Abstract
The present paper is a sequel to the paper by Karchev (Condensed Matter 20 February 2017). We report the numerical solutions of the system of equations, which describes the electrodynamics of s-wave superconductors without normal quasi-particles for time-independent fields and half-plane superconductor geometry. The results are: (i) the applied magnetic field increases the Ginzburg–Landau (GL) coherence length and suppresses the superconductivity; (ii) the applied electric field decreases GL coherence length and supports the superconductivity; (iii) if the applied magnetic field is fixed and the applied electric field increases, the London penetration depth of the magnetic field decreases. The main conclusion is that by applying electric field at very low temperature where there are no normal quasi-particles one increases the critical magnetic field. This result is experimentally testable.
PACS:
74.20.-z; 74.20.Mn; 71.10.-w
1. Introduction
The system of Maxwell equations for a relativistically covariant theory of s-wave superconductivity without normal quasi-particles is derived in [1]. We report the numerical solutions of the system for time-independent fields and half-plane superconductor geometry. The results are: (i) the applied magnetic field increases the Ginzburg–Landau (GL) coherence length and suppresses the superconductivity; (ii) the applied electric field decreases GL coherence length and supports the superconductivity; (iii) if the applied magnetic field is fixed and the applied electric field increases, the London penetration depth of the magnetic field decreases. The main conclusion is that by applying electric field at very low temperature (where there are no normal quasi-particles), one increases the critical magnetic field. This result is experimentally testable.
2. The System of Equations
The system of equations which describes the electrodynamics of s-wave superconductors reads as [1]:
where is the electric field, is the magnetic field, and is the local density of Cooper pairs. The parameter is the magnetic permeability, and is the electric permittivity of the superconductor. We assume that they do not change their values when the system undergoes normal-to-superconductor transition. The parameter
where T is the temperature and is the critical temperature, is positive when the system is in a superconducting state. The charge of the Cooper pair is .
The vector and the scalar Q are supplementary fields. It is important to stress that the gauge-invariant vector and the scalar Q take part in Equations (2) and (4) as a magnetic vector and electric scalar potentials, while in Equation (1) is a supercurrent and in Equation (3) is the density of the superconducting quasi-particles. This dual contribution of the new fields is the basis of the electrodynamics of superconductors.
We focus on the system of equations with time-independent fields given by
It is important to note that the system of equations for static electrodynamics does not split into systems of equations for electric and magnetic fields. One can do this by assuming that and Q are zero in Equation (11) and is a constant. Thus, one arrives at the conclusion that the electric field also penetrates a certain distance, just as the magnetic field does [2]. This approximation is not correct.
To elucidate the interplay between electric–magnetic fields and superconductivity, we consider the system of Equations (7)–(11) for fields which depend on the z coordinate only. Then, the system of equations for the fields , , , , and adopts the form
It is convenient to introduce dimensionless functions , and of a dimensionless distance , where
is the Ginzburg–Landau coherence length and
In Equations (21), , the applied electric field is , and the applied magnetic field is . The representations of the electric and magnetic fields by means of and are the following:
The system of Equations (17)–(19), rewritten in terms of the new functions, reads:
In Equations (23), is the Ginzburg–Landau parameter
which satisfies for type I superconductors and for type II ones. The parameters and have the representation
For semi-infinite superconductors, with a surface of the superconductor orthogonal to the z-axis, the boundary conditions are given by
3. Numerical Solutions
If neither electric nor magnetic fields are applied, the equation for the dimensionless function
is exactly solvable [3,4], and the solution for is
It is more convenient to study a system of first-order differential equations. To this end, we introduce three new functions and rewrite the system (23) in the form
We proceed by numerically solving the system (29)–(34) for and different values of and . The solutions for the density of Cooper pairs as a function of are depicted in Figure 1.
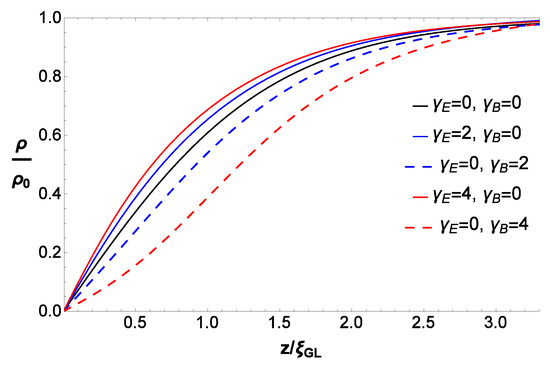
Figure 1.
Density of Cooper pairs as a function of . (i) Dashed lines—when magnetic field is applied; (ii) Solid lines—when the electric field is applied; (iii) The line in the middle—neither electric nor magnetic fields are applied.
The curve in the middle (black) is the solution (28) when neither electric nor magnetic fields are applied. It is the reference solution. The two dashed curves below the reference one are solutions when magnetic field is applied (), and the two solid line curves above the reference one are the solutions when electric field is applied ().
The Ginzburg–Landau coherence length measures the distance over which the superconducting order parameter increases up to the bulk value, measured from the surface of the superconductor (). If we set in Equation (28) , we obtain . We can use this relation as a definition of the GL coherence length when electric field is applied, and when magnetic field is applied. When electric field is applied, the solution satisfies for , and when magnetic field is applied, the solution satisfies for . The dashed curves in Figure 1 show that , and the GL coherence length increases whenthe applied magnetic field increases, while and the GL coherence length decreases when the applied electric field increases. Therefore, one concludes that the applied electric field decreases the GL coherence length, which means that the electric field supports the superconductivity, while the applied magnetic field increases the GL coherence length, which means that the magnetic field destroys the superconductivity.
The next calculations are achieved for a fixed value of the applied magnetic field and different electric fields. The result is depicted in Figure 2.
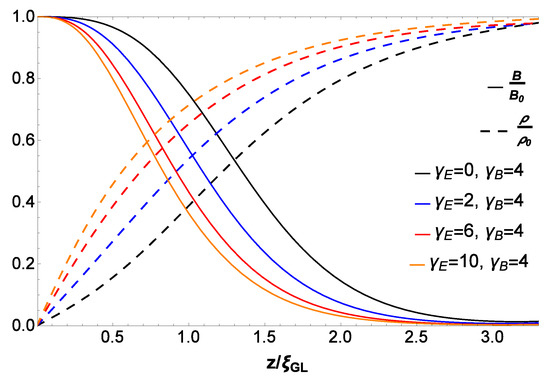
Figure 2.
The dashed lines are the density of Cooper pairs as a function of for fixed value of the applied magnetic field and different values of applied electric fields. The solid lines are the magnetic field in the interior of the superconductor when different electric fields are applied.
The dashed lines correspond to the solutions for the density of Cooper pairs as a function of . They show that even in the presence of an applied magnetic field the increase of the applied electric field decreases the GL coherence length. The solid lines show the magnetic field in the interior of the superconductor when different electric fields are applied. The curves show that London penetration for the magnetic field decreases. The main conclusion is that under the application of an electric field at very low temperatures where there are no normal quasi-particles, the critical magnetic field is increased. This can be experimentally tested.
4. Summary
The superconductor is not an ideal conductor [5]. If we place an ideal metal in a constant magnetic field at temperature and then decrease the temperature to temperatures below , the magnetic field remains unchanged. On the other hand, if the magnetic field is zero at temperatures above and we switch it on at temperature , it remains zero inside the ideal metal. Therefore, the final state depends on the order in which actions are taken, while the superconductor expels the magnetic field and the order of events does not matter. In the present paper, we discuss another important difference. The normal quasi-particles in an ideal metal completely screen the applied electric field. When the electrons form Cooper pairs in superconducting state, they permit the penetration of the applied electric field; further, the electric field decreases the distance over which the superconducting order parameter increases up to the bulk value (Ginzburg–Landau coherence length). This is our main result.
The aim of the present paper was to present the results obtained by solving the system of equations, which describes the electrodynamics of s-wave superconductors without normal quasi-particles for time-independent fields and half-plane superconductor geometry. The objective was to elucidate the interplay between applied magnetic and electric fields and superconductivity. The overall conclusion is that the applied magnetic field destroys the superconductivity while the applied electric field supports it. The figures show that when the electric field is applied, the density of Cooper pairs increases. Therefore, if we apply an electric field at low temperature, increases and we can increase the temperature to decrease to the initial value, but at higher temperature. Hence, by means of an applied electric field we can increase the temperature without destroying the superconductivity.
The first attempt to detect an electric field in a superconductor was carried out by London [6]. In the London experiment, the capacity of a capacitor with superconducting plates was measured. At temperatures below the superconducting transition temperature, the change in capacity of the condenser when the superconductivity is destroyed by magnetic field indicates a penetration of an electric field in the superconductor. The experiment failed—no change in capacity of the mercury condenser was observed. A possible explanation is that the critical temperature of mercury is K and the experiment was carried out at K. At this temperature, the density of normal quasiparticles is still high and they screen the electric field. We hope that the experiment will be successful if one repeats it at temperatures lower than 1 K.
It is most promising to study the influence of electric field on superconductivity with materials that possess an insulator–superconductor transition. We can apply an electric field near the critical superconductor–insulator transition temperature. One example is sulfur hydride [7]. The temperature dependence of the resistance, measured at different pressures, shows that the material undergoes a superconductor–insulator transition at 129 GPa.
The London brothers’ theory of superconductivity is an extension of classical electrodynamics [2]. They supplemented the Maxwell system of equations with a set of equations. The generalized Maxwell–London equations are discussed in [8,9]. The phenomenological Ginzburg–Landau theory [10] generalizes the London one, including the order parameter. The present paper expands the GL theory by adding the electric field.
The results raise new questions. For example, the result that the applied electric field increases the critical magnetic field at low temperature makes important the question of the impact of the electric field on Abrikosov vortexes [3,11].
Author Contributions
Both authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karchev, N. Electrodynamics of s-Wave Superconductors Using First-Order Formalism. Condens. Matter 2017, 2, 20. [Google Scholar] [CrossRef]
- London, F.; London, H. The Electromagnetic Equations of the Supraconductor. Proc. R. Soc. Lond. Ser. A 1935, 149, 71–88. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; McGraw-Hill Book Company: New York, NY, USA, 1975. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; McGraw-Hill Book Company: New York, NY, USA, 2003. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 7th ed.; John Wiley and Sons: Chichester, UK, 1996. [Google Scholar]
- London, H. An Experimental Examination of the Electrostatic Behaviour of Supraconductors. Proc. R. Soc. Lond. 1936, 155, 102–110. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofonov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Melvin, M.A. The New Classical Electrodynamics. Nature 1953, 171, 890–892. [Google Scholar] [CrossRef]
- Arbab, A.I. On the electric and magnetic properties of conductors. Adv. Stud. Theor. Phys. 2011, 5, 595–607. [Google Scholar]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20, 1064–1082. [Google Scholar]
- Abrikosov, A.A. On the magnetic properties of superconductors of the second group. Zh. Eksp. Teor. Fiz. 1957, 32, 1442–1445, Translated by Soviet Phys. JETP 1957, 5, 1174. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).