Analysis of the Efficient High-Temperature in Situ Photoluminescence from GaN Layers during Epitaxial Growth

Abstract

Photoluminescence (PL) in GaN or InGaN layers monitored during epitaxial growth at high temperatures permits a quasi-continuous in situ characterization of opto-electronic properties. Therefore, epitaxial parameters can now be optimized at the earliest possible stage. A pulsed and high-power UV laser was required for PL excitation at high temperatures. Herein, the underlying nonlinear mechanism was studied via time-resolved PL experiments and rate equation-based modeling. A temperature-activated and saturable path for quenching over defects was identified. Beyond the saturation threshold, reasonably-intensive PL sets in. At high temperatures not only is the near band gap-PL present, but also—as a new observation—a defect-assisted PL emerges. Apart from these specific electronic transitions in high-temperature PL of GaN, a simple, but reasonably predictive model of the luminescent thin film has been set up to track down interference fringes in the PL spectra. It is worth mentioning that the spectral PL modulation (aiming at the Purcell effect) is often mixed up with ordinary Fabry–Pérot interference. A distinction has become key to properly analyze the spectral signatures of high-temperature PL in order to provide a reliable in situ characterization of GaN layers during epitaxial growth.

1. Introduction

Photoluminescence (PL) is a classical contact-less and well-established tool for semiconductor characterization [1]. It is, thus, highly applicable to the direct band gap semiconductor gallium nitride (GaN) and its relatives, all of which are well-known for their high PL quantum efficiency. Although the required technical components have already been available for many years, the quasi-continuous PL scanning of GaN and InGaN epitaxial layers at high temperatures—typically at 700 °C or even higher if, e.g., metal organic chemical vapor deposition (MOCVD) is considered—was, however, developed and reported quite recently [2,3,4]. We have already demonstrated that reasonably strong PL spectra from GaN and InGaN layers were obtained during growth in a quasi-commercial MOCVD reactor at temperatures around 1050 °C for GaN and 730 °C for InGaN, which provided a useful correlation with the composition of the deposited In_xGa_1−xN layers, permitting MOCVD process optimization at the earliest possible stage. This is interesting because device optimization in the sense of targeting, e.g., a particular emission wavelength, as well as a better yield for the designated light emitting diode (LED) structure is now accessible within such an in situ PL technique. The in situ PL signal also carries other information from the epitaxial layer growth [2,3], e.g., it correlates with the layer thickness and, hence, with the growth rate (while exploring the interference pattern in the PL spectra), with the layer temperature (via redshift, broadening, and attenuation of the PL with increasing temperature), with the interface roughness (while analyzing, e.g., the modulation depth of the interference pattern in the PL spectrum), and with the (self-) absorption coefficient (given by the attenuation of the PL interference pattern toward shorter wavelengths). Interestingly, we observed in our various in situ high-temperature PL measurements [2,3,4] that the general PL behavior at high temperatures was quite similar [4] (regardless of a potential difference in peak wavelengths) for a bulk GaN substrate layer and a multi-quantum well (MQW) InGaN structure for LED devices. Therefore, our considerations apply for both the bulk GaN and also for the more complex InGaN structures, rendering such a high-temperature PL characterization/monitoring scheme quite general.

In situ PL at high temperatures also correlates with the intrinsic quality of the semiconductor lattice itself because PL emission is typically affected by electronically-effective defects, such as radiative and non-radiative recombination centers in the semiconductor [1,5]. Defect monitoring at high temperatures is a new quality in this paper and may become relevant for in situ monitoring. The demand for a non-invasive, instantaneous, and (quasi-)continuous method for monitoring epitaxial layer growth in a hot MOCVD environment with narrow optical access leaves virtually no other alternative than optical techniques in the infrared, visible, and UV spectral range. Therefore, this research exclusively refers to optically-available information at high temperatures.

In an MOCVD growth process high UV excitation densities are needed to obtain reasonable PL signals at high temperatures [2,3,4]. The excitation is provided by a repetitive (up to 20 Hz) pulsed near-UV laser with a high peak power density (in the order of MW/cm²) providing short pulses in the order of ns, with approximately 1–10 mW average power. As previously shown, a repetitive pulsed excitation (a) promotes sufficient PL at high temperatures and (b) neither damages the material nor interferes with the epitaxial growth [3]. In contrast, a continuous UV laser with equivalent power emission (e.g., 10 mW, continuous wave, CW) is hardly capable to excite reasonably efficient PL at those high temperatures. Even when increasing the CW laser power and power density by focusing the beam to small spot sizes, the PL signal remains poor, whereas the semiconductor material gets damaged, or even fully destroyed, by the intense CW laser spot.

These findings from our previous experiments [2,3,4] indicates an onset of a non-linear PL process inside the hot semiconductor layer. Laser excitation using repetitive short UV pulses with MW/cm² power densities and an average power of 10 mW turns out to be far more efficient than an equivalent CW UV laser excitation of 10 mW. Therefore, the aim of this study is to both explore the mechanisms responsible for these particular experimental findings and to retrieve additional characteristic signatures from the hot GaN layer.

The obtained PL spectra regularly contain interference fringes, which could be analyzed for a thickness or growth rate determination. Similar—but not identical—interference measurements with external light sources are already well established in thin film monitoring. However, there are subtle differences between thin film interference fringes from external illumination and from an internal PL process. These differences are frequently missed in the scientific discourse of PL spectra from thin films. This contribution describes and models these two different and photonic effects in thin films. For better clarity, the photonic effects are presented and discussed separately from the electronic transitions.

Therefore, the remainder of the paper is organized as follows: Section 1.1 introduces characteristic electronic transitions in high-temperature PL and Section 1.2 examines the characteristic photonic effects in thin luminescent layers. The experimental methods and models for electronic transitions and photonic effects are introduced in Section 2.1 and Section 2.2. The results of both topics are presented in Section 3.1 and Section 3.2, followed by conclusions in Section 4.

1.1. Considerations for Characteristic Electronic Transitions in High-Temperature PL

Referring to the above mentioned and superlinear excitation mechanisms [2,3,4] it is to note that a similar non-linearity in the GaN material or InGaN MQW material is already present at room temperature and can be readily visualized using, e.g., a sapphire wafer coated with GaN/InGaN MQW layers (representing the standard material system for LEDs) illuminated by a conventional UV fluorescence lamp (i.e., a “black light” at 350–400 nm) with a low irradiation density in the order of 10¹–10² µW/cm². At these low excitation densities, the LED wafer will not emit the characteristic emission wavelengths of the LED (e.g., blue light around 450 nm). Instead, a rather effective and pale-yellowish fluorescence (centered at approximately 570 nm, 2.2 eV) is observed, which is readily visible to the naked eye. This yellowish emission, which we term as the “yellow band” (YB) is attributed to defects in the GaN lattice [5,6].

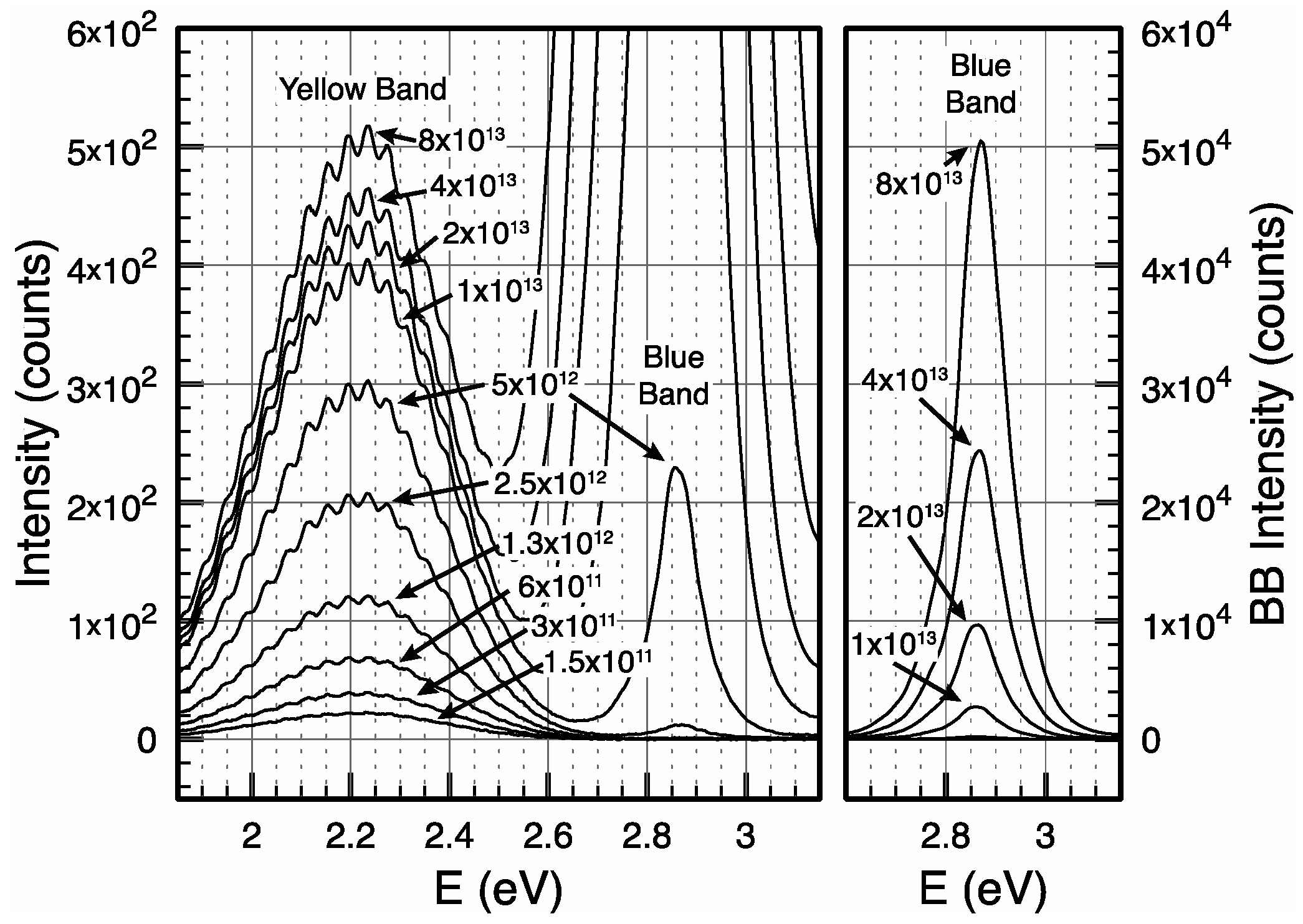
When increasing the excitation density on the wafer, e.g., by using a CW HeCd pump laser beam at 325 nm with some mW/mm² or with an ordinary electronic injection current of several mA/mm² through the LED chip, the designated wavelength, namely, the blue light at 450 nm, clearly dominates the PL emission. This is the expected emission associated to the InGaN band gap and herein denoted as the “blue band” (BB); however, it certainly also covers the near-UV wavelength range for GaN at room temperature.

Both the YB and BB emissions emerge from competing relaxation processes, and the interplay between these processes is found to be similar for simple GaN or complex InGaN MQW [4].

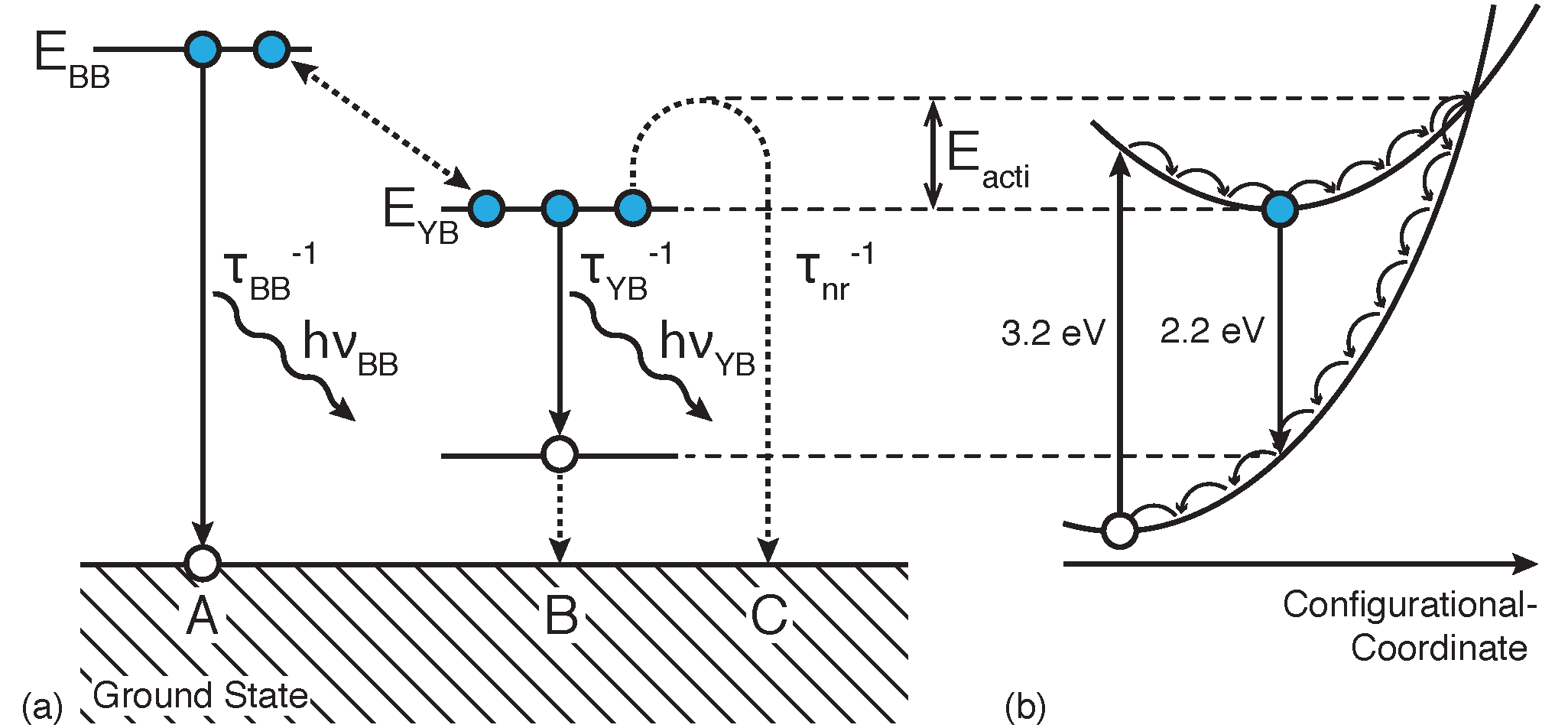
A non-equilibrium carrier in a BB state can relax into a vacant YB state (Figure 1) and, subsequently, emit a yellowish light at the expense of the BB emission. Since both the YB defect density and the defects’ individual recombination rates at room temperature are limited, the YB provides a quenching process for the BB that is easily saturated [5] (e.g., in a conventional LED at few mA injection current). Thus, above certain excitation thresholds, the BB gains intensity and will clearly dominate the PL emission at room temperature; however, the saturated YB is still present with considerably weaker relative intensities (as later shown in Section 3.1). The competition between BB and YB is experimentally observable in GaN bulk material and also—very similar—in more complex InGaN MQW samples, as shown later in Section 3.1. As very common in luminescence, a transfer from BB inside an InGaN quantum well to YB even outside of the quantum well (GaN) can readily occur via energy transfer, an actual escape of carriers from the QW is not required for this process. Energy transfer over a distance of several nm between two insulated luminescence centers (=high potential barrier between them) is a common, efficient, and fast process, such as non-radiative near-field dipole-dipole interactions, like Förster resonance energy transfer (FRET). The energies, but not the particles are transferred. In the resonance case (the emission level fits the absorption level), the transfer can quickly occur over several nm and energy transfer readily passes potential barriers. This explains the similar behavior of GaN and InGaN MQW.

As a conjecture of this research, the YB defects not only convert the excitation energy into an emission of yellowish light with a comparably slow and saturable recombination process [5,8], but such defects (or those which closely interact) also establish an additional parallel recombination channel, which is thermally activated and non-radiative. At room temperature, this non-radiative recombination is slow and not very effective. Hence, the luminescence efficiency of high quality GaN samples reaches rather high internal quantum yields virtually at 100% [9,10,11]. However, at higher temperatures, the non-radiative recombination process drastically accelerates and efficiently overtakes—i.e., quenches—both the YB and BB emissions rendering the overall PL to be affected at higher temperatures.

Nevertheless, when providing UV excitation at a higher rate (i.e., at higher power densities) that exceeds the thermally-quenching process, reasonably intensive BB and YB emissions are possible. The thermally-activated fast non-radiative recombination pathway over a limited number of defects is finally limited and can, therefore, be saturated with sufficient excitation power. As experimentally observed, this single mechanism turned out to be well-suited to describe the non-linear PL phenomena at high temperatures. The nonlinear behavior, as described here, may promote the irreplaceability of high (peak) power density UV excitation when sufficient PL emission at high temperatures is needed, e.g., for monitoring the growth of InGaN quantum wells inside a quasi-industrial MOCVD system via PL emission [2,3]. At room temperature (and above) only the near band gap BB and the broad YB emissions are visible. Other, more detailed, spectral features associated with, e.g., excitons or defined defect levels [5], are merely present at low temperatures, rendering them either blurred or dark at high temperatures, or even unobservable.

Since the prominent YB defects, together with closely-interacting dark defect states, are conjectured to play a governing role as a temperature-activated quenching path [7], their nature must be discussed in more detail. Although the YB luminescence and associated defects have been extensively studied, a detailed prescription towards an efficient PL at high temperatures is still lacking. In the following, the characteristic features of YB defects are briefly outlined along with the comprehensive review by Reshchikov et al. [5].

A considerable number of rather different, but mostly point-like, defects are associated with the YB-PL, such as Ga vacancies, complexes, and intentional or unintentional impurities [5]. For investigating the nature of the YB, 35 elements were implanted in GaN and most of them appear to increase the YB luminescence [5,12]. Additional experiments and calculations support the theory of gallium vacancies or impurities (such as carbon) are responsible for the YB [5,6]. The diversity of such luminescent defects in GaN and their possible transitions are considerably high. Therefore, it is remarkable that the collective behavior of all of these different defects can be represented just by one effective defect around the YB level modeled with rather few parameters, such as a single defect density and the relevant transition channels. With its broadband emission at around 2.2 eV, the apparent significant Stokes shift at excitation energies >3 eV and the temperature-independent peak emission wavelength [1,5], this defect can be associated with a typical luminescence center with strong electron-lattice coupling, whose configuration coordinate (CC) model is illustrated in Figure 1b [1,5,7]. Furthermore, the effective YB defect must be considered as an acceptor because the luminescent GaN layers are typically n-conducting, with free electron densities of approximately 10¹⁸ cm⁻³ at room temperature [13]. Therefore, the relevant non-equilibrium carriers are usually holes, and these interact with, more or less, deep acceptor levels above the valence band. The ground state of the YB acceptor in Figure 1a was achieved by a complete filling of the defect with electrons. In the ground state, the acceptor can capture a hole, which in n-GaN can be generated by a UV photon, from the valence band.

Alternatively, a UV excitation at around 3.2 eV [5] can directly lift an electron from the acceptor to the conduction band, or to suitable donor levels, leaving a hole behind. The bound hole in the acceptor represents the excited state of the YB defect. The excited state quickly relaxes via multiphonon emissions (as indicated in Figure 1b by the cascaded relaxation process) to a minimum, i.e., to a somewhat shifted coordinate of the underlying nucleus. The more the apparent shift of the coordinate of the excited state with respect to the ground state, the stronger the electron-lattice coupling of the system, which is characterized by the Huang-Rhys factor [1,5]. This factor is approximately 6.5 for the YB defect [14], which indicates a strong electron-lattice coupling. For this reason, only approximately 2.2 eV is available for the photon emission at the typical YB center wavelength, however, for an excitation energy of 3.2 eV. The excess energy is thermalized by multiple phonon emissions. The strong Stokes shift results in negligible self-absorption of the emitted light. In contrast, the short-wavelength wing of the BB luminescence usually undergoes notable self-absorption in either the GaN or InGaN material system. The YB transition back to a ground state occurs via capturing a free or bound electron (from a donor level) followed by photon emission and the elimination of the bound hole while restoring the ground state of the defect.

It should be noted that, for a luminescent center with strong electron-lattice coupling and, thus, with a significant coordinate offset between both dispersion parabolas in the schematic CC diagram (cf. Figure 1b), a crossover point between the excited and the ground exists at a certain energy level. At elevated temperatures, the electrons in the excited state can absorb a sufficient number of phonons (i.e., thermal excitation from the environment) while approaching the crossover point from which they can thermalize to the ground state without any photon emission. This is a well-known mechanism [1,5,15,16] for a thermally-activated non-radiative recombination channel of a luminescent center with high electron-lattice coupling, which is capable of providing the aforementioned quenching of the YB and BB.

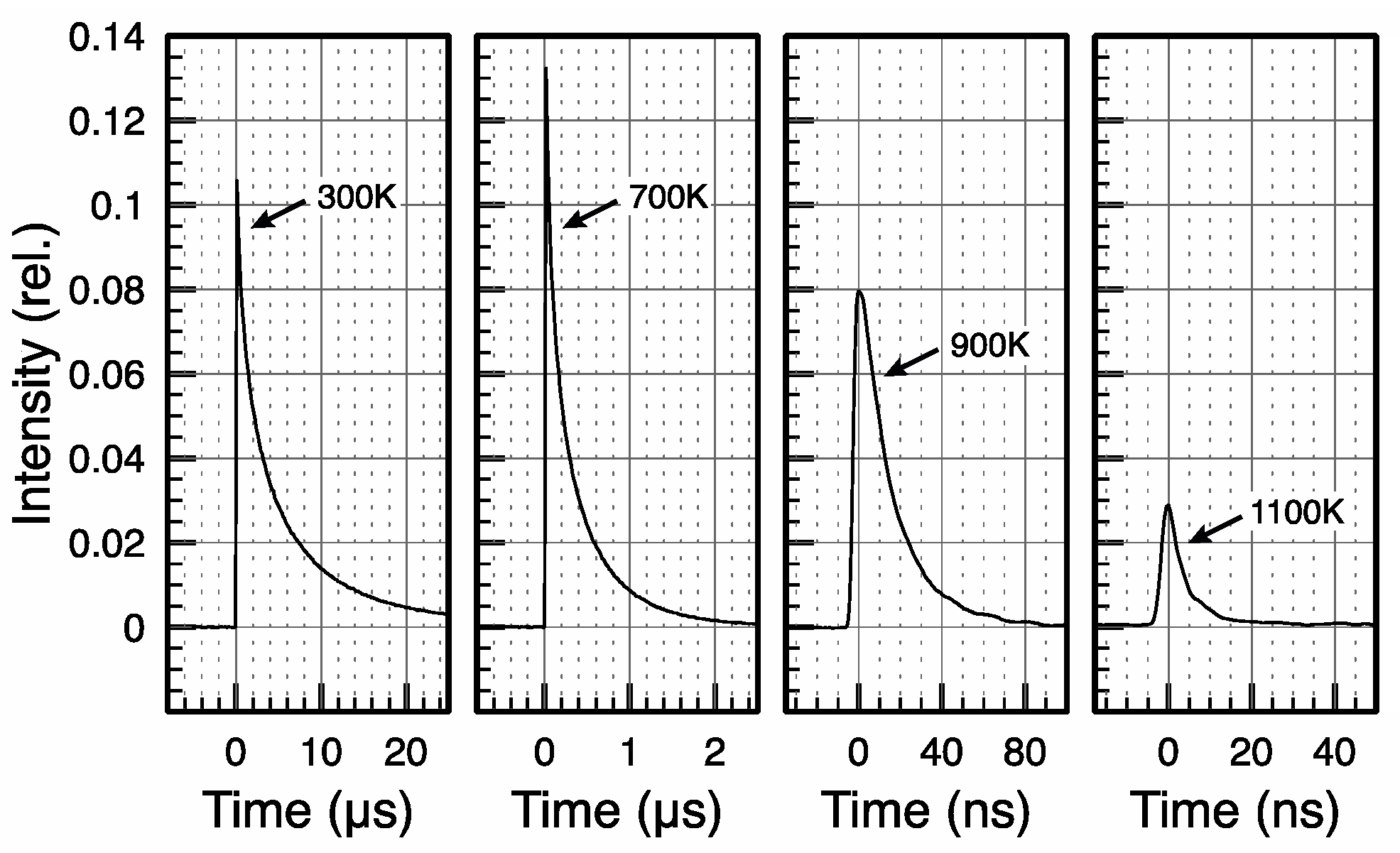
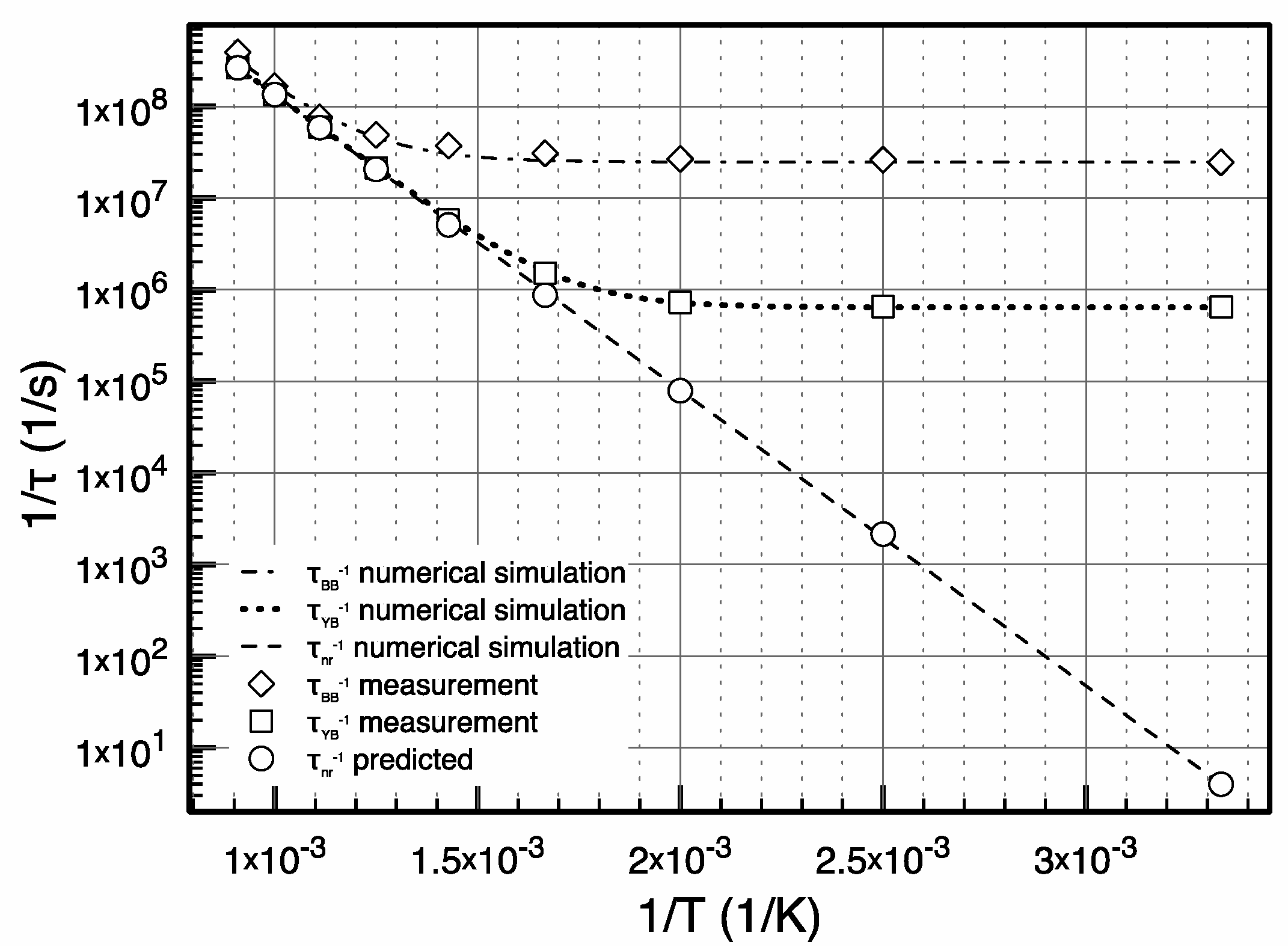
The activation energy for such temperature quenching of the YB luminescence is reported [7] in the order of approximately 0.9 eV at low excitation densities, as well as at relatively moderate temperatures (<700 K) [5]. However, when reaching a high excitation power at typically 20 W/cm² [5,15,16], which is actually far less than applied here, a lowered activation energy of around 0.65 eV was observed in [5,15], which is similar to the values found in this study. It remains unclear how the proper quenching mechanism becomes effective: whether at high temperatures the YB defects, themselves, either quench the excitation or whether an energy transfer occurs towards certain other invisible defects providing a similar outcome for the temperature activated quenching. Currently, these two contributions are hardly distinguishable for the reported PL methods. However, the proposed PL model neither requires, nor involves, such additional transitions for explaining the above observations. In our model for rather high temperatures and high-quality samples (the designated application), just the broad BB and the broad YB remain. There is nothing more observable, as mentioned above and as previously shown [2,3,4] in high-temperature PL spectra. Just these two bands, their individual behavior, and their interaction are modeled.

Thus, to flesh out the proposed model the aforementioned three major recombination pathways have to be considered (cf. Figure 1b): the BB emission (transition A) with a certain rate over the material band gap, which is tapped and eventually quenched by the luminescent and saturable YB defects (transition B), where the YB defects are simultaneously depopulated by a temperature activated non-radiative relaxation process (transition C).

1.2. Considerations for Characteristic Photonic Effects in Thin Luminescent Layers

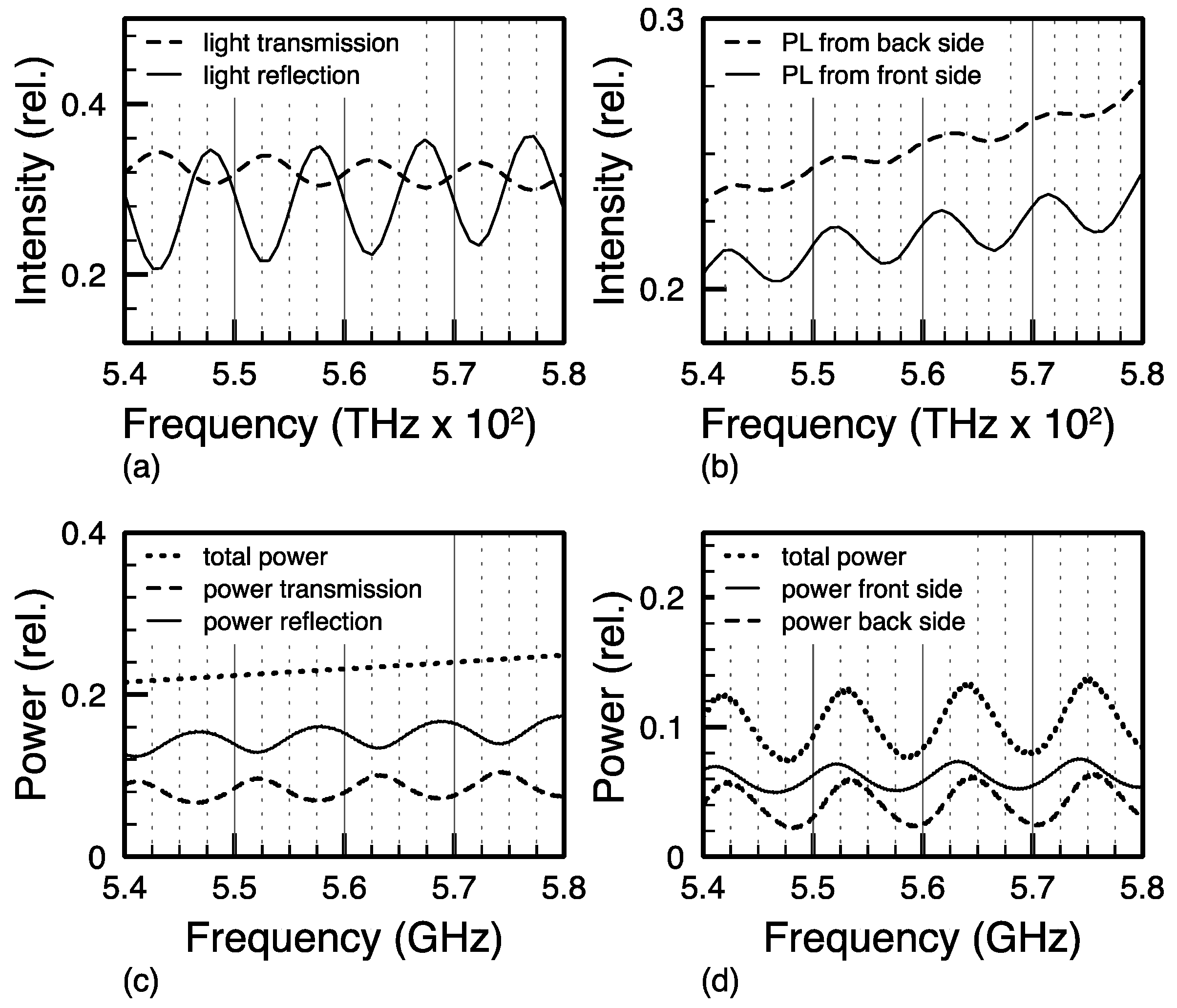
In addition to the microscopic electronic PL mechanism, macroscopic photonic effects have to be taken into account. The broadband YB emission (with strong stokes shift and virtually no self-absorption) from the thin GaN layer showed a typical and almost regularly observed modulation in the luminescence spectra (e.g., Section 3.1) that is commonly linked to Fabry–Pérot interference fringes. The latter can be directly assigned to the layer thickness and the index of refraction of the thin film. Interestingly, this interpretation seems to not be exactly right as the actual Fabry–Pérot oscillations (FPO) are usually retrieved from external white light illumination of thin films, whereas the nearly-identical modulation pattern observed in the present experiment stems from the PL as an internal light source intrinsic to the luminescent thin film.

It can be argued that a FPO cannot be held responsible for the modulation pattern of internal PL due to principal reasons: When considering a lossless optically-smooth thin film with a certain index of refraction, energy conservation is immediately applicable. Given an experiment with external white light illumination, the interference fringes of the thin film´s reflection spectra must find its exact counterparts to a 180° phase shift in the film´s transmission spectra. Both spectra, when superimposed, must reproduce the smooth spectrum of the original white light source, without any interference modulation. Such results are regularly achieved in sufficiently careful experiments. Hence, when looking at the modulation of the YB’s luminescence spectra from thin GaN films (e.g., Section 3.1), similar interference fringes can be observed in the PL spectra emitted from the film´s front side. Inside the film an internal white light source is active and no self-absorption of the emitted white light is assumed. However, when inspecting the back side of the thin film, the modulation pattern in the emitted PL spectra looks the same, but without a 180° phase shift. This is due to symmetry because there is no difference between the front and back of a free-standing, homogeneous thin film with a built-in light source (i.e., the PL). In the lossless case this necessarily implies that the atomic emission itself has to undergo a spectral modulation, aiming at what is known as the Purcell effect [17,18,19,20,21]. Therefore, the Purcell effect presented here represents not only a conventional interference, but an imprint of the (macroscopic) thin film cavity on the spontaneous emission process itself.

In order to scrutinize the various aforementioned contributions to the PL modulation an intuitive frequency-scaled 1D equivalent circuit model of the optically-activated one-dimensional InGaN/GaN thin-film layer system is presented (cf. Section 2.2). The model is based on RF transmission lines mimicking the light propagation in the corresponding layers while using broadband voltage sources either placed externally (white light illumination) or internally (active luminescence) for the optical excitation of the layer system. The electrical equivalent circuit model, thus, allows a one-dimensional simulation of the spectral features of PL emission from the overall layer stack providing clarification of the observed interference/luminescence effects, even for arbitrarily complex layer structures.

2. Materials and Methods

2.1. Experimental Methods and Models for Electronic Transitions in High-Temperature PL

The experimental setup for measuring both the decay time and the spectrum of the PL is similar to the setup used in previous investigations [4]. Samples (1 cm²) of a blue InGaN LED structure on a sapphire substrate and a 3.4 µm GaN buffer on a sapphire substrate (provided by AIXTRON SE, Herzogenrath, Germany) served as test structures.

These test samples were placed on a temperature-controlled susceptor. As previously shown [2,3,4], this setup sufficiently reproduces the conditions of in situ PL monitoring in a real MOCVD system (AIX2600G3-HT, Aixtron SE, Herzogenrath, Germany). In the PL monitoring setup shown in Figure 2 the PL was excited by a frequency-tripled Nd:YAG laser at a wavelength of 355 nm (1 HP 355-300, Crylas, Berlin, Germany), with a reduced pulse energy of 88 μJ, a rated pulse length of 1.3 ns, and a repetition rate of 20 Hz. The laser light is guided through a fiber and widened (without lens optics) to a conical beam providing an illumination spot with a diameter of 1.6 mm, up to 60 mm, on the test sample that is mounted on top of the susceptor. The peak power density on the wafer surface is, thus, reduced to a maximum of 34 kW/cm² (8 × 10¹³ photons/pulse/cm²). This is comparably low with respect to the power densities (MW/cm²) that have been recently applied within a prior setup [2,3,4] and allows the observation of the influence of the excitation density and non-linear effects. A mode scrambler was used to provide a homogeneous beam profile. To record the decay time of the PL ranging from µs to ns, a photomultiplier tube (PMT) (H10721-01, Hamamatsu Photonics, Hamamatsu, Japan) was connected over a short coax cable (50 Ω) to a sufficiently fast oscilloscope (OSC) (DSO-X 3024A, Agilent, Santa Clara, CA, USA) with a 50 Ω terminal impedance. The overall system’s decay time for a laser pulse (355 nm), resulting from the serial signal chain summing up contributions, such as the laser pulse decay time, the PMT response time, and the OSC response time, was observed to be 1.5 ± 0.3 ns, which represents the limit of temporal resolution for the observable PL decays. A combination of suitable colored glass filters (CGF) UG11 (1 mm thickness) and BG39 (1 mm) were placed in front of the laser for passing the UV excitation (at 355 nm) and strongly suppressing the other undesired emission wavelengths as the laser sub-harmonics at 532 nm, 1064 nm, and the internal diode pump laser at 808 nm. In front of the PMT (Figure 2), a stack of colored glass filters (CGF) and a notch filter (RazorEdge LP 355, Semrock, Rochester, NY, USA) distinctively suppressed the UV excitation (at 355 nm) and passed the BB PL around 440 nm for InGaN with the used CGF BG24 (2 mm), BG39 (1 mm), and the YB PL around 610 nm, which is clearly apart from the blue emission, using CGF OG590 (2 mm) and BG39 (1 mm). A metal-based neutral density (ND) filter was used to adapt the total signal levels (Figure 2). In addition to the time-resolved PL measurements of the BB and YB in the PMT, additional spectral information was obtained with a fiber-optic spectrometer (QE 65000, Ocean Optics, Dunedin, FL, USA) aiming at the spectral range of 305–1100 nm, while ignoring the temporal evolution.

For analyzing the various recombination processes associated to the PL, as shown in Figure 1, a simple, but sufficient, rate equation model was applied for the determination of the total excitation density N(t) (i.e., of the non-equilibrium holes, either bound or free), with the following input parameters: initial excitation N(0), the YB defect density D, the fixed radiative recombination rates (experimentally-derived at 300 K, where no influence of non-radiative quenching is present due to high PL quantum efficiency) for the BB and YB, as well as the activation energy E_acti (experimentally-derived from the corresponding Arrhenius plot), and the (vibrational) attempt frequency ν_nr (experimentally-derived from the Arrhenius plot) for thermal quenching.

The resulting dynamic of the excitation density is assumed to be similar to the case-distinguishing differential Equation (1) which includes the above-described mechanisms and at still moderate excitation densities, i.e., with the equilibrium majority carrier density being larger than N:

$$-\frac{dN}{dt}=\{\begin{array}{ll}\frac{N-D}{{\mathsf{\tau }}_{\mathrm{BB}}}+D\times \left(\frac{1}{{\mathsf{\tau }}_{\mathrm{YB}}}+{\nu }_{nr}\times e^{-\frac{E_{acti}}{k_{B}T}}\right)& \mathrm{for} N\left(t\right)>D \\ N\times \left(\frac{1}{{\mathsf{\tau }}_{\mathrm{YB}}}+{\nu }_{nr}\times e^{-\frac{E_{acti}}{k_{B}T}}\right)& \mathrm{for} N\left(t\right)< D\end{array}$$

(1)

A thermally-activated redistribution of YB excitation states to the BB states by applying Fermi–Dirac statistics for the local equilibrium between YB excitation and BB excitation was not explicitly applied here, because no defined energy level or energy distribution of the heterogeneous YB acceptors were accessible. The dynamic behavior according to Equation (1) was numerically solved in the framework of a temporal finite-difference scheme:

• Start the numerical calculation N(t) for a given temperature T and given initial excitation N(0).
• Within a sufficiently short time step Δt, calculate the relative decrease of N: (a) a decrease of the BB population with the radiative recombination rate 1/τ_BB; (b) a decrease of the YB population with the radiative recombination rate 1/τ_YB; and (c) an additional decrease of the YB population over the thermally-activated and non-radiative path 1/τ_nr (temperature-dependent rate from the Arrhenius equation).
• Redistribute the remaining total non-equilibrium population N(t) to the YB states until saturation density D, with the excess non-equilibrium population allocated to BB states.
• Loop back to step 2.

2.2. Experimental Methods and Models for Photonic Effects in Thin Luminescent Layers

For modeling the interference effects of PL emission within optical thin films, as observed in Section 3.1, the aforementioned frequency-scaled 1D equivalent circuit model of the layer system has been used. As shown in Figure 3 the model consists of a multi-section transmission line (TL) circuit operating in a (downscaled) frequency range of 5.4–5.8 GHz. Each individual TL represents a single layer of the processed InGaN wafer together with the free space at both sides of the wafer. The impedances (Z) of both TL₁ and TL₅ are, therefore, assigned to 377 Ω, which corresponds to the impedance of free space. The time delays for TL₁ and TL₅ were set to 2 µs, which corresponds to a physical length of approximately 11,200 wavelengths at 5.6 GHz. When translated to optical frequencies this would correspond to a distance of only 6 mm (i.e., 11,200 times 535 nm) yielding a scaling factor for the RF model of 10⁵. The characteristic impedances of TL₂, TL₃, and TL₄ were adjusted in proportion to the reciprocal value of the corresponding layer’s refractive index n_i. Hence, for TL₂ and TL₃—namely for the InGaN and GaN layer with n_2,3 = 2.6 [22]—the impedances were set both to 145 Ω, and for TL₄ representing the sapphire substrate with n₄ = 1.7 [23], the characteristic impedance amounts to 221 Ω. The physical lengths/time delays of TL₂ and TL₃ were chosen according to the scaling factor and the optical path lengths to mimic the corresponding layer thicknesses within the LED wafer. Hence, TL₂ = 0.017 ns and TL₃ = 4.51 ns, which compares to 0.097 λ and 25.27 λ at 5.6 GHz, standing for a 20 nm-thick InGaN MQW system and a 5.2 µm GaN buffer layer, both values which are close to the dimensions of the real sample. The resistors R₁ and R₂ with 377 Ω represent perfect wave impedance matching for outgoing waves mimicking free space conditions—without reflection—for both infinite half spaces. The RF equivalent circuit model was introduced into LT-SPICE, a numerical electrical circuit simulator where two different cases were analyzed: (a) the intrinsic illumination scenario: the emission signals were picked up at the front and back side of the wafer for a built-in PL light source between the InGaN MQW system and the GaN layer; and (b) the external illumination scenario: the wafer is illuminated by an external white light source, which is located 6 mm away from the front layer surface.

In the scaled RF circuit model the front and back side signals were determined by the power dissipated in the terminations R₁, R₂. The broadband light sources were represented by a frequency-swept AC voltage source with 1 V amplitude. Both voltage sources were weakly coupled using a series capacitor with only 0.01 pF (i.e., 28 kΩ at 5.6 GHz). The reasoning for this intentional mismatch is provided in the framework of the intrinsic light source scenario, where the weak electrodynamic coupling of an atomic oscillator to the surrounding cavity has to be maintained. As such a dipole source is very small compared to the emitted wavelength, a weak capacitive coupling to the cavity volume is appropriate, at least in the context of classical electrodynamics. An alternative, and rather simple, argument for weak coupling is sketched along a single emission event of the atomic dipole oscillator. If an atomic luminescence center emits a single photon with an energy of 2 eV (i.e., λ = 620 nm or f = 480 THz) into free space, this would be caused by a 2 V drop of one electron. In a classical electronic picture the maximally possible discharge current is associated with an emission event lasting about one single period and may, therefore, amount to (1.6 × 10⁻¹⁹ As)/(2 × 10⁻¹⁵ s) = 80 µA. Thus, the characteristic coupling impedance of the single atomic emitter would be at least 2 V/80 µA = 25 kΩ.

3. Results

3.1. Experimental and Numerical Results for Electronic Transitions

Figure 4 shows the PL spectra of an InGaN MQW test sample from which the non-linear interaction of both BB and YB emissions at room temperature can be deduced depending on the excitation density. A much-related interplay between BB and YB is readily observable and also well-known from simple GaN without complex InGaN MQW, e.g., [24]. Since these spectra were excited with rather short UV pulses (~1.3 ns), it is evident that the defect states already existing at room temperature may rapidly capture the excitation holes from the BB levels in the MQW (within less than 1 ns); as virtually no BB PL was detectable at low excitation densities around 1.3 × 10¹² photons/puls/cm² (cf. Figure 4). The latter corresponds to a power density of 540 W/cm² within the 1.3 ns UV pulse. From a quantitative comparison of both BB and YB emission spectra a considerably high internal quantum efficiency of more than 65% was deduced for the YB transition when the internal quantum efficiency of the BB transition was set to 100% [9]. The immediate effectiveness of vacant defect states is essential for the above reasoning. Furthermore, a considerable fraction of effective defects was observable as YB PL at room temperature due to high quantum efficiency. Although the provided amount of non-equilibrium holes (~1.3 × 10¹² cm⁻²) was not sufficient to saturate the number of present defects in the GaN, the situation totally changed when the excitation density is gradual increased within only one order of magnitude. At approximately 2.5 × 10¹² cm⁻², the BB emission set in and strongly gained intensity at higher excitation densities. Conversely, the YB emission tends to saturate and follows a distinct sub-linear behavior with increasing excitation intensities. The BB intensity, beyond the total saturation of YB, increases linearly (beyond the higher power at about 2 × 10¹³ photons/puls/cm² cf. Figure 4) and not superlinearly with excitation. In the herein-described scenario the excitation density is still small with respect to the equilibrium electron density. Therefore, the BB intensity increases linearly (beyond saturation of YB) and not in a quadratic dependence.

Additionally, inherently evident from Figure 4 is the intimate connection between YB and BB: Before observing the BB linear behavior, the YB had to be saturated. Furthermore, (from quantitative comparison and energy conservation described before) there is virtually no other process present besides the observable YB and BB in Figure 4.

Approximately 5 × 10¹²–10 × 10¹² cm⁻² of defect density were needed to be effective within the GaN thin-film sample, which, when considering a sample thickness of 3.4 µm, a penetration depth of the UV excitation of 1 µm [25], and a diffusion length of the holes up to approximately 1 µm [26] yielding an electronically-active YB defect density of approximately 5 × 10¹⁶–10 × 10¹⁶ cm⁻³ for this sample. When looking to the time-resolved PL signal from YB and BB at room temperature (300 K) (Figure 5 and Figure 6), a relatively prolonged lifetime (Figure 6 τ_YB = 6.4 × 10⁻⁶ s) of the YB states with respect to the BB recombination (Figure 6 τ_BB = 2.4 × 10⁻⁸ s) was observable. Therefore, once a YB defect level was occupied, a certain time had to pass until it could depopulate another BB excitation. Thus, at room temperature, the defect-associated quenching channel in GaN emitters can be easily saturated with the power density of the excitation.

Notably, the situation changes at higher temperatures: although the YB intensity was rapidly decreasing at increasing temperature for the PL spectra without time resolution (e.g., shown in [4]), and then not visible anymore, the time-resolved analysis shows (cf. Figure 5) that the initial YB intensity was barely affected even by considerable temperatures and even at low excitation densities. Instead, only the decay time, and not the initial amplitude, was significantly lowered at higher temperatures. Hence, the defect associated YB emission becomes observable, even at rather high temperatures, thereby offering additional and potentially valuable information from an in situ PL measurement about defects in the newly-growing GaN layers. At much higher excitation densities in MOCVD, which are possible, it would certainly still be observable.

The reciprocal of the now-observable YB decay time consists of the sum of the recombination rates from YB emission 1/τ_YB and the parallel and non-radiative recombination 1/τ_nr (Figure 1). The Arrhenius plot of the total YB recombination rate, as shown in Figure 6, revealed a rather constant radiative recombination rate at low temperatures and an additional temperature-activated rate toward higher temperatures. The activation energy deduced from the Arrhenius equation was approximately 0.64 eV. Thus, a considerably high and predominantly non-radiative recombination rate of more than 10⁸ s⁻¹ was obtained at high temperatures above 1000 K.

The YB defects rapidly (e.g., below 1 ns, evident from Figure 4) catch the carriers from the BB level while getting saturated. At room temperature (300 K), the luminescent decay rate of the YB (transition B) is approximately 1/τ_YB = 10⁵ s⁻¹, which reflects a comparably slow and easily saturable process with respect to the BB decay (transition A) with approximately 1/τ_BB = 10⁷ s⁻¹. However, at high temperatures (e.g., 1100 K) the non-radiative relaxation rate over the defects (transition C) increases towards 10⁹ s⁻¹. The non-equilibrium carriers can then be depopulated more efficiently from the BB level. Therefore, at this elevated temperature, approximately 10⁹ (non-equilibrium) holes per second for each present defect must be provided to saturate this quenching rate before reasonably strong PL emission can be observed. This is possible with a pulsed laser in the MW range, which produces ns pulses at moderate pulse energies in the µJ to mJ range. The resulting excitation flux density at 1 MW/cm² is approximately 2 × 10²⁴ photons per second, per cm². An analysis based on the corresponding rate equations (cf. Section 4) predicted that this is enough to saturate each defect (even for high defect densities up to 10¹⁹ cm⁻³) in the µm-thin-film with as much as 10⁹ non-equilibrium holes per second.

Once recombined, the defect will rapidly capture another excitation carrier from the BB. Therefore, the decay rates in the BB and YB are finally governed by the temperature activated non-radiative decay. Conversely, more and more power density must be applied for overcompensating the quenching process at high temperatures; however, because time constants are rather short, a short laser pulse with moderate energy can suffice.

Figure 6 depicts an Arrhenius plot containing both the experimental and numerical modeling results of the PL’s “cascaded” recombination channels where the following modeling parameters are identified: the activation energy of 0.64 eV for thermal quenching of the YB, the vibrational attempt frequency ν_nr = 2.5 × 10¹¹ s⁻¹, which is derived from Arrhenius plot and is associated to the resulting thermally-activated non-radiative recombination rate that ranges from irrelevant 4 s⁻¹ at 300 K up to 2.6 × 10⁸ s⁻¹ at 1100 K, the excitation density (10 × 10¹² cm⁻²), and the YB defect density (5 × 10¹² cm⁻²). This rate-equation model of the transitions underlying the PL emission is, therefore, reasonably apt to quantify the efficiencies and the temperature behavior of the measured YB and BB, as shown in Figure 6. As already mentioned, the numerical model does not include a gradual distribution of excitation between BB and YB. Notably, such a gradual distribution was already implicitly involved in the model data. For example, the measured YB decay rate 1/τ_YB (Figure 6) already includes an additional depopulation of the YB over a BB emission, even at room temperature (see Figure 4, e.g., at 2.5 × 10¹² cm⁻²). Therefore, since the presented model is already adapted to the measured decay rates, an additional consideration by applying a Fermi–Dirac-Statistics was not performed, since defined energy levels for the YB are not readily available. The rate equations are only an approximate representation of the YB and BB dynamics. Nevertheless, in the high-temperature regime and for the high-quality samples used here, they reasonably describe the observations.

3.2. Experimental and Numerical Results for Photonic Effects in Thin Luminescent Layers

In addition to the time dependence and the temperature behavior of the PL, a numerical analysis of the PL emission from the InGaN/GaN thin-film layer system was carried out using the frequency-scaled electrical equivalent circuit model. Its comparison to experimental data is shown in Figure 7 and discussed in the following.

The broad YB emission spectrum as observed in Figure 4 shows distinct interference fringes with both coinciding maxima and minima when recorded from either the front or the back side of the emitting layer system (cf. Figure 7b). This is not surprising due to the symmetry argument for the thin film with an internal light source as earlier provided in Section 1.2. The opposite applies to the external light source illumination scenario where the spectral responses of the reflected and transmitted light support a coincidence now between the reflection maxima and transmission minima, and vice versa (cf. Figure 7a), which is reasoned by simple energy conservation (for a virtually non-absorbing layer system). These observations were fully supported by the corresponding simulations using the frequency-scaled electrical equivalent circuit model as shown in Figure 7c,d. The visible discrepancies between the measured and simulated data were mainly assigned to rough surface scattering at the back side of the used sapphire wafer.

It is impossible to explain the observed PL spectra (with in-phase fringes from front and back sides) on the basis of conventional Fabry–Pérot interference within a non-absorbing material system. In Figure 7b, a lower overall emission intensity (signals from front and backside together) is apparent at, e.g., 557 THz and a higher overall emission at 552 THz. With only passive mechanisms and interference, the overall decrease at 557 THz could only be explained with a somehow effective absorption in the thin film. However, there is virtually no absorption around 2.2 eV (560 THz) in a µm thin GaN film.

Even to the contrary, notable absorption in the film suppresses the observed oscillations; see e.g., spectra in Figure 4 towards 2.8 eV (BB) and also seen in many previous spectra towards the absorption edge. Thus, it cannot be passive Fabry–Pérot interference, but must be an active imprint on the emission process itself.

Thus, the power delivery of the internal source itself was spectrally modulated by the sandwiching of the resonator structure. It cannot be explained via passive interference filtering, but must incorporate a spectral modulation of the emission process itself. With this convenient electrodynamic model, an even more complex staple of layers can be readily simulated. A quantum mechanical description of a photon emission process under the influence of a more macroscopic resonator was not required. When applying an in situ PL technique during MOCVD of GaN layers, the described Purcell effect must be applied to the spectral data (symmetrical in-phase fringe effect), rather than matching the more familiar FPO (asymmetrical and energy conserving) to this kind of data.

4. Conclusions

The modeling of optical thin films with electrodynamic transmission lines as an analogue model reasonably describes spectral interference effects, reflection, and transmission of a luminescent thin film staple. The model distinguishes conventional Fabry–Pérot interference from external light sources and the Purcell effect from spontaneous luminescence emission within a thin film. The Purcell effect, and not Fabry–Pérot interference, must be adapted for these in situ PL techniques.

The electronic transition results aim at a temperature-activated and non-radiative recombination channel in the GaN material system, which can, even at high MOCVD temperatures, be saturated with a sufficiently high excitation density. Therefore, the indirectly-observed and non-radiative recombination channels are quantitatively limited and likely assigned to a certain defect concentration in the GaN material.

Fortunately, a pulsed UV laser can readily provide sufficient excitation density at still-tolerable pulse energies. Thereby, an efficient PL excitation is possible even at high temperatures, and such PL signals can be utilized for in situ monitoring of growing crystal layers during MOCVD epitaxy. In situ PL offers valuable information about the growing material [2,3]. The layer thickness and the directly-linked growth rate are accessible via the Purcell effect, the actual surface temperature as a crucial parameter in MOCVD can be derived. Additionally, the roughness, self-absorption coefficient, and the composition In_xGa_1−xN is available, as already shown in previous contributions [2,3].

Through determining the excitation threshold for PL at high temperatures, even the concentration of electronically-active defects is observable, as described for the first time here. The threshold provides in situ information for the electronic material’s quality regarding the newly-growing crystal layer at the earliest possible stage, here described for the first time with convenient in situ PL methods. With the experience of our prior work [2,3,4] we are very confident that the threshold can be practically applied in real MOCVD processes, since even less excitation power is required [2,3]. The performance of a device is typically affected by the semiconductor’s defect density. The proposed PL technique, for example, can be applied for in situ monitoring and optimizing the electronic quality of growing GaN buffer layers as a substrate for InGaN MQW structures intended for LED or laser diodes. It should be noted that only high-quality samples (as designated for the application) are investigated in this study. In case of more and unintended non-radiative recombination centers, even at room temperature, the in situ PL signal at higher temperatures drastically decreases. Such a drastic decrease of the in situ PL is already a characterization criterion, itself, for quality monitoring.

The in situ investigation of more impure samples opens up an extended field for future investigations. The current manuscript only presents the basic observations and relations for high-quality samples.

However, the lifetime and the efficiency of laser diodes strongly depend on the material quality and the semiconductor’s defect density, which can now be observed and corrected during growth. Furthermore, material’s imperfections are held responsible for noise, reduced carrier mobility, and/or reduced breakdown thresholds in nitride-FETs for high-performance RF applications. It can be anticipated that adapted PL methods will also apply to the important and closely-related GaN-AlGaN system.