1. Introduction
The spin galvanic effect and its inverse manifestation have been intensively investigated over the past decade both for their intrinsic fundamental interest [
1] and for their application potential in future generation electronic and spintronics technology [
2,
3]. The non-equilibrium generation of a spin polarization perpendicular to an externally applied electric field is referred to as the inverse spin galvanic effect (ISGE), whereas the spin galvanic effect (SGE) is its Onsager reciprocal, whereby a spin polarization injected through a nonmagnetic material creates a charge current in the direction perpendicular to the spin polarization. As an all-electrical method of generating and detecting spin polarization in nonmagnetic materials, both of these effects may be used for applications such as spin-based field effect transistors [
4,
5,
6,
7] and magnetic random access memory (MRAM) [
8,
9].
The ISGE, also known as the Edelstein effect or current-induced spin polarization, was originally proposed by Ivchenko and Pikus [
10], and observed by Vorob’ev et al. in tellurium [
11]. Later, the ISGE was theoretically analyzed by Edelstein in a two-dimensional electron gas (2DEG) with Rashba spin-orbit coupling (SOC) [
12] and also by Lyanda-Geller and Aronov [
13,
14]. Notice that the SGE in the spin-charge conversion is sometimes referred to as the inverse Rashba–Edelstein effect. The SGE has been observed experimentally in GaAs quantum wells (QWs) by Ganichev et al. [
15,
16], where the spin polarization was detected by measuring the current produced by circularly polarized light. In semiconducting structures, the ISGE can be measured by optical methods such as Faraday rotation, linear-circular dichroism in transmission of terahertz radiation and time resolved Kerr rotation [
1,
17,
18,
19]. Very recently, a new way of converting spin to charge current has been experimentally developed by Rojas-Sánchez et al., where, by the spin-pumping technique, the non-equilibrium spin polarization injected from a ferromagnet into a Ag/Bi interface yields an electrical current [
20]. Successively, the SGE has also been observed in many interfaces with strong spin-orbit splitting, including metals with semiconductor giant SOC or insulators such as Fe/GaAs [
21] or Cu/Bi
O
[
22].
Generally speaking, the SGE can be understood phenomenologically by symmetry arguments. Electrical currents and spin polarizations are polar and axial vectors, respectively. In centro-symmetric systems, polar and axial vectors transform differently and no SGE effect is expected. In restricted symmetry conditions, however, polar and axial vectors components may transform similarly. Consider, for instance, the case of electrons confined in the xy plane with the mirror reflection through the yz plane. Under such a symmetry operation, the electrical currents along the the x and y directions transform as and . The spin polarizations transform as the components of angular momentum, and we have and . Hence, one expects a coupling between and or between and . Such a coupling is the SGE.
At a microscopic level, the strength of the coupling is due to the SOC. Usually, the SOC is classified as extrinsic and intrinsic, depending on the origin of the electrical potential. The intrinsic SOC arises due to the crystalline potential of the host material or due to the confinement potential associated with the device structure. On the other hand, the extrinsic SOC is due to the atomic potential of random impurities, which determine the transport properties of a given material. The majority of the studies on SGE/ISGE has focused on the Rashba SOC (RSOC) for electrons moving in the
xy plane, which was originally introduced by Rashba [
23] to study the properties of the energy spectrum of non-centrosymmetric crystals of the CdS type and later successfully applied to the interpretation the two-fold spin splitting of electrons and holes in asymmetric semiconducting heterostructures [
24]. RSOC is classified as being due to structure inversion asymmetry (SIA), which is responsible for the confinement of electrons in the
xy plane. In addition, one may also consider the SOC arising from the bulk inversion asymmetry (BIA), usually referred to as Dresselhaus SOC (DSOC) [
25]. Both RSOC and DSOC modify the energy spectrum by introducing a momentum-dependent spin splitting. This also can be understood quite generally on the basis of symmetry considerations. In a solid spin degeneracy for a couple of states with opposite spin and with cristalline wave vector
is the result of both time reversal invariance and parity (space inversion invariance). By breaking the parity, as, for instance, in a confined 2DEG, the spin degeneracy is lifted and the Hamiltonian acquires an effective momentum-dependent magnetic field, which is the SOC. As a result, electron states can be classified with their chirality in the sense that their spin state depends on their wave vector. In a such a situation, scalar disorder, although not directly acting on the spin state, influences the spin dynamics by affecting the wave vector of the electrons and holes. Spin relaxation arising in this context is usually referred to as the Dyakonov–Perel (DP) mechanism.
Extrinsic SOC originates from the potential that is responsible for the scattering from an impurity. In this case, before and after the scattering event, there is no direct connection between the wave vector and the spin of the electron. The scattering amplitude can be divided in spin-independent and spin-dependent contributions
where
and
are the unit vector along the direction of the momentum before and after the scattering and
is the vector of the Pauli matrices. As explained by Lifshits and Dyakonov [
26], different combinations of the amplitudes
A and
B correspond to specific physical processes. The
describes the total scattering rate, whereas
is associated with the Elliott–Yafet (EY) spin relaxation rate. Interference terms between the two amplitudes yield coupling among the currents. In more detail, the combination
describes the skew scattering, which is responsible for the coupling between the charge and spin currents, whereas
gives rise to the swapping of spin currents.
As noted [
1], when both intrinsic and extrinsic SOC are present, the non-equilibrium spin polarization of the ISGE depends on the ratio of the DP and EY spin relaxation rates. This was analyzed in [
27] by means of the Keldysh non-equilibrium Green’s function within an SU(2) gauge theory-description of the SOC. Successively, a parallel analysis by standard Feynman diagrams for the Kubo formula was carried out in [
28]. These theoretical studies indeed confirmed that the ratio of DP to EY spin relaxation is able to tune the value of the ISGE. Such tuning is also affected by the value of the spin Hall angle due to the fact that spin polarization and spin current are coupled in the presence of intrinsic RSOC.
Recently, it has been shown theoretically [
29] that the interplay of intrinsic and extrinsic SOC gives rise to an additional spin torque in the Bloch equations for the spin dynamics and affects the value of the ISGE. This additional spin torque, which is proportional to both the EY spin relaxation rate and to the coupling constant of RSOC, has been derived in [
29] in the context of the SU(2) gauge theory formulation mentioned above. Although the SU(2) gauge theory is a very powerful approach, in order to emphasize the physical origin of this new torque, it is very useful to also show how the same result can be obtained independently by using the diagrammatic approach of the Kubo linear response theory. This is the aim of the present paper. In this paper, we obtain an analytical formula of the ISGE in the presence of the Rashba, Dresselhaus and impurity SOC. In a 2DEG, we will show that the intrinsic and extrinsic SOC act in parallel as far as relaxation to the equilibrium state is concerned.
The model Hamiltonian for a 2DEG in the presence of SOC reads
where
is the vector of the components of the momentum operator, and
and
are the Pauli matrices and the coordinate operators,
m is the effective mass, and
and
are the Rashba and Dresselhaus SOC constants.
represents a short-range impurity potential and finally
is the effective Compton wave length describing the strength of the extrinsic SOC. We assume the standard model of white-noise disorder potential with
and Gaussian distribution given by
.
,
and
are the single-particle density of states per spin in the absence of SOC, the impurity concentration and the scattering amplitude, respectively.
is the elastic scattering time at the level of the Fermi Golden Rule. From now on, we work with units such that
.
The layout of the paper is as follows. In the next section, we formulate the ISGE (the SGE can be obtained similarly by using the Onsager relations [
30]) in terms of the Kubo linear response theory. In
Section 3, we derive an expression for the ISGE in the presence of the RSOC and extrinsic SOC. This case with no DSOC, where it is important by itself, allows for understanding the origin of the additional spin torque in a situation which is technically simpler to treat with respect to the general case when both RSOC and DSOC are different from zero. In
Section 4, we expand our results to the specific case when the both RSOC and DSOC, as well as SOC from impurities, are present. We show how our result can be seen as the stationary solution of the Bloch equations for the spin dynamics. We comment briefly on the relevance of our result for the interpretation of the experiments. Finally, we state our conclusions in
Section 5.
2. Linear Response Theory
In this section, we use the standard Kubo formula of linear response theory to derive the ISGE in the presence of extrinsic and intrinsic SOC. The in-plane spin polarization to linear order in the electric fields is given by
where
is the external electric fields with frequency
and
is the frequency-dependent Edelstein conductivity [
31] given by the Kubo formula [
32]
where the trace symbol includes the summation over spin indices. We keep the frequency dependence of
in order to obtain the Bloch equations for the spin dynamics. In Equation (
4),
is the renormalized spin vertex relative to a polarization along the
i-axis, required by the standard series of ladder diagrams of the impurity technique [
33,
34].
are the
bare number current vertices. In the plane-wave basis, their matrix elements from state
to state
read
The latter term
in Equations (
5) and (
6), which depends explicitly on disorder, is of order
and originates from the last term in the Hamiltonian of Equation (
2). Such a term gives rise to the side-jump contribution to the spin Hall effect [
35,
36] due to the extrinsic SOC. The side-jump and skew-scattering contributions to the spin Hall effect in the presence of RSOC have been considered in [
27,
37,
38]. A similar analysis of the side-jump and skew-scattering contributions to the ISGE has been carried out within the SU(2) gauge theory formualtion in [
27] and, more recently, in [
28] by standard Kubo formula diagrammatic methods. For this reason, we will not repeat such an analysis here, where we concentrate instead on the contributions generated by the first term on the right-hand side of Equations (
5) and (6).
Within the self-consistent Born approximation, the last two terms of the Hamiltonian (
2) yield an effective self-energy when averaging over disorder. The self-energy is diagonal in momentum space and has two contributions due to the spin independent and spin dependent scattering [
31,
39]
whereas the imaginary part of the first term gives rise to the standard elastic scattering time
The second one is responsible for the EY spin relaxation. From the point of view of the scattering matrix introduced in the previous section (cf. Equation (
1)), the two self-energy contributions correspond to the Born approximation for the
and
, respectively. Given the self-energy (
7), the retarded Green function is also diagonal in momentum space and can be expanded in the Pauli matrix basis in the form
where
The above
is the Green’s function corresponding to the two branches in which the energy spectrum splits due to the SOC. The factor
with
and
describes the dependence in momentum space of the SOC, when both RSOC and DSOC are present. Notice that inversion in the two-dimensional momentum space (
) leaves the factor
invariant, since it corresponds to
. As a consequence,
, whereas
is invariant. This observation will turn out to be useful later when evaluating the renormalization of the spin vertices. The advanced Green’s function is easily obtained via the relation
. In the expression for
,
is a band-dependent time relaxation and plays an important role in our analysis. In order to obtain this term, we note that, after momentum integration over
in Equation (
7), the imaginary part of the retarded self-energy reads
Above, we indicate with
the Fermi momentum without RSOC and DSOC and with
the
-dependent momenta of the two spin-orbit split Fermi surfaces. To the lowest order in the spin-orbit splitting, we have
where
. The momentum factors originate from the square of the vector product in the second term of Equation (
7). The factor
is due to the
inner momentum, which, upon integration, is eventually fixed at the Fermi surface in the absence of RSOC and DSOC. More precisely, when evaluating the momentum integral, one ends up by summing the contributions of the two spin-orbit split bands in such a way that the
- and
-dependent shift of the two Fermi surfaces cancels out in the sum. However, the
outer momentum remains unfixed. Its value will be fixed by the poles of the Green function in a successive integration over the momentum. Then, the
-dependent relaxation times of the two Fermi surfaces read
where
with the standard expression for the EY spin relaxation rates
In order to evaluate Equation (
4), we need the renormalized spin vertex
, whose explicit dependence on
and
has been dropped for simplicity’s sake. In the absence of impurity scattering, this vertex has its
bare form in terms of Pauli matrices as expected for spin operators
. The superscript
indicates the bare character of the vertex. As shown below, multiple impurity scattering taken into account by ladder diagrams yields the renormalized vertex
, which, in general, will be a matrix in spin space and can then be represented by an expansion in Pauli matrices
.
For vanishing RSOC or DSOC, symmetry reveals that the renormalized spin vertices share the same matrix structure of the bare ones
, i.e., in this case, the renormalized vertex differs by the bare one just by a factor. This is the case in Equation (
20) below. However, when both RSOC and DSOC are present, symmetry arguments again indicate that
and
are not simply proportional to
and
, but acquire both
and
components. By following the standard procedure [
39], after projecting over the Pauli matrix components, the vertex equation reads
where
Once the spin vertices are known, the Edelstein conductivities from Equation (
4) can be put in the orm
with the
bare Edelstein conductivities given by
The bare Edelstein conductivities are those one would obtain by neglecting the vertex corrections due to the ladder diagrams. It is useful to point that one could have adopted the alternative route to renormalize the number current vertices and use the bare spin vertices. Indeed, this was the route followed originally by Edelstein [
31]. Since the renormalized number of current vertices in the DC zero-frequency limit vanish [
34], the evaluation of the Edelstein conductivity reduces to a bubble with bare spin vertices and the current vertices in the absence of RSOC and DSOC.
3. Inverse Spin-Galvanic Effect in the Rashba Model
To keep the discussion as simple as possible, in this section, we confine first to the case when only RSOC is present. We will derive the spin polarization,
, when an external electric field is applied along the
x direction. Then, in the next section, we will evaluate the Bloch equation in the more general case when both RSOC and DSOC are present. In the case
, the renormalized spin vertex
is simply proportional to
, which means that
. Upon the integration over momentum in Equation (
16), only
is non-zero and the other eight possibilities of
in
are zero. The cases
,
,
and
vanish because of angle integration, whereas the two other cases
and
cancel each other out after taking the trace in Equation (
16).
As a result, we finally obtain (in the diffusive approximation
)
where the integral
has been evaluated in
Appendix A
with the total spin relaxation rate being
. Here,
defines the DP spin relaxation rate due to the RSOC. Notice that, in the absence of SOC, the vertex becomes singular by sending to zero the frequency, signaling the spin conservation in that limit. One sees that the EY and DP relaxation rates simply add up. This then gives
. Physically, in the zero-frequency limit, the factor
counts how many impurity scattering events are necessary to relax the spin. In the diffusive regime
, i.e., many impurity scattering events are necessary to erase the memory of the initial spin direction.
By neglecting the contribution from the extrinsic SOC in Equation (
5) for the current vertex, the bare conductivity
naturally separates in two terms
and
due to the components
and
of the number current vertex. The expression for
reads
In the above
,
and
refer to the Fermi momentum, density of states and quasiparticle time in the ±-band. To order
, one has
By including the contribution of the quasiparticle time in the ±-band from Equation (
13), one gets
where
.
The evaluation of
is more direct. It gives
Combining both contributions with accuracy up to order
gives
By combining the vertex correction Equation (
20) and the bare conductivity
in Equation (
18), we get the following contribution to the frequency-dependent spin polarization
with
.
This is not the full story yet, as we are going to explain. What we have learned up to now is that the momentum dependence of the EY self-energy on the two spin-split Fermi surfaces yields an extra term to the Edelstein polarization. Such a momentum dependence can also modify the vertex corrections—the integrals
in Equation (
17)—which lead to the renormalized spin vertex. To appreciate this aspect, we notice that, in evaluating such integrals in the absence of the RSOC, the moduli of
and
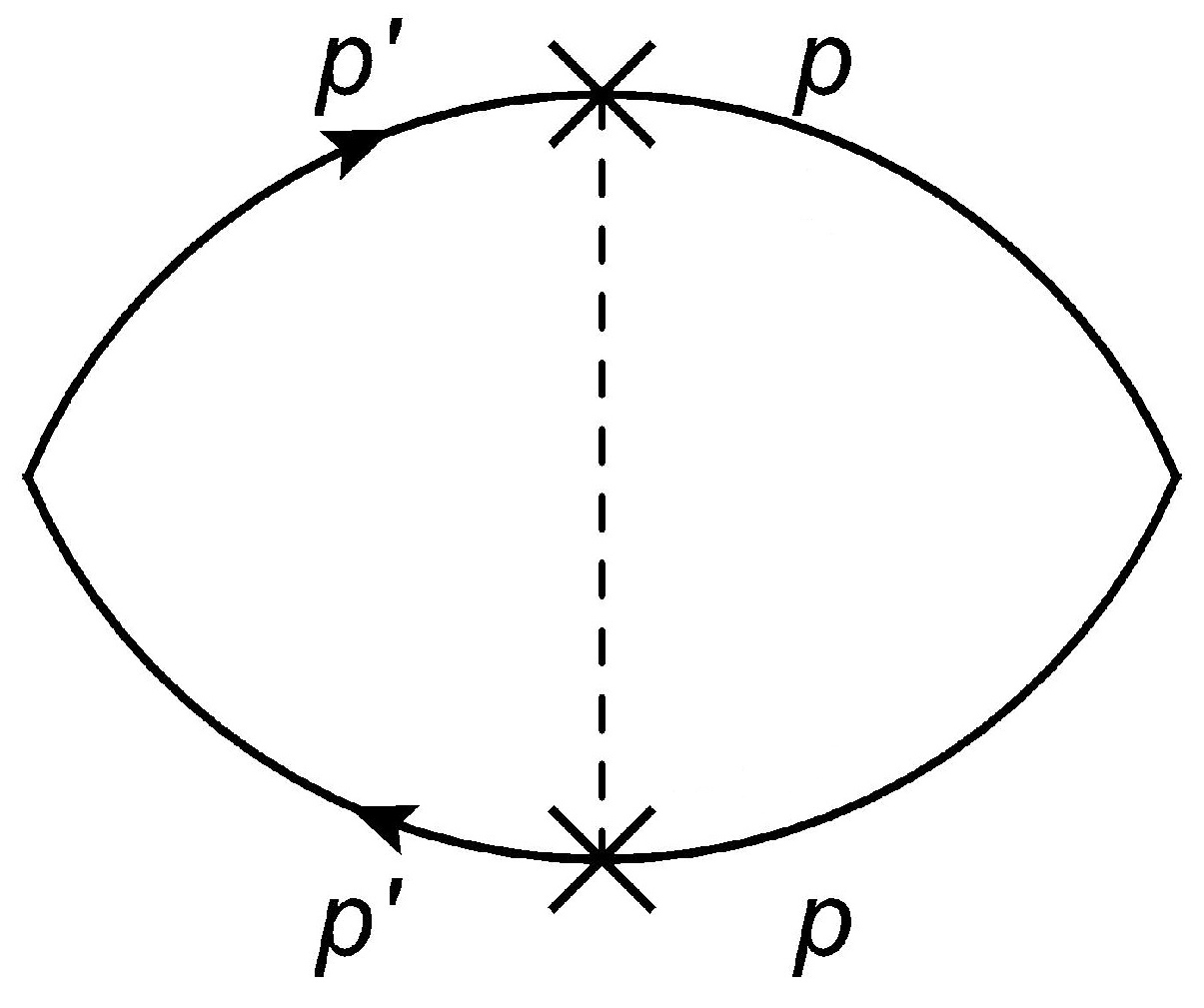
are taken at the Fermi surface in the absence of spin splitting. We emphasize that taking into account the momentum dependence on the Rashba-split Fermi surfaces one instead gets an extra contribution. Consider the diagram of
Figure 1. After integration over
, the left side of the diagram gives
If we set
, we would recover the standard diagrammatic calculation in the absence of intrinsic RSOC. By combining the above left side with the rest of the diagram, one gets an additional contribution to the bare conductivity
To this expression, we must subtract the one obtained by replacing
, which is already accounted for in the ladder summation. Hence, the extra vertex part (
) modifies the spin polarization to give the second contribution
Hence, by summing the above result with Equation (
27), the total spin polarization reads
In the diffusive regime, terms in
in the second round brackets on the right-hand side of Equation (
30), which are responsible for higher-order frequency dependence, can be neglected. In the zero-frequency limit, Equation (
30) has two main contributions described by the two terms in the last round brackets. The first term is responsible for the Edelstein result [
31] due to the intrinsic SOC, whereas the second one, which arises to order
, is an additional contribution to the spin polarization due to the extrinsic SOC. In the Rashba model without extrinsic SOC, only the first term is present, and, indeed, Equation (
30) reduces to it when
. After Fourier transforming, the above equation can be written in the form of the Bloch equation
The terms on the right-hand side describe the various torques controlling the spin dynamics. The first term, which includes DP and EY contributions, is the spin relaxation torque, whereas the second term represents the spin generation torque. The above result coincides with that obtained in [
29] by the SU(2) gauge theory formulation. We have then succeeded in showing by diagrammatic methods the origin of the EY-induced spin torque discussed by [
29]. In the next section, we will generalize this result to the case when both RSOC and DSOC are present.
4. Inverse Spin-Galvanic Effect in the Rashba–Dresslhaus Model
As we have seen in the previous Section, the size and form of the ISGE is greatly modified by the presence of the EY spin relaxation due to the extrinsic SOC. To analyze this fact more generally, we focus here on the model with RSOC and DSOC as well as SOC from impurities. In order to evaluate Equation (
4) for the Edelstein conductivity, we need the renormalized spin vertex
. For vanishing RSOC or DSOC, the renormalized spin vertices share the same matrix structure of the bare ones
. However, when both RSOC and DSOC are explicitly taken into account,
and
are not only simply proportional to
and
, but also acquire components on both
and
. By following the procedure shown in Equation (
16) and upon integration over momentum, the vertex equation for
reduces to
while that for
is
where
where
indicated the average over the momentum directions. The technical points of the calculation in Equation (
34) are given in
Appendix A at the end of the paper. In the diffusive regime,
and
are the DP relaxation rates due to the total intrinsic spin-orbit strength and the interplay of RSOC/DSOC, respectively. For vanishing DSOC, Equation (
34) reduces to the same expression in Equation (
20) as expected in the Rashba model. However, with both RSOC and DSOC, spin relaxation is anisotropic and one needs to diagonalize the matrix on the left-hand side of Equations (
32) and (
33). Such a matrix then identifies the spin eigenmodes. Having in mind to derive the Bloch equations governing to spin dynamics, we rewrite Equation (
3) by using Equation (
18)
where, by virtue of Equations (
32) and (
33),
In the diffusive regime, we can safely neglect the factor
with respect to unity in the denominator in front of the matrix and in the off diagonal elements of the matrix. The quantities
appearing on the right-hand side of Equation (
35) can be evaluated by standard techniques. However, some care is required when evaluating the momenta due to the extrinsic SOC at the spin-split Fermi surfaces, as we did in Equation (
28). The final result for the bare conductivities reads
with
We take the angular average over the DP relaxation rates in Equations (
36)–(
40)
where
,
are the DP relaxation rates due to RSOC and DSOC in the diffusive approximation. By inserting the above expression into Equations (
37)–(
40) and vertex correction in Equation (
36) and using Equation (
35), we may write the expression of the ISGE components in a form reminiscent of the Bloch equations
Indeed, by performing the anti-Fourier transform with respect to the frequency
, Equation (
47) can be written as
where
represents the internal SOC field induced by the electric current. The
and
are the DP and EY relaxation matrix
Equation (
48) is the main result of our paper. It shows that the intrinsic and extrinsic SOC act in parallel as far as relaxation to the equilibrium state is concerned, i.e., the DP and EY spin relaxation matrices add up. However, as far as the spin generation torques are concerned, DP and EY processes have opposite signs. This is in full agreement with the result of [
29] once we also take into account the spin generation torque due to side-jump and skew-scattering processes discussed diagramatically in [
28]. This is simply obtained by multiplying the DP relaxation matrix
in the second term on the right-hand side of Equation (
48) by the factor
, where
and
are the spin Hall angles for extrinsic and intrinsic SOC.
To develop some quick intuition, one may notice that again for
and
, Equation (
47) reproduces the Edelstein result for the Rashba model [
12]. Furthermore, when also
, it reproduces the frequency-dependent spin polarization for the Rashba model as shown in the previous section. When
and
, we see that the ISGE, due to the interplay of the extrinsic and intrinsic SOC, gets an additional spin torque, suggesting that the EY spin-relaxation is detrimental to the Edelstein effect. The diagrammatic analysis reported here provides the following interpretation. The EY spin relaxation depends on the Fermi momentum. When there are two Fermi surfaces with different Fermi momenta, the one with the smaller momentum undergoes less spin relaxation of the EY type than the one with larger momentum. On the other hand, the ISGE arises precisely because there is an unbalance among the two Fermi surfaces with respect to spin polarization. For a given momentum direction, the larger Fermi surface contributes more to the Edelstein polarization than the smaller Fermi surface. Hence, the combination of these two facts suggests a negative effect from the interplay of Edelstein effect and EY spin relaxation. By neglecting the EY relaxation, one sees that the DP terms can cancel each other out if the RSOC and DSOC strengths are equal. This cancellation or anisotropy of the spin accumulation could be used to determine the absolute values of the RSOC and DSOC strengths under spatial combination of spin dependent relaxation.
Finally, we comment on the relevance of our theory with respect to existing experiments [
40]. These show that the current-induced spin polarization does not align along the internal magnetic field
due to the SOC. According to our Equation (
48), this may occur due to the presence of the extrinsic SOC both in the spin relaxation torque and in the spin generation torque. Indeed, when the extrinsic SOC is absent, the spin polarization must necessarily align along the
field. Hence, our theory could, in principle, provide a method to measure the relative strength of intrinsic and extrinsic SOC.