1. Introduction
Soon after the discovery of cuprate high-temperature superconductors [
1], the search for the understanding of their chemical and electronic properties with nuclear magnetic resonance (NMR) began, see e.g., [
2,
3,
4,
5,
6]. NMR is a powerful local probe that measures the electron–nucleus interaction at particular nuclear sites through its effect on the nuclear levels. Thus, one has access to high and low energy properties at the atomic level of resolution as a function of temperature, pressure, and magnetic field [
7]. In particular, NMR gives access to the electronic susceptibility also below the critical temperature of superconductivity (
) through shift and relaxation measurements [
8].
For ordinary metals, it was known long ago, even well before the advent of NMR, that the high electronic density of states at the Fermi surface will cause special nuclear relaxation [
9] in metals, which is closely related to the later observed spin shift (Knight shift [
10]) in metals [
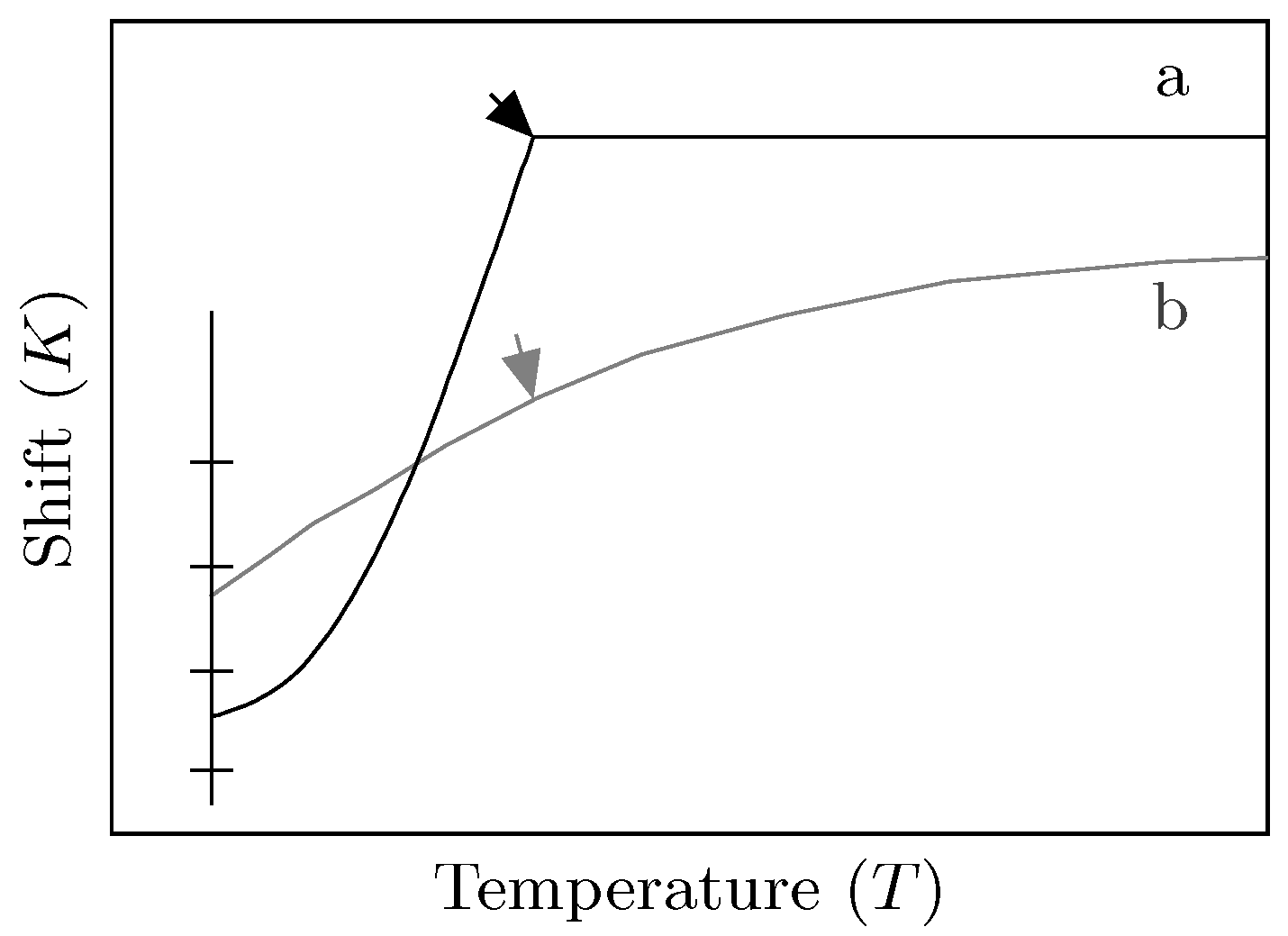
11]. Indeed, for Fermi liquids that become classical superconductors with spin-singlet pairing, these spin moments vanish and lead to the disappearance of nuclear shift (Yosida function) [
12] (cf.
Figure 1) and relaxation (the Hebel–Slichter peak constituted the first proof of the Bardeen–Cooper–Schrieffer (BCS) theory that predicted coherence peaks just below
) [
13].
The superconducting cuprates descend from antiferromagnets by doping, and this raised the question of how the Cu electronic spin will engage in conductivity and superconductivity, and how this can be monitored with NMR, as a function of doping and temperature.
It was soon established that the highly doped materials show nearly Fermi liquid-like behavior and that the pairing appears to favor spin singlet formation. However, at lower doping, but still above
, shifts and relaxation showed pronounced differences to a Fermi liquid. This behavior was believed to be due to the opening of a spingap, as the pseudogap was called when it was discovered with NMR [
14]. The NMR hallmark of the pseudogap is the drop in Knight shift with decreasing temperature above
, cf.
Figure 1.
It has to be pointed out that NMR of the cuprates is quite complex for a number of reasons.
First, the presence of crystallographically inequivalent sites in the large unit cells can cause different, overlapping resonance lines even for a single isotope.
Second, the presence of symmetry disturbing dopants leads to structural inhomogeneities that can cause large NMR linewidths. This is true in particular for nuclei with spin greater than 1/2 () through electric quadrupole interaction, thus, also for the Cu () and O () nuclei in the CuO plane.
Third, and difficult to distinguish from chemical inhomogeneity, there is electronic inhomogeneity that was predicted and detected early on, e.g., [
15,
16,
17,
18]. While present in all cuprates [
19,
20,
21,
22,
23], it is not well understood so that its consequences for the various experimental probes are not clear. In NMR, one finds various degrees of line broadening in the various cuprates (see e.g., [
24]) typically caused by concomitant charge and spin density variations [
25]. The results cannot be dismissed as being due to sample quality, since even chemically highly ordered systems can show tremendous electronic inhomogeneity [
26,
27,
28]. More recently, as will be addressed below, even the magnetic field was shown to influence the NMR splittings [
29] and broadening [
30]. Nevertheless, the average shift appears to be an important and reliable parameter.
Fourth, a limited penetration depth in the normal and superconducting state leads to uncertainties and signal-to-noise problems, and, finally, a partial diamagnetism in the mixed state below complicates NMR shift referencing. These and other complications are reasons for slow experimental progress, and they left uncertainties in the interpretation of the data.
Here, we will be concerned with shift analysis only since understanding relaxation involves a spectral range of fluctuations that may include not only the magnetic field, but also the electric field gradient. The simple uniform magnetic response, on the other hand, is responsible for the shifts for which quadrupolar effects can be eliminated much more easily. In addition, since Cu NMR does not require isotope exchange, which, for O, always has the risk of changing the doping level. We will focus on the most abundantly reported Cu shifts here and only discuss other shifts occasionally.
We will begin with remarks of concern for shift measurements, which help clarify shift referencing and other uncertainties. Then, we will repeat the early shift phenomenology before summarizing recent findings regarding the failure of the single-component description, which leads us to introducing a new shift phenomenology based on the available literature data. In this phenomenology, we will highlight special observations in the shifts that question a number of earlier conclusions and hopefully help theories to advance the understanding of the electronic properties of the cuprates.
2. Frequencies, Shifts, and Splittings
In the most simple NMR experiment, the center of gravity of the Fourier transform of a nuclear free induction decay after a
pulse determines the resonance frequency (
). Often,
coincides with the peak of the resonance line, which serves as measure of the shift. For this to be true, the radio frequency (RF) pulse excitation should be large compared to the width of a resonance line, but this is often not the case in the cuprates, not even for a single magnetic transition. Fortunately, the broadening is mostly inhomogeneous from short and long-range shift variations [
25] and one employs selective techniques (such as frequency stepping) to map out the spectral distribution of resonances approximately in lengthy experiments. Large and often temperature dependent linewidths hamper the exact determination of shifts, especially for the non-stoichiometric cuprates, and decrease NMR sensitivity. These are reasons why the lineshapes for the determination of the shifts are not always reported. Nevertheless, it appears that the Cu frequencies are quite reliable.
Loss of the NMR signal in the cuprates is of serious concern. In the superconducting state, RF penetration becomes exceedingly small, while above
, it is only limited by the anisotropic normal state conductivity. This favors the use of (oriented) powders that, on the other hand, are less favorable for orientation dependent studies. In addition, some underdoped cuprates show a sudden signal loss at some critical temperature similar to what was observed for spin glasses [
31]. Thus, one has to be aware that NMR could miss important signals. Signal intensity issues have not been properly addressed with most experiments adding to uncertainties. Perhaps the strongest evidence, however, that the observed NMR signals do represent the bulk properties is the fact that the quadrupole splittings measured with NMR account for the average chemical doping [
32,
33,
34].
For reasons of symmetry, the crystal c-axis coincides with that of the local magnetic field at the nuclei if the external field () is parallel to c (). This must be correct for orbital as well as spin shift tensors (). Likewise, the largest principle component of the electric field gradient at the Cu nucleus must point in the same c-direction (). Given a rather small or vanishing orthorhombic distortion, the direction of the other two principle axes of all of the tensors are not known with certainty, but the asymmetry of all tensors is expected to be rather small. For planar oxygen nuclei, the situation is very different, as the direction of the -bond in the plane dominates local symmetry and the asymmetry perpendicular to the -bond is expected to be much larger (in and out of the plane).
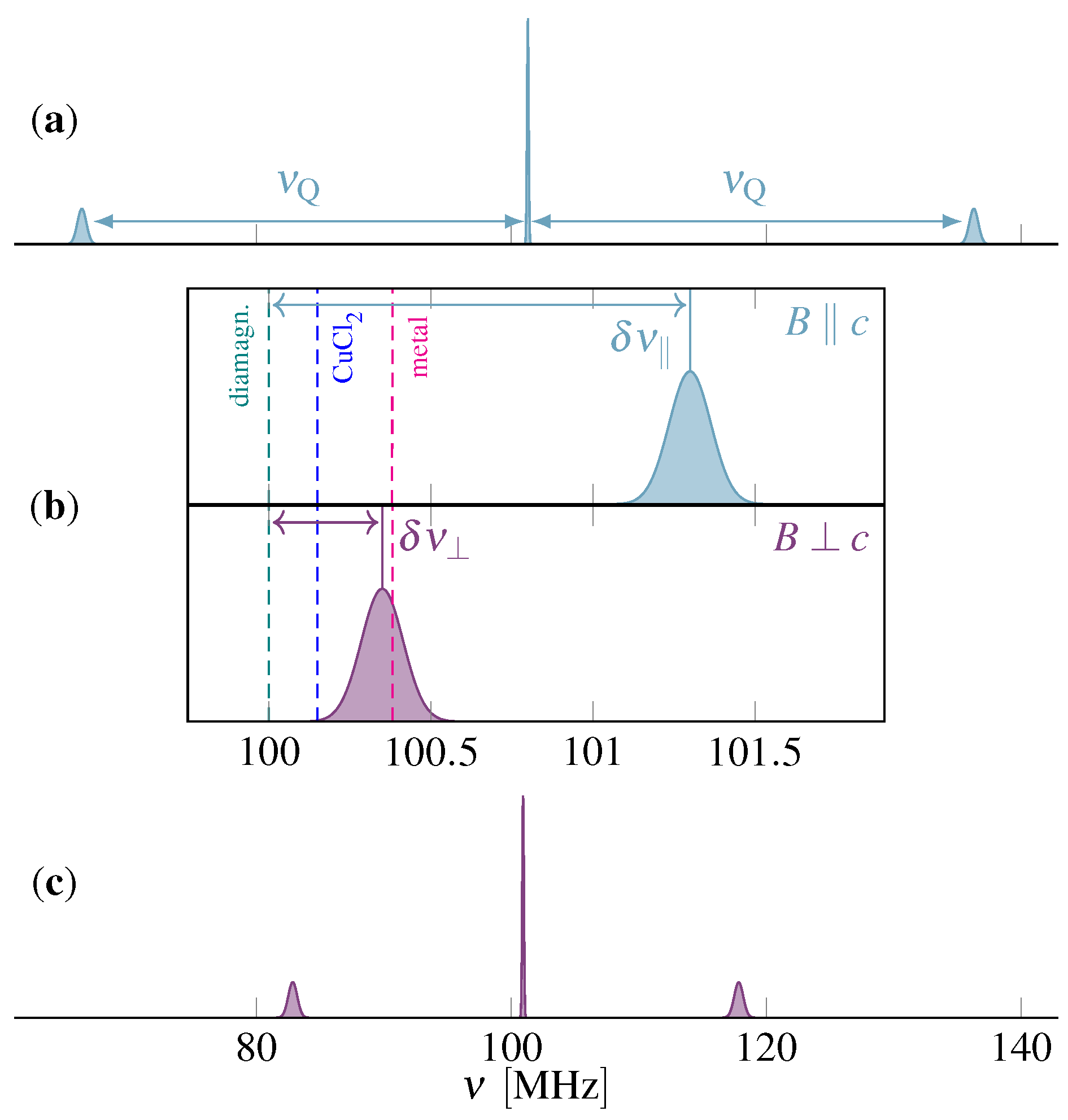
For
Cu with
, we expect three resonance lines due to the quadrupole interaction. With the field along the high symmetry axis (
), one has in the leading order for a dominating Zeeman term,
where
denotes the
= 3 transitions of the
Cu nucleus and
is the quadrupole splitting, cf.
Figure 2. Any magnetic frequency shift affects all transitions the same way so that we can discuss all shifts just for the central (
) transition, cf.
Figure 2.
If the magnetic field is perpendicular to the crystal c-axis (), the central transition () is affected by quadrupole related shifts in higher order. However, if has been determined from measurements for , the magnetic shift can be calculated from (for given tensor orientation).
For the discussion of the Cu shift, we can focus on
in (
1) that is measured with respect to a reference material resonating under identical conditions in the same field (
) at
, so that the NMR shift in frequency units is given by,
This NMR frequency shift is influenced by the diamagnetic shielding contribution from the core electrons (which is similar for all materials) and a paramagnetic Van Vleck term due to mixing with excited states depending on the chemical structure. The latter is the determining factor for the importance of the chemical shift. Electronic spin effects are expected to alter the NMR resonance frequency [
7,
35], in particular since the hyperfine coupling amplifies spin effects over those from orbital motion of free carriers (in the absence of strong spin-orbit coupling). Obviously, one would like to use as reference a material that has a shift dominated by the core electrons only. Then, the (isotropic) shifts
relate to interesting effects (Van Vleck and spin effects). Unfortunately, shift referencing in the cuprates varies, i.e., most of the early published NMR work relied on CuCl as a reference, a material that was later shown to have a significant Van Vleck contribution (
= −0.15%) [
36]. In order to use the magnitude of the NMR shift to relate to other probes or theory, one has to make sure that the shifts are properly referenced. All shifts shown here have been corrected where possible, cf. also
Appendix A.
Since one expects the mentioned frequency shifts to be proportional to the magnetic field [
7], one typically uses relative shift values that are proportional to the uniform susceptibilities (spin and orbital),
where we defined orbital (
) and spin (
) shift contributions.
Currently, it is not fully known whether the shifts in the cuprates are indeed proportional to the field. There have been reports of a field dependence of
K [
37] in high fields, and high fields were shown to induce charge density variations [
38] as well. Even moderate fields were shown to be able to induce distributions of quadrupolar splittings [
30]. However, some field dependent measurements have been performed and nuclear quadrupole resonance (NQR) experiments (
) show the absence of significant static magnetism. The study of the field dependence of the shifts is problematic since, at low magnetic fields, the rather large quadrupole interaction for Cu makes precise magnetic shift measurements difficult, apart from lowering the NMR intensity that is nearly quadratic in the field. We stipulate that the field dependence of
K at lower fields (≈10 T) can be neglected.
If one expects macroscopic shielding effects, an internal shift reference is to be used. This can be rather difficult, but comparison with the NMR shift of other nuclei within the same sample can be helpful. This has been employed rarely [
27,
39,
40,
41], rather, the diamagnetism in the mixed state was estimated based on phenomenological theory. This adds some uncertainty to the NMR shifts at low temperatures in the typical fields used (the distance between fluxoids is small compared to the penetration depth, which makes the overall field variation small in terms of shift and linewidth effects).
Lastly, one needs to mention the availability of single crystals. Since large enough crystals were rarely available, stacks of small crystals or c-axis aligned powders were used for shift measurements. This makes measurements in the a-b-plane difficult, e.g., if there was a sizable asymmetry in the plane. In addition, if one measures the shifts with the magnetic field in the CuO plane, higher order quadrupole effects are important and both tensors’ principal axes do not necessarily share the same directions in the plane. Unfortunately, shift differences upon rotating the magnetic field in the CuO plane are sparse.
Considering all the effects mentioned above, Cu NMR is quite reliable if the linewidth is not exceedingly large. The shifts vary over a large range as a function of temperature and doping so that partial diamagnetism is less important. Nevertheless, one has to be aware of discrepancies.
3. Early Shift Phenomenology
In early shift experiments, the decrease of shift for
at low temperatures was interpreted as evidence for spin singlet pairing, and the decrease of shift above
marked the discovery of the pseudogap. A more detailed picture was discussed in particular based on data from YBa
2Cu
3O
6+y aligned powders and single crystals [
5,
6,
35,
42,
43].
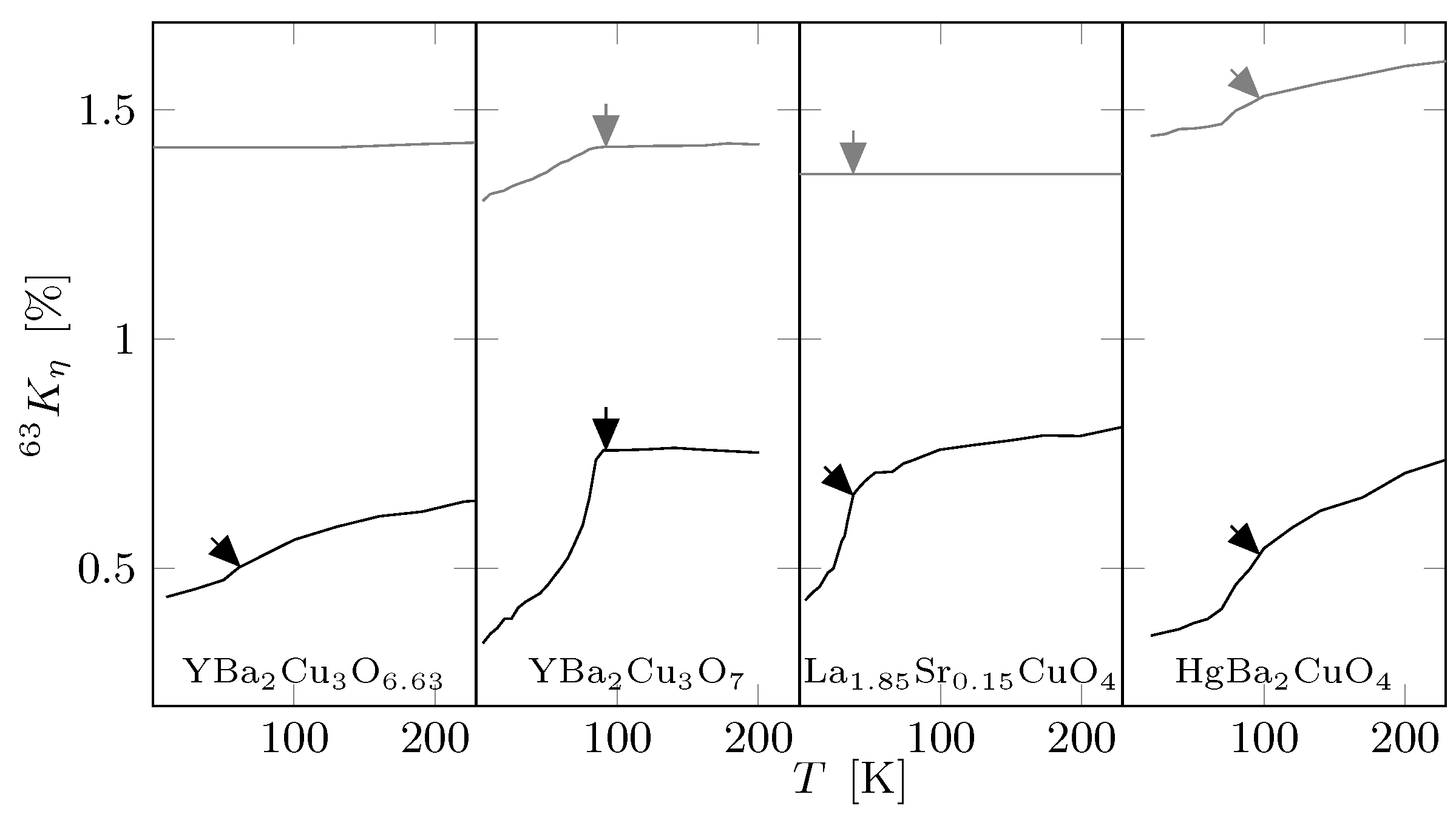
For this important family, the underdoped materials, cf.
Figure 3 (left panel), show pseudogap behavior for
, but
is rather temperature independent; the stoichiometric, slightly overdoped material shows a temperature independent
above about
, cf.
Figure 3 (second from left), below
, the shift decreases; for
, after the diamagnetic correction, the shift appeared almost unchanged.
Figure 3 also shows quite different temperature dependent shifts observed in other cuprates. La
Sr
CuO
exhibits Fermi liquid-like behavior for
and no temperature dependence for
. The situation is again different for HgBa
CuO
, where there is a sizable shift also present for
.
The shifts remaining at the lowest temperatures in both directions of the magnetic field (with regard to the crystal
c-axis) were believed to be orbital shifts. The then determined orbital shift anisotropy was close to what one expected for an isolated Cu
ion in the square planar arrangement of the CuO
plane. Similarly, the quadrupole splitting was in support of such a Cu
state [
35]. These findings entail the presence of a nearly half filled
orbital. As a consequence, one expected a negative spin shift from core polarization and dipolar effects for
(
), but a much smaller and positive shift for
(
). This can be reliably estimated but is also known from experiments on other such Cu
ions [
35,
44]. However, this was not observed, cf.
Figure 3, and it was concluded that a more complicated hyperfine scenario must be correct, one that involves also an isotropic term
B,
where the two susceptibilities are from Cu and O spins, respectively.
denotes the anisotropic onsite hyperfine constant and
B the so-called transferred hyperfine term.
It was noted early on that the Cu
spin may exchange through planar O and thus involve the Cu
state, which should lead to an isotropic shift term [
45] that could explain the data in terms of a single fluid, rather than in terms of Cu and O spins [
46]. This can be tested with NMR since a single electronic fluid has a single susceptibility. If one defines the change of the spin susceptibility
between any two temperatures
and
by
, proportional shift changes
at all nuclei should be found,
if
j denotes a particular isotope or lattice site and
the effective hyperfine constant. This is different from what one would expect if (
4) were applicable, with different temperature dependences for
and
(and
).
With experiments on YBa
2Cu
3O
6.63, it was concluded from shifts for Cu and O in the plane that a single susceptibility is at work [
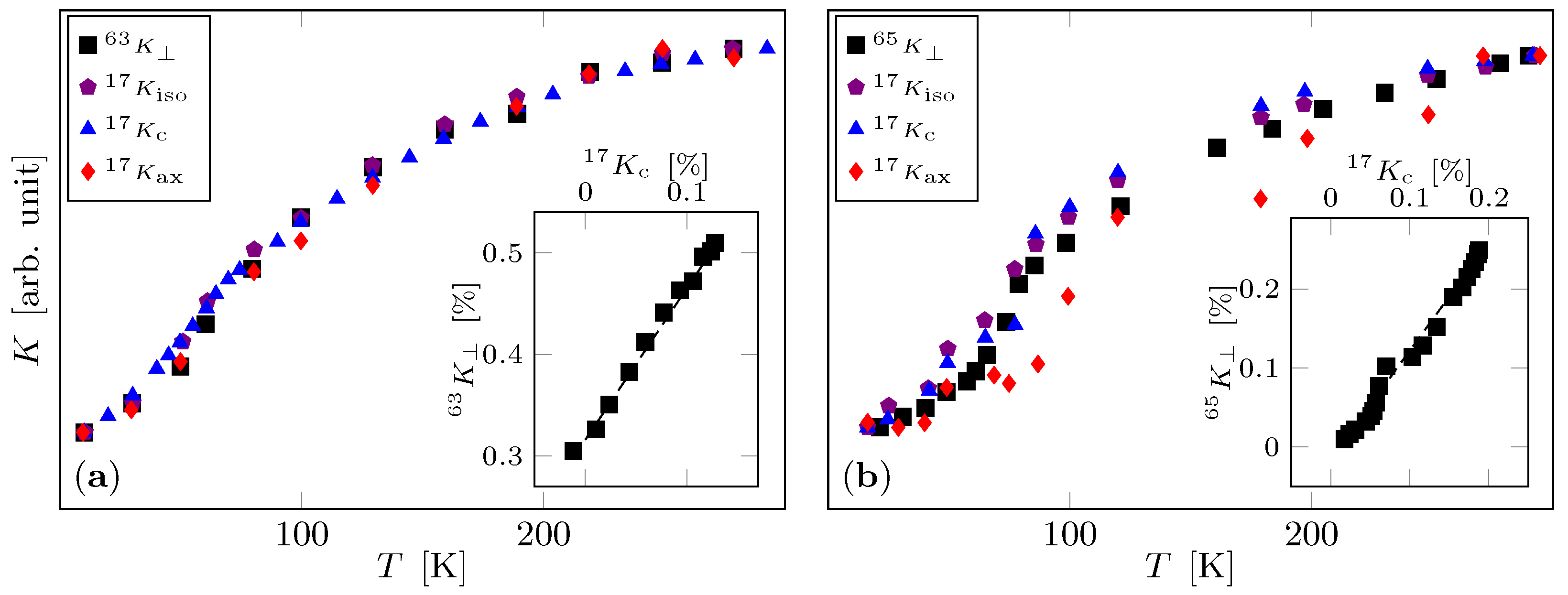
43], cf.
Figure 4a, in strong support of the single fluid scenario. In a second set of experiments on YBa
2Cu
4O
8 [
47], cf.
Figure 4b, the same conclusion was reached, although a slight deviation could be seen that was still, however, within the error bars. Note that there is no temperature dependent shift for Cu and
. These findings influenced theory considerably, although doubts of a single-band scenario persisted [
48,
49,
50,
51].
The adopted single fluid picture had to explain the absence of the spin shift for
through an accidental cancellation of the hyperfine terms, i.e.,
with
. While questioned, this coincidence was widely accepted, e.g., [
52], even for other families, such as La
Sr
CuO
, cf.
Figure 3. Other materials showed temperature dependent shifts also in
, which pointed to a violation of the accidental cancellation in these systems. However, for HgBa
CuO
and near room temperature, cf.
Figure 3, we can have
, which requires a rather large change in the hyperfine scenario.
4. Failure of the Single Fluid Model
La
Sr
CuO
was assumed to be governed by a single fluid, but its planar Cu and O shifts showed apparently different temperature dependences (cf.
Figure 5). NMR shifts, if stripped of uncertainties such as the the diamagnetic response below
, must hold definite answers. With a series of shift measurements on La
1.85Sr
0.15CuO
4 by using the apical oxygen NMR signal as an internal shift reference, it was shown beyond a doubt that this material violates the single fluid scenario and that two susceptibilities with different temperature dependences are required for the understanding of the data [
40] (cf.
Figure 5). Then, similar to (
4), one has to describe the shifts by
where
are effective hyperfine constants for the coupling to the two electronic spin components. Note that a third susceptibility must be introduced (
) since a coupling between any two spin components with susceptibilities
and
will lead to a coupling susceptibility (
) where the field at component 2 induces a polarization of component 1. It was found that the two susceptibilities discernible with NMR experiments (
and
) showed rather different temperature dependences. One susceptibility (that dominates the Cu shifts) shows a Fermi liquid-like behavior in that it is temperature independent above about
, but falls off rapidly as the temperature is lowered, while the other susceptibility (that dominates the planar O shift) is temperature dependent already above
and must be related to the pseudogap feature (the hyperfine coefficients
are given in [
40]).
While these experiments showed that the single fluid picture is not universal, it did not explain why other systems could be understood with one susceptibility, in particular the underdoped stoichiometric compound YBa
2Cu
4O
8 that is known to have very narrow NMR lines, which makes it a benchmark system. Within the error bars of early NMR, cf.
Figure 4b, a sudden change near
is indicated, which raises the question how one could further investigate this compound. Obviously, the application of pressure, strong enough to change the electronic properties slightly, but weak enough to leave the chemical structure unscathed, is a desirable tool. Such experiments, based on a new high-pressure NMR cell design [
53], could be performed recently. Since Cu has strong orbital shifts,
O NMR was employed as the oxygen orbital shift is expected to be rather weak on general grounds. As a function of pressure (that is known to raise
), it was found that a two component scenario was necessary to understand the change in the shift [
54]. With increasing pressure, a Fermi liquid-like component appears in the data (amplified by a factor of about 9 at about 6 GPa compared to the ambient pressure data). Thus, this benchmark system weakly breaks the single-fluid picture at ambient pressure, but fails to behave as such at higher pressure. These experiments showed the failure of a single-fluid description in another family of materials, while agreeing with previously published accounts [
47]. Thus, it appeared that the single-fluid picture emerging through NMR was rather accidental.
In a parallel set of experiments, the HgBa
CuO
family of materials was investigated [
26,
27,
41]. These materials are tetragonal and have a single CuO
plane similar to the La
Sr
CuO
family. Thus, any multi-component behavior must result from the plane (and, e.g., any influence from other spin components such as in the CuO-chains for the YBa
2Cu
3O
6+y family can be excluded). Furthermore, the widely held belief was that, since doping occurs further away from the CuO
plane, these systems must be much more homogeneous compared to La
Sr
CuO
. However, in first experiments on high quality single crystals, it was found that, while the Hg NMR shows very narrow lines, the Cu nuclei in the plane have a similar quadrupolar broadening of the satellite transitions due to charge variations as in La
1.85Sr
0.15CuO
4 [
26], which was ascribed to charge density order only very recently [
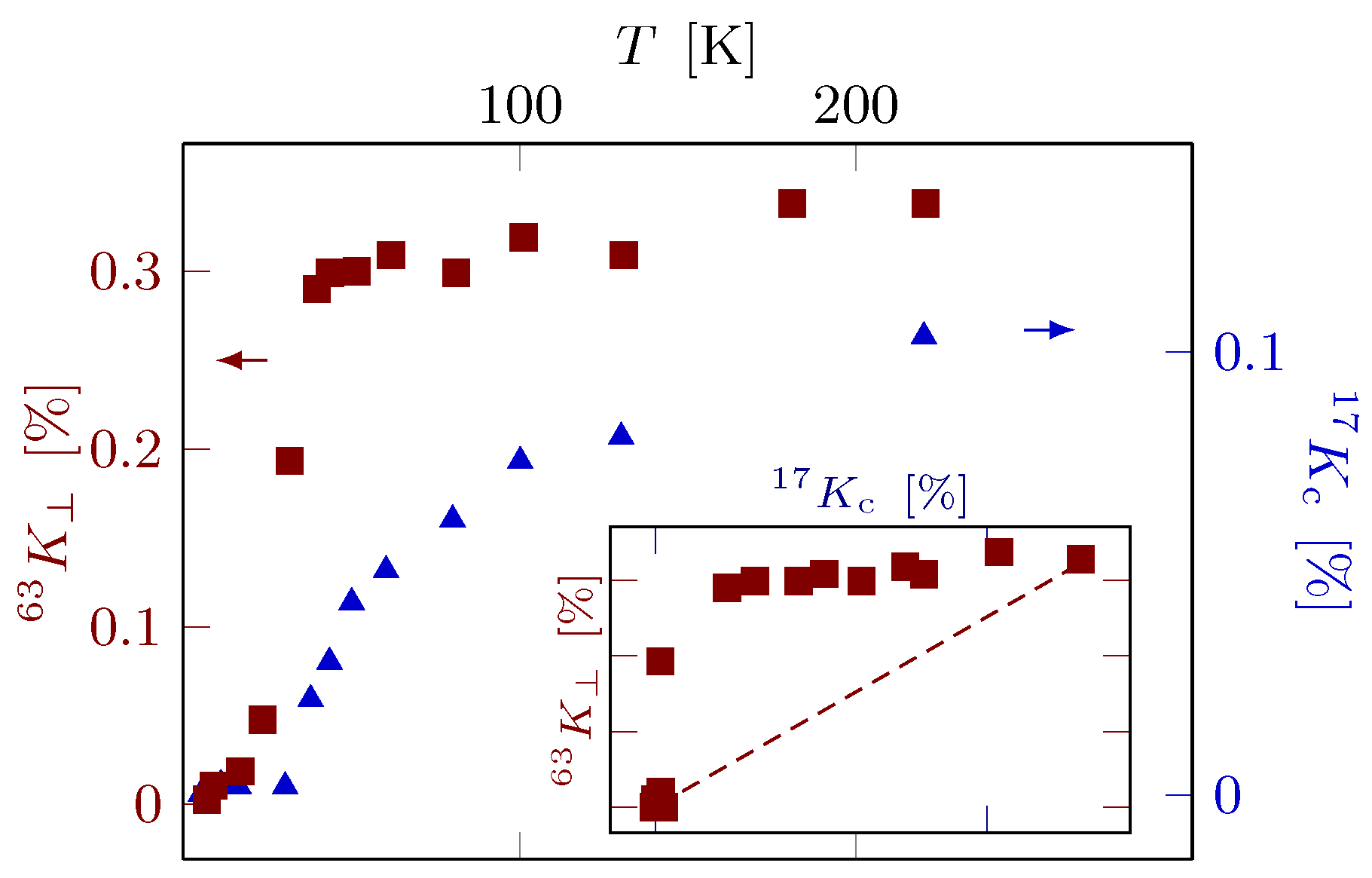
55] (but may not explain all doping and temperature dependences observed with NMR).
An important difference of the HgBa
CuO
family of cuprates compared to YBa
2Cu
3O
6+y and La
Sr
CuO
is the presence of a temperature dependent shift also for
for Cu. By comparing the shifts for Cu and both directions of the field, it became obvious that, for an underdoped system, the changes in shift with temperature in both directions were not proportional to each other, while the optimally doped material did show proportional changes [
41]. On the other hand, Hg NMR showed that also the optimally doped system is not a single fluid [
56]. In order to understand this somewhat mysterious behavior, more systems were studied [
27]. With the new samples, it became apparent that there was a third shift component that had a different Cu shift anisotropy, easily recognizable for underdoped and overdoped samples. However, while this component was temperature independent at higher temperatures, the temperature where it rapidly vanished was different from
(only for the underdoped sample investigated earlier is this temperature close to its
= 74 K). Furthermore, this component changes sign at optimal doping so that it is absent in the data. This new component can be recognized easily in a shift–shift plot, where
is plotted against
(cf.
Figure 6).
All of the data could be analyzed with these three susceptibilities, and it was argued that one of the susceptibilities could be due to the coupling of two spin components (cf. (
7)). Interestingly, the Fermi liquid-like component shares the same anisotropy as the pseudogap component [
27].
While all of these experiments made it clear that the approach used up to now that interprets the cuprate NMR shifts fails, and despite some support from the phenomenological theory [
57] that used the earlier findings within a generalized two-fluid scenario, the single-fluid approach is still being adopted (e.g., [
58,
59]), perhaps since a unifying, new phenomenology for the NMR data analysis is missing. With the new understanding of the cuprate phase diagram in terms of NMR that has two charge components (at Cu and O) [
34], we decided to take a closer look at all available Cu shift data, which led us eventually to introduce a new, contrasting NMR shift phenomenology that will be discussed below.
5. Contrasting Cu Shift Phenomenology
We collected data from the literature where Cu shifts were reported with the magnetic field parallel and perpendicular to the
c-axis of the crystal. The shift reference was checked and changed to the diamagnetic part if necessary, as described in
Section 2. The individual plots of shift vs. temperature can be found in the
Supplementary Materials as well as the references collected in the
Appendix A, where the reader can also find information about the changes applied to the data.
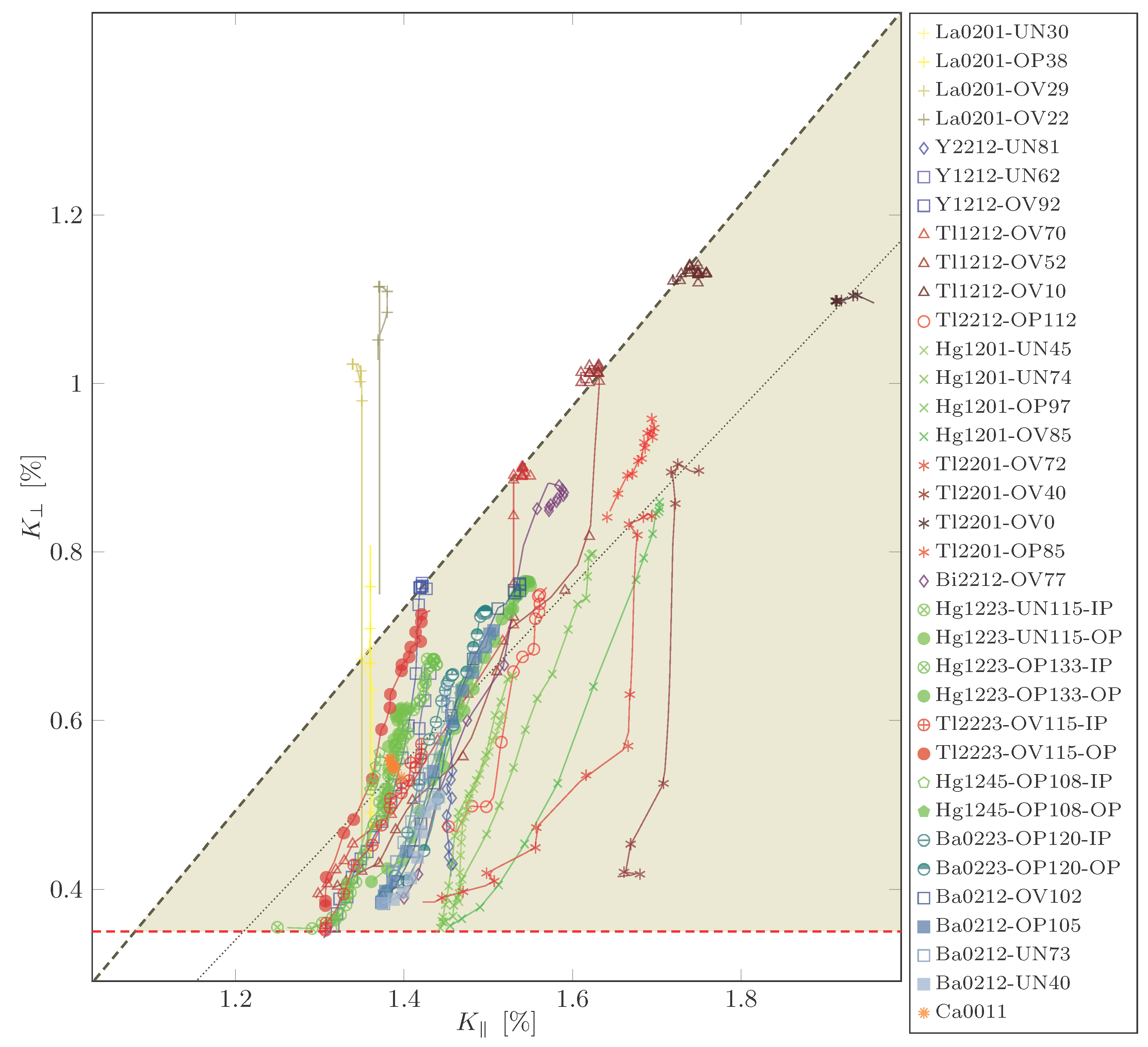
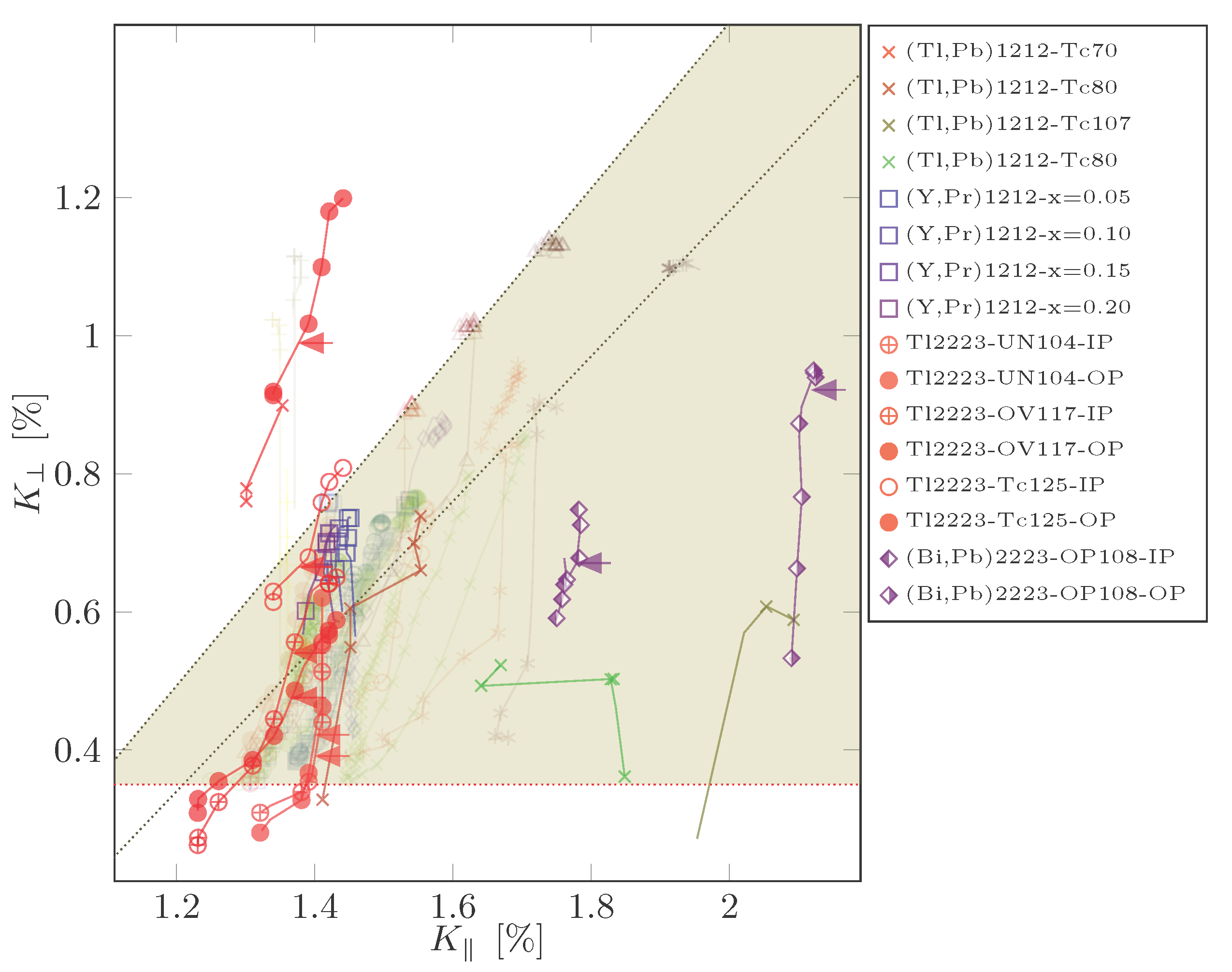
A first overview is shown in
Figure 7 where we use the plot already discussed in more detail in
Figure 6 [
27,
41]. It has
as a function of
with temperature as an implicit parameter. Note that both axes have the same scale.
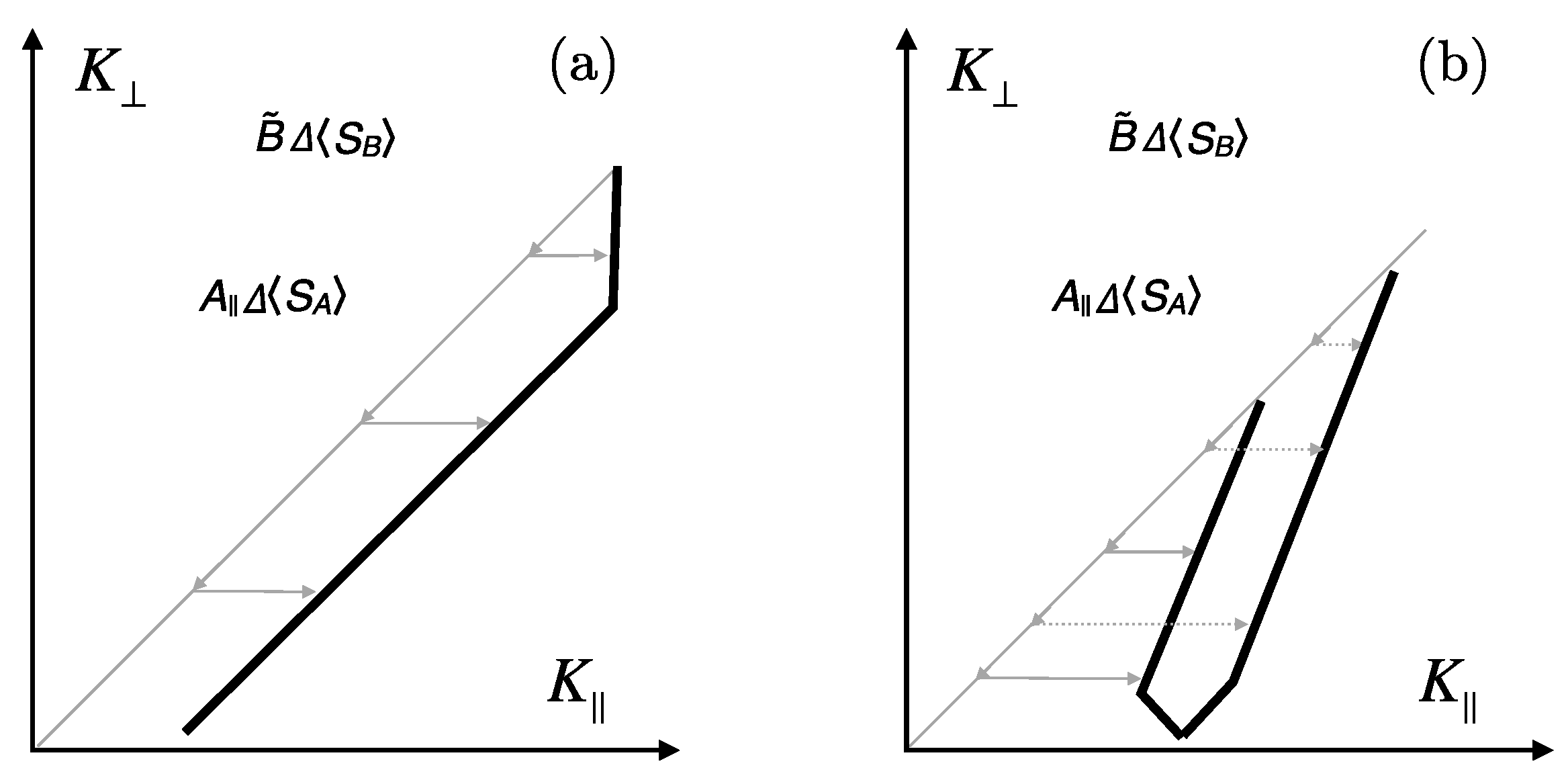
We would like to summarize what we think are key observations in
Figure 7, before we discuss these points in greater detail below:
- A
Common : all shifts for meet at a similar low-temperature shift point , dashed red line.
- B
Large spread for : for different families have rather different low-temperature shifts 1.2–2.0%.
- C
Isotropic shift line: for overdoped systems and high temperatures, many points make up a line with slope , as expected from isotropic hyperfine coupling (dashed diagonal line). There may be other isotropic lines for other families, and one of them is indicated by the dotted line.
- D
New orbital shifts: the isotropic shift line and the common intersect at and , which defines an orbital shift pair.
- E
Shift triangle: practically all temperature dependent shifts are found below the main isotropic shift line, i.e., for almost all cuprates, very different from what was assumed so far.
- F
Characteristic slopes: a few typical slopes dominate the figure, and .
We would like to discuss these six points somewhat further before we draw conclusions about the electronic liquid.
(A) The fact that reaches similar values at low temperatures independent from doping has been taken as the hallmark of spin singlet pairing. Slight differences in could stem from variations in the orbital shift, the life-time of the electronic states, differences in macroscopic diamagnetism, quadrupole interaction (charge density variations), or even somewhat different field-dependent shifts. While partial diamagnetism may shift somewhat up at low temperatures, it appears to be a very reliable shift.
(B) Most systems have temperature dependent shifts for (), contrary to the systems analyzed early on. In fact, these shifts can be rather large, which would require very different hyperfine scenarios assuming the traditional shift phenomenology. However, at low temperatures, these shifts do not converge to a similar as for . Given the rather ubiquitous CuO plane, it appears difficult to understand the differences only in terms of variable orbital shifts.
(C) A great number of shifts for overdoped systems above
(
) define a line with a slope of nearly 1, i.e.,
, where we denote with
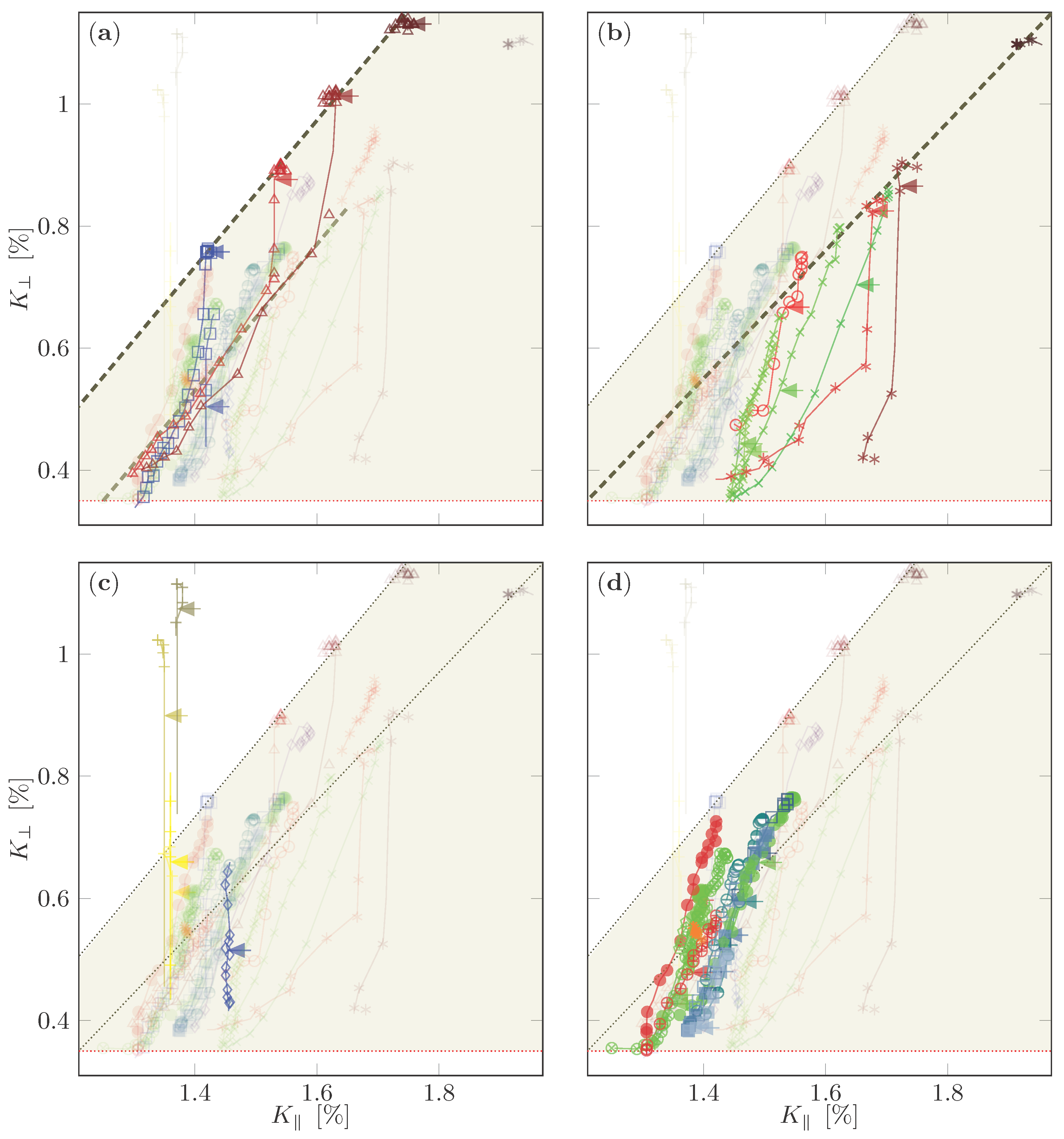
the change with respect to doping. Changing temperature has a very different effect than changing doping. Apparently, this isotropic shift line varies somewhat between families (dotted and dashed lines in
Figure 8b). Since most of the
involve the overdoped, temperature independent shift range, one might be inclined to assign this line to a shift due to a simple (Fermi) liquid that reigns in the overdoped systems at high temperatures and to which the nuclei couple predominantly with an almost isotropic hyperfine coefficient. We also note that there is a parallel line to the dominant isotropic line: after a drop at
as the temperature is lowered, the shifts disappear as a function of temperature (not doping) in an isotropic fashion for Tl1212 (cf.
Figure 8a).
(D) The isotropic shift lines intersect
and define orbital shifts
. This may indicate slight differences in the orbital shift for different families. The new values for the orbital shift are much closer to what is expected from first principle calculations that predict an orbital shift anisotropy of about 2.4 [
36].
(E) Another striking observation in
Figure 7 is the fact that almost all experimental shifts are below the highest isotropic line (or the isotropic line for the family), i.e.,
at all temperatures. If the diagonal lines define a Fermi liquid of carriers with isotropic coupling the action of the gaps, as the temperature is lowered, leads to a stronger decrease of
than
.
(F) When looking at
Figure 7, certain other straight line segments can be identified. Next to the isotropic shift line, one recognizes a somewhat steeper slope that was described first with the HgBa
CuO
family of cuprates [
27,
41]. It was assumed that it is caused by the anisotropy of a hyperfine coupling coefficient. The offsets between the lines were believed to be due to another shift component that disappears below a characteristic temperature
. For YBa
2Cu
3O
7 (Y1212), the special slope appears well below
, while, for other samples (e.g., the HgBa
CuO
(Hg1201) family), it appears above and below
, and this is shifted by doping. For a given family, the low-temperature shift values meet at the same point, while there is an offset between families (of the size of what is observed even between members of a single family at higher temperatures). Another much steeper slope with
can be found as well (cf.
Figure 8c). It is important for underdoped YBa
2Cu
3O
6+y (Y1212), La
Sr
CuO
(La0201), and some Tl compounds in some range of temperatures.
6. Discussion
A number of systems [
27,
40,
41,
51] were shown to fail for a single fluid model explanation, as summarized in
Section 4. In particular, one of the benchmark systems (YBa
2Cu
4O
8) was found to be just at the brink of failing for the single fluid picture, as application of modest pressure revealed [
54]. Most of the evidence came from contrasting temperature dependences of the shifts for different nuclei, but also just for a single nucleus and different orientations of the external field [
27,
41,
51]. Since the Cu shift data appear quite reliable, as discussed above, we gathered available data and applied the same shift referencing. The data were then plotted in
Figure 7 as
(with temperature as an implicit parameter).
By inspecting
Figure 7, we pointed to a number of rather reliable facts that lead to our new shift phenomenology for the cuprates. The first such fact is that the low-temperature shifts for
converge to the same shift for all materials, which must determine the orbital shift
, perhaps the only assumption that survives the old picture. Quite the opposite, the shifts for
do not converge towards a common value. While it is possible that the orbital shift in this direction does depend on the family of materials, there must be an unexplained, residual shift left at the lowest temperatures. Part of the evidence comes from the plot itself (as already mentioned), but also first principle calculations predicted an orbital shift anisotropy of
, a number that appears rather reliable also on general grounds [
36], and hints at an orbital term
%, much closer to what we determine (
%) from
Figure 7. We know from the HgBa
CuO
family, investigated with great care earlier [
27,
41], that this additional shift is probably present at Hg, as well as planar O, which favors a spin contribution.
Another very reliable observation is what we call the isotropic shift line, a line with a slope of nearly one (
) in
Figure 7. Probably, there are few such lines with slightly different slopes for different families (cf. also
Figure 8b). These lines clearly show that the extent of parallel and perpendicular shifts must be similar, very different from earlier conclusions, but in support of what we just stated above. This most likely calls for a much larger isotropic hyperfine coefficient
, again contrary to what has been assumed in the early phenomenology. The nearly isotropic shift lines also define an orbital shift
together with
that is much closer to what is expected from the discussion above. Perhaps slightly different points of intersection of the nearly isotropic shift lines with a common
define slightly different orbital shifts for different families.
Another remarkable observation is that almost all shift data are found below the diagonal (nearly isotropic) shift line, i.e., when lowering the temperature so that either the pseudogap or the superconducting gap sets in falls faster than . Furthermore, this happens interestingly enough along a small number of rather fixed slopes . This must point to special properties of the fluid.
How can we understand the findings with a minimal amount of assumptions that do not rest on particular theoretical pictures? Based on the chemical bonding, we expect an isotropic term that involves the Cu
orbital (in various possible ways). If the related hyperfine coefficient
is sufficiently large (we just use
instead of 4
), it explains why any spin density
creates the nearly isotropic shift line. We write,
where we added an anisotropic term
so that
since the isotropic lines deviate only slightly from slope 1 and since the local chemistry demands an involvement of the
orbital. Its bare onsite core polarization, dipolar, and spin-orbit contributions are quite well known and lead to an overall anisotropy
with a negative
and an almost vanishing
[
35,
44]. Thus, spin density in this orbital will predominantly change
, i.e., it will lead to a shift change that is nearly on a horizontal line in
Figure 7. Without having to speculate about the details of the electronic fluid(s), one would then guess that what is needed in order to explain the temperature dependences of the data in
Figure 7 is a change of spin density in the
orbital leading to
(nearly horizontal change) and a concommittant change for the isotropic part
(cf.
Figure 9). The special slopes discussed above would then tell us about the allowed ratios
that make up the few special slopes in
Figure 7.
In the above model and in view of the figures above, decreasing the temperature leads to basically two different behaviors.
(1) Systems that undergo a superconducting transition without a preceding shift decrease (from the action of the pseudogap) rapidly lose (with the large slope) a certain amount of predominantly . As the temperature decreases further, both shifts fall parallel to the isotropic line. This indicates a certain, rapid decrease in that creates a similar shift change as , followed by a change in only.
(2) Systems that lose shifts by the action of the pseudogap as the temperature is lowered, before the shift change from the superconducting gap that appears, behaves differently. Here, the slope is about 2.4 with which the shifts break away from the isotropic line. This slope is not interrupted by crossing . Only at very low temperatures do the changes in shifts break away from the special slope according to the following phenomenology: after is fully established, still falls for the overdoped systems; for the underdoped systems, the change in is still not completed when that in is exhausted. This scenario is apparent for the HgBaCuO family, and, for other systems, the typical deviations from the linear slopes hint at the same behavior. For optimal doping, the shifts appear to follow the high-temperature slope down to the lowest values.
At the lowest temperatures, there must be negative spin density left in the orbital, which may be difficult to detect with uniform susceptibility measurements that suffer from the Meissner response and notorious contributions from Curie defects at low temperatures.
We would like to note that, in the extensive analysis of the failure of the single fluid scenario for La
1.85Sr
0.15CuO
4, it was already reported [
40] that the coupling of the Cu nucleus to the Fermi liquid-like component was 8.6 times larger than its coupling to the other component, and that the planar oxygen was found to only weakly couple to the Fermi liquid-like component. Thus, for systems where the temperature dependence of the Cu shift is not dominated by the Fermi liquid-like component, Cu and O should show a similar temperature dependence. This explains why the single fluid behavior was detected with some of the materials early on. The action of the superconducting gap with its pronounced, sudden drop in shift at
is not always seen in the Cu data (cf.
Figure 7), but hardly for planar oxygen. This explains why the Fermi liquid-like component as a second shift component can easily be missed.
Finally, we would like to discuss the findings in view of the NMR phase diagram [
34] that was suggested recently. We do not observe an immediate trend relating
to the NMR shifts in
Figure 7. However, there appears to be a subtle connection to the charge distribution between planar Cu and O measured by NMR [
33]. The degree of covalency of the planar Cu-O bond, i.e., the hole distribution between Cu and O that is set by material chemistry and is related to the charge transfer gap, was shown to set the maximum
and superfluid density [
33,
34]. In
Figure 8c, the La
Sr
CuO
family, having the lowest O hole content and the lowest maximum
, is limited to a very narrow window of
–
% such that doping and increasing temperature only affect an increase in
. The Y-based materials with higher O hole content already in the parent material and higher
cover a wider range of
–
% while changes in
are dominating. Finally, the Hg, Tl and Bi-based materials that show the highest O hole contents and correspondingly highest
span the entire range of observed
as a function of doping and temperature, where, interestingly, the range of observed
decreases with an increase of adjacent CuO
layers. We note that these materials, particularly the single-layer materials (Hg1201, Tl2201), show the greatest spread,
–
%, and, for high temperatures, they fall on the isotropic shift line (
). The double-layer materials of Tl1212 span a slightly smaller range,
–
%, and, for high temperatures, they fall on the nearly isotropic shift line (
) together with double-layer YBa
2Cu
3O
6+y. The triple (Hg1223, Tl2223) and quintuple (Hg1245) layer materials are limited to
–
%,
Figure 8d.
Therefore, while we do not find an obvious relation of the shift phenomenology to , materials with increased O hole content (at the expense of that at Cu) do show much larger isotropic shifts at high temperatures.