Ultrafast Transport Transient in n-Doped ZnS in Wurtzite and Zincblende Phases

Abstract

In this paper, we analyzed the ultrafast transient transport in n-doped ZnS in wurtzite and zincblende phases, driven far away from equilibrium by an electric field. Through the numerical solution of associate quantum transport equations based on the Non-Equilibrium Statistical Operator Method, the time evolution of the electron drift velocity and the non-equilibrium temperature of electrons and phonons were obtained, analyzing the dependence on the electric field strength.

1. Introduction

Zinc sulfide (ZnS) is a wide band-gap semiconductor, which crystallizes in zincblende (ZB) or wurtzite (WZ) phases. In recent decades, we have witnessed a large expansion in the study of the wide-gap and strongly-polar semiconductors. This is a consequence of the realization of the long-awaited possibility of growing satisfactory samples, leading to the increased development of electronic and opto-electronic devices of large technological and industrial interest (blue diodes, blue lasers, etc.) [1,2,3,4,5,6]. The zinc sulfide semiconductor has been investigated in a host of new materials as an application of thin-film technology [7,8,9]. Thin-film electroluminescent devices have become of great interest, since they offer a possible means of achieving a high-resolution, light-weight, compact video display panel for computer terminals or flat-panel displays. Electroluminescent devices offer significant advantages over other existing technologies such as cathode ray tubes, plasma, and liquid-crystal displays [10,11].

As a general rule, the transport properties in zinc sulfide semiconductor have been calculated using Monte Carlo simulations [12,13] and Boltzmann transport equations [14]. Seeking a better understanding of the carrier transport in ZnS(WZ) and in ZnS(ZB), a theoretical study of the electron drift velocity was performed in this work. For this, we used a kinetic theory for far-from equilibrium systems: the “Non-Equilibrium Statistical Operator Method” [15], which provides an elegant, practical, and physically clear picture of irreversible processes [16,17]; for example, in far-from equilibrium semiconductors [18,19,20,21,22], which is the case considered here. This method was used in numerous works for studying transport processes and kinetic phenomena (e.g., [23,24,25]).

Through the numerical solution of associate quantum transport equations based on the Non-Equilibrium Statistical Operator Method, the time evolution of the electron drift velocity, and the non-equilibrium temperature of electrons and phonons (optical and acoustic) were obtained in n-doped zinc sulfide, in wurtzite and zincblende phases, analyzing the dependence on the electric field strength.

2. Transport Equations

In this paper, we consider the case of the n-doped semiconductor ZnS in contact with a reservoir at temperature $T_0$ with a constant applied electric field $\mathcal{E}$. The electric field drives the system out of equilibrium, and the time-dependent macroscopic state is described in terms of a statistical thermodynamics for irreversible systems based on the Non-Equilibrium Statistical Operator Method [15,16,17].

In the present case, the non-equilibrium thermodynamic state of the system is characterized by the macrovariables: carriers’ linear momentum along the direction of the electric field $\mathcal{E}$: $\mathbf{P}\left(t\right)$; carriers’ energy, $E_e\left(t\right)$; the energy of the longitudinal optical phonons, $E_{lo}\left(t\right)$; and the energy of the acoustic phonons, $E_{ac}\left(t\right)$. The transversal optical phonons have been ignored because the deformation potential interaction with electrons in the conduction band is negligible [26].

On the other hand, the basic intensive non-equilibrium variables are the electron drift velocity, $\mathbf{v}\left(t\right)$; the non-equilibrium temperature (or quasitemperature) of electrons, $T_e^{*}\left(t\right)$; the non-equilibrium temperature of longitudinal optical phonons, $T_{lo}^{*}\left(t\right)$; and the non-equilibrium temperature of acoustic phonons, $T_{ac}^{*}\left(t\right)$.

We emphasize that the basic intensive non-equilibrium variables $\{\mathbf{v}\left(t\right),T_e^{*}\left(t\right),T_{lo}^{*}\left(t\right),T_{ac}^{*}\left(t\right)\}$ are associated, respectively, to the macrovariables: $\{\mathbf{P},E_e\left(t\right),E_{lo}\left(t\right),E_{ac}\left(t\right)\}$ [27].

We shall restrict the situation to the conditions of weak-to-moderate electric field intensities so that the parabolic band approximation is acceptable; i.e., we take ${ϵ}_{\mathbf{k}}={\hslash }^2\mathbf{k}·m^{*}\mathbf{k}/2$. However, nonparabolicity and side valleys in a conduction band is significant in high-field transport processes (e.g., [28]).

The equations of evolution for these basic macrovariables are derived in the nonlinear quantum kinetic theory described in [27]. They are

$$\frac{d{E}_e\left(t\right)}{dt}=-\frac{e\mathcal{E}}{m^{*}}·\mathbf{P}\left(t\right)+J_{E,lo}^{\left(2\right)}\left(t\right),$$

(1)

$$\frac{d\mathbf{P}\left(t\right)}{dt}=-nVe\mathcal{E}+{\mathbf{J}}_{\mathbf{P}}^{\left(2\right)}\left(t\right),$$

(2)

$$\frac{d{E}_{lo}\left(t\right)}{dt}=J_{lo}^{\left(2\right)}\left(t\right)-J_{lo,an}^{\left(2\right)}\left(t\right),$$

(3)

$$\frac{d{E}_{ac}\left(t\right)}{dt}=J_{ac}^{\left(2\right)}\left(t\right)+J_{lo,an}^{\left(2\right)}\left(t\right)-J_{ac,dif}^{\left(2\right)}\left(t\right).$$

(4)

In Equation (1), the first right-hand term accounts for the rate of energy transferred from the electric field to the carriers, and the second term accounts for the transfer of the excess energy of the carriers to the phonons. In Equation (2), the first right-hand term is the driving force generated by the presence of the electric field. The second term is the rate of momentum transfer due to interaction with the phonons and ionized impurities. In Equations (3) and (4), the first right-hand term describes the rate of change of the energy of the phonons due to interaction with the electrons. More precisely, they account for the gain, the energy transferred to them from the hot carriers, and then the sum of contributions $J_{lo}^{\left(2\right)}\left(t\right)$ and $J_{ac}^{\left(2\right)}\left(t\right)$ is equal to the last term in Equation (1), with change of sign. The second term in Equation (3) accounts for the rate of transfer of energy from the optical phonons to the acoustic phonons via anharmonic interaction. The contribution $J_{lo,an}^{\left(2\right)}\left(t\right)$ is the same but with different sign in Equations (3) and (4). Finally, the last term in Equation (4) is the diffusion of heat from the ac phonons to the reservoir. We notice that $dn/dt=0$ because the concentration n of electrons is fixed by doping. The detailed expressions for the collision operators are given in [27].

3. Results

The set of coupled differential Equations (1)–(4) were resolved numerically for $T_0=$ 300 K and $n={10}^{17}$ cm${}^{-3}$. The time evolution of the basic intensive non-equilibrium variables $\{T_e^{*}\left(t\right)$,$T_{lo}^{*}\left(t\right)$,$T_{ac}^{*}\left(t\right)$,$\mathbf{v}\left(t\right)\}$ were obtained for different values of the electric field strength. To perform the numerical calculations, for the particular case of n-doped ZnS(WZ) and ZnS(ZB), we have used the same parameters listed in Table I of [19].

Figure 1 shows the time evolution towards the steady state of the electron drift velocity in n-doped ZnS(WZ) (Figure 1a) and in ZnS(ZB) (Figure 1b) for four different values of the electric field strength with $T_0=$ 300 K and $n={10}^{17}$ cm${}^{-3}$. It can be noticed that the larger electron drift velocity corresponds to ZnS(WZ), which can be ascribed to the fact that the electrons have a smaller effective mass in ZnS(WZ) than in ZnS(ZB). It is verified that the steady state is attained after a transient time on the order of about 0.3 ps. The electron drift velocity is proportional to the relaxation time, which is composed of the contributions due to scattering by phonons and by impurities. It depends on the macrostate of the system; that is, on the non-equilibrium temperature (or quasitemperature) of electrons $T_e^{*}\left(t\right)$, the non-equilibrium temperature of longitudinal optical phonons $T_{lo}^{*}\left(t\right)$, the non-equilibrium temperature of acoustic phonons $T_{ac}^{*}\left(t\right)$, as well as the concentration of carriers n and the lattice temperature $T_0$.

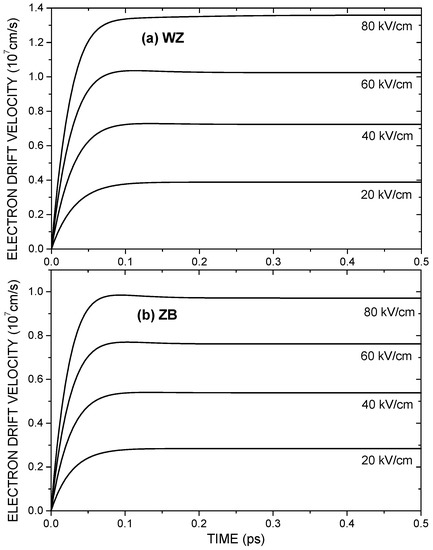
Figure 1. Evolution towards the steady state of the electron drift velocity in (a) ZnS(WZ) and (b) ZnS(ZB) for four values of the electric field strength, with $T_0=$ 300 K and $n={10}^{17}$ cm${}^{-3}$. WZ: wurtzite; ZB: zincblende.

The Figure 2 shows the time evolution towards the steady state of the non-equilibrium temperature of electrons $T_e^{*}\left(t\right)$ in n-doped ZnS(WZ) (Figure 2a) and in ZnS(ZB) (Figure 2b) for four different values of the electric field strength with $T_0=$ 300 K and $n={10}^{17}$ cm${}^{-3}$. It is verified that the steady state is attained after a transient time on the order of subpicoseconds and that the larger electron non-equilibrium temperature corresponds to ZnS(WZ), which has a smaller electron effective mass than ZnS(ZB).

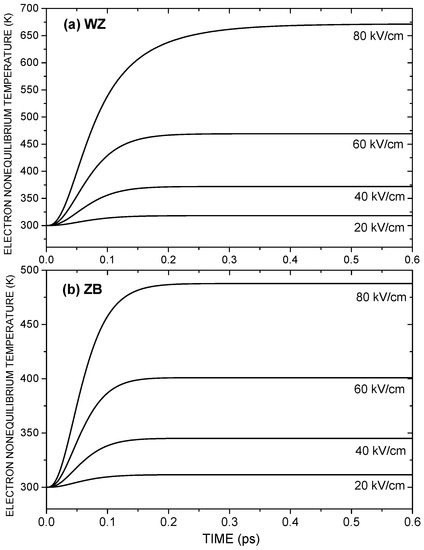
Figure 2. Evolution towards the steady state of the non-equilibrium temperature of electrons $T_e^{*}\left(t\right)$ in (a) ZnS(WZ) and (b) ZnS(ZB) for four values of the electric field strength, with $T_0=$ 300 K and $n={10}^{17}$ cm${}^{-3}$.

Figure 3 shows the time evolution towards the steady state of the non-equilibrium temperature of longitudinal optical phonons $T_{lo}^{*}\left(t\right)$ in n-doped ZnS(WZ) (Figure 3a) and in ZnS(ZB) (Figure 3b) for four different values of the electric field strength with $T_0=$ 300 K and $n={10}^{17}$ cm${}^{-3}$. The longitudinal optical phonons are little heated (less than 1.4%) compared to the lattice temperature $T_0=300$ K. Moreover, the non-equilibrium temperature of acoustic phonons (not shown here) keeps almost at room temperature ($T_{ac}^{*}\left(t\right)\simeq T_0$).

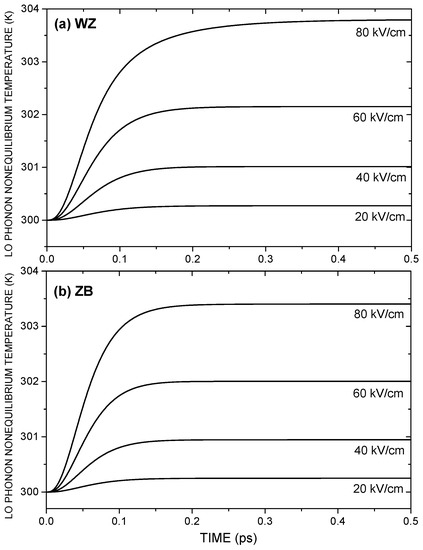
Figure 3. Evolution towards the steady state of the non-equilibrium temperature of longitudinal optical phonons $T_{lo}^{*}\left(t\right)$ in (a) ZnS(WZ) and (b) ZnS(ZB) for four values of the electric field strength, with $T_0=$300 K and $n={10}^{17}$ cm${}^{-3}$.

Figure 4 and Figure 5 show the “bird’s eye view” of the time evolution toward the steady state of the electron drift velocity and the non-equilibrium temperature of electrons. The results in Figure 1 and Figure 4 show a “slight overshoot” behavior in a higher electric field range. No overshoot occurs when the momentum relaxation time—which is smaller than the energy relaxation time shortly after application of the electric field — becomes predominantly larger than the other [29].

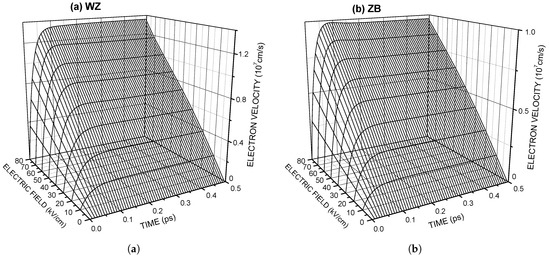
Figure 4. The “bird’s eye view” of the time evolution toward the steady state of the electron drift velocity in (a) ZnS(WZ) and (b) ZnS(ZB).

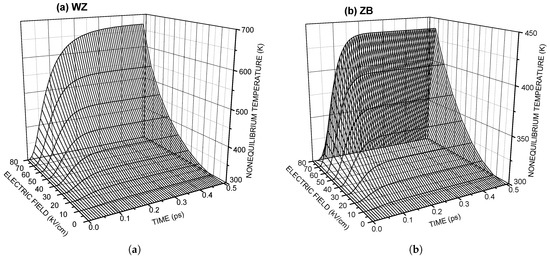
Figure 5. The “bird’s eye view” of the time evolution toward the steady state of the non-equilibrium temperature of electrons in (a) ZnS(WZ) and (b) ZnS(ZB).

4. Final Comments

The non-equilibrium electron and phonon temperatures and the electron drift velocity were calculated in the transient state for the n-doped zinc sulfide (in wurtzite and zincblende phases) in the presence of moderate-to-high electric fields. Of course, they depend on the non-equilibrium macroscopic state of the sample. The main result is that the larger electron drift velocity corresponds to ZnS(WZ), which can be ascribed to the fact that the electrons have a smaller effective mass in ZnS(WZ) than in ZnS(ZB). From the point of view of device applications, it is extremely important to compare the properties of the different phases of a particular material. For instance, one phase can be more suitable than another in some applications, making it more attractive for certain device applications.