de Gennes–Suzuki–Kubo Quantum Ising Mean-Field Dynamics: Applications to Quantum Hysteresis, Heat Engines, and Annealing

Abstract

We briefly review the early development of the mean-field dynamics for cooperatively interacting quantum many-body systems, mapped to pseudo-spin (Ising-like) systems. We start with (Anderson, 1958) pseudo-spin mapping the BCS (1957) Hamiltonian of superconductivity, reducing it to a mean-field Hamiltonian of the XY (or effectively Ising) model in a transverse field. Then, we obtain the mean-field estimate for the equilibrium gap in the ground-state energy at different temperatures (gap disappearing at the transition temperature), which fits Landau’s (1949) phenomenological theory of superfluidity. We then present in detail a general dynamical extension (for non-equilibrium cases) of the mean-field theory of quantum Ising systems (in a transverse field), following de Gennes’ (1963) decomposition of the mean field into the orthogonal classical cooperative (longitudinal) component and the quantum (transverse) component, with each of the component following Suzuki–Kubo (1968) mean-field dynamics. Next, we discuss its applications to quantum hysteresis in Ising magnets (in the presence of an oscillating transverse field), to quantum heat engines (employing the transverse Ising model as a working fluid), and to the quantum annealing of the Sherrington–Kirkpatrick (1975) spin glass by tuning down (to zero) the transverse field, which provides us with a very fast computational algorithm, leading to ground-state energy values converging to the best-known analytic estimate for the model. Finally, we summarize the main results obtained and draw conclusions about the effectiveness of the de Gennes–Suzuki–Kubo mean-field equations for the study of various dynamical aspects of quantum condensed matter systems.

1. Introduction

The first significant theory of cooperatively interacting many-body quantum condensed matter systems is the Bardeen–Cooper–Schrieffer (BCS) theory [1] of superconductivity, proposed in 1957. The theory had been spectacularly successful in explaining several experimentally observed outstanding features of the superconducting phase of condensed matter (without any external magnetic field). The following year, in an intriguing publication [2], Anderson showed that the BCS theory is, in effect, a mean field theory of the Cooper pair (cooperatively) interacting electrons (mapped to XY spins) in the presence of a quantum (transverse) field of strength given by the free electron energy (effectively to the mean-field theory of Ising systems in transverse fields). The strength of the mean field on each of the pseudo spins (corresponding to the wave vectors of the electrons near the Fermi surface) would be given by the square root of the sum of the squares of the free electron energy and the sum of the square of the Cooper pair energies (gap parameter). This would lead to the self-consistent gap equation of the BCS. Assuming that the gap vanishes at the transition temperature, one can find the celebrated BCS relation between the gap magnitude at zero temperature and the superconducting transition temperature (see Section 2).

Though the BCS theory is a mean-field one for a quantum cooperative system (effectively a mean-field theory of XY or Ising systems in transverse fields), the transition (at $T_c$, from a superconducting phase to a normal phase) is not a quantum transition; it is driven by (classical) thermal fluctuations. Furthermore, it does not consider any dynamic aspect of the transition; rather, it is an equilibrium transition. Soon after, a mean-field theory of quantum transitions (driven by quantum fluctuations) for many-body condensed matter systems (e.g., in the context of ferro-para electric transitions in Potassium Dihydrogen Phosphate or KDP) was developed. Model systems of such transitions (driven by quantum tunneling of hydrogen ions or protons in oxygen double-wells at each site) were developed by de Gennes and others (see, e.g., [3,4]). Here, the ‘softening’ of long-wavelength or low-frequency collective modes of protons would give rise to dipole moments, inducing dipole–dipole interaction and ferroelectricity in KDP. They calculated (see also [5]) the collective tunneling frequency in such simplified models that could induce softening of those collective modes (driven by the tunneling field at different temperatures, including zero temperature for purely quantum ones) in such cooperative order–disorder transition systems. This then generally led to the study of the static behavior of quantum phase transitions in many-body systems employing the transverse field Ising models (see, e.g., [6,7,8,9]). The mean-field study of the transitions in these transverse-field Ising models had wider applications in tunneling-mode softening studies of quantum ANNNI models, used to study various modulated phases in materials with regularly competing interactions (see, e.g., [10] for the earliest study). First reports on similar studies in transverse Ising models were made in [11] for random transverse-field case and in [12] for a spatially modulated longitudinal-field case. The earliest study of the static transition properties of Mattis and Edwards–Anderson Ising spin glass in transverse fields was reported in [13].

Soon, dynamical behavior of transverse field Ising systems under externally driven fields received the attention and dynamic hysteresis in pure ising magnets, employing the Suzuki–Kubo mean field dynamics [14], in both classical (see, e.g., [15]) and quantum [16] Ising systems (where the longitudinal field and the tunneling or transverse field varied periodically with time in the respective cases). Afterwards, this mean field quantum dynamics for heat engines with pure Ising system as working fluid (with both longitudinal and transverse fields varying cyclically as the bath temperature changes from that of the heat source to that of the sink) was studied [17] to show that quantum heat engine efficiencies can approach the Carnot value while the corresponding classical engine can not. Recently, this de Gennes–Suzuki–Kubo mean-field Ising dynamics has been applied to the celebrated problem of quantum annealing [18,19,20,21,22] to estimate the ground state energy of the randomly frustrated spin glass model of the Sherrington–Kirkpatrick (SK) variety [23,24] where the best analytic estimate (up to tenth decimal place exists [25]) and the numerical study of the quantum annealing gives [26] very fast convergence (with comparable scaling results on the fluctuations) as seen also [27] for the classical annealing (just with Suzuki–Kubo dynamics).

We intend to develop here the most general form of de Gennes–Suzuki–Kubo quantum Ising mean field dynamical equations in Section 3.1 and then study them numerically for the special cases of dynamic hysteresis in quantum Ising systems (in Section 3.2), for the increased efficiencies of the quantum Ising heat engines (in Section 3.3) and for the quantum annealing study the ground state energy for the SK model (in Section 3.4). Finally, we will summarize (in Section 4) the main results discussed here in different cases and highlight the elegance and prospect of the de Gennes–Suzuki–Kubo quantum Ising mean-field dynamical equation to study various many-body dynamic behaviors of quantum condensed matter systems.

2. Anderson’s Pseudo-Spin Mapping of BCS Hamitonian & Mean Field Theory of BCS Superconductivity

2.1. Landau’s Phenomenological Theory of Superfluidity and Superconductivity

Helium-4 ($H{e}^4$) when cooled below $4.2$ K, becomes liquid. If liquid $H{e}^4$ was placed in a container, with the liquid filled almost to the edge, then there would be constant dripping of $H{e}^4$ from the container. This indicates the disappearance of friction or viscosity of $H{e}^4$ (in the surface layers). There were attempts to explain this from Bose–Einstein condensation. However, this was not a system of free particles, but an interacting system. Therefore, it is not a Bose gas, but a Bose liquid. Hence, the superfluidity cannot be explained through Bose–Einstein condensation. Landau suggested the following scenario (see, e.g., [28,29]).

For free particles, the dispersion relation reads ${ϵ}_k\sim k^2$. However, such a free particle dispersion cannot show superfluidity. Landau assumed that for interacting Boson systems the dissipation relation may become ${ϵ}_k\sim ck$ (for electron systems ${ϵ}_k\sim \Delta +c{k}^2$ is possible, see Figure 1) and that might lead to frictionless flow. He considered the superfluid system consisting of the (quantum) fluid placed in contact with a (classical) massive wall or surface. If some friction is encountered in the flow, then energy of the fluid and, hence, the momentum has to change. This change in momentum is to be taken up by the classical mass in contact with the liquid.

If it can be shown that this heavy mass cannot accept every excitation satisfying the energy and momentum conservations, then the fluid has no other choice but to flow without friction.

If v and $v^{\prime }$ denote velocities of the classical mass before and after energy exchange, then from energy conservation

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}M{v}^{\prime 2}={\displaystyle \frac{1}{2}}M{v}^2+{ϵ}_k,\end{array}$$

(1)

and for momentum conservation

$$\begin{array}{c}\hfill M{v}^{\prime }=Mv+\hslash k.\end{array}$$

Squaring and dividing the above equation by $2M$ we get

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2M}}{M}^2{v}^{\prime 2}={\displaystyle \frac{1}{2}}M{v}^2+{\displaystyle \frac{1}{2M}}{\hslash }^2{k}^2+\hslash vk.\end{array}$$

Subtracting this from Equation (1), we get

$$\begin{array}{c}\hfill {ϵ}_k={\displaystyle \frac{1}{2M}}{\hslash }^2{k}^2+\hslash vk.\end{array}$$

Since M is very large, the above energy-momentum conservation is satisfied for

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{{ϵ}_k}{k}}\right|}_{min}=\hslash v.\end{array}$$

(2)

If ${ϵ}_k=c{k}^2$, then the above condition is satisfied for all non-vanishing velocities, indicating the possibility of exchange of energy and momentum. Hence no super-fluidity. However, if ${ϵ}_k=ck$ (as in the cases of phonon and roton excitations) then only for $v>c$, the condition is satisfied. For lower values of v, one gets flow without resistance or superfluidity. The other case of interest is ${ϵ}_k=\Delta +k^2$ where one also gets superfluidity for $\Delta \ne 0$ and this can occur for the BCS theory of superconductivity discussed next.

2.2. Mean Field Theory of BCS Superconductivity

The resistivity in some materials practically vanishes when the temperature is reduced below a critical value. These materials then also become completely diamagnetic. This is called superconductivity. Superconductivity can not be a property of free electrons. In a lattice, electrons are of course not free. Apart from the Coulomb repulsion among them they face a fluctuating periodic potential (electron–phonon scattering). It is observed that replacement of atoms by their isotopes induce changes in the superconductivity onset temperature. This is called the isotope effect, which often relates the critical temperature ($T_c$) with the mass (M) of the atoms by a relation like $M^{1/2}{T}_c=constant$. When we change the atomic mass, we basically do nothing to the electron but only change the phonon modes. This led to the belief that superconductivity is due to electron–electron interactions, mediated by phonons. Cooper showed that the maximum value of the effective interaction between the electron pairs can become attractive when the electron pairs are near the Fermi surface and they have opposite spin states and momentum vectors. The BCS Hamiltonian can be written, with k, $k^{\prime }$ denoting the momenta of electrons and $\tilde{k}$ for phonons and $C^{†}$, C denoting, respectively, the electron creation and destruction operators, as (see for, e.g., [2,30])

$$\begin{array}{c}\hfill H={\displaystyle \sum _k}{ϵ}_k^0{C}_k^{†}{C}_k+{\displaystyle \sum _{k,k^{\prime },\tilde{k}}}{V}_{k{k}^{\prime }\tilde{k}}{C}_{k+\tilde{k}}^{†}{C}_{k^{\prime }-\tilde{k}}^{†}{C}_k{C}_{k^{\prime }}.\end{array}$$

(3)

We assume here $V_{k{k}^{\prime }\tilde{k}}\equiv -V$, the maximum value of the effective attractive interaction when k and $k^{\prime }(=-k)$ pairs (with opposite spin states) are formed and k’s are near Fermi vector. Then the Hamiltonian can be written as

$$\begin{array}{c}\hfill H={\displaystyle \sum _k}{ϵ}_k^0{C}_k^{†}{C}_k-V{\displaystyle \sum _{k{k}^{\prime }}}{C}_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}{C}_k{C}_{-k}.\end{array}$$

(4)

Because of pairing of electrons, we have ($k,-k$) and ($k^{\prime },-k^{\prime }$) pairs, both having the same energy ${ϵ}_k^0$. Hence, the Hamiltonian takes the form

$$\begin{array}{c}\hfill H={\displaystyle \sum _k}{ϵ}_k^0\left(C_k^{†}{C}_k+C_{-k}^{†}{C}_{-k}\right)-V{\displaystyle \sum _{k{k}^{\prime }}}{C}_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}{C}_k{C}_{-k}.\end{array}$$

We choose ${\displaystyle \sum _k}{ϵ}_k^0=0$. Therefore,

$$H=-{\displaystyle \sum _k}{ϵ}_k^0\left(1-C_k^{†}{C}_k-C_{-k}^{†}{C}_{-k}\right)-V{\displaystyle \sum _{k{k}^{\prime }}}{C}_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}{C}_k{C}_{-k}.$$

The last term is still not in a diagonal form. We intend to map this Hamiltonian (in the lowest energy states) to a pseudo spin Hamiltonian.

Let us consider only the low lying states of this Hamiltonian, namely the electron pair occupied ($\left|-\rangle \right.$) and pair unoccupied ($\left|+\rangle \right.$):

$$\begin{array}{c}\hfill \left|+\rangle \right.\equiv \left|0_k,0_{-k}\rangle \right.\left|-\rangle \right.\equiv \left|1_k,1_{-k}\rangle \right.\end{array}$$

Hence,

$$\begin{array}{c}\hfill \left(1-C_k^{†}{C}_k-C_{-k}^{†}{C}_{-k}\right)\left|+\rangle \right.=\left|+\rangle \right.\\ \hfill \left(1-C_k^{†}{C}_k-C_{-k}^{†}{C}_{-k}\right)\left|-\rangle \right.=-\left|-\rangle \right..\end{array}$$

We, therefore, make the correspondence $(1-C_k^{†}{C}_k-C_{-k}^{†}{C}_{-k})\equiv {\sigma }_k^z$.

Since $C_k^{†}{C}_{-k}^{†}\left|+\rangle \right.=\left|-\rangle \right.$,$C_k^{†}{C}_{-k}^{†}\left|-\rangle \right.=0$, $C_{-k}{C}_k\left|-\rangle \right.=\left|+\rangle \right.$ and $C_{-k}{C}_k\left|+\rangle \right.=0$, we immediately identify its correspondence with raising and lowering operators ${\sigma }^{+}/{\sigma }^{-}$:

$${\sigma }^{\pm }={\sigma }^x\pm i{\sigma }^y=\left(\begin{array}{cc}0& 0\\ 2& 0\end{array}\right)or\left(\begin{array}{cc}0& 2\\ 0& 0\end{array}\right),$$

and therefore

$$\begin{array}{c}\hfill C_k^{†}{C}_{-k}^{†}={\displaystyle \frac{1}{2}}{\sigma }_k^{-},C_{-k}{C}_k={\displaystyle \frac{1}{2}}{\sigma }_k^{+}.\end{array}$$

(5)

In terms of these spin operators we finally arrive at

$$\begin{array}{c}\hfill H=-{\displaystyle \sum _k}{ϵ}_k^0{\sigma }_k^z-{\displaystyle \frac{V}{4}}{\displaystyle {\displaystyle \sum _{k{k}^{\prime }}}}\left({\sigma }_k^x{\sigma }_{k^{\prime }}^x+{\sigma }_k^y{\sigma }_{k^{\prime }}^y\right)\end{array}$$

(6)

or,

$$\begin{array}{c}\hfill H=-{\displaystyle \sum _k}{\overrightarrow{h}}_k·{\overrightarrow{\sigma }}_k,\end{array}$$

(7)

where the effective field ${\overrightarrow{h}}_k$ components are

$$\begin{array}{c}\hfill h_k^x={\displaystyle \frac{V}{4}}{\displaystyle \sum _{k^{\prime }}}\langle {\sigma }_{k^{\prime }}^x\rangle ;h_k^y={\displaystyle \frac{V}{4}}{\displaystyle \sum _{k^{\prime }}}\langle {\sigma }_{k^{\prime }}^y\rangle ;h_k^z={ϵ}_k^0.\end{array}$$

(8)

As the $\langle {\sigma }_x\rangle$ and $\langle {\sigma }_y\rangle$ are symmetric we consider only one component (with proper counting) and hence $\left|{\overrightarrow{h}}_k\right|=\sqrt{{{ϵ}_k^0}^2+{\displaystyle \frac{V^2}{4}}{\left({\displaystyle \sum _{k^{\prime }}}\langle {\sigma }_{k^{\prime }}^x\rangle \right)}^2}$. The pseudo spin $\overrightarrow{{\sigma }_k}$ will therefore be in the direction of the field $\overrightarrow{h_k}$ and its magnitude will depend on the temperature.

• At $T=0$:

Here the spin magnitude will be its maximum and hence

$$\begin{array}{c}\hfill \langle {\overrightarrow{\sigma }}_k\rangle ={\displaystyle \frac{{\overrightarrow{h}}_k}{\left|{\overrightarrow{h}}_k\right|}}\end{array}$$

(9)

Let

$$\begin{array}{c}\hfill \langle {\sigma }_k^x\rangle =sin{\theta }_k={\displaystyle \frac{\langle h_k^x\rangle }{\left|{\overrightarrow{h}}_k\right|}}and\langle {\sigma }_k^z\rangle =cos{\theta }_k={\displaystyle \frac{\langle h_k^z\rangle }{\left|{\overrightarrow{h}}_k\right|}},\end{array}$$

Hence

$$\begin{array}{c}\hfill \langle {\sigma }_k^x\rangle ={\displaystyle \frac{{\displaystyle \sum _{k^{\prime }}}\frac{V}{2}\langle {\sigma }_{k^{\prime }}^x\rangle }{\sqrt{{{ϵ}_k^0}^2+\frac{V^2}{4}{\left({\displaystyle \sum _{k^{\prime }}}\langle {\sigma }_{k^{\prime }}^x\rangle \right)}^2}}}and\langle {\sigma }_k^z\rangle ={\displaystyle \frac{{ϵ}_k^0}{\sqrt{{{ϵ}_k^0}^2+\frac{V^2}{4}{\left({\displaystyle \sum _{k^{\prime }}}\langle {\sigma }_{k^{\prime }}^x\rangle \right)}^2}}}\end{array}$$

If we define

$$\begin{array}{c}\hfill \Delta ={\displaystyle \frac{V}{2}}{\displaystyle \sum _{k^{\prime }}}\langle {\sigma }_{k^{\prime }}^x\rangle ,\end{array}$$

(10)

then we can write

$$\begin{array}{c}\hfill \langle {\sigma }_k^x\rangle =sin{\theta }_k={\displaystyle \frac{\Delta }{\sqrt{{{ϵ}_k^0}^2+{\Delta }^2}}}and\langle {\sigma }_k^z\rangle =cos{\theta }_k={\displaystyle \frac{{ϵ}_k^0}{\sqrt{{{ϵ}_k^0}^2+{\Delta }^2}}}\end{array}$$

(11)

Putting Equation (11) on Equation (10) we get the self consistent equation for $\Delta$:

$$\begin{array}{c}\hfill \Delta ={\displaystyle \frac{V}{2}}{\displaystyle \sum _{k^{\prime }}}{\displaystyle \frac{\Delta }{\sqrt{{{ϵ}_{k^{\prime }}^0}^2+{\Delta }^2}}}.\end{array}$$

(12)

We can express this gap in Equation (12) as an integral in the following form

$$\begin{array}{c}\hfill \Delta ={\displaystyle \frac{V}{2}}\int {\displaystyle \frac{\rho \left({ϵ}_F\right)\Delta dϵ}{\sqrt{{ϵ}^2+{\Delta }^2}}},\end{array}$$

where $\rho \left({ϵ}_F\right)$ is the density of states at the Fermi level. Therefore, the so called gap equation takes the form

$$\begin{array}{c}\hfill {\displaystyle \frac{V}{2}}\int {\displaystyle \frac{\rho \left({ϵ}_F\right)dϵ}{\sqrt{{ϵ}^2+{\Delta }^2}}}=1.\end{array}$$

(13)

The ground state of the Hamiltonian (7) occurs when ${\overrightarrow{\sigma }}_k$ is aligned in the direction of ${\overrightarrow{h}}_k$. The excited state will be when the alignment of ${\overrightarrow{\sigma }}_k$ is opposite to ${\overrightarrow{h}}_k$. Hence the change in energy is $2\left|{\overrightarrow{h}}_k\right|$. Therefore,

$${ϵ}_k=2\left|{\overrightarrow{h}}_k\right|=2\sqrt{{{ϵ}_k^0}^2+{\Delta }^2}.$$

(14)

When $k\to 0$, ${ϵ}_k^0\sim k^2\to 0$, but ${ϵ}_k\ne 0$. Hence $\Delta$ represents the zero temperature energy gap, independent of k. As discussed in the previous section, the non-vanishing value of this gap $\Delta$ ensures a “superfluid” like flow of the (charged) electrons and hence superconductivity.

• At $T\ne 0$:

Here, unlike in (9), the average spin magnitude will be given by $tanh\left({\displaystyle \frac{\left|{\overrightarrow{h}}_k\right|}{k_{B}T}}\right)$. Hence

$$\begin{array}{c}\hfill \langle {\overrightarrow{\sigma }}_k\rangle ={\displaystyle \frac{{\overrightarrow{h}}_k}{\left|{\overrightarrow{h}}_k\right|}}tanh\left(\left|{\overrightarrow{h}}_k\right|/k_{B}T\right),\left|{\overrightarrow{h}}_k\right|=\sqrt{{{ϵ}_k^0}^2+{\Delta }^2},\end{array}$$

and consequently the generalization of Equation (12) would be

$$\begin{array}{c}\hfill \Delta ={\displaystyle \frac{V}{2}}{\displaystyle \sum _{k^{\prime }}}tanh\left({\displaystyle \frac{\left|{\overrightarrow{h}}_{k^{\prime }}\right|}{k_{B}T}}\right)sin{\theta }_{k^{\prime }};sin{\theta }_k={\displaystyle \frac{\Delta }{\left|{\overrightarrow{h}}_k\right|}}.\end{array}$$

(15)

The gap $\Delta$ is now a function of temperature T and if we define the critical temperature $T_c$ as the temperature where the gap $\Delta$ vanishes (see previous section); then,

$$\begin{array}{c}\hfill {\displaystyle \frac{V}{2}}{\displaystyle \sum _{k^{\prime }}}{\displaystyle \frac{1}{{ϵ}_{k^{\prime }}^0}}tanh{\displaystyle \frac{{ϵ}_{k^{\prime }}^0}{k_B{T}_c}}=1.\end{array}$$

(16)

Numerically solving Equations (15) and (16), we get

$$\begin{array}{c}\hfill 2\Delta \left(T=0\right)=3.5T_c.\end{array}$$

(17)

For most conductors (like Sn, Al, Pt), this relation is seen to be fairly accurate.

3. de Gennes–Suzuki–Kubo Quantum Ising Mean-Field Dynamical Equation

In the previous section, we have seen that the BCS theory could be seen as a mean field theory of a quantum XY system (described by Hamiltonian (6)), which in effect (because of the assumed symmetries, following Equation (8), for the thermal averages $\langle {\sigma }^x\rangle$ and $\langle {\sigma }^y\rangle$), becomes in effect a mean field theory of an Ising model in transverse field. Furthermore, in the BCS theory, we did not consider any dynamics of that quantum Ising model.

In this section, we therefore give a general dynamical mean field theory of Ising systems in transverse field (given in the next Section 3.1) and then discuss special cases of mean field theories for quantum Ising hysteresis in Section 3.2, quantum Ising heat engine in Section 3.3, and quantum annealing of the Sherrington–Kirkpatrick Ising spin glass model in Section 3.4.

3.1. Mean Field Dynamical Equation for a General Quantum Ising System

The Hamiltonian of a general Ising system in the presence of time (t) dependent transverse ($\mathsf{\Gamma }\left(t\right)$) and longitudinal magnetic field ($h\left(t\right)$) reads as

$$H\left(t\right)=-{\displaystyle \sum _{i,j}}{J}_{ij}{\sigma }_i^z{\sigma }_j^z-h\left(t\right){\displaystyle \sum _i}{\sigma }_i^z-\mathsf{\Gamma }\left(t\right){\displaystyle \sum _i}{\sigma }_i^x,$$

(18)

where $\overrightarrow{\sigma }$ denotes the Pauli spin vector, $h\left(t\right)$ and $\mathsf{\Gamma }\left(t\right)$ are the time dependent external longitudinal and transverse field, respectively. $J_{ij}$ denotes the strength of the interaction that can generally be random with specific distributions $P\left(J_{ij}\right)$ between the spins at i-th and j-th sites.

It should be noted that due to the transverse field (the noncommuting component of the cooperative part of the Hamiltonian Equation (18), the quantum dynamics of the spins ${\sigma }^z$ arises from the Heisenberg equation of motion. However, one can still expect a simplified version of the dynamical evolution in the mean-field approximation (following refs. [3,4,9,14,15,16]).

The mean-field Hamiltonian can be written as

$$H\left(t\right)=-{\displaystyle \sum _i}{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)·\overrightarrow{m_i}\left(t\right).$$

(19)

Here, the effective mean-field ${\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)$ on any spin ${\overrightarrow{m}}_i$ has two parts, the first part ${{\overrightarrow{h}}_i}^{z\mathrm{eff}}\left(t\right)$ comes from the standard cooperative interaction (Curie–Weiss type) among the spins and the second part ${h_i}^{x\mathrm{eff}}\left(t\right)$ is the transverse field.

$${\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)=h_i^{z\mathrm{eff}}\left(t\right)\widehat{z}+{h_i}^{x\mathrm{eff}}\left(t\right)\widehat{x}$$

(20)

where

$$\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)\right|={\left[{\left({\displaystyle \sum _j}{J}_{ij}{m}_j^z\left(t\right)+h\left(t\right)\right)}^2+{\mathsf{\Gamma }}^2\left(t\right)\right]}^{1/2}$$

(21)

with

$$h_i^{z\mathrm{eff}}\left(t\right)={\displaystyle \sum _j}{J}_{ij}{m}_j^z\left(t\right)+h\left(t\right)$$

(22)

and

$$h_i^{x\mathrm{eff}}\left(t\right)=\mathsf{\Gamma }\left(t\right).$$

(23)

Here, ${\overrightarrow{m}}_i\equiv \langle {\overrightarrow{\sigma }}_i\rangle$, where $<·>$ denotes the thermal average.

The generalized mean-field dynamics of the Ising spins in the presence of both longitudinal and transverse field, extending the classical Suzuki–Kubo formalism [14] can be represented (cf. [26,27]) by the following differential equation:

$${\displaystyle \frac{d{\overrightarrow{m}}_i}{dt}}=-{\overrightarrow{m}}_i+tanh\left({\displaystyle \frac{|{\overrightarrow{h}}_i^{\mathrm{eff}}|}{T}}\right){\displaystyle \frac{{\overrightarrow{h}}_i^{\mathrm{eff}}}{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\right|}}.$$

(24)

The above vector differential equation is basically first order nonlinear coupled differential equations for ${\overrightarrow{m}}_i=\langle {\overrightarrow{\sigma }}_i\rangle$. They can be explicitly rewritten as

$${\displaystyle \frac{d{m}_i^x}{dt}}=-m_i^x+tanh\left({\displaystyle \frac{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\right|}{T}}\right)·{\displaystyle \frac{\mathsf{\Gamma }}{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\right|}}$$

(25)

and

$${\displaystyle \frac{d{m}_i^z}{dt}}=-m_i^z+tanh\left({\displaystyle \frac{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\right|}{T}}\right)·{\displaystyle \frac{h_i^{z\mathrm{eff}}}{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\right|}}.$$

(26)

For discrete time (t), the above equation can be simplified to

$$m_i^x(t+1)=tanh\left({\displaystyle \frac{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)\right|}{T\left(t\right)}}\right)·{\displaystyle \frac{\mathsf{\Gamma }\left(t\right)}{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)\right|}}$$

(27)

and

$$m_i^z(t+1)=tanh\left({\displaystyle \frac{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)\right|}{T\left(t\right)}}\right)·{\displaystyle \frac{h_i^{z\mathrm{eff}}\left(t\right)}{\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)\right|}},$$

(28)

where $\left|{\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)\right|$, $h_i^{z\mathrm{eff}}\left(t\right)$ are given by Equations (21) and (22) with the corresponding variables at time t.

3.2. Quantum Ising Hysteresis and Dynamic Transition

We have studied [16] the hysteresis and dynamic phase transition in transverse Ising ferromagnet by solving the mean field dynamical Equation (for $h=0$ Equation (24)). In this case the transverse field is sinusoidally oscillating in time $\mathsf{\Gamma }\left(t\right)={\mathsf{\Gamma }}_a\cos \left(\omega t\right)$, where $\omega =2\pi f$ and f denotes the frequency of oscillation. The time dependence of $m^x\left(t\right)$ has been found to show a phase difference with that of $\mathsf{\Gamma }\left(t\right)$. This phase difference has given rise to the hysteretic response. The hysteresis loop area $A^x=\oint m^x\left(t\right)d\mathsf{\Gamma }$ has been studied as function of the frequency ($\omega$) and amplitude (${\mathsf{\Gamma }}_a$) of the oscillating transverse magnetic field and the temperature (T) of the system. Here, for evaluating $A^x$ (and also for evaluating the dynamic order parameter Q), integration over a complete cycle corresponds to the time period given by $f^{-1}$. A scaling form $A^x\sim {\mathsf{\Gamma }}_a^{\alpha }{T}^{-\beta }g\left({\displaystyle \frac{\omega }{{\mathsf{\Gamma }}_a^{\gamma }{T}^{\delta }}}\right)$ has been found through data collapse (Figure 2). The estimated (best fit) values of the exponents are $\alpha =1.75\pm 0.05$, $\beta =0.50\pm 0.02$, $\gamma =0.00\pm 0.02$ and $\delta =0.00\pm 0.02$. The scaling function $g\left(x\right)\sim {\displaystyle \frac{x}{1+{\left(cx\right)}^2}}$.

The hysteretic response is found to be associated with another dynamical response, the dynamical phase transition. The time average magnetization (longitudinal component $m^z$) over the full cycle of the oscillating magnetic field, i.e., $Q={\displaystyle \frac{\omega }{2\pi }}\oint m^z\left(t\right)dt$, transits to a nonzero value for specific set of values of the temperature (T) and the amplitude (${\mathsf{\Gamma }}_a$) of the oscillating transverse magnetic field. A comprehensive phase boundary has been drawn and shown in Figure 3. The approximate analytic form of the phase boundary has also been proposed to be as $T={\displaystyle \frac{\pi {\mathsf{\Gamma }}_a/2}{\sinh (\pi {\mathsf{\Gamma }}_a/2)}}$. This analytic form of the dynamical phase boundary matches well with that obtained numerically.

3.3. Quantum Ising Heat Engine

Following some of the original studies and results for increased efficiencies in quantum heat engines, where the working fluid of the engine is a quantum many-body system (see, e.g., [31,32]), and some of the extensive reviews (see, e.g., [33,34]) on quantum heat engines with standard quantum condensed matter working fluid, and the paper [35] considering a transverse field Ising chain as the working fluid in a Otto engine, a mean field quantum Ising system was employed as working fluid in [17]. Following [17], the mean field Equation (24) has been employed here to compare the efficiencies of a four-stroke-cycle classical (when driven along the heat cycle by the longitudinal field on the Ising system) and quantum (when driven in time along the heat cycle by transverse field, in general in presence of time independent longitudinal field) heat engines, designed in the following form (see Figure 4):

(i)

Stroke-A → B: Field (transverse field $\mathsf{\Gamma }$, in quantum case) increases linearly with time from a low value, ${\mathsf{\Gamma }}_L$, to a high value, ${\mathsf{\Gamma }}_H$) at a constant high temperature $T_H$ of the heat bath. Heat is being absorbed by the engine during this stroke. This is an isothermal ($T_H$ constant) stroke. In this isothermal stroke, the system is allowed to absorb the heat from the reservoir. The internal energy of the system (working fluid of the quantum engine) increases in this stroke.

(ii)

Stroke-B → C: The system is being cooled (linearly from $T_H$ to $T_L$) with thermalization (with the cold bath or heat sink at temperature $T_L$) where the field remains fixed.

(iii)

Stroke-C → D: This is another isothermal (at $T_L$) stroke where the field decreases linearly from ${\mathsf{\Gamma }}_H$ to ${\mathsf{\Gamma }}_L$). The heat is being released hence the internal energy is found to decrease.

(iv)

Stroke-D → E: The temperature increases linearly (from $T_L$ to $T_H$) for fixed value of ${\mathsf{\Gamma }}_L$.

Thus, in steady state, the system (working fluid, quantum Ising system here) returns to the original or initial starting point of the cycle (state) after the completion of the whole cycle. In the schematic diagram (Figure 4), the states denoted by A and E are the same with respect to all the thermodynamic parameters.

The efficiency of the quantum engine would be clearly evaluated from the changes in internal energy (of the cooperative part of the Ising Hamiltonian) absorbs heat during the steady state strokes A→B and that released during the stroke C→D in Figure 4. Denoting the heat absorbed and released by $E_{absorbed}$ and $E_{released}$, respectively, we we can express $E_{absorbed}=U\left(B\right)-U\left(A\right)$, where $U\left(A\right)$ and $U\left(B\right)$ represent the magnitudes of the internal energy at the state points A and B respectively. Similarly, $E_{released}=|U\left(D\right)-U\left(C\right)|$ (to keep is positive), where $U\left(D\right)$ and $U\left(C\right)$ represent the magnitudes of the internal energy at the state points D and C, respectively (see Figure 5). Hence, the efficiency of the engine is $\eta =(E_{absorbed}-E_{released})/E_{absorbed}$.

Following [17], the numerical solutions (with parameter values used) and the estimated values of internal energies U of the quantum Ising system (engine working fluid) at the points A, B, C and D, we get the efficiency of the quantum Ising heat engine, for different values of (fixed amount) longitudinal field, as shown in Figure 6. The study could compare the efficiencies of both classical and quantum Ising heat engines (for identical temperatures of the heat bath and heat sink). Figure 6 shows that the engine efficiency can be considerably enhanced (and brought closer to the Carnot value corresponding to the temperatures of heat source and sink) by putting a fixed optimal value for the longitudinal field. An approximate mean field type analysis supports [17] such an observation.

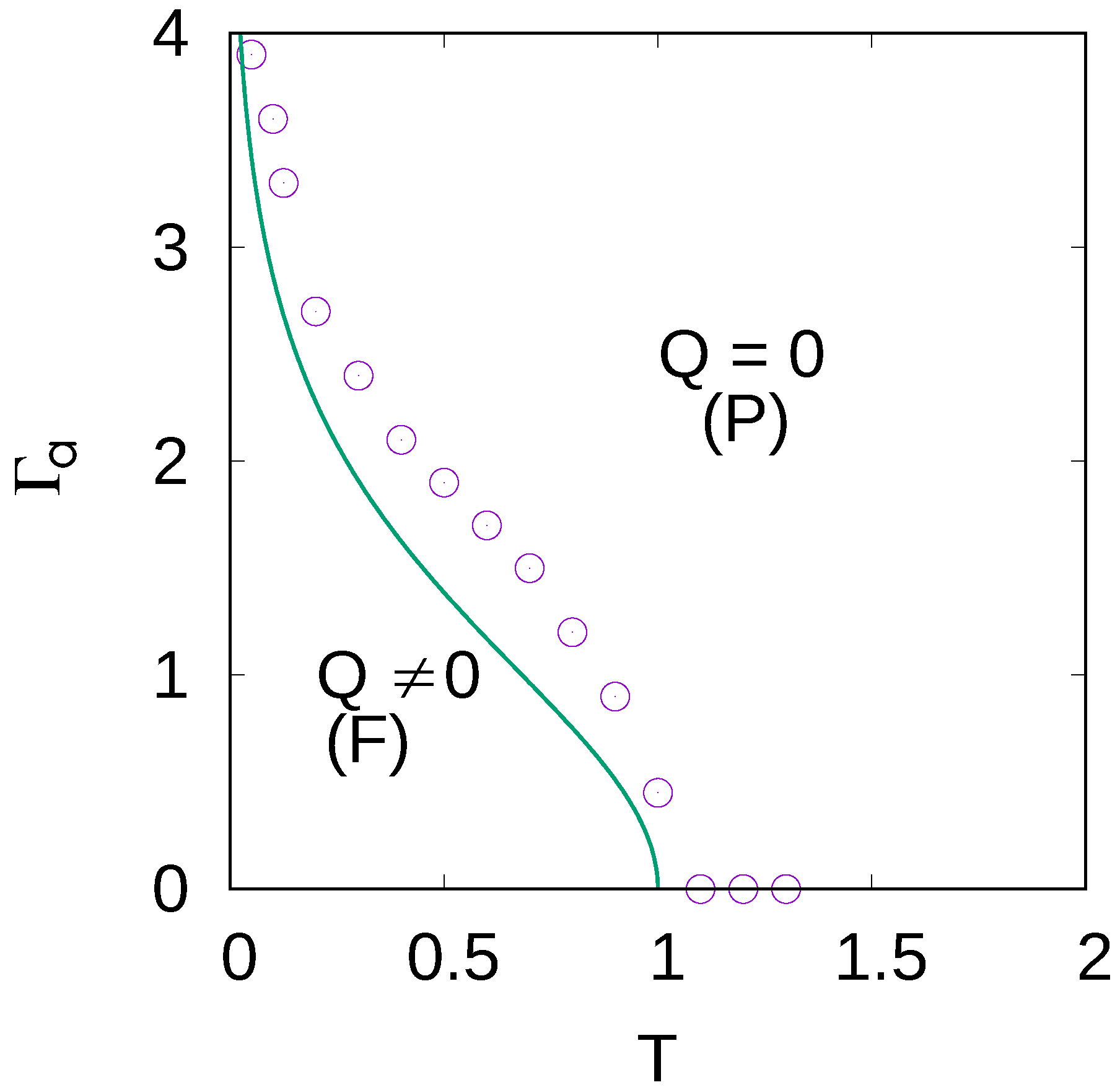
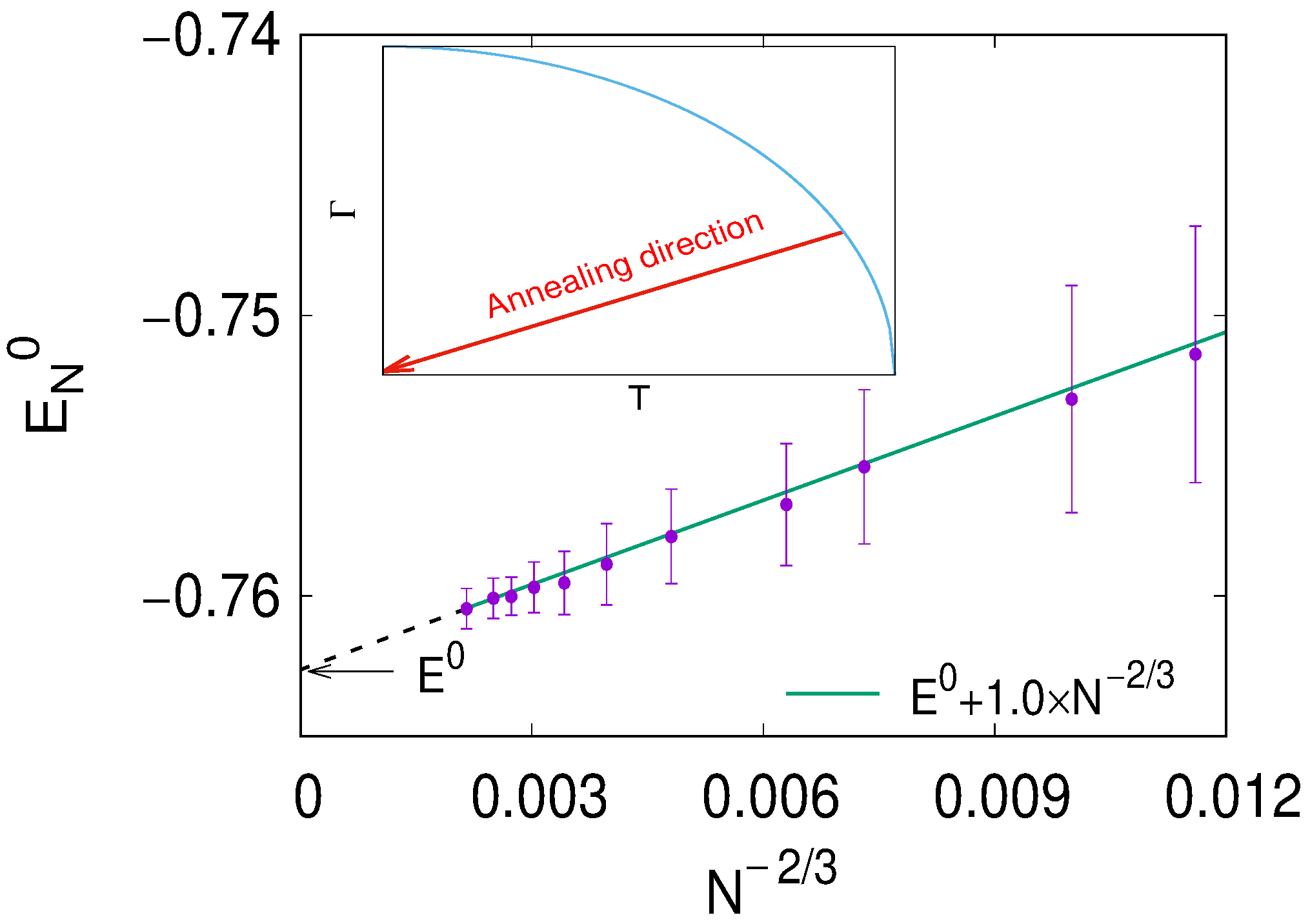
3.4. Quantum Annealing of the SK Model

After the initial (1981) attempt [13] to study the quantum Ising spin glass of the Mattis and Edwards–Anderson variety in a transverse field, the quantum Ising SK model was first studied in 1985 by Ishii and Yamamoto [36], using high-temperature expansion of the mean field free energy from set up by Thouless, Anderson and Palmer (TAP) type mean-field approximation [37]. We will discuss herein the application of quantum annealing (see, e.g., [18,19,20,21,22,38]), employing the discrete time version Equations (27) and (28) of the de Gennes–Suzuki–Kubo equation and estimate the ground state energy of the Sherrington–Kirkpatrick model [23,24]. Here, we will put $h\left(t\right)=0$ and the interactions $J_{ij}$ in Hamiltonian Equation (18) are randomly ferromagnetic and antiferromagnetic with zero average and have a Gaussian distribution:

$$P\left(J_{ij}\right)=(1/J){(N/2\pi )}^{1/2}exp[-(N/2){(J_{ij}/J)}^2],$$

(29)

with

$${\left[J_{ij}^2\right]}_{av}-{\left[J_{ij}\right]}_{av}^2=J^2/N=1/N.$$

(30)

Here, because of very weak average mean field on each spin, we have to add a reaction term coming from the second order mean field fluctuation (following TAP [37] and the modification [26] required for the low or zero temperature quantum spin-glass transitions here) in the effective mean field component: In Equation (22) after incorporating the TAP reaction term $h_i^{z\mathrm{eff}}\left(t\right)={\sum }_j{J}_{ij}{m}_j^z\left(t\right)-\left[1-q\left(t\right)\right]m_i^z\left(t\right)$ where $q=1/N{\left[{\sum }_{i=1}^N{\left(m_i^z\right)}^2\right]}_{av}$, while the x-component in Equation (23) remaining the same, i.e., $h_i^{x\mathrm{eff}}\left(t\right)=\mathsf{\Gamma }\left(t\right)$. For quantum annealing, the temperature and transverse field parameters will follow the annealing schedules:

$$T\left(t\right)=T_0[1-t/\tau ]$$

(31)

and/or

$$\mathsf{\Gamma }\left(t\right)={\mathsf{\Gamma }}_0[1-t/\tau ],$$

(32)

where at $t=0$, the temperature $T_0>T_c$ and/or ${\mathsf{\Gamma }}_0>{\mathsf{\Gamma }}_c$ and $T_c$, ${\mathsf{\Gamma }}_c$ correspond to the temperature and transverse field values at the spin glass ($q\ne 0$) and para ($q=0$) phase boundary.

We will discuss here (following [26]) the numerical results obtained from the above-mentioned coupled equations. We will solve numerically the above Equation (28) for given configurations of $m_i^z\left(t\right)$, using Equations (21) and (22) for ${\overrightarrow{h}}_i^{\mathrm{eff}}\left(t\right)$, for an N spin SK model (N in the range 25 to 10,000) averaging over configurations in the range 10,000 to 15, respectively.

For the classical case ($\mathsf{\Gamma }$ = 0 with $h=0$), the equation for $d{m}_i^z/dt$ has been already studied for classical annealing in the SK model [27].

The simplicity and affordability of the classical annealing using Suzuki–Kubo dynamics naturally raises interests in the quantum equivalent of the approach. For a pure quantum annealing (see Figure 7), the temperature is set equal to zero and the transverse field vanishes linearly with time, following Equation (32). For a mixed annealing strategy (see Figure 8), the initial values of the temperature $T_0$ and transverse field ${\mathsf{\Gamma }}_0$ are set above $T_c=0.94$ and ${\mathsf{\Gamma }}_c=0.5$ and they both vanish linearly with time following Equations (31) and (32).

In Figure 7, the ground state energy values obtained here for different system sizes are very close to what was found for purely classical annealing [39,40] for the corresponding sizes. Indeed, the power law variations with the system sizes also come out to be the same for both the ground state energies and their fluctuations. The linear annealing time $\tau$ used for the dynamics (in Equations (31) and (32)) also has the same scaling behavior as in the classical case. This implies that the algorithmic cost of both classical and quantum simulations remain the same and scale with $N^3$. The extrapolated value of the ground state energy per spin ($E^0=-0.7623\pm 0.0001$) in the infinite system size limit is also very close to the classical case ($E^0=-0.7629\pm 0.0002$). Therefore, these results indicate that the algorithmic advantage here comes from the fact that the magnetization variables ($m_i$) are made continuous due to the Suzuki–Kubo dynamics. Hence, the case of quantum annealing, which effectively makes the magnetization variables continuous through both longitudinal and transverse fields, does not bring any added advantage.

Finally, we look into the case of mixed annealing where both the temperature and transverse fields are varied simultaneously during the annealing process following Equations (31) and (32). The time scale for annealing, $\tau$, is kept the same for both of these parameters. In Figure 8, the ground state energy values and their fluctuations are plotted. The starting point of the annealing process was at $T=T_c=0.94$ for $\mathsf{\Gamma }={\mathsf{\Gamma }}_c=0.5$. Once again, the energy values are similar to what was obtained for the purely classical and quantum cases, with the same power law variations, albeit with a slightly different value for the constant a. The extrapolation to the thermodynamic limit gives a ground-state energy of $E^0=-0.7626\pm 0.0001$. Of course, the algorithmic cost also remains the same ($N^3$).

4. Conclusions & Discussion

Here, we have reviewed the recent development of a quantum many-body theory of mean-field dynamics for cooperatively interacting Ising like systems. For the static formulation, its origin could be traced back to the pseudo-spin mapping of the BCS Hamiltonian and re-derivation of the BCS superconductivity theory in 1957 and its gap equations by Anderson (in 1958), where the mean-field self-consistent equations were employed for an XY (or effectively Ising) model (with interaction strength given by those of the Cooper pairs) in a transverse field (of strength given by the free electron energy). That we have discussed in Section 2. Although the quantum nature of the BCS superconductivity transition could be studied from such a mapping, general nature of the phase transitions driven by such transverse or quantum fields, was studied a little later, in connection with the structural transitions in KDP type systems, starting with de Gennes (1963). It was extended by Brout-Muller-Thomas (1966), viewing the structural transitions as mode-softening of the collective phonon modes coupled with the electron-tunneling modes in such systems, incorporating the Suzuki–Kubo (1968) mean-field Ising dynamics in the transverse Ising model (reviewed here in Section 3.1). Such quantum phase transitions of the Ising models in transverse fields were then extensively studied, also beyond mean field theories (see e.g., [9,41], employing various analytical and computational techniques from 1970 onwards. Some of these results are discussed here. First we have discussed the general formulation of quantum mean-field dynamics, namely the deG ennes–Suzuki–Kubo dynamics for transverse Ising-like systems. Then, the hysteretic response of an Ising system to a periodically varying transverse or tunneling field, the scaling behavior of the hysteresis loop area, and the dynamic phase transition (separating the time-averaged magnetization Q from a non-zero value to zero; see Figure 3) have been discussed in Section 3.2. In the following Section 3.3, the efficiencies of both classical and quantum heat engines are compared using a quantum Ising model as working fluid and we find (see Figure 6) that the engine efficiency can be considerably enhanced (and brought closer to the Carnot value corresponding to the temperature of heat source and sink) compared to the classical Ising system by putting a fixed optimal value for the longitudinal field. Finally we have discussed in Section 3.4, the quantum annealing dynamics for estimating the ground state energy of the Sherrington–Kirpatrick spin glass model which gave a computationally very fast algorithm, leading to ground state energy comparable with the best known analytic estimate. Here we have annealed the SK spin-glass system, first by changing the transverse field from 1 to 0 keeping the temperature at zero, i.e., quantum annealing and later where both the transverse field and temperature are changed, i.e., mixed annealing. We have gotten the ground state energy per spin (in the extrapolated limit) $E^0=-0.7623\pm 0.0001$ (see Figure 7) for quantum annealing and $E^0=-0.7626\pm 0.0001$ (see Figure 8) for mixed annealing, with the fluctuation in $E^0$ reducing as $N^{-3/4}$ (see Figure 9) with the system size N, compared to the best known analytic result $E^0=-0.763166\dots$ [25]. It may be noted at this point that the mean field dynamics here for the SK model, using both pure classical annealing (with tunneling field $\mathsf{\Gamma }$ set to zero) or pure quantum annealing (with temperature T set to zero), lead uniquely to an accurate estimate ground state energy of the SK model.

Development of mean field theory for quantum many-body systems has a rich history. It started with Nobel laureates Bardeen, Cooper and Schrieffer in their 1957 theory of electron-phonon interaction induced superconductivity [1] and Nobel laureate de Gennes’ mean field theory (1963) of transverse Ising model [3] for proton tunneling induced para-ferroelectric transition in KDP crystals. Nobel laureate Anderson showed in 1958 [2] that a pseudo-spin mapping of the the BCS Hamiltonian leads to a cooperatively interacting XY model (or effectively Ising model in Fermi vector space, near the Fermi level) in a transverse or tunneling field (of strength given by the free electorn dispersion). The resulting BCS gap parameter at zero temperature ($T=0$; see Equations (14) and (17)) comes from the (pseudo-Ising) spin–spin interaction. This non-vanishing gap $\Delta$ at $T<T_c$ for the electron energy dispersion in the BCS superconductors would then induce, according to the phenomenological theory of superfluidity by Nobel laureate Landau (1949) [28], superconductivity for the charged electrons. Another Nobel Laureate Muller (together with Brout and Thomas) [4] in 1966 developed the mean field or random phase approximation for the soft mode dispersion in the transverse Ising model of KDP. The increase in transition temperature due to reduced proton tunneling (increased mass) in deuterated KDP (see, e.g., [42,43]) could also be explained. Following the initial study [13] of the quantum Ising spin glass models (of the Mattis and Edwards-Anderson variety), several attempts were made (see, e.g., [36,44]) to develop mean field theories for the free energy of the transverse Ising SK model. These were mostly based on the high temperature limit of the classical SK model TAP free energy structure (proposed by Nobel laureate Thouless et al. in 1977 [37]), which tried to incorporate the Replica Symmetry Breaking effects in the ground state, as conceived by Nobel laureate Parisi [45,46] for the classical SK model.

All these proved major advantage of the Mean field theory of transverse Ising models in studying the static transition properties of long range interacting quantum many body systems. Soon afterwards, the equilibrium classical and quantum transition behavior in short-range interacting model transverse field Ising systems started developing (see, e.g., [47,48,49,50,51,52]) and became very well established (see, e.g., the reviews in [9,41,53]). However, most of these developments were for equilibrium or static phase transition behavior of the transverse Ising systems. For applications of the model to non-equilibrium situations where the fields on the condensed matter system or even the temperature of the system changes with time, for example in dynamic hysteresis in quantum magnets (where the transverse field on the quantum Ising system changes periodically with time; see, e.g., [16,54]), or in quantum heat engines (with quantum Ising system as working fluid and both the temperature and transverse field change with time during different strokes of the engine cycles; see, e.g., [17]), or in quantum annealing of the Sherrington–Kirkpatrick model (where the tunneling field and temperature both need to be annealed down to zero; see e.g., [26]), one needs to augment the dynamics of the longitudinal and transverse components (de Gennes [3]) of the Ising spins employing the Suzuki–Kubo mean field dynamics [14]. This has been done in Section 3.1 and the final equations for the longitudinal and transverse spin components are given by Equations (25) and (26) in differential form and by Equations (27) and (28) for discrete time evolution. Some of the important results regarding the transverse magnetization loop area scaling and the dynamic transition phase diagram (separating the para or $Q=0$ and ordered ($Q>0$, where Q denotes the steady state value of the integrated longitudinal magnetization over a complete period of the transverse field), enhanced efficiency (approaching the Carnot value) of the quantum Ising heat engine and the new quantum annealing algorithm for estimating the ground state energy per spin of the SK model are discussed in Section 3.2, Section 3.3 and Section 3.4, respectively. In particular, we note the intriguing success of the mean field quantum Ising annealing algorithm following the de Gennes–Suzuki–Kubo equation, in comfortably converging to the best analytic estimate [25] for the energy of the Replica Symmetry Broken [45,46] ground state of the Sherrington–Kirkpatrick model [23]. It may be mentioned here that the observations of similar accurate estimates for the ground state energy as well of as the annealing times, as discussed in 3.4. (see [26,27] for details, see also [55] for a recent comparison in the classical case), for both classical and quantum Ising Sherrington–Kirkpatrick model suggest that “quantum supremacy” (cf. [56]) gets merged in such cases when one employs the de Gennes–Suzuki–Kubo mean field dynamics for annealing. It may be noted that the continuous nature of the magnetization variable (both in classical and quantum cases) seems to be responsible here for the major benefit in our annealing processes, where this dynamics contributes equally for both the cases in the Sherrington–Kirkpatrick system and did not show any “quantum supremacy”. However, it may further be noted that in the quantum case the order parameter (magnetization) vector has continuous dynamics for both the components (longitudinal and transverse, keeping the total magnetization magnitude constant) and this feature (in contrast to that in the classical case) can indeed help more flexible search (by navigating in higher dimension of the order parameter) for the ground state, compared to the classical annealing in the context of different systems. Some such interesting systems might be the cases of sudden quench in BCS (see e.g., [57,58]), quantum quenching dynamics [59] of BCS superconductors to Bose–Einstein (BE) condensate due to fast electromagnetic perturbations and similar many-body quantum dynamical systems. All these indicate immense prospects for such mean field quantum many-body dynamical equation obtained by combining the de Gennes [3] mean field quantum Ising model and the Suzuki–Kubo mean field (classical) Ising dynamics as proposed here.