Nanoscale Lattice Heterostructure in High-Tc Superconductors
Abstract
1. Essential Heterogeneities in Hole-Doped High-Tc Cuprate Superconductors
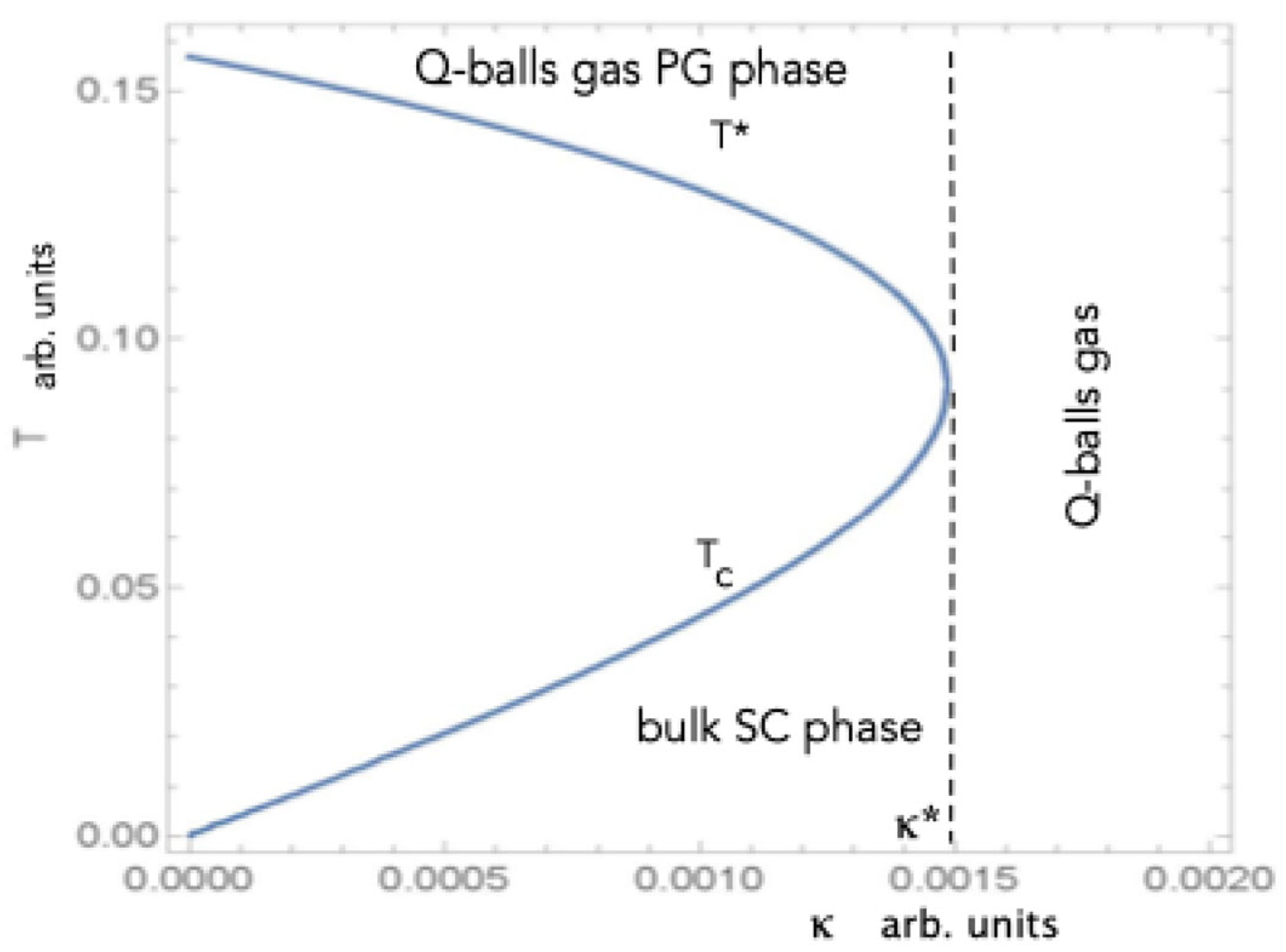
2. Q-Balls and the Role of Local Nanoscale Lattice Fluctuations in the High-Tc Superconductivity Mechanism in Cuprate Perovskites
3. Local Lattice Fluctuations in Cuprates Seen by X-Ray Spectroscopy XANES and EXAFS
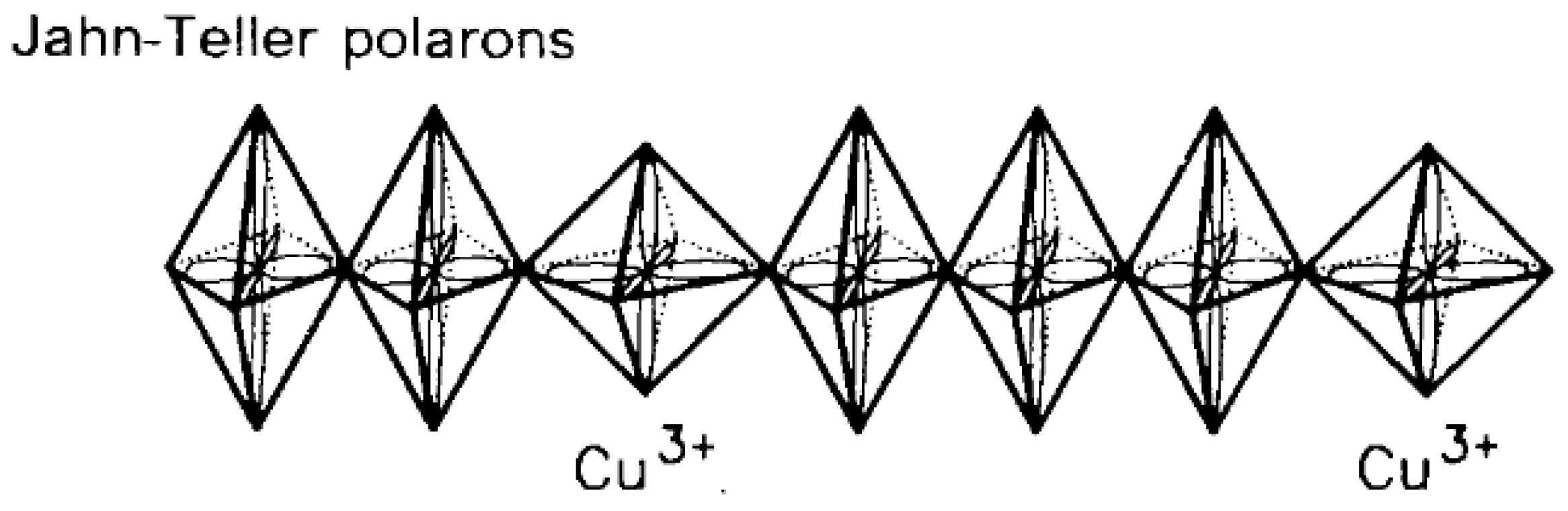
4. Internal Quantum Tunneling Polarons’ Dynamical Structure and Kuramoto Synchronization in Cuprate Superconductors
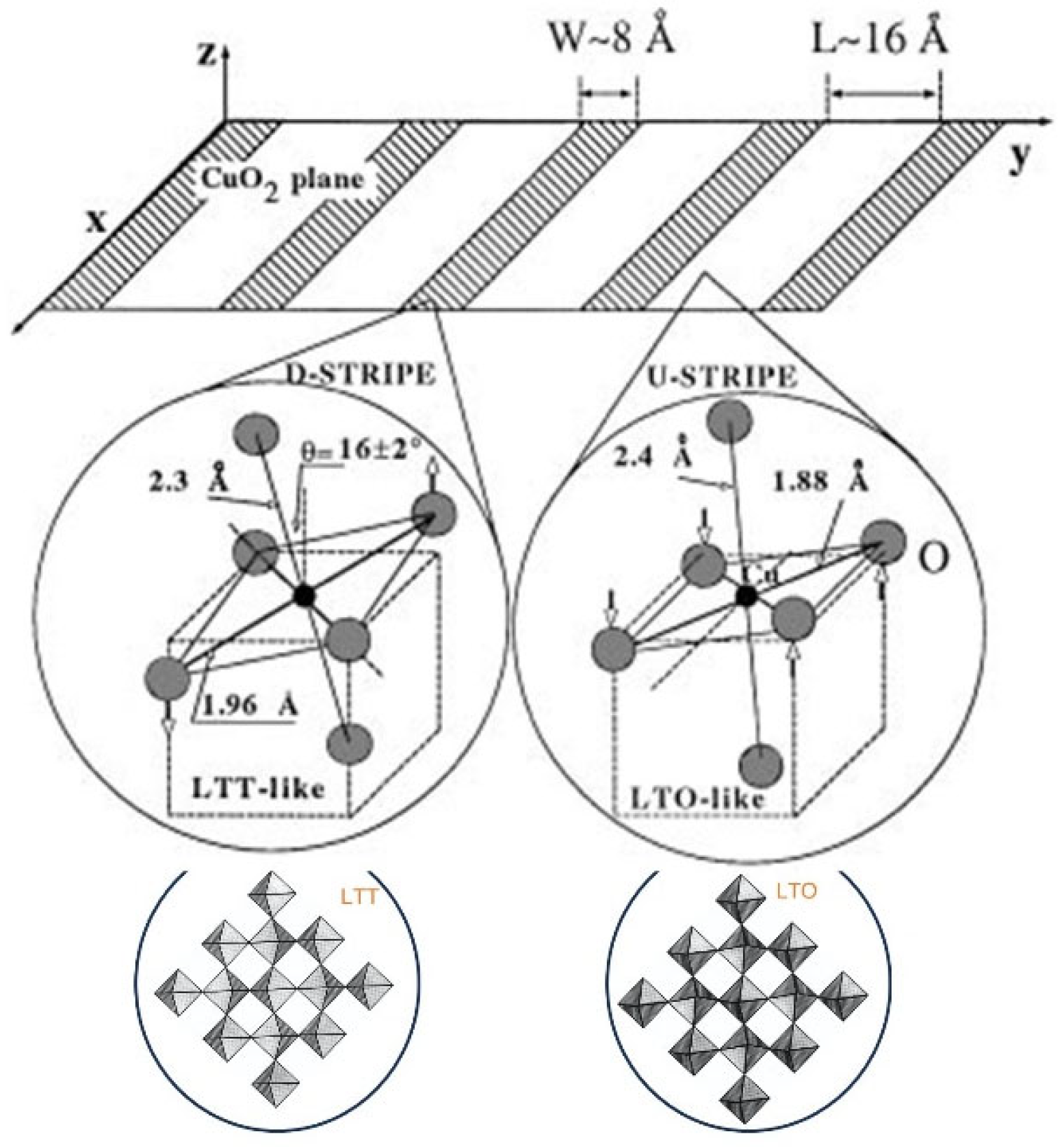
5. Polarons Nanoscale Self-Organization in Cuprate Perovkites as Seen by X-Ray Absorption Spectroscopy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides—The new approach to high-Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585. [Google Scholar] [CrossRef]
- Cardona, M.; Liu, R.; Thomsen, C.; Kress, W.; Schönherr, E.; Bauer, M.; Genzel, L.; König, W. Effect of isotopic substitution of oxygen on Tc and the phonon frequencies of high Tc superconductors. Solid State Commun. 1988, 76, 789–793. [Google Scholar] [CrossRef]
- Zech, D.; Keller, H.; Conder, K.; Kaldis, E.; Liarokapis, E.; Poulakis, N.; Müller, K.A. Site-selective oxygen isotope effect in optimally doped YBa2Cu3O6+x. Nature 1994, 371, 681–683. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Morenzoni, E.; Angst, M.; Conder, K.; Savić, I.M.; Lampakis, D.; Liarokapis, E.; Tatsi, A.; Keller, H. Site-selective oxygen isotope effect on the magnetic field penetration depth in underdoped Y0.6Pr0.4Ba2Cu3O7−δ. Phys. Rev. B 2003, 68, 220506. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope effect of the charge-stripe ordering temperature in La2−xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Zhao, G.-m.; Keller, H.; Conder, K. Unconventional isotope effects in the high-temperature cuprate superconductors. J. Phys. Condens. Matter 2001, 13, R569–R587. [Google Scholar] [CrossRef]
- Shengelaya, A.; Kochelaev, B.I.; Conder, K.; Keller, H. Electronic phase separation and unusual isotope effects in La2−xSrxCuO4 observed by electron paramagnetic resonance. In High Tc Superconductors and Related Transition Metal Oxides; Bussmann-Holder, A., Keller, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 287–302. [Google Scholar]
- Keller, H. Unconventional isotope effects in cuprate superconductors. In Structure and Bonding; Bussmann-Holder, A., Müller, K.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 114, pp. 143–169. [Google Scholar]
- Bussmann-Holder, A.; Keller, H. Polaron formation as origin of unconventional isotope effects in cuprate superconductors. Eur. Phys. J. B 2005, 44, 487–490. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Bishop, A.R.; Simon, A.; Micnas, R.; Müller, K.A. Unconventional isotope effects as evidence for polaron formation in cuprates. Europhys. Lett. 2005, 72, 423–429. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. 328 Determination of the Local Lattice Distortions in the CuO2 Plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412–3415. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef]
- Kremer, R.K.; Sigmund, E.; Hizhnyakov, V.; Hentsch, F.; Simon, A.; Müller, K.A.; Mehring, M. Percolative phase separation in La2CuO4+δ and La2-xSrxCuO4. Z. Phys. B Condens. Matter 1992, 86, 319–324. [Google Scholar] [CrossRef]
- Sigmund, E.; Müller, K. Phase Separation in Cuprate Superconductors. Proceedings of the Second International Workshop on “Phase Separation in Cuprate Superconductors” September 4–10, 1993, Cottbus, Germany; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Müller, K.A. Essential heterogeneity in hole doped cuprate superconductors. In Superconductivity in Complex Systems; Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 2005; Volume 114, pp. 1–12. [Google Scholar]
- Bussmann-Holder, A.; Keller, H. Multiband Superconductivity, Polarons, Jahn-Teller Polarons, Heterogeneity, and High-Temperature Superconductivity. Condens. Matter 2024, 9, 56. [Google Scholar] [CrossRef]
- Müller, K.A. The Unique Properties of Superconductivity in Cuprates. J. Supercond. Nov. Magn. 2014, 27, 2163–2179. [Google Scholar] [CrossRef]
- Shengelaya, A.; Müller, K.A. Perspective, The intrinsic heterogeneity of superconductivity in the cuprates. Eur. Phys. Lett. 2015, 109, 27001. [Google Scholar] [CrossRef]
- Haase, J.; Slichter, C.P.; Stern, R.; Milling, C.T.; Hinks, D.G. NMR Evidence for Spatial Modulations in the Cuprates. J. Supercond. Inc. Nov. Magn. 2000, 13, 723–726. [Google Scholar] [CrossRef]
- Rybicki, D.; Jurkutat, M.; Reichardt, S.; Kapusta, C.; Haase, J. Perspective on the phase diagram of cuprate high-temperature superconductors. Nat. Commun. 2016, 7, 11413. [Google Scholar] [CrossRef]
- Jurkutat, M.; Rybicki, D.; Sushkov, O.P.; Williams, G.V.; Erb, A.; Haase, J. Distribution of electrons and holes in cuprate superconductors as determined from 17O and 63Cu nuclear magnetic resonance. Phys. Rev. B 2014, 90, 140504. [Google Scholar] [CrossRef]
- Müller, K.A. Possible coexistence of s- and d-wave condensates in copper oxide superconductors. Nature 1995, 377, 133–135. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; La Mattina, F.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. Experimental evidence for two gaps in the high-temperature La1.83Sr0.17CuO4 superconductor. Phys. Rev. Lett. 2007, 98, 057007. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba−La−Cu−O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Furrer, A. Neutron scattering investigations of charge inhomogeneities and the pseudogap state in high-temperature superconductors. In Superconductivity in Complex Systems; Structure and Bonding; Bussmann-Holder, A., Müller, K.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 114, pp. 171–204. [Google Scholar]
- Oyanagi, H.; Zhang, C.; Tsukada, A.; Naito, M. Lattice instability in high temperature superconducting cuprates probed by x-ray absorption. J. Phys. Conf. Ser. 2008, 108, 012038. [Google Scholar] [CrossRef]
- Mukhin, S. Euclidean Q-balls of fluctuating SDW/CDE in the ‘nested’ Hubbard model of high-Tc superconductors as the origin of pseudogap and superconducting behaviors. Condens. Matter 2022, 7, 31. [Google Scholar] [CrossRef]
- Mukhin, S.I. Euclidean Q-balls of electronic spin/charge densities confining superconducting condensates as the origin of pseudogap and high-Tc superconducting behaviours. Ann. Phys. 2022, 447, 169000. [Google Scholar] [CrossRef]
- Mukhin, S. Possible manifestation of Q-ball mechanism of high-Tc superconductivity in X-ray diffraction. Condens. Matter 2023, 8, 16. [Google Scholar] [CrossRef]
- Campi, G.; Barba, L.; Zhigadlo, N.D.; Ivanov, A.A.; Menushenkov, A.P.; Bianconi, A. Q-Balls in the pseudogap phase of Superconducting HgBa2CuO4+y.Condens. Matter 2023, 8, 15. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A. Evolution of complexity in out-of-equilibrium systems by time-resolved or space-resolved synchrotron radiation techniques. Condens. Matter 2019, 4, 32. [Google Scholar] [CrossRef]
- Coleman, S. Q-balls. Nucl. Phys. 1985, 262, 263–283. [Google Scholar] [CrossRef]
- Mukhin, S.I. Q-ball mechanism of electron transport properties of high-Tc superconductors. arXiv 2025, arXiv:2504.09610. [Google Scholar] [CrossRef]
- Barisic, N.; Li, Y.; Yu, G.; Zhao, X.; Dressel, M.; Smontara, A.; Greven, M. Universal sheet resistance and revised phase diagram of the cuprate high-temperature superconductors. Prov. Natl. Acad. Sci. USA 2013, 110, 12235. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Komiya, S.; Ono, S.; Ando, Y.; Gu, G.D.; Ong, N.P. Diamagnetism and Cooper pairing above Tc in cuprates. Phys. Rev. B 2010, 81, 054510. [Google Scholar] [CrossRef]
- Balzarotti, A.; Menushenkov, A.P.; Motta, N.; Purans, J. EXAFS of the superconducting oxide BaPb1-xBixO3. Solid State Commun. 1984, 49, 887–890. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Ignatov, A.Y.; Ivanov, A.A.; Elesin, V.F.; Rudnev, I.A.; Kochubey, D.I. Polarized K-Cu XANES study of epitaxial Nd1.85Ce0.15CuO4 thin films irradiated by He+ ions. Solid State Commun. 1992, 84, 319–321. [Google Scholar] [CrossRef]
- Ignatov, A.Y.; Menushenkov, A.P.; Ivanov, A.A.; Kochubey, D.I. The local structure transformation in Nd1.85Ce0.15CuO4 films irradiated by He+ ions: Polarized EXAFS study. Phys. C 1994, 234, 69–76. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Ignatov, A.Y.; Galkin, S.G.; Ivanov, A.A.; Elesin, V.F.; Rudnev, I.A.; Chernov, V.A.; Nikitenko, S.G.; Kochubey, D.I. Radiative defects in HTSC thin films: EXAFS and XANES study. Phys. Low-Dimens. Struct. 1994, 3, 9–16. [Google Scholar]
- Menushenkov, A.P.; Ignatov, A.Y.; Chernov, V.A.; Nikitenko, S.G. Radiative Defects Structure in HTSC Thin Films: Polarized XAS Study. Nucl. Instrum. Methods Phys. Res. Sect. B 1995, 97, 151–154. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Ignatov, A.Y.; Ivanov, A.A.; Kochubey, D.I.; Chernov, V.A.; Nikitenko, S.G. Polarized XAS spectroscopy of HTSC thin films. Nucl. Instrum. Methods Phys. Res. Sect. A 1995, 359, 236–239. [Google Scholar] [CrossRef]
- Ignatov, A.Y.; Iacobucci, S.; Menushenkov, A.P.; Lagarde, P.; Ivanov, A.A. Electronic structure of Nd1.85Ce0.15CuO4−d irradiated by He+ ions: An X-ray absorption on the Cu-L3 and Ce-M4,5 edges. J. Phys. IV 1997, 7, C2-1123–C2-1124. [Google Scholar]
- Ignatov, A.Y.; Ivanov, A.A.; Menushenkov, A.P.; Iacobucci, S.; Lagarde, P. Symmetry of the free states of an electron-doped Nd2-xCexCuO4−d superconductor determined by x-ray absorption spectroscopy. Phys. Rev. B. 1998, 57, 8671–8679. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Chernikov, R.V.; Ivanov, A.A.; Sidorov, V.V.; Klementev, K.V. Double-well potential for oxygen ion vibrations in Nd2−xCexCuO4−δ. J. Phys. Conf. Ser. 2009, 190, 012093. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Kuznetsov, A.V.; Chernikov, R.V.; Ivanov, A.A.; Sidorov, V.V.; Klementev, K.V. Correlation of the local and the macroscopic properties of high-temperature superconductors. Z. Kristallogr. 2010, 225, 487–491. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Kuznetsov, A.V.; Chernikov, R.V.; Ivanov, A.A.; Sidorov, V.V.; Klementev, K.V. Low temperature anharmonicity and superconductivity in cuprates. J. Supercond. Nov. Magn. 2014, 27, 925–928. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Klementev, K.V. Extended x-ray absorption fine-structure indication of double-well potential for oxygen vibration in Ba1−xKxBiO3. J. Phys. Condens. Matter 2000, 12, 3767–3786. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Kuznetsov, A.V.; Chernikov, R.V.; Ivanov, A.A.; Sidorov, V.V.; Klementev, K.V. Role of the Perovskite-Like Lattice in the High-Temperature Superconductor Mechanism: EXAFS Data Analysis. Journal of Surface Investigation. X-Ray Synchrotron. Neutron Tech. 2013, 7, 407–421. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Ivanov, V.G.; Chepikov, V.N.; Nygaard, R.R.; Soldatenko, A.V.; Rudnev, I.A.; Osipov, M.A.; Mineev, N.A.; Kaul, A.R.; Mathon, O.; et al. Correlation of local structure peculiarities and critical current density of 2G MOCVD YBCO tapes with BaZrO3 nanoinclusions. Supercond. Sci. Technol. 2017, 30, 045003. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Ivanov, A.A.; Chernysheva, O.V.; Rudnev, I.A.; Osipov, M.A.; Kaul, A.R.; Chepikov, V.N.; Mathon, O.; Monteseguro, V.; d’Acapito, F.; et al. The influence of BaSnO3 and BaZrO3 nanoinclusions on the critical current and local structure of HTS coated conductors. Supercond. Sci. Technol. 2022, 35, 065006. [Google Scholar] [CrossRef]
- Ivanov, A.A.; Ivanov, V.G.; Menushenkov, A.P.; Wilhelm, F.; Rogalev, A.; Puri, A.; Joseph, B.; Xu, W.; Marcelli, A.; Bianconi, A. Local noncentrosymmetric structure of Bi2Sr2CaCu2O8+y by X-ray magnetic circular dichroism at Cu K-Edge XANES. J. Supercond. Nov. Magn. 2018, 31, 663–670. [Google Scholar] [CrossRef]
- Conradson, S.D.; Velasco, V.; Silva Neto, M.B.; Jin, C.-Q.; Li, W.-M.; Cao, L.-P.; Gauzzi, A.; Karppinen, M.; Perali, A.; Wimberger, S.; et al. Correlation of strontium anharmonicity with charge-lattice dynamics of the apical oxygens and their coupling to cuprate superconductivity. Supercond. Sci. Technol. 2024, 37, 025005. [Google Scholar] [CrossRef]
- Velasco, V.; Silva Neto, M.B.; Perali, A.; Wimberger, S.; Bishop, A.R.; Conradson, S.D. Evolution of charge-lattice dynamics across the Kuramoto synchronization phase diagram of quantum tunneling polarons in cuprate superconductors. Condens. Matter 2021, 6, 52. [Google Scholar] [CrossRef]
- Velasco, V.; Silva Neto, M.B.; Perali, A.; Wimberger, S.; Bishop, A.R.; Conradson, S.D. Kuramoto synchronization of quantum tunneling polarons for describing the dynamic structure in cuprate superconductors. Phys. Rev. B 2022, 105, 174305. [Google Scholar] [CrossRef]
- Conradson, S.D.; Geballe, T.H.; Jin, C.-Q.; Cao, L.-P.; Baldinozzi, G.; Jiang, J.M.; Latimer, M.J.; Mueller, O. Local structure of Sr2 CuO3.3, a 95 K cuprate superconductor without CuO2 planes. Proc. Natl. Acad. Sci. USA 2020, 117, 4565–4570. [Google Scholar] [CrossRef]
- Conradson, S.D.; Geballe, T.H.; Jin, C.-Q.; Cao, L.-P.; Gauzzi, A.; Karppinen, M.; Baldinozzi, G.; Li, W.-M.; Gilioli, E.; Jiang, J.M.; et al. Nonadiabatic coupling of the dynamical structure to the superconductivity in YSr2Cu2.75Mo0.25O7.54 and Sr2CuO3.3. Proc. Natl. Acad. Sci. USA 2020, 117, 33099–33106. [Google Scholar] [CrossRef]
- Conradson, S.D.; Raistrick, I.D.; Bishop, A.R. Axial oxygen-centered lattice instabilities and high-temperature superconductivity. Science 1990, 248, 1394–1398. [Google Scholar] [CrossRef]
- Acosta-Alejandro, M.; Mustre de León, J.; Conradson, S.D.; Bishop, A.R. Evidence for a local structural change in La2CuO4.1 across the superconducting transition. J. Supercond. 2002, 15, 355–360. [Google Scholar] [CrossRef]
- Mustre de León, J.; Acosta-Alejandro, M.; Conradson, S.D.; Bishop, A.R. Change of the in-plane Cu–O bond distribution in La2CuO4.1 across Tc. J. Phys. Chem. Solids 2008, 69, 2288–2291. [Google Scholar] [CrossRef]
- Zhang, C.J.; Oyanagi, H. Local lattice instability and superconductivity in La1.85Sr0.15Cu1−xMxO4 (M = Mn, Ni, and Co). Phys. Rev. B 2009, 79, 064521. [Google Scholar]
- Mustre de León, J.; Conradson, S.D.; Batistić, I.; Bishop, A.R. Evidence for an axial oxygen-centered lattice fluctuation associated with the superconducting transition in YBa2Cu3O7. Phys. Rev. Lett. 1990, 65, 1675–1678. [Google Scholar] [CrossRef] [PubMed]
- Allen, P.G.; Mustre de León, J.; Conradson, S.D.; Bishop, A.R. Characterization of a split axial-oxygen site in TlBa2Ca3Cu4O11 by extended X-ray-absorption fine-structure spectroscopy. Phys. Rev. B 1991, 44, 9480–9485. [Google Scholar] [CrossRef]
- Mustre de León, J.; Conradson, S.D.; Batistić, I.; Bishop, A.R. Correlation between axial-oxygen anharmonicity and Tc in YBa2Cu3O7 and related compounds. Phys. Rev. B 1991, 44, 2422–2425. [Google Scholar] [CrossRef]
- Mustre de León, J.; Batistić, I.; Bishop, A.R.; Conradson, S.D.; Trugman, S.A. Polaron origin for anharmonicity of the axial oxygen in YBa2Cu3O7. Phys. Rev. Lett. 1992, 68, 3236–3239. [Google Scholar] [CrossRef]
- Mustre de León, J.; Conradson, S.D.; Batistić, I.; Bishop, A.R.; Raistrick, I.D.; Aronson, M.C.; Garzon, F.H. Axial oxygen-centered lattice instabilities in YBa2Cu3O7: An application of the analysis of extended x-ray-absorption fine structure in anharmonic systems. Phys. Rev. B 1992, 45, 2447–2457. [Google Scholar] [CrossRef]
- Booth, C.H.; Bridges, F.; Boyce, J.B.; Claeson, T.; Lairson, B.M.; Liang, R.; Bonn, D.A. Comparison of local structure measurements from c-axis polarized XAFS between a film and a single crystal of YBa2Cu3O7−δ as a function of temperature. Phys. Rev. B 1996, 54, 9542–9554. [Google Scholar] [CrossRef] [PubMed]
- Acebrón, J.A.; Bonilla, L.L.; Pérez Vicente, C.J.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Velasco, V.; Silva Neto, M.B. Unconventional superconductivity as a quantum Kuramoto synchronization problem in random elasto-nuclear oscillator networks. J. Phys. Commun. 2021, 5, 015003. [Google Scholar] [CrossRef]
- Kuramoto, Y. Self-entrainment of a population of coupled non-linear oscillators. In International Symposium on Mathematical Problems in Theoretical Physics; Araki, H., Ed.; Springer: Berlin/Heidelberg, Germany, 1975; pp. 420–422. [Google Scholar]
- Haskel, D.; Stern, E.A.; Hinks, D.G.; Mitchell, A.W.; Jorgensen, J.D. Altered Sr environment in La2−xSrxCuO4. Phys. Rev. B 1997, 56, R521–R524. [Google Scholar] [CrossRef]
- Gao, W.B.; Liu, Q.Q.; Yang, L.X.; Yu, Y.; Li, F.Y.; Jin, C.Q.; Uchida, S. Out-of-plane effect on the superconductivity of Sr2−xBaxCuO3+δ with Tc up to 98 K. Phys. Rev. B 2009, 80, 094523. [Google Scholar] [CrossRef]
- Bersuker, I. The Jahn-Teller Effect; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Streltsov, S.V.; Khomskii, D.I. Jahn-Teller effect and spin-orbit coupling: Friends or foes? Phys. Rev. X 2020, 10, 031043. [Google Scholar] [CrossRef]
- Browne, A.J.; Krajewska, A.; Gibbs, A.S. Quantum materials with strong spin-orbit coupling: Challenges and opportunities for materials chemists. J. Mater. Chem. 2021, 9, 11640–11654. [Google Scholar] [CrossRef]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039–1263. [Google Scholar] [CrossRef]
- Capone, M.; Ciuchi, S. Polaron crossover and bipolaronic metal-insulator transition in the half-filled Holstein model. Phys. Rev. Lett. 2003, 91, 186405. [Google Scholar] [CrossRef]
- Celiberti, L.; Mosca, D.F.; Allodi, G.; Pourovskii, L.V.; Tassetti, A.; Forino, P.C.; Cong, R.; Garcia, E.; Tran, P.M.; De Renzi, R.; et al. Spin-orbital Jahn-Teller bipolarons. Nat. Commun. 2024, 15, 2429. [Google Scholar] [CrossRef]
- Bianconi, A.; Doniach, S.; Lublin, D. X-ray Ca K edge of calcium adenosine triphosphate system and of simple Ca compunds. Chem. Phys. Lett. 1978, 59, 121–124. [Google Scholar] [CrossRef]
- Bianconi, A.; Bachrach, R.Z. Al surface relaxation using surface extended X-ray-absorption fine structure. Phys. Rev. Lett. 1979, 42, 104. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Saini, N.L.; Bianconi, A. Temperature dependent lattice distortion in La1−xCexRu2 by Ru K-edge absorption spectroscopy. AIP Conf. Proc. 2001, 554, 449–455. [Google Scholar] [CrossRef]
- Menushenkov, A.P.; Klementev, K.V.; Kuznetsov, A.V.; Kagan, M.Y. Local lattice distortions and the nature of superconductivity in Ba(K)BiO3-BaPb (Bi)O3. AIP Conf. Proc. 2001, 554, 269–277. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Bianconi, G.; Saini, N.L. The strain quantum critical point for superstripes. AIP Conf. Proc. 2001, 554, 124–132. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Rossetti, T.; Lanzara, A.; Perali, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Ha, Y.N.D.H. Stripe structure in the CuO2 plane of perovskite superconductors. Phys. Rev. B 1996, 54, 12018. [Google Scholar] [CrossRef]
- Zhou, J.S.; Bersuker, G.I.; Goodenough, J.B. Non-adiabatic electron-lattice interactions in the copper-oxide superconductors. J. Supercond. 1995, 8, 541–544. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Zhou, J.S. Vibronic states in La2−xBaxCuO4. J. Supercond. 1997, 10, 309–314. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Bianconi, A. High Tc Superconductors Made by Metal Heterostructures at the Atomic Limit. European Patent N. 0733271, 27 May 1998. [Google Scholar]
- Logvenov, G.; Bonmassar, N.; Christiani, G.; Campi, G.; Valletta, A.; Bianconi, A. The superconducting dome in artificial high-Tc superlattices tuned at the Fano–Feshbach resonance by quantum design. Condens. Matter 2023, 8, 78. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Logvenov, G.; Campi, G. High-Tc superconducting dome in artificial heterostructures made of nanoscale quantum building blocks. Phys. Rev. B 2024, 110, 184510. [Google Scholar] [CrossRef]
- Campi, G.; Logvenov, G.; Caprara, S.; Valletta, A.; Bianconi, A. Kondo versus Fano in superconducting artificial high-Tc heterostructures. Condens. Matter 2024, 9, 43. [Google Scholar] [CrossRef]
- Ahmad, H.G.; Massarottti, D.; Tafuri, F.; Logvenov, G.; Bianconi, A.; Campi, G. Josephson coupling in lanthanum-based cuprate superlattices. APL Quantum 2025, 2, 016113. [Google Scholar] [CrossRef]
- Campi, G.; Alimenti, A.; Logvenov, G.; Smith, G.A.; Balakirev, F.; Lee, S.-E.; Balicas, L.; Silva, E.; Ummarino, G.A.; Midei, G.; et al. Upper critical magnetic field and multiband superconductivity in artificial high-Tc superlattices of nano quantum wells. Phys. Rev. Mater. 2025, 9, 074204. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Sboychakov, A.O.; Rakhmanov, A.L.; Kugel, K.I. Intrinsic arrested nanoscale phase separation near a topological Lifshitz transition in strongly correlated two-band metals. Supercond. Sci. Technol. 2015, 28, 024005. [Google Scholar] [CrossRef]
- Campi, G.; Innocenti, D.; Bianconi, A. CDW and similarity of the Mott insulator-to-metal transition in cuprates with the gas-to-liquid-liquid transition in supercooled water. J. Supercond. Nov. Magn. 2015, 28, 1355–1363. [Google Scholar] [CrossRef]
- Zhao, G.M.; Conder, K.; Keller, H.; Müller, K.A. Oxygen isotope effects in: Evidence for polaronic charge carriers and their condensation. J. Phys. Condens. Matter 1998, 10, 9055. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Karppinen, M.; Yamauchi, H. Control of the charge inhomogeneity and high-Tc superconducting properties in homologous series of multi-layered copper oxides. Mater. Sci. Eng. R Rep. 1999, 26, 51–96. [Google Scholar] [CrossRef]
- Karppinen, M.; Kotiranta, M.; Yamauchi, H.; Nachimuthu, P.; Liu, R.S.; Chen, J.M. O K-edge and Cu L23-edge XANES study on the concentration and distribution of holes in the (Pb2/3Cu1/3)3Sr2(Y,Ca)Cu2O8+z superconductive phase. Phys. Rev. B 2001, 63, 184507. [Google Scholar] [CrossRef]
- Karppinen, M.; Yamauchi, H. Hole-doping routes for understanding the relationship between atomic arrangements and superconductivity properties in multi-layered copper oxides. Int. J. Inorg. Mater. 2000, 2, 589–599. [Google Scholar] [CrossRef]
- Marezio, M.; Chmaissem, O.; Bougerol, C.; Karppinen, M.; Yamauchi, H.; Geballe, T.H. Overdoped cuprates with high-temperature superconducting transitions. APL Mater. 2013, 1, 021103. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Takashige, M.; Müller, K.A. Preparation and characterization of alkaline-earth substituted superconducting La2CuO4. Mater. Res. Bull. 1987, 22, 819–827. [Google Scholar] [CrossRef]
- Campi, G.; Catricala, M.; Chita, G.; Barba, L.; Shi, L.; Zhao, J.; Jin, C.; Bianconi, A. Lattice quantum geometry controlling 118 K multigap superconductivity in heavily overdoped CuBa2Ca3Cu4O10+d. Phys. Rev. Mater. 2025, 9, 094801. [Google Scholar] [CrossRef]
- Egami, T. Competing interactions in complex oxides: Polaron stability in manganites and cuprates. AIP Conf. Proc. 2001, 554, 38–47. [Google Scholar] [CrossRef]
- Lanzara, A.; Saini, N.L.; Brunelli, M.; Natali, F.; Bianconi, A.; Radaelli, P.G.; Cheong, S.W. Crossover from large to small polarons across the metal-insulator transition in manganites. Phys. Rev. Lett. 1998, 81, 878. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L. Nanoscale lattice fluctuations in cuprates and manganites. In Superconductivity in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 287–330. [Google Scholar]
- Campi, G.; Poccia, N.; Joseph, B.; Bianconi, A.; Mishra, S.; Lee, J.; Roy, S.; Nugroho, A.A.; Buchholz, M.; Braden, M.; et al. Direct visualization of spatial inhomogeneity of spin stripes order in La1.72Sr0.28NiO4. Condens. Matter 2019, 4, 77. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Joseph, B.; Mishra, S.K.; Müller, L.; Zozulya, A.; Nugroho, A.A.; Roy, S.; Sprung, M.; Ricci, A. Nanoscale inhomogeneity of charge density waves dynamics in La2−xSrxNiO4. Sci. Rep. 2022, 12, 15964. [Google Scholar] [CrossRef]
- Li, J.; Yin, W.-G.; Wu, L.; Zhu, P.; Konstantinova, T.; Tao, J.; Yang, J.; Cheong, S.-W.; Carbone, F.; A Misewich, J.; et al. Dichotomy in ultrafast atomic dynamics as direct evidence of polaron formation in manganites. npj Quant. Mater. 2016, 1, 16026. [Google Scholar] [CrossRef]
- Nguepnang, J.V.; Teguimfouet, A.K.; Kenfack-Sadem, C.; Kenfack-Jiotsa, A. Polaron dynamic and decoherence in transition metal dichalcogenides under electric field. Indian J. Phys. 2022, 96, 2001–2010. [Google Scholar] [CrossRef]
- Kim, Y.H.; Foster, C.M.; Heeger, A.J. Polarons in high Tc superconductors: IRAV modes and electronic transitions to gap states as in conducting polymers. Synth. Met. 1989, 29, 603–608. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Polaron theory of nuclear relaxation in YBa2Cu4O8 and other metal oxides. Phys. C Supercond. 1991, 182, 327–332. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Kabanov, V.V.; Ray, D.K. Polaron theory of mid-infrared conductivity a numerical cluster solution. Phys. C Supercond. 1994, 224, 247–255. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Krebs, A.B. Polarons in high-temperature superconductors. Sov. Phys. Uspekhi 1992, 35, 345. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Normal state of strongly coupled electrons and phonons: Dielectric properties, vibrational excitations and application to high-Tc superconducting metal oxides. Phys. C Supercond. 1992, 191, 115–130. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Ranninger, J. Photoemission spectroscopy of the superconducting and normal state for polaronic systems. Phys. C Supercond. 1992, 198, 360–370. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Many-body effects in the normal-state polaron system. Phys. Rev. B 1992, 46, 2838. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Mott, N.F. Spin and Charge bipolaron kinetics of high-Tc superconductors. Int. J. Mod. Phys. B 1994, 8, 2075–2109. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Mott, N.F. Polarons and Bipolarons; World Scientific: Singapore, 1995. [Google Scholar] [CrossRef]
- Alexandrov, A. Bipolaron theory of high-T oxides. In Anharmonic Properties of High-tc Cuprates-Proceedings of the International Workshop; World Scientific: Singapore, 1995; p. 179. [Google Scholar]
- Alexandrov, A.S. Bipolaron anisotropic flat bands, Hall mobility edge, and metal-semiconductor duality of overdoped high-Tc oxides. Phys. Rev. B 1996, 53, 2863. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Kabanov, V.V. Theory of superconducting Tc of doped fullerenes. Phys. Rev. B 1996, 54, 3655. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Dent, C.J. Angle-resolved photoemission in doped charge-transfer Mott insulators. Phys. Rev. B 1999, 60, 15414. [Google Scholar] [CrossRef]
- Alexandrov, A.S. d-wave Bose–Einstein condensate and tunnelling in superconducting cuprates. Phys. C Supercond. 1998, 305, 46–56. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Mott insulator–high Tc bipolaronic superconductor transition in cuprates. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 356, 197–209. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Polaron dynamics and bipolaron condensation in cuprates. Phys. Rev. B 2000, 61, 12315. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Sricheewin, C. Green’s and spectral functions of small Fröhlich polaron. Europhys. Lett. 2000, 51, 188. [Google Scholar] [CrossRef][Green Version]
- Alexandrov, A.S. Strong-coupling theory of high-temperature superconductivity. AIP Conf. Proc. 2001, 580, 1–95. [Google Scholar][Green Version]
- Alexandrov, A.S. Breakdown of the Migdal-Eliashberg theory in the strong-coupling adiabatic regime. Europhys. Lett. 2001, 56, 92. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Kornilovitch, P.E. Superlight bipolarons explain the high superconducting temperature. J. Supercond. 2002, 15, 403–408. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Kornilovitch, P.E. High-temperature superconductivity and charge segregation in a model with strong long-range electron–phonon and Coulomb interactions. Phys. Lett. A 2002, 299, 650–655. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Boson-Fermion Mixtures, d-Wave Condensate, and Tunneling in Cuprates. In Stripes and Related Phenomena; Springer: Boston, MA, USA, 2002; pp. 159–167. [Google Scholar]
- Alexandrov, A.S.; Devreese, J.T. Lattice polaron. In Advances in Polaron Physics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 53–95. [Google Scholar]
- Alexandrov, A.S.; Devreese, J.T. Advances in Polaron Physics; Springer Series in Solid-State Sciences (SSSOL); Springer: Berlin/Heidelberg, Germany, 2010; Volume 159. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Strong-coupling superconductivity beyond BCS and the key pairing interaction in cuprate superconductors. J. Phys. Conf. Ser. 2011, 286, 012012. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Devreese, J.T. Multipolaron Problem. In Advances in Polaron Physics; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2010; Volume 159. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Theory of high-temperature superconductivity in doped polar insulators. Europhys. Lett. 2011, 95, 27004. [Google Scholar] [CrossRef]
- Alexandrov, A.S. High-temperature superconductivity: The explanation. Phys. Scr. 2011, 83, 038301. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Devreese, J.T. Continuum polaron. In Advances in Polaron Physics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 11–52. [Google Scholar]
- Alexandrov, A.S. Strong-coupling theory of high-temperature superconductivity and colossal magnetoresistance. Strongly Correl. Electron Mater. Phys. Nanoeng. 2005, 5932, 18–32. [Google Scholar]
- Alexandrov, A.S. Nonadiabatic polaronic superconductivity in MgB2 and cuprates. Phys. C Supercond. 2001, 363, 231–236. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Bratkovsky, A.M. Giant thermopower and figure of merit of semiconducting polaronic nanolayers. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 153204. [Google Scholar] [CrossRef][Green Version]
- Alexandrov, A.S. Polarons in complex oxides and molecular nanowires. In Molecular Nanowires and Other Quantum Objects; Springer: Dordrecht, The Netherlands, 2003; pp. 151–166. [Google Scholar][Green Version]
- Alexandrov, A.S. Lattice polarons and switching in molecular nanowires and quantum dots. In Nanotechnology for Electronic Materials and Devices; Springer: Boston, MA, USA, 2007; pp. 305–356. [Google Scholar][Green Version]
- Salje, E.K.; Alexandrov, A.S.; Liang, W.Y. Polarons and Bipolarons in High-Tc Superconductors and Related Materials; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar][Green Version]
- Ciuchi, S.; De Pasquale, F.; Fratini, S.; Feinberg, D. Dynamical mean-field theory of the small polaron. Phys. Rev. B 1997, 56, 4494. [Google Scholar] [CrossRef]
- Ciuchi, S.; De Pasquale, F. Dynamical mean field theory of the CDW phase. J. Phys. IV 1998, 8, Pr6-99. [Google Scholar] [CrossRef]
- Ciuchi, S.; De Pasquale, F. Charge-ordered state from weak to strong coupling. Phys. Rev. B 1999, 59, 5431. [Google Scholar] [CrossRef]
- Perali, A.; Grimaldi, C.; Pietronero, L. Nonadiabatic pairing effects for tight-binding electrons interacting with phonons. Phys. Rev. B 1998, 58, 5736. [Google Scholar] [CrossRef]
- Capone, M.; Ciuchi, S.; Grimaldi, C. The small polaron crossover: Role of dimensionality. In Stripes and Related Phenomena; Springer: Boston, MA, USA, 2000; pp. 169–174. [Google Scholar]
- Perali, A.; Pieri, P.; Strinati, G.C.; Castellani, C. Pseudogap and spectral function from superconducting fluctuations to the bosonic limit. Phys. Rev. B 2002, 66, 024510. [Google Scholar] [CrossRef]
- Plakida, N. High-Temperature Cuprate Superconductors: Experiment, Theory, and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Shengelaya, A.; Müller, K.A. Superconductivity in oxides generated by percolating electron or hole bipolarons. J. Supercond. Nov. Magn. 2019, 32, 3–6. [Google Scholar] [CrossRef]
- Shengelaya, A.; Bruun, M.; Kochelaev, B.I.; Safina, A.; Conder, K.; Müller, K.A. Metallic phase in lightly doped La2−xSrxCuO4 observed by electron paramagnetic resonance. Phys. Rev. Lett. 2004, 93, 017001. [Google Scholar] [CrossRef]
- Mihailovic, D.; Kabanov, V.V.; Müller, K.A. The attainable superconducting Tc in a model of phase coherence by percolating. Europhys. Lett. 2002, 57, 254. [Google Scholar] [CrossRef]
- Müller, K.A. From single- to bipolarons with Jahn–Teller character and metallic cluster-stripes in hole-doped cuprates. In Handbook of High-Temperature Superconductivity; Schrieffer, J.R., Brooks, J.S., Eds.; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Müller, K.A. The impact of ESR (EPR) on the understanding of the cuprates and their superconductivity. EPR Newsl. 2012, 22, 5–6. [Google Scholar]
- Lanzara, A.; Bogdanov, P.V.; Zhou, X.J.; Kellar, S.A.; Feng, D.L.; Lu, E.D.; Yoshida, T.; Eisaki, H.; Fujimori, A.; Kishio, K.; et al. Evidence for ubiquitous strong electron–phonon coupling in high-temperature superconductors. Nature 2001, 412, 510–514. [Google Scholar] [CrossRef]
- Kusar, P.; Demsar, J.; Mihailovic, D.; Sugai, S. A systematic study of femtosecond quasiparticle relaxation processes in La2−xSrxCuO4. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 014544. [Google Scholar] [CrossRef]
- Calvani, P.; Capizzi, M.; Lupi, S.; Maselli, P.; Ruzicka, B. Polaronic optical absorption in semiconducting and superconducting oxides. Czechoslov. J. Phys. 1996, 46 (Suppl. S3), 1247–1248. [Google Scholar] [CrossRef]
- Liarokapis, E.; Lampakis, D.; Palles, D.; Karpinski, J.; Panagopoulos, C. A Raman view of local lattice distortions and charge transfer in cuprates. J. Phys. Chem. Solids 2006, 67, 2065–2071. [Google Scholar] [CrossRef]
- Aoki, R.; Murakami, H. Tunneling spectrum analysis regarding phonon contribution to high Tc Cooper pairing. J. Low Temp. Phys. 1996, 105, 1231–1236. [Google Scholar] [CrossRef]
- Aoki, R.; Murakami, H.; Shirai, M.; Svistunov, V.M.; Dyachenko, A.L.; Afanassyev, D.N. Tunneling spectrum indicating phonon contribution to high Tc oxide superconductivity. Czechoslov. J. Phys. 1996, 46 (Suppl. 3), 1339–1340. [Google Scholar] [CrossRef]
- Aoki, R.; Murakami, H.; Shirai, M.; Svistunov, V.M.; Afanassyev, D.N. Optical phonon contribution to the high Tc cooper-pairing investigated by tunneling spectrum. Phys. C Supercond. Appl. 1997, 282–287, 979–980. [Google Scholar] [CrossRef]
- Murakami, Y.; Werner, P.; Tsuji, N.; Aoki, H. Ordered phases in the Holstein-Hubbard model: Interplay of strong Coulomb interaction and electron-phonon coupling. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 125126. [Google Scholar] [CrossRef]
- Mihailovic, D.; Müller, K.A. The two-component paradigm for superconductivity in the cuprates. In High-Tc Superconductivity 1996: Ten Years After the Discovery; Springer: Dordrecht, The Netherlands, 1997; pp. 243–256. [Google Scholar]
- Shengelaya, A.; Bruun, M.; Kochelaev, B.I.; Safina, A.; Conder, K.; Müller, K.A. Microscopic Phase Separation and two type of quasiparticles in lightly doped La2−xSrxCuO4 observed by electron paramagnetic resonance. In Symmetry and Heterogeneity in High Temperature Superconductors. Proceedings of the NATO Advanced Study Research. Workshop on Symmetry and Heterogeneity in High Temperature Superconductors Erice, Sicily, Italy, 4–10 October 2003; Springer: Dordrecht, The Netherlands, 2006; pp. 105–116. [Google Scholar]
- Mihailovic, D.; Stevens, C.; Demsar, J.; Podobnik, B.; Smith, D.C.; Ryan, J.F. Evidence for polarons and itinerant carriers in superconductivity from time-resolved optical measurements on YBa2Cu3O7−d. J. Supercond. 1997, 10, 337–341. [Google Scholar] [CrossRef]
- Bishop, A.R.; Mihailovic, D.; De Leon, J.M. Signatures of mesoscopic Jahn–Teller polaron inhomogeneities in high-temperature superconductors. J. Phys. Condens. Matter 2003, 15, L169. [Google Scholar] [CrossRef]
- Mihailovic, D. Optical experimental evidence for a universal length scale for the dynamic charge inhomogeneity of cuprate superconductors. Phys. Rev. Lett. 2005, 94, 207001. [Google Scholar] [CrossRef]
- Liarokapis, E. Phase separation in cuprates induced by doping, hydrostatic pressure or atomic substitution. In Symmetry and Heterogeneity in High Temperature Superconductors: Proceedings of the NATO Advanced Study Research. Workshop on Symmetry and Heterogeneity in High Temperature Superconductors Erice, Sicily, Italy, 4–10 October 2003; Springer: Dordrecht, The Netherlands, 2006; pp. 117–132. [Google Scholar]
- Tajima, H.; Yerin, Y.; Perali, A.; Pieri, P. Enhanced critical temperature, pairing fluctuation effects, and BCS-BEC crossover in a two-band Fermi gas. Phys. Rev. B 2019, 99, 180503. [Google Scholar] [CrossRef]
- Yerin, Y.; Tajima, H.; Pieri, P.; Perali, A. Coexistence of giant Cooper pairs with a bosonic condensate and anomalous behavior of energy gaps in the BCS-BEC crossover of a two-band superfluid Fermi gas. Phys. Rev. B 2019, 100, 104528. [Google Scholar] [CrossRef]
- Tajima, H.; Hanai, R.; Ohashi, Y. Strong-coupling corrections to spin susceptibility in the BCS-BEC-crossover regime of a superfluid Fermi gas. Phys. Rev. A 2016, 93, 013610. [Google Scholar] [CrossRef]
- Tajima, H.; Perali, A.; Pieri, P. BCS-BEC crossover and pairing fluctuations in a two band superfluid/superconductor: AT matrix approach. Condens. Matter 2020, 5, 10. [Google Scholar] [CrossRef]
- Tajima, H.; Pieri, P.; Perali, A. Hidden pseudogap and excitation spectra in a strongly coupled two-band superfluid/superconductor. Condens. Matter 2021, 6, 8. [Google Scholar] [CrossRef]
- Tajima, H. Precursor of superfluidity in a strongly interacting Fermi gas with negative effective range. Phys. Rev. A 2018, 97, 043613. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, J.; Cai, S.; Zhao, J.; Gu, G.; Lin, C.; Yan, H.; Huang, C.; Yang, C.; Long, S.; et al. Quantum phase transition from superconducting to insulating-like state in a pressurized cuprate superconductor. Nat. Phys. 2022, 18, 406–410. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Shanenko, A.A.; Kaun, C.C.; Peeters, F.M. Metallic nanograins: Spatially nonuniform pairing induced by quantum confinement. Phys. Rev. B 2011, 83, 214509. [Google Scholar] [CrossRef]
- Saraiva, T.T.; Cavalcanti, P.J.; Vagov, A.; Vasenko, A.S.; Perali, A.; Dell’Anna, L.; Shanenko, A.A. Multiband material with a quasi-1D band as a robust high-temperature superconductor. Phys. Rev. Lett. 2020, 125, 217003. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Liu, Y.; Zhuang, C.; Shi, J.; Yao, Y.; Massidda, S.; Monni, M.; Jia, Y.; Xi, X.; Li, Q.; et al. Fully band-resolved scattering rate in MgB2 revealed by the nonlinear hall effect and magnetoresistance measurements. Phys. Rev. Lett. 2008, 101, 067001. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liu, B.T.; Hu, Y.F.; Chen, J.; Gao, H.; Shan, L.; Wen, H.H.; Pogrebnyakov, A.V.; Redwing, J.W.; Xi, X.X. Large anisotropic normal-state magnetoresistance in clean MgB2 thin films. Phys. Rev. Lett. 2006, 96, 167003. [Google Scholar] [CrossRef]
- Salasnich, L.; Shanenko, A.A.; Vagov, A.; Aguiar, J.A.; Perali, A. Screening of pair fluctuations in superconductors with coupled shallow and deep bands: A route to higher-temperature superconductivity. Phys. Rev. B 2019, 100, 064510. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Saraiva, T.T.; Vagov, A.; Vasenko, A.S.; Perali, A. Suppression of fluctuations in a two-band superconductor with a quasi-one-dimensional band. Phys. Rev. B 2022, 105, 214527. [Google Scholar] [CrossRef]
- Krasavin, A.; Vagov, A.; Vasenko, A.; Stolyarov, V.; Shanenko, A. Suppression of superconducting fluctuations in multiband superconductors as a mechanism for increasing the critical temperature (brief review). JETP Lett. 2024, 119, 233–250. [Google Scholar] [CrossRef]
- Bianconi, G. Superconductor-insulator transition on annealed complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 85, 061113. [Google Scholar] [CrossRef]
- Bianconi, G. Enhancement of Tc in the superconductor–insulator phase transition on scale-free networks. J. Stat. Mech. Theory Exp. 2012, 2012, P07021. [Google Scholar] [CrossRef]
- Bianconi, G. Superconductor-insulator transition in a network of 2d percolation clusters. Europhys. Lett. 2013, 101, 260. [Google Scholar] [CrossRef]
- Neverov, V.D.; Lukyanov, A.E.; Krasavin, A.V.; Vagov, A.; Croitoru, M.D. Spatial correlations in disorder: Impact on the superconducting critical temperature. Phys. Rev. B 2025, 111, 184514. [Google Scholar] [CrossRef]
- Maśka, M.M.; Śledź, I.D.Z.; Czajka, K.; Mierzejewski, M. Inhomogeneity-induced enhancement of the pairing interaction in cuprate superconductors. Phys. Rev. Lett. 2007, 99, 147006. [Google Scholar] [CrossRef]
- Nunner, T.S.; Andersen, B.M.; Melikyan, A.; Hirschfeld, P.J. Dopant-modulated pair interaction in cuprate superconductors. Phys. Rev. Lett. 2005, 95, 177003. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Zachmann, M.; Vagov, A.; Axt, V.; Shanenko, A.; Kettmann, P.; Papenkort, T.; Kuhn, T. Coherent dynamics of confinement-induced multiband superconductors. Phys. C Supercond. Appl. 2014, 503, 183–186. [Google Scholar] [CrossRef]
- Neverov, V.D.; Lukyanov, A.E.; Krasavin, A.V.; Vagov, A.; Croitoru, M.D. The impact of short-range (gaussian) disorder correlations on superconducting characteristics. Condens. Matter 2024, 9, 6. [Google Scholar] [CrossRef]
- Neverov, V.D.; Lukyanov, A.E.; Krasavin, A.V.; Vagov, A.; Lvov, B.G.; Croitoru, M.D. Exploring disorder correlations in superconducting systems: Spectroscopic insights and matrix element effects. Beilstein J. Nanotechnol. 2024, 15, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Arutyunov, K.Y.; Zavialov, V.V.; Sedov, E.A.; Golokolenov, I.A.; Zarudneva, A.A.; Shein, K.V.; Trun’KIn, I.N.; Vasiliev, A.L.; Konstantinidis, G.; Stavrinidis, A.; et al. Nanoarchitecture: Toward quantum-size tuning of superconductivity. Phys. Status Solidi RRL 2018, 13, 1800317. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Croitoru, M.D.; Vagov, A.; Peeters, F.M. Giant drop in the Bardeen-Cooper-Schrieffer coherence length induced by quantum size effects in superconducting nanowires. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 82, 104524. [Google Scholar] [CrossRef]
- Pickett, W.E. Colloquium: Room temperature superconductivity: The roles of theory and materials design. Rev. Mod. Phys. 2023, 95, 021001. [Google Scholar] [CrossRef]
- Kovalenko, A.N. High-temperature superconductivity: From macro- to nanoscale structures. Nanosyst. Phys. Chem. Math. 2016, 7, 941–970. [Google Scholar] [CrossRef]
- Confalone, T.; Sardo, F.L.; Lee, Y.; Shokri, S.; Serpico, G.; Coppo, A.; Chirolli, L.; Vinokur, V.M.; Brosco, V.; Vool, U.; et al. Cuprate twistronics for quantum hardware. Adv. Quantum Technol. 2025, 2500203. [Google Scholar] [CrossRef]
- Martini, M.; Lee, Y.; Confalone, T.; Shokri, S.; Saggau, C.N.; Wolf, D.; Gu, G.; Watanabe, K.; Taniguchi, T.; Montemurro, D.; et al. Twisted cuprate van der Waals heterostructures with controlled Josephson coupling. Mater. Today 2023, 67, 106–112. [Google Scholar] [CrossRef]
- Confalone, T.; Shokri, S.; Sardo, F.L.; Vinokur, V.M.; Nielsch, K.; Golam, H.; Poccia, N. Challenges in the electrical engineering of cuprate twistronics. Nat. Rev. Electr. Eng. 2025, 2, 73–74. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bussmann-Holder, A.; Haase, J.; Keller, H.; Kremer, R.K.; Mukhin, S.I.; Menushenkov, A.P.; Ivanov, A.; Kuznetsov, A.; Velasco, V.; Conradson, S.D.; et al. Nanoscale Lattice Heterostructure in High-Tc Superconductors. Condens. Matter 2025, 10, 56. https://doi.org/10.3390/condmat10040056
Bussmann-Holder A, Haase J, Keller H, Kremer RK, Mukhin SI, Menushenkov AP, Ivanov A, Kuznetsov A, Velasco V, Conradson SD, et al. Nanoscale Lattice Heterostructure in High-Tc Superconductors. Condensed Matter. 2025; 10(4):56. https://doi.org/10.3390/condmat10040056
Chicago/Turabian StyleBussmann-Holder, Annette, Jürgen Haase, Hugo Keller, Reinhard K. Kremer, Sergei I. Mukhin, Alexey P. Menushenkov, Andrei Ivanov, Alexey Kuznetsov, Victor Velasco, Steven D. Conradson, and et al. 2025. "Nanoscale Lattice Heterostructure in High-Tc Superconductors" Condensed Matter 10, no. 4: 56. https://doi.org/10.3390/condmat10040056
APA StyleBussmann-Holder, A., Haase, J., Keller, H., Kremer, R. K., Mukhin, S. I., Menushenkov, A. P., Ivanov, A., Kuznetsov, A., Velasco, V., Conradson, S. D., Campi, G., & Bianconi, A. (2025). Nanoscale Lattice Heterostructure in High-Tc Superconductors. Condensed Matter, 10(4), 56. https://doi.org/10.3390/condmat10040056










