Previous Article in Journal
Impact of Molecular π-Bridge Modifications on Triphenylamine-Based Donor Materials for Organic Photovoltaic Solar Cells
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Condensed Matter
Volume 10
Issue 4
10.3390/condmat10040053
condensedmatter-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Exploring Low Energy Excitations in the d5 Iridate Double Perovskites La2BIrO6 (B = Zn, Mg)

by
Abhisek Bandyopadhyay
1,2,*,
Dheeraj Kumar Pandey
2,
Carlo Meneghini
3,
Anna Efimenko
4,
Marco Moretti Sala
5 and
Sugata Ray
1
1
School of Materials Science, Indian Association for the Cultivation of Science, Jadavpur, Kolkata 700032, West Bengal, India
2
Department of Physics, Ramashray Baleshwar College (A Constituent Unit of L. N. Mithila University, Darbhanga), Dalsingsarai, Samastipur 848114, Bihar, India
3
Dipartimento di Scienze, Universitá Roma Tre, Via della Vasca Navale 84, 00146 Rome, Italy
4
European Synchrotron Radiation Facility (ESRF)–The European Synchrotron, 71 Avenue des Martyrs, 38000 Grenoble, France
5
Dipartimento di Fisica, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133 Milano, Italy
*
Author to whom correspondence should be addressed.
Condens. Matter 2025, 10(4), 53; https://doi.org/10.3390/condmat10040053
Submission received: 31 August 2025 / Revised: 26 September 2025 / Accepted: 29 September 2025 / Published: 6 October 2025
(This article belongs to the Section Quantum Materials)
Browse Figures
Versions Notes

Abstract

We experimentally investigate the structural, magnetic, transport, and electronic properties of two d5 iridate double perovskite materials La2BIrO6 (B = Mg, Zn). Notably, despite similar crystallographic structure, the two compounds show distinctly different magnetic behaviors. The M = Mg compound shows an antiferromagnetic-like linear field-dependent isothermal magnetization below its transition temperature, whereas the M = Zn counterpart displays a clear hysteresis loop followed by a noticeable coercive field, indicative of ferromagnetic components arising from a non-collinear Ir spin arrangement. The local structure studies authenticate perceptible M/Ir antisite disorder in both systems, which complicates the magnetic exchange interaction scenario by introducing Ir-O-Ir superexchange pathways in addition to the nominal Ir-O-B-O-Ir super-superexchange interactions expected for an ideally ordered structure. While spin–orbit coupling (SOC) plays a crucial role in establishing insulating behavior for both these compounds, the rotational and tilting distortions of the IrO6 (and MO6) octahedral units further lift the ideal cubic symmetry. Finally, by measuring the Ir-L3 edge resonant inelastic X-ray scattering (RIXS) spectra for both the compounds, giving evidence of spin–orbit-derived low-energy inter-J-state (intra t2g) transitions (below ~1 eV), the charge transfer (O 2p → Ir 5d), and the crystal field (Ir t2g → eg) excitations, we put forward a qualitative argument for the interplay among effective SOC, non-cubic crystal field, and intersite hopping in these two compounds.

1. Introduction

In contrast to the extensively studied strongly correlated 3d transition metal oxides, the heavier 5d transition metal oxides with spatially extended 5d orbitals remained largely unexplored until the puzzling Mott insulating ground state of a layered tetravalent d5 iridate Sr2IrO4 had been demonstrated by Kim et al. within the framework of a unique combination of strong SOC, large crystal electric field, and moderate on-site Coulomb repulsion [1]. The strong SOC splits the triply degenerate t2g orbitals of a low spin Ir4+ (5d5) ion into completely filled Jeff = 3/2 quartet and half-filled narrow Jeff = 1/2 doublet bands. The Jeff = 1/2 band is further split into an occupied lower Hubbard and an empty upper Hubbard band, introducing an energy gap in between them in presence of a moderate Coulomb U. It is noteworthy that under strong SOC, only the total angular momentum quantum number MJ (=Σmj) serves as ‘good quantum number’. Thus, the complex magnetic and electronic ground states of the 5d iridium oxides can be effectively described within J-picture. Consequently, these 5d iridates offer a suitable material playground for hosting a plethora of possibilities in terms of the ground states arising from delicate balance between SOC, crystal field effects, electron correlation, Hund’s exchange, noncubic crystal distortions, electron hopping, bandwidth, and superexchange interactions within a variety of crystal structures and lattice geometries [2,3,4,5,6,7]. Among them, Jeff = 1 2 magnetic Mott state has emerged as a particularly intriguing subject in recent condensed matter research of Ir4+-containing oxide materials, owing to its capacity to host a variety of unconventional magnetic phases [4,7].
Double perovskite (DP) oxides of general chemical formula A2BB’O6, on the other hand, are considered to be the most intriguing structural variant of inorganic materials for the design of novel magnetic [8] and multiferroic [9] materials by proper choice of B and B’. In this structure class, the ground state magnetic responses are mainly controlled by the B/B’ cations while A is usually nonmagnetic di- or tri-valent cations. The perfect rock-salt ordering of the corner-sharing BO6 and B’O6 octahedra introduces two interpenetrating fcc sublattices of B and B’, each of which forms a distinct frustrated tetrahedral network (as shown in Figure 1). So, the interplay of various magnetic exchange interactions, ranging from short-range nearest-neighbor (B-O-B’) to next-nearest-neighbor (B-O-B’-O-B) interactions to long-range B/B’-sublattice orderings, can lead to unique magnetic properties [10,11,12,13,14,15,16]. In addition, depending on the lattice geometry and the deviation of the B–O–B′ bond angle from the ideal 180°, as well as the presence of strong spin–orbit coupling (if either B or B′ is a 4d/5d transition metal), anisotropic exchange interactions, e.g., the Dzyaloshinskii–Moriya antisymmetric exchange, may emerge, leading to spin canting in the magnetic ground state [17,18]. In this context, Ir-based DPs with the general chemical formula La2BIr4+O6 (where B is a magnetic or nonmagnetic divalent cation) are promising and provide a fertile ground for diverse magnetic responses. Among them, compounds with B = Mg and Zn exhibit A-type antiferromagnetic (AFM) order [14,15,19]; B = Mn is ferromagnetic [20]; B = Co, Ni, and Fe possess noncollinear magnetism with either canted or helical spin structures [21,22]; and the B = Cu compound is ordered below 74 K with a spin structure comprising two orthogonal AFM sublattices and a very small canted moment [11]. Moreover, considering that Ir4+ ions are largely separated by B-site cations in a perfectly B-site ordered DP, the DP compounds with Ir at B’- and any nonmagnetic cation at B-sites are particularly suited for assessing the pure Jeff = 1 2 character in these d5 iridates.
In this work, we experimentally investigated the local (XAFS) and periodic (XRD) structures, magnetic, and electrical transport properties, as well as the Ir-L3 edge resonant-inelastic-X-ray-scattering (RIXS) spectra on two d5 iridate double perovskites La2BIrO6 (B = Mg, Zn; hereafter abbreviated as LMIO and LZIO, respectively). Despite the similar crystallographic structure, these two compounds surprisingly show difference in the magnetic responses. In field-dependent isothermal magnetization measurements, the LMIO system shows antiferromagnetic-like strictly linear M–H behavior below its transition temperature, while prominent hysteresis loops along with the significant coercivity, indicative of ferromagnetic components, appear in case of the LZIO compound below its magnetic ordering temperature. While SOC plays a crucial role in establishing insulating transport for both the samples, the structural analysis reveals the presence of tilting and rotational distortions in the IrO6 octahedra in both the compounds, which contribute to lifting out the cubic symmetry. Finally, by carrying out high-resolution low-energy and low-resolution high-energy Ir L3-edge RIXS (resonant inelastic X-ray scattering) measurements, we probed the spin–orbit-derived intra-t2g (i.e., inter-J-state) transitions (below ~1 eV), the charge transfer (O 2p  → Ir 5d), and the crystal field (Ir t2g  →  eg) excitations. These observations enable us to make a qualitative description on the effective SOC of Ir, non-cubic crystal field, Hund’s exchange, and intersite hopping in these two compounds in light of the novel Jeff = 1 2 state.

2. Results and Discussion

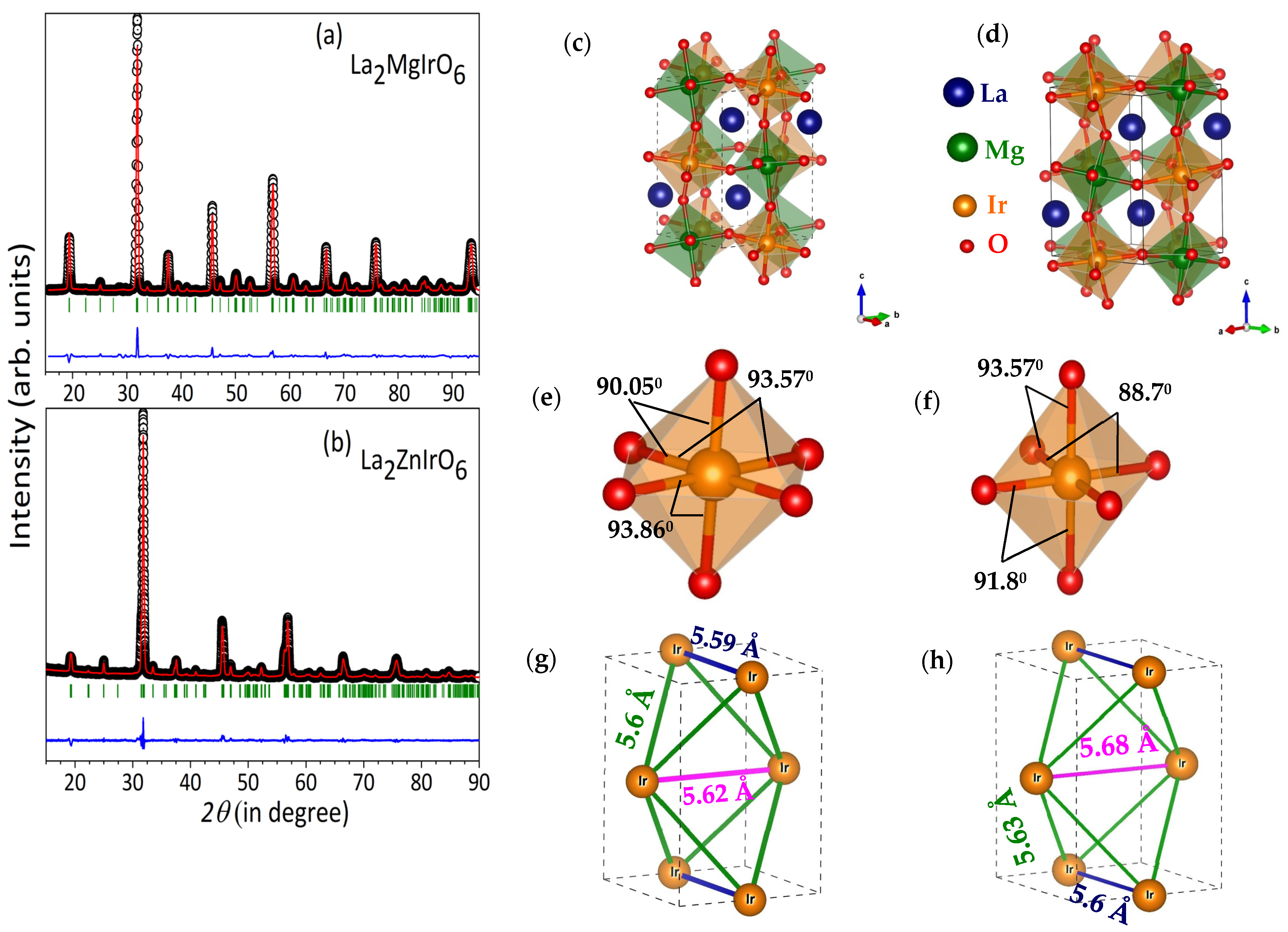
2.1. Crystal Structure from X-Ray Powder Diffraction (XRPD)

The room-temperature crystal structures of both compounds were determined by analyzing the X-ray powder diffraction (XRPD) patterns obtained from their respective polycrystalline samples, as shown in Figure 2a,b.
The Rietveld refinements clearly reveal that both LMIO and LZIO samples crystallize in a pure single phase within the monoclinic P21/n space group. The periodic (crystallographic) structure indicates the B-site alternatively occupied by Mg/Zn and Ir (Figure 2c,d) giving rise to a monoclinic distorted double perovskite structure, where the larger La cations are accommodated close to the center of the pseudocubic cavity, surrounded by the octahedral IrO6 /BO6 units. Each of the (Mg/Zn)O6 and IrO6 octahedral motifs are arranged separately in an fcc lattice, which then constructs distinct edge-shared tetrahedral networks of Ir- (Figure 1) and Zn/Mg. In addition, careful structural analysis clearly demonstrates B/B’ antisite disorder in both La2ZnIrO6 (~8%) and La2MgIrO6 (~10%), which is larger compared to the previous report [19] but resembles the neutron powder diffraction results on the similar DP compounds Sr2MgIrO6 and Sr2ZnIrO6 [23]. The refined lattice parameters, atomic positions, site-occupancy, along with the goodness factors are tabulated in Table 1.
An important structural aspect in the DP class of materials is the presence of octahedral distortion which is determined by the Goldschmidt tolerance factor [24] based on the ionic radii of the A and B site atoms. In both LMIO and LZIO samples, the monoclinic distortions originating from (i) the inter-octahedral tilting, causing the deviation of Mg/Zn-O-Ir bond angle from 180° (Table 2) as well as (ii) the intra-octahedral bond rotations, causing the O-Ir-O and O-Mg/Zn-O bond angles are different from the ideal 90° or 180° (Figure 2e,f and Table 2). In addition, each Ir ion is acted upon by a local noncubic crystal field in both the materials due to the presence of three dissimilar Ir-O bond distances (see Figure 2e,f). All these factors naturally renormalize the effective SOC strength of Ir through modification in the bandwidth, hybridization, hopping, and crystal field effects, and consequently will cause redistribution of the Ir energy levels for both the systems. It is important to note at this point that since the magnetic interactions between the Ir moments are mediated via Ir-O-Mg/Zn-O-Ir super-superexchange pathways, the Ir-O-Mg(Zn) bond angles play a crucial role in the ground state magnetism of these two DP systems. Furthermore, as envisioned from Figure 2g,h, the isosceles triangular network of Ir in both the compounds would possibly weaken the geometric exchange frustration, thus influencing the nearest-neighbor magnetic exchange interaction strengths for all of the Ir sites [25,26].

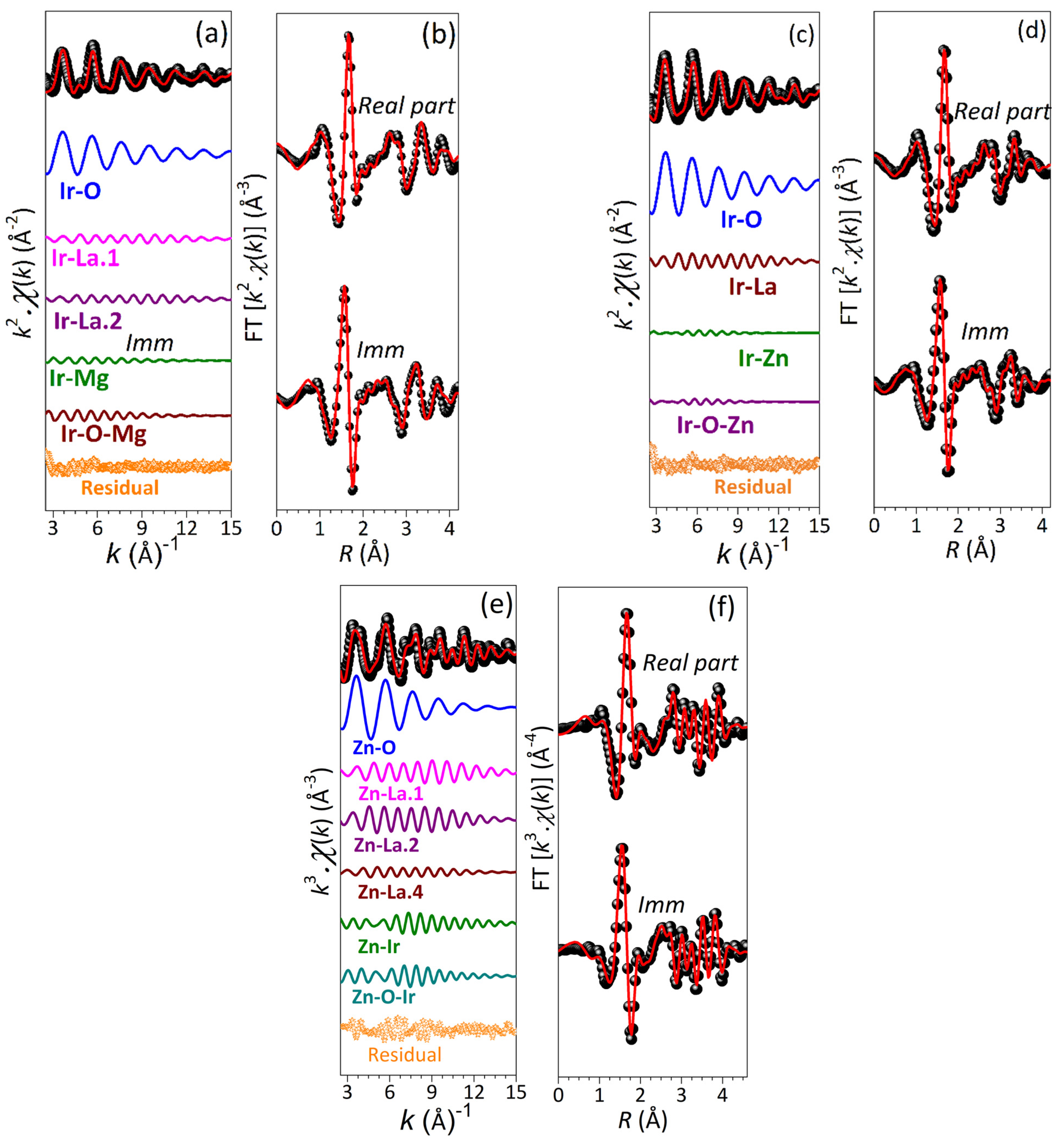
2.2. Local Structure from Extended X-Ray Absorption Fine Structure (EXAFS) Spectroscopic Study

In a perfectly B-site ordered double perovskite, each B cation is ideally surrounded by six B′ cations and no B neighbors. In contrast, in a completely disordered B-site configuration, B and B′ cations are randomly distributed, resulting in an average of three B and three B′ neighbors around each B/B′ site. The DP structure is known to be highly prone to antisite disorder [27,28], which can lead to local (non-periodic) chemical environments that differ from the globally ordered (periodic) structure revealed by crystallographic analysis [29,30,31]. Such local chemical disorder can significantly affect the physical properties of the material, potentially leading to unexpected differences in electronic and magnetic behaviors despite similar crystallographic frameworks. In such a backdrop, in order to confirm the local atomic distributions of both the DP iridates, the Ir L3-edge and the Zn K-edge EXAFS measurements were carried out. The k 2 -weighed EXAFS structural signals along with the theoretical best fit curves are shown in Figure 3a–f. The structural parameters, extracted from the Zn K as well as the Ir L3-edges EXAFS data analysis (see Figure 3), are summarized in Table 3.
The average local structure around Ir (in both LZIO and LMIO) and Zn (in LZIO) is consistent with the crystallographic structure obtained from XRD refinements. Specifically, the Ir L3-edge EXAFS analysis confirms a Mg/Zn-Ir antisite disorder of approximately 10% in both the samples. This finding is further confirmed by the Zn K-edge EXAFS data of LZIO, which coherently reports about 10% of local Zn-Ir chemical disorder around the Zn site.
For both the compounds, the average Ir-O bond lengths appear shorter compared to the average distances between Ir and nearest O lattice positions (being 2.02 Å and 2.14 Å for LMIO and LZIO, respectively).
The Ir-O nearest-neighbor distances are shorter in LMIO than LZIO, while the associated disorder, quantified by the mean square relative displacement (MSRD, σ 2 ), is very similar in both LMIO and LZIO samples. The relatively small MSRD values ( σ 2 ≃ 2 × 10 − 3 Å 2 ) indicate a well-defined and sharp Ir-O neighbor distribution in both of the cases. The Ir–Mg/Zn distributions are also comparable between the two samples. However, more pronounced differences emerge in the Ir–Mg/Zn next-nearest-neighbor region, where significantly larger disorder is observed in LZIO compared to LMIO. This different disorder may be related to the notably large MSRD of the Zn–O shell ( σ 2 ≃ 8 × 10 − 3 Å 2 ), suggesting a role of ZnO6 octahedra distortions. This trend is confirmed looking at the Zn-K edge results. Unfortunately, Mg-K edge EXAFS data are unavailable in LMIO because of the low Mg-K edge energy (EMg = 1303 eV) and the overlap with the La-MI edge (1362 eV).
From the perspective of the physical properties of these two DPs, our EXAFS data refinements clearly unfold the resulting ground state magnetic responses to be the outcome of predominant Ir-O-(Mg/Zn)-O-Ir next-nearest-neighbor conventional magnetic superexchange interactions plus the antisite disorder-driven magnetic exchange interactions through the Ir-O-Ir nearest-neighbor superexchange pathways [11,12,13,14,15,16,30,31,32,33,34].

2.3. Determination of Ir-Oxidation State from X-Ray Absorption near Edge Structure (XANES) Spectroscopy

Iridium can adopt 4+, 5+, and 6+ valence states in the octahedral symmetry typical of the perovskite and related compounds. Among them, Ir4+ and Ir6+ species are strongly magnetic [1,14,35,36], while Ir5+ is ideally nonmagnetic (Jeff = 0) or weakly magnetic [37,38,39]. The mixed-valent Ir4+/Ir5+ iridates host a wide variety of novel electronic and magnetic ground states [40,41,42,43]. Naturally the Ir-valence has a crucial role in determining the ground state physical properties of these iridates. So, to confirm the oxidation state of Ir in the two studied compounds, the Ir L3-edge XANES spectra were measured from the two samples, and the normalized spectra are presented in Figure 4a. The main peak in the pre-edge region, identified as a white-line features, correspond to an electric dipole-allowed 2p  → 5d transition of Ir. The weak shoulder in the low-energy side (dotted magenta arrows) of the respective white lines are very similar for both the compounds, as is also evident looking at the second derivative curves of the XANES spectra (Figure 4b).
There is no observable energy shift in the edge positions of these two compounds, suggesting that both samples have the same Ir-valence state. The corresponding second-derivative curves, as shown in Figure 4b, more precisely highlight the identical white-line features. A prominent doublet feature is evident in the respective second-derivative curves, and, importantly, the energy positions for both samples match exactly, as indicated by the green dotted lines in Figure 4b. In Oh symmetry, the two components of the Ir L3-edge white-line correspond to the 2 p → t 2 g (low-energy feature) and 2 p → e g (higher energy peak) transitions [44,45]. The relative intensity and peak shape corresponding to the 2 p → t 2 g transition closely match the previous reports [44,45] and hence confirm the expected 4+ oxidation state of Ir in both compounds. Notice that the shape and intensity of the contribution corresponding to the 2 p → e g transition are largely insensitive to the Ir-valence as, in low-spin configuration, the Ir-5d valence electrons preferentially occupy the lower energy t2g orbitals before occupying the higher-energy eg states.

2.4. Electrical Resistivity

The temperature-dependent electrical resistivity (ρ vs. T) between 180 and 400 K has been measured on both the samples and the results are shown in Figure 4c,d. Upon cooling, the electrical resistivity, ρ, increases continuously for both the compounds in a similar manner, indicating insulating behavior. Further, the collected ρ(T) curves were modeled using Arrhenius activated behavior, ρ(T) ~ exp(Δ/kBT) (Δ is the activation energy and kB is the Boltzmann constant) [46], shown in the insets to Figure 4c,d. In both of the cases, the Arrhenius fitting has been performed by considering two distinct regions, and the resulting two separate values of Δ, indicated by ΔI and ΔII for the two regions, are shown in the respective insets. Similarly to the many other iridates [1,38,47], the insulating character of both these materials reveals the crucial role of SOC on the electronic ground states. Our results are also in line with the previous literature reports [14,15].

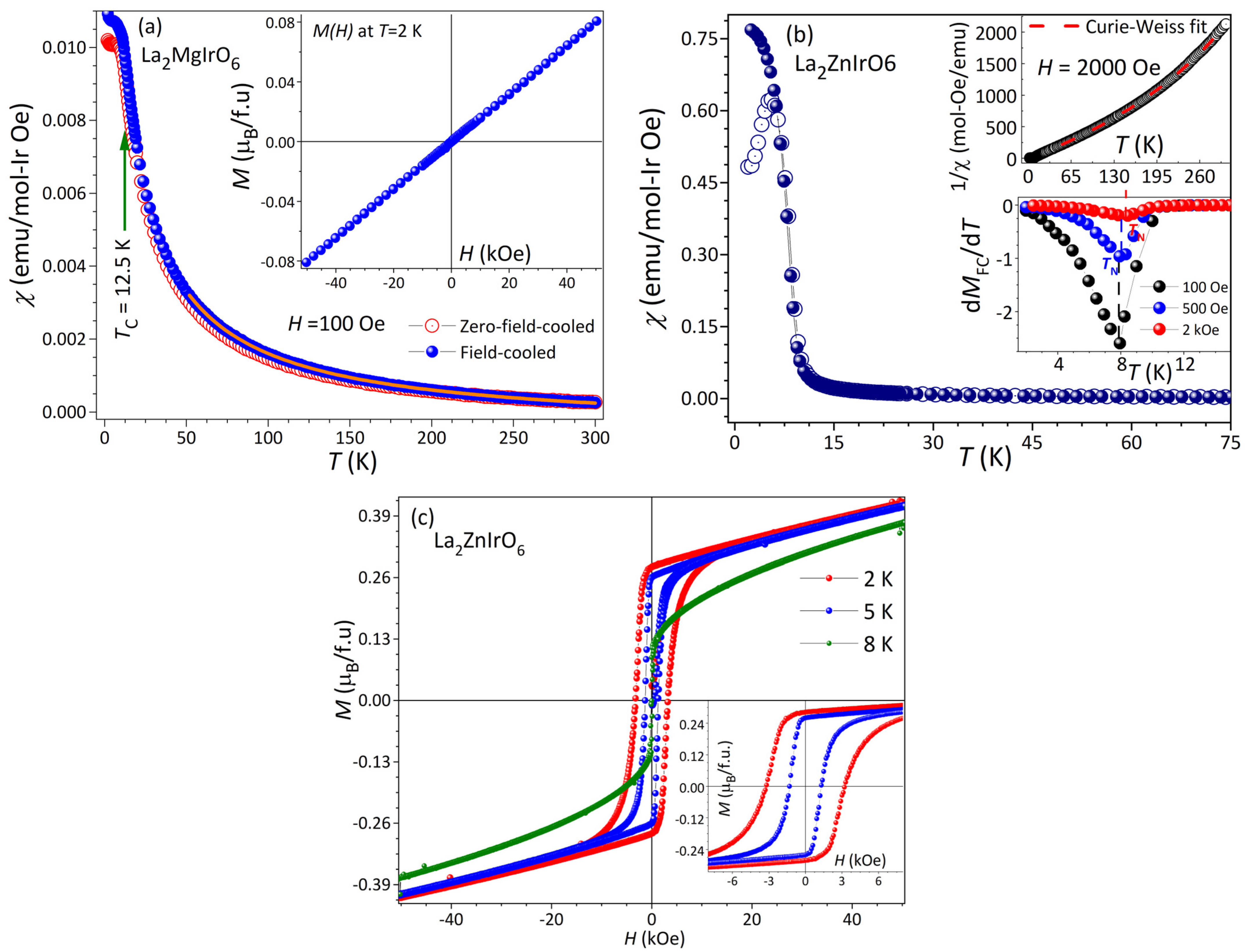
2.5. Temperature-Dependent DC Magnetic Susceptibility and Field-Dependent DC Magnetization

Next, the temperature dependence of dc magnetic susceptibility of La2MgIrO6 at 100 Oe applied magnetic field shows a weak transition at around 12.5 K (TN). Further, the 2 K M vs. H isotherm clearly demonstrates linear behavior (see inset to Figure 5a) without any sign of hysteresis and coercive field, thus refuting ferromagnetic components vis-à-vis spontaneous magnetization in this compound. Therefore, the 12.5 K transition in the χ-T data of La2MgIrO6 (Figure 5a) can be assigned to the antiferromagnetic (AFM) in nature. The transition temperature TN was further ensured from the minimum of the respective first derivative curve (dM/dT vs. T) and, most importantly, the value of TN in our present study exactly matches with the previous reports [14,19]. The Curie–Weiss fit (solid orange line in Figure 5a) on the field-cooled susceptibility data in the 50–300 K temperature range reveals an effective magnetic moment μeff ≈ 1.26 μB/Ir, which is much smaller than the theoretical spin-only moment of 1.73 μB for a low-spin Ir4+ (d5) ion with S = 1 2 . The estimated negative Weiss temperature (θCW = −5.9 K) reflects nearest-neighbor antiferromagnetic exchange between the Ir local moments. On the other hand, the temperature-dependent DC magnetic susceptibility of La2ZnIrO6 in 2 kOe applied magnetic field has been measured and the result is depicted in Figure 5b. A susceptibility maximum appears near about 5.4 K in the ZFC curve while an increase in field-cooled magnetization is evident below this temperature with a tendency of near saturation upon further lowering the temperature. Our Curie–Weiss fit [χ = χ0 + C/(T − θCW); with χ0, C, and θCW being the temperature-independent paramagnetic susceptibility, Curie constant, and Weiss temperature, respectively, shown in the top inset of Figure 5b by χ−1 vs. T plot] to the field-cooled χ (T) data in the T-range of 50–300 K yields an effective moment, μeff = (8c)1/2 = 1.43 μB/Ir4+, and only a slightly positive θCW (≈ 0.2 K).
At this point, it is noteworthy to mention that the AFM peak of ZFC magnetization (TZFC) is gradually shifted to lower temperatures with an increasing field, and also the negative θCW is systematically reduced (see Table 4), indicating competing ferro/antiferromagnetic interactions. The difference between ZFC and FC magnetization curves below TZFC, together with low-field (±6 kOe) hysteresis followed by linear high-field (>6 kOe) magnetization increase in the M-H isotherms (see Figure 5c), further suggests the presence of ferromagnetic components within an overall AFM background in LZIO or, in other words, mixed ferro/antiferromagnetic interactions in the ground state of LZIO. The transition temperature, TN, was determined from the minimum of the temperature derivative of field-cooled susceptibility, dχFC/dT, curves at different applied fields (see solid-colored lines in the bottom inset of Figure 5b). It is evident that TN is shifted towards the higher temperatures with an increasing field.
As displayed in the inset to Figure 5c, below the transition temperature (TN), the observed significant coercivity (HC ~ 3200 Oe and ~1300 Oe at 2 K and 5 K, respectively) in low applied fields (<8000 Oe) followed by linear increase in magnetization at higher fields (see Figure 5c) is typical of canted AFM spin arrangement [12] of LZIO, which is in agreement with the previous works [14,15,48,49]. In addition, the small values of spontaneous magnetization, obtained from the linear extrapolation of the high-field M-H data to zero field axis (see Table 4), the negative θCW at low applied fields (see Table 4), and finally, the absence of saturation magnetization even at highest applied 7 Tesla magnetic field, further support the noncollinear magnetism (NCM) [48] of LZIO comprising both FM and AFM components of the ordered Ir4+ moments. The spin-canting and the development of ferromagnetic interactions in LZIO possibly originate from the dominance of SOC-induced antisymmetric Dzyaloshinskii–Moriya (DM) exchange interaction over the isotropic Heisenberg AFM coupling [15]. It is hypothesized that the tilting and rotational distortions of the IrO6 octahedra (deviation of Ir-O-Zn and O-Ir-O bond angles from ideal 180° and 90°, respectively) break the spatial inversion symmetry among the Ir moments, causing NCM by introducing DM interactions between the Ir4+ moments. However, spin-polarized density functional theory (DFT) calculations predict A-type AFM ground state for both the compounds [14], but unlike LZIO, absence of spontaneous magnetization in La2MgIrO6 could be attributed to the axis of the IrO6 octahedral rotations being orthogonal to the stacking direction of the FM planes [50].
Conventional A-type antiferromagnetic order on the Ir-fcc lattice of both these compounds can invoke solely from nearest-neighbor isotropic Heisenberg AFM exchange interaction [19]. But, contrary to the spin-1/2 magnets with a large frustration parameter, f (= |θCW|/TN) ≈ 9 [27,51], both LMIO and LZIO exhibit very small values of ‘f’ (~0.5 and 0.02, respectively). It is noteworthy to state that the presence of sizeable ferromagnetic second-neighbor interaction and SOC-driven significant uniaxial Ising anisotropy within the framework of the conventional Heisenberg–Ising model (becoming symmetry allowed only under weak monoclinic crystal distortion of the IrO6 octahedra, consistent with the structural description) possibly plays crucial role to strongly reduce the frustration [52,53], hence pushing these systems towards magnetic ordering. Our results clearly point towards the importance of SOC in these two materials, and consequently, warrant us to further explore the role of strong SOC-driven directional exchange interactions on the quantum magnetism of heavy transition metal oxides.
The reduced values of the effective magnetic moment on the individual Ir4+ ion of both the compounds (obtained from Curie–Weiss fit), compared to the theoretically calculated spin-only moment of 1.73 µB for an S = 1/2 state of Ir4+, suggest a key role of orbital contribution to the Ir magnetic moments in either of these compounds, which is in agreement with the reported several 5d spin-1/2 systems [27,54,55]. Moreover, the estimated effective moments per Ir4+ of both LMIO and LZIO (~1.26 and 1.4 µB, respectively) are much smaller than that expected for a spin–orbit coupled Jeff = 1 2 pseudospin state of Ir4+ 5d5 electron configuration, pointing towards the covalent character of the Ir magnetic moments due to stronger hybridization of Ir 5d orbitals in both these DPs. Such a reduced iridium effective moment further reinforces departure from the pure Jeff = 1 2 scenario in both these systems.

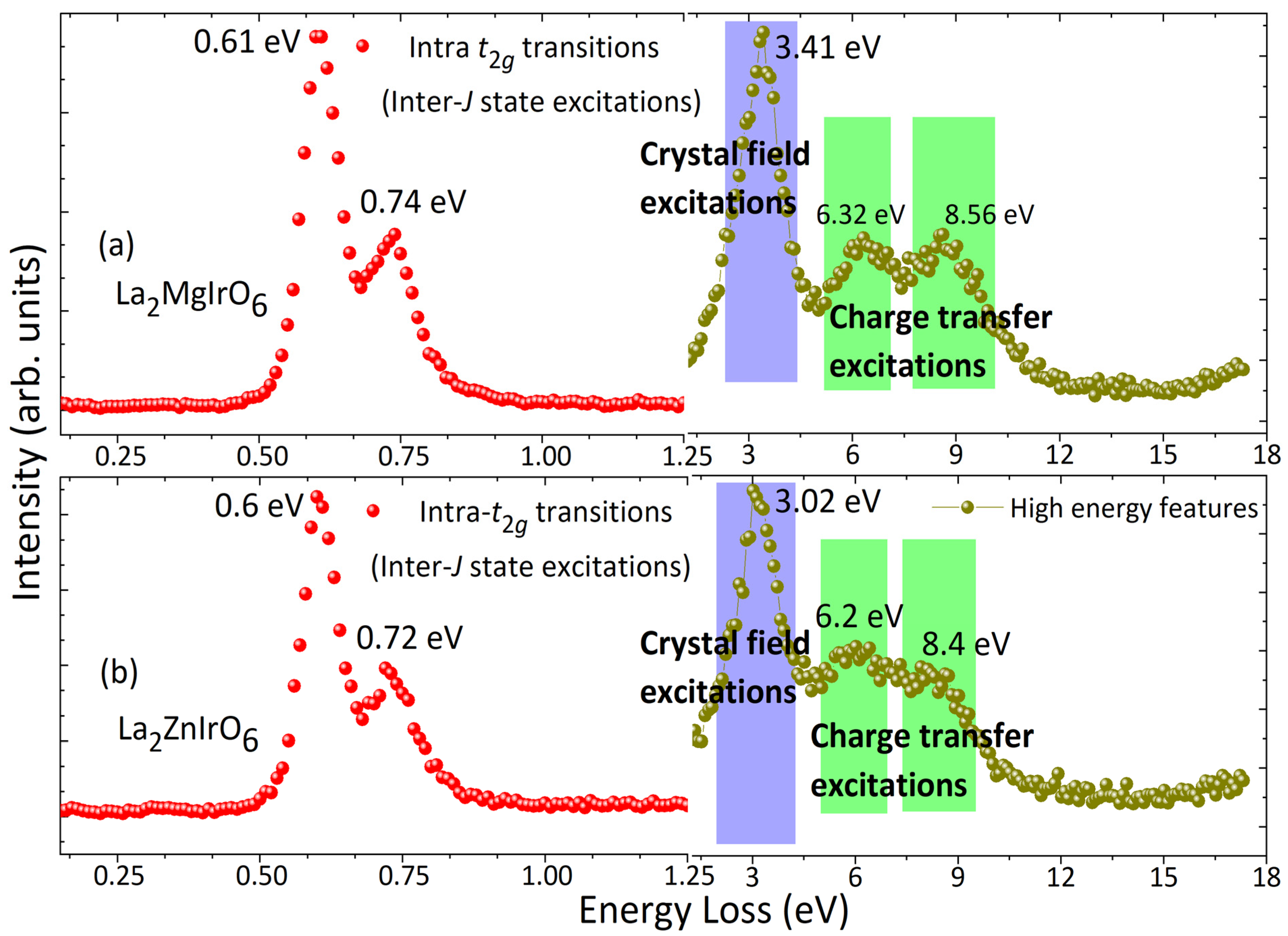
2.6. Ir L3-Edge Resonant Inelastic X-Ray Scattering (RIXS)

Ir L3-edge RIXS is a powerful technique used to assess the validity of Jeff = 1 2 candidacy in d5 iridates. In the ideal octahedral environment of an Ir4+ ion, the Jeff = 1 2 doublet ground state is separated from the Jeff = 3 2 quartet excited state by 3 2 λ (λ being the SOC strength on Ir). A non-cubic crystal field at the Ir4+ site further splits the quartet band into two doublets causing mixing between Jeff = 1 2 and 3 2 states. RIXS, at this point, can be a suitable tool to probe the crystal field excitations, and hence, a reasonable estimation of effective SOC strength and the non-cubic crystal field at the Ir4+ site of any iridate material could be possible. With this, RIXS measurements at the Ir L3-edge of both LMIO and LZIO samples have been performed at T = 300 K and the collected spectra are displayed in Figure 6. Incident photon energy was kept fixed at 11.216 keV during the experiment to enhance the inelastic features of the J multiplet, i.e., intra-t2g transitions. Increased photon counts at the particular energy losses of the measured RIXS spectrum (Figure 6a,b) refer to the specific excitations from filled to vacant electronic states. The features at the highest energy losses (ħω ≈ 6 eV and 8.5 eV, shown by the green rectangles in Figure 6) are assigned to the charge transfer excitations from the O 2p bands to unoccupied Ir t2g and eg bands, respectively [56], for both the compounds. The relatively broad nature of the charge–transfer transitions (in terms of peak shape) in La2ZnIrO6 compared to the La2MgIrO6 indicates larger electronic bandwidth of Ir in LZIO. The features observed at ~3.4 eV and 3.02 eV for LMIO and LZIO, respectively, suggest electron excitation from Ir-t2g to eg orbitals [56,57], revealing the crystal field splitting energies of the respective samples. As evident in Figure 6a,b, the higher energy of the interband t2g  →  eg excitation in LMIO relative to LZIO refers to the greater Ir-O covalency in LMIO than LZIO, and thereby a stronger crystal field effect due to smaller Ir-O distances in LMIO (in consistent with the EXAFS results; see Table 3). The prevalence of stronger Ir-O covalency favors the itinerant character of the Ir electron magnetism in LMIO over LZIO, which likely agrees with the observed lower effective Ir magnetic moments in LMIO with respect to the LZIO due to increasing Ir-O covalent interaction.
In addition, we also observed two sharp inelastic features in the high-resolution low-energy RIXS spectra of both the compounds below 1 eV (Figure 6), which are completely different from the peaks of pentavalent Ir-double perovskites [57]. The energies corresponding to the two peaks (≈0.61 eV and ≈0.74 eV for LMIO, while ≈0.6 eV and ≈0.72 eV for LZIO) match well with the expected intra-t2g transitions of d5 iridates [58]. The nature of these two intra-t2g transitions is very similar (in terms of peak position, peak splitting, and peak-width, shown in Figure 6a,b) in both the double perovskites, and these features are also consistent with the existing literature reports [59]. In such a scenario, we may therefore qualitatively infer the value of the effective spin–orbit coupling strength to be about 0.45–0.46 eV and the noncubic crystal field energy to be ~0.12 eV for both the DP iridates within the framework of single ion Hamiltonian assuming spin–orbit coupling and non-cubic crystal field effects [60,61,62]. These findings point to the fact that the estimated λ/Δnc (>3.5), being similar to the spin–orbit Mott insulator Sr2IrO4 (λ/Δnc > 2.8) [63] and the Kitaev materials Na2IrO3 and α-Li2IrO3 (λ/Δ > 4.7) [64], places both the iridates close to the Jeff = 1 2 limit.
The persistent deviation from the ideal Jeff = 1 2 state (in terms of developed smaller effective magnetic moments per Ir4+ ion relative to that of a perfect Jeff = 1 2 pseudospin state for Ir4+) could be attributed to the stronger Ir-O covalency, noncubic crystal distortion, hybridization of Ir 5d orbitals, intersite Ir-Ir hopping, ligand-mediated superexchange interaction, and bandwidth effects [65,66], which all act against the atomic SOC effect. In this context, it has been demonstrated by Nag et al. [67] and Bandyopadhyay et al. [37,47] that both hopping, noncubic crystal field, and bandwidth effects strongly influence the effective SOC strength of Ir in iridium-based oxides. As a consequence, precise estimation of effective SOC strength on Ir within the atomic limit is not at all a reasonable approach because the low-energy Ir L3-RIXS features would be the outcome of several pertinent electronic and solid-state factors in a real solid [37,47,67,68]. Therefore, to quantify the effective spin–orbit coupling strength of Ir and the resulting J-states in the two DP iridates LMIO and LZIO, further full multiplet calculations (using exact diagonalization of the effective full many-body Hamiltonian) are warranted which should include all possible electronic and solid-state effects.

3. Conclusions

In summary, we have carried out comprehensive structural (both local and global), electronic, and physical property characterizations of the two d5 Ir-double perovskites by using standard X-ray diffraction, X-ray absorption fine structure spectroscopy, electrical resistivity, and DC magnetization measurements; as well, the low-energy spin–orbit and higher energy crystal field plus charge transfer excitations of the two iridates have been probed via performing the Ir L3-edge resonant inelastic X-ray scattering experiment. Our magnetic results of conventional magnetic long-range ordering with a small frustration parameter in both the compounds clearly suggest the SOC-driven anisotropic AFM Kitaev exchange interaction together with the isotropic Heisenberg exchange to be at the root of observed magnetic behaviors. Subtle differences in the magnetic responses arise from the difference in stacking directions of their FM planes relative to the IrO6 octahedral rotation axes. Although the Ir-L3 edge RIXS spectra have been described within a single-ion description of an overall strong spin–orbit split Jeff = 1 2 pseudospin state, the noncubic crystal field effect, together with the enhanced Ir-Ir superexchange due to Mg/Zn-Ir antisite disorder and the reduced effective Ir4+ moments, would lead to the deviation from the atomic spin–orbit coupling picture by renormalizing the effective SOC strength. This might cause possible departure from the perfect Jeff = 1 2 scenario. In order to ensure the actual J state description and to estimate the effective SOC strength plus noncubic crystal field energy of these two iridate DPs, full multiplet calculations are highly warranted to implement by considering two site models (neighboring two IrO6 octahedra and switching on all kinds of interactions in between them) along with all possible electronic and solid-state effects. Our work emphasizes the crucial roles of the choice of B-site cation, and consequently, the structural distortions (in terms of tilting and rotations of the octahedra), site disorder, etc., on the ground state magnetic responses of the double perovskite class of materials. Furthermore, our comprehensive experimental study on two d5 iridate DP La2BIrO6 (B = Zn, Mg) systems evidently establish the strong impact of several pertinent solid-state and electronic factors (e.g., non-cubic crystal field, hopping, hybridization, bandwidth, etc.) against the atomic SOC effect, and hence, towards the deviation from an atomic-like spin–orbit-coupled ideal Jeff picture in the higher-d transition metal-based oxides.

4. Materials and Methods

Polycrystalline La2MIrO6 (M = Mg, Zn) samples have been synthesized by conventional solid state reaction route. Stoichiometric amount of high purity (>99.9%) starting reference oxide La2O3, ZnO, MgO, and IrO2 powders were thoroughly mixed in an agate mortar. The mixture was then calcined initially at 650° C for 12 h and finally sintered at 1000 °C for 48 h in air with few intermediate grindings. The phase purity of these samples was checked by powder X-ray diffraction (XRD) and subsequent structural characterization was performed using a Bruker AXS: D8 Advance X-ray diffractometer equipped with a Cu Kα monochromatic X-ray source. The obtained room temperature XRD data were analyzed using the Rietveld technique and the refinements were performed by FULLPROF program [69]. The Ir L3-edge X-ray absorption near edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) of both the samples have been measured at the XAFS beamline of Elettra (Trieste, Italy) synchrotron radiation facility at room temperature in standard transmission geometry. Data treatment and quantitative analysis of EXAFS have been carried out using ARTEMIS program [70]. Temperature-dependent zero-field electrical resistivity (ρ) measurements for the two samples were performed using the standard four-probe method within a temperature range of 200–400 K in a laboratory-based liquid nitrogen (down to 80 K) resistivity set up, where the sample probe consists of a sample holder being fixed at one end with a stainless-steel rod, while having a rubber cork at the opposite end. This probe becomes well-fitted in a glass-made cryostat connected with a rotary pump to evacuate the sample chamber before measurement in order to avoid possible condensation of air moisture at low T. Further, a small amount of inert He gas is inserted before the measurement to improve the thermal conductivity and temperature stability of the samples. A Keithley 2400 constant current source and a Keithley 2182A nano voltmeter were used to measure the thermal variation of ρ for these samples. Lakeshore 331 and 325 temperature controllers were also used for temperature-controlling purposes. The four-probe method for the ρ-T measurements was employed to eliminate contributions from the contact resistances of the electrodes which are in series with the sample resistance. The contacts were made using externally insulated Cu wires and the electrodes were made using conductive silver paste. Further, the temperature and magnetic field dependence of dc magnetic susceptibility were measured in the temperature range of 2–300 K and in magnetic fields up to ±50 kOe in a superconducting quantum interference device magnetometer (SQUID MPMS, Quantum Design). The resonant inelastic X-ray scattering (RIXS) experiment at the Ir L3 edge was performed at the ID20 beamline of European Synchrotron Radiation Facility (ESRF) for these two samples using π-polarized photons and a scattering geometry with 2θ ≃ 90° to suppress elastic scattering.

Author Contributions

Conceptualization, A.B. and S.R.; powder sample preparation, A.B.; methodology, A.B., C.M., A.E., and M.M.S.; software, A.B., C.M., A.E., M.M.S., and S.R.; validation, A.B., C.M., S.R., and D.K.P.; formal analysis, A.B., C.M., and S.R.; investigation, A.B. and S.R.; resources, S.R. and A.B.; data curation, A.B. and S.R.; writing—original draft preparation, A.B.; writing—review and editing, A.B., S.R., and C.M.; visualization, A.B., S.R., C.M., and D.K.P.; supervision, S.R. and A.B.; project administration, A.B. and S.R.; funding acquisition, S.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by CSIR, India and IACS. Further, Jawaharlal Nehru Centre for Advanced Scientific Research from DST-Synchrotron-Neutron project supported for performing experiments at ESRF (Proposal No. HC-2872). S.R. acknowledges the Science and Engineering Research Board (SERB), DST, India (Project no. CRG/2023/001060), and the UGC-DAE CSR scheme (CRS/2023-24/1646) for funding. The authors are grateful to the Technical Research Centre (TRC) and the Indian Association for the Cultivation of Science, Kolkata, for their research support.

Data Availability Statement

Data is contained within the article.

Acknowledgments

A.B. thanks CSIR, India, and IACS for fellowships. A.B. also acknowledges SERB, DST, India, for a National Post-Doctoral Fellowship (N-PDF, File No. PDF/2020/000785). A.B. and S.R. thank the Jawaharlal Nehru Centre for Advanced Scientific Research from DST-Synchrotron-Neutron project for performing experiments at ESRF (Proposal No. HC-2872). The authors also thank TRC-DST of IACS for providing experimental facilities. A.B and D.K.P acknowledge Lalit Narayan Mithila University for giving financial support. S.R. acknowledges the Science and Engineering Research Board (SERB), DST, India (Project no. CRG/2023/001060), and the UGC-DAE CSR scheme (CRS/2023-24/1646) for funding. The authors are grateful to the Technical Research Centre (TRC) and the Indian Association for the Cultivation of Science, Kolkata, for their research support.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kim, B.J.; Jin, H.; Moon, S.-J.; Kim, J.-Y.; Park, B.-G.; Leem, C.S.; Yu, J.; Noh, T.W.; Kim, C.; Oh, S.J.; et al. Novel Jeff = 1/2 Mott State Induced by Relativistic Spin-Orbit Coupling in Sr2IrO4. Phys. Rev. Lett. 2008, 101, 076402. [Google Scholar] [CrossRef]
  2. Pesin, D.; Balents, L. Mott physics and band topology in materials with strong spin–orbit interaction. Nat. Phys. 2010, 6, 376. [Google Scholar] [CrossRef]
  3. Jackeli, G.; Khaliullin, G. Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef] [PubMed]
  4. Wang, F.; Senthil, T. Twisted Hubbard Model for Sr2IrO4: Magnetism and Possible High Temperature Superconductivity. Phys. Rev. Lett. 2011, 106, 136402. [Google Scholar] [CrossRef] [PubMed]
  5. Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
  6. Balents, L. Spin Liquids in frustrated magnets. Nature 2010, 464, 199. [Google Scholar] [CrossRef]
  7. Chaloupka, J.; Jackeli, G.; Khaliullin, G. Kitaev-Heisenberg Model on a Honeycomb Lattice: Possible Exotic Phases in Iridium Oxides A2IrO3. Phys. Rev. Lett. 2010, 105, 027204. [Google Scholar] [CrossRef]
  8. Pardo, V.; Pickett, W.E. Compensated magnetism by design in double perovskite oxides. Phys. Rev. B 2009, 80, 054415. [Google Scholar] [CrossRef]
  9. Saha-Dasgupta, T. Ferroic properties in bi-component perovskites: Artificial superlattices and naturally forming compounds. J. Phys. Condens. Matter. 2014, 26, 193201. [Google Scholar] [CrossRef]
  10. Powell, A.V.; Gore, J.G.; Battle, P.D. The magnetic properties of iridium in mixed-metal oxides. J. Alloys Compd. 1993, 201, 73. [Google Scholar] [CrossRef]
  11. Manna, K.; Sarkar, R.; Fuchs, S.; Onykiienko, Y.A.; Bera, A.K.; Cansever, G.A.; Kamusella, S.; Maljuk, A.; Blum, C.G.F.; Corredor, L.T.; et al. Noncollinear antiferromagnetism of coupled spins and pseudospins in the double perovskite La2CuIrO6. Phys. Rev. B 2016, 94, 144437. [Google Scholar] [CrossRef]
  12. Narayanan, N.; Mikhailova, D.; Senyshyn, A.; Trots, D.M.; Laskowski, R.; Blaha, P.; Schwarz, K.; Fuess, H.; Ehrenberg, H. Temperature and composition dependence of crystal structures and magnetic and electronic properties of the double perovskites La2−xSrxCoIrO6 (0 ≤ x ≤ 2). Phys. Rev. B 2010, 82, 024403. [Google Scholar] [CrossRef]
  13. Kolchinskaya, A.; Komissinskiy, P.; Yazdi, M.B.; Vafaee, M.; Mikhailova, D.; Narayanan, N.; Ehrenberg, H.; Wilhelm, F.; Rogalev, A.; Alff, L. Magnetism and spin-orbit coupling in Ir-based double perovskites La2−xSrxCoIrO6. Phys. Rev. B 2012, 85, 224422. [Google Scholar] [CrossRef]
  14. Cao, G.; Subedi, A.; Calder, S.; Yan, J.-Q.; Yi, J.; Gai, Z.; Poudel, L.; Singh, D.J.; Lumsden, M.D.; Christianson, A.D.; et al. Magnetism and electronic structure of La2ZnIrO6 and La2MgIrO6: Candidate Jeff = 1/2 Mott insulators. Phys. Rev. B 2013, 87, 155136. [Google Scholar] [CrossRef]
  15. Zhu, W.K.; Lu, C.-K.; Tong, W.; Wang, J.M.; Zhou, H.D.; Zhang, S.X. Strong ferromagnetism induced by canted antiferromagnetic order in double perovskite iridates (La1−xSrx)2ZnIrO6. Phys. Rev. B 2015, 91, 144408. [Google Scholar] [CrossRef]
  16. Taylor, A.E.; Morrow, R.; Singh, D.J.; Calder, S.; Lumsden, M.D.; Woodward, P.M.; Christianson, A.D. Magnetic order and electronic structure of the 5d3 double perovskite Sr2ScOsO6. Phys. Rev. B 2015, 91, 100406. [Google Scholar] [CrossRef]
  17. Dzyaloshinskii, I. A Thermodynamic Theory of Weak Ferromagnetism of Antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241. [Google Scholar] [CrossRef]
  18. Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
  19. Aczel, A.A.; Cook, A.M.; Williams, T.J.; Calder, S.; Christianson, A.D.; Cao, G.-X.; Mandrus, D.; Kim, Y.-B.; Paramekanti, A. Highly anisotropic exchange interactions of jeff = 1/2 iridium moments on the fcc lattice in La2BIrO6 (B = Mg,Zn). Phys. Rev. B 2016, 93, 214426. [Google Scholar] [CrossRef]
  20. Demazeau, G.; Siberchicot, B.; Matar, S.; Gayet, C.; Largeteau, A. A new ferromagnetic oxide La2MnIrO6: Synthesis, characterization, and calculation of its electronic structure. J. Appl. Phys. 1994, 75, 4617. [Google Scholar] [CrossRef]
  21. Uhl, M.; Matar, S.F.; Siberchicot, B. Calculated magnetic and electronic properties of the double perovskites La2TIrO6 (T = Mn, Fe, Co). J. Magn. Magn. Mater. 1998, 187, 201. [Google Scholar] [CrossRef]
  22. Currie, R.C.; Vente, J.F.; Frikkee, E.; Ijdo, D. The Structure and Magnetic Properties of La2MLrO6 with M = Mg, Co, Ni, and Zn. J. Solid State Chem. 1995, 116, 199. [Google Scholar] [CrossRef]
  23. Laguna-Marco, M.A.; Kayser, P.; Alonso, J.A.; Martinez-Lope, M.J.; van Veenendaal, M.; Choi, Y.; Haskel, D. Electronic structure, local magnetism, and spin-orbit effects of Ir(IV)-, Ir(V)-, and Ir(VI)-based compounds. Phys. Rev. B 2015, 91, 214433. [Google Scholar] [CrossRef]
  24. Popov, G.; Greenblatt, M.; Croft, M. Large effects of A-site average cation size on the properties of the double perovskites Ba2−xSrxMnReO6: A d5−d1 system. Phys. Rev. B 2003, 67, 024406. [Google Scholar] [CrossRef]
  25. Wiebe, C.R.; Greedan, J.E.; Luke, G.M.; Gardner, J.S. Spin-glass behavior in the S = ½ fcc ordered perovskite Sr2CaReO6. Phys. Rev. B 2002, 65, 144413. [Google Scholar] [CrossRef]
  26. Nag, A.; Bhowal, S.; Bert, F.; Hillier, A.D.; Itoh, M.; Carlomagno, I.; Meneghini, C.; Sarkar, T.; Mathieu, R.; Dasgupta, I.; et al. Ba3MIr2O9 hexagonal perovskites in the light of spin-orbit coupling and local structural distortions. Phys. Rev. B 2018, 97, 064408. [Google Scholar] [CrossRef]
  27. Meneghini, C.; Ray, S.; Liscio, F.; Bardelli, F.; Mobilio, S.; Sarma, D.D. Nature of “Disorder” in the Ordered Double Perovskite Sr2FeMoO6. Phys. Rev. Lett. 2009, 103, 046403. [Google Scholar] [CrossRef]
  28. Bufaiçal, L.; Ferreira, L.M.; Lora-Serrano, R.; Agüero, O.; Torriani, I.; Granado, E.; Pagliuso, P.G. Physical properties of disordered double perovskite Ca2−xLaxFeIrO6. J. Appl. Phys. 2008, 103, 07F716. [Google Scholar] [CrossRef]
  29. Jana, S.; Singh, V.; Kaushik, S.D.; Meneghini, C.; Pal, P.; Knut, R.; Karis, O.; Dasgupta, I.; Siruguri, V.; Ray, S. Atomic-scale chemical fluctuation in LaSrVMoO6, a proposed half-metallic antiferromagnet. Phys. Rev. B 2010, 82, 180407. [Google Scholar] [CrossRef]
  30. Jana, S.; Singh, V.; Nag, A.; Meneghini, C.; Dasgupta, I.; Aquilanti, G.; Ray, S. LaSrVMoO6: A case study for A-site covalency-driven local cationic order in double perovskites. Phys. Rev. B 2012, 86, 014203. [Google Scholar] [CrossRef]
  31. Jana, S.; Meneghini, C.; Sanyal, P.; Sarkar, S.; Dasgupta, T.S.; Karis, O.; Ray, S. Signature of an antiferromagnetic metallic ground state in heavily electron-doped Sr2FeMoO6. Phys. Rev. B 2012, 86, 054433. [Google Scholar] [CrossRef]
  32. Sarma, D.D.; Mahadevan, P.; Saha-Dasgupta, T.; Ray, S.; Kumar, A. Electronic Structure of Sr2FeMoO6. Phys. Rev. Lett. 2000, 85, 2549. [Google Scholar] [CrossRef] [PubMed]
  33. Das, H.; Sanyal, P.; Saha-Dasgupta, T.; Sarma, D.D. Origin of magnetism and trend in Tc in Cr-based double perovskites: Interplay of two driving mechanisms. Phys. Rev. B 2011, 83, 104418. [Google Scholar] [CrossRef]
  34. Hemery, E.K.; Williams, G.V.M.; Trodahl, H.J. La-induced changes in the magnetic and electronic properties of Sr2−xLaxFeMoO6. Phys. Rev. B 2006, 74, 054423. [Google Scholar] [CrossRef]
  35. Cao, G.; Durairaj, V.; Chikara, S.; De Long, L.E.; Parkin, S.; Schlottmann, P. Non-Fermi-liquid behavior in nearly ferromag netic SrIrO3 single crystals. Phys. Rev. B 2007, 76, 100402. [Google Scholar] [CrossRef]
  36. Kayser, P.; Martínez-Lope, M.J.; Alonso, J.A.; Retuerto, M.; Croft, M.; Ignatov, A.; Fernández-Díaz, M.T. Crystal and Magnetic Structure of Sr2MIrO6 (M = Ca, Mg) Double Perovskites—A Neutron Diffraction Study. Eur. J. Inorg. Chem. 2013, 2014, 178. [Google Scholar] [CrossRef]
  37. Bandyopadhyay, A.; Chakraborty, A.; Bhowal, S.; Kumar, V.; Sala, M.M.; Efimenko, A.; Bert, F.; Biswas, P.K.; Meneghini, C.; Büttgen, N.; et al. Breakdown of atomic spin-orbit coupling picture in an apparently isolated pseudo-one-dimensional iridate: Sr3NaIrO6. Phys. Rev. B 2022, 105, 104431. [Google Scholar] [CrossRef]
  38. Nag, A.; Middey, S.; Bhowal, S.; Panda, S.K.; Mathieu, R.; Orain, J.C.; Bert, F.; Mendels, P.; Freeman, G.; Mansson, M.; et al. Origin of the Spin-Orbital Liquid State in a Nearly J = 0 Iridate Ba3ZnIr2O9. Phys. Rev. Lett. 2016, 116, 097205. [Google Scholar] [CrossRef]
  39. Khan, M.S.; Bandyopadhyay, A.; Nag, A.; Kumar, V.; Mahajan, A.V.; Ray, S. Magnetic ground state of the distorted 6H perovskite Ba3CdIr2O9. Phys. Rev. B 2019, 100, 064423. [Google Scholar] [CrossRef]
  40. Banerjee, A.; Sannigrahi, J.; Giri, S.; Majumdar, S. Observation of non-Fermi liquid behavior in hole-doped Eu2Ir2O7. Phys. Rev. B 2017, 96, 224426. [Google Scholar] [CrossRef]
  41. Porter, Z.; Zoghlin, E.; Britner, S.; Husremovic, S.; Ruff, J.P.C.; Choi, Y.; Haskel, D.; Laurita, G.; Wilson, S.D. Evolution of structure and magnetism across the metal-insulator transition in the pyrochlore iridate (Nd1−xCax)2Ir2O7. Phys. Rev. B 2019, 100, 054409. [Google Scholar] [CrossRef]
  42. Ueda, K.; Fukuda, H.; Kaneko, R.; Fujioka, J.; Tokura, Y. Evolution of possible Weyl semimetal states across the Mott transition in pyrochlore iridates induced by hole doping. Phys. Rev. B 2020, 102, 245131. [Google Scholar] [CrossRef]
  43. Zoghlin, E.; Porter, Z.; Britner, S.; Husremovic, S.; Choi, Y.; Haskel, D.; Laurita, G.; Wilson, S.D. Mapping the structural, magnetic and electronic behavior of (Eu1−xCax)2Ir2O7 across a metal–insulator transition. J. Phys. Condens. Matter 2020, 33, 055601. [Google Scholar] [CrossRef] [PubMed]
  44. Choy, J.-H.; Kim, J.-D.K.; Demazeau, G.; Jung, D.Y. LIII-Edge XANES Study on Unusually High Valent Iridium in a Perovskite Lattice. J. Phys. Chem. 1994, 98, 6258. [Google Scholar] [CrossRef]
  45. Choy, J.-H.; Kim, J.-D.K.; Hwang, S.-H.; Demazeau, G.; Jung, D.Y. XANES and EXAFS Studies on the Ir-O Bond Covalency in Ionic Iridium Perovskites. J. Am. Chem. Soc. 1995, 117, 8557. [Google Scholar] [CrossRef]
  46. Zhang, L.; Tang, Z.-J. Polaron relaxation and variable-range-hopping conductivity in the giant-dielectric-constant material CaCu3Ti4O12. Phys. Rev. B 2004, 70, 174306. [Google Scholar] [CrossRef]
  47. Bandyopadhyay, A.; Carlomagno, I.; Simonelli, L.; Sala, M.M.; Efimenko, A.; Meneghini, C.; Ray, S. Evolution of electronic and magnetic properties in a series of iridate double perovskites Pr2−xSrxMgIrO6 (x = 0, 0.5, 1.0). Phys. Rev. B 2019, 100, 064416. [Google Scholar] [CrossRef]
  48. Vogl, M.; Corredor, L.T.; Dey, T.; Mørrow, R.; Scaravaggi, F.; Wolter, A.U.B.; Aswartham, S.; Wurmehl, S.; Büchner, B. Interplay of 3d- and 5d-sublattice magnetism in the double perovskite substitution series La2Zn1−xCoxIrO6. Phys. Rev. B 2018, 97, 035155. [Google Scholar] [CrossRef]
  49. Iakovleva, M.; Fuchs, S.; Alfonsov, A.; Grafe, H.-J.; Vogl, M.; Aswartham, S.; Wurmehl, S.; Dey, T.; Büchner, B.; Vavilova, E.; et al. Static and dynamic magnetism of the Ir-based double perovskites La2BIrO6 (B = Co, Zn) probed by magnetic resonance spectroscopies. Phys. Rev. B 2018, 98, 174401. [Google Scholar] [CrossRef]
  50. Cook, A.M.; Matern, S.; Hickey, C.; Aczel, A.A.; Paramekanti, A. Spin-orbit coupled jeff = 1/2 iridium moments on the geometrically frustrated fcc lattice. Phys. Rev. B 2015, 92, 020417. [Google Scholar] [CrossRef]
  51. Wiebe, C.R.; Greedan, J.E.; Kyriakou, P.P.; Luke, G.M.; Gardner, J.S.; Fukaya, A.; Gat-Malureanu, M.; Russo, P.L.; Savici, A.T.; Uemura, Y.J. Frustration-driven spin freezing in the S=1/2 fcc perovskite Sr2MgReO6. Phys. Rev. B 2003, 68, 134410. [Google Scholar] [CrossRef]
  52. Seehra, M.S.; Giebultowicz, T.M. Magnetic structures of fcc systems with nearest-neighbor and next-nearest-neighbor exchange interactions. Phys. Rev. B 1988, 38, 11898. [Google Scholar] [CrossRef]
  53. Lefmann, K.; Rischel, C. Quantum effects in magnetic structures on the fcc lattice. Eur. Phys. J. B 2001, 21, 313. [Google Scholar] [CrossRef]
  54. de Vries, M.A.; Mclaughlin, A.C.; Bos, J.-W.G. Valence Bond Glass on an fcc Lattice in the Double Perovskite Ba2YMoO6. Phys. Rev. Lett. 2010, 104, 177202. [Google Scholar] [CrossRef] [PubMed]
  55. Aharen, T.; Greedan, J.E.; Bridges, C.A.; Aczel, A.A.; Rodriguez, J.; MacDougall, G.; Luke, G.M.; Imai, T.; Michaelis, V.K.; Kroeker, S.; et al. Magnetic properties of the geometrically frustrated S=½ antiferromagnets, La2LiMoO6 and Ba2YMoO6, with the B-site ordered double perovskite structure: Evidence for a collective spin-singlet ground state. Phys. Rev. B 2010, 81, 224409. [Google Scholar] [CrossRef]
  56. Ishii, K.; Jarrige, I.; Yoshida, M.; Ikeuchi, K.; Mizuki, J.; Ohashi, K.; Takayama, T.; Matsuno, J.; Takagi, H. Momentum-resolved electronic excitations in the Mott insulator Sr2IrO4 studied by resonant inelastic x-ray scattering. Phys. Rev. B 2011, 83, 115121. [Google Scholar] [CrossRef]
  57. Nag, A.; Bhowal, S.; Chakraborty, A.; Sala, M.M.; Efimenko, A.; Bert, F.; Biswas, P.K.; Hillier, A.D.; Itoh, M.; Kaushik, S.D.; et al. Origin of magnetic moments and presence of spin-orbit singlets in Ba2YIrO6. Phys. Rev. B 2018, 98, 014431. [Google Scholar] [CrossRef]
  58. Kim, Y.-J.; Clancy, J.P.; Gretarsson, H.; Cao, G.; Singh, Y.; Kim, J.; Upton, M.H.; Casa, D.; Gog, T. Probing electronic excitations in iridates with resonant inelastic x-ray scattering and emission spectroscopy techniques. arXiv 2018, arXiv:1805.03612. [Google Scholar] [CrossRef]
  59. Aczel, A.A.; Clancy, J.P.; Chen, Q.; Zhou, H.D.; Reig-i-Plessis, D.; MacDougall, G.J.; Ruff, J.P.C.; Upton, M.H.; Islam, Z.; Williams, T.J.; et al. Revisiting the Kitaev material candidacy of Ir4+ double perovskite iridates. Phys. Rev. B 2019, 99, 134417. [Google Scholar] [CrossRef]
  60. Liu, X.; Katukuri, V.M.; Hozoi, L.; Yin, W.G.; Dean, M.P.M.; Upton, M.H.; Kim, J.; Casa, D.; Said, A.; Gog, T.; et al. Testing the Validity of the Strong Spin-Orbit-Coupling Limit for Octahedrally Coordinated Iridate Compounds in a Model System Sr3CuIrO6. Phys. Rev. Lett. 2012, 109, 157401. [Google Scholar] [CrossRef]
  61. Hozoi, L.; Gretarsson, H.; Clancy, J.P.; Jeon, B.-G.; Lee, B.; Kim, K.H.; Yushankhai, V.; Fulde, P.; Casa, D.; Gog, T.; et al. Longer-range lattice anisotropy strongly competing with spin-orbit interactions in pyrochlore iridates. Phys. Rev. B 2014, 89, 115111. [Google Scholar] [CrossRef]
  62. Sala, M.M.; Ohgushi, K.; Al-Zein, A.; Hirata, Y.; Monaco, G.; Krisch, M. CaIrO3: A Spin-Orbit Mott Insulator Beyond the jeff = 1/2 Ground State. Phys. Rev. Lett. 2014, 112, 176402. [Google Scholar] [CrossRef]
  63. Lu, X.; Olalde-Velasco, P.; Huang, Y.; Bisogni, V.; Pelliciari, J.; Fatale, S.; Dantz, M.; Vale, J.G.; Hunter, E.C.; Chang, J.; et al. Dispersive magnetic and electronic excitations in iridate perovskites probed by oxygen K-edge resonant inelastic x-ray scattering. Phys. Rev. B 2018, 97, 041102(R). [Google Scholar] [CrossRef]
  64. Gretarsson, H.; Clancy, J.P.; Liu, X.; Hill, J.P.; Bozin, E.; Singh, Y.; Manni, S.; Gegenwart, P.; Kim, J.; Said, A.H.; et al. Crystal-Field Splitting and Correlation Effect on the Electronic Structure of A2IrO3. Phys. Rev. Lett. 2013, 110, 076402. [Google Scholar] [CrossRef]
  65. Paramekanti, A.; Singh, D.J.; Yuan, B.; Casa, D.; Said, A.; Kim, Y.-J.; Christianson, A.D. Spin-orbit coupled systems in the atomic limit: Rhenates, osmates, iridates. Phys. Rev. B 2018, 97, 235119. [Google Scholar] [CrossRef]
  66. Takegami, D.; Kasinathan, D.; Wolff, K.K.; Altendorf, S.G.; Chang, C.F.; Hoefer, K.; Melendez-Sans, A.; Utsumi, Y.; Meneghin, F.; Ha, T.D.; et al. Charge-transfer energy in iridates: A hard x-ray photoelectron spectroscopy study. Phys. Rev. B 2020, 102, 045119. [Google Scholar] [CrossRef]
  67. Nag, A.; Bhowal, S.; Sala, M.M.; Efimenko, A.; Dasgupta, I.; Ray, S. Hopping-Induced Ground-State Magnetism in 6H Perovskite Iridates. Phys. Rev. Lett. 2019, 123, 017201. [Google Scholar] [CrossRef]
  68. Revelli, A.; Sala, M.M.; Monaco, S.G.; Becker, P.; Bohatý, L.; Hermanns, M.; Koethe, T.C.; Fröhlich, T.; Warzanowski, P.; Lorenz, T.; et al. Resonant inelastic x-ray incarnation of Young’s double-slit experiment. Sci. Adv. 2019, 5, eaav4020. [Google Scholar] [CrossRef] [PubMed]
  69. Carvajal, J.R. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B 1993, 192, 55–69. [Google Scholar] [CrossRef]
  70. Newville, M. EXAFS analysis using FEFF and FEFFIT. J. Synchrotron Rad. 2001, 8, 322. [Google Scholar] [CrossRef] [PubMed]
Condensedmatter 10 00053 g001
Figure 1. Edge-shared tetrahedral network formed out of individual B/B’ cations (green spheres) of a cubic double perovskite structure.
Figure 1. Edge-shared tetrahedral network formed out of individual B/B’ cations (green spheres) of a cubic double perovskite structure.
Condensedmatter 10 00053 g001
Condensedmatter 10 00053 g002
Figure 2. (a,b) Rietveld refined XRD patterns of the two samples. Open black circles and the continuous red line represent the experimentally observed data and the theoretically calculated pattern, respectively. The continuous blue line represents the difference between the observed and calculated patterns while the vertical green ticks indicate the Bragg peak positions. The refined crystal structures for (c) La2MgIrO6 and (d) La2ZnIrO6; IrO6 octahedral rotational distortion (deviation of O-Ir-O bond angles from ideal 90°) for (e) La2MgIrO6 and (f) La2ZnIrO6. Finally, the isosceles Ir triangles, with the dissimilar Ir-Ir distances for (g) La2MgIrO6 and (h) La2ZnIrO6 compounds.
Figure 2. (a,b) Rietveld refined XRD patterns of the two samples. Open black circles and the continuous red line represent the experimentally observed data and the theoretically calculated pattern, respectively. The continuous blue line represents the difference between the observed and calculated patterns while the vertical green ticks indicate the Bragg peak positions. The refined crystal structures for (c) La2MgIrO6 and (d) La2ZnIrO6; IrO6 octahedral rotational distortion (deviation of O-Ir-O bond angles from ideal 90°) for (e) La2MgIrO6 and (f) La2ZnIrO6. Finally, the isosceles Ir triangles, with the dissimilar Ir-Ir distances for (g) La2MgIrO6 and (h) La2ZnIrO6 compounds.
Condensedmatter 10 00053 g002
Condensedmatter 10 00053 g003
Figure 3. Ir L3-edge k2 weighted experimental EXAFS data (shaded black circles) and respective best fits (red solid line) for La2MgIrO6 (a) and La2ZnIrO6 (c) samples. The contributions from the individual single and multiple scattering paths (solid colored line) and the residual [k2χexp—k2χth] (open orange stars) are also indicated for these two samples; vertically shifted for clarity. (b,d) Fourier transforms of the respective experimental data (shaded black circles) and the theoretical fitted (solid red line) curves. The real (Real part) and the imaginary parts (Imm) are shown; vertically shifted for clarity. In addition, (e) The Zn K-edge k3 weighted experimental EXAFS data (shaded black circles) and the corresponding best fit (red solid line) for La2ZnIrO6 sample. The contributions from the individual single and multiple scattering paths (solid colored line) and also the residual [k2χexp—k2χth] (open orange stars) are also indicated; vertically shifted for clarity. (f) Fourier transforms of the experimental data (shaded black circles) and the theoretical fitted (solid red line) curve. The real (Real part) and the imaginary parts (Imm) are shown; vertically shifted for clarity.
Figure 3. Ir L3-edge k2 weighted experimental EXAFS data (shaded black circles) and respective best fits (red solid line) for La2MgIrO6 (a) and La2ZnIrO6 (c) samples. The contributions from the individual single and multiple scattering paths (solid colored line) and the residual [k2χexp—k2χth] (open orange stars) are also indicated for these two samples; vertically shifted for clarity. (b,d) Fourier transforms of the respective experimental data (shaded black circles) and the theoretical fitted (solid red line) curves. The real (Real part) and the imaginary parts (Imm) are shown; vertically shifted for clarity. In addition, (e) The Zn K-edge k3 weighted experimental EXAFS data (shaded black circles) and the corresponding best fit (red solid line) for La2ZnIrO6 sample. The contributions from the individual single and multiple scattering paths (solid colored line) and also the residual [k2χexp—k2χth] (open orange stars) are also indicated; vertically shifted for clarity. (f) Fourier transforms of the experimental data (shaded black circles) and the theoretical fitted (solid red line) curve. The real (Real part) and the imaginary parts (Imm) are shown; vertically shifted for clarity.
Condensedmatter 10 00053 g003
Condensedmatter 10 00053 g004
Figure 4. (a) Ir L3-XANES (X-ray absorption near edge structure) spectra for the two samples; (b) second derivative curves of the respective normalized absorption spectra, indicating white-line features more prominently. The green-dashed lines correspond to Ir 2p → t2g (lower-energy) and Ir 2p → eg (higher energy) transitions; Temperature dependence of electrical resistivity for (c) La2ZnIrO6 and (d) La2MgIrO6. Inset: corresponding Arrhenius fitting.
Figure 4. (a) Ir L3-XANES (X-ray absorption near edge structure) spectra for the two samples; (b) second derivative curves of the respective normalized absorption spectra, indicating white-line features more prominently. The green-dashed lines correspond to Ir 2p → t2g (lower-energy) and Ir 2p → eg (higher energy) transitions; Temperature dependence of electrical resistivity for (c) La2ZnIrO6 and (d) La2MgIrO6. Inset: corresponding Arrhenius fitting.
Condensedmatter 10 00053 g004
Condensedmatter 10 00053 g005
Figure 5. (a) Zero-field-cooled (open red circles) and field-cooled (shaded blue circles) dc magnetic susceptibility vs. temperature, χ (T), variations under 100 Oe applied magnetic field for La2MgIrO6. Inset: 2 K M vs. H isotherm. (b) Amount of 2 kOe zero-field-cooled (open circles) and field-cooled (shaded circles) dc magnetic susceptibility data for La2ZnIrO6. Top inset: corresponding Curie–Weiss fit showing inverse susceptibility (1/χ) vs. temperature plot in the 50–300 K temperature range. Bottom inset: temperature dependence of dM/dT for three different applied fields, indicating the transition temperature TN for each of the fields from the minimum of the respective curves. (c) M vs. H isotherms for La2ZnIrO6 at three different temperatures. Inset: expanded views of the respective M (H) curves to highlight the coercivity and remanence.
Figure 5. (a) Zero-field-cooled (open red circles) and field-cooled (shaded blue circles) dc magnetic susceptibility vs. temperature, χ (T), variations under 100 Oe applied magnetic field for La2MgIrO6. Inset: 2 K M vs. H isotherm. (b) Amount of 2 kOe zero-field-cooled (open circles) and field-cooled (shaded circles) dc magnetic susceptibility data for La2ZnIrO6. Top inset: corresponding Curie–Weiss fit showing inverse susceptibility (1/χ) vs. temperature plot in the 50–300 K temperature range. Bottom inset: temperature dependence of dM/dT for three different applied fields, indicating the transition temperature TN for each of the fields from the minimum of the respective curves. (c) M vs. H isotherms for La2ZnIrO6 at three different temperatures. Inset: expanded views of the respective M (H) curves to highlight the coercivity and remanence.
Condensedmatter 10 00053 g005
Condensedmatter 10 00053 g006
Figure 6. Ir L3-edge RIXS spectrum of La2MgIrO6 (a) and La2ZnIrO6 (b) with the left side of each spectrum showing high-resolution low-energy excitations within the SOC multiplets and the right side representing the low-resolution high-energy features.
Figure 6. Ir L3-edge RIXS spectrum of La2MgIrO6 (a) and La2ZnIrO6 (b) with the left side of each spectrum showing high-resolution low-energy excitations within the SOC multiplets and the right side representing the low-resolution high-energy features.
Condensedmatter 10 00053 g006
Table 1. Results of the Rietveld refinement carried out on La2MgIrO6 and La2ZnIrO6 XRPD data (300 K). The refinements were carried out using a single phase with monoclinic P21/n space group. Unit cells parameters and statistical refinement quality factors for La2MgIrO6 are as follows: a = 5.5868(2) Å, b = 5.6243(2) Å, c = 7.9105(1) Å; α = γ = 90°, β = 90.018(1)°; The fixed or constant values are labeled by asterisk (*). Rp = 13.1, Rwp= 14.1, Rexp= 7.46, and χ2 = 3.57; unit cells parameters and statistical refinement quality factors for La2ZnIrO6 are as follows: a = 5.5988(7) Å, b = 5.6819(0) Å, c = 7.9395(1) Å; α = γ = 90°, β = 90.021(8)°; Rp = 13.9, Rwp = 12.8, Rexp = 6.91, and χ2 = 3.43.
Table 1. Results of the Rietveld refinement carried out on La2MgIrO6 and La2ZnIrO6 XRPD data (300 K). The refinements were carried out using a single phase with monoclinic P21/n space group. Unit cells parameters and statistical refinement quality factors for La2MgIrO6 are as follows: a = 5.5868(2) Å, b = 5.6243(2) Å, c = 7.9105(1) Å; α = γ = 90°, β = 90.018(1)°; The fixed or constant values are labeled by asterisk (*). Rp = 13.1, Rwp= 14.1, Rexp= 7.46, and χ2 = 3.57; unit cells parameters and statistical refinement quality factors for La2ZnIrO6 are as follows: a = 5.5988(7) Å, b = 5.6819(0) Å, c = 7.9395(1) Å; α = γ = 90°, β = 90.021(8)°; Rp = 13.9, Rwp = 12.8, Rexp = 6.91, and χ2 = 3.43.
SampleAtomOccupancyxyz
La2MgIrO6La10.4999(1)0.5349(1)0.2495(2)
Mg1/Ir10.9188(2)/0.08120.500
Ir2/Mg20.9188 */0.0812 00.50
O110.2109(4)0.1985(2)−0.0425(1)
O210.2698(4)0.7278(5)−0.0502(1)
O310.4267(5)−0.0168(2)0.2576(4)
La2ZnIrO6La10.5019(2)0.5457(3)0.2481(5)
Zn1/Ir10.8965(6)/0.1035 0.500
Ir2/Z20.8965 */0.1035 00.50
O110.2153(6)0.2002(4)−0.0341(3)
O210.3016(5)0.7325(4)−0.0522(5)
O310.4063(5)−0.0223(5)0.2364(6)
Table 2. An estimation of octahedral distortions in the form of deviated bond angles.
Table 2. An estimation of octahedral distortions in the form of deviated bond angles.
Type of DistortionConnectivityLa2MgIrO6La2ZnIrO6
TiltingIr-O3-Mg/Zn156.00(1)°149.50(1)°
Ir-O2-Mg/Zn155.47(5)°151.86(2)°
Ir-O1-Mg/Zn152.10(6)°155.56(4)°
RotationalO1-Ir-O389.94(6)°93.57(2)°
O1-Ir-O293.57(4)°91.27(4)°
O2-Ir-O386.13(5)°88.17(6)°
Table 3. Local structure parameters extracted from the Ir L3 and Zn K-edges EXAFS fittings. In order to reduce correlation among the parameters, constraints were applied, namely x as the fraction of Ir-O-Mg/Zn configurations, i.e., NIr-O-Mg/Zn = 6x and NIr-O-Ir = 6(1 − x). The fixed or constrained values are labeled by *. The absolute mismatch between the experimental data and the best fit are as follows: R2 = 0.013 and 0.018 corresponding to the Ir L3 edge fittings of LMIO and LZIO, respectively, while R2 = 0.019 for the Zn K-edge EXAFS data fitting of LZIO.
Table 3. Local structure parameters extracted from the Ir L3 and Zn K-edges EXAFS fittings. In order to reduce correlation among the parameters, constraints were applied, namely x as the fraction of Ir-O-Mg/Zn configurations, i.e., NIr-O-Mg/Zn = 6x and NIr-O-Ir = 6(1 − x). The fixed or constrained values are labeled by *. The absolute mismatch between the experimental data and the best fit are as follows: R2 = 0.013 and 0.018 corresponding to the Ir L3 edge fittings of LMIO and LZIO, respectively, while R2 = 0.019 for the Zn K-edge EXAFS data fitting of LZIO.
Sample with Absorption EdgeShellNσ2(102 Å2)R(Å)
La2ZnIrO6
(Ir-L3 edge)		Ir-O6.0 *0.21(3)2.009(4)
Ir-La14.0 *0.43(5)3.25(2)
Ir-La24.0 *0.43 *3.43(3)
Ir-Zn/Ir (SS)5.3(2)/0.71.68(4)4.01(2)
Ir-O-Zn/Ir (MS)10.7 */1.31.68 *4.07(3)
La2MgIrO6
(Ir-L3 edge)		Ir-O6.0 *0.22(3)1.995(5)
Ir-La14.0 *0.75(5)3.27(6)
Ir-La24.0 *0.75 *3.43(2)
Ir-Mg/Ir (SS)5.2(2)/0.80.55(3)3.98(2)
Ir-O-Mg/Ir (MS)10.4 */1.60.55 *4.02(2)
La2ZnIrO6
(Zn-K edge)		Zn-O6.00.77(2)2.078(4)
Zn-La12.0 *0.66(5)3.26(5)
Zn-La24.0 *0.97(7)3.44(4)
Zn-La32.0 *0.97 *3.72(6)
Zn-Ir/Zn5.4(2)/0.60.81(6)3.98(2)
Zn-O-Ir/Zn10.8 */1.20.81 *4.04(6)
Table 4. Results obtained from the temperature-dependent DC magnetic susceptibility curves and M vs. H isotherms for LZIO.
Table 4. Results obtained from the temperature-dependent DC magnetic susceptibility curves and M vs. H isotherms for LZIO.
H (Oe)TZFC(K)TN(K)µeff(µB/Ir4+)ΘCW(K) T(K)MS (µB/f.u.)
1008.57.91.63−7.03 20.292
χ vs. T 5006.158.11.47−2.12M vs. H50.278
20005.38.451.430.2 80.209
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bandyopadhyay, A.; Pandey, D.K.; Meneghini, C.; Efimenko, A.; Sala, M.M.; Ray, S. Exploring Low Energy Excitations in the d5 Iridate Double Perovskites La2BIrO6 (B = Zn, Mg). Condens. Matter 2025, 10, 53. https://doi.org/10.3390/condmat10040053

AMA Style

Bandyopadhyay A, Pandey DK, Meneghini C, Efimenko A, Sala MM, Ray S. Exploring Low Energy Excitations in the d5 Iridate Double Perovskites La2BIrO6 (B = Zn, Mg). Condensed Matter. 2025; 10(4):53. https://doi.org/10.3390/condmat10040053

Chicago/Turabian Style

Bandyopadhyay, Abhisek, Dheeraj Kumar Pandey, Carlo Meneghini, Anna Efimenko, Marco Moretti Sala, and Sugata Ray. 2025. "Exploring Low Energy Excitations in the d5 Iridate Double Perovskites La2BIrO6 (B = Zn, Mg)" Condensed Matter 10, no. 4: 53. https://doi.org/10.3390/condmat10040053

APA Style

Bandyopadhyay, A., Pandey, D. K., Meneghini, C., Efimenko, A., Sala, M. M., & Ray, S. (2025). Exploring Low Energy Excitations in the d5 Iridate Double Perovskites La2BIrO6 (B = Zn, Mg). Condensed Matter, 10(4), 53. https://doi.org/10.3390/condmat10040053

Article Metrics

Back to TopTop