Mott Law exp(T₀/T)^1/4 and Scaling Properties of the Oxygen-Deficient Tenorite CuO_0.75

Abstract

The novel sub-stoichiometric copper oxide CuO_0.75 was prepared via the slow oxidation of Cu₂O. This compound retains the original crystallographic structure of tenorite CuO, despite the considerable presence of disordered oxygen vacancies. CuO_0.75 resembles the mixed valence oxide Cu²⁺/Cu¹⁺, while the unit cell contains one oxygen vacancy. Performance-wise, the electric resistivity and magnetic susceptibility data follow the Anderson–Mott localization theories. The exponential localization decay length was found to be α⁻¹ = 2.1 nm, in line with modern scaling research. Via cooling, magnetic double-exchange interaction, mediated by oxygen, results in Zener conductivity at T~122 K, which is followed by antiferromagnetic transition at T~51 K. The obtained results indicate that the CuO_0.75 compound can be perceived as a showcase material for the demonstration of a new class of high-performance magnetic materials.

1. Introduction

Before the development of localization theories in disordered systems, Landauer [1] put forward the systematic calculation of the electric conductivity of metals containing point defects and derived the equation σ = e²/h·[ΣT_i], in which summation is extended over scattering obstacles. This equation is widely used in semiconducting nanostructures, and the pre-factor is named the Landauer quantum conductance, which is considered in various localization theories, such as the quantum Hall effect, and symbolizes a route toward greater universality in solid-state research.

This groundbreaking progress regarding localization in disordered systems, followed by Anderson [2] and Mott [3], triggered a further intensive search for the universality of magnetic and electric properties in solid-state physics, optics, etc. The quantum mechanical functions in localized systems are confined to a finite region and they decay exponentially at higher distances. The localization phenomena cover various materials [4,5] and optics [6,7,8]. However, experimental data derived from the real objects are scarce and dominantly restricted to resistive measurements [9,10], while the accompanying magnetic effects, superimposed with resistivity data, are rare in the scientific literature.

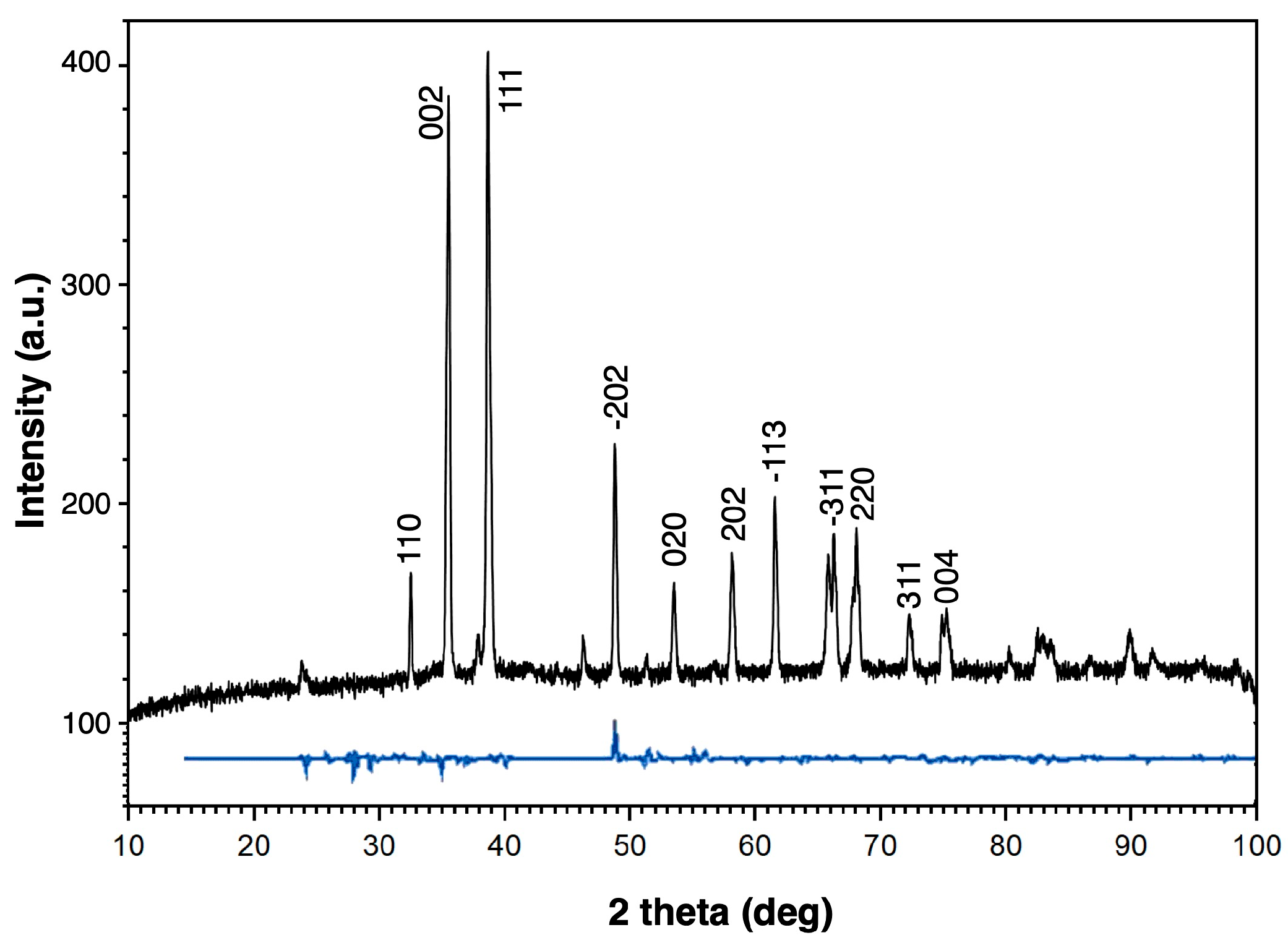
This paper aims to describe the preparation of the sub-stoichiometric copper oxide CuO_0.75, indicated by disordered oxygen vacancies, while the X-ray diffraction data demonstrate the maintenance of the original structure of the tenorite CuO. In addition to the resistivity, CuO_0.75 displays an interesting set of magnetic effects, which start by cooling from T~122 K and are followed by antiferromagnetic transition (AF) at T~51 K. In the next step, the experimental data are discussed in terms of Mott and Anderson theories, as well as modern scaling models. However, difficulties arise from the fact that theories and models dominantly deal with metals, while CuO_0.75 is not metallic, as indicated by its huge dielectric permittivity ε~1.3 × 10³, evaluated separately in these experiments.

2. Experiment

Oxygen-deficient CuO_0.75 was produced from the powdered cuprous oxide Cu₂O with a particle size of 0.5 microns and heated at 388 K in a 4 bar oxygen atmosphere. Prior to the reaction, the powder was heated in vacuum at 423 K in order to remove the traces of gases such as water vapor, CO₂ and SO₂. The slow reaction was monitored for 10–12 days by use of a pressure gauge and terminated when the oxygen pressure reduced to the value indicating the necessary stoichiometry for CuO_0.75. The final product was a raw and hard cluster. The oxygen content was additionally verified by means of decomposition in a 2 bar H₂ atmosphere at 673 K.

The powder obtained by means of subsequent regrinding of the raw cluster (R-sample) was pressed into pellets 8 mm in diameter and d = 0.9 mm in thickness. Raw CuO_0.75 is an insulator, but it was observed that conductance may be induced by applying a DC current starting at 1 µA and gradually increasing up to 1.5 mA during repeated annealing–cooling cycles (DC–samples) in an argon atmosphere. The annealing temperature was 908 K, while the final conductivity of DC samples at room temperature (RT) saturated at 0.08–1.25 × 10⁻² Ω⁻¹m⁻¹. The modification of materials containing highly polarized dipoles using currents was published elsewhere [11,12], and this effect is ascribed to the formation of clusters. More recent findings [13,14] may provide some introductory ideas and hints regarding the possible stimulation of disorder and the corresponding increase in conductivity via the use of conducting currents.

3. Results

Copper oxide (CuO) is a narrow-band p-type semiconductor and crystallographic unit cell belonging to the monoclinic group C2/c with cell dimensions a = 0.4683 nm, b = 0.3421 nm, c = 0.5129 nm; α = 90°, β = 90°, γ = 99.784°. The unit cell contains four unit formulas, and its density is ρ = 5.94 g·cm⁻³, while the oxygen-deficient form CuO_0.75 exhibits a density of ρ = 5.64 g·cm⁻³. Due to it having one oxygen vacancy per unit cell, CuO_0.75 is expected to be a mixed valence oxide with an equal number of Cu²⁺ and Cu⁺ cations. In this respect, CuO_0.75 resembles the copper oxide Cu₄O₃, known as paramelaconite, with the structure indicating CuO₂ chains along the c-axis [15]. Paramelaconite, however, exhibits a pyrochlore crystal lattice, while CuO_0.75 preserves the original CuO structure, as is visible in the XRD data recorded for CuO_0.75, as shown in Figure 1. CuO_0.75 samples have a foreign substance content of ~3%; 1.4% Cu₂O, 0.7% Cu₄O₃, 0.3% Cu₂S, and 0.7% Cu.

High-resolution measurements of AC susceptibility were performed on R and DC samples using a Cryobind susceptometer, and real and imaginary parts are shown in Figure 2. Measurements were performed at 231 Hz and 1.26 Oe (zero-peak) for the (a) R sample and (b) DC sample. The samples exhibit a surprising temperature dependence regarding their susceptibility, and several features are included. When cooling from RT, the AC magnetic susceptibility displays three features. Down to T = 122 K, susceptibility obeys paramagnetic behavior, and the plot of 1/(χ′(T) − χ′_P) versus T is shown in Figure 3. Pauli susceptibility was evaluated as χ′_P = 6.5 × 10⁻⁶ emu/g·Oe, while the density of states (DOS) at Fermi energy was calculated [16] from χ′_P = μ₀·μ_B²·N(E_F), giving N(E_F) = 2.8 × 10⁴⁶ Joule⁻¹ m⁻³. The Fermi energy E_F was separately derived from the number of states n = 1/V₀ = 2.4 × 10²⁸ m⁻³, and V₀ indicates the volume of the crystallographic unit cell. The Fermi wave number is given as k_F = (3π²·n)^1/3, and E_F = 3.3 eV. The next feature appears in the DC sample at T = 101 K, and it correlates with a temperature transition leading to the melting of localized states and the appearance of additional magnetic interactions which result in Zener conductivity and magnetic helical phases. Both the DC and R samples undergo, at T = 51 K, an AF transition, which reflects their similarity to paramelaconite, indicated by the AF at T = 42 K, as reported by Pinsard-Gaudart and co-workers [17]. However, a sharp peak in imaginary susceptibility indicates the survival of residual ferromagnetic correlations, i.e., weak ferromagnetism in the temperature interval of 51 < T < 122 K. The horizontal dashed line in Figure 2 shows the contribution of the Pauli susceptibility after the removal of the contributions of foreign components; the latter were subtracted after an independent measurement of the susceptibility of commercial Cu₂O previously heated in vacuum at T = 850 K.

Figure 4 presents the resistance of the DC sample measured using a cooling and heating cycle in the range of 80–415 K. The inset shows the specimen’s (1) arrangement with in-pressed gold wires, 100 microns in diameter, acting as probes providing four resistance measurements. A copper–constantan thermocouple (2) consisting of 50-micron wires was covered by a silk weave (3). The thermocouple was separated from the pellet by a 30-micron mica foil (6). The pellet was glued using heat-resistant glue to the ceramic plate (5). In order to eliminate the contribution of parasitic intrinsic thermopower, the cooling–heating cycle was applied slowly and extended up to 44 days. The liquid nitrogen level in the surrounding cooling bath was kept constant, while evaporation was compensated by the introduction of the fresh liquid nitrogen via drop-by-drop flow. The linear dependence of lnρ on T^−1/4 is evident down to T_C = 122 K, when lnρ starts to deviate with further heating, which is followed by a sharp downturn at T = 101 K. The linear dependence of lnρ on T^−1/4 is the characteristic behavior of the disordered three-dimensional (3D) system indicated by localization of the electronic states. Anderson put forward that, in disordered systems, diffusion theories of the conductivity must be replaced by models based on quantum jumps between the localized states. Continuing on such a course, Mott developed a theory [18] of variable range hopping, and the logarithm of the resistivity was derived as

lnρ = 2αR + 1/(4απ/3)k_BTR³N(E_F) R = [αk_BTN(E_F)]^−1/4

(1)

where 1/α and R are the localization length and hopping range, respectively. This expression was fitted to the measured dependence of lnρ on T^−1/4 in the temperature interval of 122–415 K when the metallic state is set up by further heating, as is shown in the inset of Figure 4. An evaluation of the localization length gives an α⁻¹ in the order of 10⁻¹⁰ m. This result contradicts the activation energy required for the formation of the hopping process and given (36 [18]) by the model independent expression, W = α³/N(E)~170 eV. The cause of this discrepancy may be the derivation of Equation (1) without consideration of the dielectric properties of materials. CuO_0.75 displays enormous dielectric permittivity, which in turn reduces activation energy. We consider in this paper the localization decay length, as derived from the above-cited activation energy expression, to be α⁻¹ = 2.1 nm.

The measured electric conductance of CuO_0.75 at T = 415 K was G₀ = 1.5 × 10⁻²Ω⁻¹, and the evaluated conductivity was σ₀ = 0.17 Ω⁻¹·cm⁻¹. An attempt to compare this value to the Mott metallic conductivity σ_min = π²·e²/8·z·h·c (31 [18]) must consider the dielectric permittivity of CuO_0.75, which in the temperature interval of 100–415 K is ε = 1.3 × 10³. The renormalized value reads σ = ε·σ₀~221 Ω⁻¹·cm⁻¹, and it is comparable to the Mott conductivity σ_min = 300 Ω⁻¹·cm⁻¹. In further calculations, we replace the lattice parameter c with α⁻¹ for distant localized scatters.

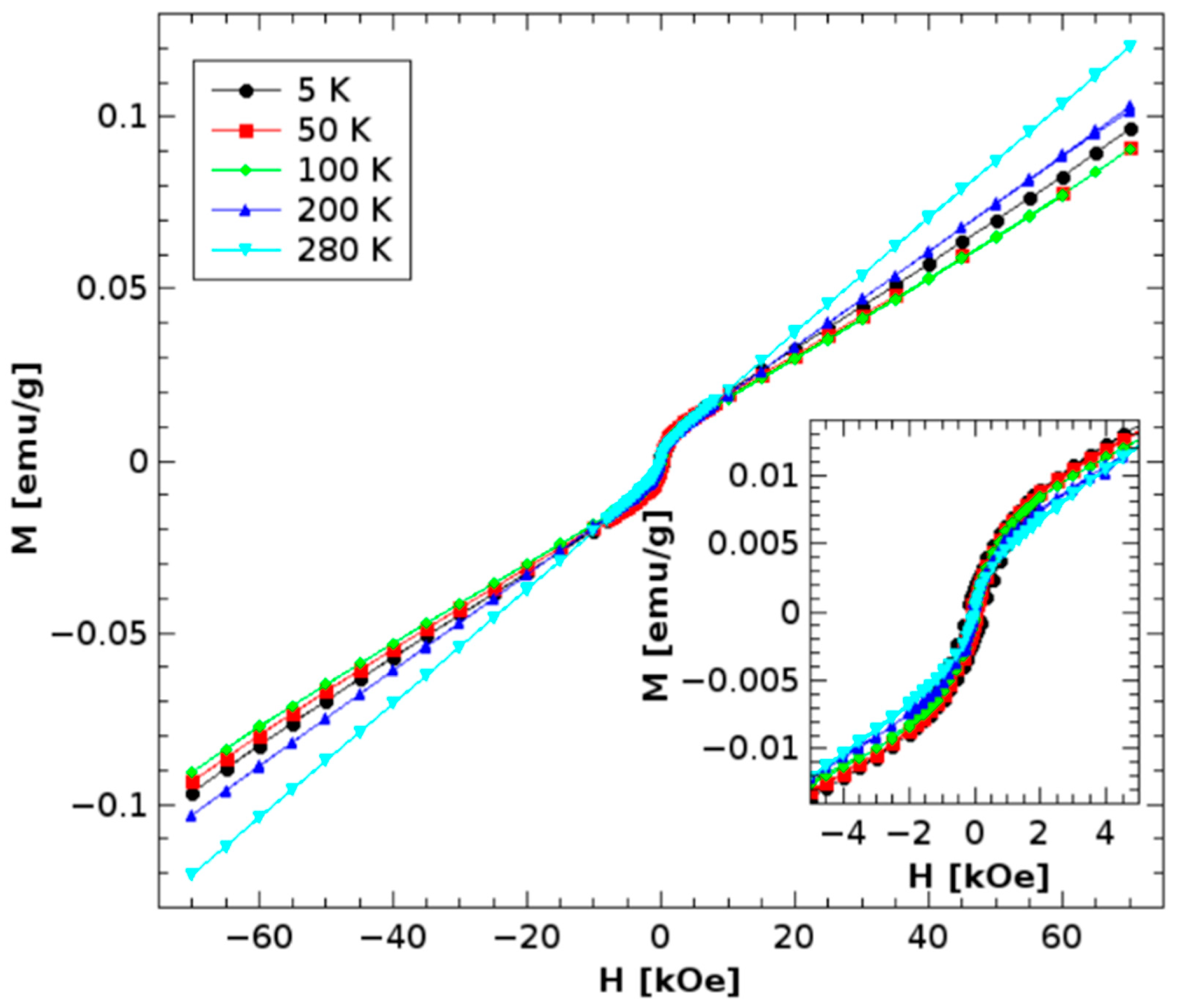
The measurements of hysteresis loops, performed through the use of a SQUID magnetometer, are presented in Figure 5. First of all, they show a generally near-linear response, with a relatively small slope and small magnetization below 0.1 emu/g even in a field of 50 kOe in all three temperature ranges, which is in accordance with other presented results, since the antiferromagnetic and Pauli paramagnetic phases have relatively small magnetic responses. However, there is some notable irreversibility and nonlinearity in fields below 1 kOe, where hysteresis begins at 5 K, with coercivity around 400 Oe, decreasing to around 100 Oe at a temperature of 50 K. Above 100 K, loops become closed and reversible with the uncertainty of the superconducting magnet field. The bending of loops into an S-shape around small fields in the order of ~kOe could originate from the superparamagnetism of spin nanoclusters, which may reflect the localized states bound to distinct regions. Cooling down to the antiferromagnetic phase, open hysteresis develops, which theoretically could originate from the blocking of spin-clusters, but weak ferromagnetism is a more probable explanation. Other specific techniques using neutron reflection should provide a more precise explanation. However, this result opens questions for further study and presents potential applications of the material in spintronics, and even more so in other broken-symmetry-based devices.

4. Discussion

Following [17], the magnetic double-exchange interaction calculated in paramelaconite (Cu₄O₃) between the nearest-neighbor Cu²⁺ cations Cu²⁺–O–Cu²⁺ (NN) is E = 48.3 K. Such a mechanism may also be present in CuO_0.75. In addition, oxygen vacancies may also be involved in the double-exchange of Cu²⁺–Vo–Cu²⁺ or Cu²⁺–Vo–Cu⁺.

The reduction in the resistance of CuO_0.75 below 122 K may be explained by Zener’s model of magnetic double-exchange conductivity. This model was originally applied to the resistance [19] properties of strontium-doped manganite (La_1–xSr_x)MnO₃. An exchange is favored by the polarization of the hopping electrons between aligned cation spins Mn⁴⁺–O–Mn³⁺, which in turn enhances the electric conductance and the magnetization due to the itinerant electron contribution. Zener evaluated the electric conductance G_Z = x·e²E/h·k_BT. E and x are the exchange energy and fraction of ions involved in the exchange, respectively. G_Z reduces the resistance divergence T^−1/4 in CuO_0.75 at T < 122 K, giving rise to possible fluid conductance. The calculated Zener conductivity reads σ_Z~380 Ω⁻¹·cm⁻¹, while relative dielectric permittivity is absent in the evaluation.

Thouless [20] introduced dimensionless conductance g = G·h/e². However, the ratio of the measured and Landauer conductance is impractical for testing the scaling theories experimentally, since the measured conductance G is dependent on the sample thickness d, due to there being no uniquely defined parameter. We introduce dimensionless conductivity g = ε·α⁻¹·G·h/d·e², and g gives the Thouless energy E_T = g·Δ. Δ = 18.8 meV is the above-evaluated level spacing, and from the resistance at T = 415 K, Thouless energy reads E_T = 9.8 meV, giving T_C = 132 K, which should be compared to the transition temperature T = 122 K. The Thouless energy and corresponding temperature mark the melting of the localized to extended states, while, upon heating, the T^−1/4 regime starts at temperature T = 122 K and extends up to 415 K.

In the next step, an attempt is presented to compare the resistance data to the scaling model put forward by Abrahams and co-workers (AALR) [21]. A problem arises in defining the universal scaling length L based on given experimental data. The choice proposed by AALR is the mean free path l, although l is questionable because of a strong dependence on temperature. Following a search for common points for the AALR model, Mott theory, and our experimental data, we introduce localization decay L = α⁻¹ as a scaling length, since it is independent of temperature. AALR theory introduces the parameter β = d(lng)/d(lnL), indicating that β = 0 at the metal–insulator transition. The comparatively easy calculation for the case of CuO_0.75 starts with the elimination of the temperature in Equation (1), which gives the dimensionless conductivity g = (h·L·σ₀·ε·e²)exp − R/L. This expression matches the AALR result for the 3D system. In addition, the authors identify a pre-factor with Mott conductivity giving to this quantity the scaling form 2π·e²g_c/L₀^d−2. More algebra results in β = d(lng)/d(lnL) = 1 − R/L giving β = 0 for R = L at T = 318 K, comparable to the MI transition temperature T = 415 K.

5. Conclusions

In conclusion, a novel copper oxide CuO_0.75 was prepared. This compound is represented by one oxygen vacancy per unit cell and exhibits the crystallographic structure of tenorite CuO. In the interval of 122–415 K, electric resistance is temperature-dependent according to Mott’s law exp[(T₀/T)^1/4]. Anderson’s theory of localization and Mott’s theory of variable hopping were successfully applied, and the characteristic length of exponential decay of the localized state was evaluated as α⁻¹ = 2.1 nm, while the variable hopping range is R = 2.3 × 10⁻⁹ m at T = 122 K. It has been shown that Mott’s concept of minimum conductivity in metals σ_min may be extended to the nonmetal CuO_0.75, giving rise to a possible universal physical constant. In addition, σ_min has been evaluated by taking into account a calculated [22] ratio of critical localization potential and band width V_crit/B = 2, confirming this result to be correct. Dimensionless Thouless conductivity g was calculated and the corresponding Thouless energy E_T, converted to temperature, gives T~114 K. In order to apply the scaling theory of Abrahams and co-workers (AALR), L = α⁻¹ is chosen as a scaling length. At T = 122 K, magnetic measurements reveal the transition to a double-exchange interaction indicated by Zener conductivity, which is comparable to the Mott conductivity σ_min. CuO_0.75 undergoes an antiferromagnetic transition at T = 51 K.