The Defect Charge Effect on Magnetic Anisotropy Energy and Dzyaloshinskii–Moriya Interaction of the I Vacancy and 3d Transition Metal Co-Doped Monolayer CrI3
Abstract
:1. Introduction
2. Results and Discussion
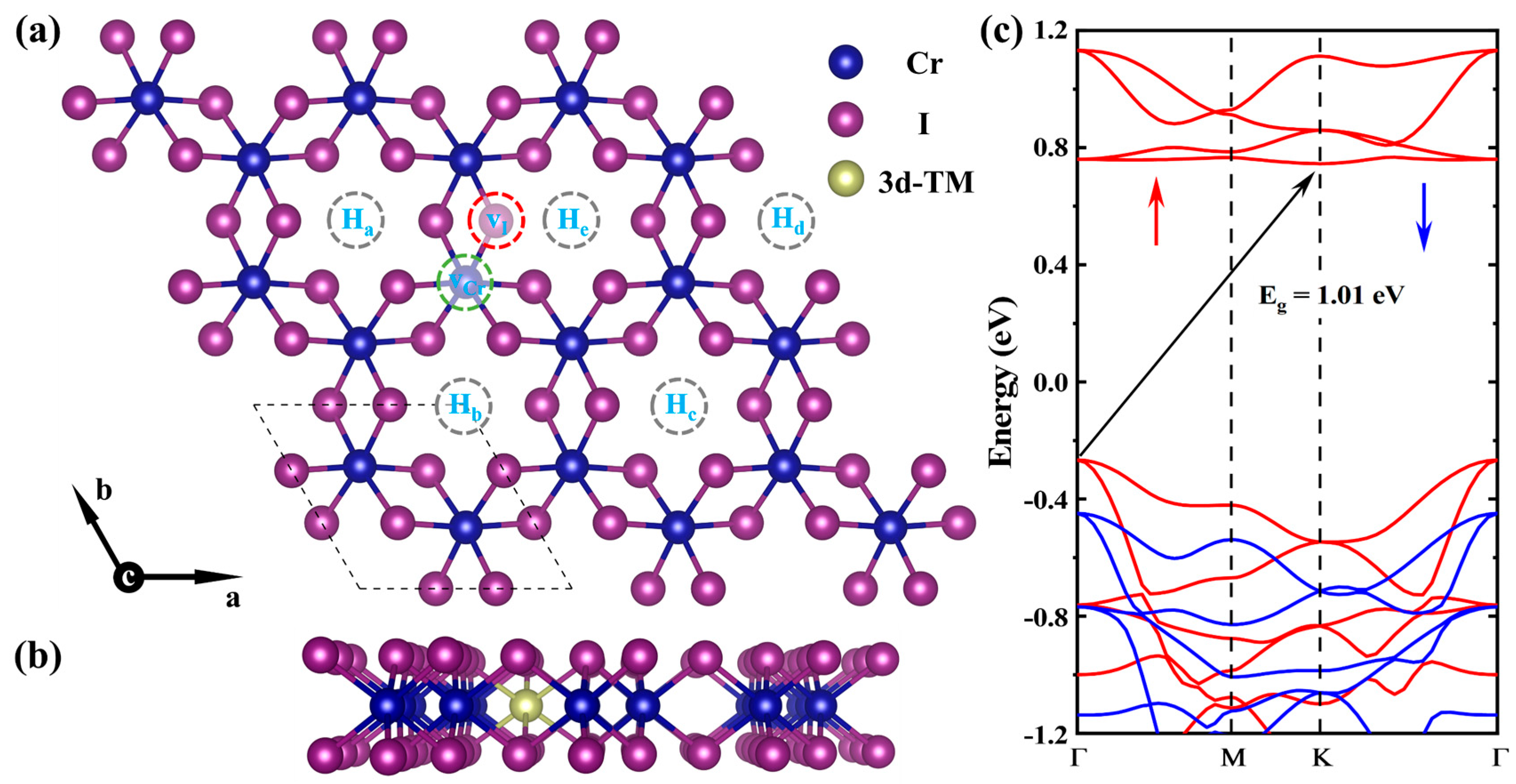
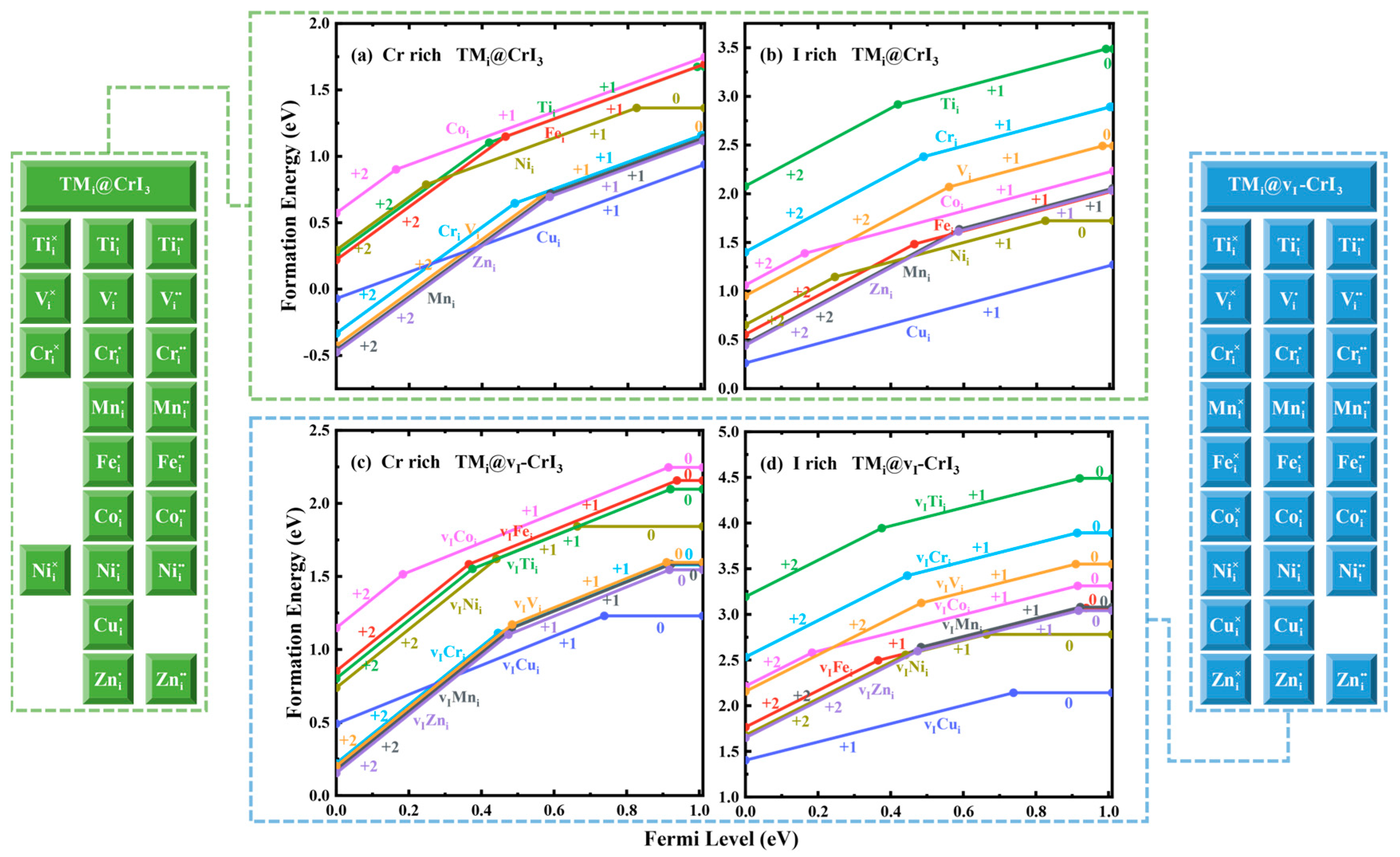
2.1. The Formation Energy of Point Defect in CrI3
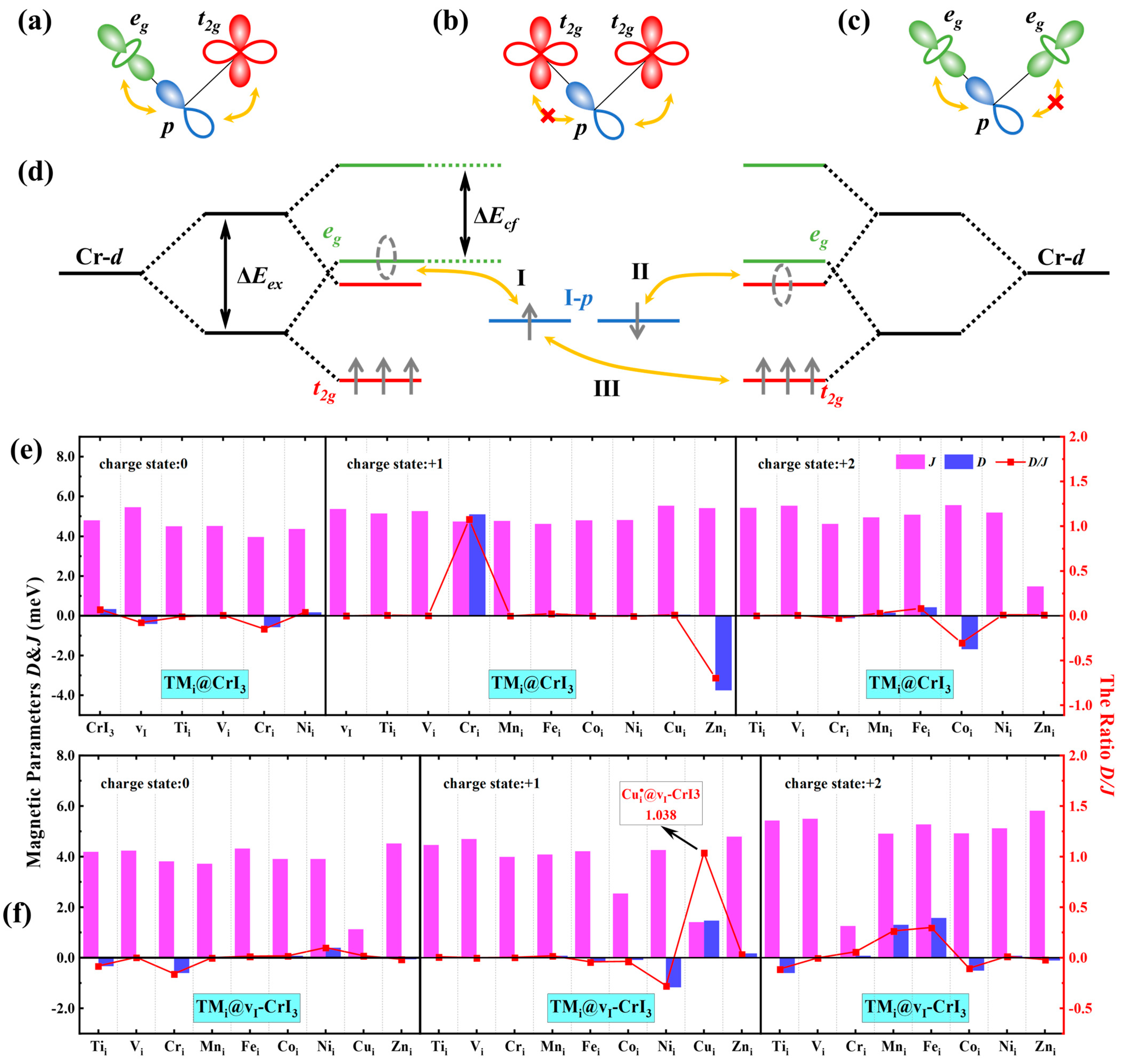
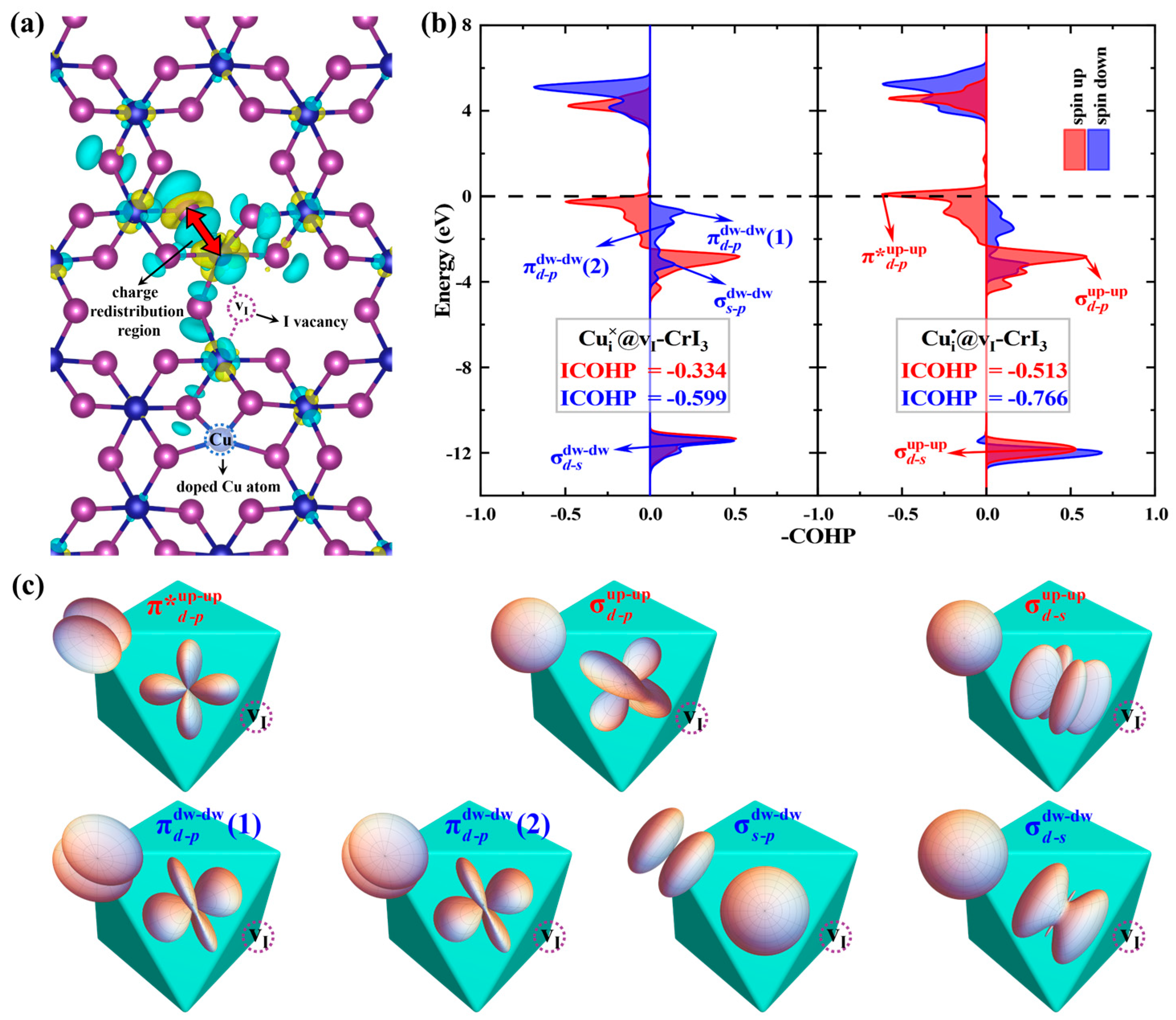
2.2. Magnetic Exchange Interactions
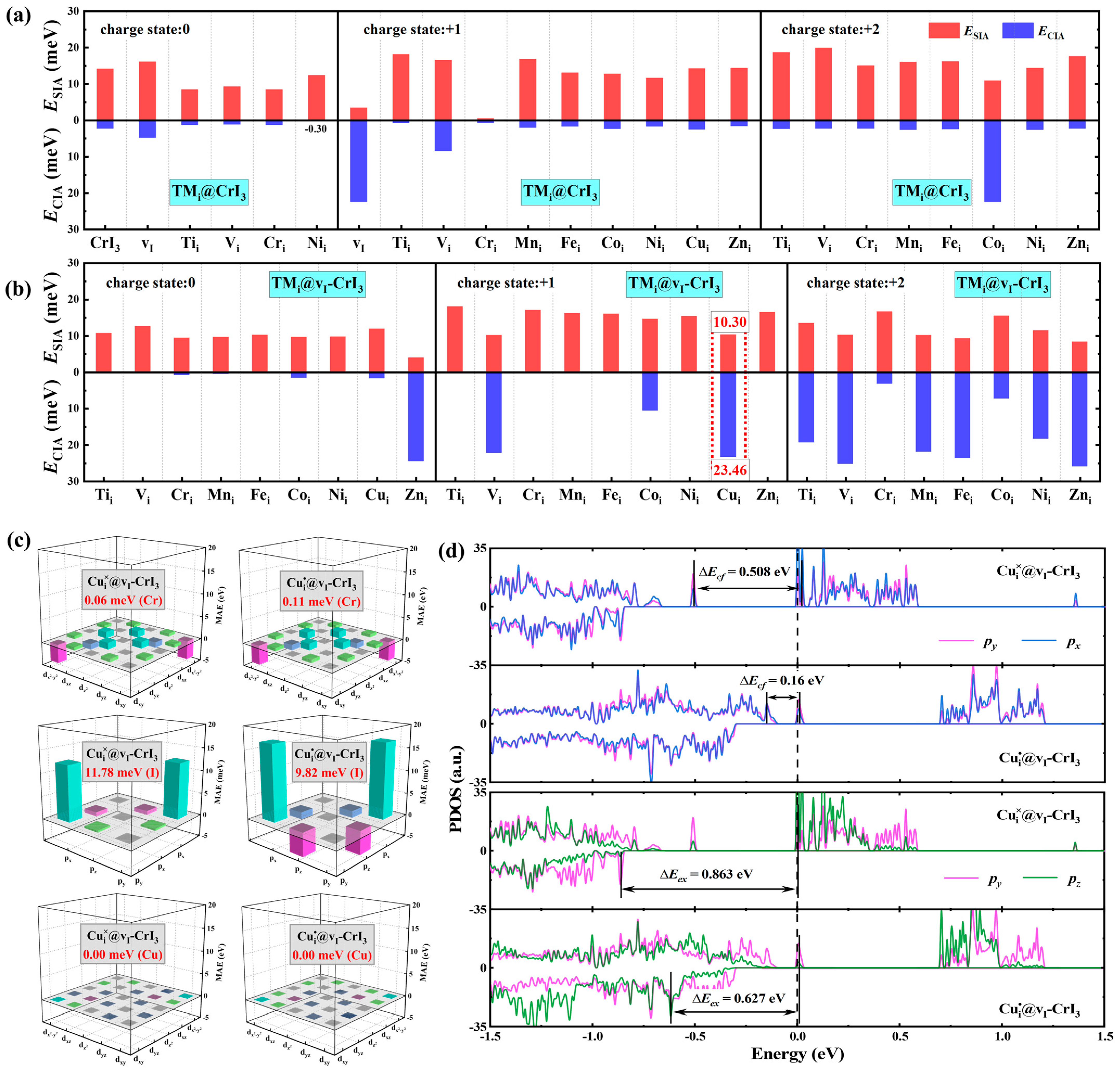
2.3. Magnetic Anisotropy Energy
3. Conclusions
4. Computational Details
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xing, S.; Zhou, J.; Zhang, X.; Elliott, S.; Sun, Z. Theory, properties and engineering of 2D magnetic materials. Prog. Mater Sci. 2023, 132, 101036. [Google Scholar] [CrossRef]
- Chen, B.; Zeng, M.; Khoo, K.H.; Das, D.; Fong, X.; Fukami, S.; Li, S.; Zhao, W.; Parkin, S.S.P.; Piramanayagam, S.N.; et al. Spintronic devices for high-density memory and neuromorphic computing—A review. Mater. Today 2023, 70, 193–217. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.; Zheng, Z.; Zhang, Z.; Lin, K.; Sun, X.; Wang, G.; Wang, J.; Wei, J.; Vallobra, P.; et al. Ferrimagnets for spintronic devices: From materials to applications. Appl. Phys. Rev. 2023, 10, 011301. [Google Scholar] [CrossRef]
- Gibertini, M.; Koperski, M.; Morpurgo, A.F.; Novoselov, K.S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 2019, 14, 408–419. [Google Scholar] [CrossRef]
- Yang, F.; Hu, P.; Yang, F.F.; Chen, B.; Yin, F.; Sun, R.; Hao, K.; Zhu, F.; Wang, K.; Yin, Z. Emerging enhancement and regulation strategies for ferromagnetic 2D transition metal dichalcogenides. Adv. Sci. 2023, 10, 2300952. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, Z.; Gao, Y.; Wang, H.; Gao, J.; Zhao, J. Selecting dual atomic clusters supported on two-dimensional biphenylene with significantly optimized capability to reduce carbon monoxide. J. Mater. Chem. A 2024, 12, 2748–2759. [Google Scholar] [CrossRef]
- Bijker, R. Phase transitions and spontaneously broken symmetries. Fundam. Phys. 2009, 3, 51–60. [Google Scholar]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one-or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.; Bogdanov, A.; Monchesky, T. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Butenko, A.; Leonov, A.; Rößler, U.; Bogdanov, A. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857–2897. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.; Bo, L.; Zhao, R.; Hu, C.; Ji, L.; Chen, W.; Li, Y.; Zhang, Y.; Zhang, X. The modes of skyrmionium motion induced by vacancy defects on a racetrack. J. Magn. Magn. Mater. 2021, 537, 168173. [Google Scholar] [CrossRef]
- Smiri, A.; Jaziri, S.; Lounis, S.; Gerber, I.C. DFT+ U investigation of magnetocrystalline anisotropy of Mn-doped transition-metal dichalcogenide monolayers. Phys. Rev. Mater. 2021, 5, 054001. [Google Scholar] [CrossRef]
- Langer, R.; Mustonen, K.; Markevich, A.; Otyepka, M.; Susi, T.; Błoński, P. Graphene Lattices with Embedded Transition-Metal Atoms and Tunable Magnetic Anisotropy Energy: Implications for Spintronic Devices. ACS Appl. Nano Mater. 2022, 5, 1562–1573. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, M.; Zhu, X.; Tan, C.; Wang, J.; Albarakati, S.; Aloufi, N.; Algarni, M.; Farrar, L.; Wu, M.; et al. Tailoring Dzyaloshinskii–Moriya interaction in a transition metal dichalcogenide by dual-intercalation. Nat. Commun. 2021, 12, 3639. [Google Scholar] [CrossRef]
- Banik, S.; Chattopadhyay, M.K.; Tripathi, S.; Rawat, R.; Jha, S.N. Large positive magnetoresistance and Dzyaloshinskii–Moriya interaction in CrSi driven by Cr 3d localization. Sci. Rep. 2020, 10, 12030. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Soriano, D.; Katsnelson, M.I.; Fernández-Rossier, J. Magnetic Two-Dimensional Chromium Trihalides: A Theoretical Perspective. Nano Lett. 2020, 20, 6225–6234. [Google Scholar] [CrossRef]
- Song, T.; Cai, X.; Tu, M.W.-Y.; Zhang, X.; Huang, B.; Wilson, N.P.; Seyler, K.L.; Zhu, L.; Taniguchi, T.; Watanabe, K.; et al. Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Science 2018, 360, 1214–1218. [Google Scholar] [CrossRef]
- Lee, Y.C.; Chang, S.W.; Chen, S.H.; Chen, S.L.; Chen, H.L. Optical Inspection of 2D Materials: From Mechanical Exfoliation to Wafer-Scale Growth and Beyond. Adv. Sci. 2022, 9, 2102128. [Google Scholar] [CrossRef]
- Islam, M.A.; Serles, P.; Kumral, B.; Demingos, P.G.; Qureshi, T.; Meiyazhagan, A.; Puthirath, A.B.; Abdullah, M.S.B.; Faysal, S.R.; Ajayan, P.M.; et al. Exfoliation mechanisms of 2D materials and their applications. Appl. Phys. Rev. 2022, 9, 041301. [Google Scholar] [CrossRef]
- Yi, M.; Shen, Z. A review on mechanical exfoliation for the scalable production of graphene. J. Mater. Chem. A 2015, 3, 11700–11715. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Y.; Li, P.; Wang, J.; Zhou, S.; Zhao, J.; Guo, D.; Zhong, D. Imaging Vacancy Defects in Single-Layer Chromium Triiodide. J. Phys. Chem. Lett. 2021, 12, 2199–2205. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Bai, Y.; Tang, J.; Wang, P.; You, Y.; Xu, G.; Xu, F. Growth of high-quality CrI3 single crystals and engineering of its magnetic properties via V and Mn doping. J. Alloys Compd. 2022, 908, 164573. [Google Scholar] [CrossRef]
- Thiel, L.; Wang, Z.; Tschudin, M.A.; Rohner, D.; Gutiérrez-Lezama, I.; Ubrig, N.; Gibertini, M.; Giannini, E.; Morpurgo, A.F.; Maletinsky, P. Probing magnetism in 2D materials at the nanoscale with single-spin microscopy. Science 2019, 364, 973–976. [Google Scholar] [CrossRef]
- Wang, R.; Su, Y.; Yang, G.; Zhang, J.; Zhang, S. Bipolar doping by intrinsic defects and magnetic phase instability in monolayer CrI3. Chem. Mater. 2020, 32, 1545–1552. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, X.; Shen, X.; Krasheninnikov, A.V.; Chen, Z.; Sun, L. Enhancing Ferromagnetism and Tuning Electronic Properties of CrI3 Monolayers by Adsorption of Transition-Metal Atoms. ACS Appl. Mater. Interfaces 2021, 13, 21593–21601. [Google Scholar] [CrossRef]
- Pizzochero, M. Atomic-scale defects in the two-dimensional ferromagnet CrI3 from first principles. J. Phys. D Appl. Phys. 2020, 53, 244003. [Google Scholar] [CrossRef]
- Guo, Y.; Yuan, S.; Wang, B.; Shi, L.; Wang, J. Half-metallicity and enhanced ferromagnetism in Li-adsorbed ultrathin chromium triiodide. J. Mater. Chem. C 2018, 6, 5716–5720. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, L.; Zhou, Q.; Li, Y.; Yuan, S.; Chen, Q.; Dong, S.; Wang, J. Surface Vacancy-Induced Switchable Electric Polarization and Enhanced Ferromagnetism in Monolayer Metal Trihalides. Nano Lett. 2018, 18, 2943–2949. [Google Scholar] [CrossRef]
- Zhang, J.-M.; Zhu, W.; Zhang, Y.; Xiao, D.; Yao, Y. Tailoring magnetic doping in the topological insulator Bi2Se3. Phys. Rev. Lett. 2012, 109, 266405. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Zhang, A.; Feng, Z.; Wang, W. Theoretical Insights on the Charge State and Bifunctional OER/ORR Electrocatalyst Activity in 4d-Transition-Metal-Doped g-C3N4 Monolayers. ACS Appl. Mater. Interfaces 2024. [Google Scholar] [CrossRef] [PubMed]
- Yue, S.; Li, D.; Zhang, A.; Yan, Y.; Yan, H.; Feng, Z.; Wang, W. Rational design of single transition-metal atoms anchored on a PtSe2 monolayer as bifunctional OER/ORR electrocatalysts: A defect chemistry and machine learning study. J. Mater. Chem. A 2024, 12, 5451–5463. [Google Scholar] [CrossRef]
- Xu, H.; Li, D.; Deng, M.; Liu, X.; Feng, Z.; Wang, W. Intrinsic point defects and the n-type dopability of Bi2MoO6 with higher photocatalytic performance: A hybrid functional study. Phys. Rev. Mater. 2023, 7, 045401. [Google Scholar] [CrossRef]
- Kuklin, A.V.; Begunovich, L.V.; Gao, L.; Zhang, H.; Ågren, H. Point and complex defects in monolayer PdSe2: Evolution of electronic structure and emergence of magnetism. Phys. Rev. B 2021, 104, 134109. [Google Scholar] [CrossRef]
- Chen, S.; Huang, C.; Sun, H.; Ding, J.; Jena, P.; Kan, E. Boosting the Curie temperature of two-dimensional semiconducting CrI3 monolayer through van der Waals heterostructures. J. Phys. Chem. C 2019, 123, 17987–17993. [Google Scholar] [CrossRef]
- McGuire, M.A.; Dixit, H.; Cooper, V.R.; Sales, B.C. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem. Mater. 2015, 27, 612–620. [Google Scholar] [CrossRef]
- Dillon Jr, J.; Olson, C. Magnetization, resonance, and optical properties of the ferromagnet CrI3. J. Appl. Phys. 1965, 36, 1259–1260. [Google Scholar] [CrossRef]
- Zhang, T.; Grzeszczyk, M.; Li, J.; Yu, W.; Xu, H.; He, P.; Yang, L.; Qiu, Z.; Lin, H.; Yang, H. Degradation chemistry and kinetic stabilization of magnetic CrI3. J. Am. Chem. Soc. 2022, 144, 5295–5303. [Google Scholar] [CrossRef]
- Kazim, S.; Mastrippolito, D.; Moras, P.; Jugovac, M.; Klimczuk, T.; Ali, M.; Ottaviano, L.; Gunnella, R. Synchrotron radiation photoemission spectroscopy of the oxygen modified CrCl3 surface. Phys. Chem. Chem. Phys. 2023, 25, 3806–3814. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, M.; Zhao, R.; Liu, X.; Shen, J.; Huang, H.; Shen, S.; Zhang, L.; Zhang, J.; Zheng, X. Degradation effect and magnetoelectric transport properties in CrBr3 devices. Materials 2022, 15, 3007. [Google Scholar] [CrossRef] [PubMed]
- Mastrippolito, D.; Swiatek, H.; Moras, P.; Jugovac, M.; Gunnella, R.; Lozzi, L.; Benassi, P.; Klimczuk, T.; Ottaviano, L. Intense and stable room-temperature photoluminescence from nanoporous vanadium oxide formed by in-ambient degradation of VI3 crystals. J. Lumin. 2022, 251, 119137. [Google Scholar] [CrossRef]
- Hine, N.; Frensch, K.; Foulkes, W.; Finnis, M. Supercell size scaling of density functional theory formation energies of charged defects. Phys. Rev. B 2009, 79, 024112. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, L. High-throughput calculation and machine learning of two-dimensional halide perovskite materials: Formation energy and band gap. Mater. Today Commu. 2023, 35, 105841. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Dou, K.; He, Z.; Du, W.; Dai, Y.; Huang, B.; Ma, Y. d0 Magnetic Skyrmions in Two-Dimensional Lattice. Adv. Funct. Mater. 2023, 33, 2301817. [Google Scholar] [CrossRef]
- Chen, T.; Guo, C.; Sengupta, P.; Poletti, D. Effects of staggered Dzyaloshinskii-Moriya interactions in a quasi-two-dimensional Shastry-Sutherland model. Phys. Rev. B 2020, 101, 064417. [Google Scholar] [CrossRef]
- Du, W.; Dou, K.; He, Z.; Dai, Y.; Huang, B.; Ma, Y. Spontaneous magnetic skyrmions in single-layer CrInX3 (X = Te, Se). Nano Lett. 2022, 22, 3440–3446. [Google Scholar] [CrossRef]
- Luo, H.-B.; Zhang, H.-B.; Liu, J.P. Strong hopping induced Dzyaloshinskii–Moriya interaction and skyrmions in elemental cobalt. npj Comput. Mater. 2019, 5, 50. [Google Scholar] [CrossRef]
- Shanavas, K.; Satpathy, S. Electronic structure and the origin of the Dzyaloshinskii-Moriya interaction in MnSi. Phys. Rev. B 2016, 93, 195101. [Google Scholar] [CrossRef]
- Janson, O.; Rousochatzakis, I.; Tsirlin, A.A.; Belesi, M.; Leonov, A.A.; Rößler, U.K.; Van Den Brink, J.; Rosner, H. The quantum nature of skyrmions and half-skyrmions in Cu2OSeO3. Nat. Commun. 2014, 5, 5376. [Google Scholar] [CrossRef] [PubMed]
- Romming, N.; Pralow, H.; Kubetzka, A.; Hoffmann, M.; von Malottki, S.; Meyer, S.; Dupé, B.; Wiesendanger, R.; von Bergmann, K.; Heinze, S. Competition of Dzyaloshinskii-Moriya and higher-order exchange interactions in Rh/Fe atomic bilayers on Ir (111). Phys. Rev. Lett. 2018, 120, 207201. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Ren, X.; Xie, J.; Cheng, B.; Liu, W.; An, T.; Qin, H.; Hu, J. Magnetic switches via electric field in BN nanoribbons. Appl. Surf. Sci. 2019, 480, 300–307. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Lang, N.D.; Ehrenreich, H. Pressure Dependence of Curie Temperature in Ni. J. Appl. Phys. 1967, 38, 1316–1318. [Google Scholar] [CrossRef]
- Yekta, Y.; Hadipour, H.; Şaşıoğlu, E.; Friedrich, C.; Jafari, S.A.; Blügel, S.; Mertig, I. Strength of effective Coulomb interaction in two-dimensional transition-metal halides MX2 and MX3 (M = Ti, V, Cr, Mn, Fe, Co, Ni; X = Cl, Br, I). Phys. Rev. Mater. 2021, 5, 034001. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kim, K.; Ko, K.-T.; Seo, J.; Kim, J.S.; Jang, T.-H.; Kim, Y.; Kim, J.-Y.; Cheong, S.-W.; Park, J.-H. Giant Magnetic Anisotropy Induced by Ligand L S Coupling in Layered Cr Compounds. Phys. Rev. Lett. 2019, 122, 207201. [Google Scholar] [CrossRef]
- Lu, X.; Fei, R.; Zhu, L.; Yang, L. Meron-like topological spin defects in monolayer CrCl3. Nat. Commun. 2020, 11, 4724. [Google Scholar] [CrossRef]
- Xu, C.; Feng, J.; Xiang, H.; Bellaiche, L. Interplay between Kitaev interaction and single ion anisotropy in ferromagnetic CrI3 and CrGeTe3 monolayers. npj Comput. Mater. 2018, 4, 57. [Google Scholar] [CrossRef]
- Lado, J.L.; Fernández-Rossier, J. On the origin of magnetic anisotropy in two dimensional CrI3. 2D Mater. 2017, 4, 035002. [Google Scholar] [CrossRef]
- Wang, D.-s.; Wu, R.; Freeman, A. First-principles theory of surface magnetocrystalline anisotropy and the diatomic-pair model. Phys. Rev. B 1993, 47, 14932. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Cococcioni, M.; De Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Webster, L.; Yan, J.-A. Strain-tunable magnetic anisotropy in monolayer CrCl3, CrBr3, and CrI3. Phys. Rev. B 2018, 98, 144411. [Google Scholar] [CrossRef]
- Jiang, P.; Li, L.; Liao, Z.; Zhao, Y.; Zhong, Z. Spin direction-controlled electronic band structure in two-dimensional ferromagnetic CrI3. Nano Lett. 2018, 18, 3844–3849. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Mi, W.; Wang, X. Spin-dependent electronic structure and magnetic anisotropy of 2D ferromagnetic Janus Cr2I3X3 (X = Br, Cl) monolayers. Adv. Electron. Mater. 2020, 6, 1900778. [Google Scholar] [CrossRef]
- Van de Walle, C.G.; Neugebauer, J. First-principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 2004, 95, 3851–3879. [Google Scholar] [CrossRef]
- Vasyutinskii, B.; Kartmazov, G.; Finkel, V. Problems of the structure of chromium at temperatures of 700–1700 C. Fiz. Met. Metalloved. 1961, 12, 141–142. [Google Scholar]
- Shimomura, C.; Takemura, K.; Fujii, Y.; Minomura, S.; Mori, M.; Noda, Y.; Yamada, Y. Structure analysis of high-pressure metallic state of iodine. Phys. Rev. B 1978, 18, 715. [Google Scholar] [CrossRef]
- Yin, W.-J.; Wei, S.-H.; Al-Jassim, M.M.; Turner, J.; Yan, Y. Doping properties of monoclinic BiVO4 studied by first-principles density-functional theory. Phys. Rev. B 2011, 83, 155102. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Deng, M.; Shen, H.; Li, H.; Ding, J. Effects of native defects and cerium impurity on the monoclinic BiVO4 photocatalyst obtained via PBE + U calculations. Phys. Chem. Chem. Phys. 2020, 22, 25297–25305. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, P.; Deng, M.; Shen, H.; Feng, Z.; Li, H. Hybrid density functional theory study of native defects and nonmetal (C, N, S, and P) doping in a Bi2WO6 photocatalyst. ACS Omega 2020, 5, 29081–29091. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. npj Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Lany, S.; Zunger, A. Assessment of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: Case studies for ZnO and GaAs. Phys. Rev. B 2008, 78, 235104. [Google Scholar] [CrossRef]
- Komsa, H.-P.; Pasquarello, A. Finite-size supercell correction for charged defects at surfaces and interfaces. Phys. Rev. Lett. 2013, 110, 095505. [Google Scholar] [CrossRef] [PubMed]
- Komsa, H.-P.; Berseneva, N.; Krasheninnikov, A.V.; Nieminen, R.M. Charged point defects in the flatland: Accurate formation energy calculations in two-dimensional materials. Phys. Rev. X 2014, 4, 031044. [Google Scholar] [CrossRef]
- Singh, A.; Singh, A.K. Atypical behavior of intrinsic defects and promising dopants in two-dimensional WS2. Phys. Rev. Mater. 2021, 5, 084001. [Google Scholar] [CrossRef]
- Singh, A.; Singh, A.K. Origin of n-type conductivity of monolayer MoS2. Phys. Rev. B 2019, 99, 121201. [Google Scholar] [CrossRef]
- Manjanath, A.; Hsu, C.-P.; Kawazoe, Y. Tuning the electronic and magnetic properties of pentagraphene through the C1 vacancy. 2D Mater. 2020, 7, 045024. [Google Scholar] [CrossRef]
- Singh, A.; Manjanath, A.; Singh, A.K. Engineering defect transition-levels through the van der Waals heterostructure. J. Phys. Chem. C 2018, 122, 24475–24480. [Google Scholar] [CrossRef]
- Noh, J.-Y.; Kim, H.; Kim, Y.-S. Stability and electronic structures of native defects in single-layer MoS2. Phys. Rev. B 2014, 89, 205417. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Ju, L.; Yang, G.; Yuan, D.; Feng, Z.; Wang, W. The charge effects on the hydrogen evolution reaction activity of the defected monolayer MoS2. Phys. Chem. Chem. Phys. 2023, 25, 10956–10965. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Wei, S.-H. Overcoming the Doping Bottleneck in Semiconductors. Comp. Mater. Sci. 2004, 30, 337–348. [Google Scholar] [CrossRef]
- Tracy, J.W.; Gregory, N.W.; Lingafelter, E.C. Crystal structure of chromium(II) bromide. Acta Crystallogr. 1962, 15, 672–674. [Google Scholar] [CrossRef]
- Ferrari, A.; Giorgio, F. Crystal structure of the iodides of divalent metals. Atti Accad. Naz. Lincei Cl. Fis. Mat. Nat. Rend. 1929, 10, 522. [Google Scholar]
- Wang, H.-C.; Botti, S.; Marques, M.A. Predicting stable crystalline compounds using chemical similarity. npj Comput. Mater. 2021, 7, 12. [Google Scholar] [CrossRef]
- Sakuma, T. Crystal structure of β-CuI. J. Phys. Soc. Jpn. 1988, 57, 565–569. [Google Scholar] [CrossRef]
- Cable, J.; Wilkinson, M.; Wollan, E.; Koehler, W. Neutron diffraction investigation of the magnetic order in MnI2. Phys. Rev. 1962, 125, 1860. [Google Scholar] [CrossRef]
- Ketelaar, J. Die Kristallstruktur des Nickelbromids und-jodids. Z. Für Krist.-Cryst. Mater. 1934, 88, 26–34. [Google Scholar] [CrossRef]
- Angelkort, J.; Senyshyn, A.; Schönleber, A.; Smaalen, S.v. Temperature-dependent neutron diffraction on TiI3. Z. Für Kristallographie 2011, 226, 640–645. [Google Scholar] [CrossRef]
- Lomova, T.N.; Tyulyaeva, E.Y. New Trends in the Direct Synthesis of Phthalocyanine/Porphyrin Complexes. In Direct Synthesis of Metal Complexes; Elsevier: Amsterdam, The Netherlands, 2018; pp. 239–278. [Google Scholar]
- Hirakawa, K.; Kadowaki, H.; Ubukoshi, K. Study of frustration effects in two-dimensional triangular lattice antiferromagnets–neutron powder diffraction study of VX2, X ≡ Cl, Br and I. J. Phys. Soc. Jpn. 1983, 52, 1814–1824. [Google Scholar] [CrossRef]
- Pinsker, Z.; Tatarinova, L.; Novikova, V. Electronographic determination of the structure of zinc iodide. Zh. Fiz. Khim 1946, 20, 243. [Google Scholar]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, G.; Yang, Q.; Zhang, K.; Yang, J.; Ge, G.; Wang, W. The Defect Charge Effect on Magnetic Anisotropy Energy and Dzyaloshinskii–Moriya Interaction of the I Vacancy and 3d Transition Metal Co-Doped Monolayer CrI3. Condens. Matter 2025, 10, 29. https://doi.org/10.3390/condmat10020029
Ji G, Yang Q, Zhang K, Yang J, Ge G, Wang W. The Defect Charge Effect on Magnetic Anisotropy Energy and Dzyaloshinskii–Moriya Interaction of the I Vacancy and 3d Transition Metal Co-Doped Monolayer CrI3. Condensed Matter. 2025; 10(2):29. https://doi.org/10.3390/condmat10020029
Chicago/Turabian StyleJi, Guangtian, Qingqing Yang, Kun Zhang, Jueming Yang, Guixian Ge, and Wentao Wang. 2025. "The Defect Charge Effect on Magnetic Anisotropy Energy and Dzyaloshinskii–Moriya Interaction of the I Vacancy and 3d Transition Metal Co-Doped Monolayer CrI3" Condensed Matter 10, no. 2: 29. https://doi.org/10.3390/condmat10020029
APA StyleJi, G., Yang, Q., Zhang, K., Yang, J., Ge, G., & Wang, W. (2025). The Defect Charge Effect on Magnetic Anisotropy Energy and Dzyaloshinskii–Moriya Interaction of the I Vacancy and 3d Transition Metal Co-Doped Monolayer CrI3. Condensed Matter, 10(2), 29. https://doi.org/10.3390/condmat10020029






