Terahertz Time-Domain Spectroscopy of Substituted Gadolinium Gallium Garnet
Abstract
1. Introduction
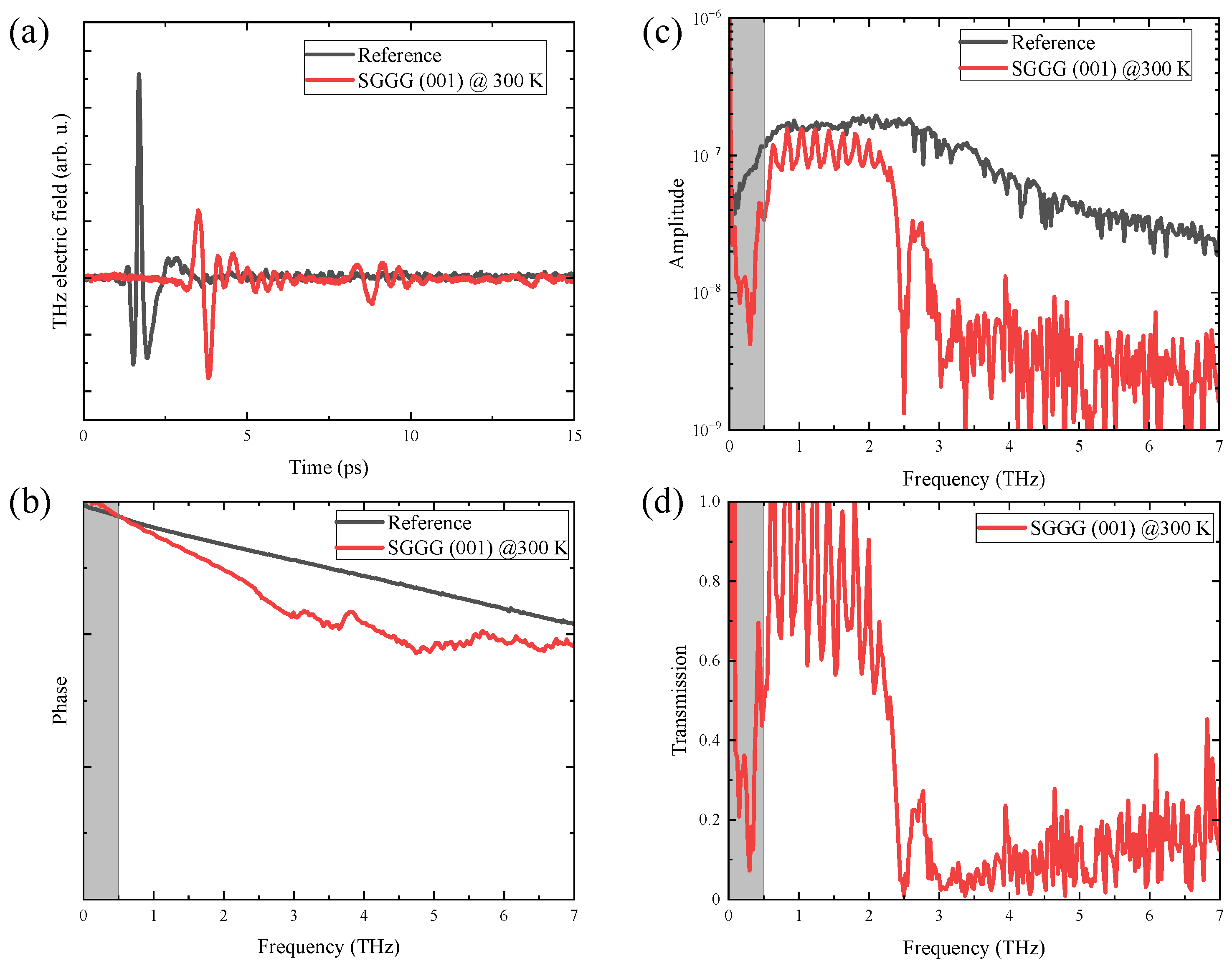
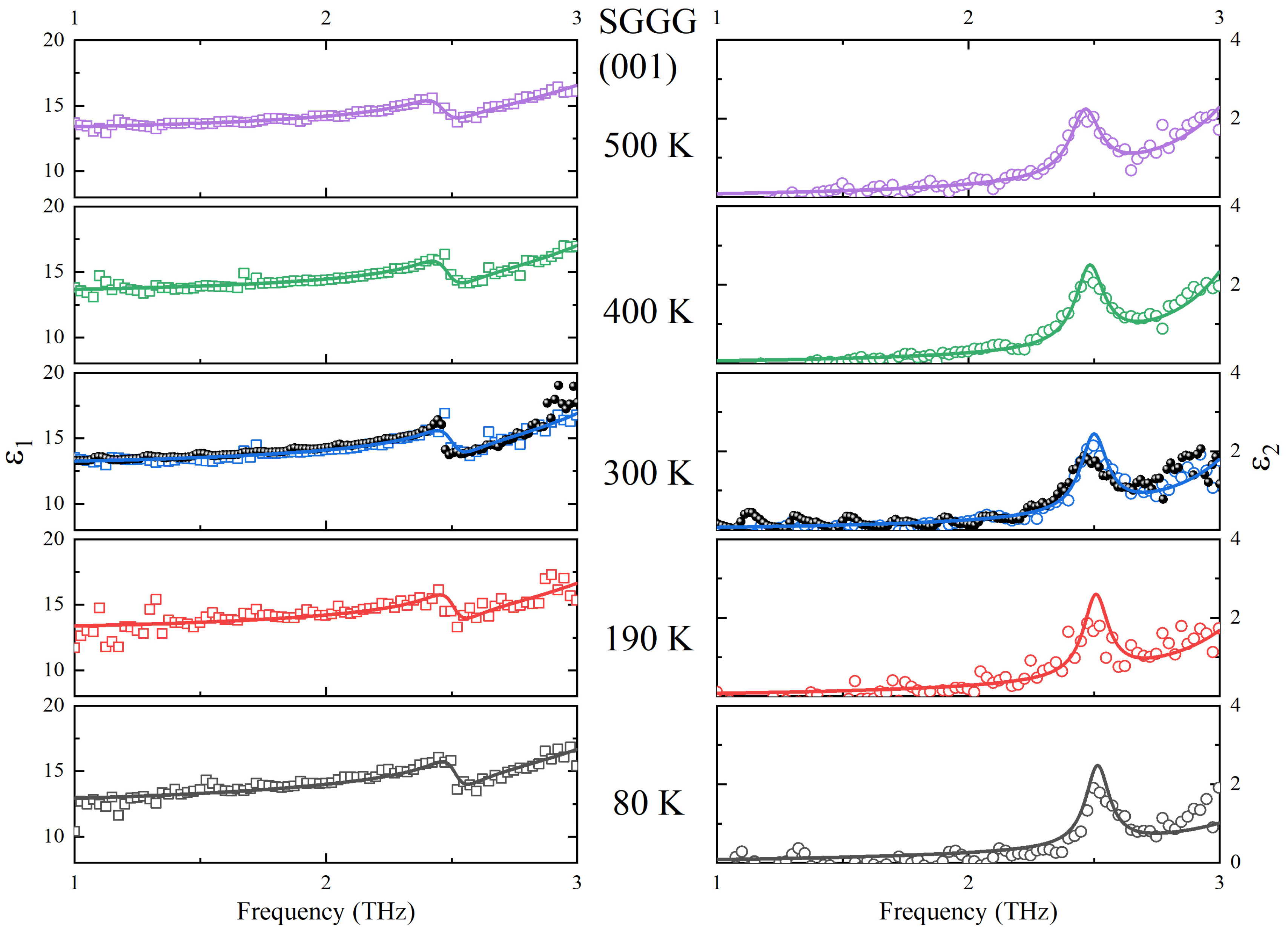
2. Results and Discussion
- (i)
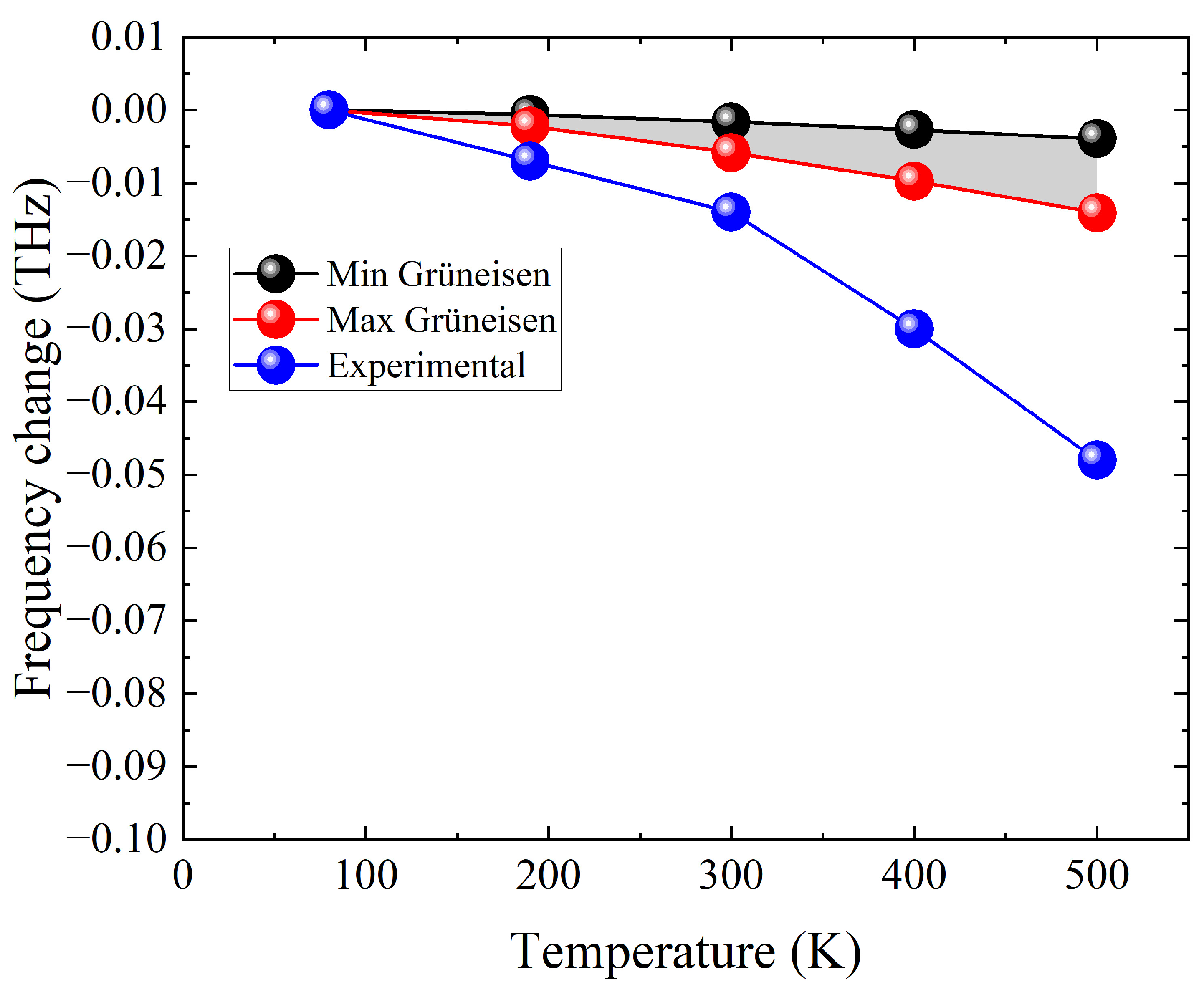
- Temperature-dependent Lattice Constants: Take the GGG temperature-dependent lattice constant change for SGGG discussion. The lattice constants of GGG at various temperatures refer to several previous studies [18,19]. Because the doping percentages of other elements are less than 1% each, the lattice constants of SGGG at various temperatures can refer to GGG for the approximation.
- (ii)
- Grüneisen parameter: Take the Grüneisen parameter in the range from 0.5 to 1.8 for the TO1 phonon for SGGG. This is the range for the Grüneisen parameter of the TO1 phonon of Yttrium Aluminum Garnet (YAG) [20]. The best approximation for SGGG is GGG, but there was no report that provides its Grüneisen parameter and pressure-dependent phonon behaviors. Moreover, since the phonon change caused by the lattice constant change is proportional to the cell volume change and the rate, the Grüneisen parameter, primarily affects the relative shift of the phonon frequency with respect to a reference point.
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ueda, J.; Tanabe, S. Review of Luminescent Properties of Ce3+-Doped Garnet Phosphors: New Insight into the Effect of Crystal and Electronic Structure. Opt. Mater. X 2019, 1, 100018. [Google Scholar] [CrossRef]
- Karipbayev, Z.T.; Kumarbekov, K.; Manika, I.; Dauletbekova, A.; Kozlovskiy, A.L.; Sugak, D.; Ubizskii, S.B.; Akilbekov, A.; Suchikova, Y.; Popov, A.I. Optical, Structural, and Mechanical Properties of Gd3Ga5O12 Single Crystals Irradiated with 84Kr+ Ions. Phys. Status Solidi B Basic. Res. 2022, 259, 202100415. [Google Scholar] [CrossRef]
- Sokolov, N.S.; Fedorov, V.V.; Korovin, A.M.; Suturin, S.M.; Baranov, D.A.; Gastev, S.V.; Krichevtsov, B.B.; Maksimova, K.Y.; Grunin, A.I.; Bursian, V.E.; et al. Thin Yttrium Iron Garnet Films Grown by Pulsed Laser Deposition: Crystal Structure, Static, and Dynamic Magnetic Properties. J. Appl. Phys. 2016, 119, 023903. [Google Scholar] [CrossRef]
- Jin, C.; Li, R.; Liu, Y.; Zhang, L.; Zhang, J.; Sun, P.; Luo, Z.; Jiang, J. Efficient and Stable Gd3Ga5O12:Cr3+ Phosphors for High-Performance NIR LEDs. Adv. Opt. Mater. 2023, 11, 2300772. [Google Scholar] [CrossRef]
- Martinazzoli, L.; Kratochwil, N.; Gundacker, S.; Auffray, E. Scintillation Properties and Timing Performance of State-of-the-Art Gd3Al2Ga3O12 Single Crystals. Nucl. Instrum. Methods Phys. Res. A 2021, 1000, 165231. [Google Scholar] [CrossRef]
- Du, S.; Yang, Q.; Fan, X.; Wang, M.; Zhang, H. A Compact and Low-Loss Tunable Bandpass Filter Using YIG/GGG Film Structures. IEEE Microw. Wirel. Compon. Lett. 2022, 33, 259–262. [Google Scholar] [CrossRef]
- Holzmann, C.; Ullrich, A.; Ciubotariu, O.T.; Albrecht, M. Stress-Induced Magnetic Properties of Gadolinium Iron Garnet Nanoscale-Thin Films: Implications for Spintronic Devices. ACS Appl. Nano Mater. 2022, 5, 1023–1033. [Google Scholar] [CrossRef]
- Sarker, M.S.; Nakamura, S.; Yamahara, H.; Seki, M.; Tabata, H. Multifrequency Spin-Wave Propagation for Parallel Data Processing Using Microstructured Yttrium Iron Garnet Thin Films. IEEE Trans. Magn. 2022, 58, 4300706. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Zhang, H.; Luo, J.; Quan, C.; Han, Z.; Qiao, Y.; Chen, Y.; Wang, Z.; Cheng, M.; et al. Effect of Ca2+/Mg2+/Zr4+ Concentrations on the Characteristics of Substituted Gadolinium Gallium Garnet Single Crystals with Large Lattice Parameter. J. Alloys Compd. 2023, 965, 171467. [Google Scholar] [CrossRef]
- Sabbaghi, M.; Hanson, G.W.; Weinert, M.; Shi, F.; Cen, C. Terahertz Response of Gadolinium Gallium Garnet (GGG) and Gadolinium Scandium Gallium Garnet (SGGG). J. Appl. Phys. 2020, 127, 025104. [Google Scholar] [CrossRef]
- Adachi, M.; Yamahara, H.; Kawabe, S.; Matsui, H.; Tabata, H. Strong Optical Reflection of Rare-Earth Garnets in the Terahertz Regime by Reststrahlen Bands. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 89, 205124. [Google Scholar] [CrossRef]
- Adachi, M.; Matsui, H.; Seki, M.; Yamahara, H.; Tabata, H. High-Temperature Terahertz Absorption Band in Rare-Earth Gallium Garnet. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 91, 085118. [Google Scholar] [CrossRef]
- Papagelis, K.; Arvanitidis, J.; Vinga, E.; Christofilos, D.; Kourouklis, G.A.; Kimura, H.; Ves, S. Vibrational Properties of (Gd1-xYx) 3Ga5O12 Solid Solutions. J. Appl. Phys. 2010, 107, 113504. [Google Scholar] [CrossRef]
- Neu, J.; Schmuttenmaer, C.A. Tutorial: An Introduction to Terahertz Time Domain Spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101. [Google Scholar] [CrossRef]
- Dorney, T.D.; Baraniuk, R.G.; Mittleman, D.M. Material Parameter Estimation with Terahertz Time-Domain Spectroscopy. J. Opt. Soc. Am. A 2001, 18, 1562–1571. [Google Scholar] [CrossRef]
- Helal, M.A.; Mori, T.; Kojima, S. Terahertz Time-Domain Spectroscopy and Raman Scattering Studies of Incipient Ferroelectric BaZrO3. Ferroelectrics 2016, 499, 107–114. [Google Scholar] [CrossRef]
- Zhu, S.; Zheng, W. Temperature-Dependent Phonon Shifts in van Der Waals Crystals. J. Phys. Chem. Lett. 2021, 12, 5261–5270. [Google Scholar] [CrossRef] [PubMed]
- Kolmakova, N.P.; Levitin, R.Z.; Orlov, V.N.; Vedernikov, N.F. Magnetoelastic properties of rare-earth paramagnetic garnets: Magnetostriction and thermal expansion. J. Magn. Magn. Mater. 1990, 87, 218–228. [Google Scholar] [CrossRef]
- Nakajima, K.; Machida, K. Thermal expansion of gallium garnets and Bi-substituted iron garnet epitaxial thick films. J. Cryst. Growth 1988, 92, 23–25. [Google Scholar] [CrossRef]
- Monteseguro, V.; Rodríguez-Hernández, P.; Muñoz, A. Yttrium Aluminium Garnet under Pressure: Structural, Elastic, and Vibrational Properties from Ab Initio Studies. J. Appl. Phys. 2015, 118, 245902. [Google Scholar] [CrossRef]
- Berdel, K.; Rivas, J.G.; Bolívar, P.H.; De Maagt, P.; Kurz, H. Temperature Dependence of the Permittivity and Loss Tangent of High-Permittivity Materials at Terahertz Frequencies. IEEE Trans. Microw. Theory Tech. 2005, 53, 1266–1271. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Sawada, H. Electron Density Study of Garnets: Z3Ga5O12; Z=Nd, Sm, Gd, Tb. J. Solid State Chem. 1997, 132, 300–307. [Google Scholar] [CrossRef]
- Gong, C.; Kawayama, I.; Murakami, H.; Teramoto, T.; Tonouchi, M. Intensity-Dependent Self-Induced Dual-Color Laser Phase Modulation and Its Effect on Terahertz Generation. Sci. Rep. 2021, 11, 498. [Google Scholar] [CrossRef] [PubMed]
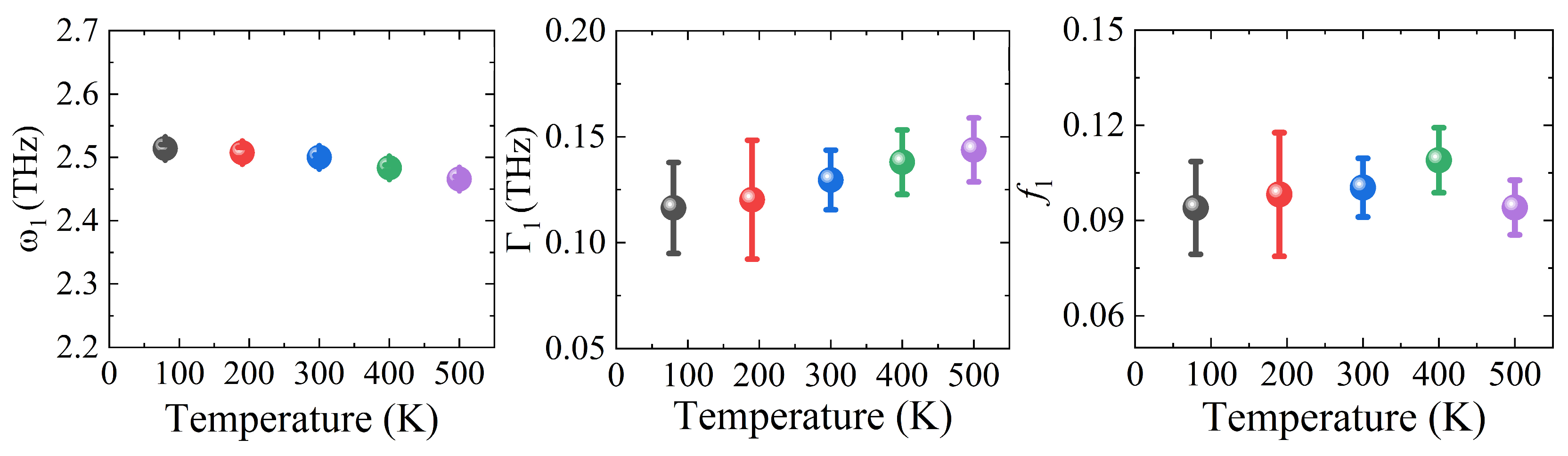
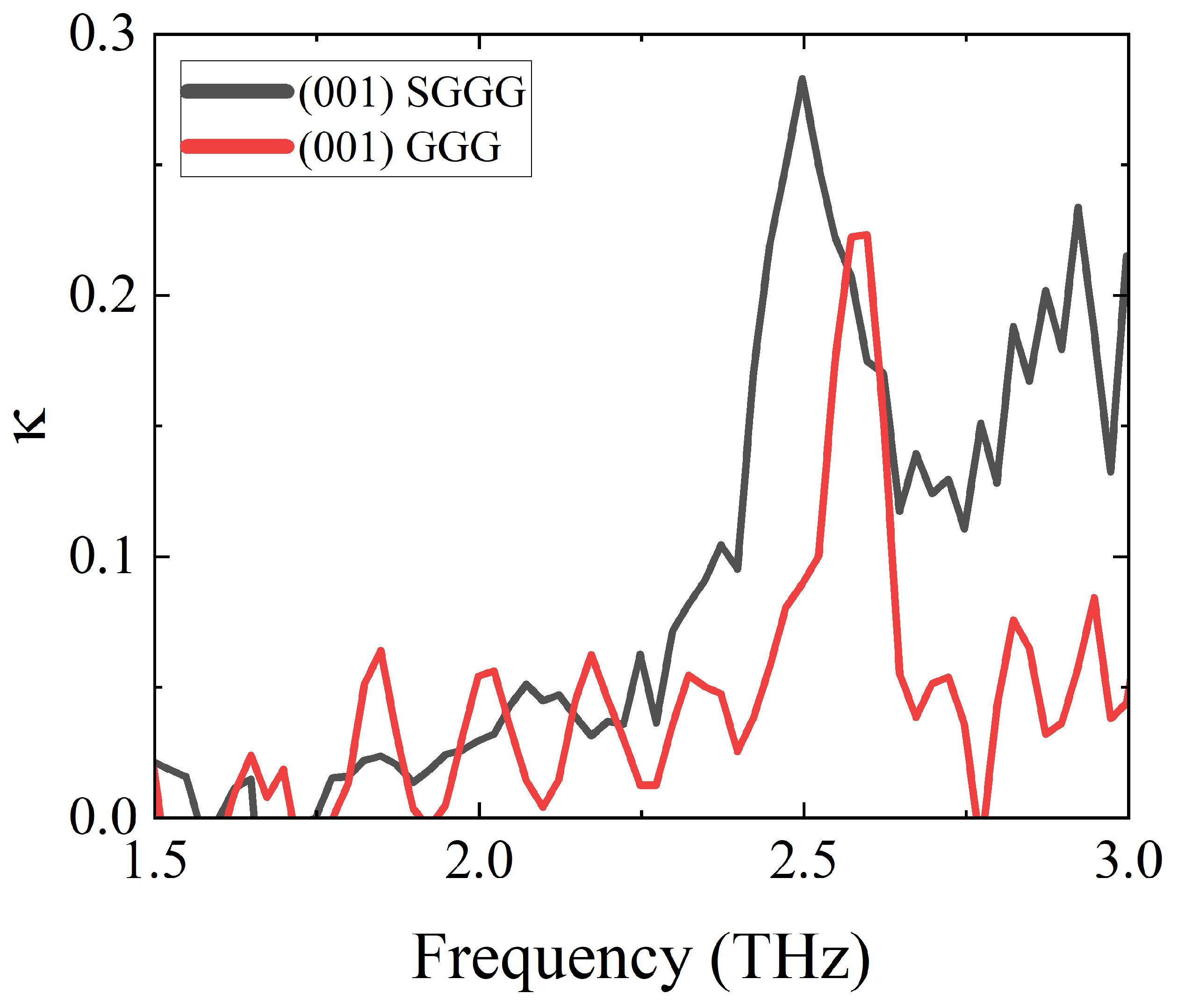

| 80 K | 190 K | 300 K | 400 K | 500 K | |
|---|---|---|---|---|---|
| SGGG (001) | |||||
| (THz) | 2.514 | 2.507 | 2.500 | 2.484 | 2.466 |
| (THz) | 0.110 | 0.120 | 0.130 | 0.138 | 0.144 |
| 0.095 | 0.098 | 0.100 | 0.109 | 0.094 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Xu, J.; Murakami, H.; Yamahara, H.; Seki, M.; Tabata, H.; Tonouchi, M. Terahertz Time-Domain Spectroscopy of Substituted Gadolinium Gallium Garnet. Condens. Matter 2025, 10, 1. https://doi.org/10.3390/condmat10010001
Wang K, Xu J, Murakami H, Yamahara H, Seki M, Tabata H, Tonouchi M. Terahertz Time-Domain Spectroscopy of Substituted Gadolinium Gallium Garnet. Condensed Matter. 2025; 10(1):1. https://doi.org/10.3390/condmat10010001
Chicago/Turabian StyleWang, Ke, Junchao Xu, Hironaru Murakami, Hiroyasu Yamahara, Munetoshi Seki, Hitoshi Tabata, and Masayoshi Tonouchi. 2025. "Terahertz Time-Domain Spectroscopy of Substituted Gadolinium Gallium Garnet" Condensed Matter 10, no. 1: 1. https://doi.org/10.3390/condmat10010001
APA StyleWang, K., Xu, J., Murakami, H., Yamahara, H., Seki, M., Tabata, H., & Tonouchi, M. (2025). Terahertz Time-Domain Spectroscopy of Substituted Gadolinium Gallium Garnet. Condensed Matter, 10(1), 1. https://doi.org/10.3390/condmat10010001








