Status Identification in Support of Fishing Effort Estimation for Tuna Longliners in Waters near the Marshall Islands Based on AIS Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Data Preprocessing
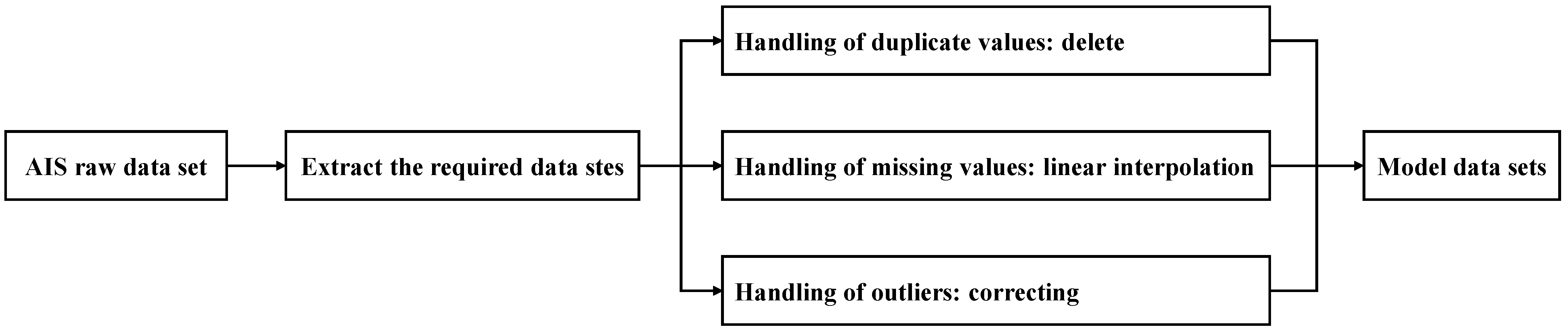
2.2.1. AIS Data Cleaning
- (1)
- Extract the MMSI, date, time, longitude, latitude, speed and course information from the original record and remove all other entries.
- (2)
- Eliminate duplicate AIS records by arranging those with the same MMSI in chronological order.
- (3)
- We used the linear interpolation method to deal with the missing values of sailing speed. The linear interpolation method sets the fishing vessel in a status of uniform linear motion between trajectory points, and this method can effectively interpolate the missing values of AIS data within short time period. Assume that the missing data of a fishing vessel at time tm was Vm, denoted as (tm, Vm), and the complete data before and after were (ti, Vi), (tj, Vj). The missing value interpolation formula is:
- (4)
- Delete latitude, longitude, heading and speed data that are out of range.
- (5)
- Final integration of data for subsequent studies.
2.2.2. Calculation of Distance between Trajectory Points
2.2.3. Calculation of Course Difference and Speed Difference
2.3. Methods
2.3.1. BP Neural Network
2.3.2. Support Vector Machine
2.3.3. Model Construction and Testing
2.3.4. Fishing Effort Estimation and Correlation Analysis
3. Results
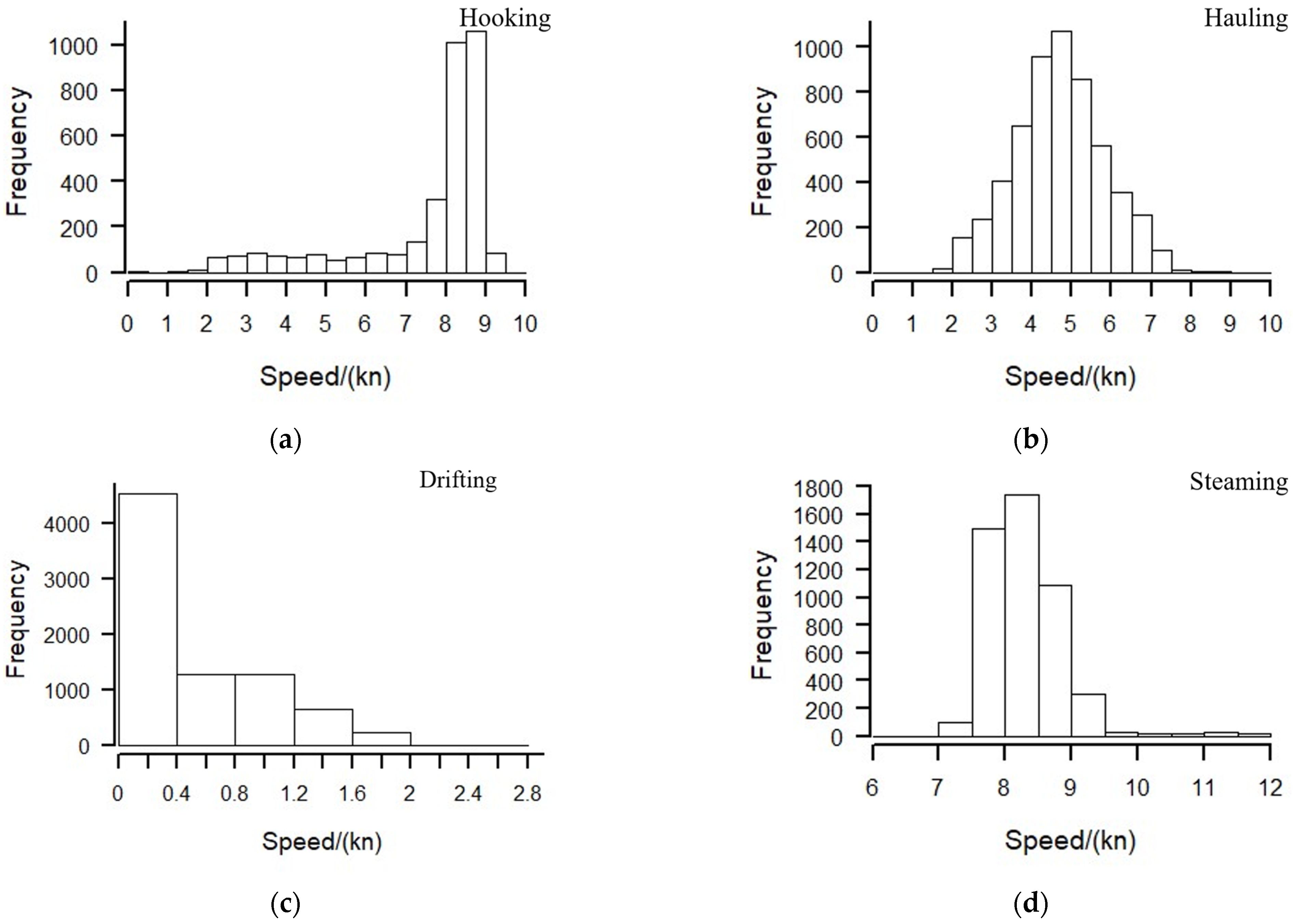
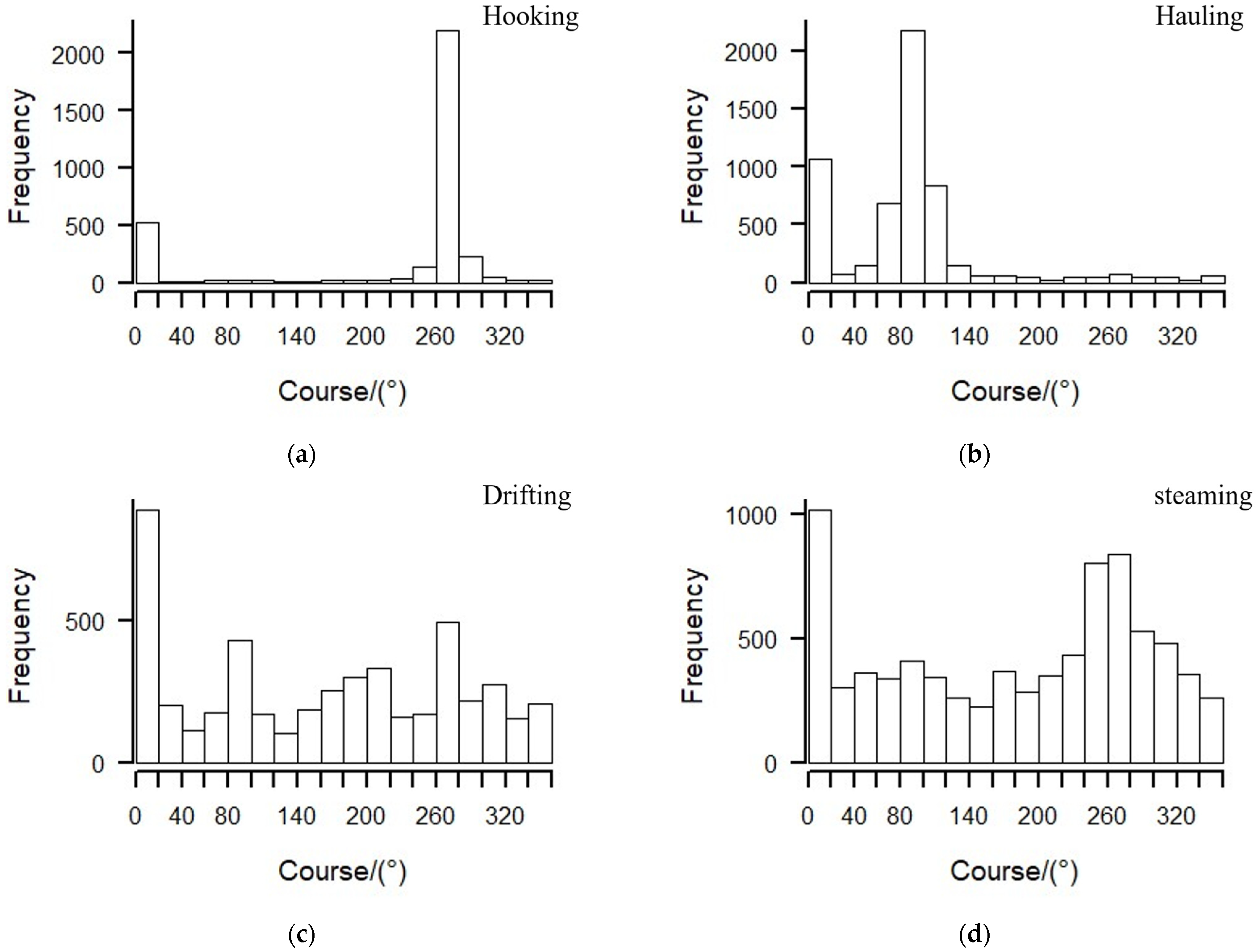
3.1. Tuna Longliner Characteristic Analysis
3.2. Threshold Screening Method
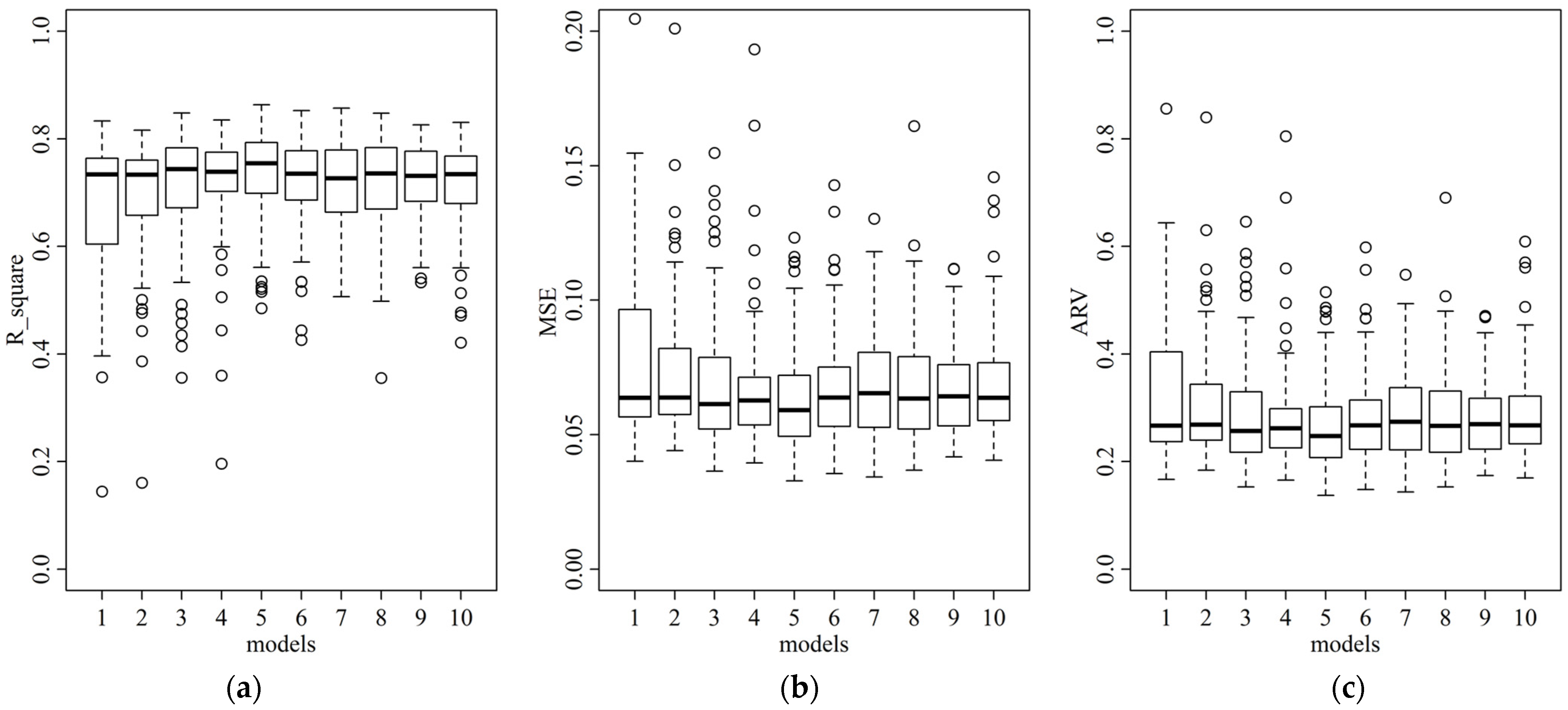
3.3. BP Neural Network Classification Models
3.4. SVM Models
3.5. Fishing Effort Statistics
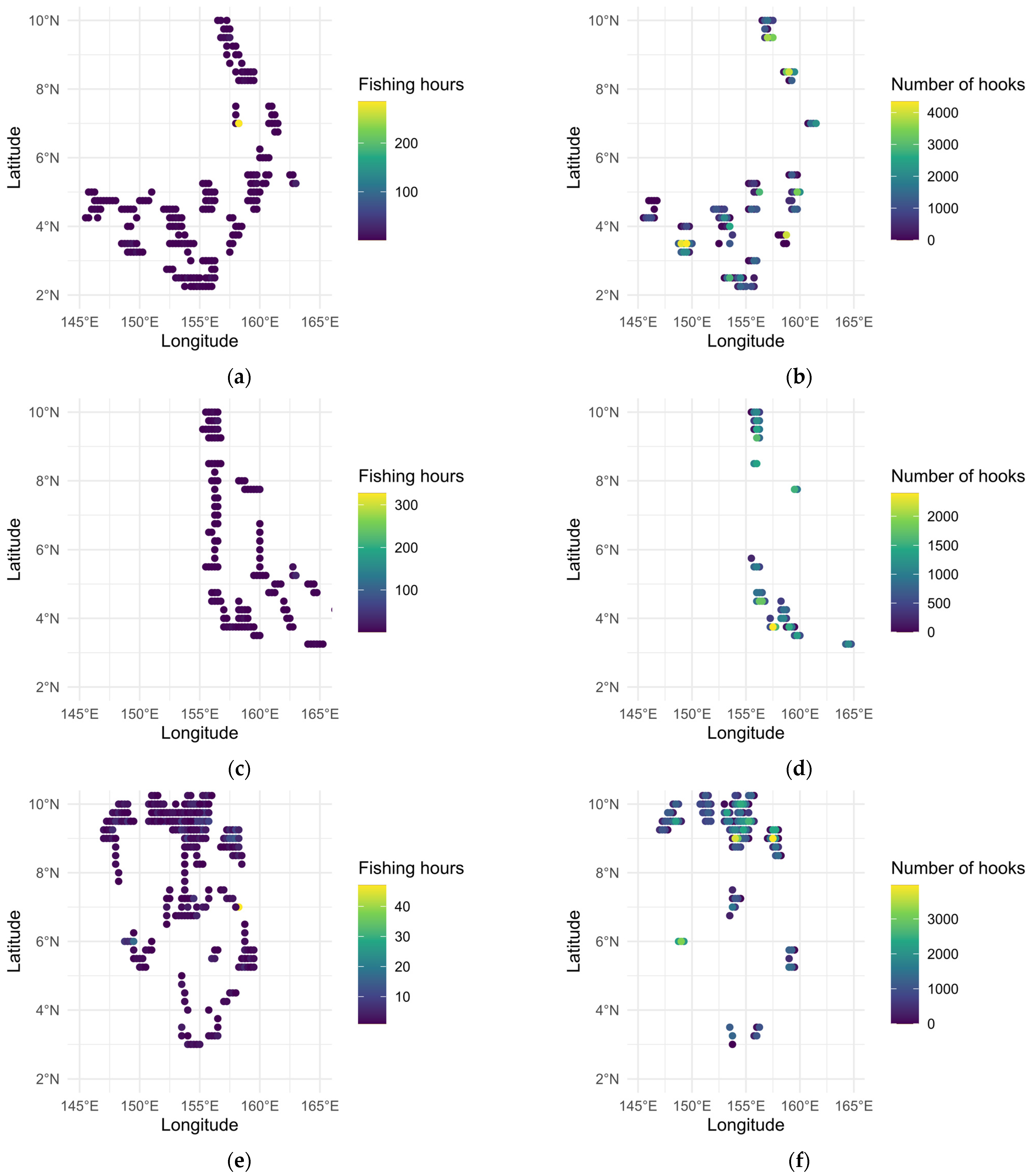
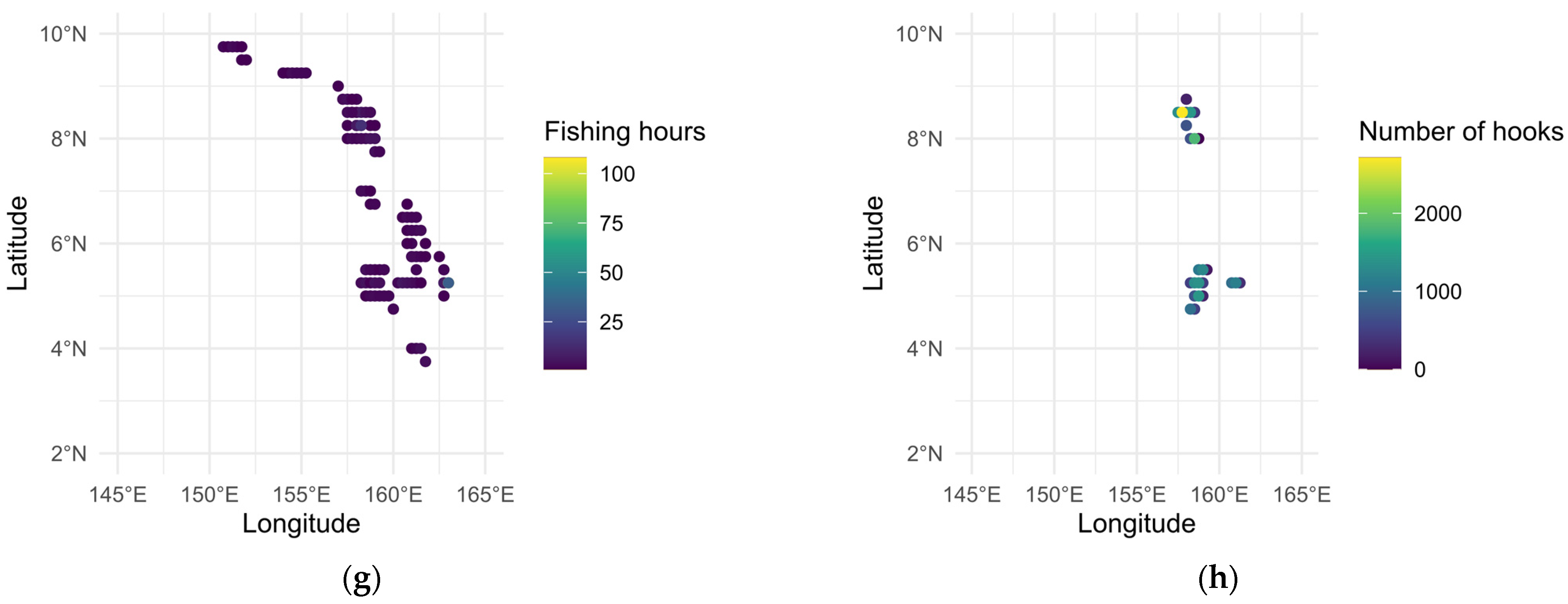
3.6. Spatial Distribution of Fishing Effort
3.7. Spatial Correlation Analysis
4. Discussion
4.1. The Reliability of This Study Are High
4.2. SVM Is the Optimal Method
4.3. AIS Data Are More Suitable for the Fishing Effort Spatial Distribution Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Russo, T.; Carpentieri, P.; Fiorentino, F.; Arneri, E.; Scardi, M.; Cioffi, A.; Cataudella, S. Modeling landings profiles of fishing vessels: An application of Self-Organizing Maps to VMS and logbook data. Fish. Res. 2016, 181, 34–47. [Google Scholar] [CrossRef]
- Fonseca, T.; Campos, A.; Afonso-Dias, M.; Fonseca, P.; Pereira, J. Trawling for cephalopods off the Portuguese caost-Fleet dynamics and landing composition. Fish. Res. 2008, 92, 180–188. [Google Scholar] [CrossRef]
- Okamura, H.; Morita, S.H.; Funamoto, T.; Ichinokawa, M.; Eguchi, S. Target-based catch-per-unit-effort standardization in multispecies fisheries. Can. J. Fish. Aquat. Sci. 2018, 75, 452–463. [Google Scholar] [CrossRef]
- Yadav, V.K.; Jahageerdar, S.; Adinarayana, J. Use of different modeling approach for sensitivity analysis in predicting the Catch per Unit Effort (CPUE) of fish. Indian J. Geo-Mar. Sci. 2020, 49, 1729–1741. [Google Scholar]
- Mullowney, D.R.; Dawe, E.G. Development of performance indices for the Newfoundland and Labrador snow crab (Chionoecetes opilio) fishery using data from a vessel monitoring system. Fish. Res. 2009, 100, 248–254. [Google Scholar] [CrossRef]
- Walters, C. Folly and fantasy in the analysis of spatial catch rate data. Can. J. Fish. Aquat. Sci. 2003, 60, 1433–1436. [Google Scholar] [CrossRef]
- Janette, L.; South, A.B.; Simon, J. Developing reliable, repeatable, and accessible methods to provide high-resolution estimates of fishing-effort distributions from vessel monitoring system (VMS) data. ICES J. Mar. Sci. 2010, 67, 1260–1271. [Google Scholar]
- Bertrand, S.; Burgos, J.M.; Gerlotto, F.; Atiquipa, J. Lévy trajectories of Peruvian purse-seiners as an indicator of the spatial distribution of anchovy (Engraulis ringens). ICES J. Mar. Sci. 2005, 62, 477–482. [Google Scholar] [CrossRef]
- Natale, F.; Gibin, M.; Alessandrini, A.; Vespe, M.; Paulrud, A. Mapping Fishing Effort through AIS Data. PLoS ONE 2015, 10, e0130746. [Google Scholar] [CrossRef]
- Murawski, S.A.; Wigley, S.E.; Fogarty, M.J.; Rago, P.J.; Mountain, D.G. Effort distribution and catch patterns adjacent to temperate MPAs. ICES J. Mar. Sci. 2005, 62, 1150–1167. [Google Scholar] [CrossRef]
- Gerritsen, H.; Lordan, C. Integrating vessel monitoring systems (VMS) data with daily catch data from logbooks to explore the spatial distribution of catch and effort at high resolution. ICES J. Mar. Sci. 2011, 68, 245–252. [Google Scholar] [CrossRef]
- Bez, N.; Walker, E.; Gaertner, D.; Rivoirard, J.; Gaspar, P. Fishing activity of tuna purse seiners estimated from vessel monitoring system (VMS) data. Can. J. Fish. Aquat. Sci. 2011, 68, 1998–2010. [Google Scholar] [CrossRef]
- Walker, E.; Gaertner, D.; Gaspar, P.; Bez, N. Fishing activity of tuna purse estimated from VMS data and validated by observers’ data. Collect. Vol. Sci. Pap. 2010, 65, 2376–2391. [Google Scholar]
- Murray, L.G.; Hinz, H.; Hold, N.; Kaiser, M.J. The effectiveness of using CPUE data derived from Vessel Monitoring Systems and fisheries logbooks to estimate scallop biomass. ICES J. Mar. Sci. 2013, 70, 1330–1340. [Google Scholar] [CrossRef]
- James, M.; Mendo, T.; Jones, E.; Orr, K.; McKnight, A.; Thompson, J. AIS data to inform small scale fisheries management and marine spatial planning. Mar. Policy 2018, 91, 113–121. [Google Scholar] [CrossRef]
- Kroodsma, D.; Mayorga, J.; Hochberg, T.; Miller, N.; Boerder, K.; Ferretti, F.; Wilson, A.; Bergman, B.; White, T.; Block, B.; et al. Tracking the Global Footprint of Fisheries. Science 2018, 359, 904–908. [Google Scholar] [CrossRef]
- Yang, S.L.; Zhang, S.M.; Yuan, Z.H.; Dai, Y.; Zhang, H.; Zhang, B.B.; Fan, W. Calculating the fishing intensity of offshore longline fleets on fishing grounds based on their fishing characteristics. J. Fish. Sci. China 2020, 27, 307–314. [Google Scholar]
- Yang, S.L.; Zhang, S.M.; Zhou, W.F.; Cui, X.S.; Zhang, B.B.; Fan, W. Calculating the fishing effort of longline fishing vessel in the western and central pacific ocean using AIS. Trans. Chin. Soc. Agric. Eng. 2020, 36, 198–203. [Google Scholar]
- Nieblas, A.; Barde, J.; Louys, J.; Assan, C.; Imzilen, T.; Dalleau, C.; Gerry, C.; Chassot, E. Global Atlas of AIS-Based Fishing Activity—Challenges and Opportunities; FAO: Rome, Italy, 2019. [Google Scholar]
- Iriondo, A.; Santiago, J.; Murua, H.; Granado, I.; Taconet, M.; Kroodsma, D.; Miller, N.; Fernandes, J. FAO Area 67—AIS-Based Fishing Activity in the Northeast Pacific; FAO: Rome, Italy, 2019. [Google Scholar]
- Yuan, Z.H.; Yang, D.H.; Fan, W.; Zhang, S.M. On fishing grounds distribution of tuna longline based on satellite automatic identification system in the Western and Central Pacific. Mar. Fish. 2018, 40, 649–659. [Google Scholar]
- Bordalo, M.P.; Figueiredo, I. Extraction and classification of longline fishing trips from vessel monitoring systems data with sequential recording gaps. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 34, 1–7. [Google Scholar]
- Song, L.M.; Lv, K.K.; Yang, J.L.; Hu, Z.X. Otolith morphology of bigeye tuna in Marshall Islands waters. J. Shanghai Ocean Univ. 2012, 21, 884–891. [Google Scholar]
- Cheng, X.; Zhang, F.; Chen, X.J.; Wang, J.T. Application of Artificial Intelligence in the Study of Fishing Vessel Behavior. Fishes 2023, 8, 516. [Google Scholar] [CrossRef]
- Ciaburro, G.; Venkateswaran, B. Neural Networks with R: Smart Models Using CNN, RNN, Deep Learning, and Artificial Intelligence Principles; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Wang, P.; Wang, P.; En, F. Neural Network Optimization Method and Its Application in Information Processing. Math. Probl. Eng. 2021, 2, 10. [Google Scholar] [CrossRef]
- Li, Z.; Ye, Z.; Wan, R.; Zhang, C. Model selection between traditional and popular methods for standardizing catch rates of target species a case study of Japanese Spanish mackerel in the gillnet fishery. Fish. Res. 2015, 161, 312–319. [Google Scholar] [CrossRef]
- Chang, S.K.; Yuan, T.L. Deriving high-resolution spatiotemporal fishing effort of large-scale longline fishery from vessel monitoring system (VMS) data and validated by observer data. Can. J. Fish. Aquat. Sci. 2014, 71, 1363–1370. [Google Scholar] [CrossRef]
- Marza, I.M. VMS Data Analyses and Modeling for the Monitoring and Surveillance of Indonesian Fisheries. Ph.D. Thesis, Computer Vision and Pattern Recognition. Ecole Nationale Supérieure Mines-Télécom Atlantique, Nantes, France, 2017. [Google Scholar]
- Witt, M.J.; Godley, B.J. A step towards seascape scale conservation: Using vessel monitoring systems (VMS) to map fishing activity. PLoS ONE 2017, 2, e1111. [Google Scholar] [CrossRef] [PubMed]
- Robards, M.D.; Silber, G.K.; Adams, J.D.; Arroyo, J.; Lorenzini, D.; Schwehr, K.; Amos, J. Conservation science and policy applications of the marine vessel Automatic Identification System (AIS)—A review. Bull. Mar. Sci. 2016, 92, 75–103. [Google Scholar] [CrossRef]
- Guo, S.Q.; Mou, J.M.; Chen, L.Y.; Chen, P.F. Improved Kinematic Interpolation for AIS Trajectory Reconstruction. Ocean Eng. 2021, 234, 109256. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Meng, Q.; Xiao, Z.; Fu, X.J. A novel ship trajectory reconstruction approach using AIS data. Ocean Eng. 2018, 159, 165–174. [Google Scholar] [CrossRef]
- Huang, H.G.; Hong, F.; Liu, J.; Liu, C.; Feng, Y.; Guo, Z.W. FVID: Fishing Vessel Type Identification Based on VMS Trajectories. J. Ocean Univ. China 2019, 18, 403–412. [Google Scholar] [CrossRef]
- Yang, S.L.; Shi, H.M.; Fan, W.; Zhang, H.; Fei, Y.J.; Zhang, H. Spatial distribution of squid fishing vessel operations in the southwest Atlantic Ocean and its relationship with environmental factors. J. Fish. Sci. China 2022, 29, 365–376. [Google Scholar]
- Shono, H. Application of support vector regression to CPUE analysis for southern bluefin tuna Thunnus maccoyii and its comparison with conventional methods. Fish Sci. 2014, 80, 879–886. [Google Scholar] [CrossRef]
- Mao, J.M.; Chen, X.J.; Jing, Y. Forecasting fishing ground of Thunnus alalunga based on BP neural network in the South Pacific Ocean. Acta Oceanol. Sin. 2016, 38, 34–43. [Google Scholar]
- Yang, S.L.; Zhang, Y.; Zhang, H.; Fan, W. Comparison and analysis of different model algorithms for CPUE standardization in fishery. Trans. Chin. Soc. Agric. Eng. 2015, 31, 259–264. [Google Scholar]
- Yuan, H.C.; Gu, Y.T.; Wang, J.T.; Chen, Y.; Chen, X.J. Study on the Medium and Long Term of Fishery Forecasting Based on Neural Network. In Proceedings of the Artificial Intelligence and Computational Intelligence: 4th International Conference, AICI 2012, Chengdu, China, 26–28 October 2012; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2012; pp. 626–633. [Google Scholar]
- Campbell, R.A. CPUE standardisation and the construction of indices of stock abundance in a spatially varying fishery using general linear models. Fish. Res. 2014, 70, 209–227. [Google Scholar] [CrossRef]
- Ward, P.; Hindmarsh, S. An overview of historical changes in the fishing gear and practices of pelagic longliners, with particular reference to Japan’s Pacific fleet. Rev. Fish Biol. Fish. 2007, 17, 501–516. [Google Scholar] [CrossRef]
- Gunawardane, N.; Ariyarathna, M.; Amarasinghe, U.; de Croos, D. Validating the fishing locations reported in the logbooks using the positional data of vessel monitoring systems in the multi-day fishery of Sri Lanka. Sri Lanka J. Aquat. Sci. 2023, 28, 11–28. [Google Scholar] [CrossRef]

| Actual | Fishing Status | Non-Fishing Status | |
|---|---|---|---|
| Estimated | |||
| Fishing status | 8498 | 1727 | |
| Non-fishing status | 508 | 11,540 | |
| Actual | Fishing Status | Non-Fishing Status | |
|---|---|---|---|
| Estimated | |||
| Fishing status | 5486 | 498 | |
| Non-fishing status | 354 | 7996 | |
| Actual | Fishing Status | Non-Fishing Status | |
|---|---|---|---|
| Estimated | |||
| Fishing status | 2586 | 121 | |
| Non-fishing status | 213 | 3914 | |
| Actual | Fishing Status | Non-Fishing Status | |
|---|---|---|---|
| Estimated | |||
| Fishing status | 6025 | 468 | |
| Non-fishing status | 263 | 9189 | |
| Actual | Fishing Status | Non-Fishing Status | |
|---|---|---|---|
| Estimated | |||
| Fishing status | 2602 | 175 | |
| Non-fishing status | 116 | 3942 | |
| Month | January | June | July | August | September | October | November |
|---|---|---|---|---|---|---|---|
| Pearson’s correlation coefficient | 0.88 | 0.98 | 0.88 | 0.79 | 0.84 | 0.99 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Song, L.; Jiang, K. Status Identification in Support of Fishing Effort Estimation for Tuna Longliners in Waters near the Marshall Islands Based on AIS Data. Fishes 2024, 9, 66. https://doi.org/10.3390/fishes9020066
Lu Z, Song L, Jiang K. Status Identification in Support of Fishing Effort Estimation for Tuna Longliners in Waters near the Marshall Islands Based on AIS Data. Fishes. 2024; 9(2):66. https://doi.org/10.3390/fishes9020066
Chicago/Turabian StyleLu, Zhengwei, Liming Song, and Keji Jiang. 2024. "Status Identification in Support of Fishing Effort Estimation for Tuna Longliners in Waters near the Marshall Islands Based on AIS Data" Fishes 9, no. 2: 66. https://doi.org/10.3390/fishes9020066
APA StyleLu, Z., Song, L., & Jiang, K. (2024). Status Identification in Support of Fishing Effort Estimation for Tuna Longliners in Waters near the Marshall Islands Based on AIS Data. Fishes, 9(2), 66. https://doi.org/10.3390/fishes9020066







