Abstract
As quantum computing continues to advance, it threatens the long-term protection of traditional cryptographic methods, especially in biometric authentication systems where it is important to protect sensitive data. To overcome this challenge, we present a comprehensive, privacy-preserving framework for multimodal biometric authentication that can easily integrate any two binary-encoded modalities through feature-level fusion, ensuring that all sensitive information remains encrypted under a CKKS-based homomorphic encryption scheme resistant to both classical and quantum-enabled attacks. To demonstrate its versatility and effectiveness, we apply this framework to the retinal vascular patterns and palm vein features, which are inherently spoof-resistant and particularly well suited to high-security applications. This method not only ensures the secrecy of the combined biometric sample, but also enables the complete assessment of recognition performance and resilience against adversarial attacks. The results show that our approach provides protection against threats such as data leakage and replay attacks while maintaining high recognition performance and operational efficiency. These findings demonstrate the feasibility of integrating multimodal biometrics with post-quantum cryptography, giving a strong, privacy-oriented authentication solution suitable for mission-critical applications in the post-quantum era.
1. Introduction
Contemporary developments in information technology have been accompanied by an escalation of cyber threats and heightened concerns about data privacy, making secure and efficient authentication mechanisms more urgent than ever. The growing sophistication of cyberattacks, coupled with the pervasive dissemination of sensitive information across online platforms, has revealed inadequacies in conventional authentication schemes. Furthermore, the prospect of practical quantum computers presents a novel class of threats to established security infrastructures. In particular, Shor’s algorithm [1] has demonstrated that the hardness assumptions underlying RSA and elliptic-curve cryptosystems (ECC) can be broken in polynomial time on a quantum machine, while Grover’s algorithm [2] has shown that the effective key lengths of symmetric systems are considerably reduced, thereby increasing their susceptibility to brute-force attacks. In response, the National Institute of Standards and Technology (NIST) has initiated a process to standardise post-quantum cryptographic (PQC) algorithms [3]. These factors together create a pressing need for authentication methods that are resilient to both classical and quantum-enabled adversaries, without imposing unacceptable costs on usability or runtime performance [4].
Biometric authentication systems (BASs) have emerged as a viable alternative to traditional authentication methods by leveraging unique physiological or behavioural characteristics that are inherently difficult to replicate. However, the literature documents clear limitations of unimodal approaches: spoofing attacks, sensitivity to environmental variation, and constrained discriminatory capacity within and across subject classes [5,6]. These weaknesses have driven interest in multimodal approaches, because fusing multiple traits can compensate for modality-specific failures. Among fusion strategies, feature-level fusion has been shown to produce richer, more discriminative templates by combining distinctive feature representations at an early stage, thereby enabling richer discriminatory information and improved security [7]. Despite progress on fusion techniques and on template protection, there remains a need for systematic studies that unite high-quality feature-level fusion with cryptographic protection that targets long-term, post-quantum resilience, while quantifying the resulting trade-offs among recognition accuracy, computational cost and resistance to quantum-enabled adversaries.
Within the spectrum of biometric modalities, retinal vascular patterns and palm vein structures have garnered particular attention due to their exceptional security attributes and operational reliability [8]. Retinal scans capture the intricate vascular patterns within the eye, which are remarkably stable over an individual’s lifetime and extremely difficult to duplicate, while palm vein recognition utilises near-infrared (NIR) imaging to extract subdermal vein patterns, offering a contactless and user-friendly method of acquisition that is inherently resistant against common spoofing techniques [9]. The fusion of these two traits at the feature level yields a powerful biometric signature that is hard to counterfeit, making it suitable for high-security and mission-critical applications. Regardless of their advantages, deploying high-security biometric systems raises major privacy concerns since, unlike passwords, compromised biometric data cannot be changed and may have lasting effects [10]. In response, researchers have investigated advanced cryptographic measures, homomorphic encryption (HE) and lattice-based methods, to protect biometric data effectively without sacrificing accuracy [11]. These approaches demonstrate considerable potential but also reveal a trade-off between strong privacy guarantees and the computational demands of real-time operation [12].
Motivated by these observations, this study proposes a generic, privacy-preserving framework for multimodal biometric authentication that seamlessly integrates any two biometric modalities via a feature-level fusion strategy, ensuring that sensitive information remains encrypted under a CKKS-based homomorphic encryption scheme designed to withstand both classical and quantum-enabled adversaries. To validate the framework’s versatility and effectiveness, we present a case study that pairs retinal vascular and palm vein features, both of which, owing to their unique structural patterns and inherent spoof-resistance, are particularly suited to be used in high-security applications. In response to the associated challenges, this work contributes to the field of security in several key ways. This study makes three main contributions. First, it presents a unified multimodal authentication framework that fuses any two binary-encoded modalities at the feature level while securing data with a CKKS-based homomorphic encryption scheme resilient to classical and quantum attacks. Second, it offers a quantitative evaluation of the trade-offs between security, recognition accuracy, and computational performance, highlighting the practical impact of privacy-preserving encryption. Third, it situates biometric template protection within the post-quantum cryptographic landscape, explicitly aligning the framework with ongoing NIST standardisation efforts to ensure long-term relevance and operational feasibility.
The remainder of this paper is organised as follows. Section 2 provides a comprehensive review of the relevant literature on unimodal and multimodal biometric systems, post-quantum cryptographic algorithms, and homomorphic encryption. Section 3 details the proposed authentication framework, including feature-level fusion strategy and CKKS-based encrypted matching, as well as the assumptions and evaluation metrics that underpin our analysis. Section 4 presents the experimental setup, parameter tuning results, performance evaluation, and security analysis. Finally, Section 5 summarises the key findings, discusses implications for future research, and outlines potential avenues for refining secure, privacy-preserving authentication systems in mission-critical contexts.
2. Background
2.1. Unimodal Biometric Systems and Their Limitations
The deployment of biometric systems for authentication and identification has traditionally relied upon the utilisation of a single physiological or behavioural characteristic, a paradigm conventionally referred to as a unimodal biometric system. Formally, such a system can be defined by the tuple , in which is the measurable space of raw biometric samples, the function represents the feature extraction mechanism mapping the raw biometric sample to a d-dimensional Euclidean feature space, serves as a similarity or distance measure, and denotes the decision threshold. The process of verification within such a system is framed as a binary hypothesis test, where (the null hypothesis) states that the live input and the stored template belong to the same individual, while (the alternative hypothesis) asserts that they belong to different individuals. The decision regarding the claimed identity of the user is made by computing the matching score between a live input and a stored template, and subsequently using a threshold-like function [13] to compare s against to determine whether the live input matches the stored template, thereby confirming or rejecting the claimed identity. Under this framework, two error probabilities are of primary concern: (i) the false acceptance rate (FAR), which quantifies the likelihood of incorrectly accepting an imposter as a legitimate user, and (ii) the false rejection rate (FRR), which measures the probability of erroneously rejecting a legitimate user. The overall performance of a biometric system is typically evaluated using the receiver operating characteristic (ROC) curve, which illustrates the trade-off between FAR and FRR across various decision thresholds [14]. Despite their conceptual simplicity and relatively low implementation cost, unimodal systems present three fundamental weaknesses:
- vulnerability to spoofing attacks due to the reliance on a single biometric modality,
- sensitivity to noise and variability arising from environmental conditions, sensor characteristics, and user presentation, all of which introduce stochastic deviations in the extracted feature vectors,
- lack of universality and distinctiveness across heterogeneous populations, leading to increased intra-class variability and decreased inter-class separability and thus to unacceptably high error rates [15].
2.2. Multimodal Biometric Systems and Fusion Strategies
The limitations inherent in unimodal biometric systems have motivated the transition towards the development of multimodal biometric systems, which leverage the complementary strengths of multiple biometric traits to improve recognition accuracy and security. In a multimodal biometric system, the decision-making process is extended to incorporate multiple biometric modalities, each of which is characterised by its own feature extraction and matching processes. This extension can be represented by the tuple , where each is a measurable space of raw samples for the ith modality and each projects observations into a real-vector space of dimension . The individual modality matcher assigns a similarity (or distance) score to any pair of feature vectors in the ith modality. The fusion operator is responsible for combining the information from the M modalities at one of three levels: feature-level (), score-level (), or decision-level (), each possessing distinct mathematical characteristics and operational trade-offs [5]. The feature-level fusion approach makes use of the operator which combines the feature vectors from each modality into a single unified feature vector that encapsulates the information from all modalities. This is particularly advantageous in scenarios where the modalities exhibit complementary characteristics, as it allows for the integration of diverse information sources at an early stage, thereby enhancing the discriminative power of the resulting feature vector [7]. The feature-level fusion operator can be implemented in various ways, such as concatenation, averaging, or more complex methods like canonical correlation analysis (CCA) or principal component analysis (PCA) [6]. In the case of concatenation, the feature vectors from each modality are combined into a single high-dimensional vector, which is then used for matching against the stored template. This approach allows for the preservation of the unique characteristics of each modality while creating a unified representation that can be processed by a single matcher. In score-level fusion, the individual modality scores are aggregated by the operator which combines them using a variety of methods, including weighted sum, product rules, or rank-based techniques, resulting in a composite score S, which is then thresholded [16]. While more modular and often less computationally demanding than feature-level fusion, this approach inevitably leads to the discarding of some raw feature information and thus tends to offer slightly lower accuracy. Finally, decision-level fusion combines the binary outcomes of the individual modality matchers into a single decision using the operator , which can be implemented using majority voting or other consensus-based methods. This approach is computationally efficient and straightforward to implement, as it relies solely on the binary outputs of individual modality matchers. However, by operating at such a high level of abstraction, it often fails to leverage the complementary information available across different biometric traits, which can lead to suboptimal recognition performance in practice [17].
2.3. Post-Quantum and Privacy-Preserving Cryptography
The imminent arrival of large-scale quantum computers constitutes a fundamental threat to the security of contemporary public-key infrastructures, which rely upon the presumed intractability of certain number-theoretic problems for classical computers. Shor’s algorithm demonstrates that, in a quantum model, both integer factorisation and the computation of discrete logarithms can be performed in time polynomial in the bit-length n of the input, specifically , which is exponentially faster than the best-known classical algorithms [1]. This has profound implications for widely used public-key cryptosystems such as RSA and ECC, which rely on the difficulty of these problems for their security. For instance, breaking a 2048-bit RSA key with the general number field sieve (GNFS) [18] requires operations, which is roughly the same protection as a 112-bit symmetric cipher in presence of quantum adversaries. A 3072-bit RSA key, by contrast, is estimated to be equivalent in strength to a 128-bit symmetric key [19]. Elliptic-curve cryptography over a 256-bit prime field (e.g., NIST P-256), which classically needs operations to solve the discrete logarithm problem, is reduced by Shor’s method to polynomial time with respect to the curve size, effectively nullifying its 128-bit security margin [20]. At the same time, Grover’s algorithm provides a quadratic speedup for brute-force search on symmetric keys, reducing the exhaustive search complexity for a n-bit symmetric cipher from to quantum queries and thus halving its effective security [2]. As a result, to preserve a classical n-bit security level against quantum threats, one must employ a -bit key. For example, although AES-256 resists classical brute-force attacks at a complexity of , under Grover’s algorithm its security is reduced to quantum operations [19]. Similar considerations apply to cryptographic hash functions: the preimage resistance of a 256-bit hash, such as SHA-256, is reduced from to against quantum attacks, while its collision resistance, classically bounded by the birthday paradox at , can be further reduced to roughly quantum steps using the Brassard-Høyer-Tapp algorithm [21]. In response to these emerging threats, the National Institute of Standards and Technology (NIST) has initiated a process to standardise post-quantum cryptographic (PQC) algorithms that are secure against both classical and quantum adversaries [3].
While the transition to PQC secures the underlying channels and storage of biometric templates against quantum-enabled eavesdroppers, it does not by itself eliminate the privacy risks inherent in handling biometric data. Any leakage, whether through database breaches, side-channel attacks, or inadvertent exposure during computation, can result in irreversible identity compromise, given the immutable nature of biometric traits. Traditional template-protection mechanisms, such as cancelable features [22] or fuzzy vault-based biometric cryptosystems [23], provide some level of obfuscation but often lack rigorous security proofs under strong adversarial models. Moreover, they have been shown to be susceptible to a range of attacks, including hill-climbing, inversion and record-linkage attacks [24]. In contrast, homomorphic encryption offers a mathematically rigorous alternative by enabling computation directly on encrypted data, thus preserving privacy without revealing the underlying biometric information. Among existing HE schemes, CKKS [25] offers an efficient solution for approximate arithmetic over encrypted vectors, making it particularly suitable for feature-level biometric matching. Its security derives from the Ring Learning with Errors (RLWE) problem, which is widely considered resistant to both classical and currently known quantum attacks [26,27]. By adopting parameters consistent with recognised post-quantum recommendations, CKKS provides a practical level of long-term protection while supporting real-time processing. Consequently, biometric systems can execute feature extraction and matching on encrypted representations without disclosing sensitive information, maintaining both operational efficiency and quantum-resilient confidentiality even in the event of a security breach.
2.4. Fully Homomorphic Encryption
A cryptographic scheme is said to be homomorphic if it supports certain algebraic operations, specifically addition and/or multiplication, directly on ciphertexts, such that decrypting the result of these operations yields exactly the same outcome as applying the same operations to the corresponding plaintexts. This capability allows to perform secure computation over encrypted data without exposing the underlying values, thereby preserving confidentiality throughout the processing pipeline. Formally, let and be two plaintext values, and denote by and their ciphertexts under public key . Let and be the encryption and decryption functions, respectively, where is the secret key, thus:
A fully homomorphic encryption (FHE) scheme additionally ensures that
where ⊞ and ⊠ denote homomorphic addition and multiplication. Consequently, arbitrary arithmetic expressions can be evaluated in the encrypted domain without exposing raw data [28]. Prominent FHE schemes include the NTRU-based scheme introduced by Hoffstein et al. [29], the Brakerski-Vaikuntanathan (BV) scheme [30], and the Gentry-Peikert-Vaikuntanathan (GPV) scheme [31], each offering a distinct balance between computational efficiency and cryptographic security, depending on the underlying hardness assumptions and structural design. The NTRU scheme is based on the hardness of the shortest vector problem (SVP) in lattices, while the GPV and BV schemes rely on the learning with errors (LWE) problem, which is also lattice-based. The latter two schemes are particularly notable for their ability to support bootstrapping [32], a process that refreshes ciphertexts to reduce noise accumulation during homomorphic operations, thus enabling arbitrary depth computations. For applications involving real-valued data the CKKS scheme [25] is particularly well-suited, since it natively supports approximate computations over complex numbers rather than being confined to exact integer operations. In contrast to integer-only schemes (e.g., BFV or BGV), CKKS reduces both ciphertext growth and noise accumulation through its rescaling mechanism and it leverages Single Instruction, Multiple Data (SIMD) batching to pack many plaintext slots into a single ciphertext, thereby enabling highly parallelised processing and significantly improving throughput.
Basic Notation
At its core, a homomorphic encryption system comprises several algebraic structures and algorithms that, when combined, enable computation over encrypted data. In this framework, it is crucial to distinguish between three hierarchical levels of information representation, each fulfilling a specific role in the overall functionality of the system. First, the message m represents the raw input, typically expressed as a floating-point scalar or vector, which must undergo an encoding transformation based on modular integer arithmetic in order to be suitable for the cryptographic scheme.
Second, the plaintext p refers to the encoded form of the message, represented either as a nonnegative integer or as a polynomial with integer coefficients in the plaintext space, and serves as the direct input to the encryption algorithm. Following the encryption process, the plaintext p can be decrypted back to its original form, either as the original message m or as the result of homomorphic computations performed on the encrypted data. In this sense, the plaintext serves as a bridge between the raw data and its encrypted representation, allowing for secure processing while maintaining the integrity of the underlying information. Third, the ciphertext constitutes the encrypted version of the plaintext, expressed as large integers or structured polynomials that conceal all information about the underlying data until decryption is performed. The ciphertext is generated by applying the encryption function to the plaintext p, and it can be decrypted back to its original form using the decryption function . Table 1 summarises these and other notational conventions.

Table 1.
Summary of notation and definitions.
3. Materials and Methods
3.1. Proposed Framework
This study introduces a novel privacy-preserving multimodal biometric authentication framework that integrates any two modalities through feature-level fusion, while ensuring the security of sensitive biometric data using a post-quantum homomorphic encryption scheme. Designed for high-security environments, the framework minimises the risk of unauthorised access while providing strong protection against both classical and quantum-capable adversaries. A detailed protocol-level view of the system is provided in Figure 1.
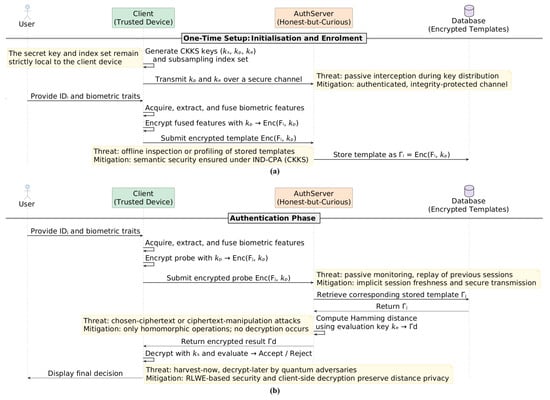
Figure 1.
High-level protocol overview of the proposed PQC enabled privacy-preserving multimodal biometric authentication system: (a) initialisation and enrolment phase, and (b) authentication phase.
3.1.1. Feature-Level Fusion
Choosing the right fusion strategy really comes down to the needs of the specific application, whether the goal is to maximise accuracy, reduce computation time, or keep the overall system design simple. In environments where security is a top priority and preventing unauthorised access is critical, feature-level fusion often proves to be the most effective option. By combining information from different biometric sources early on, it captures a deeper and more detailed profile of each individual. This does not just boost recognition performance, it also helps the system stand up better against spoofing and other potential threats [7]. In our setup, we implement the feature-level fusion operator, , using a straightforward concatenation method. This means we take the feature vectors from each modality and join them into one combined vector. That unified vector is then used for matching against stored templates. Bringing everything together at this early stage allows the system to draw on a richer pool of information, giving the fused representation a much stronger ability to distinguish between users [5].
Let and denote the Boolean feature vectors extracted from any two modalities. To combine these complementary streams of information at the earliest possible stage, the feature-level fusion operator is defined by concatenation, a process that is both linear and injective. This operator maps the Cartesian product of the two Boolean spaces into a higher-dimensional Boolean hypercube:
where is the unified Boolean vector representing the union of the two modalities, and is the total dimension of the fused feature space.
Although this operator preserves all modality-specific indicators optimising the available discriminative content, the dimension d may prove intractable for subsequent processing. In order to reduce the dimensionality of the feature space to a manageable value a data-independent dimensionality reduction approach based on the sparse random-coordinate subsampling operator is employed. Formally, let be an index set selected uniformly at random (without replacement) once at system initalisation and define the subsampling operator as:
where is the reduced Boolean vector of length k. To justify this reduction, let be two arbitrary feature vectors and let be the Hamming distance (HD) between them, and since each coordinate is retained with probability , the expectation of the subsampled HD satisfies:
Furthermore, by Hoeffding’s inequality [33], for any and any fixed pair , the probalibity that the subsampled distance deviates from its expectation by more than is bounded by . Thus, by choosing ensures, with probability at least , that
Although alternative fusion strategies, such as learned binary hashing [34,35] or Bloom-filter-style encodings [36], offer more compact representations or probabilistic guarantees, they generally require additional learning, introduce approximation errors, and complicate homomorphic evaluation. In contrast, feature-level concatenation preserves all modality-specific information and allows direct, linear operations on encrypted vectors, which ensures maximum discriminative content and straightforward integration with CKKS-based Hamming-distance matching. Therefore, for the purposes of our framework, concatenation provides the most effective balance between accuracy, security, and computational simplicity.
3.1.2. Homomorphic Encryption Scheme
The proposed framework makes use of the CKKS encryption scheme, which is a public-key, approximate homomorphic encryption method, rooted in the RLWE problem, and supports operations like addition, multiplication, rotation, and conjugation. Although the results are not perfectly accurate, they are close enough for practical use with encrypted real numbers. What follows is a general overview of the scheme, guided by its fundamental principles. Among these parameters, particular attention must be given to the security parameter, denoted by , which quantifies the scheme resistance to cryptographic attacks, reflecting the computational effort an adversary would need to compromise the encryption. An attack would be guaranteed to succeed with operations (e.g., or denotes 128-bit or 256-bit security, respectively). This level of security is influenced by the choice of other parameters, such as the modulus degree n, coefficient modulus q, and the noise distribution . Naturally, a larger means higher security, but it also translates to greater computational costs and a slightly tighter noise budget. CKKS handles arithmetic with real values, where both plaintext and ciphertext exist within a polynomial ring, , where is the coefficient modulus and is the cyclotomic polynomial . This ring comprises polynomials with degrees up to and integer coefficients from 0 to . A plaintext under CKKS consists of a single polynomial, whereas a ciphertext typically contains two or more. Notably, noise is inherent to the CKKS ciphertext and cannot be exactly separated post-encryption. To maintain acceptable precision through successive homomorphic operations, the ciphertext is scaled by a factor , mitigating rounding errors and preserving the integrity of computations [37].
Basic Principles and Supported Operations
A public-key FHE scheme is formally defined by its parameters and a set of probabilistic polynomial-time (PPT) algorithms: . For a given parameter set, the key generation algorithm produces:
- the secret key , an n-degree polynomial from a uniform ternary distribution with coefficients in , is strictly for decryption and must remain private;
- the public key is a pair of polynomials used for encryption. Here, and , with a being a random polynomial sampled uniformly from and e a random error polynomial per HE standards [38];
- the evaluation keys, derived from , allow the server to perform homomorphic multiplications and slot rotations without ever exposing the secret key itself. In practice, the relinearisation keys shrink a multiplied ciphertext back to its standard form, while the Galois keys enable cyclic shifts of the packed data slots.
CKKS encryption and decryption algorithms are based on the RLWE problem. The public encryption algorithm uses the public key and a message m (encoded as plaintext ) to produce a ciphertext :
Here, u is from a random ternary Gaussian distribution, and are error polynomials. The first element, , contains the concealed plaintext, and the second, , holds auxiliary decryption data. Plaintext p is approximately retrieved by the decryption algorithm , which uses both the secret key and ciphertext :
This approximation is valid if the noise remains sufficiently small, ensuring closely matches the original plaintext. As homomorphic addition and multiplication in CKKS, they rely on polynomial arithmetic in . For two ciphertexts and , encrypting plaintexts and :
- Addition produces , encrypting ;
- Multiplication outputs , encrypting . This operation results in a ciphertext with three polynomials, unlike the two-polynomial input. To manage size and noise growth post-multiplication, relinearisation, rescaling, and modulus switching procedures are applied [39].
Cryptographic Parameters
The homomorphic encryption standard recommends a set of parameters that achieve roughly 128-bit security, assuming the secret key is sampled from a uniform ternary distribution as , where each coefficient is independently and uniformly drawn from the set . At its core, the scheme depends on three key choices:
- The security parameter , which sets the security level by guiding choices for polynomial degree n and coefficient modulus q;
- The polynomial degree n sets the dimension of the ring via the cyclotomic polynomial and determines the ciphertext slot count, enabling larger modulus bit sizes and more complex homomorphic operations;
- The ciphertext modulus q, a large integer composed of smaller prime moduli , each satisfying , with L denoting how many layers of multiplication can be handled before the noise grows too large.
The scaling factor is another parameter used to encode real numbers onto polynomials with integer coefficients via a float-to-fixed-point conversion. For accurate encoding, real values are scaled by and rounded to the nearest integer: , where . This parameter impacts both result precision and the number of allowable operations before overflow. Parameter selection involves trade-offs. A large coefficient modulus q permits more homomorphic operations and expands the noise budget, but it also increases computational overhead and may reduce processing speed due to larger numerical values. Similarly, a higher polynomial degree n enhances security yet amplifies computational complexity. An increased security parameter improves encryption strength but leads to greater computational workload and larger ciphertext dimensions. A specified security level for is assured when operations adhere to the parameter configurations in Table 2 for an error standard deviation approximately equal to [38].

Table 2.
Recommended values for the parameters, polynomial degree n and default coefficient modulus bit-length , are provided for three security levels , considering an error standard deviation of [38].
3.1.3. Key Management and Operational Controls
The proposed privacy-preserving multimodal biometric authentication framework operates through two main phases: enrolment and authentication, as illustrated in Figure 1. In our design the client (enrollee) retains the secret key (), while the public key () is published to the server for encryption. Evaluation keys required for homomorphic processing (e.g., relinearisation and Galois keys) are generated by the client at enrolment and uploaded to the server over a secure channel; these keys permit the server to perform ciphertext relinearisation and vector rotations without enabling decryption. To limit exposure, clients may use per-user keys (preferred) or per-tenant keys as an operational trade-off: per-user keys maximise isolation but preclude cross-user ciphertext batching on a single key, whereas shared keys enable larger SIMD packing at the cost of weaker key separation. Key rotation is supported via periodic re-enrolment or targeted rekeying: when a rotation is required, the client generates a fresh key pair and either re-encrypts and re-uploads templates under the new key or provisions key-switching material explicitly; we recommend scheduled rotation (for example quarterly or on suspected compromise) combined with re-enrolment when practical. To mitigate denial-of-service (DoS) risks and replay attacks, the system requires encrypted per-session nonces and authenticators to prevent replay, and employs server-side rate limiting and anomaly detection to throttle abusive or bulk evaluation requests. Resource-intensive operations, such as generating or uploading evaluation keys, are performed over authenticated and rate-limited channels to prevent resource exhaustion. Lastly, key information is auditable and logged so that any dubious provisioning can be quickly identified and revoked.
3.1.4. Distance Computation
To perform matching in the homomorphically encrypted domain, the Hamming distance is employed on the reduced Boolean feature vectors due to its straightforward bitwise interpretability and its compatibility with subsampled signatures. Let denote the full concatenated feature vector of dimension , and let the subsampling operator produce the k-bit vector . Given two such subsampled signatures, and , corresponding respectively to the query and the enrolled template, the Hamming distance quantifies the number of differing bits between them and serves as a measure of dissimilarity between the two feature vectors.
Formally, the Hamming distance is defined by
where ⊻ denotes the Boolean XOR. In the encrypted domain, direct bitwise operations such as XOR are not natively supported due to the arithmetic nature of homomorphic encryption schemes. To overcome this limitation, the XOR operation between two binary values and is algebrically expressed as
This formulation allows the XOR operation to be evaluated within the encrypted domain, enabling the computation of the Hamming distance using supported arithmetic operations. As a result, the Hamming distance between two binary vectors and can be reformulated as the sum of squared differences of their corresponding elements:
Each reduced vector is first slot-packed into a CKKS plaintext vector and scaled by a fixed-point factor to ensure that the plaintext lies within the CKKS plaintext space , after which it is encrypted yielding the ciphertext with . The vector of component-wise XORs is then computed in the encrypted domain by means of the identity in Equation (12):
where ⊞, ⊟ and ⊠ denote CKKS homomorphic addition, subtraction and multiplication, respectively. The final encrypted Hamming distance is obtained by summing the k components of into a single ciphertext slot, making use of the SIMD packing property of the CKKS scheme, which allows for efficient parallell processing of multiple plaintext slots within a single ciphertext. This aggregation is performed through a balanced sequence of ciphertext rotations and additions, collectively denoted by the operator , which yields the final encrypted distance as follows:
Decryption of using the secret key yields an approximate plaintext encoding of the Hamming distance:
with any approximation error kept negligible by choosing the CKKS scale factor and modulus chain to exceed the accumulated noise from the k homomorphic multiplications and the additions.
3.2. Assumptions and Threat Model
In developing our CKKS-based multimodal authentication framework, we make several foundational assumptions. Firstly, to construct multimodal identities, we pair biometric samples drawn from two separate datasets, each collected from disjoint user sets, thereby creating synthetic identities for evaluation. This approach, widely adopted in the multimodal biometrics literature, is motivated by two related concerns: (i) it prevents spurious cross-modality correlations that can arise when traits are jointly collected from the same subjects, and (ii) it emulates the practical unlinkability of distinct physiological characteristics in cases where naturally paired samples are not available [40,41,42,43,44]. In this way, the methodology provides a rigorous and reproducible basis for assessing the discriminative power of feature-level fusion, ensuring that reported gains reflect genuine complementarity between modalities rather than artefacts of the dataset, thereby enhancing the generalisability of the results. Secondly, each biometric modality yields a stable, fixed-length binary feature vector through preprocessing and binarisation; these vectors are concatenated into a single binary signature and then subsampled via a data-independent operator to produce a compact k-bit representation. We further assume a standard client-server architecture in which the client, a trusted device, holds the secret key and performs feature extraction, subsampling and encryption under the public key, while the server, which possesses only the public and evaluation keys, carries out homomorphic matching without ever decrypting the data. All protocol metadata and ciphertexts traverse an authenticated, integrity-protected channel; the adversary may intercept but not tamper with messages undetected. Key generation and distribution of evaluation keys are assumed to occur in a secure, one-time setup phase, as described in Section 3.1.3.
Our threat model attributes to the adversary the ability to record arbitrary ciphertexts in transit (“passive eavesdropping”), to examine all stored encrypted templates and query ciphertexts on the server (“honest-but-curious” behaviour), and even to harvest today ciphertexts with the intent to decrypt them once quantum capabilities mature (“harvest-now, decrypt-later”). The adversary may also attempt replay attacks reusing previously captured authentication exchanges to impersonate legitimate users, and may submit crafted ciphertexts to the server in an effort to infer information (“chosen-ciphertext attack”). We further consider stronger, deployment-relevant adversaries: (i) a “malicious server” that deviates from the protocol to gather extra information or return forged responses; (ii) “server-enrollee collusion”, where an insider or compromised enrollee cooperates with the server to reconstruct or link other users’ templates; (iii) “offline template-reconstruction” attackers who obtain ciphertext archives and attempt statistical or learning-based inversion; and (iv) “timing and cache side-channel” adversaries able to observe execution time or microarchitectural leakage. We assume the adversary may hold arbitrary computational resources bounded by the estimated hardness of Ring-LWE under our chosen parameters, but does not hold users’ secret keys unless explicitly stated. Against these capabilities, our framework is required to satisfy the following security objectives: (i) semantic security (IND-CPA/IND-CCA), ensuring intercepted ciphertexts reveal no information about the underlying binary vectors; (ii) distance privacy, so that homomorphic evaluation yields only an encrypted distance and leaks no additional correlation or bit-level data; (iii) replay-attack resistance, achieved by incorporating fresh encrypted nonces in each session; (iv) post-quantum confidentiality, guaranteeing that even a future quantum adversary cannot recover secret key or plaintexts from stored ciphertexts; (v) correctness, in that the homomorphically computed Hamming distance decrypts exactly to the integer result up to negligible rounding, under the chosen CKKS parameters; (vi) robustness to malicious servers and collusion, by ensuring the server has no access to secret keys, by limiting information returned in responses, and by supporting per-user keying where operationally feasible; (vii) resilience to offline reconstruction and inversion attacks, by relying on semantic security, fresh randomness per encryption, and conservative parameter selection; and (viii) resistance to timing and microarchitectural channels, via constant-shape evaluation, constant-time primitives and implementation guidelines that avoid secret-dependent memory access. To clarify the adversary’s capabilities and our corresponding security goals, Table 3 summarises the principal threat vectors and the protective properties our system must deliver.

Table 3.
Principal adversary capabilities and security objectives.
3.3. Evaluation Metrics
In order to assess the practical trade-offs inherent in a post-quantum secure multimodal system, we consider three broad categories of metrics: recognition performance, computational efficiency, and cryptographic robustness. Each provides insight into a different dimension of system behaviour.
- Recognition performance is aimed at assessing whether a subject’s claimed identity matches their verified identity by testing the hypothesis [45]:The null hypothesis assumes that the claim is genuine, while the alternative indicates an impostor attempt. Such a test is inherently prone to two types of error: the false acceptance rate (FAR), which refers to the probability of incorrectly accepting a false claim (type I error), and the false rejection rate (FRR), which refers to the probability of wrongly rejecting a valid claim (type II error). The genuine acceptance rate (GAR), often used instead of FRR, measures the likelihood of correctly accepting a genuine identity. The relationship between FAR and FRR as the decision threshold varies is typically illustrated by the detection error trade-off (DET) curve, and the point where these two error rates are equal is known as the equal error rate (EER).
- Computational efficiency considers the impact of homomorphic encryption on practical implementation by estimating the end-to-end latency, throughput, and communication overhead of the system. End-to-end latency refers to the total time required to complete an entire authentication request, from biometric sample acquisition to final decision output, and is divided into client-side operations (feature extraction, encryption, decryption) and server-side operations (homomorphic evaluation and template lookup). Throughput is quantified by how many full authentication operations the system can handle per second in the steady-state scenario, reflecting its scalability and overall performance, especially under concurrent access. Communication overhead is the average ciphertext size exchanged between server and client, with ciphertexts in CKKS much larger than corresponding plaintexts. This action provides a gauge of the bandwidth requirement of the system and aids in identifying its suitability for deployment into networks with limited capacity.
- Cryptographic security is measured by the bit-level security that comes from the chosen CKKS modulus chain, based on the Ring-LWE hardness problem. The parameters depend on the scale, modulus sizes, and polynomial degree but only those configurations that meet the strict requirements for post-quantum security are considered good. The noise budget consumption during homomorphic evaluation is monitored to ensure that decryption produces the correct Hamming distance within the expected error bounds. Additionally, the maximum subsample length k that can be managed without depleting the noise budget is documented, referencing the statistical concentration bounds on the subsampled Hamming-distance estimator.
4. Results
4.1. Experimental Data
In this section, we describe the datasets used in our experiments with respect to the chosen modalities: retinal and palm vein biometrics. Since no multimodal datasets are publicly available for this specific combination, we introduce a harmonisation and synthetic pairing procedure aimed at creating a multimodal experimental set from publicly available single-modal data.
4.1.1. Datasets
This study makes use of two publicly available biometric databases to develop and assess our framework. The chosen datasets are the Retina Identification Database (RIDB) [46] and the Multi-Spectral Palmprint Database (MSPD) [47] both of which offer a varied collection of samples well suited to evaluating BASs.
The RIDB contains 100 high-resolution colour fundus images from 20 healthy adult participants, each contributing five unique retinal scans taken under consistent imaging conditions. These images were acquired using a TOPCON TRC-50EX non-mydriatic fundus camera with a 45° field of view, a device known for its reliability and precision in clinical ophthalmology. In order to facilitate optimal visualisation of the retinal vasculature and to ensure sufficient image clarity for subsequent analytical procedures, all subjects underwent pharmacological pupil dilation immediately prior to image acquisition, achieving an average pupil diameter of approximately 4.0 mm, thereby reducing the likelihood of artefacts related to insufficient illumination or limited field exposure. Each fundus image was saved in JPEG format as a 24-bit colour file and possesses a native spatial resolution of pixels, providing detailed visual information suitable for a variety of computational analysis tasks.
The CASIA MSPD consists of a collection of multispectral palmprint and palm vein images acquired from a total of 100 different individuals and, for each subject, six near-infrared (NIR) images of both the left and right hands were captured across two temporally separated acquisition sessions, yielding a total of 7200 images. Acquisition was performed using a dedicated NIR imaging device under unconstrained hand-placement conditions, thereby more closely simulating real-world scenarios in which users may not precisely align their hands with pre-defined positioning guides. Each image is represented as an 8-bit grayscale JPEG file with a native spatial resolution of pixels, offering sufficient detail for the extraction and analysis of the subtle vascular patterns that characterise palm vein biometrics. In the context of our experiments, only the NIR sub-band that corresponds specifically to the visualisation of palm vein structures is utilised for feature extraction, as this spectral range provides the highest contrast and most consistent visibility of the subcutaneous vein patterns that serve as the primary biometric cue in this modality [48].
Together, these two datasets allow us to evaluate our feature-level fusion method within a post-quantum homomorphic encryption setting, ensuring that both the distinct vascular features of the retina and the subcutaneous vein patterns of the palm are tested under realistic changes in subject identity, recording sessions, and capture conditions. Table 4 outlines the main attributes of each dataset, and Figure 2 presents example images that highlight the distinctive qualities of both biometric modalities.

Table 4.
Summary of the datasets used in this study.
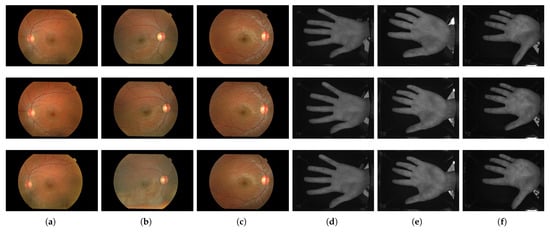
Figure 2.
Representative biometric samples from three individuals across both modalities. Each column corresponds to a single subject and includes three samples per modality: (a–c) retinal fundus images from the RIDB dataset, (d–f) palm vein images from the CASIA MSPD dataset.
4.1.2. Multimodal Dataset Harmonisation Through Synthetic Subject Pairing
To test the proposed multimodal authentication framework, it is essential to have a dataset that contains biometric samples from the same subjects across both modalities. Formally, let denote the biometric datasets associated with n distinct modalities, and let represent the set of unique subject identifiers in dataset , where . In an ideal scenario, the truly multimodal dataset would comprise only those individuals in the intersection
thereby ensuring data availability for every subject and modality. However, since the RIDB and CASIA MSPD datasets do not share any common subjects, we employ a synthetic subject pairing strategy to create a unified multimodal dataset. This approach allows the creation of virtual multimodal identities through a one-to-one synthetic mapping between users from each unimodal dataset, thereby enabling the integration of diverse biometric traits while preserving statistical independence across modalities. Since no real overlap exists between subject sets, the number of synthetic multimodal identities is constrained by the smallest cardinality among the unimodal datasets, specifically:
Therefore, this ensures that the harmonised dataset remains balanced and that each synthetic identity within the aggregated dataset is linked to a complete set of corresponding samples for every modality. In our specific application we employed the dataset harmonisation procedure through the following steps.
- Subject sampling: a subset of N users are randomly selected from each unimodal dataset, where N corresponds to the minimum cardinality among the available subject pools, thereby guaranteeing uniform representation and ensuring that the resulting synthetic multimodal population is not biased by disparities in dataset size.
- Synthetic pairing: a bijective association is then established between the selected subjects from each modality, resulting in N synthetic identities, each of which integrates biometric samples from one subject in each unimodal dataset, thus simulating subject profiles in the absence of real-world identity overlap.
- Sample standardisation: for each synthetic identity, a fixed number of biometric samples is selected from each modality in order to ensure uniform sample representation. In addition, samples are chosen from different sessions to preserve intra-subject variability and reflect realistic biometric acquisition conditions.
- Identifier normalisation: each synthetic subject is assigned a unique and consistent identifier, ensuring reliable cross-referencing throughout the dataset, and simplifying subsequent processing stages.
- Integrity validation: a final verification procedure confirms that each synthetic identity includes the required number of valid, non-corrupted biometric samples across all modalities, thus ensuring the completeness and integrity of the dataset prior to downstream processing.
Table 5 summarises the characteristics of the harmonised multimodal dataset, which comprises 20 synthetic subjects, each associated with 5 retinal and 6 palm vein samples, yielding a total of 100 retinal and 120 palm vein images.

Table 5.
Summary of the harmonised multimodal dataset.
4.2. Feature Extraction
To derive a robust and highly discriminative representation of the vascular patterns inherent in both retinal and palm vein biometrics, each modality is processed through a carefully structured sequence of preprocessing and feature extraction steps. These operations are designed to highlight the most informative structures and produce compact feature vectors compatible with the subsequent stages of the processing pipeline. In the retinal pipeline, raw fundus images are first normalised and enhanced by localising the optic disc via the Circle Hough Transform (CHT), followed by a coordinate transformation from Cartesian to polar space to straighten vessel paths, and then subjected to a Laplacian-of-Gaussian filter coupled with morphological opening and closing to accurately extract the blood vessel network [28]. The resulting binary vessel map of dimensions pixels is subsequently vectorised to yield the retinal feature template of size . In the near-infrared palm vein pipeline, sensor and environmental noise are initially attenuated, after which a locally adaptive binarisation identifies the hand silhouette to define a precise region of interest and extract its coordinates [49]; the ROI, of dimensions pixels, is then processed to enhance contrast and sharpness of vein patterns, and filtered with a Laplacian-of-Gaussian operator to emphasise linear structures [48]. Finally, morphological operations are used to further refine the vascular image, resulting in a stable feature map represented as a vector of size . The following subsections present a comprehensive exposition of each algorithmic component, detailing the underlying mathematical models, parameterisation strategies, and practical implementation aspects that support the feature-level fusion framework. Figure 3 illustrates the feature extraction pipelines for both modalities, highlighting the key steps involved in transforming raw biometric images into compact binary feature vectors.
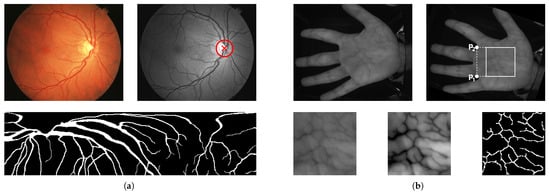
Figure 3.
Feature extraction pipelines for retinal and palm vein modalities: (a) the retinal pipeline includes optic disc localisation, polar transformation, and vessel extraction, while (b) the palm vein pipeline involves region of interest definition, contrast enhancement, morphological processing, and vessel extraction.
4.3. Experimental Environment
All computational experiments take place within a virtualised testbed, hosted on a physical machine equipped with an Intel Core i5-1135G7 processor operating at a base frequency of 2.42 GHz, and provisioned with 8 GB of physical RAM. The host system runs a 64-bit installation of Microsoft Windows 11 (version 24H2, codename Germanium). Within this environment, a virtual machine is configured with one dedicated virtual CPU and 4 GB of RAM. It operates under a 64-bit installation of the Debian GNU/Linux distribution (version 12.4.0), using the XFCE desktop environment to minimise graphical overhead and conserve system resources. The implementation makes use of Python 3.11.2 alongside the Microsoft SEAL library [50], which is accessed through its official Python bindings. These bindings are developed using pybind11, a lightweight header-only library that enables Python to work directly with C++ code. By exposing SEAL’s core encryption primitives directly, the Python interface preserves fine-grained control over parameter selection and operational detail, thereby supporting experimentation and prototyping of privacy-preserving computations.
4.4. Parameter Tuning
In this section, the parameters that determine both the statistical reliability of the subsampling procedure and the cryptographic integrity of the CKKS scheme are jointly optimised. The subsample length k not only determines how closely the HD estimation concentrates around its mean, and thus directly influencing matching accuracy, but also fixes the number of homomorphic operations required for comparison. Specifically, evaluating the HD over a k-bit signature necessitates k multiplications (ignoring multiplication by a known constant) and additions to implement the bitwise XOR logic and accumulating the result. It is therefore critical that the CKKS parameters are chosen so that the aggregate noise remains strictly below the decryption threshold.
4.4.1. Subsampling Dimension
Recall from Section 3.1.1 that Hoeffding’s inequality implies, for any two Boolean vectors and any ,
to ensure that the deviation is at most with probability at least , it is required that:
Table 6 summarises k-values for common choices of relative error and confidence level () based on the above inequality, given the total dimension of the fused feature space, where represents the sum of the individual feature vector dimensions detailed in Section 4.2. For a practical trade-off between computational efficiency and matching accuracy, a relative error of with offers an appealing compromise, since it reduces the original dimension d by slightly more than an order of magnitude while ensuring that the subsampled Hamming distances concentrate within of their expected values with a confidence level of .

Table 6.
Minimal subsample length k as a function of desired relative error , at confidence level with .
4.4.2. Homomorphic Encryption Parameters
The selection of CKKS parameters is guided by the requirement to ensure that the noise growth during homomorphic evaluation does not exceed the decryption threshold, thereby guaranteeing that the final Hamming distance can be accurately decrypted.
As described earlier, the comparison between two subsampled k-length feature vectors involves k homomorphic multiplications (ignoring multiplication by a known constant) and additions. In CKKS, each homomorphic multiplication increases the ciphertext scale and is typically followed by a rescaling step that consumes one modulus prime from the chain; consequently, the number of primes must exceed the maximum multiplicative depth of the evaluation circuit. Our Hamming-distance computation (binary vector product followed by packed summation) requires at most one multiplication per packed slot plus one rescaling step for global correctness, while additional primes provide headroom for rotations, relinearisation, and implementation safety margins. These operations must be performed within a noise budget that remains strictly above the decryption threshold. To support this level of computation, parameter sets are chosen to ensure at least 128-bit post-quantum security under the Ring-LWE assumption. This includes selecting a polynomial modulus degree n, coefficient modulus size, and an initial scale factor for encoding. However, rather than working directly with a single large coefficient modulus q, we decompose it into a product of smaller, coprime primes:
Here and are the outer primes, which furnish headroom for final decryption, and are the inner primes, each of which permits one level of multiplication before rescaling. The number L of inner primes therefore sets the maximum sequential multiplication depth. These are some key considerations to keep in mind when selecting the CKKS parameters: (i) the maximum multiplicative depth that can be supported is closely related to how many inner primes are used; (ii) as the overall size of the primes increases, performance tends to degrade, resulting in longer computation times and greater memory requirements; (iii) the size of the primes also directly affects the level of precision that can be achieved, both for whole numbers and decimal places.
According to the recommendations of the API libraries [51], a good approach to select the bit-length of each prime in the modulus chain of this cryptographic scheme depends on several aspects, as outlined below [39].
- The bit precision of the integer is equal to the difference in the size of the inner and outer primes. For instance, the use of 25-bit inner primes and 35-bit outer primes gives a precision of 10 bits. It indicates that, in cases of processing data, where the input or output values can be greater than , the selection of prime numbers with a bigger difference will be the correct solution to avoid errors.
- The bit precision of the fractional part also corresponds roughly to the number of bits of the scaling factor (i.e., ) which is supposed to be of the same order as the bit-length of the inner primes.
- If the highest accuracy when decrypting is desired, outer primes in the chain must be 60-bit length; otherwise, their size must be changed according to the specific needs.
- In order to make the system more secure, the size of outer primes must be longer than that of inner primes by at least 10 bits.
If the initial scale of the ciphertexts is , after multiplication, their scale will increase to , and after the scaling process, it will adapt to . Assuming that , then will be approximately equal to , for every . In this way, it is possible to keep the scale around during processing. Also recall that, given a number of levels equal to L, we can perform a maximum of L multiplications (scaling), which corresponds to eliminating L primes from the coefficient modulus. When the coefficient modulus is reduced to a single prime, it must be slightly larger than by a few bits to ensure the integrity of the plaintext value before the decimal point. For the best result, the moduli used are preferably selected to be of the size within the range from 20 up to 60 bits. To meet the multiplicative-depth requirements of the Hamming-distance evaluation and also to achieve 128-bit post-quantum security, we adopt a polynomial modulus degree of and a modulus chain with bit-lengths , for a total . The initial CKKS scale is set so that , and the error distribution standard deviation is chosen in line with common RLWE instantiations (approximately ). The wider outer primes in the chain provide additional noise-budget headroom for rotations, relinearisation and rescaling, while the 20-bit inner prime (equal to ) preserves precision through the intermediate rescaling steps. Furthermore, the 16-bit gap between the inner and outer primes creates a sufficient margin to accommodate the maximum possible Hamming distance, thereby guaranteeing exact decryption of the result without rounding error and maintaining the noise budget safely above the threshold. The estimated hardness of these parameters against a wide set of classical and quantum attacks is shown in Section 4.5.3, confirming that they meet the desired security level.
4.5. Performance Evaluation
In this section we assess our framework according to three complementary perspectives: recognition performance, computational efficiency and cryptographic robustness. Each perspective sheds light on a different aspect of the system, and together they support a holistic understanding of its strengths and limitations.
4.5.1. Recognition Performance
We assess the recognition performance of our privacy-preserving multimodal framework by homomorphically computing the Hamming distance between binary feature vectors derived from fused retinal and palm vein samples. All matching is performed under encryption using the CKKS scheme, with the final similarity scores recovered through decryption. As outlined in Section 3.3, performance is evaluated using the detection error trade-off curve, which captures the system’s behaviour over a wide range of decision thresholds, and the equal error rate, which provides a concise indicator of recognition accuracy. Figure 4 presents the DET curve for our approach, with the EER clearly marked. The proposed multimodal system achieves an EER of , with a GAR of at the operating point where false acceptance and false rejection are balanced. The GAR remains high across several orders of magnitude, going beyond when the FAR is and dropping only to when the FAR is . This indicates a clear impostor and genuine score distribution separation, ensuring the system to always retain discriminative capability even under stringent security requirements. We also measured the numerical differences between plaintext and CKKS-encrypted Hamming-distance evaluations using the same feature extractor and matching pipeline.
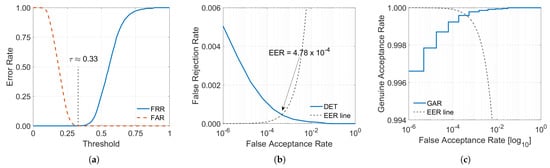
Figure 4.
Recognition performance of the proposed privacy-preserving multimodal authentication system: (a) FAR and FRR curves as functions of the decision threshold, illustrating the trade-off between rejecting genuine users and accepting impostors, (b) DET curve with the EER marked, highlighting the system’s behaviour across operating points, and (c) semi-logarithmic ROC curve showing the relationship between GAR and FAR, reflecting the system’s discriminative capability.
The mean absolute error (MAE) between plaintext and encrypted distances equals 0.3428, confirming that the approximate arithmetic of CKKS introduces only minimal numerical deviation, with negligible impact on matching decisions at the adopted operating threshold. The plaintext Hamming-distance computation requires approximately 0.035 ms per comparison, whereas the average time per authentication, including the complete homomorphic evaluation, amounts to 0.0167 s. Although the encrypted evaluation is several orders of magnitude slower than the plaintext computation, it remains sufficiently efficient for practical authentication scenarios (see Section 4.5.2 for full timing and memory breakdown).
Table 7 compares the performance of the proposed multimodal system against various unimodal baselines of retinal and palm vein biometrics using the same datasets and verification protocol. The multimodal system is observed to outperform all single-modality systems consistently in recognition accuracy. The best-performing unimodal method achieves an equal error rate just above 0.1%, whereas the proposed system reduces it to below 0.05%, representing an improvement of nearly 50% relative to the strongest individual matcher. These results indicate that the proposed feature-level fusion strategy effectively allow to capture complementary information from the two modalities, leading to a more discriminative and robust representation than either modality can provide alone.

Table 7.
Recognition performance of the proposed multimodal authentication system, compared to unimodal systems grouped by modality.
4.5.2. Computational Efficiency and Memory Usage
In order to assess the practicality of our privacy-oriented multimodal-based authentication framework, we measure both runtime and memory requirements for the four core cryptographic operations: (i) key generation, (ii) encryption, (iii) homomorphic evaluation (matching), and (iv) decryption. To estimate the total computation time each section of the code is executed 200 times, and the average value is used for analysis. The results of these measurements are summarised in Table 8, which provides a detailed breakdown of the time taken for each operation, as well as the total time required for a complete authentication cycle, including key generation. The memory footprint for each component is also presented in Table 9, which details the size of the keys, plaintexts, ciphertexts, and intermediate buffers used during the computation.

Table 8.
Measured runtime for each stage of homomorphic Hamming distance evaluation using , a 92-bit coefficient modulus, a scale factor of , and a subsample length of , chosen to fit a single CKKS ciphertext for maximal SIMD packing.

Table 9.
Estimated peak memory footprint during homomorphic computation of Hamming distance using the CKKS scheme with , a 92-bit coefficient modulus, a scale factor of , and a subsample length of .
1. Key generation: this process, which is performed using the cryptographic parameters specified in Section 4.4, requires about 87 milliseconds on average and includes the time for the secret key generation, the public key derivation, and the auxiliary keys computation. Though this process is computationally expansive, it is a one-time setup cost that does not need to be repeated for each authentication operation. Once generated, the keys can be securely stored and reused for all subsequent encryption and matching operations. The memory footprint is mainly determined the storage of the Galois keys which take up around 18 MB. Along with the secret key (192 kB), the public key (384 kB), and the relinearisation keys (768 kB), the total memory usage is still less than 20 MB. This keeps the procedure relatively lightweight for modern computing platforms and keeps the balance of both time and memory requirements.
2. Encryption: to begin the encryption process, the 4096-bit feature vector is first encoded into a plaintext polynomial using the CKKS scheme. The purpose of this step is to pack the binary values into the available complex slots of the plaintext polynomial, to apply the scaling factor, and to get the data ready for encryption. The packing and encoding tasks are on average performed in less than 1 millisecond, whereas the encryption utilising NTT and noise sampling takes approximately 3 milliseconds. In terms of memory usage, the plaintext polynomial occupies around 128 kB, while the ciphertext, which is the encrypted representation of the plaintext, requires approximately 256 kB.
3. Homomorphic evaluation: matching two encrypted vectors consists of a bitwise exclusive OR operation, which requires k (ignoring multiplication by a known constant) parallel multiplications along with additions, followed by additions to accumulate the Hamming weight. Thanks to SIMD packing, the entire multiplication layer executes in one step. The average runtime for this evaluation is around 12 milliseconds, including any required relinearisation and rescaling, while the resulting ciphertext, which holds the Hamming distance, is approximately 128 kB in size. The CKKS slot capacity and chosen k determine three linked trade-offs: discrimination, batching efficiency, and cryptographic cost. For our setting a single ciphertext supports up to 4096 slots, so permits full single-ciphertext packing and maximal SIMD throughput. For one must either increase n (raising parameter and security costs) or split the signature across multiple ciphertexts (increasing communication, rotations, and latency). Reducing k reduces per-comparison cost but may degrade discrimination if too many features are discarded. In practice k should be selected to balance recognition performance against latency, memory, and the available slot capacity.
4. Decryption: the ciphertext produced by the evaluation phase is first decrypted using the secret key, recovering a plaintext polynomial of approximately 64 kB. On average, decryption is completed in approximately 0.1 milliseconds. Following decryption, a separate decoding operation is required to convert the complex-valued polynomial back into an interpretable numerical result. This step, which includes inverse scaling and unpacking, is completed in an additional 0.3 milliseconds. The combined process is fast, memory-efficient, and requires no further allocations beyond the ciphertext and output buffer.
4.5.3. Cryptographic Robustness and Security Analysis
To ensure that our privacy-preserving multimodal authentication framework is both secure and functional, we analyse the cryptographic properties of the CKKS scheme under which it operates, verifying that the selected parameters meet the necessary security standards, confirm that the homomorphic operations yield correct results, and show that the system is resilient against potential attacks.
It is useful to place our framework within the broader landscape of privacy-preserving biometric techniques. Systems based on BFV and BGV schemes also rely on the same Ring-LWE hardness assumption but perform exact integer arithmetic, which substantially increases ciphertext expansion and multiplicative depth when evaluating vector operations. Although our biometric signatures are binary, the proposed framework uses CKKS due to its superior computational efficiency in vectorised homomorphic operations. The approximate arithmetic supported by CKKS allows simultaneous packed processing of large binary feature vectors, significantly reducing latency and memory usage compared with BFV/BGV implementations of equivalent security strength [58,59]. On the other hand, cancelable and hybrid methods perform a lightweight obfuscation of features through non-invertible transforms or helper data, yet their security is mostly heuristic and they are susceptible to inversion or record-linkage attacks [22,23,24]. Trusted Execution Environments (TEEs) and Secure Multiparty Computation (MPC) offer alternative paradigms; however, the former depend on hardware trust and are susceptible to side-channel leakage [60], while the latter introduce significant communication and latency costs [61]. Table 10 summarises the qualitative trade-offs among these methods. Overall, CKKS achieves a reasonable balance of cryptographic strength and computing efficiency, making it ideal for real-time multimodal authentication in post-quantum scenarios.

Table 10.
Qualitative comparison of privacy-preserving approaches for biometric matching.
- Security level of parameters: our primary target to achieve at least 128-bit post-quantum security (equivalent to 256-bit classical security) under the Ring-LWE assumption, which protects against “harvest-now, decrypt-later” attacks. Accordingly, we select polynomial modulus degree and a coefficient modulus chain with bit-lengths (total ), in accordance with the recommended parameters in Table 2. The security of the chosen CKKS parameters was assessed using the LWE Estimator [26], considering multiple attack strategies. Table 11 summarises the estimated work factors for for the most effective primal and dual attack families under typical reduction-shape models [63,64,65,66,67]. Classical costs are reported in of the estimated operation count, while quantum costs conservatively assume a square-root speedup. All attacks yield effective security well above the 128-bit post-quantum threshold, confirming the robustness of the selected parameters.
 Table 11. Estimated hardness of the adopted CKKS parameter set (, bits, ) against standard LWE attacks under different reduction-shape models (outputs from LWE estimator [27]) along with their corresponding quantum-cost approximations.
Table 11. Estimated hardness of the adopted CKKS parameter set (, bits, ) against standard LWE attacks under different reduction-shape models (outputs from LWE estimator [27]) along with their corresponding quantum-cost approximations. - Correctness under noise growth: CKKS is inherently approximate, and each homomorphic multiplication followed by rescaling reduces the available precision due to scale growth and modulus reduction. To ensure that all operations yield correct results, we track the remaining modulus size and ciphertext scale at each stage of the Hamming-distance evaluation. In all trials the estimated remaining precision exceeded 16 bits at the end of evaluation, well above the minimum 12-bits required for error-free decryption; indeed no decryption failures were observed, demonstrating that our parameter choices maintain correctness throughout the computation.
- Resistance to attacks: the system is designed to minimise susceptibility to known cryptanalytic and side-channel attacks by enforcing a fixed sequence of homomorphic operations, thereby precluding adaptive behaviours that could be exploited through chosen-ciphertext or oracle-based techniques. Since no bootstrapping or iterative decryption is required, and the server operates within the honest-but-curious model without access to secret keys or decryption queries, the opportunities for malicious inference are significantly reduced. To prevent statistical correlations between ciphertexts, fresh encryption randomness is sampled for every input. Each ciphertext also includes a unique freshness nonce for each session, which prevents attackers from reusing previously captured data in a replay attempt. The Galois keys, required for internal vector manipulations, are generated securely during initialisation and are never exposed to adversaries. Taken together, these measures ensure that no exploitable structure is introduced at runtime and that all cryptographic operations remain semantically secure against both passive and active threats.
5. Conclusions
This study presented a privacy-preserving framework for multimodal biometric authentication that combines any two binary-encoded modalities using feature-level fusion, ensuring that sensitive information remains encrypted under a post-quantum secure homomorphic encryption scheme.
The system, which fused retinal and palm vein features at the representation level, not only significantly outperformed the single-modality baselines but also achieved an equal error rate of 0.048%, effectively halving the error while improving genuine acceptance rates at low false-acceptance thresholds.
From a computational perspective, once the cryptographic keys are generated, a single authentication instance constitutes approximately 16% of the overall pipeline cost, with homomorphic evaluation of the Hamming distance representing roughly 75% of the per-instance workload and about 12% of the overall pipeline computation. The full transient memory footprint for one authentication cycle reaches approximately 20.32 MB, excluding the secret key and decrypted plaintexts which are handled locally and with Galois keys forming the largest contribution to persistent storage.
The framework is also highly scalable and can operate efficiently using input vectors up to the full CKKS slot capacity, supporting a wide range of biometric representations with a polynomial degree of 8192 and 4096 encrypted slots. The modular design allows straightforward extension to additional binary modalities or higher-dimensional feature vectors with minimal adjustments to the encryption parameters.
The cryptographic robustness of the solution, ensured by the selected CKKS parameters, provide robust post-quantum guarantees, while protocol-level defenses prevent replay and adaptive attacks. Fixed operation sequences and regulated key usage ensure semantic security against both passive and active adversaries, minimising exposure to attack vectors. This approach is crucial, as biometric data forms the core of identity verification in high-security contexts, where breaches or privacy violations have severe consequences.
In practical terms, the proposed framework is well suited to decentralised and cloud-based biometric authentication, as sensitive templates remain encrypted throughout the entire process, mitigating the risk of data breaches and fully complying with regulatory and ethical standards on data minimisation and user consent. By ensuring that any single party has no access to raw biometric data, the system enables secure identity authentication while maintaining operational reliability, even across federated and cloud platforms. These capabilities render it particularly applicable in high-security and mission-critical scenarios, where operation functionality and privacy protection are equally important.
Author Contributions
Conceptualisation, D.P. and P.L.M.; formal analysis, D.P.; investigation, D.P.; methodology, D.P.; software, D.P.; validation, P.L.M.; writing—original draft, D.P.; writing—review and editing, P.L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AES | Advanced Encryption Standard |
| BAS | Biometric Authentication System |
| BDD | Bounded Distance Decoding |
| CASIA | Chinese Academy of Sciences Institute of Automation |
| CCA | Canonical Correlation Analysis |
| CHT | Circle Hough Transform |
| CKKS | Cheon-Kim-Kim-Song |
| DET | Detection Error Trade-off |
| DOS | Denial of Service |
| ECC | Elliptic Curve Cryptography |
| EER | Equal Error Rate |
| FAR | False Acceptance Rate |
| FHE | Fully Homomorphic Encryption |
| FRR | False Rejection Rate |
| GNFS | General Number Field Sieve |
| GSA | Geometric Series Assumption |
| HD | Hamming Distance |
| HE | Homomorphic Encryption |
| IND-CCA | Indistinguishability under Chosen Ciphertext Attack |
| IND-CPA | Indistinguishability under Chosen Plaintext Attack |
| LDA | Linear Discriminant Analysis |
| LWE | Learning with Errors |
| MAE | Mean Absolute Error |
| MPC | Multiparty Computation |
| MSPD | Multi-Spectral Palmprint Database |
| NIR | Near-Infrared |
| NIST | National Institute of Standards and Technology |
| NTT | Number Theoretic Transform |
| PCA | Principal Component Analysis |
| PPT | Probabilistic Polynomial Time |
| PQC | Post-Quantum Cryptography |
| RIDB | Retina Identification Database |
| RLWE | Ring Learning with Errors |
| ROC | Receiver Operating Characteristic |
| RSA | Rivest-Shamir-Adleman |
| SHA | Secure Hash Algorithm |
| SIMD | Single Instruction, Multiple Data |
| SVP | Shortest Vector Problem |
| TEE | Trusted Execution Environment |
| uSVP | Unique Shortest Vector Problem |
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (STOC), Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Alagic, G.; Bros, M.; Ciadoux, P.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Liu, Y.K.; Miller, C.; et al. Status Report on the Fourth Round of the NIST Post-Quantum Cryptography Standardization Process; U.S. Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2025.
- Yang, W.; Wang, S.; Cui, H.; Tang, Z.; Li, Y. A review of homomorphic encryption for privacy-preserving biometrics. Sensors 2023, 23, 3566. [Google Scholar] [CrossRef] [PubMed]
- Ross, A.; Jain, A.K. Multimodal biometrics: An overview. In Proceedings of the 12th European Signal Processing Conference, Vienna, Austria, 6–10 September 2004; pp. 1221–1224. [Google Scholar]
- Jain, A.; Nandakumar, K.; Ross, A. Score normalization in multimodal biometric systems. Pattern Recognit. 2005, 38, 2270–2285. [Google Scholar] [CrossRef]
- Sarangi, P.P.; Nayak, D.R.; Panda, M.; Majhi, B. A feature-level fusion based improved multimodal biometric recognition system using ear and profile face. J. Ambient Intell. Humaniz. Comput. 2022, 13, 1867–1898. [Google Scholar] [CrossRef]
- Meng, X.; Yin, Y.; Yang, G.; Xi, X. Retinal identification based on an improved circular gabor filter and scale invariant feature transform. Sensors 2013, 13, 9248–9266. [Google Scholar] [CrossRef]
- Palma, D.; Montessoro, P.L. Biometric-based human recognition systems: An overview. In Recent Advances in Biometrics; IntechOpen: London, UK, 2022; Chapter 2; pp. 23–43. [Google Scholar]
- Waheed, Z.; Akram, M.U.; Waheed, A.; Khan, M.A.; Shaukat, A.; Ishaq, M. Person identification using vascular and non-vascular retinal features. Comput. Electr. Eng. 2016, 53, 359–371. [Google Scholar] [CrossRef]
- Özcan, A.Ş.; Ayduman, C.; Türkoğlu, E.R.; Savaş, E. Homomorphic encryption on GPU. IEEE Access 2023, 11, 84168–84186. [Google Scholar] [CrossRef]
- Marcolla, C.; Sucasas, V.; Manzano, M.; Bassoli, R.; Fitzek, F.H.; Aaraj, N. Survey on fully homomorphic encryption, theory, and applications. Proc. IEEE 2022, 110, 1572–1609. [Google Scholar] [CrossRef]
- Blanchini, F.; Casagrande, D.; Fabiani, F.; Giordano, G.; Palma, D.; Pesenti, R. A threshold mechanism ensures minimum-path flow in lightning discharge. Sci. Rep. 2021, 11, 280. [Google Scholar] [CrossRef] [PubMed]
- Palma, D.; Montessoro, P.L.; Giordano, G.; Blanchini, F. A dynamic algorithm for palmprint recognition. In Proceedings of the IEEE International Conference on Communications and Network Security (CNS), Florence, Italy, 28–30 September 2015; pp. 659–662. [Google Scholar]
- A. El_Rahman, S.; Alluhaidan, A.S. Enhanced multimodal biometric recognition systems based on deep learning and traditional methods in smart environments. PLoS ONE 2024, 19, e0291084. [Google Scholar] [CrossRef]
- Snelick, R.; Uludag, U.; Mink, A.; Indovina, M.; Jain, A. Large-scale evaluation of multimodal biometric authentication using state-of-the-art systems. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 450–455. [Google Scholar] [CrossRef] [PubMed]
- Delac, K.; Grgic, M. A survey of biometric recognition methods. In Proceedings of the Proceedings. Elmar-2004. 46th International Symposium on Electronics in Marine, Zadar, Croatia, 8–18 June 2004; pp. 184–193. [Google Scholar]
- Lenstra, A.K.; Lenstra, H.W. The Development of the Number Field Sieve; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993; Volume 1554. [Google Scholar]
- Chen, L.; Chen, L.; Jordan, S.; Liu, Y.K.; Moody, D.; Peralta, R.; Perlner, R.A.; Smith-Tone, D. Report on Post-Quantum Cryptography; U.S. Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016; Volume 12.
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Brassard, G.; Høyer, P.; Tapp, A. Quantum cryptanalysis of hash and claw-free functions. In Proceedings of the LATIN’98: Theoretical Informatics: Third Latin American Symposium, Campinas, Brazil, 20–24 April 1998; Springer: Berlin/Heidelberg, Germany; pp. 163–169. [Google Scholar]
- Bringer, J.; Chabanne, H. An authentication protocol with encrypted biometric data. In Proceedings of the International Conference on Cryptology in Africa, Casablanca, Morocco, 11–14 June 2008; pp. 109–124. [Google Scholar]
- Juels, A.; Sudan, M. A fuzzy vault scheme. Des. Codes Cryptogr. 2006, 38, 237–257. [Google Scholar] [CrossRef]
- Abdullahi, S.M.; Sun, S.; Wang, B.; Wei, N.; Wang, H. Biometric template attacks and recent protection mechanisms: A survey. Inf. Fusion 2024, 103, 102144. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Proceedings of the 23rd International Conference on the Theory and Applications of Cryptology and Information Security (ASIACRYPT), Hong Kong, China, 3–7 December 2017; pp. 409–437. [Google Scholar]
- Albrecht, M.; Chase, M.; Chen, H.; Ding, J.; Goldwasser, S.; Gorbunov, S.; Halevi, S.; Hoffstein, J.; Laine, K.; Lauter, K.; et al. Homomorphic Encryption Standard. Cryptology ePrint Archive, Paper 2019/939. 2019. Available online: https://eprint.iacr.org/2019/939 (accessed on 1 February 2025).
- Albrecht, M.; Player, R.; Scott, S. On the Concrete Hardness of Learning with Errors. Cryptology ePrint Archive, Paper 2015/046. 2015. Available online: https://eprint.iacr.org/2015/046 (accessed on 1 February 2025).
- Palma, D.; Montessoro, P.L. For Your Eyes Only: A Privacy-Preserving Authentication Framework based on Homomorphic Encryption and Retina Biometrics. IEEE Access 2024, 12, 183688–183706. [Google Scholar] [CrossRef]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Proceedings of the International Algorithmic Number Theory Symposium, Portland, OR, USA, 21–25 June 1998; pp. 267–288. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing (STOC), Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput. 2014, 43, 831–871. [Google Scholar] [CrossRef]
- Gentry, C. A Fully Homomorphic Encryption Scheme. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Hoeffding, W. Probability inequalities for sums of bounded random variables. In The Collected Works of Wassily Hoeffding; Springer: New York, NY, USA, 1994; pp. 409–426. [Google Scholar]
- Liu, H.; Wang, R.; Shan, S.; Chen, X. Deep supervised hashing for fast image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2064–2072. [Google Scholar]
- Lin, K.; Lu, J.; Chen, C.S.; Zhou, J. Learning compact binary descriptors with unsupervised deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1183–1192. [Google Scholar]
- Gomez-Barrero, M.; Rathgeb, C.; Li, G.; Ramachandra, R.; Galbally, J.; Busch, C. Multi-biometric template protection based on bloom filters. Inf. Fusion 2018, 42, 37–50. [Google Scholar] [CrossRef]
- Schlüter, N.; Binfet, P.; Darup, M.S. A brief survey on encrypted control: From the first to the second generation and beyond. Annu. Rev. Control 2023, 56, 100913. [Google Scholar] [CrossRef]
- Albrecht, M.; Chase, M.; Chen, H.; Ding, J.; Goldwasser, S.; Gorbunov, S.; Halevi, S.; Hoffstein, J.; Laine, K.; Lauter, K.; et al. Homomorphic encryption standard. In Protecting Privacy Through Homomorphic Encryption; Springer: Cham, Switzerland, 2021; pp. 31–62. [Google Scholar]
- Palma, D.; Montessoro, P.L.; Loghi, M.; Casagrande, D. A Privacy-Preserving System for Confidential Carpooling Services Using Homomorphic Encryption. Adv. Intell. Syst. 2025, 7, 2400507. [Google Scholar] [CrossRef]
- Ammour, N.; Bazi, Y.; Alajlan, N. Multimodal approach for enhancing biometric authentication. J. Imaging 2023, 9, 168. [Google Scholar] [CrossRef]
- Canuto, A.M.; Pintro, F.; Xavier-Junior, J.C. Investigating fusion approaches in multi-biometric cancellable recognition. Expert Syst. Appl. 2013, 40, 1971–1980. [Google Scholar] [CrossRef]
- Nagar, A.; Nandakumar, K.; Jain, A.K. Multibiometric cryptosystems based on feature-level fusion. IEEE Trans. Inf. Forensics Secur. 2012, 7, 255–268. [Google Scholar] [CrossRef]
- Nandakumar, K.; Jain, A.K. Multibiometric template security using fuzzy vault. In Proceedings of the 2008 IEEE Second International Conference on Biometrics: Theory, Applications and Systems, Washington, DC, USA, 29 September–1 October 2008; pp. 1–6. [Google Scholar]
- Sutcu, Y.; Li, Q.; Memon, N. Secure biometric templates from fingerprint-face features. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–6. [Google Scholar]
- Palma, D.; Blanchini, F.; Montessoro, P.L. A system-theoretic approach for image-based infectious plant disease severity estimation. PLoS ONE 2022, 17, e0272002. [Google Scholar] [CrossRef] [PubMed]
- Akram, M.U.; Salam, A.A.; Khawaja, S.G.; Naqvi, S.G.H.; Khan, S.A. RIDB: A dataset of fundus images for retina based person identification. Data Brief 2020, 33, 106433. [Google Scholar] [CrossRef] [PubMed]
- Chinese Academy of Sciences Institute of Automation. CASIA Multi-Spectral Palmprint Image Database V1.0. Available online: http://english.ia.cas.cn/db/201611/t20161101_169937.html (accessed on 1 February 2025).
- Palma, D.; Blanchini, F.; Giordano, G.; Montessoro, P.L. A dynamic biometric authentication algorithm for near-infrared palm vascular patterns. IEEE Access 2020, 8, 118978–118988. [Google Scholar] [CrossRef]
- Palma, D.; Montessoro, P.L.; Giordano, G.; Blanchini, F. Biometric palmprint verification: A dynamical system approach. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2676–2687. [Google Scholar] [CrossRef]
- Microsoft SEAL (Release 4.1). Microsoft Research, Redmond, WA, 2023. Available online: https://github.com/Microsoft/SEAL (accessed on 1 February 2025).
- Ibarrondo, A.; Viand, A. Pyfhel: Python for homomorphic encryption libraries. In Proceedings of the 9th Workshop on Encrypted Computing & Applied Homomorphic Cryptography, Seoul, Republic of Korea, 15 November 2021; pp. 11–16. [Google Scholar]
- Fatima, J.; Syed, A.M.; Akram, M.U. A secure personal identification system based on human retina. In Proceedings of the 2013 IEEE Symposium on Industrial Electronics & Applications, Kuching, Malaysia, 22–25 September 2013; pp. 90–95. [Google Scholar]
- Waheed, Z.; Waheed, A.; Akram, M.U. A robust non-vascular retina recognition system using structural features of retinal image. In Proceedings of the 2016 13th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 12–16 January 2016; pp. 101–105. [Google Scholar]
- Mirmohamadsadeghi, L.; Drygajlo, A. Palm vein recognition with local binary patterns and local derivative patterns. In Proceedings of the 2011 International Joint Conference on Biometrics (IJCB), Washington, DC, USA, 11–13 October 2011; pp. 1–6. [Google Scholar]
- Zhou, Y.; Kumar, A. Human identification using palm-vein images. IEEE Trans. Inf. Forensics Secur. 2011, 6, 1259–1274. [Google Scholar] [CrossRef]
- Kang, W.; Wu, Q. Contactless palm vein recognition using a mutual foreground-based local binary pattern. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1974–1985. [Google Scholar] [CrossRef]
- Ma, X.; Jing, X.; Huang, H.; Cui, Y.; Mu, J. Palm vein recognition scheme based on an adaptive Gabor filter. IET Biom. 2017, 6, 325–333. [Google Scholar] [CrossRef]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive. 2012. Available online: https://eprint.iacr.org/2012/144 (accessed on 1 February 2025).
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory (TOCT) 2014, 6, 1–36. [Google Scholar] [CrossRef]
- Costan, V.; Devadas, S. Intel SGX Explained. Cryptology ePrint Archive. 2016. Available online: https://eprint.iacr.org/2016/086 (accessed on 1 February 2025).
- Mohassel, P.; Zhang, Y. SecureML: A system for scalable privacy-preserving machine learning. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 19–38. [Google Scholar]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Schnorr, C.P. Lattice reduction by random sampling and birthday methods. In Proceedings of the Annual Symposium on Theoretical Aspects of Computer Science, Berlin, Germany, 27 February–1 March 2003; pp. 145–156. [Google Scholar]
- Chen, Y.; Nguyen, P.Q. BKZ 2.0: Better lattice security estimates. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Seoul, Republic of Korea, 4–8 December 2011; pp. 1–20. [Google Scholar]
- Liu, M.; Nguyen, P.Q. Solving BDD by enumeration: An update. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 25 February –1 March 2013; pp. 293–309. [Google Scholar]
- Micciancio, D.; Regev, O. Lattice-based Cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; p. 147. [Google Scholar]
- Albrecht, M.R. On dual lattice attacks against small-secret LWE and parameter choices in HElib and SEAL. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, 30 April–4 May 2017; pp. 103–129. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).