A Privacy-Preserving Scheme for V2V Double Auction Power Trading Based on Heterogeneous Signcryption and IoV

Abstract

As electric vehicles (EVs) gain popularity, the existing public charging infrastructure is struggling to keep pace with the rapidly growing demand for the immediate charging needs of EVs. V2V power trading has gradually attracted widespread attention and development. EVs need to transmit sensitive information, such as transaction plans, through communication entities in the Internet of Vehicles (IoV). This could lead to leaks of sensitive information, thereby threatening the fairness of transactions. In addition, due to the differences in the cryptographic systems of entities, communication between entities faces challenges. Therefore, a privacy-preserving scheme for V2V double auction power trading based on heterogeneous signcryption and IoV is proposed. Firstly, a heterogeneous signcryption algorithm is designed to realize secure communication from certificateless cryptography to identity-based cryptography. Secondly, the scheme employs a pseudonym mechanism to protect the real identities of EVs. Furthermore, a verification algorithm is designed to verify the information sent by EVs and ensure the traceability and revocation of malicious EVs. The theoretical analysis shows that the proposed scheme could serve common security functions, and the experiment demonstrates that the proposed scheme reduces communication costs by about 14.56% and the computational cost of aggregate decryption by 80.51% compared with other schemes in recent years.

1. Introduction

Rapid economic development has led to increasingly serious problems, such as environmental pollution and energy demand. Electric vehicles (EVs) have experienced explosive growth due to their low-carbon and environmental protection characteristics [1]. They are widely considered to be the best alternative to fuel vehicles and have become a focal point for scholars in the field of Internet of Vehicles (IoV). From 2022 to 2023, global EVs achieved explosive growth, with deliveries reaching 10.5 million units, an increase of 55% over 2021. The Chinese market is particularly prominent, with sales increasing by 82% year-on-year [2].

As the number of EVs surges, public charging infrastructures are facing significant pressure, which could easily lead to problems such as charging congestion, unreasonable layout, and insufficient charging facilities, causing users to have range anxiety about EVs. V2V (Vehicle-to-Vehicle) electricity transaction has been developed as a new, flexible electricity transaction method that can effectively supplement the V2G (Vehicle-to-Grid) method. EVs with surplus power can charge other EVs through a DC-DC bidirectional converter and reduce the damage of heavy-load charging to the power grid [3]. With the help of technologies such as IoV, real-time communication interaction, sharing of physical location, charging and discharging requirements, and energy prices can be established [4]. EV users can flexibly choose to buy or sell electricity at any time according to battery status, electricity price, and transaction plans. Compared with traditional charging methods, this breaks through the limitations of time and space and allows charging and discharging operations to be performed at any time and place, which not only makes up for the shortage of charging facilities but also reduces the range anxiety of users [5,6].

However, EVs communicate in a non-fully trusted environment. Malicious attackers may intercept, modify, replay, and delete information during transmission, which will affect all users in the entire network and cause sensitive information leakage, further affecting transaction fairness [7]. Meanwhile, due to factors such as the movement of EVs and channel interference, the communication environment is complex and dynamic, and it is very necessary to adapt to diverse environments [8]. With the continuous development of cryptographic systems, entities in IoV are likely to be in different cryptographic systems due to differences in computing power. For example, EVs and RSUs have insufficient computing power, so it is not a good idea to adopt a high-cost scheme, while the platform agent (PA) and auction center (AC) can bear relatively large costs due to their large computing power. In addition, different manufacturers are likely to adopt different cryptographic systems for different EVs to achieve information transmission. Therefore, in order to enhance users’ dependence on and trust in an IoV environment with limited physical resources and provide support for reliable V2V power trading, it is crucial to implement a secure communication mechanism that can protect user privacy and support cross-cryptographic systems.

In V2V power trading, EV trading parties often use auctions to solve the electricity allocation problem [9]. Among the most prevalent auction models are the reverse auction (RA), where buyers solicit bids from sellers, and the double auction (DA), which allows multiple buyers and sellers to submit bids simultaneously.

1.1. Related Work

To encourage more users to participate in V2V power trading, many research efforts have focused on utilizing auction mechanisms to maximize user benefits. The authors of [10] use RA based on the dynamic pricing strategy to realize peer-to-peer (P2P) transactions between EVs, improving the profit of seller EVs with insufficient price competitiveness and reducing the cost of buyer EVs. Ref. [11] proposes a DA mechanism based on the Bayesian game method for V2V and V2G electricity transaction architecture based on blockchain. Ref. [12] designed a V2V electricity transaction platform with DA and high flexibility to increase the economic benefits of participants and reduce energy consumption from the power grid. While these schemes can bring economic benefits to users and reduce grid losses, they fail to consider privacy issues during transactions. A leak of sensitive information not only risks the privacy of EV users but also threatens the integrity of transactional fairness. Additionally, as the awareness of privacy protection increases among users, these schemes are less likely to encourage user participation in V2V electricity transactions. Therefore, it is critical to ensure users’ privacy and the security of transaction plans.

To address the above issues, many scholars have proposed schemes based on cryptographic technology. These are broadly classified into three types: traditional public key cryptography (PKC), identity-based cryptography (IBC), and certificateless cryptography (CLC). In the CLC scheme, the user’s private key is not completely generated by itself but also partially generated by a key generation center (KGC). It can solve the certificate management and key trusteeship problems in PKI and IBC, and its efficiency and security are enhanced. Boneh et al. [13] first proposed aggregate signatures, which aggregate multiple signatures into one signature and verify the aggregate signature using bilinear maps. For resource-constrained network nodes, aggregate signatures can solve the problem of high computational burden and reduce overhead. To ensure the security of data transmission between entities, Zheng proposed a signcryption scheme that can realize encryption and signatures in one logical step and achieve data confidentiality and unforgeability at the same time [14]. When there are many users, aggregate signcryption can merge multiple signcryption messages into one, which is suitable for environments with limited computing resources and bandwidth, such as IoV and smart grids [15]. Dohare et al. [16] proposed a certificateless aggregate signcryption (CLASC) scheme based on bilinear maps for cloud–fog-centered Industry 4.0, which uses fog nodes to reduce the computational cost of the cloud. However, this scheme does not meet the conditional privacy protection needs and easily leaks the user’s real identity. Dai et al. [17] proposed a CLASC scheme using ECC for vehicle-mounted sensor networks and conducted a security analysis under the random oracle model (ROM); it can achieve the same level of security with a shorter key and has the characteristics of small storage space and low bandwidth. However, when communication in the IoV is attacked or tampered with, the impact will spread to the entire network. Therefore, it is necessary to adopt a revocation and supervision mechanism for malicious EVs, but this is not considered in [17]. In addition, the research scheme in the above literature is suitable for cryptographic environments using the same system parameters and does not support heterogeneous communication across cryptographic systems.

For heterogeneous cryptographic environments, Jin et al. [18] proposed a heterogeneous signcryption scheme, from the CLC environment of wireless sensor networks to the IBC environment of server networks. Ali et al. [19] proposed a heterogeneous signcryption scheme in an IBC-to-PKI environment for vehicle self-organizing networks and achieved conditional privacy protection. In [20], the authors proposed a heterogeneous aggregation signcryption scheme in a PKI-to-IBC environment and combined network slicing with IoV to achieve batch verification. The above schemes use complex bilinear mapping, which leads to high computational costs. To reduce these costs, PAN et al. [21] proposed a heterogeneous signcryption scheme from IBC to PKI suitable for drone networks. Zhou et al. [22] proposed a secure communication scheme from CLC to PKI for heterogeneous communication issues in IoV. This scheme is built based on ECC and uses an online/offline signcryption approach to reduce costs. This scheme did not use complex bilinear mapping, but it does not fall under the application environment of this paper.

1.2. Contributions

In summary, there is a possibility of sensitive information about plans and user identities being leaked in V2V power trading. Therefore, it is necessary to consider cross-cryptographic systems with secure communication and to hide the real identities of users. Meaning, being able to track and revoke malicious EVs is also crucial. The main contributions of this paper are as follows:

(1)

A privacy-preserving scheme for V2V double auction power trading based on heterogeneous signcryption and IoV is proposed. The seller EVs can charge during periods of low load in accordance with the demand response policy and earn income by selling the electricity, which not only meets the instant charging needs of EVs but also helps to reduce range anxiety.

(2)

A heterogeneous signcryption algorithm from a CLC-to-IBC cryptographic system is improved, utilizing ECC and integrating the aggregation method in the scheme to achieve greater computational efficiency.

(3)

A pseudonym mechanism is implemented for EV users engaged in V2V power trading to protect the real identities of these users. It also provides a verification algorithm to verify the information and ensures the tracking of malicious EVs and the revocation of their eligibility to participate in V2V power trading.

(4)

The security analysis of this scheme is carried out based on ROM, and the performance comparison analysis is carried out through experiments. The scheme has certain advantages in both communication and computational costs.

1.3. Roadmap

The remainder of this paper is organized as follows: Section 2 reviews related technologies, such as ECC; difficult problems; and blockchain. Section 3 describes the scheme model. Section 4 details the implementation of the proposed scheme. Section 5 presents the security of the scheme. Section 6 conducts performance analysis. Finally, Section 7 summarizes the main contributions of the paper and discusses future research.

2. Preliminaries

2.1. Elliptic Curve Cryptography

Elliptic curve cryptography is a public key cryptosystem based on the algebraic structure of elliptic curves, and its security relies on the intractability of the elliptic curve discrete logarithm problem. Assume that $q > 3$ is a large prime number, and $E$ is the point group of the non-singular elliptic curve defined by $y^2=x^3+ax+b (mod q)$ over the finite field $F_q$, where $a,b\in F_q$, $4a^3+27b^2\ne O (mod q)$. The operations and definitions of $E$ are as follows:

(1)

Point addition: For different points, $P,Q$, on $E$, the sum of points $P$ and $Q$, denoted as $R=P+Q$, is the point where the line through $P$ and $Q$ intersects the elliptic curve, $E$. If $P=Q$, then $R=P+P=2P$, determined by the intersection of the tangent line of $P$ and $E$.

(2)

Point multiplication: For $E$; point $P$; and an integer, $d$, satisfying $d\ge 1$, $dP$ is defined as point $P$ added $d$ times; that is, $dP=P+\cdots +P$.

Based on the above group operation, the elliptic curve discrete logarithm problem (ECDLP) can be constructed. As shown in the following difficult problem, the difficulty of solving the ECDLP makes it possible to build a public key cryptosystem: select a base point, G, with order n on the elliptic curve group, E, where n is a very large prime number. The user randomly selects an integer, $k\in [1,n-1]$, as the private key and then calculates the point such that $P=kG$. $P$ is the public key of the user. Even if the attacker knows the public key, $P,$ and base point, G, the private key, $k$, cannot be calculated through an effective algorithm because it needs to solve ECDLP. Furthermore, ECC requires a much smaller key size when providing the same security level. This gives ECC a significant advantage in environments with limited computing power, storage space, and bandwidth (such as IoV and blockchain).

2.2. Difficult Problem

Based on the definition of elliptic curve cryptography, consider $G=\{\left(x,y\right)\in E/x,y\in F_q\}\cup \{O\}; G$ is an additive cyclic group. If $P\in E\left(F_q\right)$, it is a generator of the group. There are the following definitions.

(1)

Elliptic curve discrete logarithmic problem (ECDLP): For a given point, $X,aX$, where $X\in G$ and $a\in Z_q^{\ast }$, it is computationally difficult to find $a$. For sufficiently small numbers, ϵ, the probability that a probabilistic polynomial time-constrained $\left(PPT\right)$ adversary, $\mathcal{C}$, can solve ECDLP is negligible.

(2)

Elliptic curve computational Diffie–Hellman (ECCDH): For a given $P,X=aP,Y=bP$, i.e., a tuple $\left(P,aP,bP\right)$, where $a,b\in Z_q^{\ast }$, the ECCDH problem is to compute $abP$. For a sufficiently small number, $ϵ$, any $PPT$ adversary, $\mathcal{C}$, can solve ECDDH with negligible probability.

2.3. Blockchain

Blockchain is a decentralized, distributed ledger technology that operates on a P2P network. It securely records transactions and data, characterized by decentralization, immutability, and transparency. It can establish a reliable record of transactions between distrusting parties. Through a consensus mechanism, different nodes can reach a consensus on the order and status of transactions, ensuring the stability of the entire network. Common consensus mechanisms include Proof of Work (PoW), Proof of Stake (PoS), Delegated Proof of Stake (DPoS), Practical Byzantine Fault Tolerance (PBFT), and Proof of Reputation (PoR) [23].

Structurally, a blockchain consists of blocks linked in chronological order. Each block contains a batch of transaction data, a timestamp, and the hash value of the previous block, forming an irreversible data chain. This structure combines advanced technologies such as cryptography, distributed data storage, smart contracts, and consensus mechanisms to ensure data integrity and source authentication, further enhancing the security and credibility of the system.

2.4. Security Model

According to the description of the security model in [24], the attacker is denoted as $\mathcal{A}$ and can be divided into two types: type I ${(\mathcal{A}}_1$) and type II ${(\mathcal{A}}_2)$. ${\mathcal{A}}_1$ can obtain the master private key of a KGC and calculate the partial private key of EVs, but it cannot modify the public key of EVs. Conversely, ${\mathcal{A}}_2$ can replace the public key of EVs with a specified value but cannot obtain the master private key of the KGC. Challenger $\mathcal{C}$ will interact with ${\mathcal{A}}_1$ and ${\mathcal{A}}_2,$ respectively, in what are called Game I and Game II.

$\mathcal{A}$ is an active attacker with the capabilities of eavesdropping, tampering, and replaying, which can be used to carry out active attacks. The game between challenger $\mathcal{C}$ and attacker $\mathcal{A}$ can be divided into three stages: the start of the game, the game process, and the end of the game. Concretely, the following security goals should be considered in our proposed scheme:

• Confidentiality: Data transmitted by EVs is kept secret from attackers; even eavesdroppers cannot access its contents. Only authorized entities can access it.
• Integrity: This ensures that data signed by EVs has not been modified during V2V power trading.
• Authentication: Any attempt by an attacker to modify transmitted data should be detected, ensuring that only authorized entities can access the transmitted data.
• Non-repudiation: This prevents EVs from repudiating previously sent data. If accepted by a communicating entity, this action cannot be denied.

3. Scheme Design and Realization

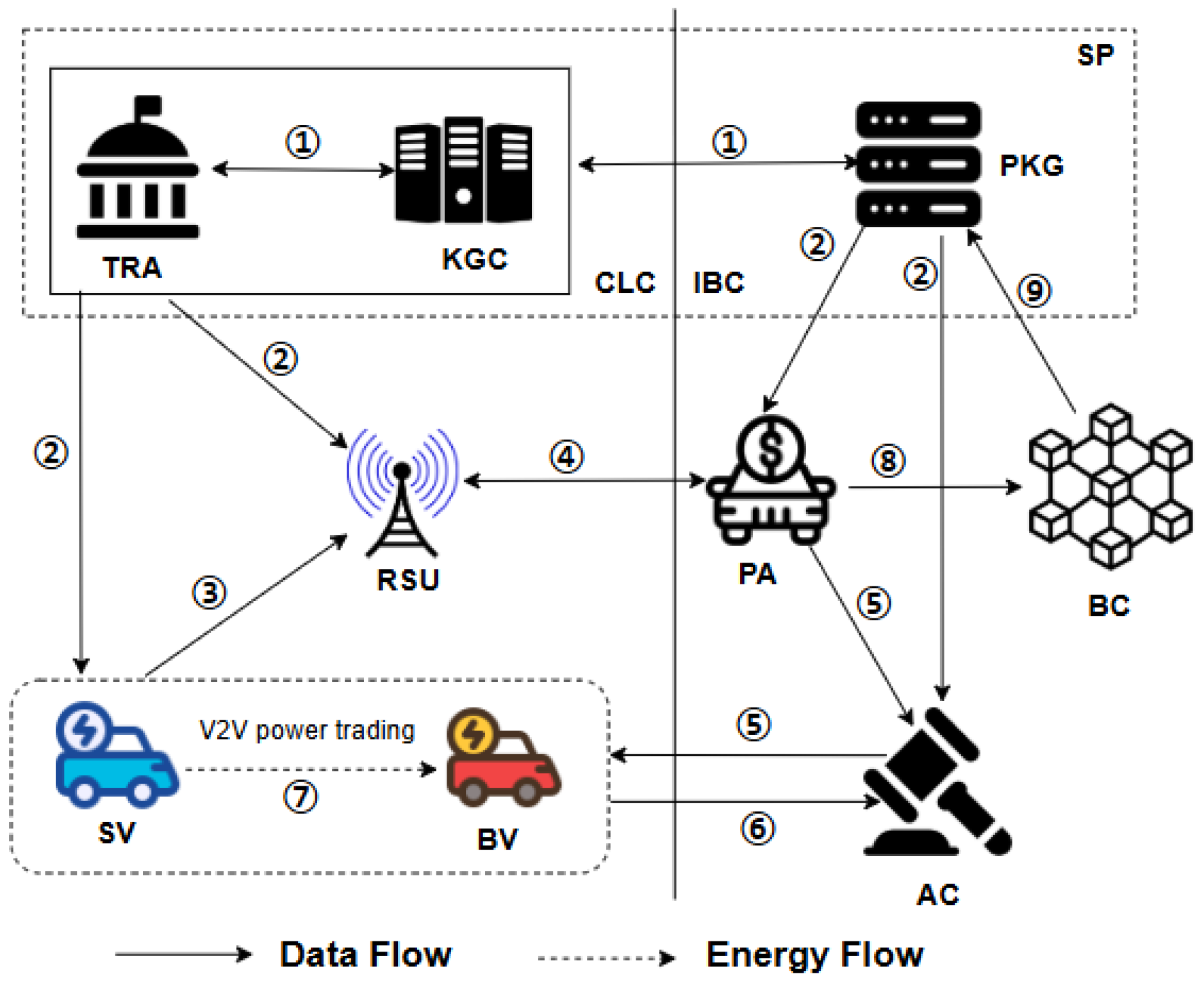
3.1. Scheme Overall Design Framework

3.1.1. Scheme Design Ideas

In order to ensure the security of heterogeneous communication between entities in IoV, a heterogeneous signcryption algorithm is designed. To protect the privacy of users’ real identities, the scheme utilizes pseudonyms to facilitate communication in cryptographic systems. Thus, EVs can submit transaction plans using pseudonyms. Furthermore, due to the constrained computational capabilities of the OBU, ECC is selected over bilinear pairing operations to minimize computational cost and improve overall efficiency. Finally, the verification algorithm is given to verify information and ensure that EV users exhibiting malicious behavior can be tracked and revoked.

3.1.2. Scheme Model

EVs are divided into BVs and the SVs in our proposed scheme. They transmit electricity plans to the nearest RSUs via IoV. The RSUs then aggregate these plans, which are then received by the PA. The PA initially matches the trading plans based on the principle of price priority. If successful, the results are forwarded to the AC for collection. The AC notifies the BV of the results, and then, the BV selects a suitable SV and notifies the PA via the AC. Based on location information, EVs arrive at the designated location to execute a transaction. Once the transaction is complete, the PA reaches consensus on the transaction information and uploads it to the BC for review. Figure 1 shows the design of the system model of V2V power trading.

Table 1. The meaning of the transaction symbols.

Symbol	Meaning
SP	Service provider
KGC	Key generation center
TRA	Trust regulatory authority
PKG	Private key generator
BV/SV	Buyer/seller electric vehicle
RSU	Roadside units
PA	Platform agent
AC	Auction center
BC	Blockchain

shows the meaning of the transaction symbols. The system primarily consists of the following key entities.

SP: A service provider, including the TRA, KGC, and PKG, responsible for providing system parameters and registration services to various entities. The KGC and TRA belong to the CLC cryptographic system, while the PKG belongs to the IBC cryptographic system.

TRA: A fully trusted authority responsible for registering RSUs and EVs in the system and generating some of the system’s public parameters. It also has a list of real EV identities and supervises EVs in conjunction with the KGC.

KGC: A partially trusted entity responsible for generating partial private keys and pseudonyms for EVs and owning their pseudonym list.

PKG: Generates public and private keys for the PA and AC.

EVs: These are divided into BVs and SVs, equipped with a bidirectional charging and discharging system and an OBU, with limited computing and storage capabilities, and can communicate wirelessly with the RSU within a range of 300 m to transmit relevant information to the RSU [25]. They are also equipped with smart meters to record transaction volume.

RSUs: A key component of IoV, these are semi-trusted entities typically located along roadsides or at intersections. They offer far superior computing power, information storage, and attack resistance than OBUs. They utilize wireless channels for high-speed communication with OBUs, providing services to EVs on the road. Acting as a communication intermediary between PA and EVs, they aggregate and forward EV signcrypted information to the PA to improve efficiency.

PA: As the organizer of V2V power trading, this verifies the authenticity and legitimacy of the information, collects transaction plans for preliminary matching, and transmits the transaction results to the AC. It also acts as a node in the blockchain and participates in consensus.

AC: This collects the initial list of matched transactions from the PA. If a BV wins an auction among multiple SVs, the AC creates a winning set and transmits it to the BV. The BV selects the SV it intends to trade with, and then, the AC notifies both parties of the transaction plan.

BC: This stores transaction records in a distributed manner for query by EVs, the PA, and the SP.

3.1.3. Scheme Execution Process

According to the above entities and system model, Figure 1, the timing diagram of the scheme is designed, as shown in Figure 2, and the specific execution process of each stage is provided.

(1)

The TRA, KGC, and PKG generate master keys and system parameters.

(2)

The TRA combines the KGC to generate keys for the RSU, and the PKG generates keys for the PA and AC. The EVs send their real identities to the TRA, which maintains the list, $R_l$; generates pseudonyms; and sends them to the KGC. The KGC generates partial private keys for them and maintains the pseudonym list, $P_l$, to supervise the pseudonyms. The EVs combine their own secret values and partial private keys to generate their own public and private keys.

(3)

The EVs signencrypt their own transaction plans and send them to the surrounding RSUs.

(4)

The RSU validates the collected information, consolidates it, and forwards it to the PA. The PA verifies the authenticity and legitimacy of the aggregated information and decrypts it to obtain the specific transaction plan. The PA then calls the smart contract deployed in the BC and independently determines the winning SV based on the principle of price priority. Finally, the initial list of matched transactions is forwarded to the AC.

(5)

The AC collects auction information through the PA and obtains the initial list of matched transactions. If a BV wins the auction out of multiple SVs, the AC creates a winner set and transmits it to the corresponding BV for the final selection.

(6)

The BV selects the intended SV from the winner set for the transaction. After receiving the transaction plan selected by the BV, the AC deletes the remaining results from the set and sends the plan to the PA.

(7)

The successfully matched pair of EVs conducts the transaction based on the agreed-upon transaction information, including price, volume, and location.

(8)

Upon transaction completion, both EVs sign the record and submit it to the PA. The PA then validates the record via a consensus algorithm. Once consensus is achieved, the record is uploaded to the BC for review by the EVs, PA, and TRA.

(9)

If the TRA receives a complaint, it will check the electricity transactions on the BC to identify malicious EVs and then combine with the KGC to track the real identity and revoke its participation qualification.

3.1.4. Scheme Symbol Definition

Based on Figure 1 and Figure 2, the symbols and definitions involved in the scheme are as follows in

Table 2. The symbols and definitions in the scheme.

Symbol	Meaning
$\mathrm{SP}\oplus$	Bitwise XOR operation
$H_i$	One-way secure hash function
$q,P$	Order and generators of group G
$Z_q^{\ast }$	The set of positive integers smaller than q
$E$	Elliptic curves over finite fields
$G$	$\mathrm{Cyclic} \mathrm{groups} \mathrm{of} \mathrm{order} q$$\mathrm{defined} \mathrm{on} E$
$\lambda$	System security parameter
$k,P_{pub}$	KGC’s master private key and public key
$k_t,T_{pub}$	TRA’s master private and public key
$k_p,P_1$	PKG master key and public key
$I{D}_i,P_{I{D}_i}$	$\mathrm{The} \mathrm{real} \mathrm{identity} \mathrm{and} \mathrm{pseudonym} \mathrm{of} \mathrm{the} E{V}_i$
$S{K}_{I{D}_i}=\left(a_{I{D}_i},b_{I{D}_i}\right)$	$\mathrm{The} \mathrm{private} \mathrm{key} \mathrm{of} E{V}_i$
$P{K}_{I{D}_i}=\left(C_{I{D}_i},D_{I{D}_i}\right)$	$\mathrm{The} \mathrm{public} \mathrm{key} \mathrm{of} E{V}_i$
$m_i$	Electricity transaction information
${m_i}^{\prime }$	Heterogeneous signcryption information
M	Aggregated signcryption information

.

3.2. Scheme Detailed Realization

3.2.1. System Parameter Setting

Given the system security parameter, $\mathsf{\lambda }$, KGC selects a large prime number, $\mathrm{p},\mathrm{q}>2^{\mathsf{\lambda }}$, and assumes $\mathrm{G}=⟨\mathrm{P}⟩$ is an additive cyclic group of order $\mathrm{q}$ on $\mathrm{E}$. The KGC selects a random number, $\mathrm{k}\in {\mathrm{Z}}_{\mathrm{q}}^{\ast }$; calculates ${\mathrm{P}}_{\mathrm{p}\mathrm{u}\mathrm{b}}=\mathrm{k}\mathrm{P}$; and selects five secure hash functions: ${\mathrm{H}}_0:\{\mathrm{0,1}{\}}^{\ast }\times \mathrm{G}\to {\mathrm{Z}}_{\mathrm{q}}^{\ast }$, ${\mathrm{H}}_1:\mathrm{G}\times \{\mathrm{0,1}{\}}^{\ast }\to \{\mathrm{0,1}{\}}^{\ast }$, ${\mathrm{H}}_2:\{\mathrm{0,1}{\}}^{\ast }\times \mathrm{G}\times \mathrm{G}\to {\mathrm{Z}}_{\mathrm{q}}^{\ast }$, ${\mathrm{H}}_3:\mathrm{G}\to {\mathrm{Z}}_{\mathrm{q}}^{\ast }$, ${\mathrm{H}}_4:\{\mathrm{0,1}{\}}^{\ast }\times \{\mathrm{0,1}{\}}^{\ast }\times \mathrm{G}\times \{\mathrm{0,1}{\}}^{\ast }\to {\mathrm{Z}}_{\mathrm{q}}^{\ast }$. The TRA selects a random number, ${\mathrm{k}}_{\mathrm{t}}\in {\mathrm{Z}}_{\mathrm{q}}^{\ast }$, and calculates ${\mathrm{T}}_{\mathrm{p}\mathrm{u}\mathrm{b}}={\mathrm{k}}_{\mathrm{t}}\mathrm{P}$. In addition, the PKG selects a random number, ${\mathrm{k}}_{\mathrm{p}}\in {\mathrm{Z}}_{\mathrm{q}}^{\ast }$, and calculates ${\mathrm{P}}_1={\mathrm{k}}_{\mathrm{p}}\mathrm{P}$. Then, it publishes the system public parameters: $\{\mathrm{G},\mathrm{P},\mathrm{q},\mathrm{E},{\mathrm{P}}_{\mathrm{p}\mathrm{u}\mathrm{b}},{\mathrm{T}}_{\mathrm{p}\mathrm{u}\mathrm{b}},{\mathrm{P}}_1,{\mathrm{H}}_{\mathrm{i}}\}$.

3.2.2. PA and AC Registration (IBC)

The PA and AC are the receivers of the IBC cryptographic system and need to send their real identity information to the PKG for registration. Here, we will take PA registration as an example, and AC registration is the same. After receiving it, the PKG verifies the legitimacy of the identity and selects a random number, $k_{PA}\in Z_q^{\ast }$; calculates ${P_{PA}=k}_{PA}P$ and $h_{PA}=H_0\left(I{D}_{PA},P_{PA}\right)$; and then calculates the private key, $s_{PA}=k_{PA}+k_p{h}_{PA}$, and obtains the public key, ${\mathrm{p}}_{PA}=s_{PA}P=P_{PA}+P_1{h}_{PA}$, and sends $\left(p_{PA},s_{PA}\right)$ to the PA through a secure channel.

3.2.3. EVs and RSU Registration (CLC)

EVs participating in V2V power trading must first register to obtain authorization. To ensure the anonymity of the information transmitted during V2V transactions, the TRA will generate a pseudonym for EVs before they join the system.

$\mathrm{E}{\mathrm{V}}_{\mathrm{i}}$ selects a random number, ${\mathrm{r}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}\in {\mathrm{Z}}_{\mathrm{q}}^{\ast }$; calculates ${\mathrm{R}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}={\mathrm{r}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}\mathrm{P}$; and sends $\left(\mathrm{I}{\mathrm{D}}_{\mathrm{i}},{\mathrm{R}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}\right)$ to the TRA. The TRA checks whether it is in the list, ${\mathrm{R}}_{\mathrm{l}}=\{\mathrm{I}{\mathrm{D}}_1,\mathrm{I}{\mathrm{D}}_2,\dots ,\mathrm{I}{\mathrm{D}}_{\mathrm{n}}\}$. If so, it rejects the request. Otherwise, the TRA obtains the current time, ${\mathrm{t}}_{\mathrm{i}}$; selects a random number ${\mathrm{x}}_{\mathrm{i}}\in {\mathrm{Z}}_{\mathrm{q}}^{\ast }$; calculates ${\mathrm{X}}_{\mathrm{i}}={\mathrm{x}}_{\mathrm{i}}\mathrm{P}$ and sets ${\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},1}}={\mathrm{R}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}$ and ${\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},2}}=\mathrm{I}{\mathrm{D}}_{\mathrm{i}}\oplus {\mathrm{H}}_1\left({\mathrm{k}}_{\mathrm{t}}{\mathrm{R}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}},{\mathrm{P}}_{{\mathrm{R}\mathrm{S}\mathrm{U}}_{\mathrm{i}}}{\mathrm{t}}_{\mathrm{i}}\right)$; and obtains the pseudonym ${\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}=\left({\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},1}},{\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},2}},{\mathrm{t}}_{\mathrm{i}}\right)$. The TRA sends the pseudonym to the KGC. After receiving it, the KCG will maintain a pseudonym list, ${\mathrm{P}}_{\mathrm{l}}$; supervise the pseudonym; and execute the partial key generation algorithm: Firstly, we select a random number,$k_{I{D}_i}\in Z_q^{\ast }$, and calculate $D_{I{D}_i}=k_{I{D}_i}P$. Then, let $h_{I{D}_i}=H_2\left(P_{I{D}_i}{,D}_{I{D}_i},P_{pub}\right)$, and calculate ${ b}_{I{D}_i}=\left(k_{I{D}_i}+h_{I{D}_i}k\right)mod q$. The KGC takes the partial key, $\left(b_{I{D}_i},D_{I{D}_i}\right)$.

The KGC sends the partial key, $\left(b_{I{D}_i},D_{I{D}_i}\right)$, to the TRA. The TRA sends $\left(b_{I{D}_i},D_{I{D}_i},X_i,t_i\right)$ to $E{V}_i$. $E{V}_i$ calculates $P_{I{D}_{i,1}}=r_{I{D}_i}{X}_i$ and $P_{I{D}_{i,2}}=I{D}_i\oplus H_1\left({r_{I{D}_i}T}_{pub},{P_{{RSU}_i},t}_i\right)$, obtains pseudonym $P_{I{D}_i}=\left(P_{I{D}_{i,1}},P_{I{D}_{i,2}},t_i\right)$, calculates $h_{I{D}_i}=H_2\left(P_{I{D}_i},D_{I{D}_i},P_{pub}\right)$, and determines whether $b_{I{D}_i}P=D_{I{D}_i}+h_{I{D}_i}{P}_{pub}$ holds. If not, $E{V}_i$ will regenerate; otherwise, a key generation algorithm is executed to obtain its own public and private key. Firstly, based on the known real identity, $\mathrm{I}{\mathrm{D}}_{\mathrm{i}}$, and partial key, $\left({\mathrm{b}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}},{\mathrm{D}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}\right)$, we select a random number, $a_{I{D}_i}\in Z_q^{\ast }$, and calculate $A_{I{D}_i}=a_{I{D}_i}P$ and $C_{I{D}_i}=A_{I{D}_i}+D_{I{D}_i}$. The private key is $S{K}_{I{D}_i}=\left(a_{I{D}_i},b_{I{D}_i}\right),$ and the public key is $P{K}_{I{D}_i}=\left(C_{I{D}_i},D_{I{D}_i}\right)$.

The RSU registration process is similar. However, since EVs use pseudonyms for communication, there is no need to generate pseudonyms for the RSU at the same time. Therefore, the RSU’s public and private key generation process can be simplified. The specific process is the same as above. The private and public key of the RSU is $\left(a_{RS{U}_i},b_{RS{U}_i}\right)$ and $P_{RS{U}_i}=\left(C_{RS{U}_i},D_{RS{U}_i}\right)$; then, we publish the public key information of the RSU.

3.2.4. EVs Generate Heterogeneous Signcryption

During the V2V power trading process, EVs conduct buying and selling transactions based on their own needs and formulate their own transaction plan information, $m_i$, including the amount of electricity to be bought/sold, the expected purchase and sale price of electricity, their own location, etc. To ensure the privacy of the information, heterogeneous signcryption of $m_i$ is required before EV transmission, and then, it is forwarded to the nearby RSU after signcryption.

$E{V}_i$ chooses $y_i\in Z_q^{\ast }$; calculates $Y_i=y_{i}P$; and generates the current timestamp, $T_{i,1}\in \{0,1{\}}^{\ast }$. Then, it calculates $U_i=m_i\oplus H_3\left(y_i{p}_{PA}\right)$ and ${ h}_4=H_4\left(U_i,P_{I{D}_i},P{K}_{I{D}_i},T_{i,1}\right)$ and gets the value of $V_i=y_i+\left(b_{I{D}_i}+r_{I{D}_i}\right)h_4$. So, the final signcryption information is $m_i^{\prime }=\left(U_i,V_i,Y_i\right)$, and it sends a ciphertext, $\{m_i^{\prime },T_{i,1},P_{I{D}_i},P{K}_{I{D}_i},U_i\}$, to the nearby RSU through wireless radio transmission.

3.2.5. RSU Generate Aggregated Signcryption

When the RSU receives the signcryption information of $n$ EVs within a certain period, it first generates the current timestamp, $T_{i,1}^{\ast }$, and calculates $\left|T_{i,1}^{\ast }-T_{i,1}\right|$ to check if it is $\le ∆T$. If this is satisfied, it is within the validity period. It also checks whether the pseudonym $P_{I{D}_i}$ has expired and is in $P_l$. If it has not expired and is not in $P_l$, the value of $n$ is judged. If $n=1$, a single signcryption verification algorithm is executed to perform a single signcryption verification: firstly, we calculate ${{\mathrm{h}}^{\prime }}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}={\mathrm{H}}_2\left({\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}}{,\mathrm{D}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}},{\mathrm{P}}_{\mathrm{p}\mathrm{u}\mathrm{b}}\right)$ and ${{\mathrm{h}}^{\prime }}_4={\mathrm{H}}_4\left({\mathrm{U}}_{\mathrm{i}},{\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}},\mathrm{P}{\mathrm{K}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i}}},{\mathrm{T}}_{\mathrm{i},1}\right)$. Then, we determine whether Equation (1) holds true:

$$V_{i}P=Y_i+\left(D_{I{D}_i}+{h^{\prime }}_{I{D}_i}{P}_{pub}+R_{I{D}_i}\right){h^{\prime }}_4$$

(1)

If Equation (1) is established, it indicates that the RSU verification is passed; otherwise, it will be rejected. If $n>1$, the RSU will aggregate the received $n$ pieces of information into an aggregated ciphertext.

The process of aggregation signcryption employs the small exponential test technique [26]. The RSU selects a random number, $s,$ that is small enough to calculate $V={\sum }_{i=1}^n{c}_i{V}_i$, where $c_i=\{c_1,c_2,\dots ,c_n\}$ and $c_i\in \left[1,2^s\right]$. The RSU will obtain the aggregated signcryption information, $M=\{U_1,U_2,\dots ,U_n,V,Y_1,Y_2,\dots ,Y_n\}$ and then send the aggregated signcryption information, $M$, together with $\{P_{I{D}_i},P{K}_{I{D}_i},T_{i,1},U_i\}$, to the PA.

3.2.6. PA Verification and Decryption

The PA receives the aggregated signcryption information from the RSUs in each region and checks its validity as above. If it passes, it executes the aggregated signcryption verification algorithm to batch-verify whether the signcryption is valid. Firstly, we calculate ${h^{\prime }}_{I{D}_i}=H_2\left(P_{I{D}_i}{,D}_{I{D}_i},P_{pub}\right)$ and ${h^{\prime }}_{4,i}=H_4\left(U_i,P_{I{D}_i},P{K}_{I{D}_i},T_{i,1}\right)$. Then, we calculate whether Equation (2) holds true:

$$VP={\mathsf{\Sigma }}_{i=1}^n{c}_i{Y}_i+\left({\mathsf{\Sigma }}_{i=1}^n{c}_i{h^{\prime }}_{I{D}_i}{h^{\prime }}_{4,i}\right)P_{pub}+{\mathsf{\Sigma }}_{i=1}^n{c}_i\left(D_{I{D}_i}+R_{{ID}_i}\right){h^{\prime }}_{4,i}$$

(2)

If Equation (2) holds, it means that the aggregate signcryption verification is successful; otherwise, it is rejected. If batch verification is invalid, all ciphertexts are deleted and re-verified, which is too inefficient. In this case, a recursive divide-and-conquer method [27] is used to track invalid or illegal signcryption. If the verification is successful, the received ciphertext is decrypted according to Equation (3) to obtain the plan information

$$m_i=U_i\oplus H_3\left(Y_i{s}_{PA}\right)$$

(3)

3.2.7. V2V Transaction Matching

After the PA successfully decrypts, V2V electricity transaction matching is carried out. The matching winner is determined based on the price priority principle to satisfy the supply and demand of both EVs. Firstly, we mark BV and SV as $\left(i,S_{b{v}_i},P_{b{v}_i},L_{b{v}_i}\right)$ and $(j,S_{s{v}_j},P_{s{v}_j},L_{s{v}_j}),$ respectively, and match them according to the power relationship between the buyer and seller ($S_{b{v}_i},S_{s{v}_j}$) and the bid price ${(P}_{b{v}_i}{,P}_{s{v}_j})$. On the basis of satisfying $S_{b{v}_i}$ and $S_{s{v}_j}$, bidding is conducted according to the principle of price priority. Smart contracts are sorted from small to large according to $P_{sv}$ and from large to small according to $P_{bv}$. According to the relationship between power consumption and sorting, the valid result set is determined. For the detailed process, refer to [28]. If EVs fail to win the bid, they can adjust their bid prices and participate again. The PA then sends all valid result sets to the AC. Upon a BV winning multiple SV auctions, the AC is responsible for creating a winning result set for it and determines the appropriate transaction location based on the positional relationship between $L_{sv}$ and $L_{bv}$ and forwards it to both EVs. The BV independently selects the SV it intends to trade with. The AC first determines the transaction plan. It then deletes all results that the BV did not select and reports this updated plan to the PA. Finally, the EVs arrive at the transaction location for the V2V power trading.

3.2.8. Transaction Consensus and Upload

When the EV transaction between the two parties is completed, the transaction information is confirmed, including the transaction power, transaction price, end time, etc. The final signature is sent to the PA to complete the consensus. The PBFT consensus algorithm is used. The detailed process is referenced in [29]. After the consensus is completed, the transaction information is packaged, a new block is generated, and the information is uploaded to the BC.

3.2.9. Malicious EV Tracking and Revocation

To ensure user privacy during the communication process between entities, EVs use pseudonyms to signcrypt electricity information. When EVs display malicious behavior, such as fraud or attack, their real identities should be tracked, and malicious attackers can be disqualified. The TRA can calculate Equation (4) to trace the real identity of EVs based on its own private keys and pseudonyms.

$$I{D}_i=P_{I{D}_{i,2}}\oplus H_1\left(k_t{X}_i,P_{{RSU}_i},t_i\right)$$

(4)

Then, the TRA stores the real identity, $I{D}_i$, of EVs to be revoked in the list, $R_l=\{I{D}_1,I{D}_2,\dots ,I{D}_n\}$, and sends its corresponding pseudonym to the KGC; the KGC stores it in the pseudonym list, $P_l$, and regularly transmits it to the PA for reporting, at which time, it will provide services for it again. In addition, the TRA can know the real identities but not obtain the transaction information of EVs, which will not threaten user privacy.

4. Scheme Analysis

4.1. Correctness

(1)

The proof of correctness of the partial private keys is shown in Equation (5):

$$b_{I{D}_i}P={(k}_{I{D}_i}+h_{I{D}_i}k)P=D_{I{D}_i}+h_{I{D}_i}{P}_{pub}$$

(5)

(2)

The proof of correctness of the single signcryption verification is as follows, as shown in Equation (6):

$$\begin{array}{cc}\hfill V_{i}P & ={(y}_i+\left(b_{I{D}_i}+r_{I{D}_i}{)h}_4\right)P\hfill \\ & ={(y}_i+({(k}_{I{D}_i}+h_{I{D}_i}k)+r_{I{D}_i}{)h}_4)P\hfill \\ & =Y_i+\left(D_{I{D}_i}+h_{I{D}_i}{P}_{pub}+R_{I{D}_i}\right)h_4 \hfill \end{array}$$

(6)

(3)

The proof of correctness of the aggregated signcryption verification is as follows, as shown in Equation (7):

$$\begin{array}{cc}\hfill VP& ={\mathsf{\Sigma }}_{i=1}^n{c}_i{V}_{i}P\hfill \\ & ={\mathsf{\Sigma }}_{i=1}^n{c}_i\left(y_i+b_{I{D}_i}+r_{I{D}_i}\right){h^{\prime }}_{4,i}P\hfill \\ & ={\mathsf{\Sigma }}_{i=1}^n{c}_i\left(y_i+\left(k_{I{D}_i}+{h^{\prime }}_{I{D}_i}k\right)+r_{I{D}_i}\right){h^{\prime }}_{4,i}P \hfill \\ & ={\mathsf{\Sigma }}_{i=1}^n{c}_i{Y}_i+\left({\mathsf{\Sigma }}_{i=1}^n{c}_i{h^{\prime }}_{I{D}_i}{h^{\prime }}_{4,i}\right)P_{pub}+{\mathsf{\Sigma }}_{i=1}^n{c}_i\left(D_{I{D}_i}+R_{i{d}_i}\right){h^{\prime }}_{4,i}\hfill \end{array}$$

(7)

(4)

The proof of the correctness of the ciphertext decryption is as follows, as shown in Equation (8):

$$\begin{array}{cc}\hfill m_i& =U_i\oplus H_3\left(Y_i{s}_{PA}\right)\hfill \\ & =U_i\oplus H_3\left(y_i{P(k}_{PA}+k_p{h}_{PA})\right)\hfill \\ & =U_i\oplus H_3\left(y_i{(P}_{PA}+P_1{h}_{PA})\right) \hfill \\ & ={ U}_i\oplus H_3\left(y_i{p}_{PA}\right)\hfill \end{array}$$

(8)

(5)

The proof of the correctness of pseudonymous tracking is as follows, as shown in Equation (9):

$$\begin{array}{cc}\hfill {\mathrm{I}\mathrm{D}}_i& ={\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},2}}\oplus {\mathrm{H}}_1\left({\mathrm{k}}_{\mathrm{t}}{X}_i,{\mathrm{P}}_{{\mathrm{R}\mathrm{S}\mathrm{U}}_{\mathrm{i}}}{\mathrm{t}}_{\mathrm{i}}\right)\hfill \\ & ={\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},2}}\oplus {\mathrm{H}}_1\left({\mathrm{k}}_{\mathrm{t}}{x}_{i}P,{\mathrm{P}}_{{\mathrm{R}\mathrm{S}\mathrm{U}}_{\mathrm{i}}}{\mathrm{t}}_{\mathrm{i}}\right)\hfill \\ & ={\mathrm{P}}_{\mathrm{I}{\mathrm{D}}_{\mathrm{i},2}}\oplus {\mathrm{H}}_1\left({\mathrm{x}}_i{T}_{pub},{\mathrm{P}}_{{\mathrm{R}\mathrm{S}\mathrm{U}}_{\mathrm{i}}}{\mathrm{t}}_{\mathrm{i}}\right)\hfill \end{array}$$

(9)

4.2. Security Analysis

4.2.1. Unforgeability

This section will use the ROM to prove two theorems. Under the ROM, the hash function is a random oracle; the attacker can only obtain the relevant output by asking the challenger.

Theorem 1. 

If the $PPT$ adversary, ${\mathcal{A}}_1$, uses the advantage of $ϵ$ to attack this scheme, $\mathcal{C}$ can solve the ECDLP with a non-negligible advantage, ${ϵ}^{\prime };$ that is, it is unforgeable under attacker ${\mathcal{A}}_1$.

Proof of Theorem 1. 

Assume that $\mathcal{C}$ is the challenger of ECDLP. For a given ECDLP example, $(P, D_{I{D}_i}=k_{I{D}_i}P)$, the goal of $\mathcal{C}$ is to solve $k_{I{D}_i}$. $\mathcal{C}$ maintains a series of lists, $L$, and selects ${P_{I{D}_i}}^{\ast }$ as the challenge identity. The interaction proceeds as follows:

Phase 1: $\mathcal{C}$ executes the initialization algorithm and provides the resulting system parameters to ${\mathcal{A}}_1$.

Phase 2: ${\mathcal{A}}_1$ adaptively queries $\mathcal{C}$ multiple times. The specific process is as follows:

$H_2$ queries: When $\mathcal{C}$ receives $H_2\left(P_{I{D}_i}{,D}_{I{D}_i},P_{pub}\right)$ queries from ${\mathcal{A}}_1$ about $P_{I{D}_i}$, $\mathcal{C}$ checks if there is a corresponding tuple in list $L_{H_2}$. If so, it returns $h_{I{D}_i}$ to ${\mathcal{A}}_1$. Otherwise, it randomly selects a random number, $k_{I{D}_i}\in Z_q^{\ast }$, and calculates $D_{I{D}_i}=k_{I{D}_i}P$ and $h_{I{D}_i}=H_2\left(P_{I{D}_i}{,D}_{I{D}_i},P_{pub}\right)$; then, it will add ($P_{I{D}_i}{,D}_{I{D}_i},P_{pub},h_{I{D}_i}$) to list $L_{H_2}$ and return it to ${\mathcal{A}}_1$.

${ H}_3$ queries: When $\mathcal{C}$ receives $H_3\left(y_i{p}_{PA}\right)$ queries from ${\mathcal{A}}_1$ about $P_{I{D}_i}$, if the corresponding tuple exists, it is returned to ${\mathcal{A}}_1$. Otherwise, $\mathcal{C}$ selects a random number, $y_i\in Z_q^{\ast }$; calculates $h_3=H_3\left(y_i{p}_{PA}\right)$; adds ($y_i{p}_{PA},h_3$) to $L_{H_3}$; and returns it to ${\mathcal{A}}_1$.

$H_4$ queries: When $\mathcal{C}$ receives $h_4$ queries from ${\mathcal{A}}_1$ about $P_{I{D}_i}$, $\mathcal{C}$ checks if list $L_{H_4}$ contains a tuple, ($U_i,P_{I{D}_i},P{K}_{I{D}_i},T_{i,1}$ ). If so, it returns $h_4$ to ${\mathcal{A}}_1$. Otherwise, $𝒞$ selects a random number, $h_4\in Z_q^{\ast }$ ; adds ($U_i,P_{I{D}_i},P{K}_{I{D}_i},T_{i,1},h_4$ ) to $L_{H_4}$ ; and returns it to ${\mathcal{A}}_1$.

Secret value queries: When $\mathcal{C}$ receives a secret value query from ${\mathcal{A}}_1$ about $P_{I{D}_i}$, it first checks whether ${P_{I{D}_i}}^{\ast }=P_{I{D}_i}$ holds. If so, it terminates the query. Otherwise, it checks whether list $L_{sk}$ contains $\left(a_{I{D}_i},b_{I{D}_i},P_{I{D}_i}\right)$. If so, it returns $\left(a_{I{D}_i},b_{I{D}_i}\right)$ to ${\mathcal{A}}_1$. Otherwise, it selects random numbers, $a_{I{D}_i},b_{I{D}_i}\in Z_q^{\ast }$ ; inserts $\left(a_{I{D}_i},b_{I{D}_i},P_{I{D}_i}\right)$ into $L_{sk}$ ; and returns $\left(a_{I{D}_i},b_{I{D}_i}\right)$ to ${\mathcal{A}}_1$.

Public key queries: When $\mathcal{C}$ receives a public key query from ${\mathcal{A}}_1$ about $P_{I{D}_i}$, it checks whether ${P_{I{D}_i}}^{\ast }=P_{I{D}_i}$ holds. If so, it randomly selects $a_{I{D}_i},k_{I{D}_i}\in Z_q^{\ast }$ ; calculates $A_{I{D}_i}=a_{I{D}_i}P,{{ D}_{I{D}_i}=k_{I{D}_i}P,C}_{I{D}_i}=A_{I{D}_i}+D_{I{D}_i}$ ; adds $\left(D_{I{D}_i},C_{I{D}_i},P_{I{D}_i}\right)$ to list $L_{pk}$ ; and returns it to $\mathcal{A}$. If not, it checks whether $\left(D_{I{D}_i},C_{I{D}_i},P_{I{D}_i}\right)$ is in $L_{pk}$. If so, it returns $\left(D_{I{D}_i},C_{I{D}_i}\right)$ to ${\mathcal{A}}_1$. If not, it executes the secret value queries and $H_2$ queries to obtain $a_{I{D}_i},b_{I{D}_i}$ and $h_{I{D}_i}$, calculates $A_{I{D}_i}=a_{I{D}_i}P$ and $D_{I{D}_i}=b_{I{D}_i}P-h_{I{D}_i}{P}_{pub}$ to get $C_{I{D}_i}$, and finally returns $\left(D_{I{D}_i},C_{I{D}_i}\right)$ to ${\mathcal{A}}_1$ and adds $\left(D_{I{D}_i},C_{I{D}_i},P_{I{D}_i}\right)$ to $L_{pk}$.

Signcryption queries: When $\mathcal{C}$ receives a signcryption query from ${\mathcal{A}}_1$ about $m_i$, it first checks whether ${P_{I{D}_i}}^{\ast }=P_{I{D}_i}$ holds. If so, it executes the secret value queries to obtain $\left(a_{I{D}_i},b_{I{D}_i}\right)$, randomly selects $y_i\in Z_q^{\ast }$, and calculates $Y_i=y_{i}P$. It then executes $H_3,H_4$ queries to obtain $h_3,h_4$, calculates $U_i=m_i\oplus h_3$, randomly selects $r_{I{D}_i}\in Z_q^{\ast }$, calculates $V_i=y_i+\left(b_{I{D}_i}+r_{I{D}_i}\right)h_4$, adds the signcryption information $m_i^{\prime }=\left(U_i,V_i,Y_i\right)$ to $L_s$, and returns it to ${\mathcal{A}}_1$. Otherwise, it generates the signcryption through the private key.

Phase 3: Through phases 1 and 2, ${\mathcal{A}}_1$ outputs valid signcryption information, $m_i^{\prime }=\left(U_i,{V^{\prime }}_i,Y_i\right)$, where $V^{\prime }$ satisfies $V_{i}P=Y_i+\left(D_{I{D}_i}+{h^{\prime }}_{I{D}_i}{P}_{pub}+R_{I{D}_i}\right){h^{\prime }}_4$. According to the bifurcation theorem [30], ${\mathcal{A}}_1$ can find more signcryption information, $m_i^{″}$ =$\left(U_i,V_i^{\ast },Y_i\right)$, that satisfies $V_i^{″}P=Y_i+\left(D_{I{D}_i}+{h^{\prime }}_{I{D}_i}{P}_{pub}+R_{I{D}_i}\right)h_4^{″}$, so we can find $\mathsf{ϵ}=\left(V_i^{″}-V_i^{\prime }\right)/\left(h_4^{″}-h_4^{\prime }\right)-k_{I{D}_i}-k{h}_{I{D}_i}^{\prime }$ so that ${\mathcal{A}}_1$ can solve the ECDLP problem with this advantage. □

Theorem 2. 

Unforgeability under attacker ${\mathcal{A}}_2.$

Proof of Theorem 2. 

$\mathcal{C}$ is the challenger; $\left(G,P,P_{pub}=kP\right)$ is the input of the hard problem, where $k\in Z_q^{\ast }$. The goal of ${\mathcal{A}}_2$ is to calculate the value of $k$. The interaction proceeds as follows:

Phase 1: $\mathcal{C}$ executes the initialization algorithm and provides the resulting system parameters to ${\mathcal{A}}_2$.

Phase 2: ${\mathcal{A}}_2$ can initiate random oracle queries for $H_2,H_3,H_4$. This process is the same as the proof of Theorem 1, above. In addition, ${\mathcal{A}}_2$ can also initiate the following queries, where $L_{psk},L_{sk},L_{pk}$ store partial private keys, private keys, and public key information, respectively. The specific process is as follows:

Partial key query: When receiving a partial private key query about ${P_{ID}}^{\ast }$, if ${P_{ID}}^{\ast }=P_{I{D}_i}$, $\mathcal{C}$ stops querying; otherwise, it checks whether $L_{psk}$ exists $\left(b_{I{D}_i},D_{I{D}_i},P_{I{D}_i}\right)$. If so, it returns $\left(b_{I{D}_i},D_{I{D}_i}\right)$ to ${\mathcal{A}}_2$. Otherwise, it randomly selects $k_{I{D}_i},h_{I{D}_i}\in Z_q^{\ast }$, then calculates ${ b}_{I{D}_i}=k_{I{D}_i}+h_{I{D}_i}k, D_{I{D}_i}=k_{I{D}_i}P$, inserts $\left(b_{I{D}_i},D_{I{D}_i},P_{I{D}_i}\right)$ into $L_{psk}$, and returns $(b_{I{D}_i},D_{I{D}_i})$ to ${\mathcal{A}}_2$.

Private key query: When receiving a private key query about ${P_{ID}}^{\ast }$, if ${P_{ID}}^{\ast }=P_{I{D}_i}$, $\mathcal{C}$ stops querying; otherwise, it checks $L_{sk}$. If $\left(P_{I{D}_i},b_{I{D}_i},a_{I{D}_i}\right)$ exists in it, it returns $\left(b_{I{D}_i},a_{I{D}_i}\right)$ to ${\mathcal{A}}_2$. Otherwise, it randomly selects $a_{I{D}_i}\in Z_q^{\ast }$, obtains $b_{I{D}_i}$ through partial key query, and then inserts $\left(P_{I{D}_i},b_{I{D}_i},a_{I{D}_i}\right)$ into $L_{sk}$ and returns $\left(b_{I{D}_i},a_{I{D}_i}\right)$ to ${\mathcal{A}}_2$.

Public key query: When receiving a public key query about ${P_{ID}}^{\ast }$, $\mathcal{C}$ checks $L_{pk}$. If $\left(P_{I{D}_i},D_{I{D}_i},C_{I{D}_i}\right)$ exists in it, it sends $\left(D_{I{D}_i},C_{I{D}_i}\right)$ to ${\mathcal{A}}_2$. If not, $\mathcal{C}$ checks $L_{psk},L_{sk}$ for a record of $P_{I{D}_i}$. If so, it obtains $D_{I{D}_i}$ and $a_{I{D}_i}$ from them, respectively, calculates $A_{I{D}_i}=a_{I{D}_i}P,C_{I{D}_i}=A_{I{D}_i}+D_{I{D}_i}$, and then returns $\left(D_{I{D}_i},C_{I{D}_i}\right)$ to ${\mathcal{A}}_2$. If no relevant record exists, it determines whether ${P_{ID}}^{\ast }=P_{I{D}_i}$. If the equation is satisfied, $\mathcal{C}$ randomly selects $k_{I{D}_i},h_{I{D}_i}\in Z_q^{\ast }$, calculates $D_{I{D}_i}=k_{I{D}_i}P,A_{I{D}_i}=h_{I{D}_i}P$, calculates $C_{I{D}_i}=A_{I{D}_i}+D_{I{D}_i}$, inserts $\left(P_{I{D}_i},D_{I{D}_i},C_{I{D}_i}\right)$ into $L_{pk}$, and returns $\left(D_{I{D}_i},C_{I{D}_i}\right)$ to ${\mathcal{A}}_2$. If the equality does not hold, $\mathcal{C}$ obtains $D_{I{D}_i}$ and $a_{I{D}_i}$ through the above partial key query and private key query, then calculates $A_{I{D}_i}=h_{I{D}_i}P$ obtains $C_{I{D}_i}=A_{I{D}_i}+D_{I{D}_i}$, and then inserts $\left(P_{I{D}_i},D_{I{D}_i},C_{I{D}_i}\right)$ into $L_{pk}$, and $\mathcal{C}$ returns $\left(D_{I{D}_i},C_{I{D}_i}\right)$ to ${\mathcal{A}}_2$.

Public key replacement query: When receiving a public key replacement query regarding ${P_{ID}}^{\ast }$, the tuple in $L_{pk}$ is replaced with $(P_{I{D}_i},{D^{\prime }}_{I{D}_i},{C^{\prime }}_{I{D}_i})$.

Signcryption query: When $\mathcal{C}$ receives a signcryption query, if ${P_{ID}}^{\ast }=P_{I{D}_i}$, the query is terminated. If the equality does not hold, $\mathcal{C}$ obtains the private key of $P_{I{D}_i}$ and runs the signcryption algorithm to generate the ciphertext $\left(U_i,V_i,Y_i\right)$, which is then sent to ${\mathcal{A}}_2$.

Phase 3: ${\mathcal{A}}_2$ generates a forged signcryption $\left({U^{\prime }}_i,{V^{\prime }}_i,{Y^{\prime }}_i\right)$ and sends it to $\mathcal{C}$ to check whether ${P_{ID}}^{\ast }=P_{I{D}_i}$ holds. If not, the forgery stops. Otherwise, the signcryption passes verification. According to the proof of Theorem 1, the value of $\mathsf{ϵ}$ can be calculated. Therefore, ${\mathcal{A}}_2$ can solve the ECDLP with this advantage.

In summary, $\mathcal{C}$ could solve the ECDLP, but this is inconsistent with the fact that the ECDLP cannot be solved. Therefore, our proposed scheme satisfies the unforgeability under the attack of adversaries ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$. □

However, the security analysis of this scheme relies on the ROM, which assumes the existence of an ideal, public “random oracle” that outputs a completely uniformly random response for any new input. However, in practice, this must be instantiated using a specific hash algorithm. Actual hash functions are deterministic, and their outputs merely appear random—that is, they satisfy pseudo-randomness—rather than the perfect randomness required by the ROM. Therefore, it is possible that a scheme proven secure by the ROM may contain vulnerabilities after being instantiated using a specific hash function. Nevertheless, the ROM remains a crucial and widely accepted theoretical tool in cryptography. ROM-based proofs ensure that the scheme itself is flawless. While this proof must exploit specific flaws in real-world hash functions, modern hash functions such as SHA-3 have been reviewed by academics and have not been found to have significant flaws. Therefore, despite relying on the ROM, the scheme still maintains a strong degree of correctness.

4.2.2. Dual System Parameters

The scheme uses different system master keys, which is more secure. If there is a problem with the IBC system and the PKG is attacked, the malicious attacker can obtain the master key of the PKG and the private key of the PA and AC, so that they can decrypt and obtain the transaction information of the EVs. However, because the CLC system is normal, the attacker cannot obtain the key of the TRA, so they cannot know the real identity of the EV and prevent its privacy leakage.

4.2.3. Authentication

In this scheme, EVs must be legally registered to participate in the system and perform subsequent operations to provide guarantees for V2V power trading. The CLC registration process for EVs is given in this paper, so this feature is achieved.

4.2.4. Non-Repudiation and Traceability

In this scheme, EVs sign their transactions when sending information. Only the signer has the private key. Therefore, our proposed scheme achieves non-repudiation of transaction information through digital signature technology. Furthermore, although a pseudonym mechanism is used in the scheme, according to the analysis in Section 3.2.9, the real identity can be tracked and revoked, so this property is achieved.

4.2.5. Resistance to Attacks

(1)

Anti-replay attack: Both pseudonymous and signed information have a timestamp, which can be used to determine whether they have expired, thus resisting replay attacks.

(2)

Anti-tampering attack: Transaction information needs to verify whether Equation (4) is true. Any tampering will ensure that it cannot pass the verification, so it can resist tampering attacks.

(3)

Anti-man-in-the-middle attack: The aggregation process uses the small index test technology, which is known in [30] to be able to resist man-in-the-middle attacks during batch verification.

To further analyze the solution’s security against potential attacks, simulation tests were conducted using the scyther (v1.1.3) formal security analysis tool. scyther is an automated security protocol analysis tool based on the Dolev–Yao attack model [31]. Attackers have the ability to obtain, eavesdrop, modify, delete, and resend messages and perform impersonation attacks, specifying EVs and RSUs as the two parties involved in verification. The scyther running results are shown in Figure 3, below. No potential attacks were detected during the communication process, indicating that the solution effectively protects against potential threats.

4.3. Privacy Analysis

4.3.1. Information Confidentiality and Integrity

EVs perform a signcryption operation on the power information, $m_i$, to obtain $m_i^{\prime }=\left(U_i,V_i,Y_i\right)$. Only the PA decrypts the ciphertext with its own private key. Under the ECDLP, the scheme achieves confidentiality. In addition, the RSU verifies whether Equation (1) is true to determine whether the information has been tampered with or forged, thus satisfying the integrity.

4.3.2. Anonymity

During the entire power information transmission process, EVs use two pseudonyms, $P_{I{D}_{i,1}}=R_{I{D}_i}$, $P_{I{D}_{i,2}}=I{D}_i\oplus H_1\left(k_t{R}_{I{D}_i},P_{{RSU}_i}, t_i\right)$, to communicate with other entities, and the pseudonym stage uses two random secret values, $r_{I{D}_i}$ and $k_t$. According to the ECCDH problem, malicious attackers cannot deduce, and the PA cannot infer the real identity based on the pseudonym. Therefore, except for the TRA and EVs themselves, other entities cannot know their real identity, satisfying anonymity.

4.3.3. Unlinkability

In this scheme, EVs use pseudonyms to transmit their own electricity transaction information, and an arbitrary random number, $T_{i,1},$ is used to sign the information, making it impossible for attackers to link the information of the same EVs. Therefore, there is no correlation between any pseudonym information, satisfying the unlinkability.

5. Performance Analysis

This section presents an analysis of the communication and computational capabilities of our proposed scheme. Furthermore, it provides a comparative performance analysis with those in [18,19,20,21,22].

5.1. Computational Analysis

Consider a bilinear map, $e:G_1\times G_1\to G_2$, with a security level of 80 bits and an elliptic curve, $E :y^2=x^3+ax+b mod p$, with additive cyclic group $G$ and order $q$, where $a,b\in Z_q^{\ast }$. $p,q$ are two large prime numbers, which are of the sizes 160 and 521 bits. Using the same environment as in [32], a computer based on the Linux operating system Ubuntu 20.04.6LTS, with Intel(R) Core (TM)i7-8850U CPU and 8.0 G RAM, is used to operate various cryptographic primitives in the MIRACL library. The symbols, definitions, and running times of each operation are presented in

Table 3. The description and runtime of the relevant operation.

Symbol	Meaning	Running Time (ms)
$T_{bp}$	Biliner pairing operation	4.2110
$T_{b{p}_{pa}}$	Biliner pairing point addition	0.0964
$T_{b{p}_{sm}}$	Biliner pairing scalar multiplication	1.8192
$T_{ec{c}_{pa}}$	Elliptic curve point addition	0.0018
$T_{ec{c}_{sm}}$	Elliptic curve scalar multiplication	0.4420
$T_{mtp}$	Map-to-point hash function	4.4060
$T_m$	Small exponent test technique multiplication operation	0.0278
$T_e$	Modular exponentiation	0.0271

.

Next, we present a detailed analysis of the computational costs associated with the schemes proposed in [18,19,20,21,22] and our proposed scheme. Because the schemes in [18,19,20] are based on bilinear mapping, the computational costs are relatively large. Refs. [21,22] are based on ECC, so the computational cost is relatively small. Ignoring the one-way hash operation with low cost, the signcryption phase in the proposed scheme requires two elliptic curve point multiplication operations. The decryption phase necessitates four-point multiplications and three-point addition operations, as shown in

Table 4. Comparison of security features of each scheme.

Reference	Signcryption (ms)	Single Verification (ms)	Aggregated Verification (ms)	Environment
Ref. [18]	$4T_{b{p}_{sm}}+3T_e$	$4T_{b{p}_{sm}}+2T_{bp}+T_e$	$n(4T_{b{p}_{sm}}+2T_{bp}+T_e)$	CLC → IBC
Ref. [19]	$2T_{b{p}_{sm}}+T_e$	$T_{b{p}_{sm}}+2T_{bp}$	$n{T}_{b{p}_{sm}}+2T_{bp}$	IBC → PKI
Ref. [20]	$T_e+4T_{ec{c}_{sm}}+T_{ec{c}_{pa}}$	$3T_{bp}+T_{ec{c}_{sm}}+T_{ec{c}_{pa}}$	$\left(n+2\right)T_{bp}+n{T}_{ec{c}_{sm}}+3n{T}_{ec{c}_{pa}}$	PKI → IBC
Ref. [21]	$2T_{ec{c}_{sm}}$	$4T_{ec{c}_{sm}}+2T_{ec{c}_{pa}}$	$\left(3n+1\right)T_{ec{c}_{sm}}+2n{T}_{ec{c}_{pa}}$	IBC → PKI
Ref. [22]	$4T_{ec{c}_{sm}}$	$3T_{ec{c}_{sm}}+T_{ec{c}_{pa}}$	$n(3T_{ec{c}_{sm}}+T_{ec{c}_{pa}}$)	CLC → PKI
Our Scheme	$2T_{ec{c}_{sm}}$	$4T_{ec{c}_{sm}}+3T_{ec{c}_{pa}}$	$\left(2n+1\right)T_{ec{c}_{sm}}+3n{T}_m+\left(3n-2\right)T_{ec{c}_{pa}}$	CLC → IBC

. The computational costs of the other schemes were analyzed similarly. The comparison of the computational cost of signcryption and decryption is shown in Figure 4. Although it has no obvious advantage over the scheme in [21], the scheme in [21] is not suitable for the heterogeneous environment of IoV, which will lead to greater privacy risks. In addition, Ref. [22] has a relatively small decryption cost, but the advantage is not obvious as the number of EVs increases. Meanwhile, there is no guarantee of tracing malicious EVs in this scheme. Furthermore, the communication analysis shows that the communication cost of this scheme is large. At the same time, the scheme proposed in this paper also has lower computational latency. As illustrated in Figure 5, its computational performance advantage becomes increasingly pronounced as the number of signcryption operations grows.

5.2. Communication Analysis

With the aim of evaluating the communication consumption of the scheme and meeting the 80-bit security level, the $p$ of the bilinear map is set to 64 bytes, and the $p$ of the ECC is set to 20 bytes. Therefore, the group element size, $\left|G_{bp}\right|$, based on the bilinear map is 128 bytes; the group element size, $\left|G_{ecc}\right|$, based on the elliptic curve is 40 bytes; the element size, $\left|Z_q^{\ast }\right|$, in $Z_q^{\ast }$ is 20 bytes; the timestamp size, $\left|T\right|$, is 4 bytes; and the size of the message, $m$, is 100 bytes.

In order to analyze these schemes, we mainly consider the ciphertext information, $m^{\prime }$, generated by heterogeneous signcryption. From Section 3.2.4, the ciphertext information is $\{m_i^{\prime },T_{i,1},P_{I{D}_i},P{K}_{I{D}_i}\}$, where $m_i^{\prime }=\left(U_i,V_i,Y_i\right),{P{K}_{I{D}_i}=\left(C_{I{D}_i},D_{I{D}_i}\right), T}_{i,1}\in T$,${\{V}_i,P_{I{D}_i}\}\in Z_q^{\ast }$, ${\{Y}_i,C_{I{D}_i},D_{I{D}_i}\}\in G_{ecc}$, and $U_i\in M$, so the communication cost of our proposed scheme is $3\left|G_{ecc}\right|+2\left|Z_q^{\ast }\right|+\left|T\right|+\left|m\right|=3\times 40+2 \times 20+4+100=264$ bytes. The calculation of other schemes is similar, as summarized in

Table 5. Comparison of communication costs.

Reference	Single Transaction Information	Cost (byte)	Environment
Ref. [18]	$4\left|Z_q^{\ast }\right|+2\left|G_1\right|+\left|G_2\right|+\left|m\right|$	438	CLC → IBC
Ref. [19]	$\left|2G_1\right|+\left|m\right|+\left|T\right|$	232	IBC → PKI
Ref. [20]	$2\left|G_{ecc}\right|+\left|m\right|+\left|Z_q^{\ast }\right|+\left|ID\right|$	264	PKI → IBC
Ref. [21]	$2\left|Z_q^{\ast }\right|+\left|G_{bp}\right|+\left|m\right|$	268	IBC → PKI
Ref. [22]	$2\left|G_{ecc}\right|+8\left|Z_q^{\ast }\right|+\left|T\right|+\left|m\right|$	343	CLC → PKI
Our Scheme	$3\left|G_{ecc}\right|+2\left|Z_q^{\ast }\right|+\left|T\right|+\left|m\right|$	264	CLC →IBC

. The schemes in [18,19,20] employ bilinear mappings. Ref. [18] has the same environment as this paper, but it incurs a higher communication cost. Refs. [19,20] have lower communication costs but require greater computational costs. At the same security level, the ECC-based scheme requires fewer elements than the bilinear mapping-based scheme. The authors of [21,22] use ECC to signcrypt information. The communication cost of [21] is similar to that of our proposed scheme, but the signcryption process does not introduce a timestamp, which makes it difficult to resist replay attacks. On the other hand, compared with the proposed scheme, the scheme in [22] exhibits a relatively high communication cost.

5.3. Security Function Analysis

A comparison of security functions in

Table 6. Comparison of security functions of each scheme.

Reference	Anonymity	Confidentiality and Integrity	Verification	Traceability	Revocability	Anti-Attack
Ref. [18]	×	√	×	√	×	×
Ref. [19]	√	√	√	×	×	√
Ref. [20]	×	√	√	√	×	√
Ref. [21]	×	√	√	√	×	×
Ref. [22]	√	√	√	×	×	√
Our Scheme	√	√	√	√	√	√

demonstrates some of the primary differences between the proposed schemes and existing schemes, such as anonymity, confidentiality, integrity, verification, traceability, revocability, and anti-attack, where a check mark, “√”, denotes that the requirement is met, and “×” indicates that it is not.

The above literature [18,19,20,21,22] all have achieved the most basic security function analysis indicators, integrity, and confidentiality. In our proposed scheme, the ciphertext is sent using a pseudonym, $P_{I{D}_i}$, to ensure anonymity and traceability through the TRA. It also achieves revocability by using an invalidation list. The scheme in [18,19,21] uses a real identity for communication, which ensures traceability but poses a risk of privacy leakage. Although [19] adopts anonymity and improves efficiency through aggregation and batch verification, it does not provide traceability in the anonymous situation and does not offer an invalidation mechanism. In addition, Ref. [22] also adopted anonymity but did not perform batch verification on the transmitted information. In addition, the scheme did not guarantee the traceability of malicious EVs. Therefore, this scheme has certain advantages in terms of security functions.

6. Discussion

In our scheme, we adopt the CLC cryptosystem with lower costs to transmit information according to the computing power of EVs and RSUs, while the PA and AC adopt the IBC cryptosystem because of the high computing power of the servers that can bear the larger cost. Our scheme uses a small exponential testing technique in the aggregation phase. Performance analysis shows that as the number of EVs (n), or the transaction volume, increases, the aggregation verification process does not increase significantly. Compared with similar paper schemes, this gives our scheme a distinct advantage in handling high throughput. In revocation management, for malicious EVs, we only use the method of maintaining the revocation list, which does not have a large overhead. Therefore, for high-mobility, mobility, and network congestion scenarios, the design choices for both aggregation and revocation ensure that the impact on overall system costs remains low, thereby supporting better scalability under challenging conditions such as high mobility and network congestion.

Regarding portability across cryptosystems, we make the following assertion:

Assume that there are EVs supporting CLC and IBC on the road at the same time. Firstly, the PKG required for the IBC system can be deployed within a controllable area (such as a smart highway demonstration zone), assigning IBC identities and private keys to the PA and AC. The RSU can be upgraded to add IBC client functionality. When EVs need to communicate with the PA or AC via the RSU, the RSU can be responsible for the conversion from CLC to IBC for EVs in the CLC system, while EVs in the IBC system can directly communicate with the same cryptographic system. Initially, newly manufactured EVs will be deployed with dual cryptographic system support and then gradually migrate to CLC, gradually replacing IBC with CLC in EVs. The same approach will be applied to RSU deployment and migration. This will allow each entity to fully leverage the advantages of its own heterogeneous cryptographic system to achieve optimal performance, ensuring that each entity uses the cryptographic system most suitable for computing power, and then gradually deploy and migrate to a wider range.

Meanwhile, as described in the deployment migration strategy above, the RSU will act as a secure protocol agent, responsible for verifying the CLC signature of EVs and converting their EVs’ requests into a format recognizable by the IBC system. EVs supported by the dual cryptographic system will be deployed and gradually transitioned to EVs supporting the CLC cryptographic system. This process does not require any hardware or software upgrades to participate in V2V power trading, thereby ensuring backward compatibility. For EV makers, from a hardware perspective, today’s smart EVs already possess sufficient computing power to handle the CLC computational burden, and the hardware cost is negligible. From a software perspective, our proposed scheme can be implemented as a software library and integrated into EVs, making it feasible. RSUs typically have greater computing power than EVs, making the CLC cryptosystem more feasible for RSU manufacturers. Furthermore, PAs and ACs, due to their strong computing power, can also handle the burden of the IBC cryptosystem. Overall, it is feasible for manufacturers to integrate this scheme.

However, this paper does not consider fund settlement and does not elaborate on the V2V transaction-matching algorithm for EVs in the PA, which will be left for subsequent research. In addition, the paper does not test our proposed scheme in a specific real-world scenario of the IoV. However, our analysis shows that our scheme has a low cost, which is a prerequisite for any connected vehicle application requiring low latency and high throughput. The good results of these indicators provide strong preliminary evidence for the efficiency and practical deployment potential of our scheme.

Next, conducting large-scale simulations and real-world tests in the IoV is the main goal of our future work. Meanwhile, we will extend the scenario to a generalized heterogeneous power trading system, where proximate available distributed energy resources can participate.

7. Conclusions

A privacy-preserving scheme for V2V double auction power trading based on heterogeneous signcryption and IoV is proposed in this paper, which ensures secure communication from CLC to IBC, provides aggregation and verification, and realizes the anonymity of EV users and guarantees their traceability and revocation of malicious EVs. The scheme is proven to be unforgeable based on the ROM. Theoretical analysis shows that our proposed scheme can protect the privacy of EV users and realize secure communication. Performance analysis shows that the proposed scheme reduces the communication cost by about 14.56% and the computational cost of aggregate decryption by 80.51%, compared with other schemes in recent years.