Abstract
Deep learning-based side-channel analysis is one of the most effective techniques for extracting and classifying sensitive information from a target device. This paper demonstrates the best-performing deep learning model for the target implementation by evaluating various deep learning architectures, including MLP, CNN, and RNN, while systematically optimizing their hyperparameters to achieve the best performance. The paper uses a case study of the Number Theoretic Transform accelerator for the CRYSTALS-Kyber key encapsulation mechanism to show that enhanced deep learning analysis can be used to break security. The best-performing deep learning-based model achieved a 96.64% accuracy in classifying pairwise coefficients of the s vector, which is used to generate the secret key with the NTT accelerator for Kyber768 and Kyber1024. For Kyber512, the model achieved an accuracy of 95.71%. The proposed approach significantly improves average training efficiency, with POIs achieving up to 1.45 times faster performance for MLP models, 10.53 times faster for CNNs, and 10.28 times faster for RNNs compared to deep learning methods without POIs, while maintaining high accuracy in side-channel analysis.
1. Introduction
Side-channel analysis (SCA) has been developed over a long period and is an important method for extracting sensitive information from hardware designs, particularly cryptographic schemes. Traditional SCA approaches such as Simple Power Analysis (SPA) [1], Differential Power Analysis (DPA) [2], Correlation Power Analysis (CPA), Template Attacks [3], and Collision Attacks [4] have been widely investigated and effectively used for retrieving secret keys in various cryptographic implementations. The current approaches to exploiting side-channel leakage are all based on either statistical analysis or modeling techniques, which search for patterns in the side-channel leakage related to secret data.
In recent years, deep learning has significantly advanced the field of SCA [5]. Deep learning-based methods offer an automated and highly effective way to analyze side-channel traces. Deep learning models such as Multi-Layer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), and Recurrent Neural Networks (RNNs) can effectively extract information from devices using side-channel traces [6,7,8]. Depending on the situation, the Hamming Weight (HW) leakage model or the Identity (ID) leakage model can be used to characterize the traces [9]. Also, direct side-channel trace patterns have been analyzed [10]. This flexibility allows the models to adapt to the specific characteristics of the side-channel traces.
Another important development in SCA is the incorporation of leakage detection, which helps identify Points of Interest (POIs) [11] in the traces. Traditional techniques like SPA and CPA often make assumptions about where leakage might occur, while more modern methods such as the Test Vector Leakage Assessment (TVLA) [12] use statistical analysis to detect significant leakage points. These POIs typically correspond to key-dependent operations or other critical stages in the cryptographic algorithm where sensitive data leaks. By refining the trace analysis, leakage detection improves the effectiveness of both traditional and deep learning-based SCA attacks.
These methodological advances highlight the growing importance of side-channel analysis, not only for evaluating classical cryptosystems but also for assessing emerging post-quantum algorithms. Post-quantum cryptography (PQC) has become essential as quantum computers pose a real threat to RSA and ECC, which underpin much of today’s secure communication [13]. To address this, the National Institute of Standards and Technology (NIST) began the process of standardizing PQC algorithms, culminating in the release of the first PQC standards in August 2024 [14]. Among these is the Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) standard, which is derived from the CRYSTALS-Kyber algorithm. ML-KEM is designed to secure key exchanges in the post-quantum era and is expected to be a critical component in future secure communications. However, like all cryptographic systems, ML-KEM is vulnerable to side-channel attacks, especially in hardware implementations where physical leakage can compromise security. Protecting against these attacks is therefore crucial to ensuring that ML-KEM can provide reliable countermeasures and robust security.
In this work, we present a case study focusing on vulnerabilities in Kyber, the foundation of ML-KEM. We leverage deep learning-based SCA combined with leakage detection techniques to evaluate potential weaknesses in its hardware implementations.
1.1. Prior Works
The significant progress in applying and refining deep learning techniques for SCA has been fully expressed, wherein researchers have increasingly enhanced their adaptability and performance. In [15], Maghrebi compared the performance of different deep learning architectures on many datasets and implementations of cryptographic algorithms to find the elements that help in successful profiled attacks. Also, Masure et al. aimed at providing extensive work to discuss how the recent advances and challenges in the applications of deep learning could serve as a solid and flexible framework for SCA-based cryptographic analyses [16].
These innovative applications of deep learning extend the scope of SCA beyond traditional approaches. Works such as deep learning-based collision attacks by Staib and Moradi show that these techniques even apply to cryptographic implementations with countermeasures [17]. Other works have focused on other components, such as feature selection and loss functions, to enhance the performance of deep learning further. Perin et al. investigated feature selection with respect to key recovery optimization [18], while Kerkhof et al. systematically compared loss functions and pointed out the benefits of SCA-dedicated designs such as the CrossEntropy Ratio (CER) [19]. As for interpretability, Yap et al. introduced a method to translate neural networks into SAT equations, thus closing the gap between transparency and high performance [20]. Rioja et al. went further by proposing AI-based assessments, which automatically implement cryptographic robustness tests to enable a more systematic and efficient pipeline analysis [21]. Wu et al. introduced the Bayesian framework for hyperparameter optimization that can simplify the tuning process and boost model performance considerably [9].
The leakage detection and identification of Points of Interest remain central to improving side-channel evaluations. Durvaux and Standaert proposed statistical methods to detect data-dependent leakages and POIs in cryptographic traces. Such methods and tools are indispensable in any accurate evaluation [11]. Bache et al. further developed this area with their contribution on multivariate Test Vector Leakage Assessment (TVLA) that utilized confidence intervals to attain efficiency and precision in evaluations [22]. Deep learning has also contributed significantly to the detection and assessment of side-channel leakages. Jung et al. came forward with a deep learning-based leakage data compression that could enable increased scalability for the side-channel attack [23]. Gupta et al. merged machine learning methods along with hypothesis testing so that it would automate the leakage detection problem [24]. Saha et al. delved into various leakage detection methodologies involving fault-induced leakages in block ciphers [25]. Moos et al. proposed the DL-LA framework, the first DL approach that showed greater efficiency over state-of-the-art classical methods grounded in t-tests [26]. In addition, gradient visualization techniques proposed by Li et al. have been effective in identifying and analyzing leakage during both pre-silicon design phases and runtime, thus providing stronger cryptographic security from the very ground [27].
1.2. Our Contributions
Current methodologies have successfully demonstrated the ability to identify and assess leakages, with many works highlighting how deep learning has improved leakage detection. By combining these detection techniques with deep learning, there is potential to uncover new and more effective strategies for side-channel analysis. To address this, we propose an expedited framework that integrates Points of Interest (POIs) into deep learning-based SCA. In contrast, the traditional way of using deep learning-based SCA did not include POIs and we compare their performance.
- Our approach identifies and filters out irrelevant leakage points from power traces, improving data quality and enhancing the performance of deep learning models. This comprehensive solution aims to optimize the entire side-channel analysis process, making it more accurate and efficient. By adding Points of Interest (PoIs), we can use simpler deep learning models with fewer layers, which speeds up data classification while also improving both the accuracy and efficiency of the analysis.
- We performed a comparison across 12 different models, including 4 models each from MLPs, CNNs, and RNNs, with varying hyperparameters. To ensure a fair evaluation, the models within each category (MLP, CNN, and RNN) were designed with similar hyperparameter configurations. Additionally, we compared the performance of these models under the following two conditions: with and without POIs, respectively. This enabled us to evaluate the influence of our suggested POI technique on the efficacy and efficiency of the models. Our objective was to determine the optimal model architecture for SCA under equivalent situations and to evaluate how the POIs improve their performances.
- We observed that during secret key generation in Kyber, the NTT operation uses a limited set of values. This makes deep learning-based SCA effective for classifying intermediate data during the NTT operation. Based on this, we clarified the idea to expose the shared secret key in Kyber KEM by extracting the coefficient pairs from the NTT operation. We modified the implementation in [28] to allow communication with a host PC for transferring data. We collected 200,000 power traces during the NTT operation and used the deep learning-based SCA to classify the coefficient pairs. This shows a potential vulnerability in Kyber KEM and highlights how deep learning can be used to extract sensitive information in cryptographic systems.
2. Background
The Background section highlights how leakage detection and deep learning methods are used to analyze and exploit side-channel information in cryptographic algorithms. It also focuses on the importance of securing the NTT operation in CRYSTALS-Kyber, a critical component in post-quantum cryptography.
2.1. Leakage Detection Approaches
Leakage detection primarily aims to identify the presence of side-channel leakage rather than directly recover secret keys. This is typically achieved through statistical or information theoretic methods applied to side-channel measurements [12,29]. Two main assessment approaches are commonly used as follows [30]:
2.1.1. Attacking-Style Assessments
These involve actual side-channel attacks, such as Differential Power Analysis (DPA) and Correlation Power Analysis (CPA), which aim to extract cryptographic keys. Metrics like correlation coefficients and mutual information are calculated to evaluate the success of the attacks. For example, in CPA, the correlation coefficient between the leakage L and a hypothetical leakage model for a guessed key K is computed as follows:
where is the covariance, and are the standard deviations of L and , respectively. A high correlation indicates a correct key guess.
2.1.2. Leakage Detection-Style Assessments
This approach evaluates whether leakage exists without attempting to recover keys. Statistical hypothesis testing is commonly used, with the null hypothesis assuming no leakage and the alternative hypothesis suggesting leakage. Welch’s t-test, employed in Test Vector Leakage Assessment (TVLA), is a widely used method. The test statistic is expressed as follows:
where are the sample means of the two datasets (e.g., fixed vs. random plaintext traces), are the sample variances, and are the sample sizes. If exceeds a predefined threshold (e.g., 4.5), is rejected, indicating potential leakage.
2.2. Deep Learning-Based Side-Channel Analysis
Many studies have used different deep learning architectures for side-channel analysis, such as Multi-Layer Perceptrons (MLPs) [16], Convolutional Neural Networks (CNNs) [20], and Recurrent Neural Networks (RNNs) [15]. This section explains these popular deep learning models and how they process time-series data for side-channel analysis.
2.2.1. Multi-Layer Perceptrons (MLPs)
Multi-Layer Perceptrons (MLPs) are fully connected feedforward neural networks designed for supervised learning tasks. Each layer in a MLP consists of a set of neurons, where the output of each neuron is computed as a weighted sum of its inputs followed by an activation function. For a single layer, the computation can be expressed as follows:
Each layer in a MLP computes its output z as a weighted sum of the input vector x using the weight matrix W and bias vector b, followed by an activation function f such as ReLU, sigmoid, or tanh. The final layer of a MLP typically uses a softmax activation function to output class probabilities for classification tasks.
2.2.2. Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs) effectively model sequences by extracting local patterns through convolutional operations. For a sequence , the 1D convolution output at position t is expressed as follows:
where is the i-th filter weight, b is the bias, and k is the kernel size. Nonlinear activations like ReLU, , add complexity. Pooling layers, such as max pooling, reduce dimensionality, as follows:
Temporal Convolutional Networks (TCNs) extend CNNs to capture long-term dependencies using dilated convolutions as follows:
where d is the dilation factor, expanding the receptive field efficiently. Extracted features are passed to dense layers, with classification probabilities computed as follows:
2.2.3. Recurrent Neural Networks (RNNs)
Recurrent Neural Networks (RNNs) process sequences step by step, maintaining a hidden state to capture temporal dependencies. For a sequence , the hidden state update is expressed as follows:
where , , and are parameters, and f is an activation function like tanh. The output at timestep t is as follows:
where g is typically softmax for classification.
2.3. NTT Operation in CRYSTALS-Kyber
The Number Theoretic Transform (NTT) is a core operation in CRYSTALS-Kyber, facilitating efficient polynomial multiplication in the ring . Kyber has three different security levels [31]. The parameter sets for each level are summarized in Table 1, demonstrating the variations in module dimension k, error parameters , and compression settings , while maintaining consistent polynomial degree n and modulus q.

Table 1.
Parameter sets for Kyber.
Kyber recommends the utilization of the Number Theoretic Transform (NTT) for optimal multiplication. NTT operation is a crucial component in the Kyber cryptographic algorithm, specifically within the Kyber Key Encapsulation Mechanism (KEM), used in key generation, encapsulation, and decapsulation processes. As described in [32], NTT is an extension of the fast Fourier transform (FFT) specifically defined within a finite field. The definition of NTT is , where . In addition, demonstrates the inverse , in which . We can efficiently compute the product of two elements f and g from using NTT and its inverse . Essentially, the product is calculated as . Applying the NTT or its inverse to a vector or matrix of elements of means that the operation is performed on each element separately. When the symbol is used with matrices or vectors, it denotes a point-wise multiplication.
During the key generation process, as described in Algorithm 1, the secret key is generated directly from using the NTT operation. Therefore, the NTT operation is an essential component for strengthening the security of CRYSTALS-Kyber KEM.
| Algorithm 1: Secret key generation for Kyber KEM |
 |
3. Side-Channel Analysis Framework
In this section, we explain the idea behind the expedited deep learning-based side-channel analysis. We highlight how optimized hyperparameter tuning helps to improve attack success rates by adapting the models to better capture leakage information from cryptographic accelerators.
3.1. Main Framework
Our proposed framework is a comprehensive method that begins by modifying cryptographic implementations to collect power traces. It then applies a leakage detection method to filter out unnecessary points, retaining only the most relevant features for analysis. Using this refined data, deep learning models are trained to classify sensitive information and choose the best-performing model. Our framework covers everything from data preparation to model evaluation, ensuring the accurate and efficient classification of sensitive information using power traces. Our proposed framework, illustrated in Figure 1, is structured into four main steps. The detailed analysis for each step is as follows:
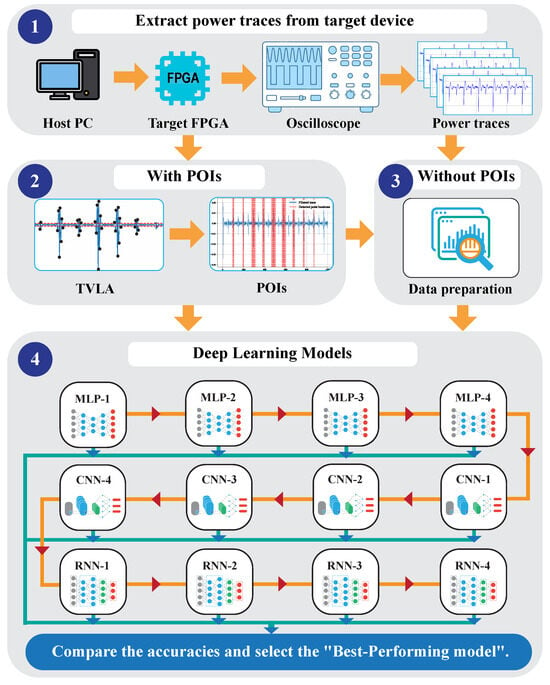
Figure 1.
Overview structure of deep learning-based SCA with and without POIs.
- Extracting power traces: In this step, the target implementation is deployed on a specially designed FPGA for side-channel analysis. Input data are sent from the host PC to the FPGA, where the FPGA performs the specified operations. After completing the computations, the results are sent back to the host PC for verification. During this operation, power traces or electromagnetic emissions are collected using specialized devices such as an oscilloscope. These traces capture the physical leakage information necessary for further analysis.
- With POIs: This step involves processing and transforming the collected traces into enhanced traces to optimize deep learning-based side-channel analysis. The transformation begins by identifying and extracting relevant leakage points using the leakage detection methods. If necessary, we can apply preprocessing techniques such as high-pass filtering to remove low-frequency noise and baseline variations, along with normalization to standardize the data.
- Without POIs: POIs are widely used in side-channel analysis, but in some cases this becomes more difficult when masking or other countermeasures are applied. This may lead to a decrease in attack performance so we also need to verify the deep learning-based analysis without the POIs. In this case we proceed directly to the trace preprocessing stage.
- Comparison between deep learning models: In the final step, we evaluate and compare the performances of various deep learning models, such as MLPs, CNNs, and RNNs, each with different hyperparameter configurations on the traces with and without POIs. Deep learning models were applied sequentially, and their classification accuracy metrics were recorded for subsequent performance comparison. This comparison helps identify the best-performing model for the target data classification. Additionally, other deep learning methods or ensemble approaches can be considered to further enhance the analysis and achieve optimal results.
3.2. Identification of Points of Interest (POIs)
Test Vector Leakage Assessment (TVLA) is one of the leakage detection statistical methods used to detect side-channel leakage in cryptographic systems [12]. Leakage detections were analyzed for Points Of Interest (POIs) [11]. TVLA is widely chosen due to its simplicity and effectiveness in identifying leakage points in side-channel traces. Our proposed POIs not only detect leakage vulnerabilities but also transform the traces into new traces by utilizing the detected significant points. We describe our POIs using statistical leakage assessment and illustrate the stages of the process with graphs, as shown in Figure 2.
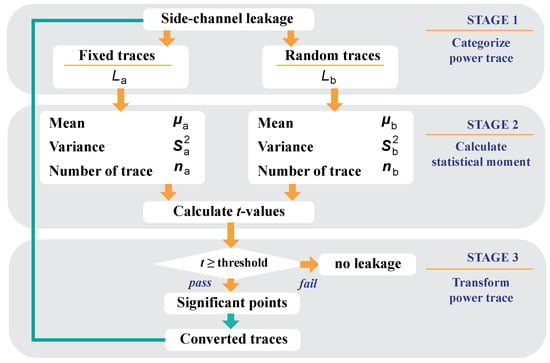
Figure 2.
Process flow for Point of Interest identification.
- Categorize Power Traces: The raw power trace data are collected, where i represents a specific time point in the trace. The power traces are divided into two groups based on input types as follows: fixed input traces and random input traces . This categorization is essential for comparative statistical analysis.
- Calculate Statistical Moments: Statistical moments such as the mean and variance are calculated for each group of traces and . The t-test formula is used to compute the t-value t for each point in the trace to identify significant points as follows:where and are the means, and are the variances, and and are the number of traces in and , respectively. A t-value exceeding the predefined threshold indicates a significant point in the trace. To determine no leakage, no observed statistic greater than 4.5 is required.
- Transform Power Traces: Significant points in the trace are retained, forming the converted trace expressed as follows:This transformation filters out irrelevant data, leaving only points with statistical significance, optimizing the trace for further analysis.
3.3. Optimizing Hyperparameters for Deep Learning Models
In this subsection, we optimize the hyperparameters for the following three architectures in our side-channel analysis framework: Multi-Layer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), and Recurrent Neural Networks (RNNs). The goal is to assess how different configurations impact classification performance while maintaining consistent structures for fair comparison.
All models adhere to the following common design principles: input traces are either raw (1000 points) or preprocessed vectors from POIs; outputs use a softmax layer; and training employs ReLU activation, the Adam optimizer, and categorical cross-entropy loss with the default learning rate. These standardizations ensure that performance differences arise from architectural and hyperparameter choices rather than inconsistencies. To balance complexity and generalization, additional units or layers were tested with dropout regularization to mitigate overfitting. The chosen hyperparameters reflect a balance between expressiveness, computational efficiency, and resistance to overfitting.
For the MLP models, one and two hidden layers were selected to systematically study the effect of depth while keeping the model interpretable and lightweight. The unit sizes of 64 and 128 were selected as common baseline values in the side-channel analysis literature, providing sufficient capacity to capture leakage patterns without excessively increasing parameter count. For the MLP models, these units allowed us to systematically examine the effect of depth, with dropout fixed at 0.1 across layers to mitigate overfitting while maintaining stability. In CNN models, 64 and 128 filters in the first convolutional layer increased representational capacity, while kernel sizes of 3 captured local correlations within neighboring points of interest. Adding a second convolutional layer in CNN-3 and CNN-4 enabled hierarchical feature extraction, and max-pooling of size 2 consistently reduced dimensionality and improved robustness against slight leakage shifts. For the RNN models, 64 and 128 recurrent units tested the impact of hidden state size on temporal dependency modeling, with a higher dropout rate of 0.2 used to counter stronger overfitting risks in sequential learning. A second recurrent layer in RNN-3 and RNN-4 further captured long-term dependencies, ensuring a fair and systematic comparison across architectures. Across all architectures, dense layers of 32–64 units provided a compact intermediate representation before the classification stage.
3.3.1. Hyperparameter Tuning for MLP Models
For the MLP models, we evaluated how the number of hidden layers and units affected performance. The following four configurations were tested (Table 2): MLP-1 and MLP-2 used a single hidden layer with 64 and 128 units, while MLP-3 and MLP-4 added a second hidden layer with 64 and 128 units, respectively. To mitigate overfitting, dropout with a rate of 0.1 was applied after each hidden and dense layer.

Table 2.
Hyperparameter tuning for MLP models.
3.3.2. Hyperparameter Tuning for CNN Models
For the CNN models, we examined how the number of convolutional layers and filters affected performance (Table 3). CNN-1 and CNN-2 used a single convolutional layer with 64 and 128 filters, while CNN-3 and CNN-4 added a second layer with 64 and 128 filters, respectively. Each convolutional layer was followed by max-pooling (size 2) and dropout (rate 0.1) to reduce overfitting. After the convolutional blocks, dense layers with 32–64 units and a softmax output were applied for classification.

Table 3.
Hyperparameter tuning for CNN models.
3.3.3. Hyperparameter Tuning for RNN Models
For the RNN models, we assessed how the number of recurrent layers and units influenced performance (Table 4). RNN-1 and RNN-2 used a single recurrent layer with 64 and 128 units, while RNN-3 and RNN-4 added a second layer with 64 and 128 units, respectively. Dropout with a rate of 0.2 was applied after each recurrent and dense layer to reduce overfitting. The recurrent blocks were followed by dense layers with 32–64 units and a softmax output for classification.

Table 4.
Hyperparameter tuning for RNN models.
4. Breaking the NTT Operation in Kyber
In this section, we present the vulnerabilities we identified in the NTT operation used in CRYSTALS-Kyber and explain how side-channel leakage can be exploited to recover the secret key. We also discuss the unprotected hardware implementation of the NTT and describe our modifications for SCA.
4.1. Idea of Breaking the NTT Operation
In hardware implementations of the NTT, negative values are avoided by working within a finite field. Using the prime modulus in CRYSTALS-Kyber, any negative result is mapped into the valid range by adding q. This ensures both the correctness and efficiency of the NTT computation.
For example, when , the possible secret-key coefficients are represented in hardware as . Similarly, when , the set is encoded as . In both cases, all coefficients remain within the finite field domain.
The NTT for 256 coefficients requires eight stages of butterfly operations. In the first stage, each butterfly combines a pair of coefficients using modular additions and multiplications with precomputed twiddle factors. Because both inputs in a butterfly share the same scaling factor in this stage, the intermediate results remain directly dependent on the underlying coefficients. Consequently, leakage from the first stage of the NTT can be exploited to recover information about the secret vector s.
It is important to note that our attack strategy does not rely on the total number of NTT executions, but rather on the ability to extract sensitive information from coefficient pairs during this initial stage. Therefore, Kyber512 with and Kyber768/1024 with exhibit comparable vulnerability to side-channel analysis, since the fundamental leakage behavior of the NTT operation remains the same across security levels.
4.2. FPGA Implementation for NTT Accelerator in Kyber
The paper [28] introduces three hardware architectures—lightweight, balanced, and high-performance—to accelerate polynomial multiplication in CRYSTALS-Kyber. While effective, these designs lack countermeasures against side-channel analysis. The lightweight version, built around a single butterfly unit, achieves notable gains for NTT, INTT, and coefficient-wise multiplication on FPGA platforms, despite its minimal resource usage.
Building on this lightweight design, we introduce two modifications to support side-channel evaluation, as shown in Figure 3. First, we integrated a USB interface for the efficient data transfer of the s-vector coefficients between the accelerator and a host PC. Second, we added a NTT register to store all 256 input coefficients, reducing memory access overhead and enabling seamless execution. Once the coefficients are loaded, the accelerator performs the NTT and returns a trigger signal to the host while power traces are recorded for analysis.
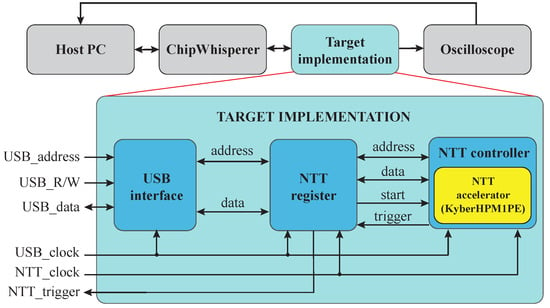
Figure 3.
Overview of the modified NTT implementation.
A hardware driver for sending and receiving data between the FPGA and the USB transceiver of the CW305 board was originally provided as part of a reference 128-bit AES implementation [33]. In our work, we modified both the register map and the target implementation to support the NTT accelerator, enabling the efficient transfer of coefficient data and synchronization with the side-channel measurement setup. The cw305_usb_reg_fe frontend translates USB transactions from the host into FPGA register-level operations, mapping reads and writes into a simple address–data bus. On a USB write, the frontend asserts a reg_write strobe together with the target reg_address and forwards the payload (reg_datao) to the internal register map. On a USB read, it asserts reg_read and drives the requested data (reg_datai) back to the host via usb_dout. By extending the USB register interface, we ensured that all input and output data for the NTT accelerator could be transferred efficiently without requiring external memory. During side-channel experiments, the host PC preloaded the 1024-bit coefficient block into the FPGA registers via USB, initiated the NTT computation by toggling control registers, and then received a trigger signal generated by NTT controller. This trigger was synchronized with the ChipWhisperer-Lite capture board, allowing the precise alignment of power traces.
To support our NTT accelerator, we extended the register memory space of the ChipWhisperer CW305 platform. In addition to the original control and status registers, we added a dedicated block of registers to store the input vector. Specifically, we allocated 128 bytes of register storage, sufficient to preload all 256 coefficients for a single NTT execution. Each coefficient is stored as a compact 4-bit hexadecimal value, allowing the efficient transfer of all coefficients from the host PC via the USB interface. Upon execution, the NTT controller sequentially expands these 4-bit hex values into the 12-bit words required by the arithmetic processing element (KyberHPM1PE). The mapping is explicitly defined as follows:
This expansion ensures compatibility with modular reduction and butterfly operations inside the NTT accelerator. The compact 4-bit format minimizes the USB payload, while the internal 12-bit expansion preserves correctness for arithmetic operations. Once all coefficients are streamed, the accelerator performs the NTT operation. The processed outputs are then written back into the extended register space, enabling the host to retrieve results through standard USB read operations.
Our measurement platform (Figure 4) consists of a ChipWhisperer-Lite, CW305 FPGA target, and PicoScope 5444D, following a well-established methodology [34]. Using this setup, we collected 100,000 traces for Kyber512 and an additional 100,000 each for Kyber768 and Kyber1024, capturing pairwise coefficient computations across all security levels. The CW305 target was clocked at 1.0 MHz, and each trace acquisition covered the entire first stage of the NTT calculation. The ChipWhisperer ADC was configured with a sampling rate of 100 MS/s and a capture length of 13,500 samples per trace, ensuring complete coverage of the relevant computation window. Power measurements were taken using the CW305’s low-noise shunt resistor circuit, with the signal amplified at 25 dB gain. The experiments were conducted in a regular laboratory environment without additional shielding, relying on stable power supply regulation and proper grounding to keep noise manageable.

Figure 4.
Measurement setup overview.
5. Verification Results
In this section, we evaluate the vulnerabilities in the NTT operation of CRYSTALS-Kyber through experimental setups, POIs, and our proposed deep learning-based SCA. We describe the methods used to analyze leakage points, and we assess the performance of various deep learning models in recovering secret key coefficients across different Kyber security levels.
5.1. Point of Interest Identification Results
We applied the TVLA method to analyze the filtered traces, comparing a fixed input set against other random inputs. The results are shown in Figure 5. This demonstrates how the TVLA test effectively identifies significant differences between the fixed and random input sets. Figure 5b further illustrates the locations of significant points’ interval.
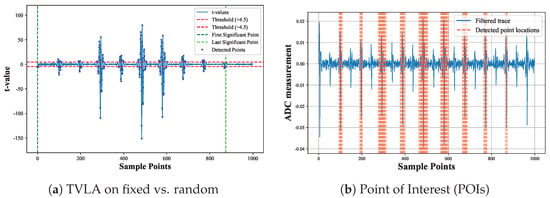
Figure 5.
Leakage detection: (a) fixed vs. random traces, (b) Point of Interest Identification.
As shown in Figure 5a, we demonstrate the effect of the TVLA in detecting the vulnerable points from the trace. In Figure 5b, the POIs are displayed with significant points identified. Using only these significant point locations, we generate a new converted trace. This trace is then normalized, making it ready for input into the deep learning model. New converted traces retain the most relevant information, improving efficiency and accuracy for deep learning-based side-channel analysis.
5.2. Performance Evaluation of Deep Learning Models
For Kyber512 with , there are seven possible coefficients, resulting in 49 input combinations for the NTT. In contrast, Kyber768 and Kyber1024 with require only 25 combinations, reflecting lower complexity. Each dataset was divided into 80% training and 20% validation according to Pareto’s principle [35].
5.2.1. Classification Performance for Kyber512
Table 5 represents the evaluation metrics for various models trained on a NTT accelerator for Kyber512. Figure 6 provides a comparison of accuracy over epochs for deep learning models with and without POIs on the NTT accelerator for Kyber512, highlighting how the models evolve during training under both scenarios.

Table 5.
Evaluation metrics for different deep learning models on the NTT accelerator for Kyber512 with and without POIs.
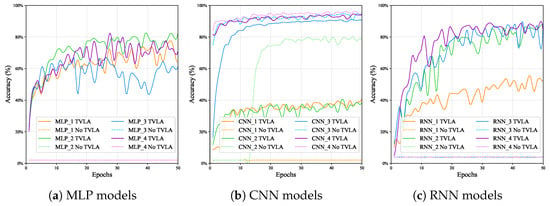
Figure 6.
Accuracy comparison of deep learning models with and without POIs on the NTT accelerator for Kyber512.
- MLP Models: MLP models perform significantly better with POIs compared to without them. Without POIs, accuracy remains low at around 2.06%, resembling random guessing. However, with POIs, accuracy improves significantly, ranging from 61.53% (MLP-3) to 82.86% (MLP-2), with F1-scores reaching as high as 74.32% (MLP-4). Training time is also 1.45 times faster on average. The results show that POIs not only boost performance but also make training more efficient. From Figure 6a, which shows accuracy over epochs, we observe that MLPs with POIs slowly improve in accuracy over epochs. However, this trend is not consistently linear and sometimes drops before rising again.
- CNN Models: CNN models demonstrate strong performance both with and without POIs. Without POIs, CNNs achieve high accuracy, ranging from 94.82% (CNN-3) to 95.71% (CNN-4), with F1-scores reaching 94.86% and 95.83%, respectively. This highlights their ability to capture spatial patterns in NTT operation data, even without leakage information. With POIs, accuracy remains high, with CNN-4 achieving 94.03% and an F1-score of 94.11%. Training becomes significantly faster, improving by an average of 16.48 times. From Figure 6b, which shows the accuracy over epochs for CNN models, we observe that CNNs achieve higher accuracy from the very beginning of training compared to MLPs and RNNs.
- RNN Models: RNN models show significant differences in performance with and without POIs. Without POIs, accuracy is approximately 2.06% and indicates random predictions. Training times are also extremely high, ranging from 2183.4 s (RNN-1) to 67328.5 s (RNN-4), making RNNs the least efficient models. With POIs, performance improves significantly, with accuracy ranging from 52.21% (RNN-1) to 87.89% (RNN-2) and F1-scores reaching a maximum of 87.85% (RNN-2). Training time decreases significantly, improving by 10.40 times for average RNNs. From Figure 6c, which shows the accuracy over epochs for RNN models, we can see that accuracy increases slowly from the beginning and requires more epochs to improve compared to CNNs.
5.2.2. Classification Performance for Kyber768 and Kyber1024
Table 6 presents the evaluation metrics for various models trained on the NTT accelerator with Kyber768 and Kyber1024. Figure 7 provides a comparison of accuracy over epochs for deep learning models with and without POIs on the NTT accelerator, highlighting how the models evolve during classification under both scenarios.

Table 6.
Evaluation metrics for different deep learning models on the NTT accelerator for Kyber768 and Kyber1024 with and without POIs.
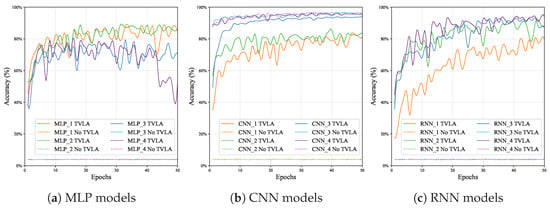
Figure 7.
Comparison between the accuracy of MLP, CNN, and RNN models on the NTT accelerator for Kyber768 and Kyber1024.
- MLP Models: The performance of MLP models shows a significant difference with and without POIs. Without POIs, MLPs perform poorly, with accuracy, precision, recall, and F1-scores all remaining at low levels. Training times remain relatively low, but the models fail to capture meaningful patterns from the data. When POIs are used, MLPs experience a significant performance boost, accuracy increasing from as low as 3.77% to over 84%, and F1-scores improving to a maximum of 86.22% for MLP-2. The training time for MLPs improved from an average of 68.8 s without POIs to 47.8 s with POIs, an improvement of 1.44-fold. From Figure 7a, we can observe that MLPs with POIs gradually improve in accuracy over time.
- CNN Models: CNN models consistently perform well, both with and without POIs. Without POIs, they achieve high accuracy, such as 96.34% (CNN-3) and 96.64% (CNN-4), with F1-scores of 96.38% and 96.63%. However, training times are high, ranging from 788.5 s (CNN-1) to 5117.9 s (CNN-4). With POIs, CNNs maintain strong performance, with CNN-4 achieving 95.25% accuracy and a 95.32% F1-score. The average training time decreased from 2651.3 s to 403.4 s, resulting in a significant improvement of 6.57 times. Figure 7b highlights that CNNs achieve high accuracy from the outset of training compared to MLPs and RNNs, demonstrating their ability to capture patterns early on.
- RNN Models: The performance of RNNs shows a big contrast between scenarios with and without POIs. Without POIs, RNNs perform poorly, with metrics such as accuracy, precision, recall, and F1-scores remaining at very low levels, indicating a failure to capture meaningful patterns. RNNs are computationally expensive, making them the least efficient models in this scenario. However, with the integration of POIs, RNNs show significant improvements. Accuracy rises in a range from 79.73% (RNN-1) to 94.08% (RNN-4), and F1-scores improve accordingly. The most substantial improvement was observed for RNNs, where the average training time dropped from 22,650.4 s to 2231.8 s, making the process 10.15 times faster. From Figure 7c, we observe that RNNs show steady improvement over time, but at a slower pace compared to CNNs.
In conclusion, the results show that POIs significantly improve the performance of MLP and RNN models. CNN-4 remains the best-performing model overall, even with POIs applied. POIs reduce training times for RNN models while improving their ability to capture relevant patterns and enhancing predictive performance. For CNNs, high-order POIs are required to match the accuracy achieved without them.
5.2.3. Comparison
There has been significant research exploring various methods for secret key recovery attacks on Kyber KEM. These work targets different operations and uses various SCA techniques. Table 7 summarizes these efforts, highlighting the target operations, types of SCA, and their respective success rates. Our work focuses specifically on the NTT operation, leveraging a deep learning-based SCA approach. While some prior works, such as [36,37], target polynomial multiplication using non-profiled or blind SCA techniques, others like [38,39] achieve message or shared key recovery through deep learning-based SCA. Additionally, ref. [40] demonstrates chosen ciphertext attacks on the inverse NTT. In comparison, our approach achieves up to 96.64% pair coefficient classification accuracy using the CNN-4 model. Although we have not yet achieved full secret key recovery, our work demonstrates an effective alternative for attacking the NTT operation, adding to the existing body of knowledge on SCA vulnerabilities in Kyber KEM.

Table 7.
Summary of secret-key recovery attacks on Kyber KEM.
6. Discussion and Future Work
Our evaluation focused on unprotected NTT implementations, and results may differ once masking or other countermeasures are applied. The deep learning models we used, including MLP, CNN, and RNN, are relatively traditional and do not explore modern architectures such as Transformers, which have shown promise in side-channel analysis. We adopted softmax as the output activation for classification because it produces normalized probability distributions across classes, simplifying accuracy evaluation. While alternatives such as sigmoid or logit-based approaches could be considered, softmax remains the most standard and interpretable choice in multi-class classification. Our analysis demonstrates that integrating POIs significantly improves classification accuracy across multiple deep learning models. In addition, although integrating POIs generally improved classification accuracy, in some cases, the top accuracy decreased after POI selection, likely because informative features outside the chosen regions were discarded.
Future work could address these limitations by increasing the number of POIs, applying adaptive POI selection strategies, and investigating advanced neural architectures to further enhance performance and robustness. We plan to investigate wider hyperparameter tuning strategies, including deeper networks, variable hidden-layer widths, and alternative activation functions, to better understand their effect on model robustness and leakage exploitation. We also aim to extend our attack evaluation to protected NTT accelerators within ML-KEM, leveraging the identified attack point to analyze resilience under masking, shuffling, and other countermeasures. Another direction is to explore modern architectures such as Transformers and attention-based models, which may offer improved feature extraction and generalization compared to traditional MLP, CNN, and RNN approaches. Our goal is to achieve complete secret key recovery for ML-KEM under realistic countermeasure settings, thereby providing a more comprehensive and practical evaluation of its side-channel resistance.
7. Conclusions
In this paper, we present a comparative deep learning-based side-channel analysis of an FPGA-based CRYSTALS-Kyber NTT accelerator. Our framework analyzes patterns in side-channel traces to classify them, helping to identify necessary intermediate values of the hardware implementation. Specifically, we classify pairs of coefficients of the NTT operation for the CRYSTALS-Kyber PQC algorithm. With the integration of POIs, the average accuracy for all MLPs increases from 3.01% to 74.08%, for CNNs from 58.98% to 77.82%, and for RNNs from 3.02% to 82.73%. These results demonstrate that our method enables deep learning models to not only work faster but also learn and classify more efficiently.
Author Contributions
M.C. and L.W. conceived and designed the study. M.C. implemented the methodology, developed the software, performed the experiments, and carried out the data analysis. X.Z., Y.Y., and M.W. contributed to methodology development and validation. L.W. and X.Z. provided supervision, resources, and project administration. M.C. drafted the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by the PQC project of JCASC (School of Integrated Circuits of Tsinghua University – Tongxin Microelectronics Co. Ltd. Joint Research Center for Automotive and Security Chip).
Data Availability Statement
The datasets used and analyzed in the current study can be made available from the corresponding author upon reasonable request. All data generated or analyzed during this study are included in this article.
Conflicts of Interest
Author Man Wei was employed by the company Tongxin Microelectronics Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Mayer-Sommer, R. Smartly analyzing the simplicity and the power of simple power analysis on smartcards. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Worcester, MA, USA, 17–18 August 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 78–92. [Google Scholar]
- Kocher, P. Differential power analysis. In Proceedings of the Advances in Cryptology (CRYPTO’99), Santa Barbara, CA, USA, 15–19 August 1999. [Google Scholar]
- Chari, S.; Rao, J.R.; Rohatgi, P. Template attacks. In Proceedings of the Cryptographic Hardware and Embedded Systems-CHES 2002: 4th International Workshop, Redwood Shores, CA, USA, 13–15 August 2002; Revised Papers 4. Springer: Berlin/Heidelberg, Germany, 2003; pp. 13–28. [Google Scholar]
- Schramm, K.; Leander, G.; Felke, P.; Paar, C. A collision-attack on AES: Combining side channel-and differential-attack. In Proceedings of the Cryptographic Hardware and Embedded Systems-CHES 2004: 6th International Workshop, Cambridge, MA, USA, 11–13 August 2004; Proceedings 6. Springer: Berlin/Heidelberg, Germany, 2004; pp. 163–175. [Google Scholar]
- Picek, S.; Perin, G.; Mariot, L.; Wu, L.; Batina, L. Sok: Deep learning-based physical side-channel analysis. ACM Comput. Surv. 2023, 55, 1–35. [Google Scholar] [CrossRef]
- Prouff, E.; Strullu, R.; Benadjila, R.; Cagli, E.; Dumas, C. Study of Deep Learning Techniques for Side-Channel Analysis and Introduction to ASCAD Database. CoRR 2018, 53, 1–45. [Google Scholar]
- Cagli, E.; Dumas, C.; Prouff, E. Convolutional neural networks with data augmentation against jitter-based countermeasures: Profiling attacks without pre-processing. In Proceedings of the Cryptographic Hardware and Embedded Systems–CHES 2017: 19th International Conference, Taipei, Taiwan, 25–28 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 45–68. [Google Scholar]
- Bazangani, O.; Eliasi, P.A.; Picek, S.; Batina, L. Can Machine Learn Pipeline Leakage? In Proceedings of the 2024 Design, Automation & Test in Europe Conference & Exhibition (DATE), Valencia, Spain, 25–27 March 2024; pp. 1–6. [Google Scholar]
- Wu, L.; Perin, G.; Picek, S. I Choose You: Automated Hyperparameter Tuning for Deep Learning-based Side-channel Analysis. IEEE Trans. Emerg. Top. Comput. 2022, 12, 546–557. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, C.; Shen, J.; Wu, Q.M.; He, D. Less Traces Are All It Takes: Efficient Side-Channel Analysis on AES. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 44, 2080–2092. [Google Scholar] [CrossRef]
- Durvaux, F.; Standaert, F.X. From improved leakage detection to the detection of points of interests in leakage traces. In Proceedings of the Advances in Cryptology–EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016; Part I 35. Springer: Berlin/Heidelberg, Germany, 2016; pp. 240–262. [Google Scholar]
- Becker, G.; Cooper, J.; DeMulder, E.; Goodwill, G.; Jaffe, J.; Kenworthy, G.; Kouzminov, T.; Leiserson, A.; Marson, M.; Rohatgi, P.; et al. Test vector leakage assessment (TVLA) methodology in practice. In Proceedings of the International Cryptographic Module Conference, Gaithersburg, MD, USA, 24–26 September 2013; Volume 1001, p. 13. [Google Scholar]
- Shaller, A.; Zamir, L.; Nojoumian, M. Roadmap of post-quantum cryptography standardization: Side-channel attacks and countermeasures. Inf. Comput. 2023, 295, 105112. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. Module-Lattice-Based Key-Encapsulation Mechanism Standard. 2024; Federal Information Processing Standards Publication 203. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.203.pdf (accessed on 15 December 2024).
- Maghrebi, H. Deep Learning Based Side Channel Attacks in Practice. Cryptology ePrint Archive. 2019. Available online: https://eprint.iacr.org/2019/578 (accessed on 20 December 2024).
- Masure, L.; Dumas, C.; Prouff, E. A comprehensive study of deep learning for side-channel analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 348–375. [Google Scholar] [CrossRef]
- Staib, M.; Moradi, A. Deep Learning Side-Channel Collision Attack. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2023, 2023, 422–444. [Google Scholar] [CrossRef]
- Perin, G.; Wu, L.; Picek, S. Exploring Feature Selection Scenarios for Deep Learning-based Side-channel Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022, 2022, 828–861. [Google Scholar] [CrossRef]
- Kerkhof, M.; Wu, L.; Perin, G.; Picek, S. No (good) loss no gain: Systematic evaluation of loss functions in deep learning-based side-channel analysis. J. Cryptogr. Eng. 2023, 13, 311–324. [Google Scholar] [CrossRef]
- Yap, T.; Benamira, A.; Bhasin, S.; Peyrin, T. Peek into the Black-Box: Interpretable Neural Network using SAT Equations in Side-Channel Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2023, 2023, 24–53. [Google Scholar] [CrossRef]
- Rioja, U.; Batina, L.; Armendariz, I.; Flores, J.L. Towards Human Dependency Elimination: AI Approach to SCA Robustness Assessment. IEEE Trans. Inf. Forensics Secur. 2022, 17, 3906–3921. [Google Scholar] [CrossRef]
- Bache, F.; Wloka, J.; Sasdrich, P.; Gueneysu, T. Multivariate TVLA—Efficient Side-Channel Evaluation using Confidence Intervals. IEEE Trans. Comput. 2023, 74, 790–804. [Google Scholar] [CrossRef]
- Jung, S.; Jin, S.; Kim, H. A Novel Side-Channel Archive Framework Using Deep Learning-Based Leakage Compression. IEEE Access 2024, 12, 105326–105336. [Google Scholar] [CrossRef]
- Gupta, P.; Ramaswamy, A.; Drees, J.P.; Hüllermeier, E.; Priesterjahn, C.; Jager, T. Automated Information Leakage Detection: A New Method Combining Machine Learning and Hypothesis Testing with an Application to Side-channel Detection in Cryptographic Protocols. In Proceedings of the 14th International Conference on Agents and Artificial Intelligence. Science and Technology Publications, Virtual, 3–5 February 2022; Volume 2, pp. 152–163. [Google Scholar] [CrossRef]
- Saha, S.; Alam, M.; Bag, A.; Mukhopadhyay, D.; Dasgupta, P. Leakage Assessment in Fault Attacks: A Deep Learning Perspective. Cryptology ePrint Archive. 2020. Available online: https://eprint.iacr.org/2020/306 (accessed on 20 December 2024).
- Moos, T.; Wegener, F.; Moradi, A. DL-LA: Deep Learning Leakage Assessment: A Modern Roadmap for SCA Evaluations. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 2021, 552–598. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Liu, Z.; Tang, M.; Ren, S. Deep Learning Gradient Visualization-Based Pre-Silicon Side-Channel Leakage Location. IEEE Trans. Inf. Forensics Secur. 2024, 19, 2340–2355. [Google Scholar] [CrossRef]
- Yaman, F.; Mert, A.C.; Öztürk, E.; Savaş, E. A hardware accelerator for polynomial multiplication operation of CRYSTALS-KYBER PQC scheme. In Proceedings of the 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 1020–1025. [Google Scholar]
- Tunstall, M.; Goodwill, G. Applying TVLA to Public Key Cryptographic Algorithms. IACR Cryptol. ePrint Arch. 2016, 2016, 513. [Google Scholar]
- Wang, Y.; Tang, M. A Survey of Side-Channel Leakage Assessment. Electronics 2023, 12, 3461. [Google Scholar] [CrossRef]
- Avanzi, R.; Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Kyber algorithm specifications and supporting documentation. NIST PQC Round 2019, 2, 1–43. [Google Scholar]
- Bisheh-Niasar, M.; Azarderakhsh, R.; Mozaffari-Kermani, M. High-speed NTT-based polynomial multiplication accelerator for post-quantum cryptography. In Proceedings of the 2021 IEEE 28th Symposium on Computer Arithmetic (ARITH), Lyngby, Denmark, 14–16 June 2021; pp. 94–101. [Google Scholar]
- Inc., N.T. ChipWhisperer: An Open-Source Side-Channel Analysis Toolchain. 2025. Available online: https://github.com/newaetech/chipwhisperer (accessed on 15 January 2024).
- Chinbat, M.; Wu, L.; Zhang, X.; Batsukh, A.; Yang, Y.; Wu, L. Evaluating Side-Channel Attack Vulnerabilities in Post-Quantum CRYSTALS-Kyber Hardware Based on Simple Power Analysis. In Proceedings of the 2023 IEEE 17th International Conference on Anti-Counterfeiting, Security, and Identification (ASID), Xiamen, China, 1–3 December 2023; pp. 46–49. [Google Scholar]
- Dunford, R.; Su, Q.; Tamang, E.; Wintour, A. The pareto principle. Plymouth Stud. Sci. 2014, 7, 140–148. [Google Scholar]
- Tosun, T.; Savas, E. Zero-Value Filtering for Accelerating Non-Profiled Side-Channel Attack on Incomplete NTT based Implementations of Lattice-based Cryptography. IEEE Trans. Inf. Forensics Secur. 2024, 19, 3353–3365. [Google Scholar] [CrossRef]
- Ravi, P.; Jap, D.; Bhasin, S.; Chattopadhyay, A. Machine Learning Based Blind Side-Channel Attacks on PQC-Based KEMs-A Case Study of Kyber KEM. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 28 October–2 November 2023; pp. 1–7. [Google Scholar]
- Ji, Y.; Wang, R.; Ngo, K.; Dubrova, E.; Backlund, L. A side-channel attack on a hardware implementation of CRYSTALS-Kyber. In Proceedings of the 2023 IEEE European Test Symposium (ETS), Venezia, Italy, 22–26 May 2023; pp. 1–5. [Google Scholar]
- Ji, Y.; Dubrova, E. A Side-Channel Attack on a Masked Hardware Implementation of CRYSTALS-Kyber. In Proceedings of the 2023 Workshop on Attacks and Solutions in Hardware Security, Copenhagen, Denmark, 30 November 2023; pp. 27–37. [Google Scholar]
- Xu, Z.; Pemberton, O.; Roy, S.S.; Oswald, D.; Yao, W.; Zheng, Z. Magnifying side-channel leakage of lattice-based cryptosystems with chosen ciphertexts: The case study of kyber. IEEE Trans. Comput. 2021, 71, 2163–2176. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).