Abstract
This paper enhances the multikey scenario in the Gentry–Sahai–Waters (GSW) fully homomorphic encryption scheme to increase its real-world applicability. We integrate the advantages of two existing GSW multikey approaches: one enabling distributed decryption and the other reducing memory requirements. We also apply the CRT decomposition and ciphertext compression techniques to the multikey settings. While leveraging the effectiveness of decomposition, we adapt the compression technique for practical cryptographic applications, as demonstrated through simulations in federated learning and multiparty communication scenarios. Our work’s potential impact on the cryptography field is significant, as it offers a more efficient and secure solution for distributed data processing in real-world scenarios, thereby advancing the state of the art in secure communication systems.
1. Introduction
As modern communication systems evolve, secure data transmission among multiple users has become increasingly crucial. Multikey encryption schemes are valuable for supporting authorized users in encrypting and decrypting shared data. However, significant challenges arise when users attempt to decrypt messages with incorrect secret keys, introducing errors that hinder accurate decryption. This issue could be more problematic in systems requiring efficient decryption across multiple users, such as federated learning and collaborative computing environments.
Our work focuses on improving the Gentry–Sahai–Waters (GSW) [1] encryption scheme, a fully homomorphic encryption (FHE) scheme that allows for arbitrary computations on encrypted data, in multikey scenarios. Mukherjee et al. (2016) [2] proposed an additional expansion phase after encryption to solve failed decryption due to incorrect keys. We build on this by integrating the distributed decryption capability from Mukherjee’s approach with the additional help of the information memory reduction method from Shen et al. (2021) [3], aiming to create a more balanced solution that reduces total memory size while maintaining decryption efficiency.
We extend the Chinese Remainder Theorem (CRT) decomposition and ciphertext compression techniques from previous research [4] into the multikey context. CRT decomposition continues to expand the message range significantly, even in multikey scenarios, making simple operations like homomorphic addition more practical. While the previously referenced ciphertext compression method (Gentry and Halevi, 2019 [5]) proved ineffective for distributed decryption in multikey scenarios, we propose an improved approach to ease the shortage. Though the execution time and memory requirements will be increased somewhat, our approach ensures the system remains secure and feasible for distributed decryption.
This work makes the following contributions to the field of fully homomorphic encryption (FHE):
- We propose a balanced expansion method that reduces total memory overhead while enabling distributed decryption.
- By extending CRT decomposition, we significantly increase the message range within the GSW scheme, covering the entire plaintext space in multikey scenarios.
- We improve ciphertext compression, ensuring it supports distributed decryption without compromising the efforts of previous expansions.
These contributions enhance the GSW encryption scheme’s applicability, efficiency, and practicality in multikey settings, opening possibilities for real-world cryptographic applications.
1.1. Related Work
1.1.1. Fully Homomorphic Encryption (FHE)
The rapid rise of cloud computing and artificial intelligence has increased reliance on remote data processing, raising significant security concerns. Fully homomorphic encryption (FHE) addresses this by enabling computations on encrypted data without decryption. Proposed by Rivest, Adleman, and Dertouzos [6] in 1978, FHE became practical with Gentry’s breakthrough in 2009 [7]. However, early schemes suffered from excessive noise and large ciphertexts, causing inefficiencies and decryption failures after limited operations.
Subsequent generations of FHE schemes aimed to improve efficiency and reduce noise. The second generation, including BV [8,9], BGV [10], and B/FV [11] schemes, allowed computations on integer vectors but still faced noise management challenges. The third generation, including GSW [1], FHEW [12], and TFHE [13], significantly improved noise handling but sacrificed data packing support.
The CKKS scheme [14] prioritizes optimized packing for efficient vector operations and calculations on real numbers. While its bootstrapping is less advanced than the third generation, CKKS significantly reduces computation time per operation, making it practical for real-world applications requiring efficient and secure data processing.
Recently, a series of studies have also focused on identity-based or multi-identity FHE constructions, which are closely related to the multikey setting [15,16,17].
1.1.2. Ciphertext Compression
Ciphertext compression has become increasingly important in encryption systems because it reduces the encrypted data’s storage and transmission overhead. Gentry and Halevi (2019) [5] introduced a compressible GSW scheme, addressing the significant storage costs associated with large volumes of ciphertext. Their work has inspired further research into adapting these techniques for multikey encryption systems.
Building on this, Shen et al. (2021) [3] extended ciphertext compression to multikey settings, effectively reducing the substantial memory requirements of expanded ciphertexts. However, it was less effective in practical distributed decryption applications. This limitation arises because the compression technique in [3] introduces correlations that can lead to message leakage, making it less reliable in distributed decryption scenarios. In response, we adapted the technique for multiparty communication scenarios to demonstrate its feasibility and potential for securely managing data across multiple users.
Our results indicate that while our approach currently requires significant computational resources for real-world cryptographic operations, it shows considerable promise in enhancing the functionality of the GSW multikey scheme.
1.2. Organization
This writeup is structured as follows: Section 2 introduces the complete encryption process of the GSW multikey scenario. Section 3 discusses two important expansion methods and our proposed balanced approach. Section 4 and Section 5 explore the application of previously researched [4] CRT decomposition and ciphertext compression techniques to the multikey setting, respectively. Section 6 presents various experimental results. Section 7 concludes the writeup with a summary and directions for future research.
2. Multikey Scheme for GSW-like Encryption
In a multi-user or multikey environment, it is essential to guarantee that other authorized users can correctly decrypt encrypted ciphertexts generated by each user to recover the original message. In the single-key scenario, when a user decrypts a message using their secret key, they can retrieve the intended message without issue. However, in a multi-user context, users will inevitably attempt decryption with wrong secret keys, making it challenging to maintain security while ensuring successful multikey operations. We will briefly review the complete GSW multikey encryption and decryption processes, followed by a discussion of distributed decryption, particularly relevant to multi-user or multiparty environments.
2.1. Notation
Before introducing the detailed key generation and encryption steps, we summarize the main notations used throughout this section:
Additional notations follow standard conventions in the LWE/GSW literature.
| Symbol | Meaning |
| G | Public gadget matrix for bit decomposition in GSW encryption |
| X | Pseudo-ciphertext generated during expansion |
| f | Mapping function used in ciphertext compression |
| Plaintext message | |
| Public key of user | |
| Secret key of user | |
| Random matrix selected during encryption | |
| LWE-related vectors used in key generation |
2.2. Key Generation
In the multikey scheme, all users possess the public keys of every other user, while each user retains only their secret key due to its sensitive nature. In a system with N users, user selects a message, encrypts it, and distributes the result to all other users for decryption. The scheme operates as follows:
- All users agree on a common matrix A from , where .
- Each user independently selects a random vector from and a vector from the distribution , which conforms to an integer-normal modulo q.
- Users then compute their vectors as , following the Learning with Errors (LWE) scheme, which was introduced by [18].
- Finally, users define their public keys and secret keys as and , respectively, and ensure that the product confirms the error model of LWE.
2.3. Encryption
The authors of [4] discovered that the error can be flexibly adjusted; both users can select their messages from the range , where and each user independently selects a random matrix . They then proceed to encrypt their messages using their respective public keys. The ciphertexts are computed as:
where . Therefore, the encryption outputs will significantly differ due to the variations in the chosen parameters.
2.4. Expansion
To ensure successful multikey execution, Mukherjee et al. [2] demonstrated that an additional expansion step is required after encryption compared to the single-key scenario. Although this increases ciphertext size, it is necessary for successful decryption of the final result.
2.4.1. Initial [2] and Our Modified Expansion
Due to our balanced approach (detailed in the next section), the final expanded ciphertext structure matches that of Mukherjee et al. [2]. For user , we need to find a “pseudo-ciphertext” that satisfies two conditions:
- , where such that and .
- .
The detailed construction of pseudo-ciphertext will be presented in Section 3.
The resulting expanded ciphertext becomes
which follows a fixed pattern. The main diagonal contains the previously encrypted ciphertext, with the number of identical ciphertexts corresponding to the number of users. The -th row is filled with all pseudo-ciphertexts, where the horizontal axis represents the user sending this information, and the vertical axis represents users receiving auxiliary information. The remaining positions contain zeros.
2.4.2. Advanced Expansion [3]
Shen et al. [3] proposed reducing the expanded ciphertext size, but this method requires splitting the previous pseudo-ciphertext into two parts. Consequently, user now needs pairs of pseudo-ciphertexts ( and ) that satisfy the following three conditions:
- , where such that .
- .
- .
The detailed construction of these pseudo-ciphertexts will be shown in Section 3. The final expanded ciphertext becomes
where , , , , and , with
Moreover, the expanded ciphertext follows a fixed placement pattern. The arrangement on the top left follows the same pattern as in Equation (1), but this time the main diagonal contains . The remaining space is filled with pseudo-ciphertexts, which are now divided into two parts, and . The first pseudo-ciphertext is placed here. Next, the bottom left and top right sections are arranged according to the sender’s position. The bottom left contains , while the top right holds . The remaining part of the bottom left section contains the second pseudo-ciphertext, and the rest of the top right section is filled with zeros. Finally, the bottom right section only contains .
2.5. Decryption
When other users attempt direct decryption with their wrong secret keys, they only recover approximate results. When user attempts decryption with their secret key, it can be expressed as follows:
where , and represents a significant error term. The additional term “” introduces significant errors, leading to incorrect results. Furthermore, since is a random matrix used by user during encryption and is not shared, other users cannot independently resolve this issue. This necessitates additional assistance from user to eliminate the “” term, which explains the need for the expansion step.
2.5.1. Combined Decryption
Since our method produces results for the pseudo-ciphertext consistent with those in the initial expansion, we consider the initial and our expansion as one group for decryption, while treating the advanced expansion as a separate group.
Initial and Our Approaches
Suppose there are N users, and the combined secret key is simply the concatenation of all secret keys:
In this case, the decryption process is
where all additional errors initially generated by the users are successfully canceled. However, since is also encrypted, the decryption process still introduces a small additional error (). Although the original more significant additional errors () are successfully eliminated, the final error magnitude remains slightly higher than that of users decrypting with the correct secret key.
Follow-Up Approach
Later, Ref. [3] discovered in Equation (2) that simply combining all secret keys would repeatedly include multiple “1”s. They suggested that these repeated “1”s could be omitted, keeping only a single “1” at the end. Thus, the combined secret key is adjusted to:
The decryption process then becomes
and thereafter, these can be divided into three parts and calculated separately,
- 1.
- 2.
- 3.
Therefore, we now know
In this setup, the first user can attempt to derive the correct answer by outputting from the first and last elements, . Similarly, the second user can attempt to derive the correct answer by outputting from the second and last elements, and so on.
Output
At this stage, irrespective of the specific expansion method employed for decryption, we adopt the same approximate method as in [4] since it is more straightforward to understand. Ultimately, all methods enable users to extract the desired message values accurately.
2.5.2. Distributed Decryption
However, combining all users’ secret keys during the decryption process raises security concerns in real-world applications. Therefore, we will examine whether these three methods can be successfully executed in a distributed decryption scenario.
Figure 1 is divided into two sections: the left side represents the combined decryption scenario, while the right side depicts the distributed decryption scenario. The distributed decryption section is further subdivided to show the elements that each user can decrypt (rows) and all the required elements (columns). For simplicity, the figure assumes only two users, with the message selected from the first user.
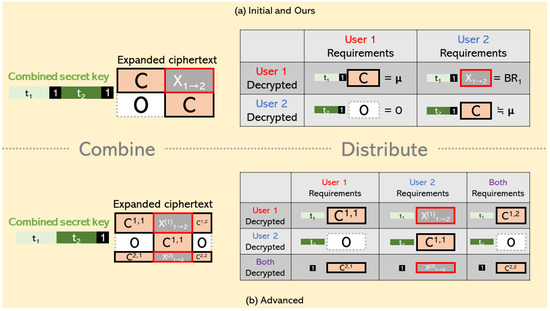
Figure 1.
Three methods for executing combined and distributed decryption scenarios.
Initial and Our Approaches
Firstly, as shown in Figure 1a, we observe that distributed decryption is carried out according to each user’s designated section, regardless of the process. In this setup, users pre-arrange an order. Each user then decrypts all elements of a specific row in the expanded ciphertext using their secret key according to their sequence.
For instance, the first user will decrypt the elements in their designated row, resulting in outputs and . The second user will decrypt their designated row similarly, producing outputs and . Since the first user selects the message, the result after decryption represents the encrypted message, while from the second user does not yield the message after decryption. In this setup, from the first user serves as auxiliary information () that needs to be transmitted to the second user. This ensures that all users obtain the necessary elements they need. Therefore, this indicates that distributed decryption is valid for both the initial and our method.
Follow-Up Approach
Due to the combined secret key adjustments, each user’s secret key must be split for decryption. Thus, in addition to decrypting their designated sections with the first part of their secret key, all users will also decrypt the last row of the expanded ciphertext.
In this case, the two users in the figure can each decrypt six elements. Both users lack two elements that they cannot obtain independently. Specifically, the first user lacks elements and , while the second user lacks elements and . Under our assumptions, the elements the first user lacks are all zeros, so they do not affect their ability to decrypt the message.
For the second user, element can be obtained by having the first user transmit it. However, even though the first user can decrypt element , it contains parts of the selected message, making it impossible to communicate with the second user. Therefore, the second user cannot obtain all the necessary elements through distributed decryption. Consequently, distributed decryption is not applicable in this scenario.
2.5.3. Noise Considerations
The proposed balanced expansion and compression are structural optimizations of ciphertext representation. These steps do not modify the underlying error distribution but only reorganize ciphertext components to reduce memory overhead. Therefore, the noise behavior essentially follows the same bounds as in Hu et al. [4]. Since no additional approximation error is introduced, the correctness guarantee of decryption is preserved in both single-key and multikey settings.
3. Multikey Expansion Methods
As previously mentioned, decryption attempts with wrong secret keys pose significant challenges in a multi-user context. To address this, Ref. [2] proposes incorporating an additional “expansion” stage following the encryption process. We will now demonstrate the generation methods for all pseudo-ciphertexts mentioned in the three expansion approaches. Section 3.1 and Section 3.3 will introduce those two existing expansion methods. Furthermore, we will combine both techniques to achieve a balanced approach, ultimately resulting in a new method applicable to multikey encryption, which will be presented in Section 3.2.
3.1. Initial Expansion [2]
3.1.1. Masking Scheme
To achieve the expansion, Ref. [2] proposes using the “masking scheme” introduced in [19]. The masking scheme requires the first user to generate significant additional helper information about the ciphertext during the encryption phase. This involves encrypting the matrix from the ciphertext equation.
Since the GSW scheme can only encrypt one scalar at a time, this generates additional helper information. Thus, is represented as , where
with and being different in each . These are then used in conjunction with all users’ vectors to compute the pseudo-ciphertext .
3.1.2. Homomorphic Linear Combination
Since all elements of are now individually encrypted into a matrix, the original “” can no longer be used. Therefore, it must be transformed into an expression that can be used within the encrypted domain. To achieve this, Ref. [2] proposes a method called “Homomorphic Linear Combination,” which is represented by
where is defined as
We can now prove the first condition for both the initial and modified expansions.
Proof.
□
Therefore, holds. The second condition can then be derived straightforwardly.
3.2. Our Modified Expansion
Subsequent experiments revealed that the expansion stage caused a significant increase in processing time, which consumed almost 90% of the entire encryption and decryption time. This is because the involvement of random matrix is crucial, and the GSW encryption scheme only encrypts one scalar at a time. As a result, the matrix requires encryptions, consuming most of the processing time. Every element in is essential for maintaining decryption accuracy, making it impossible to reduce the number of elements as a means of improvement.
Examining Equation (4) reveals that the upper half of the matrix is just a zero matrix. In practice, only the last ℓ columns of additional helper information are helpful for subsequent computations. Therefore, we considered adjusting the size of this additional helper information and modifying the matrix to remove the upper zeros in the resulting matrix. These adjustments significantly reduce both the execution time and memory usage. Ideally, the time and space required for the expansion stage could be reduced nearly times. After these adjustments, Equations (3), (4), and (5) are respectively transformed into
During the final execution of the homomorphic linear combination, our approach does not alter the resulting pseudo-ciphertext .
3.3. Advanced Expansion [3]
Their original method was designed for encryption schemes using a matrix secret key. However, since the previous two expansion methods were applied to vector secret keys, we adapted their concept and approach to work with vector secret keys for comparison purposes. Consequently, the observed improvement will be less significant than when applied to matrix secret keys. The original method from their paper is included in Appendix A.3 for reference.
3.3.1. Additional Helper Information
Upon further examination of Equation (6), it is evident that the information regarding is zero except for the last row. This insight led to the idea of splitting the additional helper information into upper and lower halves, as shown in the following
where must be the same in that pair of and .
Given the importance of the random matrix for encrypting the message, any adjustments to the expanded ciphertext and combined secret key necessitate changes in the decryption process. Following their method, the public key error introduced using a wrong secret key affects only . Since , the crucial matrix now requires encryption of only the elements in the first columns, consequently reducing the necessary additional helper information from to . This adjustment decreases memory usage by a factor of .
Additionally, due to the changes in the additional helper information, the calculation of subsequent Equation (8) also changes; that is
Initially, it required , but now it only needs .
3.3.2. Pseudo-Ciphertext
Due to the additional helper information changes, the pseudo-ciphertext is now divided according to
The first two conditions mentioned earlier can now be proven correct.
Proof.
- 1.
- 2.
□
Since the first two conditions are confirmed to be accurate, the final condition can be derived naturally.
4. Decomposition with Multikey
At this point, we extended the decomposition approach [4] to multikey scenarios. Although the performance gains in multikey were not as pronounced as in single-key scenarios, they were still notable. The entire decomposition process is illustrated in Table 1.

Table 1.
All benchmarked vector secret key schemes’ decomposition processes.
4.1. Homomorphic Addition in Multikey
When applying homomorphic addition to multikey encryption, two scenarios can occur: the messages being added are either from the same user (same key) or different users (different keys). Since we aim to simulate practical applications, the expanded ciphertext supports distributed decryption. We use the balanced method proposed in Section 3.2 for more effective experimentation.
Previous discussions indicate that auxiliary information involved in encryption and expansion introduces errors during decryption. This error increases when the information is sent to users with a wrong secret key. Consequently, the message range’s upper bound will decrease again.
4.1.1. Same Key Situation
We know that users decrypting with the wrong secret key will encounter additional errors. In the same key scenario, both messages are not chosen by the user with the wrong secret key, resulting in a double magnitude of additional errors for that user. For simplicity, assume there are only two users and messages are selected from the first user,
where , and . Although the correct calculation can ultimately be recovered with the help of auxiliary information, the cumulative error from these two messages may reach a critical threshold to fail the desired FHE computation.
4.1.2. Different Key Situation
Since both users will receive one message that they did not choose in the different key scenarios, on the one hand, the recovered result for each will include additional errors; on the other hand, these errors may contribute to providing both users with some buffer information to tolerate the error. That is,
where , and .
From the above derivation, the cumulative errors corresponding to the two users with different key scenarios consist of the correct-key and wrong-key user cases in the same key scenario, as shown in Table 2. If both scenarios involve additional homomorphic addition operations, the same key scenario will likely fail due to excessive errors generated by the second user. In contrast, different key scenarios still have a chance of success in eliminating the error because each user has some extra information provided by their computational counterpart.

Table 2.
Comparison of accumulated errors for both cases when users withhold the correct and wrong keys.
4.1.3. CRT Decomposition in Multikey
We now apply the CRT decomposition method to both scenarios. Due to the nature of the CRT decomposition, which is carry-free, parallel addition operations can be straightforwardly conducted. Since our method can continuously increase the message range’s upper bound , both users can freely choose within the entire plaintext space without restrictions.
4.2. Federated Learning
Due to the incorporation of CRT decomposition, our derived multikey FHE scheme allows for unrestricted message selection, which enables the possibility of executing multiple consecutive homomorphic additions without decryption. To demonstrate the scheme’s effectiveness, we devised a simple application for federated learning. Suppose N users participate in the computation to aggregate all their numerical data. The process is broken down into the following multiple steps and involves two rounds of communication:
- 1.
- Initial Setup. The user in the i-th position (i.e., geometric location number) possesses all users’ public keys and his own secret key, .
- 2.
- Message Selection, Encryption, and Expansion. Each user selects a message , conducts CRT decomposition, and encrypts the results. Due to differing keys, the pre-described expansion is required to prepare auxiliary error-correcting messages for other users.
- 3.
- First Communication Round. The computed expanded ciphertexts are uploaded to the cloud.
- 4.
- Homomorphic Addition. The cloud performs homomorphic addition on the N-expanded ciphertexts without decrypting them.
- 5.
- Return Result. The cloud returns the encrypted computed result to all users, who then decrypt the result according to their position-dependent decryption key , concluding the first round of communication.
- 6.
- Error Identification. The decrypted results will likely be incorrect since users will have many extra intermediaries that are not locally selected and generated.
- 7.
- Second Communication Round. The second round of communication begins as users decrypt various intermediate data and upload them to the cloud. Specifically, each user i uploads all decrypted intermediate data except those in their own designated region, that is, user i uploads decrypted data from regions 1 to and to N.
- 8.
- Classification and Final Result. The cloud classifies the received data according to each user’s needs and sends them back to the corresponding user. Each user then aggregates all received data to obtain the correct computation result.
These eight steps complete the basic federated learning application process. Following the steps mentioned above, we conducted a preliminary experiment to check if the learning process could be successfully executed. The purpose of this experiment was solely to determine the availability of execution, so no charts were generated to illustrate the effects under different security parameters. We compared the original method without decomposition and the one with CRT decomposition. To ensure practical applicability, the range of messages was allowed to be arbitrarily selected from the entire plaintext space. The CRT-involved experimental results are justified and consistent with our previous findings when the original setting is adopted. The following are some observations we obtained:
- 1.
- Original Method Without Decomposition. Even with a simple case of , the original method proved challenging due to the complexity of a single operation with an arbitrarily chosen message range, making it difficult to complete even one round of the federated learning process.
- 2.
- Method with CRT Decomposition. Although our method currently needs to work on performing many consecutive operations without intermediate decryption, experiments verify that this approach can at least successfully execute one round of federated learning in the case of , and it even has the possibility of success for .
Although our results have yet to be ready for practical application, our experimental results reveal that the GSW multikey scheme has this potential if ample computation resources are provided.
5. Multikey Ciphertext Compression
Our previous work on single-key schemes [4] found that processing and transmitting encrypted data requires substantial storage capacity. An additional expansion is necessary in the multikey context, resulting in an even more considerable memory requirement for the expanded ciphertext. Therefore, any method that can compress the involved data within these schemes would be incredibly beneficial. Consequently, we apply the PVW-like compression technique proposed in [5] to the multikey scenarios. Additionally, Ref. [3] used this compression method for the expansion approach described in Section 3.3. In the rest of this section, we extend the same compression technique to the other two expansion approaches where secret keys are in vector form.
For ease of explanation, we continue to assume only two users exist and now let the second user select the message. From the discussions on single-key schemes [4], we knew that message decomposition is necessary before compression is applied. By CRT, the original message will be split into sub-messages with smaller value ranges; let and , respectively, denote corresponding sub-messages in the plaintext and the ciphertext domains.
Since expansion is essential in the multikey settings, we write down the associated mathematical forms in the following. For Section 3.1 and Section 3.2, the ciphertext will be expanded into
while for Section 3.3, the ciphertext will be expanded into
5.1. The Compression Incurred Problems
We encountered several issues when we tried to apply the technique presented in [3], which was initially used on the matrix secret key, to the case with the vector secret key.
5.1.1. Waste of Pseudo-Ciphertext
When their ideas are transformed and applied to Section 3.3, the compression formula becomes:
Since these ciphertexts were previously expanded, must also be expanded to a vector of length .
We observed an interesting fact during the above-mentioned vectorize-key expansion. That is, when we visualize the compression formula, it becomes apparent that only the last ℓ columns of the computation are involved. Regardless of whether the first or second user chooses the message, the pseudo-ciphertext , which took the most time to compute, is not used. This means the additional helper information and the corresponding pseudo-ciphertext are wasted. This issue also appears in Section 3.1 and Section 3.2; that is
5.1.2. Unable to Handle Distributed Decryption
Exploring the potential application of the GSW encryption scheme in real-life scenarios, we attempted to implement distributed decryption. Since the pre-described advanced expansion cannot apply to distributed decryption, we used the compression technique for the initial and the modified expansions. That is, as follows
- 1.
- Initial Setup. Both users select their public keys, , and secret keys, , with all public keys publicly accessible.
- 2.
- Message Selection, Encryption, and Expansion. The second user selects the message and splits it by using bit-level decomposition, . Each of the sub-messages is then encrypted and expanded separately.
- 3.
- First Communication Round. All expanded ciphertexts are uploaded to the cloud.
- 4.
- Ciphertext Compression. The cloud compresses all received expanded ciphertexts. According to [3], only the last ℓ columns are utilized during this stage. Therefore, the compressed result becomes
- 5.
- Return Result. The cloud returns the compressed ciphertext to all users, who decrypt the received data according to their position-dependent secret keys.
- 6.
- Error Identification. The second user can decrypt and retrieve the correct message, while the first user will only obtain a zero, as shown in Table 3.
 Table 3. Decryption outcomes for the first and the second users.
Table 3. Decryption outcomes for the first and the second users. - 7.
- Second Communication Round. As before, the second user cannot decrypt any auxiliary information to assist the first user; therefore, the second round of communication is a must. Since uploading the decrypted message directly to the cloud is impractical, the first user needs help to recover the message.
5.2. The Proposed Multikey Ciphertext Compression
Our work focuses on adjusting [3]’s compression technique to solve the two problems mentioned in the previous subsection. By transforming Equation (9) used in Section 3.1 and Section 3.2 into
we can solve the “Waste of Pseudo-Ciphertext” and the “Unable to Handle Distributed Decryption” issues simultaneously. In other words, our proposed multikey ciphertext compression scheme brings the following benefits: the efficient utilization of pseudo-ciphertext and successful implementation of distributed decryption.
5.2.1. Efficient Utilization of Pseudo-Ciphertext
Our main idea is to increase the dimension of the transformation proportional to the number of users. Let denote the dimension-extended transformation of , defined as . This adjustment expands the range of ciphertext involved in the compression calculation to incorporate the previously wasted pseudo-ciphertexts into the account. Thus, the first issue in the previous subsection is solved.
5.2.2. Successful Implementation of Distributed Decryption
We devised a simple example using a multiparty communication method to demonstrate how to solve the second issue. In this case, for the n-th user, the goal is to ensure that all other users can receive the messages he selected and generated, even after compression. Our proposed scheme consists of the following steps:
- 1.
- Initial Setup. Assume all N public keys are publicly accessible, while the secret keys are exclusively owned by their respective holders.
- 2.
- Message Selection, Encryption, and Expansion. Let the n-th user select a message, split it into multiple sub-messages based on CRT and the selected moduli, and perform encryption and expansion operators.
- 3.
- First Communication Round. All expanded ciphertexts are uploaded to the cloud.
- 4.
- Ciphertext Compression. The cloud implements our modified compression method, making compressed ciphertexts significantly more prominent. As a result, the compressed result becomes
- 5.
- Return Result. The cloud then sends the compressed ciphertexts to all users, who decrypt the results according to their position-dependent secret key.
- 6.
- Error Identification. Since the n-th user selects the message, the decryption will be successful, while other users will fail to decrypt, as shown in Table 4.
 Table 4. Decryption outcomes for all users.
Table 4. Decryption outcomes for all users. - 7.
- Second Communication Round. Our proposed adjustment effectively utilizes pseudo-ciphertexts, allowing the n-th user to decrypt auxiliary information, which is then uploaded back to the cloud.
- 8.
- Classification and Final Result. Finally, the cloud distributes the auxiliary information to each user as needed. After recombination through a multipart communication process, all users can successfully receive the message, that is, .
With the aid of a simple multiparty communication process, this example demonstrates that our adjustment, despite producing a larger amount of compressed results than [3], effectively utilizes pseudo-ciphertexts, facilitating the desired applicability of distributed decryption. This improvement provides a higher potential for practically applying the GSW encryption scheme.
6. Experiments
We will compare and analyze all previously discussed content through numerical experiments, dividing them into comparing the three expansion methods and analyzing the CRT decomposition and compression techniques applied to the multikey scenario. All actual numerical data in our figures will be presented in Appendix B.
6.1. Comparative Analysis of Three Expansion Methods
This subsection compares various aspects of the expansion schemes, such as the execution time of completing encryption and decryption processes, the ciphertext size before the final decryption, the memory space required for all additional helper information, and the impact of these methods on the upper bound of the message range.
6.1.1. Memory Sizes for the Expanded Ciphertext and the Additional Helper Information
Figure 2 illustrates the size of all additional helper information required for executing the three expansion methods and the final expanded ciphertexts. The first three items in the figure represent the size of the additional helper information for each involved technique; the corresponding measure is on the right vertical axis in MB. The latter four items show the expanded ciphertext size before final decryption for a single key and the three expansion schemes; the corresponding measure is on the left vertical axis in KB.
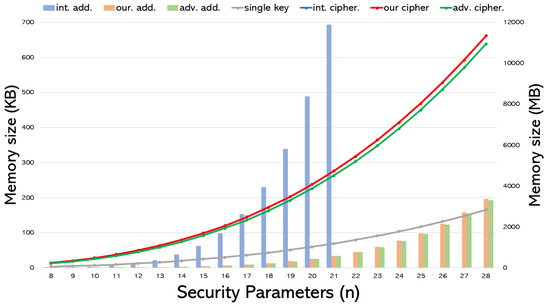
Figure 2.
Comparison of expanded ciphertext and additional helper information’s sizes across various expansion schemes.
From Figure 2, several remarks can be drawn accordingly:
- Since our proposed improvement primarily focuses on enhancing the additional helper information without altering the expanded ciphertext, the size of the additional helper information is significantly smaller than that of the initial method. In contrast, the expanded ciphertext size remains consistent with the initial process. However, the advanced approach effectively adjusts the expanded ciphertext and the additional helper information. Consequently, the advanced approach performs better in both aspects.
- Regardless of the adopted expansion method, the memory space required is significantly greater than that for single-key encryption. Both the initial and our derived methods resulted in a fourfold increase compared to the single key’s size. In contrast, the advanced approach results in it being approximately times the original size. Although multikey encryption is more practical in real-world scenarios, it inevitably faces a heavy burden in memory space.
6.1.2. Execution Time
The total execution times required for the entire encryption process using three different expansion methods are shown in Figure 3. We additionally included the time needed to execute the single-key method for comparison. The horizontal axis represents the security parameter n, where a higher value indicates a greater security level, while the vertical axis represents the execution time in milliseconds.
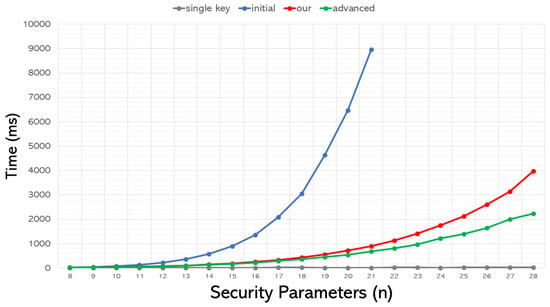
Figure 3.
Comparison of the time required for various expansion schemes to execute the encryption process.
From Figure 3, several remarks can be drawn accordingly:
- Evidently, both our and the advanced approach significantly outperform the initial method. Moreover, the time required for the advanced approach is even less than that needed for our proposed process.
- Although, with the aid of compression, both our and the advanced approach have significantly reduced the execution time, it is still considerably higher than the time required for the single-key scenario. Therefore, while the multikey approach is more applicable to real-world scenarios, it necessitates further research to speed up the execution and ensure affordable applicability.
6.1.3. Upper Bound of the Message Range
As previously addressed, users decrypting with the wrong secret key will inevitably generate additional errors after expansion. This fact makes reducing the message range’s upper bound a must as the security parameter n increases. We conduct a thorough simulation associated with this consideration to understand the concrete trend of the relationship between the growth in n and the increase in message range for various multikey scenarios. The results are shown in Figure 4, where the vertical axis represents the upper bound , expressed logarithmically. Additionally, due to its high memory requirements and execution time, the initial method is excluded from this experiment.
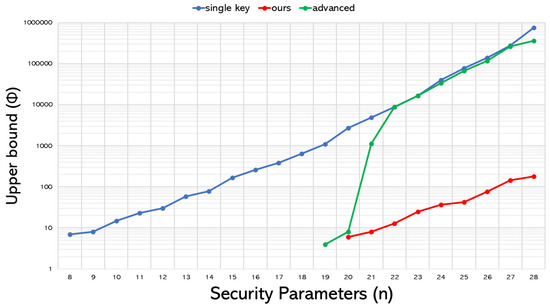
Figure 4.
Impacts of various expansion schemes on the message range’s upper bound in the multikey scenario.
From Figure 4, several remarks can be drawn accordingly:
- Our proposed method (colored in red in Figure 2) significantly reduces the upper bound compared to the correct key (single-key) condition. This reduction is necessary to ensure the successful operation of the multikey system, clearly reflecting the substantial impact of the additional error on the upper bound of the message range.
- Examining the results of the advanced approach reveals an unexpected phenomenon: from onwards, its required upper bound is almost identical to that of the original single-key counterpart. As previously addressed, the first user is responsible for integrating the first and the last elements after the completion of decryption, that isNotice that this integration resembles concatenation more than linear combination; therefore, the error does not accumulate. Instead, the first user provides two different elements to output. Knowing that the first element carries a significant error, the first user primarily uses the second element to derive the correct message. This finding allows for a substantial increase in the message range’s upper bound.
6.1.4. Concluding Remarks
Finally, we aggregate all the comparisons of these three expansion schemes into Table 5. The advanced approach excels in every category except for its inability to perform distributed decryption. We sought a balance between these two competing schemes ([2,3]) because distributed decryption is indispensable in real-world applications by combining the distributed decryption technique (cf. Section 3.1) with the effective reduction technique of additional helper information, presented in Section 3.3.

Table 5.
This table presents the integration of all performance comparison results, which are crucial for understanding the effectiveness of our proposals.
While our balanced method (indicated as Ours in Table 5) ranks second in all categories, its experimental results are nearly identical to those of the advanced approach. In other words, this combined approach effectively reduces complexity and enhances its applicability in real-world applications.
6.2. Analyzing the CRT Decomposition and Compression Techniques
Next, we will examine the impacts on the message range’s upper bound when applying the previously proposed CRT decomposition [4] and the compression techniques mentioned above to multikey scenarios. Additionally, we will briefly illustrate how the upper bound changes when performing homomorphic addition in a multikey use case, explicitly comparing the same key and different key scenarios. We aim to verify whether these changes align with our expectations.
6.2.1. Upper Bound
Figure 5 shows the upper bound simulation results associated with CRT decomposition and our suggested compression technique in single-key and multikey scenarios. It contains seven entries: the first indicates the minimum number of moduli required for CRT decomposition, followed by three entries showing the upper bound for single-key scenarios without applying any techniques, using CRT decomposition only, and using both CRT and compression. The last three entries correspond to those of multikey scenarios. The left vertical axis represents the logarithmic upper bound , while the right axis shows the number of moduli. There are no values for cases where a simple message with 0 or 1 fails.
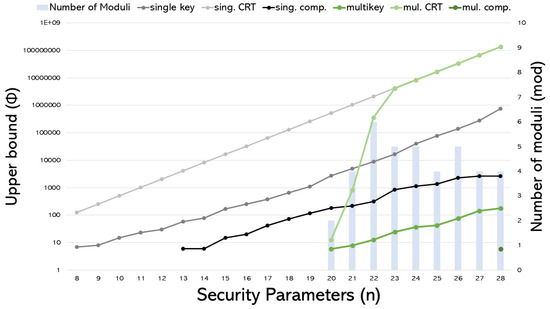
Figure 5.
Upper bound comparisons of the effectiveness of CRT decomposition and compression techniques in single-key and multikey scenarios.
From Figure 5, several remarks can be drawn accordingly:
- Our proposed CRT decomposition method [4] significantly increases the upper bound in both scenarios. Due to initially small upper bounds in multikey scenarios, is needed for conducting unrestricted upper bound selection during decomposition. Additional errors generated from wrong secret key decryption (in multikey scenarios) do affect the CRT decomposition’s obtainable upper bound. For instance, at , the ideal upper bound of will be reduced to 13 due to the wrong-key induced errors.
- Compression noticeably decreases the upper bound in both scenarios. Although multikey with compression limits the message range’s upper bound to a tiny value of 6, our suggested new compression method enables simple distributed decryption, which emulates real-world use cases more and increases its potential for practical usage.
6.2.2. Addition Operations in Multikey
Figure 6 depicts the impact on the message range’s upper bound when performing one homomorphic addition operation without CRT decomposition in the same-key and different-key scenarios. The “no addition" line represents the upper bound results of pure multikey scenarios. Performing any homomorphic operation, of course, will incur error accumulation, which in turn will reduce the allowable message range’s upper bound. As previously noted, users decrypting with the wrong secret key in the same-key scenario experienced faster error accumulation, resulting in a lower upper bound compared to the different-key scenarios.
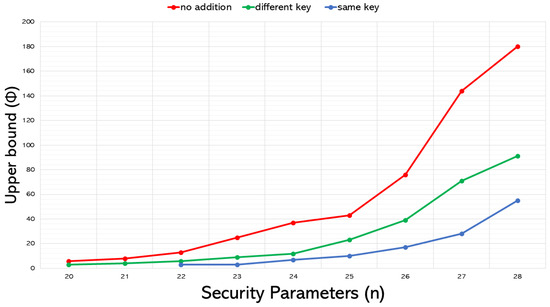
Figure 6.
Comparing the effect of performing a single homomorphic addition operation under the same-key and different-key use cases on the upper bound of the message range .
7. Future Works and Conclusions
Since the inclusion of multikey capacity to FHE schemes is crucial in modern cryptography, we proposed a feasible approach by combining methods originating from [2,3], with its applicability to distributed decryption as a critical consideration. This design will enhance the practicability of the GSW-FHE scheme in secure FML applications.
We have applied CRT decomposition and ciphertext compression techniques, suggested in our previous work [4], to the multikey scenario. CRT decomposition continues to increase the range of selectable messages effectively. Although the compression method presented in [4] seems somewhat impractical for distributed decryption use cases, we have proposed improvements to remedy this issue. While the improved scheme requires increased execution time and memory usage, it enhances the applicability of these techniques to everyday scenarios.
Although current results do not fully fit our desired expectations, they represent significant progress toward the practical deployment of the GSW-FHE schemes. Further work focuses on integrating homomorphic operations with ciphertext compression to expand the capability of direct operations on encrypted data, which is a must.
Reference [20] categorized recent advancements in multikey FHE, covering security assumptions, key generation, plaintext encryption, and ciphertext processing. Our work primarily enhances the ciphertext processing counterpart. We noted that public keys across users still share similarities, which may jeopardize the system’s security. Future work should focus on making public keys entirely distinct without affecting the decryption. Moreover, exploring and discussing other aspects of non-GSW multikey FHE schemes would no doubt be a viable research direction.
Regarding ciphertext processing, a recent work [15] discussed adjustments to extended ciphertexts. These adjustments maintain consistent dimensions across different design methods while preventing decryption failures, reducing computational overhead, lowering error levels, and supporting distributed decryption. Integrating our methods with that technology could achieve even higher effectiveness.
Author Contributions
Formal analysis, K.-W.H.; investigation, K.-W.H., W.-T.L., H.-C.W. and J.-L.W.; methodology, K.-W.H.; project administration, J.-L.W.; resources, J.-L.W.; algorithm development, K.-W.H.; supervision, W.-T.L., H.-C.W. and J.-L.W.; writing—original draft preparation, K.-W.H.; writing–—review and editing, W.-T.L., H.-C.W. and J.-L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Minister of Science and Technology, Taiwan (grant number: MOST 114-2221-E-002-101-MY3).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Matrix Secret Key
The key generation and encryption stages are nearly identical to the single-key approach when applied to the matrix secret key. The final expanded ciphertext in the expansion stage resembles the vector secret-key case’s structure. We will focus on deriving three components in the expansion stage: additional helper information , user public key combination , and pseudo-ciphertext , in this appendix.
Appendix A.1. The Initial Expansion Approach

Table A1.
Initial expansion component (matrix secret key).
Table A1.
Initial expansion component (matrix secret key).
| Initial Expansion [2] | |
|---|---|
| Additional helper information | |
| Public key combination | |
| Pseudo-ciphertext |
Table A1 presents the three components used in the expansion stage of Section 3.1, where . Following this, we need to prove that .
Proof.
□
Appendix A.2. Our Modified Expansion Approach

Table A2.
Our modified expansion component (matrix secret key).
Table A2.
Our modified expansion component (matrix secret key).
| Our Modified Expansion | |
|---|---|
| Additional helper information | |
| Public key combination | |
| Pseudo-ciphertext |
Since our modified expansion scheme focuses on reducing the memory size of the additional helper information, it does not affect the pseudo-ciphertext . In other words, the corresponding proof will be the same as that in Section 3.1, so we skip it here. Table A2 depicts the details of the three associated components.
Appendix A.3. The Advanced Expansion Approach
Next, in this subsection, we will detail the derivation of Section 3.3 for the matrix secret-key scenario; essentially, it follows the path adopted in [3]. However, we will slightly adjust the parameters to maintain consistency across various parameters. At this point, the three main components will be decomposed using the method addressed in Section 3.3. Table A3 illustrates the decomposed components in detail, where and .

Table A3.
Advanced expansion component (matrix secret key).
Table A3.
Advanced expansion component (matrix secret key).
| Advanced Expansion [3] | |
|---|---|
| Additional helper information | |
| Public key combination | |
| Pseudo-ciphertext | |
We must prove the following two formulas to obtain the above results
- ,
- ,
and demonstrate that as long as the error is within the tolerable range, the information can be correctly recovered after decryption; that is
Proof.
- 1.
- 2.
- where .
□
The correctness of the two properties is proven. Next, we will derive that the expanded ciphertext, upon decryption, also meets our desired outcome.
Proof.
and hereafter, these can also be divided into three parts and calculated separately,
- 1.
- 2.
- 3.
and therefore, we get
□
Appendix B. Numerical Data Associated with Previously Depicted Figures
This appendix details the numerical data associated with some previously depicted Figures. Table A4, Table A5, Table A6, Table A7 and Table A8 present the actual numerical results corresponding to Figure 2, Figure 3, Figure 4 and Figure 5 and Figure 6, respectively.

Table A4.
Numerical results depicted in Figure 2.
Table A4.
Numerical results depicted in Figure 2.
| n | Int. Add. (MB) | Our Add. (MB) | Adv. Add. (MB) | Single Key (KB) | Int. Cipher (KB) | Our Cipher (KB) | Adv. Cipher (KB) |
|---|---|---|---|---|---|---|---|
| 8 | 11.1154 | 1.7365 | 1.8126 | 3.625 | 14.125 | 14.125 | 12.4297 |
| 9 | 26.2816 | 3.5004 | 3.6037 | 5.1875 | 20.375 | 20.375 | 18.1875 |
| 10 | 56.6346 | 6.5782 | 6.6991 | 7.1563 | 28.25 | 28.25 | 25.5078 |
| 11 | 113.2161 | 11.6688 | 11.7830 | 9.5781 | 37.9375 | 37.9375 | 34.5781 |
| 12 | 212.7438 | 19.7228 | 19.7853 | 12.5 | 49.625 | 49.625 | 45.5859 |
| 13 | 379.5693 | 31.9971 | 31.9353 | 15.9688 | 63.5 | 63.5 | 58.7188 |
| 14 | 648.0419 | 50.1157 | 49.8214 | 20.0313 | 79.75 | 79.75 | 74.1641 |
| 15 | 1065.3169 | 76.1354 | 75.4562 | 24.7344 | 98.5625 | 98.5625 | 92.1094 |
| 16 | 1694.6486 | 112.6173 | 111.3467 | 30.125 | 120.125 | 120.125 | 112.7422 |
| 17 | 2619.2037 | 162.7037 | 160.5706 | 36.25 | 144.625 | 144.625 | 136.25 |
| 18 | 3946.4364 | 230.2005 | 226.8575 | 43.1563 | 172.25 | 172.25 | 162.8203 |
| 19 | 5812.8624 | 319.6649 | 314.6762 | 50.8906 | 203.1875 | 203.1875 | 192.6406 |
| 20 | 8390.4297 | 436.4991 | 429.3267 | 59.5 | 237.625 | 237.625 | 225.8984 |
| 21 | 11,891.7114 | 587.0491 | 577.0388 | 69.0313 | 275.75 | 275.75 | 262.7813 |
| 22 | 778.7087 | 765.0750 | 79.5313 | 317.75 | 317.75 | 303.4766 | |
| 23 | 1020.0299 | 1001.8395 | 91.0469 | 363.8125 | 363.8125 | 348.1719 | |
| 24 | 1320.8380 | 1296.9931 | 103.625 | 414.125 | 414.125 | 397.0547 | |
| 25 | 1692.3524 | 1661.5726 | 117.3125 | 468.875 | 468.875 | 450.3125 | |
| 26 | 2147.3130 | 2108.1165 | 132.1563 | 528.25 | 528.25 | 508.1328 | |
| 27 | 2700.1122 | 2650.7959 | 148.2031 | 592.4375 | 592.4375 | 570.7031 | |
| 28 | 3366.9318 | 3305.5508 | 165.5 | 661.625 | 661.625 | 638.2109 |

Table A5.
Numerical results depicted in Figure 3.
Table A5.
Numerical results depicted in Figure 3.
| n | Single Key | Initial | Our | Advanced |
|---|---|---|---|---|
| 8 | 11.32629 | 31.2462 | 20.5762 | 19.1362 |
| 9 | 11.9696 | 48.9721 | 27.5848 | 27.2867 |
| 10 | 16.13344 | 81.8141 | 37.5292 | 37.2534 |
| 11 | 16.0999 | 139.3046 | 54.4848 | 51.4700 |
| 12 | 11.232 | 224.6644 | 75.8383 | 71.8723 |
| 13 | 16.678 | 362.886 | 105.9568 | 96.2260 |
| 14 | 12.422 | 571.3308 | 143.1162 | 129.9968 |
| 15 | 15.81045 | 893.2118 | 191.0231 | 168.7586 |
| 16 | 11.605808 | 1354.1911 | 253.1195 | 219.2274 |
| 17 | 18.691 | 2095.8574 | 336.3979 | 286.0670 |
| 18 | 20.65821 | 3053.7333 | 439.8792 | 355.5583 |
| 19 | 16.8518 | 4644.4120 | 562.7427 | 449.0402 |
| 20 | 16.5372 | 6465.9700 | 711.9946 | 539.8311 |
| 21 | 11.775372 | 8963.0556 | 897.9344 | 683.5612 |
| 22 | 21.8364 | 1131.3810 | 812.7469 | |
| 23 | 22.2953 | 1420.6979 | 968.8638 | |
| 24 | 12.074 | 1749.3937 | 1219.1353 | |
| 25 | 23.3903 | 2131.9907 | 1396.8430 | |
| 26 | 21.4613 | 2601.7337 | 1637.0168 | |
| 27 | 17.24019 | 3135.2067 | 1996.0177 | |
| 28 | 28.2956 | 3982.5521 | 2227.3321 |

Table A6.
Numerical results depicted in Figure 4.
Table A6.
Numerical results depicted in Figure 4.
| n | Single Key | Ours | Advanced |
|---|---|---|---|
| 8 | 7 | ||
| 9 | 8 | ||
| 10 | 15 | ||
| 11 | 23 | ||
| 12 | 30 | ||
| 13 | 58 | ||
| 14 | 78 | ||
| 15 | 169 | ||
| 16 | 259 | ||
| 17 | 383 | ||
| 18 | 649 | ||
| 19 | 1106 | 4 | |
| 20 | 2724 | 6 | 8 |
| 21 | 4961 | 8 | 1139 |
| 22 | 8881 | 13 | 8844 |
| 23 | 16,851 | 25 | 16,836 |
| 24 | 40,185 | 37 | 33,990 |
| 25 | 78,165 | 43 | 68,005 |
| 26 | 138,984 | 76 | 117,119 |
| 27 | 277,512 | 144 | 262,287 |
| 28 | 750,000 | 180 | 361,583 |

Table A7.
Numerical results depicted in Figure 5.
Table A7.
Numerical results depicted in Figure 5.
| n | # of Moduli | Single Key | Sing. CRT | Sing. Comp. | Multikey | Mul. CRT | Mul. Comp. |
|---|---|---|---|---|---|---|---|
| 8 | 7 | 128 | |||||
| 9 | 8 | 256 | |||||
| 10 | 15 | 512 | |||||
| 11 | 23 | 1024 | |||||
| 12 | 30 | 2048 | |||||
| 13 | 58 | 4096 | 6 | ||||
| 14 | 78 | 8192 | 6 | ||||
| 15 | 169 | 16,384 | 15 | ||||
| 16 | 259 | 32,768 | 20 | ||||
| 17 | 383 | 65,536 | 42 | ||||
| 18 | 649 | 131,072 | 72 | ||||
| 19 | 1106 | 262,144 | 117 | ||||
| 20 | 2 | 2724 | 524,288 | 182 | 6 | 13 | |
| 21 | 4 | 4961 | 1,048,576 | 221 | 8 | 840 | |
| 22 | 6 | 8881 | 2,097,152 | 315 | 13 | 360,360 | |
| 23 | 5 | 16,851 | 4,194,304 | 840 | 25 | 4,194,304 | |
| 24 | 5 | 40,185 | 8,388,608 | 1155 | 37 | 8,388,608 | |
| 25 | 4 | 78,165 | 16,777,216 | 1365 | 43 | 16,777,216 | |
| 26 | 5 | 138,984 | 33,554,432 | 2310 | 76 | 33,554,432 | |
| 27 | 4 | 277,512 | 67,108,864 | 2618 | 144 | 67,108,864 | |
| 28 | 4 | 750,000 | 134,217,728 | 2652 | 180 | 134,217,728 | 6 |

Table A8.
Numerical results depicted in Figure 6.
Table A8.
Numerical results depicted in Figure 6.
| n | No Addition | Different Key | Same Key |
|---|---|---|---|
| 20 | 6 | 3 | |
| 21 | 8 | 4 | |
| 22 | 13 | 6 | 3 |
| 23 | 25 | 9 | 3 |
| 24 | 37 | 12 | 7 |
| 25 | 43 | 23 | 10 |
| 26 | 76 | 39 | 17 |
| 27 | 144 | 71 | 28 |
| 28 | 180 | 91 | 55 |
References
- Gentry, C.; Sahai, A.; Waters, B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In Proceedings of the Advances in Cryptology–CRYPTO 2013: 33rd Annual Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2013; pp. 75–92. [Google Scholar]
- Mukherjee, P.; Wichs, D. Two round multiparty computation via multi-key FHE. In Proceedings of the Advances in Cryptology–EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016; Proceedings, Part II 35. Springer: Berlin/Heidelberg, Germany, 2016; pp. 735–763. [Google Scholar]
- Shen, T.; Wang, F.; Chen, K.; Shen, Z.; Zhang, R. Compressible multikey and multi-identity fully homomorphic encryption. Secur. Commun. Netw. 2021, 2021, 6619476. [Google Scholar] [CrossRef]
- Hu, K.W.; Wang, H.C.; Lin, W.T.; Wu, J.L. Optimizing Message Range and Ciphertext Storage in Gentry–Sahai–Waters Encryption Using Chinese Remainder Theorem and PVW-like Compression Scheme. Cryptography 2025, 9, 14. [Google Scholar] [CrossRef]
- Gentry, C.; Halevi, S. Compressible FHE with applications to PIR. In Theory of Cryptography Conference; Springer: Cham, Switzerland, 2019; pp. 438–464. [Google Scholar]
- Rivest, R.L.; Adleman, L.; Dertouzos, M.L. On data banks and privacy homomorphisms. Found. Secur. Comput. 1978, 4, 169–180. [Google Scholar]
- Gentry, C. A Fully Homomorphic Encryption Scheme; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Efficient Fully Homomorphic Encryption from (Standard) LWE. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 23–25 October 2011; pp. 97–106. [Google Scholar] [CrossRef]
- Brakerski, Z.; Vaikuntanathan, V. Fully homomorphic encryption from ring-LWE and security for key dependent messages. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2011; pp. 505–524. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory (TOCT) 2014, 6, 1–36. [Google Scholar] [CrossRef]
- Fan, J.; Vercauteren, F. Somewhat practical fully homomorphic encryption. Cryptol. ePrint Arch. 2012. Available online: https://eprint.iacr.org/2012/144 (accessed on 16 August 2025).
- Ducas, L.; Micciancio, D. FHEW: Bootstrapping homomorphic encryption in less than a second. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2015; pp. 617–640. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast fully homomorphic encryption over the torus. J. Cryptol. 2020, 33, 34–91. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Proceedings of the Advances in Cryptology–ASIACRYPT 2017: 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Proceedings, Part I 23. Springer: Berlin/Heidelberg, Germany, 2017; pp. 409–437. [Google Scholar]
- Tu, G.; Liu, W.; Zhou, T.; Yang, X.; Zhang, F. Concise and Efficient Multi-Identity Fully Homomorphic Encryption Scheme. IEEE Access 2024, 12, 49640–49652. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, R.; Wei, X. A Compact Multi-Identity Fully Homomorphic Encryption Scheme Without Fresh Ciphertexts. Appl. Sci. 2025, 15, 473. [Google Scholar] [CrossRef]
- Qi, Z.; Yang, G.; Ren, X.; Zhou, Q. Compressible Identity-Based Fully Homomorphic Encryption. In Proceedings of the 2024 4th International Conference on Blockchain Technology and Information Security (ICBCTIS), Wuhan, China, 17–19 August 2024; pp. 31–35. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM (JACM) 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Clear, M.; McGoldrick, C. Multi-identity and multi-key leveled FHE from learning with errors. In Proceedings of the Advances in Cryptology–CRYPTO 2015: 35th Annual Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2015; Proceedings, Part II 35. Springer: Berlin/Heidelberg, Germany, 2015; pp. 630–656. [Google Scholar]
- Yuan, M.; Wang, D.; Zhang, F.; Wang, S.; Ji, S.; Ren, Y. An examination of multi-key fully homomorphic encryption and its applications. Mathematics 2022, 10, 4678. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).