Evaluation of Privacy-Preserving Support Vector Machine (SVM) Learning Using Homomorphic Encryption

Abstract

The requirement for privacy-aware machine learning increases as we continue to use PII (personally identifiable information) within machine training. To overcome the existing privacy issues, we can apply fully homomorphic encryption (FHE) to encrypt data before they are fed into a machine learning model. This involves generating a homomorphic encryption key pair, where the public key encrypts the input data and the private key decrypts the output. However, there is often a performance hit when we use homomorphic encryption, so this paper evaluates the performance overhead of using an SVM (support vector machine) machine learning technique with the OpenFHE homomorphic encryption library. This uses Python and the scikit-learn library to create an SVM model, which can then be used with homomorphically encrypted data inputs and then produce a homomorphically encrypted result. The experiments include a range of variables, such as multiplication depth, scale size, first modulus size, security level, batch size, and ring dimension, along with two different SVM models, SVM-poly and SVM-linear. Overall, the results show that the two main parameters that affect performance are ring dimension and modulus size, and SVM-poly and SVM-linear show similar performance levels.

1. Introduction

The rise of machine learning (ML) has led to increasing demand for large volumes of data to train accurate and effective models. However, these data often contain personally identifiable information (PII), which must be protected, especially in sensitive domains such as healthcare, finance, and the Internet of Things (IoT). For instance, in healthcare applications, training ML models on patient records can significantly improve diagnostics and treatment recommendations, but it also raises serious privacy concerns.

While data protection mechanisms such as encryption are commonly applied over the air and at rest, data are frequently left vulnerable in-process, where they are decrypted and exposed during computation. This critical gap has motivated research into privacy-preserving machine learning (PPML), which aims to enable model training and inference on encrypted or otherwise protected data.

Among the PPML techniques, homomorphic encryption (HE) provides a mathematically robust method for securing data during computation. HE thus allows arithmetic operations to be performed directly on ciphertexts, producing encrypted results that, when decrypted, match the output of the operations performed on the plaintexts. This capability is offered through different classes of HE: partial homomorphic encryption (PHE), which supports only limited operations (e.g., addition or multiplication), and fully homomorphic encryption (FHE), which supports arbitrary computations and provides the strongest privacy guarantees.

FHE schemes, particularly those based on lattice cryptography, offer a high level of security but are often computationally expensive, posing challenges for real-time or resource-constrained applications. These trade-offs must be rigorously evaluated to determine their practical applicability in machine learning workflows.

In this paper, we investigate the integration of fully homomorphic encryption into support vector machine (SVM) learning, a widely used classification algorithm known for its robustness and interpretability. An SVM model aims to define the input data within a number of different classes in a multidimensional space. This type of approach matches well with the processing of homomorphically encrypted data with matrix and vector computations of lattice methods.

Our contributions are three-fold: (1) we implement a privacy-preserving SVM model using FHE, (2) we evaluate the feasibility and performance of the model using multiple datasets and encryption parameters, and (3) we analyze the trade-offs between computational efficiency and classification accuracy. All the experiments are conducted using the OpenFHE library [1], a state-of-the-art FHE framework.

By providing an empirical evaluation of FHE-based SVMs, this work contributes to the growing field of secure machine learning and offers insights into the deployment of privacy-preserving models in sensitive data environments.

2. Background

Homomorphic encryption supports mathematical operations on encrypted data. In 1978, Rivest, Adleman, and Dertouzos [2] were the first to define the possibilities of implementing a homomorphic operation and used the RSA method. This supported multiply and divide operations [1] but not addition and subtraction. Overall, PHE supports a few arithmetic operations, while FHE supports add, subtract, multiply, and divide.

Since Gentry defined the first FHE method [3] in 2009, there have been four main generations of homomorphic encryption:

• 1st generation: Gentry’s method uses integers and lattices [4], including the DGHV method.
• 2nd generation. Brakerski, Gentry, and Vaikuntanathan (BGV) and Brakerski/Fan–Vercauteren (BFV) use a ring-learning-with-errors approach [5]. The methods are similar to each other, and there is only a small difference between them.
• 3rd generation: These include DM (also known as FHEW) and CGGI (also known as TFHE) and support the integration of Boolean circuits for small integers.
• 4th generation: CKKS (Cheon, Kim, Kim, and Song), which uses floating-point numbers [6].

Generally, CKKS works best for real number computations and can be applied to machine learning applications as it can implement logistic regression methods and other statistical computations. DM (also known as FHEW) and CGGI (also known as TFHE) are useful in the application of Boolean circuits for small integers. BGV and BFV are generally used in applications with small integer values.

2.1. Public Key or Symmetric Key

Homomorphic encryption can be implemented either with a symmetric key or an asymmetric (public) key. With symmetric key encryption, we use the same key to encrypt as we do to decrypt, whereas, with an asymmetric method, we use a public key to encrypt and a private key to decrypt. In Figure 1, we use asymmetric encryption with a public key ($pk$) and a private key ($sk$). With this, Bob, Alice, and Peggy will encrypt their data using the public key to produce ciphertext, and then we can operate on the ciphertext using arithmetic operations. The result can then be revealed by decrypting with the associated private key. In Figure 2, we use symmetric key encryption, where the data are encrypted with a secret key, which is then used to decrypt the data. In this case, the data processor (Trent) should not have access to the secret key as it could decrypt the data from the providers.

2.2. Homomorphic Libraries

There are several homomorphic encryption libraries that support FHE, including ones that support CUDA and GPU acceleration, but many have not been kept up to date with modern methods or have only integrated one method. Overall, the native language libraries tend to be the most useful as they allow the compilation to machine code. The main languages used for this are C++, Golang, and Rust, although some Python libraries exist through wrappers of C++ code. This includes HEAAN-Python and its associated HEAAN library.

One of the first libraries that supported a range of methods is Microsoft SEAL [7], with SEAL-C# and SEAL-Python. While it supports a wide range of methods, including BGV/BFV and CKKS, it has lacked significant development for the past few years. It does have support for Android and has a Node.js port [8]. Wood et al. [9] defined a full range of libraries. One of the most extensive libraries is PALISADE, which has now developed into OpenFHE. Within OpenFHE, the main implementations of this library are as follows:

• Brakerski/Fan–Vercauteren (BFV) scheme for integer arithmetic.
• Brakerski–Gentry–Vaikuntanathan (BGV) scheme for integer arithmetic.
• Cheon–Kim–Kim–Song (CKKS) scheme for real-number arithmetic (includes approximate bootstrapping).
• Ducas–Micciancio (DM) and Chillotti–Gama–Georgieva–Izabachene (CGGI) schemes for Boolean circuit evaluation.

This research paper supports the use of OpenFHE as it directly supports a range of machine learning methods, including SVM and neural networks.

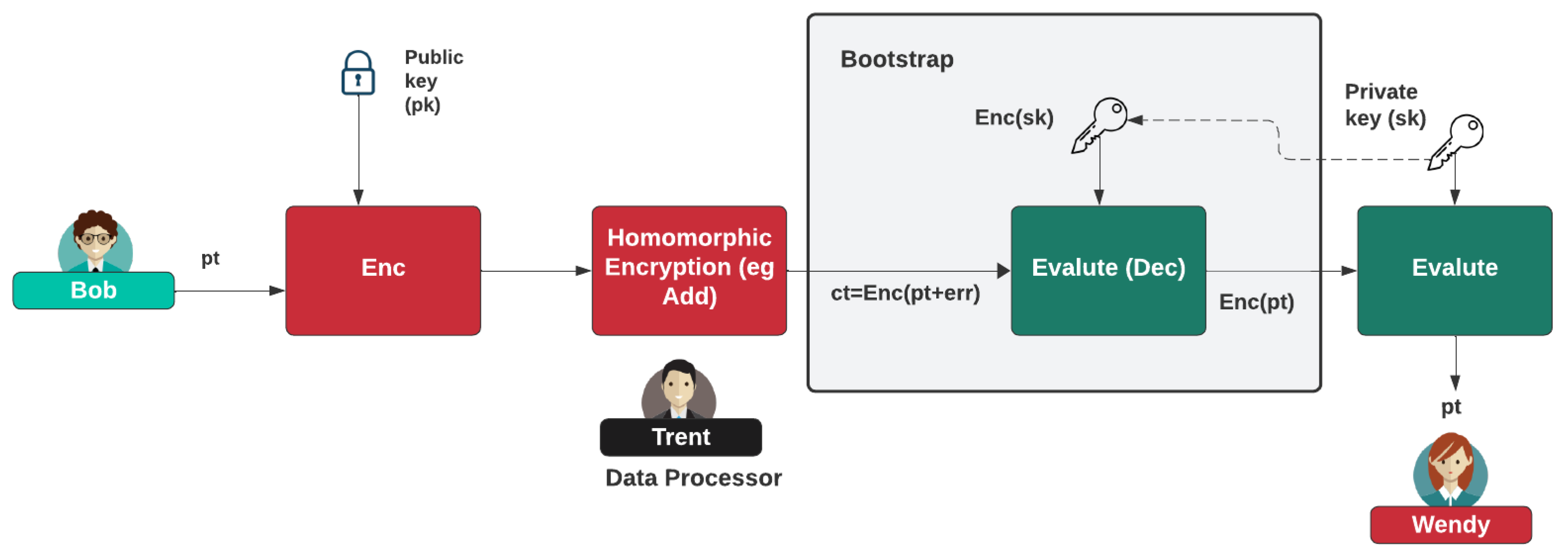
2.3. Bootstrapping

A key topic within fully homomorphic encryption is the use of bootstrapping. Within a learning-with-errors approach, we add noise to our computations. For a normal decryption process, we use the public key to encrypt data and then the associated private key to decrypt them. Within the bootstrap version of homomorphic encryption, we use an encrypted version of the private key that operates on the ciphertext. In this way, we remove the noise that can build up in the computation. Figure 3 outlines that we perform an evaluation on the decryption using an encrypted version of the private key. This will remove noise in the ciphertext, after which we can use the actual private key to perform the decryption.

The main bootstrapping methods are CKKS [6], DM [10]/CGGI, and BGV/BFV. Overall, CKKS is generally the fastest bootstrapping method, while DM/CGGI is efficient with the evaluation of arbitrary functions. These functions approximate math functions as polynomials (such as with Chebyshev approximation). BGV/BFV provides reasonable performance and is generally faster than DM/CGGI but slower than CKKS.

2.4. BGV and BFV

With BGV and BFV, we use a ring-learning-with-errors (LWE) method [5]. With BGV, we define a modulus (q), which constrains the range of the polynomial coefficients. Overall, the methods use a modulus that can be defined within different levels. We then initially define a finite group of ${\mathbb{Z}}_q$ and then make this a ring by dividing our operations with $(x^n+1)$, where $n-1$ is the largest power of the coefficients. The message can then be represented in binary as

$$m=a_{n-1}{a}_{n-2}...a_0$$

(1)

This can be converted into a polynomial with

$$\mathbf{m}=a_{n-1}{x}^{n-1}+a_{n-2}{x}^{n-2}+...+a_{1}x+a_0(modq)$$

(2)

The coefficients of this polynomial will then be a vector. Note that, for efficiency, we can also encode the message with ternary (such as with −1, 0, and 1). We then define the plaintext modulus with

$$t=p^r$$

(3)

where p is a prime number and r is a positive number. We can then define a ciphertext modulus of q, which should be much larger than t. To encrypt with the private key of $\mathbf{s}$, we implement the following:

$$(c_0,c_1)=\left({\displaystyle \frac{q}{t}}.\mathbf{m}+\mathbf{a}.\mathbf{s}+e,-\mathbf{a}\right)modq$$

(4)

To decrypt

$$m=⌊{\displaystyle \frac{t}{q}}(c_0+c_1).\mathbf{s}⌉$$

(5)

This works because

$$\begin{array}{cc}\hfill m_{recover}& =⌊{\displaystyle \frac{t}{q}}\left({\displaystyle \frac{q}{t}}.\mathbf{m}+\mathbf{a}.\mathbf{s}+e-\mathbf{a}.\mathbf{s}\right)⌉\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & =⌊\left(\mathbf{m}+{\displaystyle \frac{t}{q}}.e\right)⌉\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \approx m\hfill \end{array}$$

(8)

For two messages of $m_1$ and $m_2$, we will obtain

$$Enc(m_1+m_2)=Enc\left(m_1\right)+Enc\left(m_2\right)$$

(9)

$$Enc(m_1.m_2)=Enc\left(m_1\right).Enc\left(m_2\right)$$

(10)

2.4.1. Noise and Computation

Each time we add or multiply, the error also increases. Thus, bootstrapping is required to reduce the noise. Overall, addition and plaintext/ciphertext multiplication is not a time-consuming task, but ciphertext/ciphertext multiplication is more computationally intensive. The most computational task is typically the bootstrapping process, and the ciphertext/ciphertext multiplication process adds the most noise to the process.

2.4.2. Parameters

We thus have parameters of the ciphertext modulus (q) and the plaintext modulus (t). Both of these are typically to the power of 2. An example of q is $2^{240}$, and for t 65,537. As the value of $2^q$ is likely to be a large number, we typically define it as a $log\_q$ value. Thus, a ciphertext modulus of $2^{240}$ will be 240, defined as a $lo{g}_q$ value.

2.5. CKKS

HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) defines a homomorphic encryption (HE) library proposed by Cheon, Kim, Kim, and Song (CKKS). The CKKS method uses approximate arithmetic over complex numbers [6]. Overall, it is a level approach that involves the evaluation of arbitrary circuits of bounded (pre-determined) depth. These circuits can include add (X-OR) and multiply (AND).

HEAAN uses a rescaling procedure to measure the size of the plaintext. It then produces approximate rounding due to the truncation of the ciphertext into a smaller modulus. The method is especially useful in that it can be applied to carry out encryption computations in parallel. Unfortunately, the ciphertext modulus can become too small, where it is not possible to carry out any more operations.

The HEAAN (CKKS) method uses approximate arithmetic over complex numbers ($\mathbb{C}$) and is based on ring learning with errors (RLWE). It focuses on defining an encryption error within the computational error that will happen within approximate computations. We initially take a message (M) and convert it to a cipher message (ct) using a public key pk. To decrypt ([⟨ct,sk⟩]q), we produce an approximate value along with a small error (e).

Craig Gentry [11] outlined three important application areas within privacy-preserving genome association, neural networks, and private information retrieval. Along with this, he proposed that the research community should investigate new methods that do not involve the use of lattices.

2.5.1. Chebyshev Approximation

With approximation theory, it is possible to determine an approximate polynomial $p\left(x\right)$ that is an approximation to a function $f\left(x\right)$. A polynomial takes the form of $p\left(x\right)=a_n.x^n+a_{n-1}.x^{n-1}+a_1.x+a_0$, where $a_0...a_n$ are the coefficients of the powers, and n is the maximum power of the polynomial. In this case, we will evaluate arbitrary smooth functions for CKKS and use Chebyshev approximation. These were initially created by Pafnuty Lvovich Chebyshev. This method involves the approximation of a smooth function using polynomials.

Overall, with polynomials, we convert our binary values into a polynomial, such as 101101,

$$x^5+x^3+x^2+1$$

(11)

Our plaintext and ciphertext are then represented as polynomial values.

2.5.2. Approximation Theory

With approximation theory, we aim to determine an approximate method for a function f(x). It was Pafnuty Lvovich Chebyshev who defined a method of finding a polynomial p(x) that is approximate for f(x). Overall, a polynomial takes the form of

$$p\left(x\right)=a_n.x^n+a_{n-1}.x^{n-1}+a_1.x+a_0$$

(12)

where $a_0\dots a_n$ are the coefficients of the powers, and n is the maximum power of the polynomial. Chebyshev published his work in 1853 as “Theorie des mecanismes, connus sous le nom de parall elogrammes”. His problem statement was “to determine the deviations which one has to add to obtain an approximated value for a function f, given by its expansion in powers of $x-a$, if one wants to minimise the maximum of these errors between $x=a-h$ and $x=a+h$, h being an arbitrarily small quantity”.

3. Related Work

Homomorphic encryption supports the use of machine learning methods, and some core features include a dot product operation with an encrypted vector and logistic functions. With this, OpenFHE supports a range of relevant methods and even has a demonstrator for a machine learning method.

3.1. State of the Art

Iezzi et al. [12] defined two methods of training with homomorphic encryption:

• Private Prediction as a Service (PPaaS). This is where the prediction is outsourced to a service provider who has a pre-trained model where encrypted data are sent to the service provider. In this case, the data owner does not learn the model used.
• Private Training as a Service (PTaaS). This is where the data owner provides data to a service provider, who will train the model. The service provider can then provide a prediction for encrypted data.

Wood et al. [9] added models of

• Private outsourced computation. This involves moving computation into the cloud.
• Private prediction. This involves homomorphic data being processed into the cloud and not having access to the training model.
• Private training. This is where a cloud entity trains a model based on the client’s data.

3.2. GWAS

Blatt et al. [13] implemented the genome-wide association study (GWAS), which is a secure large-scale genome-wide association study using homomorphic encryption. The chi-squared GWAS test was implemented in OpenFHE (https://github.com/openfheorg/openfhe-genomic-examples/blob/main/demo-chi2.cpp, accessed on 20 May 2025). With this, each of the participants in the student group is given a public key from a GWAS (genome-wide association study) coordinator, who then encrypts the data with CKKS and sends them back for processing. The computation includes association statistics using full logistic regression on each variant with sex, age, and age squared as covariates. Pearson’s chi-squared test uses categories to determine if there is a significant difference between sets of data (it implements as RunChi2 from https://github.com/openfheorg/openfhe-genomic-examples/blob/main/demo-chi2.cpp, accessed on 20 May 2025).

$${\tilde{\chi }}^2={\displaystyle \frac{1}{d}}\sum _{k=1}^n{\displaystyle \frac{{(O_k-E_k)}^2}{E_k}}$$

(13)

where

• ${\tilde{\chi }}^2$ is the chi-squared test statistic.
• O is the observed frequency.
• E is the expected frequency.

Overall, the implementation involved a dataset of 25,000 individuals, and it was shown that 100,000 individuals and 500,000 single-nucleotide polymorphisms (SNPs) could be evaluated in 5.6 hours on a single server [13].

Linear Regression

The GWAS method is also implemented with linear regression for homomorphic encryption (see RunLogReg in https://github.com/openfheorg/openfhe-genomic-examples/blob/main/demo-logistic.cpp, accessed on 20 May 2025). The results show that the accuracy of both the chi-squared and linear regression tests was good. The runtime varied linearly with the number of participants in the test.

3.3. Support Vector Machines (SVMs)

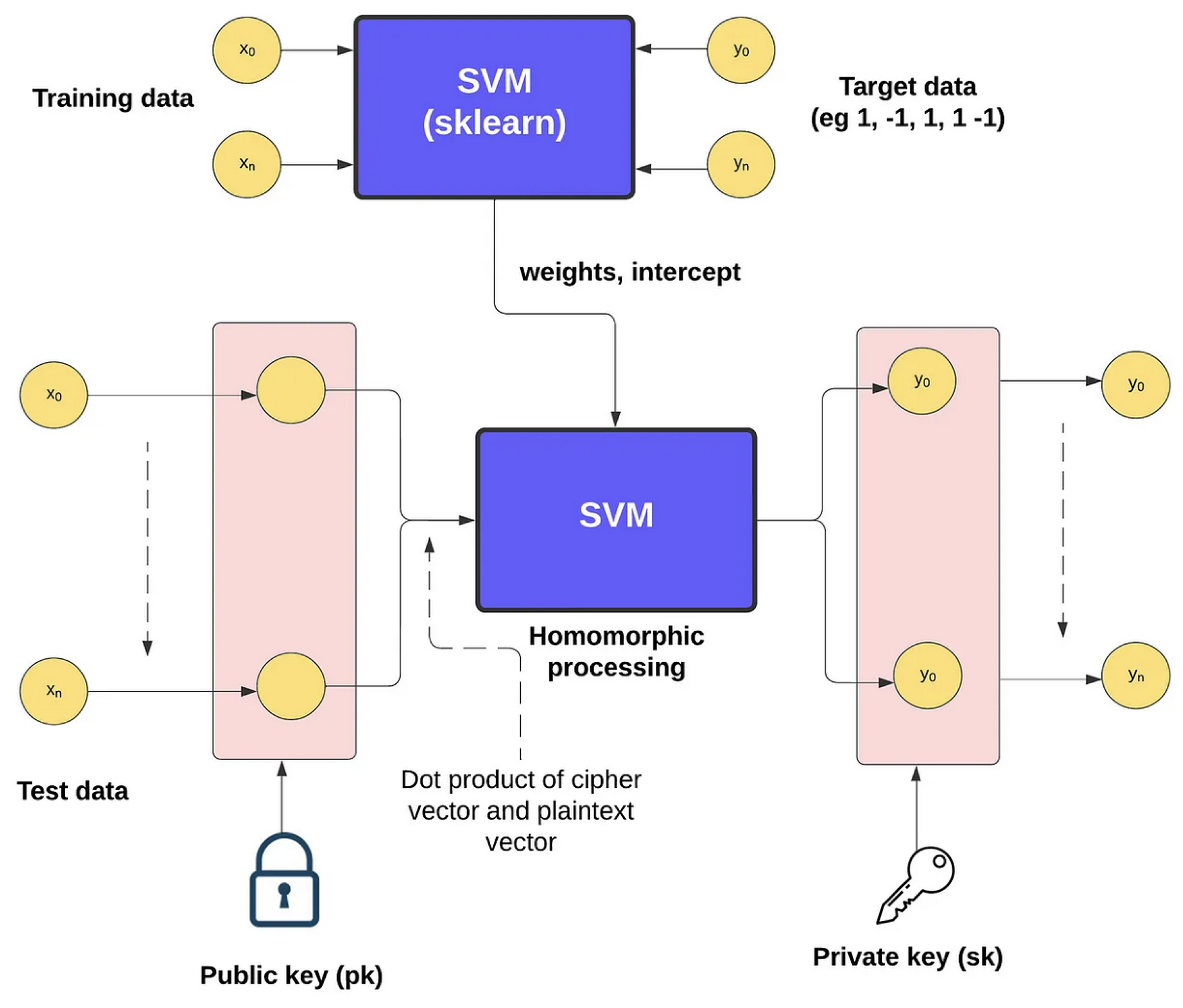
With the SVM (support vector machine) model, we have a supervised learning technique. Overall, it is used to create two categories (binary) or more (multi) and will try to allocate each of the training values into one or more categories. Basically, we have points in a multidimensional space and try to create a clear gap between the categories. New values are then placed within one of the two categories.

Overall, we split the input data into training and test data and then train with a sklearn model with unencrypted values from the training data. The output from the model includes the weights and intercepts. Next, we can encrypt the test data with the homomorphic public key and then feed the result into the SVM model. The output values can then be decrypted by the associated private key, as illustrated in Figure 4.

CKKS and SVM

The CKKS scheme is a homomorphic encryption method designed for encrypted arithmetic operations. For a given plaintext feature vector of

$$\begin{array}{c}\hfill \mathbf{x}=(x_1,x_2,\dots ,x_n)\end{array}$$

(14)

and a public key of $\mathsf{pk}$, the encryption function is

$$\mathsf{Enc}(\mathbf{x},\mathsf{pk})=c_x$$

(15)

where $c_x$ is the encrypted representation of $\mathbf{x}$ [6]. For support vector machine (SVM) classification with linear SVM, we use a linear decision function of

$$f_{\mathrm{lin}}\left(\mathbf{x}\right)={\mathbf{w}}^T\mathbf{x}+b$$

(16)

where $\mathbf{x}$ is the feature vector, $\mathbf{w}$ is the weight vector, and b is the bias term.

For classification,

$$y=\mathrm{sign}\left(f_{\mathrm{lin}}\left(\mathbf{x}\right)\right)$$

(17)

Using FHE, the computation is performed on encrypted values [6]:

$$\mathsf{Enc}\left(f_{\mathrm{lin}}\left(\mathbf{x}\right)\right)=\mathsf{Enc}({\mathbf{w}}^T\mathbf{x}+b)$$

(18)

A polynomial-kernel SVM extends the decision function to

$$f_{\mathrm{poly}}\left(\mathbf{x}\right)={({\mathbf{w}}^T\mathbf{x}+b)}^d$$

(19)

where d is the polynomial degree, and where the rest of the parameters are the same as the linear SVM. For classification,

$$y=\mathrm{sign}\left(f_{\mathrm{poly}}\left(\mathbf{x}\right)\right)$$

(20)

With homomorphic encryption, we compute this function without decrypting

$$\mathsf{Enc}\left(f_{\mathrm{poly}}\left(\mathbf{x}\right)\right)=\mathsf{Enc}\left({({\mathbf{w}}^T\mathbf{x}+b)}^d\right)$$

(21)

which follows prior encryption-based SVM work [6,11]. After computation, the result is decrypted using the $\mathbf{private}\mathbf{key}$ ($\mathsf{sk}$):

$$\mathsf{Dec}(c_f,\mathsf{sk})=f\left(\mathbf{x}\right)$$

(22)

The final classification is

$$y=\mathrm{sign}\left(\mathsf{Dec}(c_f,\mathsf{sk})\right)$$

(23)

4. Methodology

This paper explores the integration of fully homomorphic encryption (FHE) with support vector machines (SVMs) for privacy-preserving machine learning. The proposed framework employs the CKKS encryption scheme, implemented via the OpenFHE library, to enable encrypted inference while maintaining classification accuracy. Homomorphic encryption allows computations to be performed directly on encrypted data without decryption, ensuring data privacy throughout the machine learning pipeline [6]. OpenFHE is an open-source library that provides implementations of lattice-based encryption schemes, including CKKS, which supports approximate arithmetic operations on encrypted data [1].

The dataset used for this experiment is the Iris dataset, which contains measurements of iris flowers, including sepal length, sepal width, petal length, and petal width [14]. This dataset, originally introduced by Fisher [15], is widely used in machine learning research due to its simplicity and well-separated class distributions. The objective of using this dataset is to evaluate the effectiveness of the encrypted SVM framework in classifying iris species while ensuring data privacy. The dataset is publicly available from the UCI ML Repository [16].

The methodology consists of environment setup and data preprocessing. The SVM model, originally introduced by Cortes and Vapnik [17], is trained on plaintext data before being used for encrypted inference. To analyze the trade-offs between encryption security, computational efficiency, and model accuracy, the implementation is conducted using OpenFHE within a Python-based machine learning pipeline, leveraging libraries such as Scikit-Learn and NumPy [18].

4.1. Environment Setup

The encryption parameters in the fully homomorphic encryption (FHE) framework are essential for balancing security, computational efficiency, and model accuracy. The following section outlines the installation process, provides a detailed explanation of each parameter, and presents the system specifications, as shown in

Table 1. Experimental setup.

Component	Description
Compute Environment	AWS EC2 t3.medium (Two vCPUs, Intel Xeon 3.1 GHz,
	4 GB RAM)
Operating System	Ubuntu 20.04
Programming Language	Python 3.x
ML Library	scikit-learn (for SVM training and evaluation)
HE Library	OpenFHE (CKKS scheme for encrypted inference) [1]
Dataset	Iris Dataset (150 samples, four features) [15]
Preprocessing	Standardization (zero mean, unit variance), Train–Test
	Split (80–20%)
Encryption Parameters	$N,D,S,M,L,B$ (Ring Dim, Mult Depth, Scaling Factor,
	Modulus Size, Sec Level, Batch Size)
SVM Models	Linear SVM, Polynomial SVM (homomorphic kernel
	approximation) [17]
Performance Metrics	Classification Accuracy, Encryption Overhead, Inference
	Time, Memory Use, Scalability

.

4.1.1. Experimental Setup

The implementation of the encrypted SVM framework followed a structured approach to ensure efficiency and reproducibility. The setup commenced with the installation of openfhe-python, adhering strictly to the official guidelines [1]. This library provided the essential cryptographic primitives required for executing encrypted computations securely.

Following the installation, the model training phase was conducted using the model_training.py script. This process involved training an SVM classifier and saving the learned parameters, which were subsequently utilized for encrypted inference. The trained model served as the foundation for performing secure classification without exposing sensitive data.

To facilitate a standardized evaluation, the dataset was organized within the data/ directory. If necessary, the dataset could be regenerated by executing the get_data.py script, ensuring consistency and reproducibility across experiments.

For encrypted inference, two dedicated scripts were employed: encrypted_svm_ linear.py and encrypted_svm_poly.py. These scripts enabled inference using linear- and polynomial-kernel SVM models, respectively, allowing for a comprehensive assessment of encrypted classification performance under different kernel settings. Through this structured approach, the framework effectively demonstrated the feasibility of privacy-preserving machine learning using homomorphic encryption.

4.1.2. Encryption Parameters

Homomorphic encryption relies on several key parameters that impact computational efficiency, security, and accuracy [6]. The primary encryption parameters used in this study are

• Ring Dimension (N): Defines the size of the polynomial ring used in encryption. A larger N increases security but also raises computational cost [5]. Typical values include $N=2^{10},2^{12},2^{14},\dots$.
• Multiplication Depth (D): Represents the number of consecutive multiplications a ciphertext can undergo before noise accumulation becomes a limiting factor [11]. Higher D enables more complex computations, which is essential for polynomial-kernel approximation in SVM.
• Scaling Factor (S): Determines the precision of fixed-point arithmetic in CKKS encryption. A higher S improves numerical accuracy but increases computational complexity [19].
• First Modulus Size (M): Defines the initial modulus size, impacting ciphertext precision and computational overhead [20].
• Security Level (L): Specifies the cryptographic strength of encryption (e.g., 128-bit, 192-bit, or 256-bit security). A higher L enhances security but introduces additional computational costs [21].
• Batch Size (B): Represents the number of encrypted values processed in parallel. A larger B improves computational efficiency, particularly for batch inference.

These parameters significantly impact the feasibility of encrypted machine learning. In our experiments, we analyze their influence on classification accuracy, encryption overhead, and inference efficiency.

4.1.3. System Specifications

The system was deployed on an AWS EC2 t3.medium instance, equipped with two virtual CPUs (Intel Xeon 3.1 GHz) and 4 GB of RAM, providing a balanced environment for machine learning and encrypted computations. Python was used as the primary programming language for software, enabling seamless integration between machine learning and encryption frameworks. scikit-learn then supports the training and evaluation of traditional SVM models, ensuring a robust baseline for comparison. Meanwhile, OpenFHE is used to perform encryption, ciphertext operations, and homomorphic inference, thus enabling secure computation without compromising model performance.

4.2. Data Preprocessing

Data preprocessing is a crucial step to ensure reliable and efficient machine learning, particularly when incorporating homomorphic encryption [22]. In this study, we use the Iris dataset (150 samples, four features) and apply standardization to achieve zero mean and unit variance, improving model stability. The data are then split into 80% training and 20% testing to enable fair evaluation. Given the constraints of encrypted computation, categorical features are appropriately encoded. These steps help to maintain accuracy while minimizing computational overhead in secure inference.

4.2.1. Dataset Overview

The Iris dataset is a widely recognized benchmark in machine learning, frequently employed for evaluating classification algorithms [19]. It provides a structured framework for distinguishing between different iris flower species based on their physical attributes. The dataset consists of 150 samples, each representing an individual iris flower, and is characterized by 4 key features: sepal length, sepal width, petal length, and petal width, all measured in centimeters. These features enable effective classification by capturing the morphological differences among species.

The dataset comprises 3 distinct classes, each containing 50 samples, corresponding to 3 species: Iris setosa (label ‘0’), Iris versicolor (label ‘1’), and Iris virginica (label ‘2’). It is well structured, balanced, and contains no missing values, making it particularly suitable for both educational purposes and experimental evaluations in machine learning research.

Due to its simplicity and interpretability, the Iris dataset is commonly used for demonstrating data preprocessing techniques, exploratory data analysis, and classification models, including support vector machines (SVMs) and decision trees [17]. Furthermore, its features can be visualized through pair plots, enabling an intuitive understanding of feature relationships and class separability.

In this study, the Iris dataset serves as a controlled environment for analyzing the effects of homomorphic encryption on SVM classification. By leveraging its structured nature, we facilitate a reliable comparison between traditional and encrypted inference methods, allowing for a comprehensive assessment of computational performance and classification accuracy.

The Iris dataset is a classic benchmark for machine learning algorithms, favored for its simplicity and accessibility. It is widely used in educational settings and can be easily accessed through libraries like scikit-learn in Python.

4.2.2. Data Preprocessing and Feature Encoding

To ensure robust and efficient encrypted classification, the dataset was subjected to a systematic preprocessing pipeline implemented by get_data.py. This process involved feature selection, transformation, and structuring to optimize the data for FHE-based machine learning.

The dataset contains 150 rows (samples) and 4 columns (4 predictive features): sepal length, sepal width, petal length, and petal width. There is one target column of species classification. Standardization was applied to normalize values, ensuring a mean ($\mu$) of approximately zero and a standard deviation ($\sigma$) of approximately unity. This improves model performance by placing features on a similar scale. The data were split into 120 training samples and 30 test samples, ensuring a well-balanced split for model evaluation. Furthermore, categorical labels were encoded into numerical representations to facilitate seamless integration into the machine learning framework.

This preprocessing stage establishes a structured and standardized foundation for encrypted SVM training. Harmonizing feature distributions, optimizing data representation, and preparing the dataset for secure computation enhance both the accuracy and efficiency of privacy-preserving machine learning.

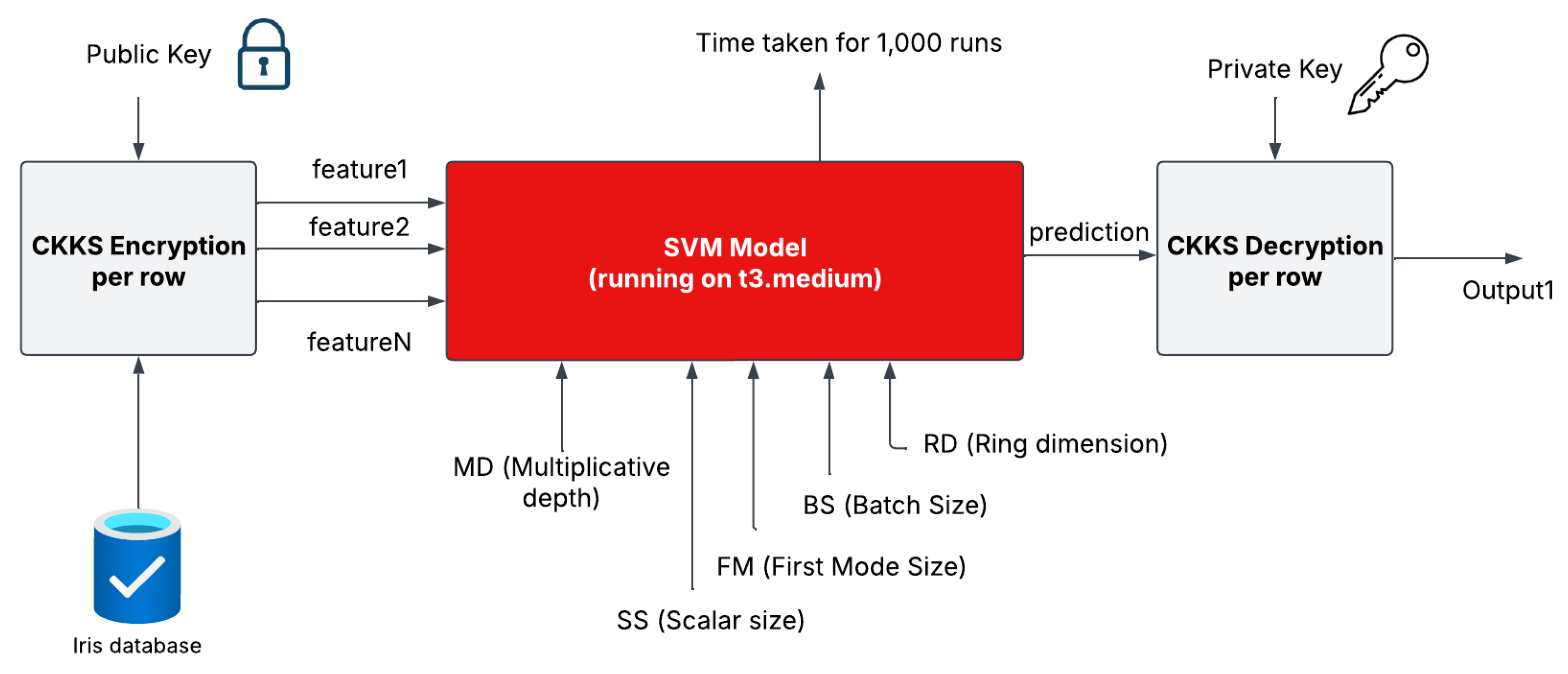
5. Implementation

This section presents the approach used to implement privacy-preserving classification using FHE. The support vector machine (SVM) model is adapted to operate on encrypted data using the CKKS encryption scheme [6].

The implementation consists of dataset preprocessing, encryption of feature vectors, SVM training, and encrypted classification. The process follows established principles from privacy-preserving machine learning [23]. The overall workflow is visualized in Figure 5.

The evaluation of the impact of homomorphic encryption on machine learning performance involves a number of experiments measuring key performance metrics. Classification accuracy was assessed by comparing encrypted and non-encrypted inference, with the SVM model achieving high accuracy. Computation time was also analyzed, including encryption, inference, and decryption durations. Additionally, the scale-up runtime was examined by calculating the ratio of non-encrypted to encrypted execution times.

Memory overhead was evaluated to determine the effect of homomorphic encryption on resource consumption, particularly memory use. Finally, scalability was assessed by analyzing performance variations as the ring dimension and multiplication depth increased.

5.1. Encryption Using CKKS

The CKKS encryption scheme was employed to encrypt feature vectors, allowing privacy-preserving computations on floating-point values [6]. CKKS supports approximate arithmetic operations, making it well suited for machine learning applications. The encryption parameters used in our experiments were selected based on a balance between computational efficiency and security. The multiplicative depth (D) ranged from 1 to 7, scaling factor (S) values varied between 10 and 50, and the first modulus size (M) was tested at 20, 30, 40, 50, and 60. The security level (L) was evaluated at 128-bit, 192-bit, and 256-bit configurations. Batch sizes (B) included 128, 256, 512, 1024, 2048, and 4096. The ring dimension (N) was tested at $2^{14}$ (16,384), $2^{15}$ (32,768), $2^{16}$ (65,536), and $2^{17}$ (131,072), providing insights into the scalability of homomorphic encryption in machine learning.

5.2. Encrypted Classification Algorithm

In this work, we propose an FHE-based approach for SVM classification that supports both linear and polynomial kernels. The classification process involves encrypting the feature vector and model parameters, performing homomorphic computations to evaluate the decision function, and decrypting the result to obtain the classification outcome. The detailed steps are outlined in Algorithm 1, which describes the encrypted inference procedure for both linear and polynomial SVM models.

Algorithm 1 Homomorphic SVM Classification [6,11]

Require: Feature vector $\mathbf{x}$, public key $\mathsf{pk}$, private key $\mathsf{sk}$, degree d (for polynomial SVM) Ensure: Classification result y  1:  Encrypt Features: $c_x\leftarrow \mathsf{Enc}(\mathbf{x},\mathsf{pk})$ (Equation (15))  2:  Encrypt Model Parameters:  3:     $c_w\leftarrow \mathsf{Enc}(\mathbf{w},\mathsf{pk})$  4:     $c_b\leftarrow \mathsf{Enc}(b,\mathsf{pk})$  5:  Compute Encrypted Decision Function:  6:  if linear SVM then  7:      $c_f\leftarrow \mathsf{Enc}({\mathbf{w}}^T\mathbf{x}+b)$ (Equation (18))  8:  else polynomial SVM  9:      $c_f\leftarrow \mathsf{Enc}\left({({\mathbf{w}}^T\mathbf{x}+b)}^d\right)$ (Equation (21)) 10:  end if 11:  Decrypt the Result: $f\left(\mathbf{x}\right)\leftarrow \mathsf{Dec}(c_f,\mathsf{sk})$ (Equation (22)) 12:  Classify Output: $$y\leftarrow \left\{\begin{array}{cc}1,\hfill & f\left(\mathbf{x}\right)\ge 0\hfill \\ -1,& f\left(\mathbf{x}\right)<0\end{array}\right.\left(\mathrm{Equation}\right(23\left)\right)$$ 13:  return y

5.3. Model Training

The model training example is given in Appendix A.

6. Results

The experimental results provide a comprehensive evaluation of the impact of homomorphic encryption on SVM inference. We implement both linear SVM and polynomial SVM kernels to investigate how different model complexities influence encrypted computation. A key observation is the trade-off between encryption depth and computational efficiency, where higher security parameters lead to increased execution time and memory consumption. This behavior is consistent with the theoretical complexity of homomorphic encryption, which introduces overhead due to polynomial arithmetic and ciphertext expansion. Our comparison between linear and polynomial kernels further highlights the performance differences under encrypted settings, demonstrating the cost–benefit trade-offs when applying homomorphic encryption to models of varying computational depth.

Beyond computational cost, the study examines the extent to which encrypted inference preserves classification accuracy. By systematically tuning the encryption parameters, particularly ring dimension and modulus size, we explore their critical roles in determining both performance efficiency and security guarantees. Larger ring dimensions and modulus sizes enhance cryptographic strength but also increase computational overhead and memory use, thereby impacting inference latency and scalability. In the context of fully homomorphic encryption (FHE), these parameters govern the depth of allowable computations and the noise budget, which in turn affect the feasibility of complex operations such as SVM decision functions. Understanding this trade-off is essential for optimizing privacy-preserving machine learning pipelines. The following sections present a detailed discussion of these findings, grounded in both empirical observations and theoretical considerations.

Table 2 and Table 3 include the gathered data. MD is multiplicative depth, SS is scalar size, FM is first mod size, BS is batch size, and RD is ring dimension. AEA is average encryption accuracy, NEA is non-encrypted accuracy, AET is average encryption time, and ANT is average non-encryption time.

• Execution Time: This metric reflects the total time taken to complete inference operations, comparing encrypted and plaintext implementations. It serves as a direct indicator of the computational overhead introduced by homomorphic encryption, which is particularly sensitive to parameter configurations such as ring dimension and multiplicative depth.
• Memory Use: Although memory consumption is not explicitly tabulated, it is inherently influenced by cryptographic parameters. Larger ring dimensions and deeper circuits result in bulkier ciphertexts and increased memory demands during intermediate computations.
• Model Accuracy: We compare the classification performance using average encrypted accuracy (AEA) and non-encrypted accuracy (NEA). Our empirical results demonstrate negligible differences between the two, indicating that model accuracy is well preserved under encryption.

These metrics are supported by detailed results and visual comparisons in Table 2 and Table 3, which showcase the trade-offs between security, computational efficiency, and classification performance under varying cryptographic parameter settings. This analysis underscores the feasibility of encrypted inference with minimal compromise in model utility.

Table 2. Results for SVM-linear.

MD	SS	FM	SL	BS	RD	AEA	NEA	AET	ANT	Scale-Up
1	30	60	128	1024	16,384	0.967	0.967	0.643458	0.000623	1032.838
2	30	60	128	1024	16,384	0.967	0.967	0.782	0.000067	1172.735
3	30	60	128	1024	16,384	0.967	0.967	0.924	0.000161	1397.215
4	30	60	128	1024	16,384	0.967	0.967	1.101	0.000613	1794.548
5	30	60	128	1024	16,384	0.967	0.967	1.283	0.000624	2056.393
6	30	60	128	1024	16,384	0.967	0.967	1.391	0.000627	2097.537
7	30	60	128	1024	16,384	0.967	0.967	1.530	0.000658	2324.503
1	10	60	128	1024	16,384	0.817	0.967	0.649	0.000067	9697.24
1	20	60	128	1024	16,384	0.967	0.967	0.672	0.000065	10,332.49
1	30	60	128	1024	16,384	0.967	0.967	0.651	0.000073	8919.69
1	40	60	128	1024	16,384	0.967	0.967	0.650	0.000029	22,431.52
1	50	60	128	1024	16,384	0.967	0.967	0.650	0.000027	24,084.56
1	30	20	128	1024	16,384	0.967	0.967	0.627	0.000076	8251.12
1	30	30	128	1024	16,384	0.967	0.967	0.632	0.000067	9434.24
1	30	40	128	1024	16,384	0.967	0.967	0.635	0.000074	8573.4
1	30	50	128	1024	16,384	0.967	0.967	0.643	0.000065	9905.05
1	30	60	128	1024	16,384	0.967	0.967	0.641	0.000067	9574.09
1	30	60	192	1024	16,384	0.967	0.967	0.204	0.000184	1108.59
1	30	60	256	1024	16,384	0.967	0.967	0.197	0.000188	1050.52
1	30	60	512	1024	16,384	0.967	0.967	0.201	0.000191	1050.31
1	30	60	1024	1024	16,384	0.967	0.967	0.198	0.000193	1023.06
1	30	60	2048	1024	16,384	0.967	0.967	0.202	0.000193	1048.5
1	30	60	4096	1024	16,384	0.967	0.967	0.647	0.000711	910.78
1	30	60	128	128	16,384	0.967	0.967	0.198	0.000109	1817.4
1	30	60	128	256	16,384	0.967	0.967	0.195	0.000107	1822.5
1	30	60	128	512	16,384	0.967	0.967	0.196	0.000109	1808.7
1	30	60	128	1024	16,384	0.967	0.967	0.200	0.000109	1834.9
1	30	60	128	2048	16,384	0.967	0.967	0.206	0.000109	1878.6
1	30	60	128	4096	16,384	0.967	0.967	0.213	0.000109	1945.3
1	30	60	128	1024	16,384	0.967	0.967	0.638	0.000662	963.82
1	30	60	128	1024	32,768	0.967	0.967	1.265	0.000624	2026.52
1	30	60	128	1024	65,536	0.967	0.967	2.583	0.00067	3646.68
1	30	60	128	1024	131,072	0.967	0.967	5.103	0.00065	8245.34

Table 2. Results for SVM-linear.

MD	SS	FM	SL	BS	RD	AEA	NEA	AET	ANT	Scale-Up
1	30	60	128	1024	16,384	0.967	0.967	0.643458	0.000623	1032.838
2	30	60	128	1024	16,384	0.967	0.967	0.782	0.000067	1172.735
3	30	60	128	1024	16,384	0.967	0.967	0.924	0.000161	1397.215
4	30	60	128	1024	16,384	0.967	0.967	1.101	0.000613	1794.548
5	30	60	128	1024	16,384	0.967	0.967	1.283	0.000624	2056.393
6	30	60	128	1024	16,384	0.967	0.967	1.391	0.000627	2097.537
7	30	60	128	1024	16,384	0.967	0.967	1.530	0.000658	2324.503
1	10	60	128	1024	16,384	0.817	0.967	0.649	0.000067	9697.24
1	20	60	128	1024	16,384	0.967	0.967	0.672	0.000065	10,332.49
1	30	60	128	1024	16,384	0.967	0.967	0.651	0.000073	8919.69
1	40	60	128	1024	16,384	0.967	0.967	0.650	0.000029	22,431.52
1	50	60	128	1024	16,384	0.967	0.967	0.650	0.000027	24,084.56
1	30	20	128	1024	16,384	0.967	0.967	0.627	0.000076	8251.12
1	30	30	128	1024	16,384	0.967	0.967	0.632	0.000067	9434.24
1	30	40	128	1024	16,384	0.967	0.967	0.635	0.000074	8573.4
1	30	50	128	1024	16,384	0.967	0.967	0.643	0.000065	9905.05
1	30	60	128	1024	16,384	0.967	0.967	0.641	0.000067	9574.09
1	30	60	192	1024	16,384	0.967	0.967	0.204	0.000184	1108.59
1	30	60	256	1024	16,384	0.967	0.967	0.197	0.000188	1050.52
1	30	60	512	1024	16,384	0.967	0.967	0.201	0.000191	1050.31
1	30	60	1024	1024	16,384	0.967	0.967	0.198	0.000193	1023.06
1	30	60	2048	1024	16,384	0.967	0.967	0.202	0.000193	1048.5
1	30	60	4096	1024	16,384	0.967	0.967	0.647	0.000711	910.78
1	30	60	128	128	16,384	0.967	0.967	0.198	0.000109	1817.4
1	30	60	128	256	16,384	0.967	0.967	0.195	0.000107	1822.5
1	30	60	128	512	16,384	0.967	0.967	0.196	0.000109	1808.7
1	30	60	128	1024	16,384	0.967	0.967	0.200	0.000109	1834.9
1	30	60	128	2048	16,384	0.967	0.967	0.206	0.000109	1878.6
1	30	60	128	4096	16,384	0.967	0.967	0.213	0.000109	1945.3
1	30	60	128	1024	16,384	0.967	0.967	0.638	0.000662	963.82
1	30	60	128	1024	32,768	0.967	0.967	1.265	0.000624	2026.52
1	30	60	128	1024	65,536	0.967	0.967	2.583	0.00067	3646.68
1	30	60	128	1024	131,072	0.967	0.967	5.103	0.00065	8245.34

Table 3. Results for SVM-poly.

MD	SS	FM	SL	BS	RD	AEA	NEA	AET	ANT	Scale-Up
1	30	60	128	1024	16,384	0.967	0.967	0.648	0.000708	915.2
2	30	60	128	1024	16,384	0.967	0.967	0.783	0.000730	1093.3
3	30	60	128	1024	16,384	0.967	0.967	0.919	0.000763	1405.0
4	30	60	128	1024	16,384	0.967	0.967	1.097	0.000629	1527.7
5	30	60	128	1024	16,384	0.967	0.967	1.288	0.000773	1665.7
6	30	60	128	1024	16,384	0.967	0.967	1.399	0.000712	1954.9
7	30	60	128	1024	16,384	0.967	0.967	1.562	0.000715	2248.4
1	10	60	128	1024	16,384	0.784	0.967	0.649	0.000067	973.8
1	20	60	128	1024	16,384	0.967	0.967	0.671	0.000065	1032.4
1	30	60	128	1024	16,384	0.967	0.967	0.651	0.000073	889.4
1	40	60	128	1024	16,384	0.967	0.967	0.650	0.000029	1033.9
1	50	60	128	1024	16,384	0.967	0.967	0.650	0.000027	1036.4
1	30	20	128	1024	16,384	0.967	0.967	0.627	0.000076	927.7
1	30	30	128	1024	16,384	0.967	0.967	0.632	0.000067	940.1
1	30	40	128	1024	16,384	0.967	0.967	0.634	0.000074	941.8
1	30	50	128	1024	16,384	0.967	0.967	0.643	0.000065	998.1
1	30	60	128	1024	16,384	0.967	0.967	0.641	0.000067	961.3
1	30	60	192	1024	16,384	0.967	0.967	0.203	0.000184	1090.9
1	30	60	256	1024	16,384	0.967	0.967	0.197	0.000188	1049.6
1	30	60	512	1024	16,384	0.967	0.967	0.201	0.000191	1052.2
1	30	60	1024	1024	16,384	0.967	0.967	0.197	0.000193	1023.7
1	30	60	2048	1024	16,384	0.967	0.967	0.202	0.000193	1048.9
1	30	60	4096	1024	16,384	0.967	0.967	0.646	0.000711	908.7
1	30	60	128	128	16,384	0.967	0.967	0.641	0.000067	961.3
1	30	60	128	256	16,384	0.967	0.967	0.204	0.000184	1090.9
1	30	60	128	512	16,384	0.967	0.967	0.197	0.000188	1049.6
1	30	60	128	1024	16,384	0.967	0.967	0.201	0.000191	1052.2
1	30	60	128	2048	16,384	0.967	0.967	0.198	0.000193	1023.7
1	30	60	128	4096	16,384	0.967	0.967	0.202	0.000193	1048.9
1	30	60	128	1024	16,384	0.967	0.967	0.680	0.000747	910.6
1	30	60	128	1024	32,768	0.967	0.967	1.269	0.000668	1951.5
1	30	60	128	1024	65,536	0.967	0.967	2.549	0.000604	3935.1
1	30	60	128	1024	131,072	0.967	0.967	5.245	0.000687	7716.4

Table 3. Results for SVM-poly.

MD	SS	FM	SL	BS	RD	AEA	NEA	AET	ANT	Scale-Up
1	30	60	128	1024	16,384	0.967	0.967	0.648	0.000708	915.2
2	30	60	128	1024	16,384	0.967	0.967	0.783	0.000730	1093.3
3	30	60	128	1024	16,384	0.967	0.967	0.919	0.000763	1405.0
4	30	60	128	1024	16,384	0.967	0.967	1.097	0.000629	1527.7
5	30	60	128	1024	16,384	0.967	0.967	1.288	0.000773	1665.7
6	30	60	128	1024	16,384	0.967	0.967	1.399	0.000712	1954.9
7	30	60	128	1024	16,384	0.967	0.967	1.562	0.000715	2248.4
1	10	60	128	1024	16,384	0.784	0.967	0.649	0.000067	973.8
1	20	60	128	1024	16,384	0.967	0.967	0.671	0.000065	1032.4
1	30	60	128	1024	16,384	0.967	0.967	0.651	0.000073	889.4
1	40	60	128	1024	16,384	0.967	0.967	0.650	0.000029	1033.9
1	50	60	128	1024	16,384	0.967	0.967	0.650	0.000027	1036.4
1	30	20	128	1024	16,384	0.967	0.967	0.627	0.000076	927.7
1	30	30	128	1024	16,384	0.967	0.967	0.632	0.000067	940.1
1	30	40	128	1024	16,384	0.967	0.967	0.634	0.000074	941.8
1	30	50	128	1024	16,384	0.967	0.967	0.643	0.000065	998.1
1	30	60	128	1024	16,384	0.967	0.967	0.641	0.000067	961.3
1	30	60	192	1024	16,384	0.967	0.967	0.203	0.000184	1090.9
1	30	60	256	1024	16,384	0.967	0.967	0.197	0.000188	1049.6
1	30	60	512	1024	16,384	0.967	0.967	0.201	0.000191	1052.2
1	30	60	1024	1024	16,384	0.967	0.967	0.197	0.000193	1023.7
1	30	60	2048	1024	16,384	0.967	0.967	0.202	0.000193	1048.9
1	30	60	4096	1024	16,384	0.967	0.967	0.646	0.000711	908.7
1	30	60	128	128	16,384	0.967	0.967	0.641	0.000067	961.3
1	30	60	128	256	16,384	0.967	0.967	0.204	0.000184	1090.9
1	30	60	128	512	16,384	0.967	0.967	0.197	0.000188	1049.6
1	30	60	128	1024	16,384	0.967	0.967	0.201	0.000191	1052.2
1	30	60	128	2048	16,384	0.967	0.967	0.198	0.000193	1023.7
1	30	60	128	4096	16,384	0.967	0.967	0.202	0.000193	1048.9
1	30	60	128	1024	16,384	0.967	0.967	0.680	0.000747	910.6
1	30	60	128	1024	32,768	0.967	0.967	1.269	0.000668	1951.5
1	30	60	128	1024	65,536	0.967	0.967	2.549	0.000604	3935.1
1	30	60	128	1024	131,072	0.967	0.967	5.245	0.000687	7716.4

6.1. Key Performance Metrics

To evaluate the performance and practicality of encrypted SVM inference, we introduce and analyze three key performance metrics: execution time, memory use, and model accuracy. These metrics collectively provide a comprehensive view of the computational and predictive trade-offs involved when deploying homomorphic encryption (HE) in machine learning workflows:

6.1.1. Classification Accuracy

Table 4. Classification accuracy comparison.

Model	Accuracy (%)
SVM (Plaintext)	96.7
SVM (Encrypted)	96.7

presents the classification accuracy of plaintext and encrypted SVM models. The results show that, in this experiment, homomorphic encryption has no significant impact on model accuracy as both versions achieve similar performance. This confirms the effectiveness of the CKKS encryption scheme in preserving the integrity of machine learning inference.

6.1.2. Computational Overhead

Homomorphic encryption introduces additional computational costs due to the encryption, encrypted inference, and decryption steps.

Table 5. Runtime analysis (s).

Operation	Plaintext	Encrypted
Feature Encryption	-	0.2029
Inference	0.0002	0.2029
Decryption	-	0.0001

compares the execution times for the plaintext and encrypted models.

The encrypted inference process is around 1000 times slower than plaintext execution, primarily due to polynomial evaluations performed under encryption.

6.1.3. Scalability and Resource Utilization

Scalability ensures stable performance as data grow, while resource utilization optimizes computational efficiency. Balancing encryption parameters helps to maintain security, accuracy, and performance.

6.1.4. Impact of Ring Dimension

The effect of increasing the ring dimension on encrypted inference time is shown in

Table 6. Homomorphic scale-up with varying ring dimensions.

MD	SS	FM	SL	BS	RD	SVM-Linear	SVM-Poly
1	30	60	128	1024	16 K	963.8	910.6
1	30	60	128	1024	32 K	2026.5	1851.7
1	30	60	128	1024	64 K	3646.7	3935.1
1	30	60	128	1024	128 K	8245.3	7716.4

and Figure 6. Larger ring dimensions increase computation time due to expanded ciphertext size.

6.1.5. Impact of Multiplication Depth on FHE Scale-Up

Table 7. Homomorphic scale-up for SVM-linear and SVM-poly with varying multiplication depth.

MD	SS	FM	SL	BS	RD	SVM-Linear	SVM-Poly
1	30	60	128	1024	16,384	1032.8	915.2
2	30	60	128	1024	16,384	1172.7	1093.3
3	30	60	128	1024	16,384	1397.2	1460.5
4	30	60	128	1024	16,384	1794.5	1527.7
5	30	60	128	1024	16,384	2056.4	1665.7
6	30	60	128	1024	16,384	2097.5	1954.9
7	30	60	128	1024	16,384	2324.5	2248.4

presents the effect of increasing multiplication depth D on encrypted inference speed, as visualized in Figure 7.

The experimental results highlight key trade-offs in homomorphic encryption for SVM inference. Table 4 confirms that the encrypted SVM model maintains 96.7% accuracy, similar to the plaintext model, demonstrating that CKKS encryption does not affect classification performance. Table 5 shows that encrypted inference is approximately 1000 times slower than plaintext inference, primarily due to the polynomial evaluations under encryption. This slowdown arises from the computational complexity of homomorphic operations, particularly ciphertext multiplication and relinearization [6]. Unlike plaintext arithmetic, where multiplication is a constant-time operation, homomorphic multiplication involves modular reductions, rescaling, and key-switching, leading to significant overhead [24].

6.2. Comparison Between Linear and Polynomial SVMs Under Fully Homomorphic Encryption (FHE)

In this subsection, we present a comparison between the linear SVM and polynomial SVM kernels within the context of fully homomorphic encryption (FHE). We evaluate these two kernels based on their computational costs, training and prediction times, scalability, and accuracy when applied to encrypted data. The results highlight the trade-offs between the linear SVM, which is computationally efficient, and the polynomial SVM, which offers flexibility for non-linearly separable data but incurs higher computational overhead under FHE.

6.2.1. Computational Efficiency and Prediction Time

As shown in

Table 8. Comparison of linear SVM vs. polynomial SVM under fully homomorphic encryption. For the datasets used in this study, both models exhibited similar accuracy, indicating that kernel selection did not significantly impact classification performance under FHE.

Feature	Linear SVM	Polynomial SVM
Computational Complexity	Low (Efficient operations)	High (Polynomial evaluations)
Prediction Time	Fast	Slower
Scalability	More scalable	Less scalable
Training Time	Faster	Slower
Accuracy on Non-linear Data	Dataset-dependent	Dataset-dependent
Accuracy on Linear Data	Dataset-dependent	Dataset-dependent
Observed Accuracy in Iris Dataset	no significant difference observed	no significant difference observed
Homomorphic Encryption Cost	Lower (Fewer operations)	Higher (Complex operations)
Suitability for Non-linear Data	Suitable if performance is critical	Suitable if flexibility is needed

, the linear SVM kernel performs significantly better in terms of computational efficiency under FHE. The training time and prediction time for the linear SVM are noticeably shorter compared to the polynomial SVM due to the simplicity of its operations, which primarily involve dot products and linear transformations.

In contrast, the polynomial SVM kernel requires more complex polynomial operations, such as raising values to powers and performing cross-products, resulting in significantly longer prediction times and higher overall computational overhead. This discrepancy is especially apparent when performing encrypted inference as the homomorphic operations involved with the polynomial SVM are more demanding.

6.2.2. Scalability and Homomorphic Cost

The scalability of each kernel under FHE is a critical consideration. Our results indicate that the linear SVM is much more scalable in encrypted environments. The prediction process involves fewer homomorphic operations, making it more suitable for datasets where real-time predictions are required. On the other hand, the polynomial SVM demonstrates poorer scalability as the cost of homomorphic encryption increases substantially with larger datasets. The multiple ciphertext comparisons required for polynomial-kernel evaluations lead to increased computational cost and slower performance.

6.2.3. Accuracy and Suitability for Non-Linear Data

Although the linear SVM is generally faster, the polynomial SVM can offer better performance when dealing with non-linearly separable data. Our experiments confirm that the polynomial SVM tends to have slightly higher accuracy for certain types of data, particularly when the data exhibit complex decision boundaries. However, the accuracy benefit of the polynomial SVM is marginal compared to its significantly higher computational cost under FHE.

In contrast, the linear SVM performs well on linearly separable problems and maintains stable accuracy with minimal overhead when operating under encryption. This makes it a better choice in scenarios where efficiency is prioritized over handling complex non-linear decision boundaries.

Overall, the kernel choice in FHE-SVM models significantly affects both performance and efficiency. The linear SVM is preferable when computational efficiency and scalability are prioritized, especially in real-time prediction scenarios. On the other hand, the polynomial SVM can be useful for non-linearly separable data but requires careful consideration due to the higher computational overhead and longer prediction times induced by the polynomial operations under FHE. Our findings suggest that the linear SVM is generally a better fit for FHE-based machine learning applications given its lower homomorphic cost and faster execution, while the polynomial SVM can be explored for more complex datasets in future work where performance trade-offs are acceptable.

6.2.4. Impact of Multiplication Depth

Table 7 and Figure 7 illustrate the significant impact of increasing multiplication depth on execution time. Specifically, for the polynomial-kernel SVM, inference time rises from 915.2 s at depth 1 to 2248.4 s at depth 7. This exponential growth is attributed to the core properties of homomorphic encryption, where multiplication depth governs the number of consecutive homomorphic multiplications that can be performed before ciphertexts must be refreshed via bootstrapping [11].

As the multiplicative depth increases, several compounding factors contribute to performance degradation:

• Noise Growth: Each homomorphic multiplication operation amplifies ciphertext noise. To manage this, relinearization and rescaling are required after multiplications, both of which are computationally expensive [6].
• Larger Ciphertexts and Moduli: Supporting deeper computation necessitates larger ciphertext modulus values, which increase ciphertext size and memory consumption [25], thereby slowing down arithmetic operations and raising storage requirements.
• Bootstrapping Overhead: Once the noise exceeds the permissible threshold, bootstrapping becomes necessary to refresh ciphertexts. This operation is known to be one of the most computationally intensive components of homomorphic encryption [24,26].

Beyond the computational costs, we also assess the impact of encryption on model accuracy. As detailed in Section 6.1.1 (Classification Accuracy), Table 4 presents the classification accuracy of plaintext and encrypted SVM models. The results indicate that homomorphic encryption has no significant effect on model accuracy, with both the encrypted and plaintext versions achieving comparable performance. Specifically, for the experiments conducted, encryption using the CKKS scheme preserves the integrity of the machine learning inference, showing negligible deviation in accuracy [6].

To mitigate the computational challenges associated with increasing multiplication depth, several optimization strategies have been proposed and discussed in prior work. While not all the techniques were implemented in this study, they provide valuable insights for future work aimed at improving the efficiency of encrypted machine learning:

• Ciphertext Packing: Batching multiple data points into a single ciphertext using SIMD-style encoding can enhance throughput while reducing the computational costs of each operation [25].
• Approximate Arithmetic: The use of schemes like CKKS for approximate arithmetic allows for real-valued computations with controlled error, providing an efficient balance between precision and performance [6].
• Efficient Bootstrapping: Recent advancements in partial and lazy bootstrapping techniques [26] offer opportunities to reduce the frequency and cost of bootstrapping, which is one of the most computationally expensive operations in FHE.
• Hardware Acceleration: Utilizing GPUs or FPGAs for homomorphic encryption operations can help to alleviate latency and memory constraints, making encrypted machine learning more feasible in large-scale applications.

These observations highlight the critical role of optimization and careful parameter tuning in making homomorphic encryption a viable solution for privacy-preserving machine learning while ensuring that model accuracy remains unaffected.

To address these challenges, several optimization strategies have been explored or proposed in the literature. While not all of these techniques were implemented in the current study, they offer promising directions for enhancing the efficiency and practicality of encrypted inference:

• Ciphertext Packing: By encoding multiple data points into a single ciphertext using batching techniques, the overall throughput can be significantly improved while reducing the number of required operations [25].
• Approximate Arithmetic: Employing schemes like CKKS allows for efficient fixed-point computations with controllable error, reducing overhead in applications where exact precision is not critical [6].
• Efficient Bootstrapping: Recent improvements in bootstrapping algorithms, including partial and lazy bootstrapping techniques [26], offer potential reductions in execution time.
• Hardware Acceleration: Parallelization via GPUs or FPGA-based implementations may further alleviate latency and memory bottlenecks, making encrypted machine learning more feasible at scale.

These findings reinforce the need for careful parameter tuning and algorithmic optimization when deploying homomorphic encryption in privacy-preserving machine learning workflows. They also provide a roadmap for future work aimed at minimizing computational costs while maintaining strong security guarantees.

6.2.5. Limitations and Future Work

While the proposed approach demonstrates promising results, certain limitations must be addressed to enhance its practical applicability. The most significant challenge lies in the high computational cost of homomorphic encryption, which leads to substantial execution time overhead. This limitation poses a significant barrier to real-time applications, particularly in scenarios where rapid inference is required. Furthermore, the large memory footprint associated with ciphertext storage presents scalability concerns, especially for deployment on resource-constrained devices.

The increased computational burden can be attributed to the underlying complexity of homomorphic encryption operations, which involve polynomial arithmetic over large integer rings [6]. The reliance on number-theoretic transforms (NTTs) for polynomial multiplication introduces an inherent O(n.log n) computational cost, while the quadratic complexity of matrix–vector operations within SVM classification further compounds execution time [11]. Additionally, the trade-off between multiplication depth and accuracy, dictated by the hardness of the ring-learning-with-errors (RLWE) problem, influences both performance and security [5].

To mitigate these challenges, future research should explore hardware acceleration techniques, such as leveraging GPUs and FPGAs, to enhance computational efficiency [27]. Additionally, optimizing the encryption parameters—such as ring dimension and coefficient modulus selection—can significantly reduce latency and memory consumption [6]. Exploring alternative cryptographic schemes, such as hybrid encryption approaches (typically merging a fast symmetric encryption scheme with a secure asymmetric encryption scheme to balance efficiency and security), may further improve the feasibility of encrypted machine learning in real-world applications [28].

7. Conclusions

The use of homomorphic encryption in machine learning holds great potential for privacy-aware learning. However, it introduces computational overhead, which must be carefully managed. This paper demonstrates that using an extracted SVM model is an effective method for creating a privacy-preserving model capable of processing encrypted data.

To identify the key parameters influencing performance, we evaluate several factors, including multiplication depth, scale size, first modulus size, security level, batch size, and ring dimension, along with two different SVM models: SVM-poly and SVM-linear.

Our findings reveal that ring dimension and modulus size are the two most influential parameters affecting system performance. In particular, increasing the dimension of the ring from $16,384$ to $131,072$ led to a substantial increase in the training time from 915.2 to 7716.4 s, representing an 8.4x increase in the execution time. Despite the higher computational cost, the model’s accuracy remained consistent across all the parameter configurations. Furthermore, both the linear SVM and polynomial SVMs demonstrated comparable performance trends, suggesting that the choice in kernel has a limited effect on the overall impact of homomorphic encryption with respect to performance overhead.

In conclusion, while homomorphic encryption introduces substantial computational overhead, the trade-off between security and performance can be optimized by carefully tuning parameters such as ring dimension and modulus size. Our study provides a data-driven basis for future work aiming to make encrypted machine learning more efficient and practical without compromising model accuracy.