Dynamic Sharding and Monte Carlo for Post-Quantum Blockchain Resilience
Abstract
1. Introduction
2. Related Work
- Volumetric assaults overburden transaction queues, increasing network slowness;
- Protocol-based attacks, such as Sybil and Eclipse attacks, threaten consensus integrity;
- Consumption of resources attacks, which target CPUs, memory, or disks.
- Transaction success rate: this indicator measures the percentage of legitimate transactions that are successfully handled. A high transaction success rate implies resilience to congestion and DDoS attacks, whereas a low success rate reflects system inefficiencies and weaknesses [41];
- Transaction latency: this metric measures the time it takes for a transaction to be confirmed and is a direct indicator of blockchain scalability. Increased delay during attacks reveals inefficiencies in resource management and network congestion [42];
- Resource consumption (CPU, memory, and disk usage): these characteristics define the computational cost associated with various blockchain topologies. High CPU and memory consumption represent processing inefficiencies, but efficient resource allocation demonstrates the effectiveness of dynamic sharding in reducing attack-induced bottlenecks [43].
- Dynamic sharding allows for agility and effective resource utilization;
- Post-quantum cryptography (Falcon): to combat quantum threats;
- Monte Carlo simulations: used for stochastic simulation of attack scenarios.
3. Methodology
3.1. Introduction
- The DDoS attack simulation and resource monitoring phase comprises simulating high-traffic DDoS attacks on both blockchain systems. The attacks are intended to stress the network by flooding it with transactions, and the system’s response is measured using metrics such transaction success rates, latency, and resource utilization (CPU, memory, and disk usage). This phase allows for a direct comparison of the performance of sharded and non-sharded systems under comparable situations;
- Monte Carlo simulations and resource monitoring model randomized attack severity and traffic patterns. Each iteration provides heterogeneity in congestion levels, transaction failures, and resource contention, allowing a probabilistic assessment of the durability of blockchain designs. Similarly, resource utilization measurements are collected during this phase to assess the efficiency of shard-based distribution in dealing with dynamic conditions.
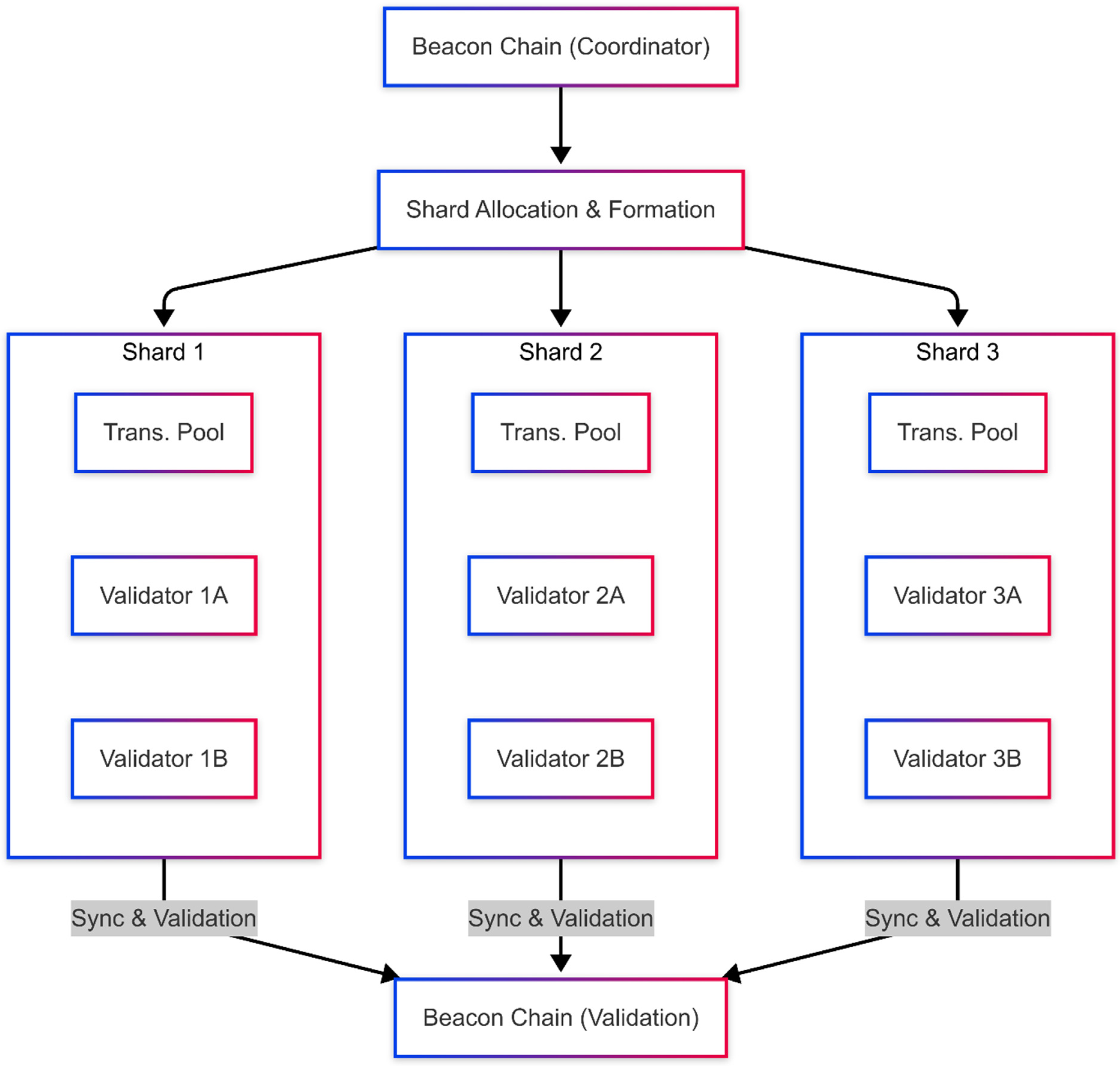
3.2. Experimental Blockchain Architectures
- The non-sharded blockchain processes all transactions collectively by a single validation pool, making it very vulnerable to network congestion and delays, especially during attacks;
- In contrast, the sharded blockchain design distributes transactions across several independent shards. Each shard maintains a subset of transactions, which reduces overall system congestion and increases scalability. This design ensures that the failure of a single shard does not compromise the overall integrity of the blockchain.
| Algorithm 1 Dynamic Shard Allocation Strategy based on Transaction Load and Network Congestion |
| Input: transaction_load, shard_threshold, max_shards, congestion_level Output: Updated shard allocations 1. Initialize shard_count ← Initial number of shards 2. Monitor real-time transaction_load and congestion_level 3. While system is running do: 4. If transaction_load > shard_threshold AND shard_count < max_shards then: 5. Increase shard_count by 1 (create new shard) 6. Redistribute active transactions among all shards 7. If congestion_level < predefined_safe_limit AND shard_count > 1 then: 8. Merge least active shards to optimize resource utilization 9. Update shard allocations and broadcast changes to nodes 10. Repeat process periodically |
3.3. Comparative Analysis of Sharding Strategies
- Static sharding (e.g., Ethereum 2.0) pre-allocates transactions to fixed shards, which improves scalability but exposing individual shards to targeted DDoS attacks;
- Hybrid sharding introduces limited adaptability, which reduces the risk of targeted attacks but still results in synchronization delays;
- Dynamic sharding constantly redistributes transactions and validator assignments, preventing adversaries from forecasting shard allocations. While dynamic sharding improves security and performance, it requires more computational resources.
3.4. DDoS Attack Simulation
- Objective:
- ○
- Evaluate the transaction success rate, latency, and resource utilization (CPU, memory, disk usage) under stress. Also, compare the ability of the sharded blockchain to handle network congestion against the non-sharded blockchain;
- Configurations:
- ○
- Transaction volume: high-frequency transaction submissions to overwhelm the network;
- ○
- Attack duration: sustained over a specific time frame to evaluate long-term resilience;
- ○
- Distribution: transactions randomly assigned to nodes to replicate adversarial scenarios.
| Algorithm 2 Simulation of Transaction Performance and Resource Utilization During Attack |
| Input: attack_duration, transaction_rate, blockchain_mode Output: transaction success/failure rate, resource utilization 1. Initialize transaction_success ← 0 2. Initialize transaction_failure ← 0 3. Start attack_timer ← 0 4. While attack_timer < attack_duration do 5. Generate incoming_transactions ← transaction_rate per second 6. If blockchain_mode = “Sharded” then: 7. Distribute transactions across shards 8. Process transactions in parallel Else: 9. Process all transactions in a single validation pool 10. For each transaction in incoming_transactions: 11. If network congestion or node overload then: 12.transaction_failure← transaction_failure + 1 Else: 13.transaction_success← transaction_success + 1 14. Record CPU, memory, and disk usage at this timestep 15. Increment attack_time 16. Compute success_rate ← transaction_success/(transaction_success+transaction_failure) 17. Return success_rate, resource_metrics |
- Monitoring:
- ○
- Resource consumption metrics (CPU, memory, and disk usage) are recorded in real-time using ressource.py;
- ○
- These metrics are analyzed post-simulation to identify performance bottlenecks and compare the efficiency of the architectures;
- Rationale:
- ○
- While post-quantum cryptographic schemes like Falcon secure blockchains against quantum-based attacks, they remain vulnerable to traditional attack vectors such as DDoS;
- ○
- This simulation examines whether the sharding mechanism can mitigate these vulnerabilities and improve the scalability of post-quantum blockchains.
3.5. Monte Carlo Simulation
3.5.1. Key Objectives
- To evaluate how varying levels of network congestion, transaction volumes, and failure probabilities impact blockchain performance;
- To statistically analyze resource consumption patterns (CPU, memory, disk usage) under diverse adversarial conditions;
- To assess whether the sharded blockchain consistently outperforms the non-sharded architecture across multiple scenarios.
3.5.2. Simulation Design
- Randomized inputs: we have two scripts, one for a sharded architecture and another one for a non-sharded architecture. They generate thousands of iterations with different attack conditions. These include varying transaction frequencies, congestion levels, and shard-specific corruption probabilities;
- Metrics recorded: each iteration captures transaction success rates, latency, and resource consumption (CPU, memory, disk usage) to build a robust dataset for comparison;
- Iteration count: thousands of iterations are performed to ensure statistical reliability and identify consistent performance trends.
| Algorithm 3 Iterative Simulation of Transaction Success and Failure Rates under Variable Load |
| Input: total_iterations = 10000 Output: success rate and failure rate of transactions 1. Initialize transaction_success ← 0 2. Initialize transaction_failure ← 0 3. For i from 1 to total_iterations do: 4. Generate transaction_load ∈ [low_load, high_load] 5. If system_mode = “Sharded” then: 6. Assign transactions to shards dynamically 7. Execute transactions in parallel Else: 8. Process all transactions in a single validation pool 9. For each transaction: 10. If network congestion or shard overload: 11. transaction_failure ←transaction_failure + 1 Else: 12. transaction_success← transaction_success + 1 13. Compute success_rate ← transaction_success/total_iterations 14. Compute failure_rate ← transaction_failure/total_iterations 15. Return success_rate, failure_rate |
3.5.3. Monte Carlo Simulation Parameters
- Number of iterations:
- b.
- Input parameter distributions:
- Transaction interarrival time: in blockchain systems, transaction arrivals follow an exponential distribution with a rate parameter of λ = 0.05 transactions per millisecond, reflecting the bursty character of transaction flows. This distribution is used to accurately model both normal operating conditions and periods of congestion caused by DDoS attacks;
- Attack intensity (DDoS load): represented by a Poisson distribution with requests per second mean values μ = {50, 100, 500}, simulating different attack magnitudes;
- Shard workload distribution: assumed to follow a normal distribution (μ = 500 transactions; σ = 100), dynamically adjusted through load-balancing mechanisms;
- Transaction size: modeled with a log-normal distribution (μ = 250 bytes; σ = 50), reflecting variations in transaction complexity;
- Validator processing time: defined using a gamma distribution (k = 2; θ = 30 ms), based on empirical benchmarks from blockchain validation processes.
- c.
- Experimental Conditions:
- Baseline scenario: normal transaction volume, no attack;
- Moderate attack: 100 malicious transactions per second targeting random shards;
- Severe attack: 500 malicious transactions per second directed at a specific shard;
- Adaptive sharding response: dynamic sharding activated with real-time workload redistribution.
- d.
- Probabilistic Modeling:
- S0 (normal operation): shards operate optimally with balanced workloads;
- S1 (mild congestion): transaction queues increase due to sudden transaction surges;
- S2 (severe congestion): validation delays grow significantly, affecting throughput;
- S3 (shard overload): one or more shards become unresponsive due to excessive load.
- e.
- Transaction Failure Handling:
- Network congestion: queue overflow probability p = 0.15 under attack conditions;
- Shard overload: probability p = 0.10 in worst-case scenarios where the shard exceeds its maximum capacity;
- Timeout failures: transactions exceeding 5 × the normal processing time are considered lost.
- f.
- Validation and Real-World Comparison:
- Empirical data from Ethereum 2.0 testnets, particularly sharding proposals;
- Historical DDoS attack logs on blockchain networks, providing real-world insights into attack patterns and mitigations;
- Theoretical models of blockchain scalability, validating the consistency of the Monte Carlo results with prior research.
3.6. Simulation Framework and Methodological Flow
4. Results and Analysis
4.1. DDoS Simulation Results
- (a)
- Transaction Latency:
- (b)
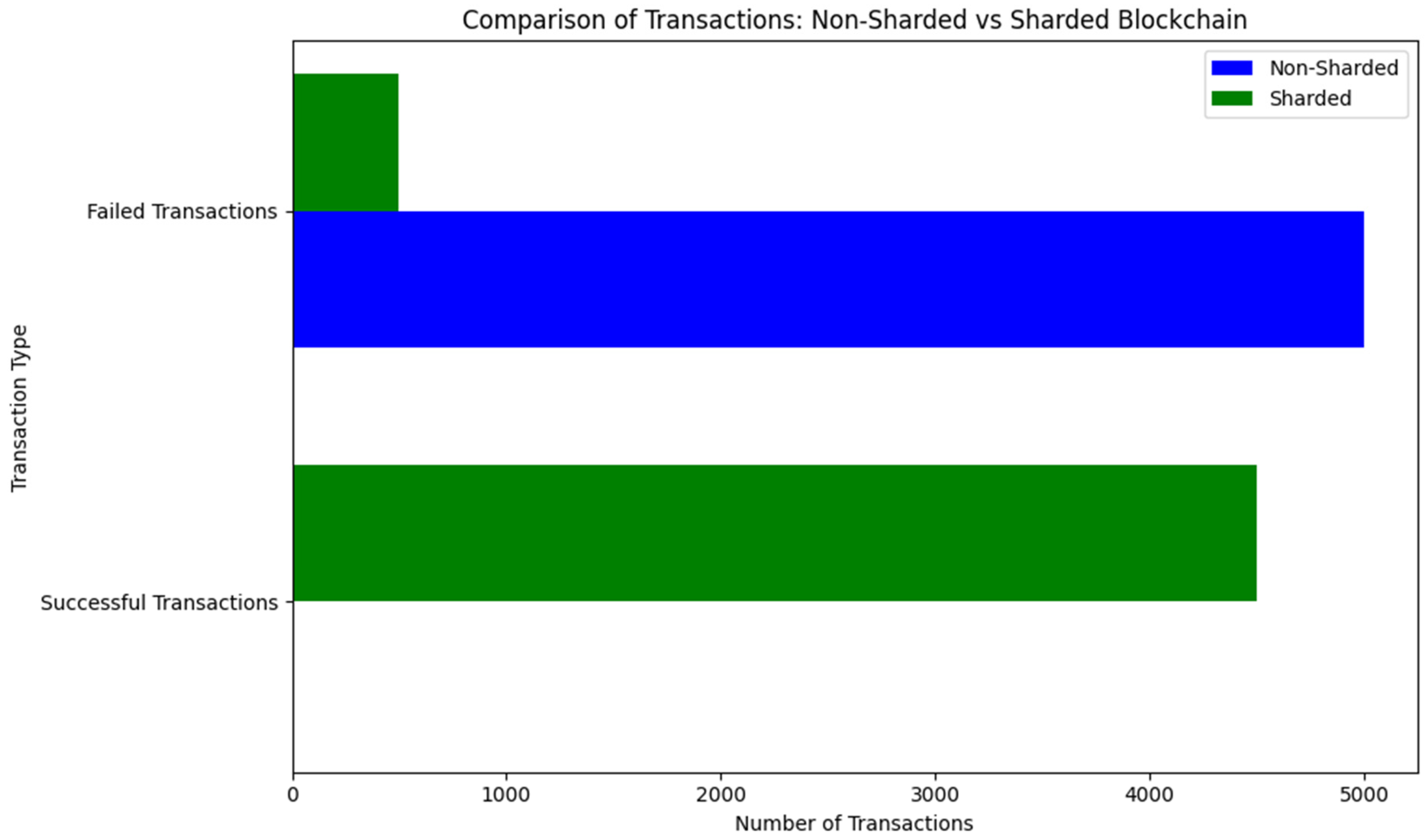
- Transaction Success Rates:
- (c)
- CPU Utilization:
- (d)
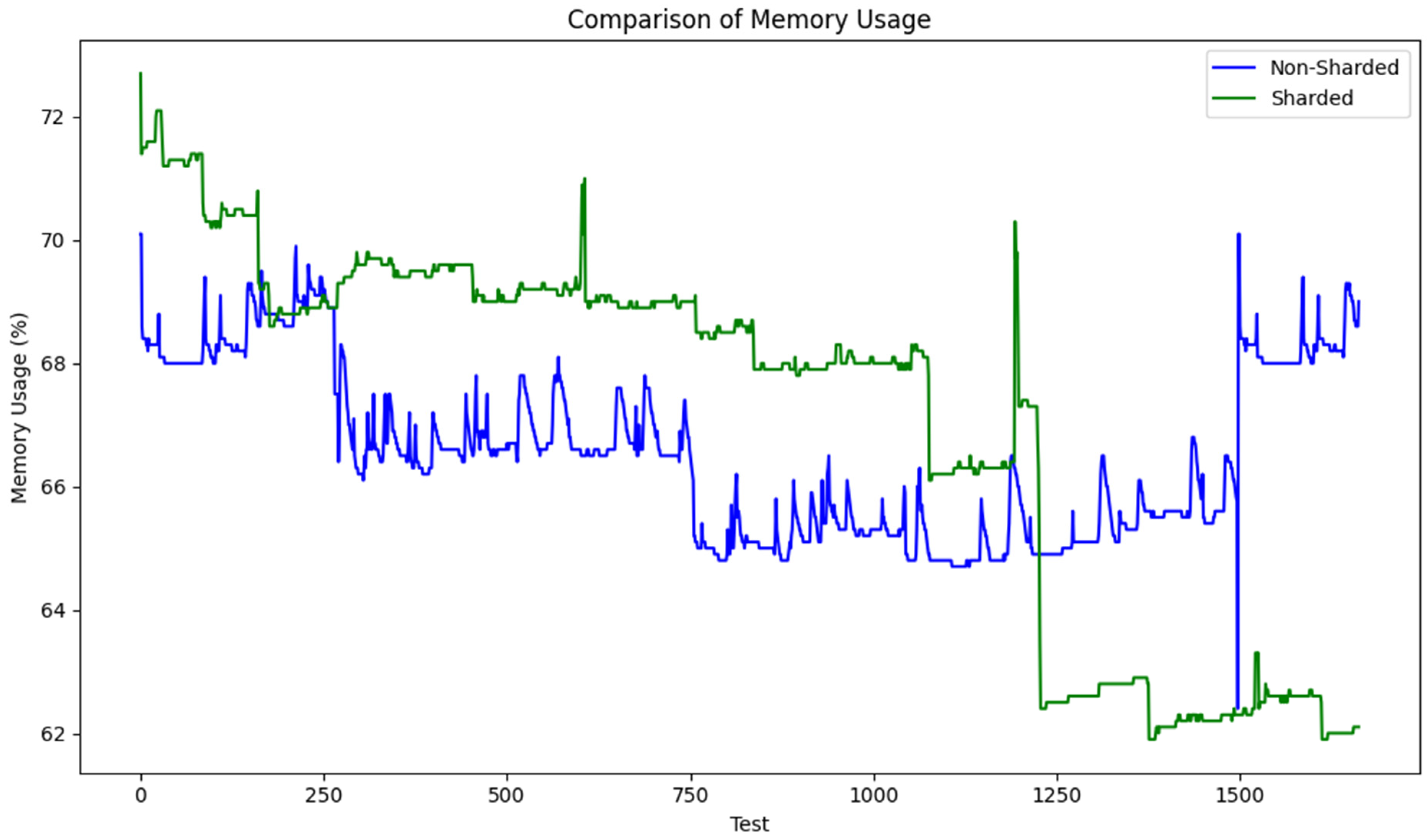
- Memory Usage:
- (e)
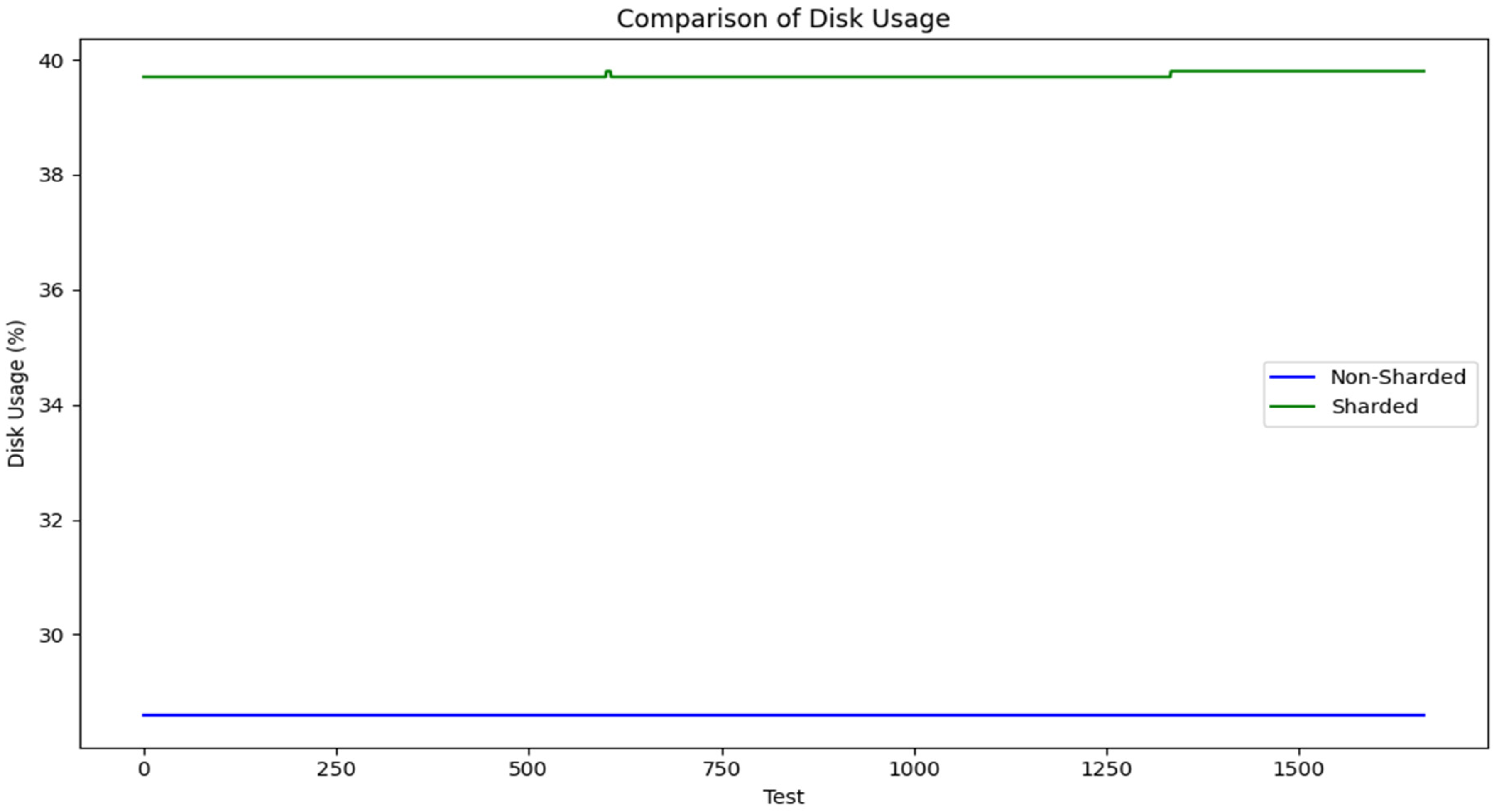
- Disk Usage:
4.2. Monte Carlo Simulation Results
- (a)
- Cumulative Transaction Success
- The cumulative number of successful transactions remains below 750 after 10,000 iterations, indicating that even without direct attacks, the non-sharded architecture struggles with scalability;
- The linear growth pattern of successful transactions confirms that the non-sharded blockchain is highly constrained by its centralized validation process, making it less efficient in handling transaction load;
- Compared to the expected performance of the sharded blockchain, the non-sharded system exhibits a significantly lower transaction success rate, reinforcing its susceptibility to congestion over time.
- (b)
- Advanced Cumulative Success Analysis:
- (c)
- Resource Utilization:
- The non-sharded blockchain exhibited frequent spikes, often nearing full capacity, signaling strain due to centralized transaction processing;
- The sharded blockchain maintained lower and more stable CPU utilization, reducing the risk of overloading the system.
- The non-sharded architecture experienced rapid and uneven memory consumption, frequently reaching saturation. This led to performance degradation during high transaction volumes;
- Sharded systems managed memory resources efficiently across shards, maintaining a balanced and predictable utilization.
- The non-sharded blockchain encountered bottlenecks due to its centralized data writing operations, resulting in inconsistent disk usage patterns;
- The sharded blockchain demonstrated consistent and steady disk utilization, leveraging distributed storage demands to prevent overload.
4.3. Statistical Significance Tests
4.3.1. Methodology for Statistical Testing
- The Shapiro–Wilk test for normality: was performed to examine if the performance parameters (transaction success rate, latency, and resource usage) have a normal distribution;
- Student’s t-test: once the normality assumption was granted, we used an independent two-sample t-test to compare the means of sharded and non-sharded blockchain designs;
- Mann-Whitney U test: in situations where normality was not proven, we used this non-parametric test to determine whether one distribution consistently produces greater results than another;
- Binomial exact test: given the enormous imbalance of successful transactions between the two topologies, we used an exact binomial test to see if the difference was statistically significant.
4.3.2. Results of Statistical Tests
- Transaction success rate: the binomial exact test showed a p-value < 0.00001, indicating a substantial increase in transaction success rates in the sharded architecture compared to the non-sharded version;
- CPU usage: the Shapiro–Wilk test showed that CPU utilization data are not regularly distributed (p < 0.0001). The sharded blockchain significantly reduced CPU utilization, as validated by the Mann–Whitney U test (p < 0.0001);
- Memory usage: similarly, the Mann–Whitney U test showed that memory consumption is significantly lower in the sharded blockchain (p < 0.0001), suggesting more efficient resource allocation;
- Disk usage: the Shapiro–Wilk normality test confirmed that disk usage values in both sharded and non-sharded architectures consist of constant values (p = 1.000 for both distributions), indicating no variance in the dataset. Given this, neither the t-test nor the Mann–Whitney U test could be meaningfully applied. While no statistical tests could be conducted due to the dataset’s lack of variation, the findings demonstrate that sharded architectures require additional disk space to allow scalability and decentralized processing.
4.3.3. Interpretation and Implications
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994. [Google Scholar]
- Boneh, D.; Shoup, V. A Graduate Course in Applied Cryptography. Version 0.5. Stanford University. 2020. Available online: https://toc.cryptobook.us (accessed on 1 October 2024).
- Ducas, L.; Prest, T. Falcon: Fast-Fourier lattice-based compact signatures over NTRU. In Proceedings of the Post-Quantum Cryptography Conference, Fort Lauderdale, FL, USA, 9–11 April 2018. [Google Scholar]
- NIST. Post-Quantum Cryptography Standardization. 2023. Available online: https://csrc.nist.gov/ (accessed on 1 January 2025).
- Wani, S.; Imthiyas, M.; Almohamedh, H.; Alhamed, K.M.; Almotairi, S.; Gulzar, Y. Distributed Denial of Service (DDoS) Mitigation Using Blockchain—A Comprehensive Insight. Symmetry 2021, 13, 227. [Google Scholar] [CrossRef]
- Manikumar, D.V.V.S.; Maheswari, B.U. Blockchain Based DDoS Mitigation Using Machine Learning Techniques. In Proceedings of the 2020 Second International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 15–17 July 2020; pp. 794–800. [Google Scholar] [CrossRef]
- Kshetri, N. Can blockchain strengthen the internet of things? IT Prof. 2017, 19, 68–72. [Google Scholar] [CrossRef]
- Buterin, V. Sharding FAQs. 2017. Available online: https://vitalik.eth.limo/general/2017/12/31/sharding_faq.html (accessed on 7 February 2025).
- Liu, X.; Xie, H.; Yan, Z.; Liang, X. A Survey on Blockchain Sharding. ISA Trans. 2023, 141, 30–43. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Dahhak, H.; Afifi, N.; Hilal, I. Security Analysis of Classical and Post-Quantum Blockchains. J. Comput. Inf. Syst. 2024, 64, 1–14. [Google Scholar] [CrossRef]
- Shi, S.; Wang, J.; Zhang, K. Resilience against DDoS attacks in blockchain networks. J. Distrib. Comput. Syst. 2021, 35, 45–58. [Google Scholar]
- Kokoris-Kogias, E.; Jovanovic, P.; Gasser, L.; Gailly, N.; Syta, E.; Ford, B. OmniLedger: A secure, scale-out, decentralized ledger via sharding. In Proceedings of the IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 20–24 May 2018; Volume 19, pp. 583–598. [Google Scholar]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography: Quantum-resistant algorithms. Commun. ACM 2017, 60, 57–64. [Google Scholar]
- Wan, L.; Eyers, D.; Zhang, H. Evaluating the Impact of Network Latency on the Safety of Blockchain Transactions. In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain), Atlanta, GA, USA, 14–17 July 2019; pp. 194–201. [Google Scholar] [CrossRef]
- Alajlan, R.; Alhumam, N.; Frikha, M. Cybersecurity for Blockchain-Based IoT Systems: A Review. Appl. Sci. 2023, 13, 7432. [Google Scholar] [CrossRef]
- Chaganti, R.; Bhushan, B.; Ravi, V. The role of Blockchain in DDoS attacks mitigation: Techniques, open challenges and future directions. arXiv 2022, arXiv:2202.03617. [Google Scholar]
- Raikwar, M.; Gligoroski, D. DoS Attacks on Blockchain Ecosystem. arXiv 2022, arXiv:2205.13322. [Google Scholar]
- Liu, Y.; Liu, J.; Vaz Salles, M.A.; Zhang, Z.; Li, T.; Hu, B.; Henglein, F.; Lu, R. Building Blocks of Sharding Blockchain Systems: Concepts, Approaches, and Open Problems. arXiv 2021, arXiv:2102.13364. [Google Scholar] [CrossRef]
- Doger, M.; Ulukus, S. Transaction Capacity, Security and Latency in Blockchains. arXiv 2024, arXiv:2402.10138. [Google Scholar]
- Zhang, L.; Zhang, F. Understanding Waiting Time in Transaction Fee Mechanism: An Interdisciplinary Perspective. arXiv 2023, arXiv:2305.02552. [Google Scholar]
- Sousa, M.; Silva, R. Hierarchical sharding to mitigate DDoS attacks in large-scale blockchain systems. IEEE Trans. Netw. Secur. 2022, 10, 45–62. [Google Scholar]
- Roughgarden, T. Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559. arXiv 2020, arXiv:2012.00854. [Google Scholar]
- Kumar, R.; Gupta, M. Sharding in distributed databases: Challenges and opportunities for blockchains. Database Syst. J. 2020, 12, 123–140. [Google Scholar]
- Han, R.; Yu, J.; Lin, H.; Chen, S.; Veríssimo, P.E. On the Security and Performance of Blockchain Sharding. Cryptol. Eprint Arch. 2021. Available online: https://eprint.iacr.org/2021/1276 (accessed on 1 December 2024).
- Bulgakov, A.L.; Aleshina, A.V.; Smirnov, S.D.; Demidov, A.D.; Milyutin, M.A.; Xin, Y. Scalability and Security in Blockchain Networks: Evaluation of Sharding Algorithms and Prospects for Decentralized Data Storage. Mathematics 2024, 12, 3860. [Google Scholar] [CrossRef]
- Kokoris-Kogias, E.; Jovanovic, P.; Ford, B. Scalability improvements in blockchain through sharding. ACM Trans. Blockchain 2019, 3, 1–25. [Google Scholar]
- Zhang, Y.; Yang, X.; Liu, J. Adaptive sharding strategies for dynamic blockchain networks. Blockchain Res. J. 2021, 6, 33–49. [Google Scholar]
- Shi, Y.; Liu, H.; Chen, X. DDoS mitigation in sharded blockchain systems: A review and evaluation. IEEE Commun. Surv. Tutor. 2021, 23, 203–220. [Google Scholar]
- Li, X.; Zhang, Y.; Zhao, W. Sharding-based blockchain systems: Enhancing resilience against DDoS attacks. Blockchain Secur. J. 2021, 4, 99–115. [Google Scholar]
- Han, K.; Wang, S.; Li, Z. Hybrid sharding for secure and scalable blockchain applications. Int. J. Blockchain Stud. 2020, 8, 78–93. [Google Scholar]
- Wang, L.; Zhao, M. Multi-layer sharding for enhanced blockchain resilience. Distrib. Ledger Res. 2021, 5, 88–110. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Buchmann, J.; Dahmen, E.; Hofheinz, D. Post-quantum signatures. J. Cryptol. 2008, 21, 377–410. [Google Scholar]
- NIST. Post-Quantum Cryptography Standardization Project. 2021. Available online: https://csrc.nist.gov/projects/post-quantum-cryptography (accessed on 1 January 2025).
- Falcon Development Team. Fast-Fourier lattice-based compact signatures. In Proceedings of the Post-Quantum Cryptography Conference, Fort Lauderdale, FL, USA, 9–11 April 2018. [Google Scholar]
- Chen, L.; Li, W.; Yu, H. Falcon integration into blockchain systems: A feasibility study. J. Blockchain Res. 2020, 7, 45–63. [Google Scholar]
- Han, Y.; Zhang, L.; Li, P. Lattice-based cryptography for blockchain quantum resistance. IEEE Blockchain Lett. 2021, 3, 12–18. [Google Scholar]
- Bernstein, D.J.; Lange, T. Quantum-resistant cryptography and its applications. Adv. Cryptol. 2019, 25, 87–95. [Google Scholar]
- Falcon Development Team. Falcon: Fast-Fourier Lattice-Based Compact Signatures over NTRU. 2020. Available online: https://falcon-sign.info/ (accessed on 1 November 2024).
- Bappy, F.H.; Zaman, T.S.; Sajid, M.S.I.; Pritom, M.M.A.; Islam, T. Maximizing Blockchain Performance: Mitigating Conflicting Transactions through Parallelism and Dependency Management. arXiv 2024, arXiv:2407.01426. [Google Scholar]
- Esmaili, M.; Christensen, K. Performance modeling of public permissionless blockchains: A survey. arXiv 2024, arXiv:2402.18049. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, G.; Sun, C.; Wang, X.; Wang, Y.; Zhang, M.; Ni, W.; Liu, R.P.; Reeves, A.; Georgalas, N. TBDD: A New Trust-based, DRL-driven Framework for Blockchain Sharding in IoT. arXiv 2024, arXiv:2401.00632. [Google Scholar] [CrossRef]
- Monte The Application of Monte Carlo Simulation to Assess the Value at Risk in Cryptocurrency. Available online: https://www.researchgate.net/publication/383997972_The_Application_of_Monte_Carlo_Simulation_to_Assess_the_Value_at_Risk_in_Cryptocurrency (accessed on 1 November 2024).







| References | DDoS | Sharding | Post-Quantum Cryptography | Falcon | Quantum Threats | Monte Carlo Simulations | Scalability | Resilience |
|---|---|---|---|---|---|---|---|---|
| Ref. [12] | X | X | ||||||
| Ref. [13] | X | X | ||||||
| Ref. [14] | X | X | ||||||
| Ref. [24] | X | |||||||
| Ref. [27] | X | X | ||||||
| Ref. [9] | X | X | ||||||
| Ref. [28] | X | X | ||||||
| Ref. [29] | X | X | X | |||||
| Ref. [30] | X | X | X | |||||
| Ref. [31] | X | X | X | |||||
| Ref. [32] | X | X | X | |||||
| Ref. [33] | X | X | ||||||
| Ref. [34] | X | X | ||||||
| Ref. [35] | X | |||||||
| Ref. [36] | X | X | ||||||
| Ref. [37] | X | X | ||||||
| Ref. [38] | X | |||||||
| Ref. [39] | X | |||||||
| Ref. [40] | X | |||||||
| Ref. [41] | X | |||||||
| Ref. [42] | X | X | ||||||
| Ref. [44] | X | X | X |
| Criteria | Static Sharding | Hybrid Sharding | Dynamic Sharding |
|---|---|---|---|
| Scalability | High | Moderate High | Very High |
| DDoS Resilience | Low | Moderate | High |
| Resource Allocation | Fixed | Partially Adaptive | Fully Adaptive |
| Synchronization Overhead | Low | Moderate | High |
| Implementation Complexity | Low | Moderate | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajar, D.; Afifi, N.; Hilal, I. Dynamic Sharding and Monte Carlo for Post-Quantum Blockchain Resilience. Cryptography 2025, 9, 22. https://doi.org/10.3390/cryptography9020022
Hajar D, Afifi N, Hilal I. Dynamic Sharding and Monte Carlo for Post-Quantum Blockchain Resilience. Cryptography. 2025; 9(2):22. https://doi.org/10.3390/cryptography9020022
Chicago/Turabian StyleHajar, Dahhak, Nadia Afifi, and Imane Hilal. 2025. "Dynamic Sharding and Monte Carlo for Post-Quantum Blockchain Resilience" Cryptography 9, no. 2: 22. https://doi.org/10.3390/cryptography9020022
APA StyleHajar, D., Afifi, N., & Hilal, I. (2025). Dynamic Sharding and Monte Carlo for Post-Quantum Blockchain Resilience. Cryptography, 9(2), 22. https://doi.org/10.3390/cryptography9020022






