SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximation †
Abstract
:1. Introduction
- 1.
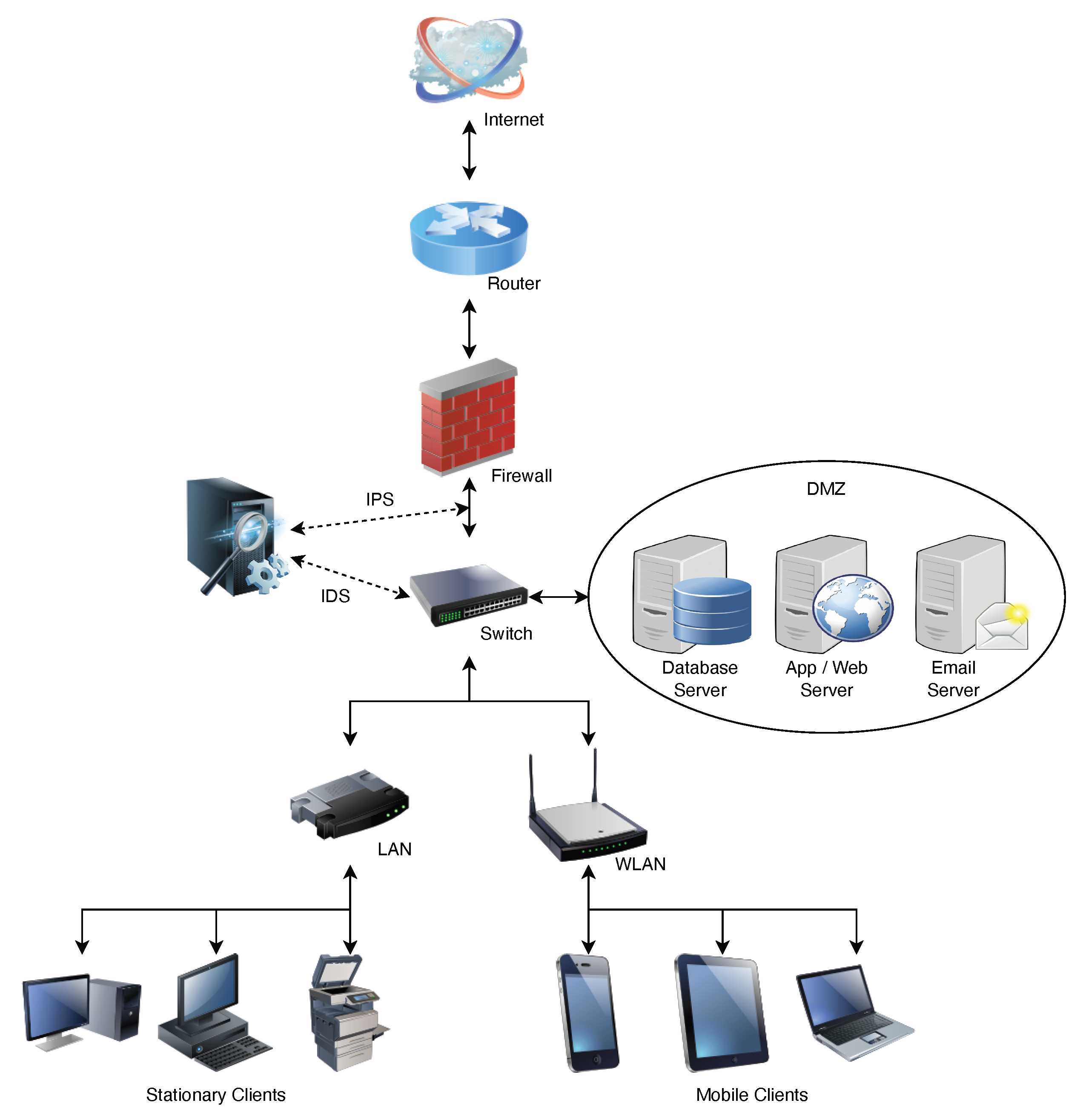
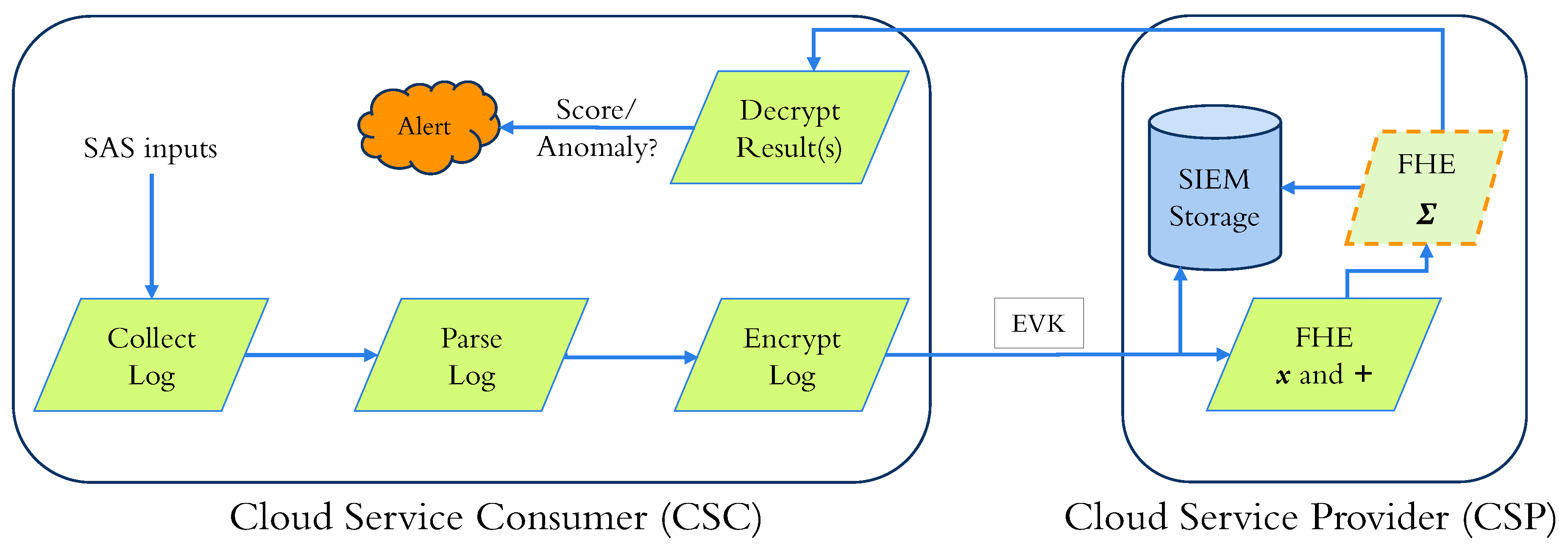
- A “log collector” to collect logs from diverse applications operating on a SAS.
- 2.
- A “transmitter” that sends logs to the SIEM, which is usually encrypted to safeguard against eavesdropping in the communication channel.
- 3.
- A “receiver” to amass, store, decrypt, and ascertain the transmitted logs’ integrity.
- 4.
- A “parser” to convert the data into a structured form used by the SIEM vendor to process the decrypted logs for storage and analysis.
- 5.
- An “anomaly detector” that uses proprietary algorithms to render parsed logs and transmit alerts for anomalies.
1.1. Contributions
- First, we formulate a supervised binary classification problem for log anomaly detection and implement it with the CKKS cryptosystem (in Section 4).
- Second, we propose novel ANN-based third-degree sigmoid approximations in the intervals and (in Section 5).
- Third, we evaluated the performance of various sigmoid approximations in the encrypted domain, and our results showed better accuracy and -ratio (in Section 6).
1.2. Organization
- First, we describe the building blocks of our protocols in Section 2, where we review FHE in Section 2.1 and present polynomial approximations for the sigmoid activation function in Section 5.
- Next, we review the previous work in Section 3.
- Then, we describe our methodology in Section 4.
- Finally, we discuss our experimental results in Section 6.
2. Background
2.1. Fully Homomorphic Encryption
- —generates a key pair.
- —encrypts a plaintext.
- —decrypts a ciphertext.
- —evaluates an arithmetic operation on ciphertexts.
- : generates a secret key () for decryption, a public key () for encryption, and a publicly available evaluation key (). The secret key () is a sample from a random distribution over . The public key () is computed aswhere a is sampled from a uniform distribution over , and e is sampled from an error distribution over . is utilized for relinearization after the multiplication of two ciphertexts.
- : encrypts a message m into a ciphertext c utilizing the public key (). Let v be sampled from a distribution over . Let and be small errors. Then, the message m is encrypted as
- : decrypts a message c into a plaintext m utilizing the secret key (). The message m can be recovered from a level l ciphertext thanks to the function . Note that with CKKS, the capacity of a ciphertext reduces each time a multiplication is computed.
- : estimates the function f on the encrypted inputs using the evaluation key .
2.2. Polynomial Approximations
2.2.1. Taylor
2.2.2. Fourier
2.2.3. Pade
2.2.4. Chebyshev
2.2.5. Remez
- 1.
- Solve the system of linear equationsfor the unknowns and E.
- 2.
- Use as coefficients to form a polynomial .
- 3.
- Find the set M of points of local maximum error .
- 4.
- If the errors at every are alternate in sign (+/−) and of equal magnitude, then is the minimax approximation polynomial. If not, replace X with M and repeat the abovementioned steps.
2.2.6. ANN
3. Related Work
- 1.
- Encode: The data are encoded to control their scope, granularity, and randomness.
- 2.
- Shuffle: The encoded data are shuffled to break their linkability and guarantee that individual data items become “lost in the crowd” of the batch.
- 3.
- Analyze: The anonymous, shuffled data are analyzed by a specific analysis engine that averts statistical inference attacks on analysis results.
- 1.
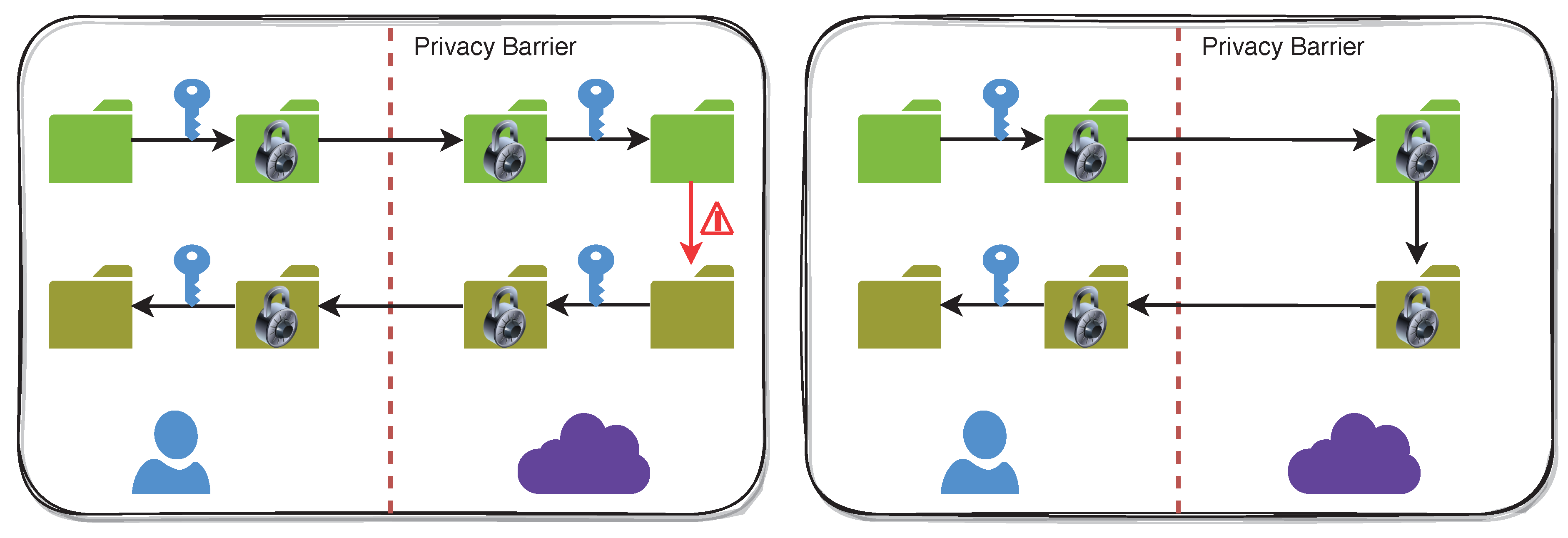
- Ubiquitous configuration—This is similar to other works and sends an encrypted result for every log entry.
- 2.
- Aggregate configuration—This reduces communication and computation requirements by sending a single result for a block of log entries.
4. Proposed Solution
- 1.
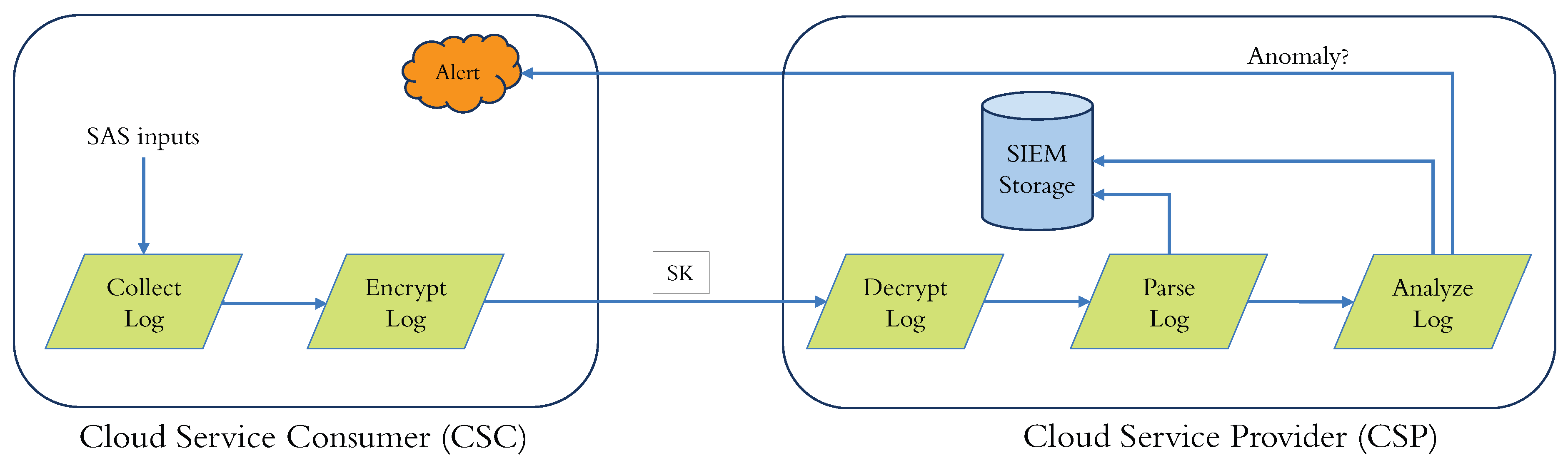
- Ubiquitous—The SIEM sends one encrypted result per user input.
- 2.
- Aggregate—Only one result is sent to the encrypted domain for all the user inputs. This technique helps reduce communication costs and uses much fewer resources on the SAS to decrypt a single encrypted result rather than one encrypted result per encrypted input.
5. Sigmoid Approximation
6. Experimental Analysis
6.1. Evaluation Criteria
- Precision is the proportion of correctly predicted positive results (true positive, TP) to the total predicted positive results (TP + false positive, FP). It is also known as the positive predictive value.
- Recall is the proportion of correctly predicted positive results (TP) to the total actual positive results (TP + false negative, FN). It is also known as sensitivity or specificity.
- Accuracy is the proportion of all correct predictions (TP + TN) to the total number of predictions made (TP + FP + TN + FN). It can be calculated as precision divided by recall or .
- The F1-score is a measure that considers both precision and recall. It is calculated as the harmonic mean of the precision and recall.
- The -ratio is measured for the sigmoid activation function with binary outcomes and calculated as the ratio of the sum of all predicted labels to the sum of all actual labels.
6.2. Datasets
6.3. Test Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cloud Object Storage—Amazon S3—Amazon Web Services. Available online: https://aws.amazon.com/s3/ (accessed on 16 October 2023).
- Azure Blob Storage | Microsoft Azure. Available online: https://azure.microsoft.com/en-us/products/storage/blobs/ (accessed on 16 October 2023).
- S.3195—Consumer Online Privacy Rights Act. 2021. Available online: https://www.congress.gov/bill/117th-congress/senate-bill/3195 (accessed on 16 October 2023).
- TITLE 1.81.5. California Consumer Privacy Act of 2018 [1798.100–1798.199.100]. 2018. Available online: https://leginfo.legislature.ca.gov/faces/codes_displayText.xhtml?division=3.&part=4.&lawCode=CIV&title=1.81.5 (accessed on 16 October 2023).
- EUR-Lex—02016R0679-20160504—EN—EUR-Lex. 2016. Available online: https://eur-lex.europa.eu/eli/reg/2016/679/2016-05-04 (accessed on 16 October 2023).
- Durumeric, Z.; Ma, Z.; Springall, D.; Barnes, R.; Sullivan, N.; Bursztein, E.; Bailey, M.; Halderman, J.A.; Paxson, V. The Security Impact of HTTPS Interception. In Proceedings of the 24th Annual Network and Distributed System Security Symposium, NDSS, San Diego, CA, USA, 26 February–1 March 2017. [Google Scholar]
- Principles for the Processing of User Data by Kaspersky Security Solutions and Technologies | Kaspersky. Available online: https://usa.kaspersky.com/about/data-protection (accessed on 16 October 2023).
- Nakashima, E. Israel hacked Kaspersky, then Tipped the NSA That Its Tools Had Been Breached. 2017. Available online: https://www.washingtonpost.com/world/national-security/israel-hacked-kaspersky-then-tipped-the-nsa-that-its-tools-had-been-breached/2017/10/10/d48ce774-aa95-11e7-850e-2bdd1236be5d_story.html (accessed on 16 October 2023).
- Perlroth, N.; Shane, S. How Israel Caught Russian Hackers Scouring the World for U.S. Secrets. 2017. Available online: https://www.nytimes.com/2017/10/10/technology/kaspersky-lab-israel-russia-hacking.html (accessed on 16 October 2023).
- Temperton, J. AVG Can Sell Your Browsing and Search History to Advertisers. 2015. Available online: https://www.wired.co.uk/article/avg-privacy-policy-browser-search-data (accessed on 16 October 2023).
- Taylor, S. Is Your Antivirus Software Spying On You? | Restore Privacy. 2021. Available online: https://restoreprivacy.com/antivirus-privacy/ (accessed on 16 October 2023).
- Karande, V.; Bauman, E.; Lin, Z.; Khan, L. SGX-Log: Securing system logs with SGX. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–6 April 2017; pp. 19–30. [Google Scholar]
- Paccagnella, R.; Datta, P.; Hassan, W.U.; Bates, A.; Fletcher, C.; Miller, A.; Tian, D. Custos: Practical tamper-evident auditing of operating systems using trusted execution. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 23–26 February 2020. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. Faster Fully Homomorphic Encryption: Bootstrapping in Less Than 0. In 1 Seconds. In Proceedings of the Advances in Cryptology—ASIACRYPT 2016, Hanoi, Vietnam, 4–8 December 2016; Cheon, J.H., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–33. [Google Scholar]
- Brakerski, Z. Fully Homomorphic Encryption Without Modulus Switching from Classical GapSVP. In Proceedings of the 32nd Annual Cryptology Conference on Advances in Cryptology—CRYPTO 2012, Santa Barbara, CA, USA, 19–23 August 2012; Volume 7417, pp. 868–886. [Google Scholar] [CrossRef]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive, Report 2012/144. 2012. Available online: https://eprint.iacr.org/2012/144 (accessed on 16 October 2023).
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. Cryptology ePrint Archive, Report 2016/421. 2016. Available online: https://eprint.iacr.org/2016/421 (accessed on 16 October 2023).
- Frery, J.; Stoian, A.; Bredehoft, R.; Montero, L.; Kherfallah, C.; Chevallier-Mames, B.; Meyre, A. Privacy-Preserving Tree-Based Inference with Fully Homomorphic Encryption. arXiv 2023, arXiv:2303.01254. [Google Scholar]
- Boudguiga, A.; Stan, O.; Sedjelmaci, H.; Carpov, S. Homomorphic Encryption at Work for Private Analysis of Security Logs. In Proceedings of the ICISSP, Valletta, Malta, 25–27 February 2020; pp. 515–523. [Google Scholar]
- Trivedi, D.; Boudguiga, A.; Triandopoulos, N. SigML: Supervised Log Anomaly with Fully Homomorphic Encryption. In Proceedings of the International Symposium on Cyber Security, Cryptology, and Machine Learning, Beer Sheva, Israel, 29–30 June 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 372–388. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. Fully Homomorphic Encryption without Bootstrapping. Cryptology ePrint Archive, Paper 2011/277. 2011. Available online: https://eprint.iacr.org/2011/277 (accessed on 16 October 2023).
- Trivedi, D. Brief Announcement: Efficient Probabilistic Approximations for Sign and Compare. In Proceedings of the 25th International Symposium on Stabilization, Safety, and Security of Distributed Systems, Jersey City, NJ, USA, 2–4 October 2023; pp. 289–296. [Google Scholar]
- Zhao, J.; Mortier, R.; Crowcroft, J.; Wang, L. Privacy-preserving machine learning based data analytics on edge devices. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–7 February 2018; pp. 341–346. [Google Scholar]
- Wang, L. Owl: A General-Purpose Numerical Library in OCaml. 2017. Available online: http://xxx.lanl.gov/abs/1707.09616 (accessed on 16 October 2023).
- Ray, I.; Belyaev, K.; Strizhov, M.; Mulamba, D.; Rajaram, M. Secure logging as a service—Delegating log management to the cloud. IEEE Syst. J. 2013, 7, 323–334. [Google Scholar] [CrossRef]
- The Tor Project | Privacy & Freedom Online. Available online: https://www.torproject.org/ (accessed on 16 October 2023).
- Zawoad, S.; Dutta, A.K.; Hasan, R. SecLaaS: Secure logging-as-a-service for cloud forensics. In Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security, Hangzhou, China, 8–10 May 2013; pp. 219–230. [Google Scholar]
- Zawoad, S.; Dutta, A.K.; Hasan, R. Towards building forensics enabled cloud through secure logging-as-a-service. IEEE Trans. Dependable Secur. Comput. 2015, 13, 148–162. [Google Scholar] [CrossRef]
- Rane, S.; Dixit, A. BlockSLaaS: Blockchain assisted secure logging-as-a-service for cloud forensics. In Proceedings of the International Conference on Security & Privacy, Jaipur, India, 9–11 January 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 77–88. [Google Scholar]
- Bittau, A.; Erlingsson, Ú.; Maniatis, P.; Mironov, I.; Raghunathan, A.; Lie, D.; Rudominer, M.; Kode, U.; Tinnes, J.; Seefeld, B. Prochlo: Strong privacy for analytics in the crowd. In Proceedings of the 26th Symposium on Operating Systems Principles, Shanghai, China, 28–31 October 2017; pp. 441–459. [Google Scholar]
- Paul, J.; Annamalai, M.S.M.S.; Ming, W.; Al Badawi, A.; Veeravalli, B.; Aung, K.M.M. Privacy-Preserving Collective Learning With Homomorphic Encryption. IEEE Access 2021, 9, 132084–132096. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Remez, E.Y. Sur le calcul effectif des polynomes d’approximation de Tschebyscheff. CR Acad. Sci. Paris 1934, 199, 337–340. [Google Scholar]
- Chen, H.; Gilad-Bachrach, R.; Han, K.; Huang, Z.; Jalali, A.; Laine, K.; Lauter, K. Logistic regression over encrypted data from fully homomorphic encryption. BMC Med. Genom. 2018, 11, 3–12. [Google Scholar] [CrossRef]
- Module: tf.keras.losses | TensorFlow v2.13.0. Available online: https://www.tensorflow.org/api_docs/python/tf/keras/losses (accessed on 16 October 2023).
- API Reference. Available online: https://scikit-learn.org/stable/modules/classes.html#module-sklearn.metrics (accessed on 16 October 2023).
- Huelse. Huelse/Seal-Python: Microsoft Seal 4.x for Python. 2022. Available online: https://github.com/Huelse/SEAL-Python (accessed on 9 May 2022).
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning, Prague, Czech Republic, 23–27 September 2013; pp. 108–122. [Google Scholar]
- Canadian Institute for Cybersecurity. NSL-KDD | Datasets | Research | Canadian Institute for Cybersecurity. 2019. Available online: https://www.unb.ca/cic/datasets/nsl.html (accessed on 16 October 2023).
- Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A.A. A detailed analysis of the KDD CUP 99 data set. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, 8–10 July 2009; IEEE: New York, NY, USA, 2009; pp. 1–6. [Google Scholar]
- He, S.; Zhu, J.; He, P.; Lyu, M.R. Loghub: A Large Collection of System Log Datasets towards Automated Log Analytics. arXiv 2008, arXiv:2008.06448. [Google Scholar]
- He, P.; Zhu, J.; Zheng, Z.; Lyu, M.R. Drain: An online log parsing approach with fixed depth tree. In Proceedings of the 2017 IEEE International Conference on Web Services (ICWS), Honolulu, HI, USA, 25–30 June 2017; IEEE: New York, NY, USA, 2017; pp. 33–40. [Google Scholar]
- Trivedi, D. GitHub-Devharsh/Chiku: Polynomial Function Approximation Library in Python. 2023. Available online: https://github.com/devharsh/chiku (accessed on 16 October 2023).
- Cheon, J.H.; Kim, D.; Kim, D.; Lee, H.H.; Lee, K. Numerical method for comparison on homomorphically encrypted numbers. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 415–445. [Google Scholar]
- Lee, E.; Lee, J.W.; No, J.S.; Kim, Y.S. Minimax approximation of sign function by composite polynomial for homomorphic comparison. IEEE Trans. Dependable Secur. Comput. 2021, 19, 3711–3727. [Google Scholar] [CrossRef]
- Boura, C.; Gama, N.; Georgieva, M.; Jetchev, D. CHIMERA: Combining Ring-LWE-Based Fully Homomorphic Encryption Schemes. Cryptology ePrint Archive, Report 2018/758. 2018. Available online: https://eprint.iacr.org/2018/758 (accessed on 16 October 2023).

| Configuration | Encryption | Decryption | ||
|---|---|---|---|---|
| Time | Size | Time | Size | |
| Ubiquitous Aggregate | ||||
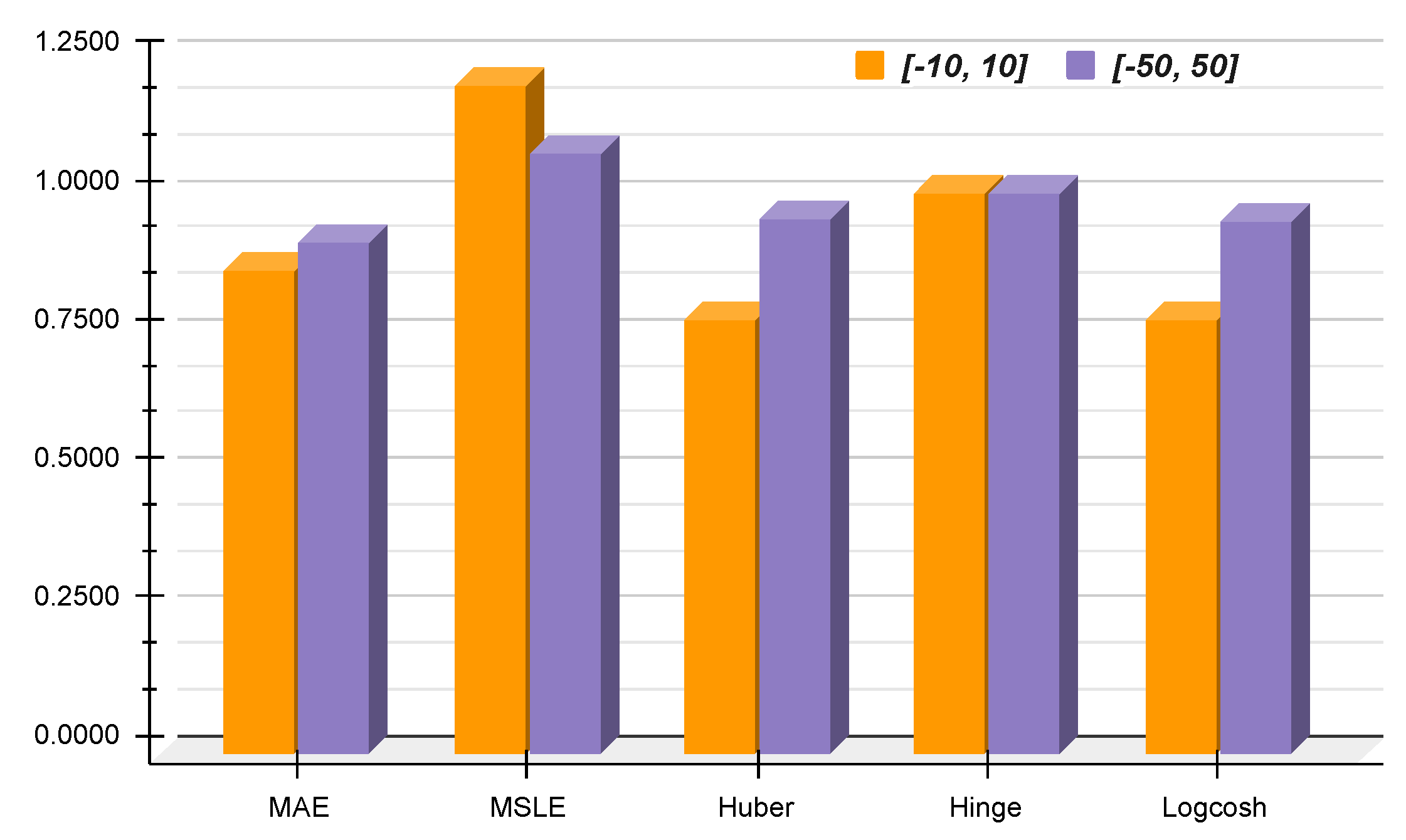
| Interval | Method | MAE | MSLE | Huber | Hinge | Logcosh |
|---|---|---|---|---|---|---|
| 0.0793 | 0.0020 | 0.0039 | 0.5593 | 0.0039 | ||
| 0.0691 | 0.0024 | 0.0031 | 0.5646 | 0.0031 | ||
| 0.1363 | 0.0115 | 0.0138 | 0.5475 | 0.0136 | ||
| 0.1255 | 0.0124 | 0.0132 | 0.5534 | 0.0131 |
| Dataset | Type | Accuracy | Precision | Recall | F1-Score | -Ratio |
|---|---|---|---|---|---|---|
| NSL-KDD | Full (100%) | 0.4811 | 0.4811 | 1.0000 | 0.6497 | 2.0782 |
| Test (20%) | 0.4832 | 0.4832 | 1.0000 | 0.6515 | 2.0695 | |
| HDFS | Full (100%) | 0.4999 | 0.4999 | 1.0000 | 0.6666 | 2.0000 |
| Test (20%) | 0.5016 | 0.5016 | 1.0000 | 0.6681 | 1.9934 |
| Dataset | Model | Scale | Method | Accuracy | Precision | Recall | F1-Score | -Ratio |
|---|---|---|---|---|---|---|---|---|
| NSL-KDD | LR | Plain | 0.9352 | 0.9502 | 0.9138 | 0.9317 | 0.9966 | |
| 0.7923 | 0.9272 | 0.6186 | 0.7421 | 0.6336 | ||||
| 0.3865 | 0.3083 | 0.2167 | 0.2545 | −2.1720 | ||||
| 0.9330 | 0.9486 | 0.9108 | 0.9293 | 1.0633 | ||||
| 0.9351 | 0.9498 | 0.9139 | 0.9315 | 1.0753 | ||||
| 0.9342 | 0.9502 | 0.9116 | 0.9305 | 1.0667 | ||||
| 0.9120 | 0.9213 | 0.8942 | 0.9076 | 1.0666 | ||||
| 0.3870 | 0.3087 | 0.2169 | 0.2548 | −2.1649 | ||||
| 0.9341 | 0.9501 | 0.9115 | 0.9304 | 1.0634 | ||||
| 0.9352 | 0.9502 | 0.9138 | 0.9317 | 1.0752 | ||||
| 0.9341 | 0.9501 | 0.9115 | 0.9304 | 1.0668 | ||||
| 0.9350 | 0.9537 | 0.9096 | 0.9311 | 1.0660 | ||||
| SVM | Plain | 0.9330 | 0.9550 | 0.9039 | 0.9287 | 1.0614 | ||
| 0.9326 | 0.9550 | 0.9031 | 0.9283 | 1.0993 | ||||
| 0.7743 | 0.9262 | 0.5790 | 0.7126 | 0.7872 | ||||
| 0.9312 | 0.9522 | 0.9029 | 0.9269 | 1.1190 | ||||
| 0.8426 | 0.8194 | 0.8649 | 0.8649 | 1.0569 | ||||
| 0.9239 | 0.9407 | 0.8993 | 0.9195 | 1.1110 | ||||
| 0.9311 | 0.9574 | 0.8974 | 0.9264 | 1.0489 | ||||
| 0.7762 | 0.9302 | 0.5804 | 0.7148 | 0.7876 | ||||
| 0.9330 | 0.9550 | 0.9039 | 0.9287 | 1.1189 | ||||
| 0.9330 | 0.9550 | 0.9039 | 0.9287 | 1.0566 | ||||
| 0.9329 | 0.9551 | 0.9036 | 0.9287 | 1.1111 | ||||
| 0.9318 | 0.9604 | 0.8958 | 0.9270 | 1.0489 | ||||
| HDFS | LR | Plain | 0.9683 | 0.9412 | 0.9992 | 0.9693 | 1.0001 | |
| 0.5308 | 0.5167 | 0.9992 | 0.6812 | 292.6803 | ||||
| 0.3616 | 0.4178 | 0.6928 | 0.5213 | 1545.6206 | ||||
| 0.5561 | 0.5306 | 0.9993 | 0.6931 | 71.6765 | ||||
| 0.8899 | 0.8203 | 0.9995 | 0.9011 | 0.7862 | ||||
| 0.5560 | 0.5305 | 0.9994 | 0.6931 | 62.0974 | ||||
| 0.8932 | 0.8249 | 0.9992 | 0.9037 | 0.7784 | ||||
| 0.3616 | 0.4178 | 0.6927 | 0.5212 | 1542.8804 | ||||
| 0.5564 | 0.5307 | 0.9992 | 0.6932 | 71.5496 | ||||
| 0.8908 | 0.8216 | 0.9992 | 0.9018 | 0.7835 | ||||
| 0.5565 | 0.5308 | 0.9992 | 0.6933 | 61.9845 | ||||
| 0.8930 | 0.8247 | 0.9992 | 0.9036 | 0.7794 | ||||
| SVM | Plain | 0.9681 | 0.9402 | 1.0000 | 0.9692 | 0.8649 | ||
| 0.5605 | 0.5330 | 1.0000 | 0.6953 | 36.6039 | ||||
| 0.5513 | 0.5278 | 1.0000 | 0.6910 | 198.8704 | ||||
| 0.6356 | 0.5793 | 0.9988 | 0.7333 | 8.5442 | ||||
| 0.9263 | 0.9385 | 0.9130 | 0.9256 | 0.6254 | ||||
| 0.6397 | 0.5820 | 1.0000 | 0.7358 | 7.4514 | ||||
| 0.9682 | 0.9406 | 0.9998 | 0.9693 | 0.6478 | ||||
| 0.5518 | 0.5281 | 1.0000 | 0.6912 | 198.5042 | ||||
| 0.6357 | 0.5793 | 1.0000 | 0.7336 | 8.5288 | ||||
| 0.9681 | 0.9402 | 1.0000 | 0.9692 | 0.6253 | ||||
| 0.6399 | 0.5821 | 1.0000 | 0.7359 | 7.4376 | ||||
| 0.9682 | 0.9404 | 1.0000 | 0.9693 | 0.6482 |
| Dataset | Model | Scale | Method | Average | Total (CPU) | |||
|---|---|---|---|---|---|---|---|---|
| Encryption | Decryption | Sigmoid | User | System | ||||
| NSL-KDD | LR | 15.9451 | 1.2736 | 25.0283 | 21,229.5304 | 31.1183 | ||
| 15.8492 | 1.2750 | 24.8478 | 14,151.9965 | 21.6079 | ||||
| 16.3591 | 1.3128 | 25.6645 | 57,907.9974 | 192.8575 | ||||
| 15.9845 | 1.2882 | 25.1456 | 7098.8882 | 12.2847 | ||||
| 16.4581 | 1.3294 | 25.8525 | 50,652.5642 | 173.5452 | ||||
| 16.5453 | 1.3044 | 26.1130 | 21,864.5342 | 86.9118 | ||||
| 16.3382 | 1.2872 | 25.6880 | 14,527.2336 | 63.9331 | ||||
| 16.2095 | 1.2866 | 25.3791 | 72,326.0694 | 229.5827 | ||||
| 16.4056 | 1.2930 | 25.8025 | 7249.1064 | 44.1778 | ||||
| 16.2132 | 1.2683 | 25.5183 | 65,122.4439 | 209.3589 | ||||
| SVM | 15.9461 | 1.2854 | 25.1386 | 21,342.9889 | 37.2623 | |||
| 16.0024 | 1.2769 | 25.1158 | 14,240.9221 | 27.7670 | ||||
| 16.3930 | 1.3225 | 25.7013 | 34,780.6294 | 69.3801 | ||||
| 16.1102 | 1.2971 | 25.3295 | 7138.4435 | 17.5237 | ||||
| 16.0584 | 1.2954 | 25.1713 | 79,472.3131 | 241.1018 | ||||
| 16.0374 | 1.2567 | 25.0808 | 43,369.0540 | 144.5788 | ||||
| 15.9906 | 1.2657 | 25.0830 | 36,270.2810 | 133.6592 | ||||
| 16.1845 | 1.2751 | 25.3623 | 41,969.1462 | 86.2903 | ||||
| 16.4235 | 1.3000 | 25.8985 | 29,143.3392 | 110.3346 | ||||
| 15.9473 | 1.2531 | 25.1184 | 93,679.2789 | 260.7503 | ||||
| HDFS | LR | 16.3908 | 1.2578 | 25.4707 | 28,191.8944 | 96.0272 | ||
| 16.4117 | 1.2704 | 25.3694 | 56,176.0993 | 249.5097 | ||||
| 16.2385 | 1.3113 | 25.1131 | 83,989.0793 | 355.9741 | ||||
| 16.1082 | 1.2582 | 24.9673 | 27,724.1933 | 75.9279 | ||||
| 15.9611 | 1.2891 | 24.7696 | 55,177.6614 | 119.2686 | ||||
| 16.0785 | 1.1416 | 24.8503 | 27,533.3271 | 43.9969 | ||||
| 16.1325 | 1.1467 | 24.6902 | 28,002.8715 | 42.0600 | ||||
| 16.1544 | 1.1475 | 24.7477 | 55,939.1609 | 88.9075 | ||||
| 16.0655 | 1.1504 | 25.0016 | 82,767.8606 | 171.9368 | ||||
| 16.4731 | 1.1875 | 25.5487 | 110,748.7027 | 309.8314 | ||||
| SVM | 16.3642 | 1.2677 | 25.4733 | 82,902.0987 | 212.2604 | |||
| 16.0238 | 1.2588 | 24.7493 | 27,494.7062 | 61.8813 | ||||
| 15.9412 | 1.2864 | 24.7108 | 54,953.8687 | 107.4183 | ||||
| 16.1825 | 1.2757 | 25.0942 | 138,438.5341 | 379.7756 | ||||
| 16.3706 | 1.3089 | 25.4166 | 35,159.2336 | 121.3245 | ||||
| 16.6737 | 1.1933 | 25.8361 | 83,201.7236 | 274.1485 | ||||
| 15.9010 | 1.1333 | 24.5346 | 27,335.2857 | 46.0062 | ||||
| 16.0024 | 1.1422 | 24.6981 | 54,971.1042 | 97.4169 | ||||
| 15.9279 | 1.1375 | 24.6168 | 27,384.4133 | 46.0062 | ||||
| 15.9141 | 1.1383 | 24.5868 | 27,388.0323 | 43.6415 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trivedi, D.; Boudguiga, A.; Kaaniche, N.; Triandopoulos, N. SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximation. Cryptography 2023, 7, 52. https://doi.org/10.3390/cryptography7040052
Trivedi D, Boudguiga A, Kaaniche N, Triandopoulos N. SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximation. Cryptography. 2023; 7(4):52. https://doi.org/10.3390/cryptography7040052
Chicago/Turabian StyleTrivedi, Devharsh, Aymen Boudguiga, Nesrine Kaaniche, and Nikos Triandopoulos. 2023. "SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximation" Cryptography 7, no. 4: 52. https://doi.org/10.3390/cryptography7040052
APA StyleTrivedi, D., Boudguiga, A., Kaaniche, N., & Triandopoulos, N. (2023). SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximation. Cryptography, 7(4), 52. https://doi.org/10.3390/cryptography7040052







