XOR Chain and Perfect Secrecy at the Dawn of the Quantum Era †
Abstract
:1. Introduction
1.1. Research Motivation
- 1.
- Scientific: There has been little research on key reusing under OTP. According to [7], a key that is derived from quantum key distribution (QKD) can be reused without risk if an attacker’s presence is not discovered during quantum transmission. On the other hand, it has not been demonstrated that OTP perfect secrecy cannot be efficiently achieved. Indeed, chaos systems have been used as pseudo-random number generators (PRNGs), and chaotic cryptography-based systems have been investigated [8,9]. Yet, keys and ciphertext can exhibit short periods, and there is no systematic method for detecting weak keys [10]. It has been demonstrated that OTP is equivalent to finding the initial condition on a pair of binary maps [11]. In this work, we will introduce a cryptosystem that we call 3-encryption, which uses the rule of triple cancellation to achieve perfect secrecy.
- 2.
- Technological: Because it is well-known that current public key data protection mechanisms do not resist quantum cryptanalysis, the development of new cryptographic security schemes must be prioritized. Despite the fact that the National Institute of Standards and Technology (NIST) has published a set of post-quantum algorithms, the security evaluations and discussions of such algorithms (regarding potential vulnerabilities) are ongoing. These algorithms are used in encryption, signing, and key establishment. Nevertheless, our basic scheme can be simultaneously used for block chaining, data encryption, and digital signatures. As a result, we envision a multifunctional cryptographic platform that is capable of providing integrated security services.
- 3.
- Security: We will demonstrate that the encryption scheme is capable of achieving perfect secrecy. Surprisingly, our algorithm’s security properties are evaluated using XOR, hash, and integer addition, which are simple to analyze, and require no complex mathematical formalism. In the appendix of this document, we will show how the encryption method achieves perfect secrecy.
1.2. State of the Art
- -
- -
- -
- Error-correcting codes are the foundation of code-based cryptography, functioning well for public key encryption. To ensure security, nearly all implemented algorithms in this class employ large keys. The McEliece public key encryption system and the Niederreiter cryptosystem are the most representative examples of code-based cryptography [16,17].
- -
- -
- Isogeny-based cryptography relies on the difficulty of finding a certain mapping (called isogeny) between two given supersingular elliptic curves. The Diffie–Hellman and elliptic curve Diffie–Hellman key-exchange methods can be replaced with the supersingular isogeny Diffie–Hellman key exchange (SIKE) as a quantum-resistant alternative [20].
- -
1.3. Perfect Secrecy
- -
- The number of possible keys is greater than or equal to the number of possible plaintexts.
- -
- The key is selected uniformly at random from the key space.
- -
- A key should only be used once.
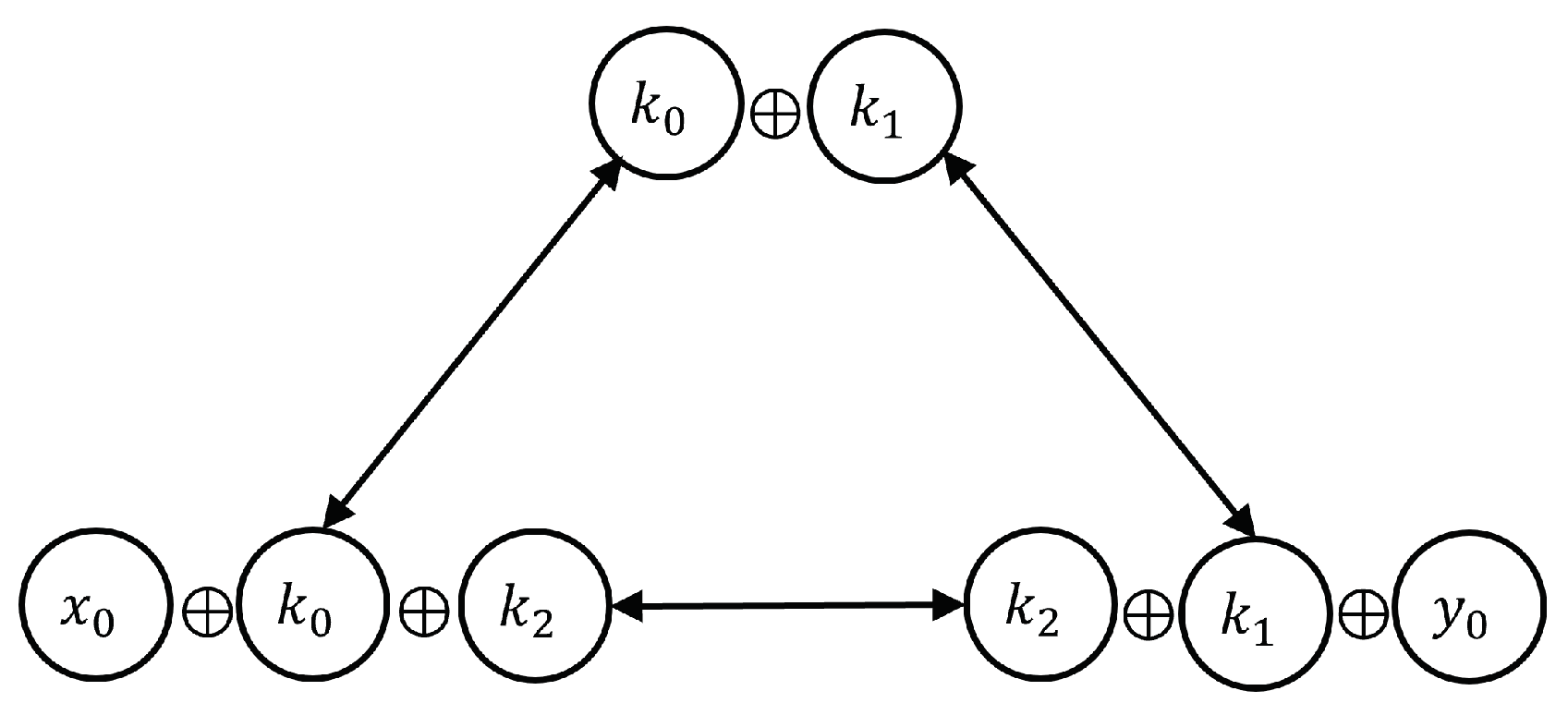
1.4. Triple XOR Cancellation Rule
1.5. Proposal of Our Approach
- -
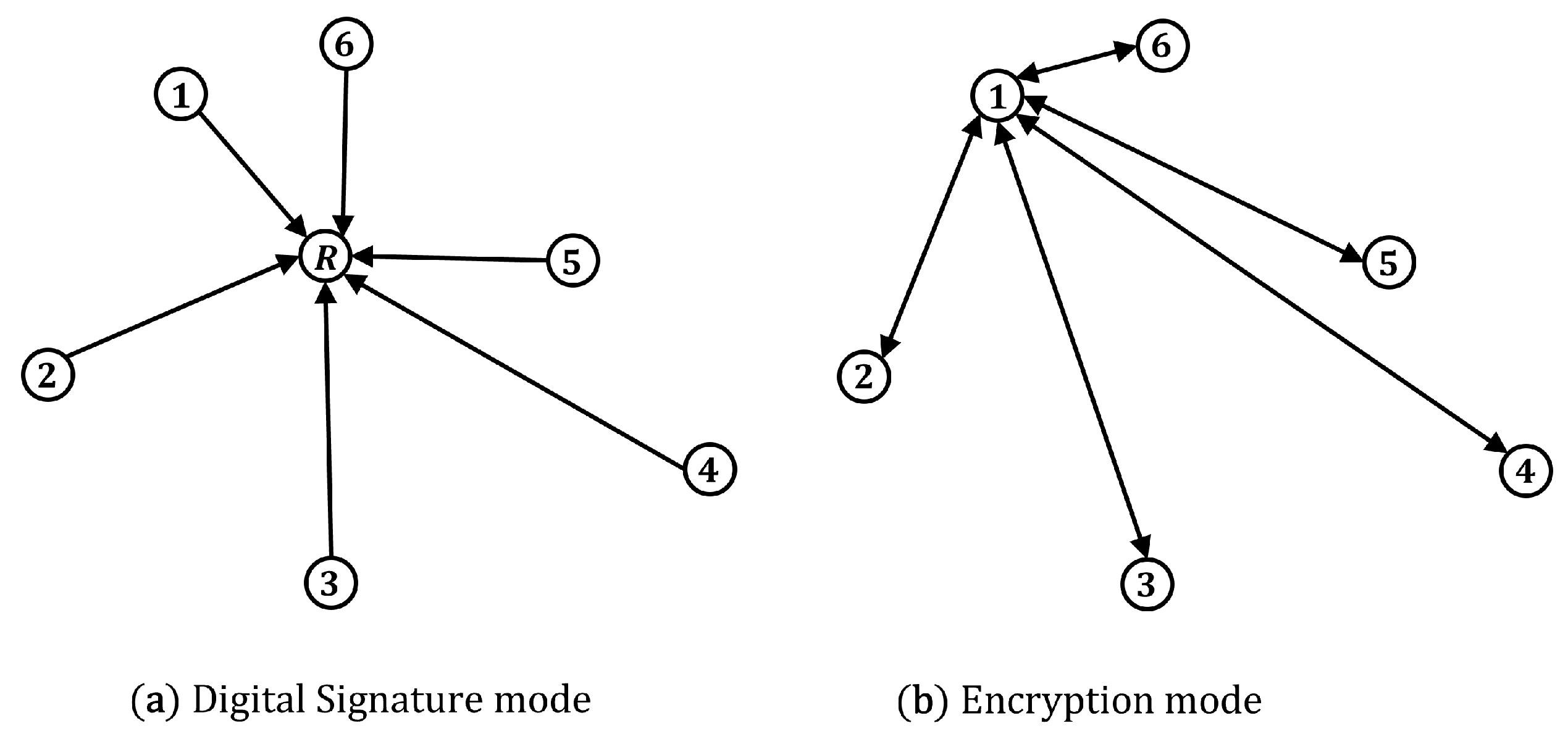
- Digital signature: It is impossible for the adversary to send a message pretending to be from her because each user has a public key in their name. By using the XOR signature algorithm, users can make sure that the current message is connected to every previous message in the chain, starting with the user identification message. This topic will be discussed in Section 2.
- -
- XOR chain: The XOR signature model has allowed us to define a new approach to the blockchain system that we call the XOR chain. We will first present a hash function-based game called Crypto Bingo in order to conceptualize the XOR chain. Section 3 covers this subject.
- -
- Data encryption: The messages are encrypted so that it is impossible for the attacker to see their content; however, authorized recipients can recover the messages in original plain text. Section 4 of the document will address XOR encryption. In Appendix A, we show the perfect secrecy demonstration.
2. Digital Signature
2.1. The Hash Chain Protocol
- 1.
- Alice and Bob generate their hash chain, which allows them to define their public and private keys.
- 2.
- They share their public keys over the public channel.
- 3.
- Alice computes and publishes it along m.
- 4.
- Bob—or any user who wants to verify the signature—just computes h, then .
- 5.
- Alice shares a new public key.
- -
- An attacker can only exploit the hash values at the right-hand side of the signature hash in the current hash chain, which implies that .
- -
- After a message is signed, some hash points to the left of the signature hash always remain unused in the previous hash chain.
- 1.
- Given that Alice has previously published , to sign the message , Alice computes to obtain , then she publishes it along .
- 2.
- Using and , Bob computes and verifies two conditions:
- (i)
- .
- (ii)
- .
2.2. Digital Signatures Based on HMAC
- 1.
- . Alice signs the message (m) by applying the HMAC function and using her private key .
- 2.
- . Bob sends his private key to Alice.
- 3.
- . Alice verifies Bob’s authenticator because she computes , which returns Bob’s public key . Then she sends and the message (m) to Bob.
- 4.
- . Bob verifies Alice’s authenticator
The HMAC Signature Method
2.3. Digital XOR Signature
2.3.1. Security Analysis
2.3.2. Key Renewal
- -
- , ,
- -
- , ,
- -
- , ,
- -
- ⋮
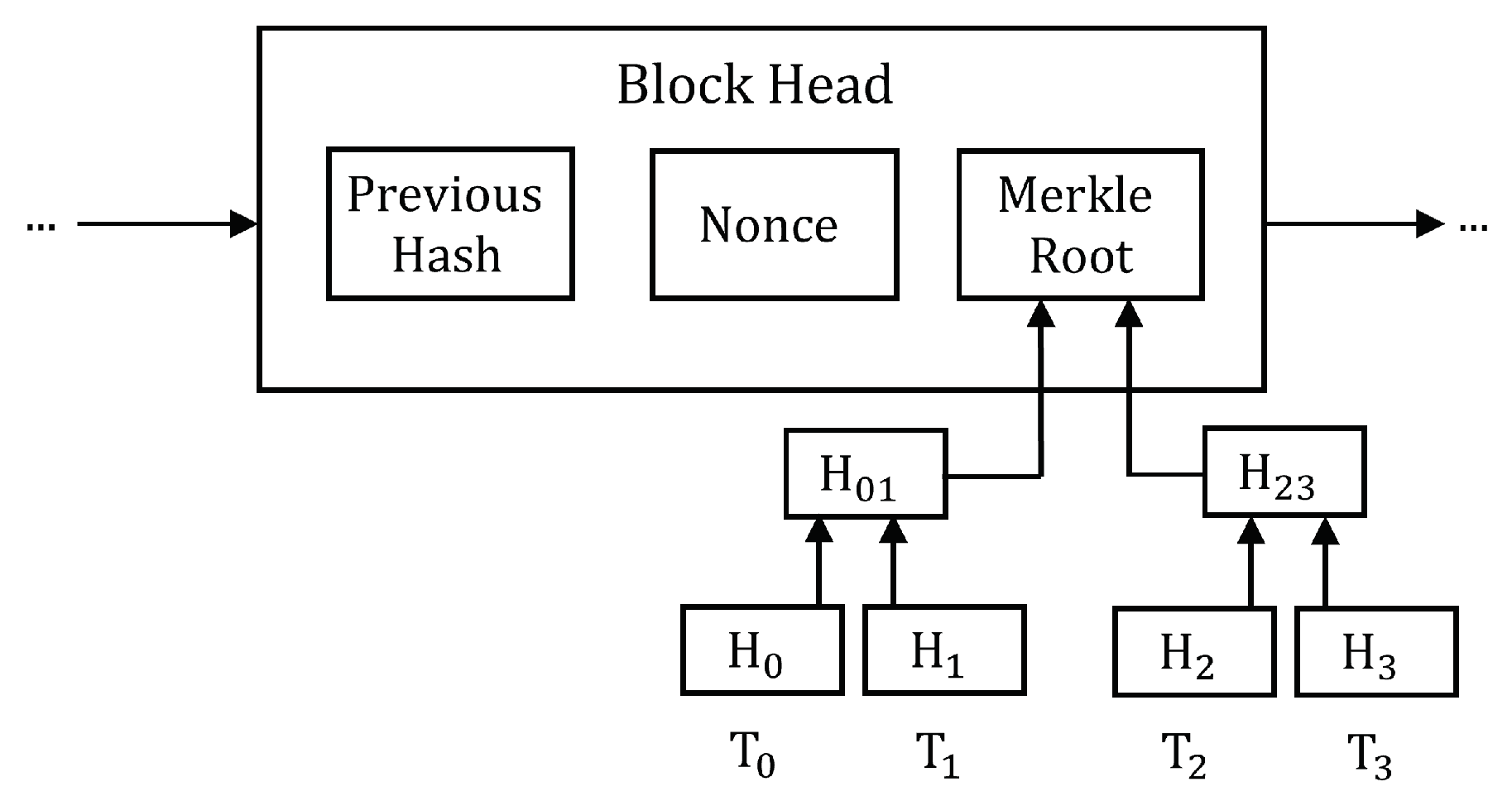
3. Blockchain
3.1. Crypto Bingo
- -
- In the first round, the root player computes and registers into the game, where and (instead of because there is no a previous winner). In addition, players compute and register into the game. Then the root player announces and the player whose failed the fewest number of bits wins. This value corresponds to the minimum Hamming distance, denoted as . It is clear that the probability of obtaining the correct bits (e.g., 256 bits) is quite low. The winner is allowed to place his block into the chain. Let be the winning player with . To be verified, the root player publishes , while player 1 announces . Then, all players verify that they correspond to and , respectively.
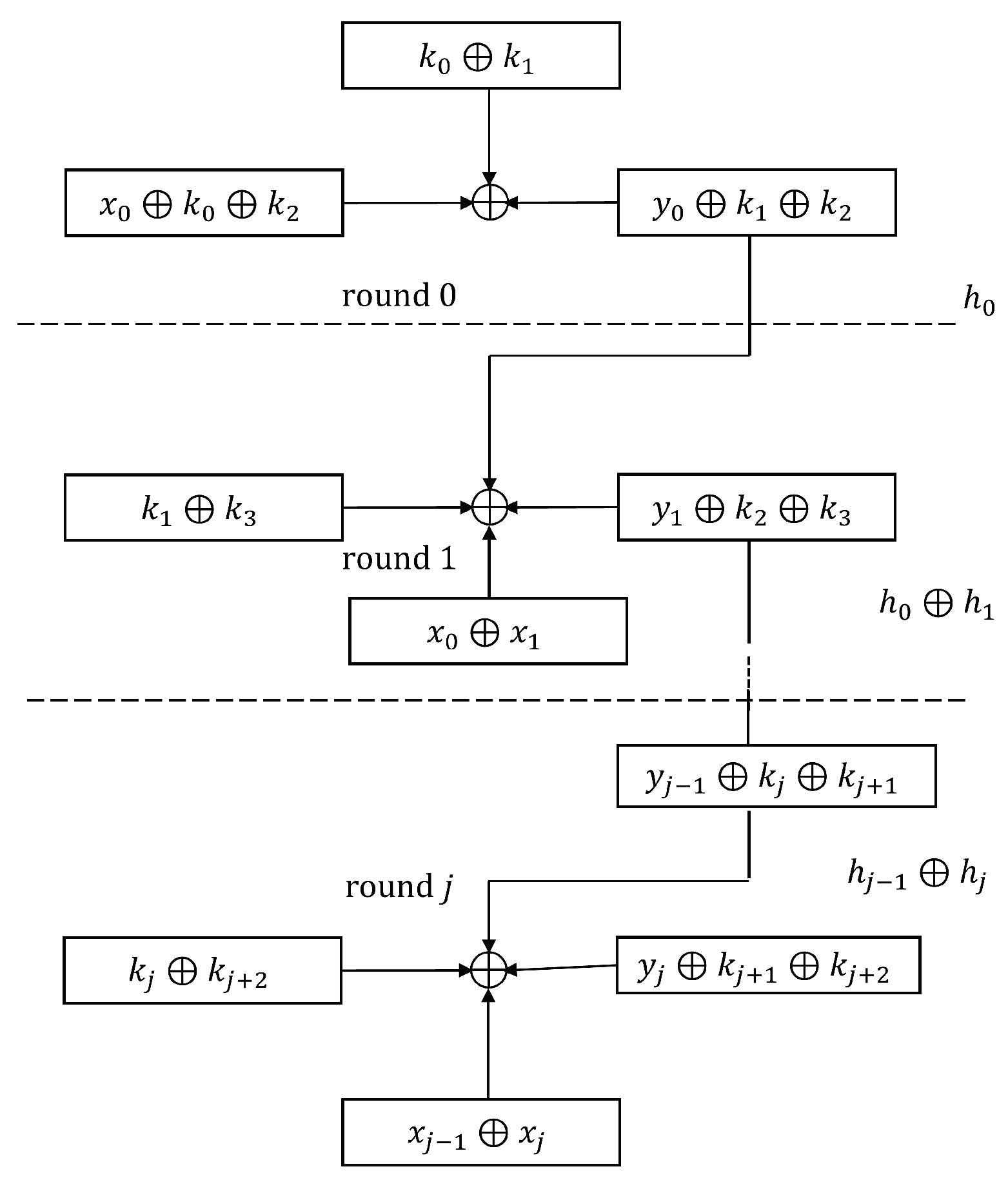
3.2. XOR Chain
- -
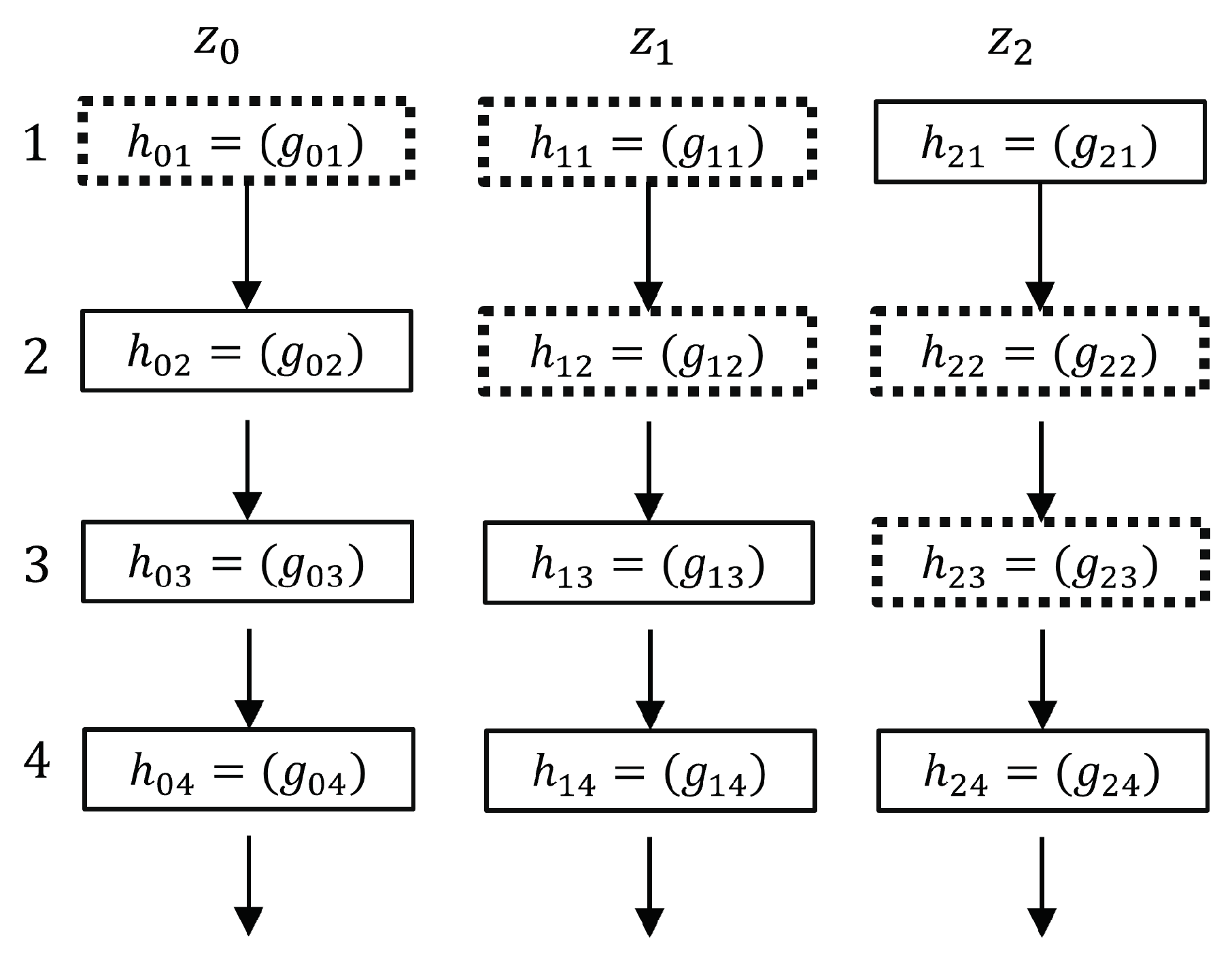
- Round 0 (registration phase): Using his numbers, , the root player, denoted as , registers in the public DB, where , and . In addition, stores in DB, where . But computes , so that is the root of his Merkle tree. Then, all players select their own set of numbers, for example, chooses , , , , and , so that they match the public keys of .
- -
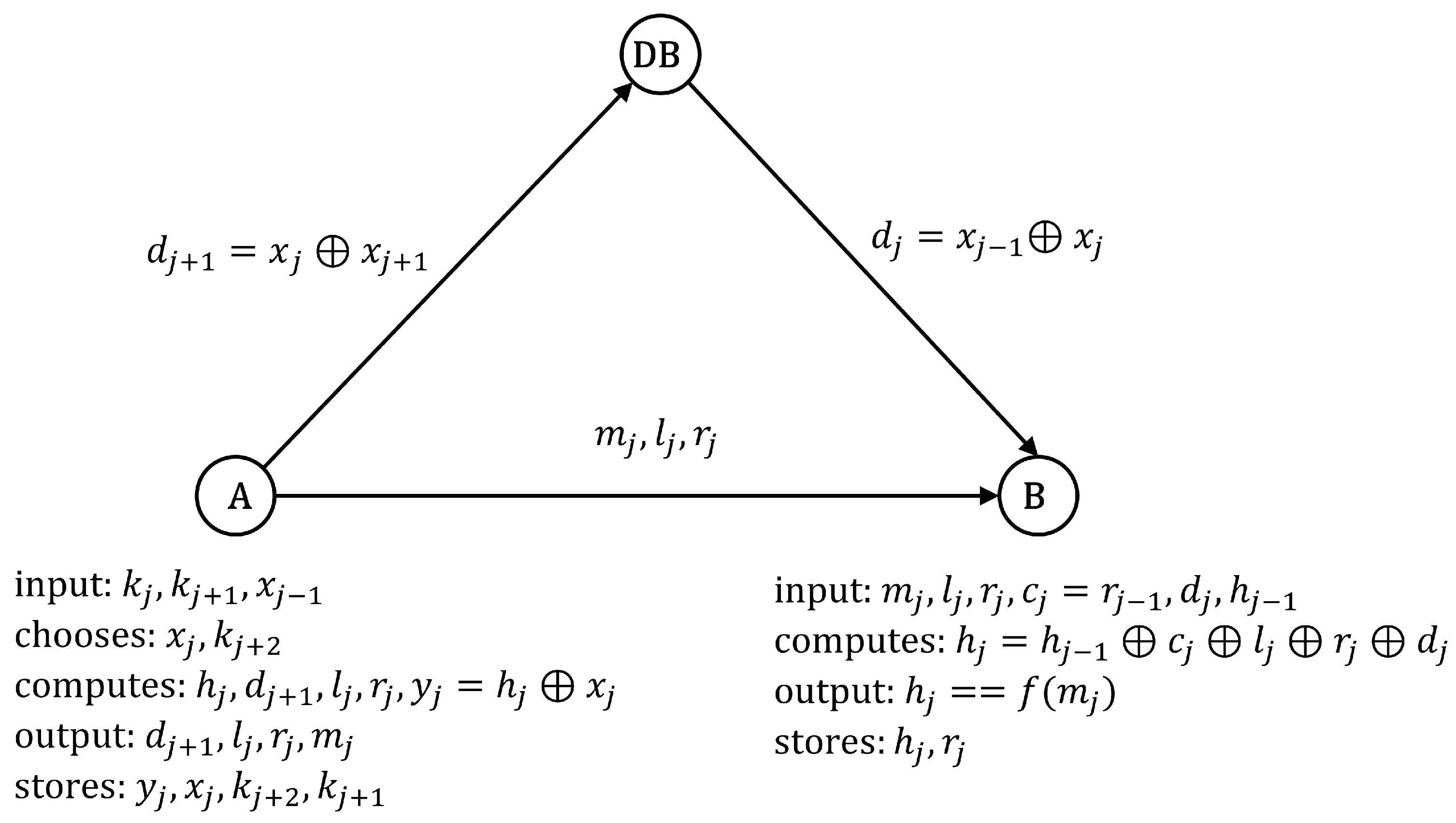
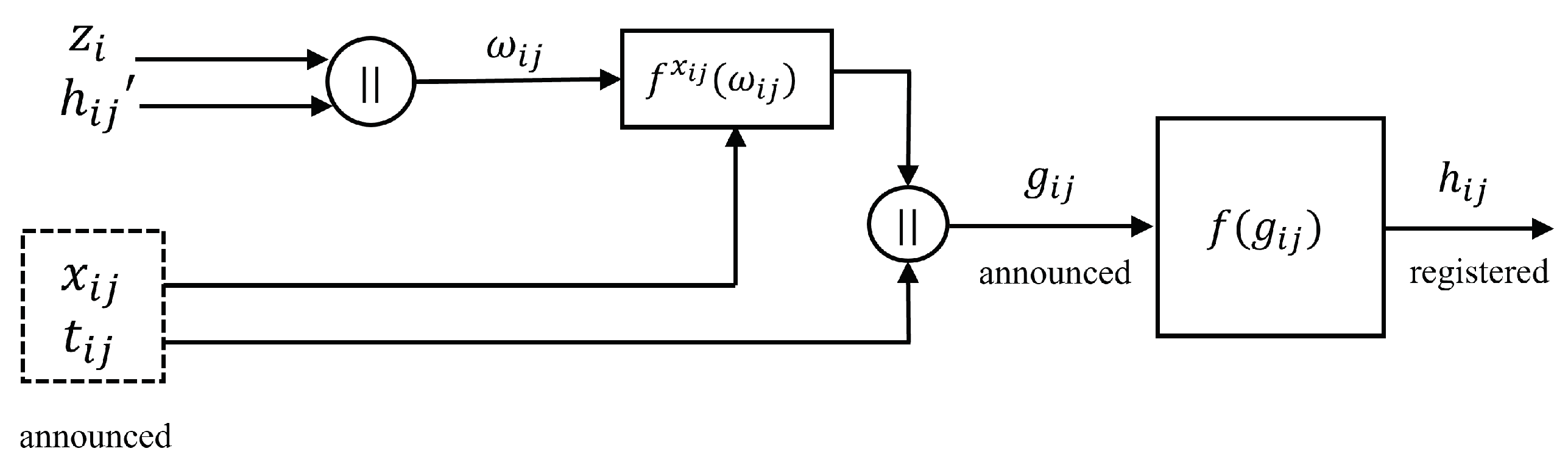
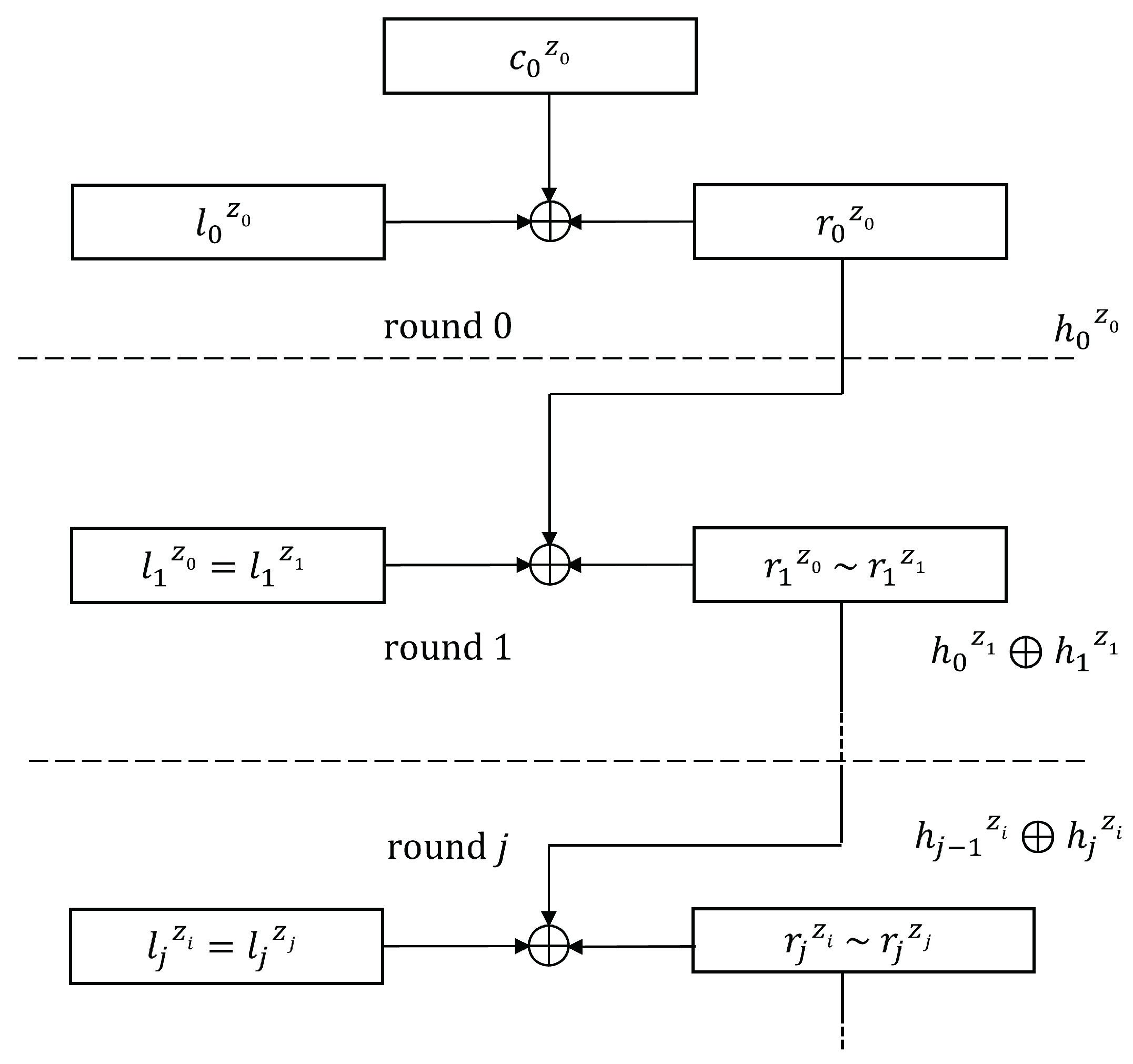
- Round 1: All nodes, for example, using , compute and . But chooses his numbers, so that yields the root of his Merkle tree. Then, publishes in DB to the rest of the nodes. Now, node publishes in DB, where and . All nodes, for example, using , obtain and . But chooses , so that (as illustrated in Figure 9). Then, publishes in DB to the rest of the nodes. If the nodes (or the majority of them) agree that has the minimum distance to , then wins the first round. Now, DB removes the auxiliary data from the other nodes but permanently stores , and to enable all nodes to verify because . Before the next round takes place, each node, say , selects its numbers again, ensuring that , where is the root of the Merkle tree that belongs to . However, is the root of the Merkle tree of the node.
4. Data Encryption
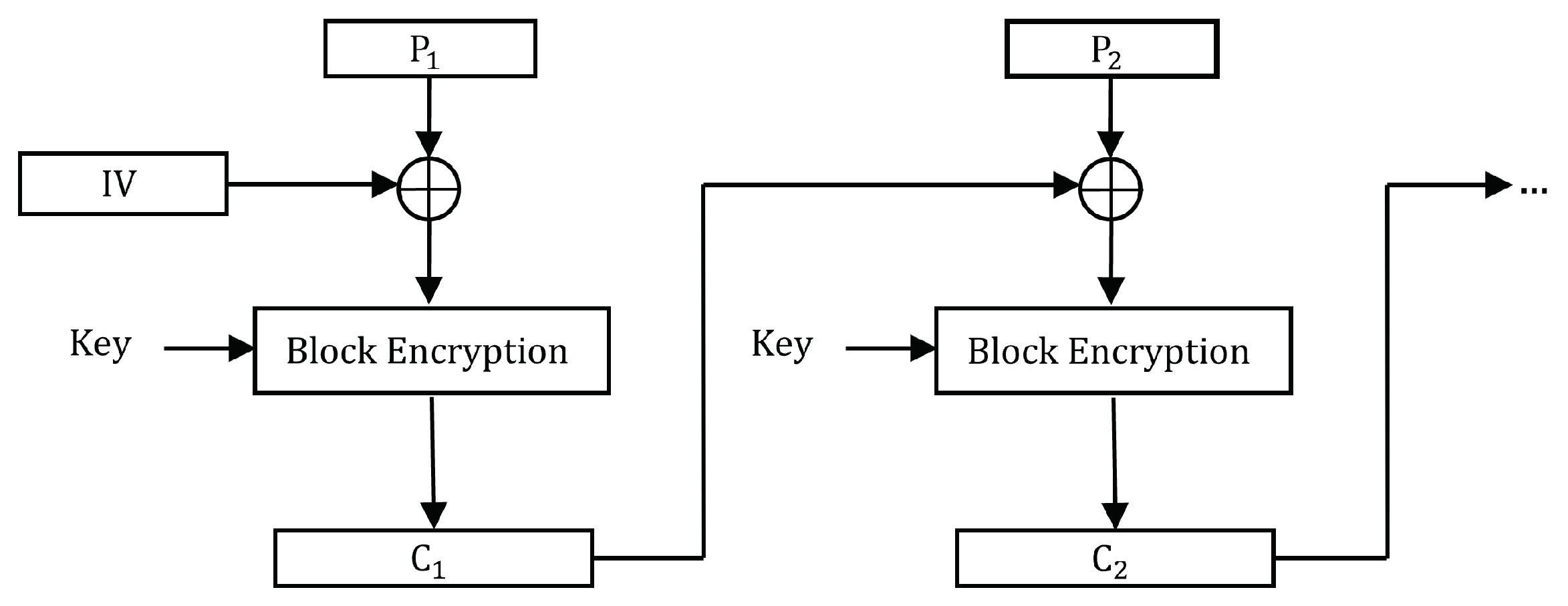
4.1. CBC Mode Encryption
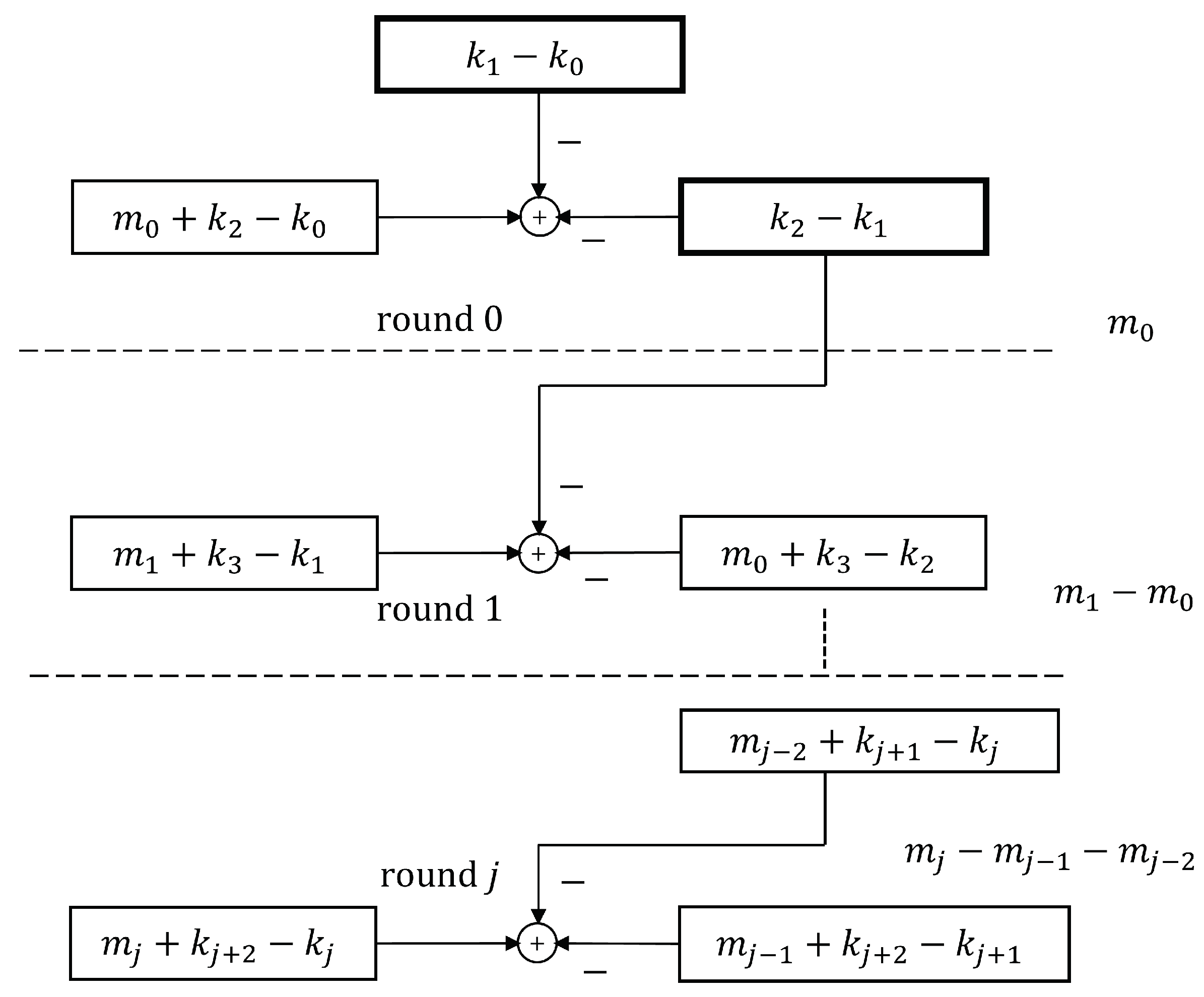
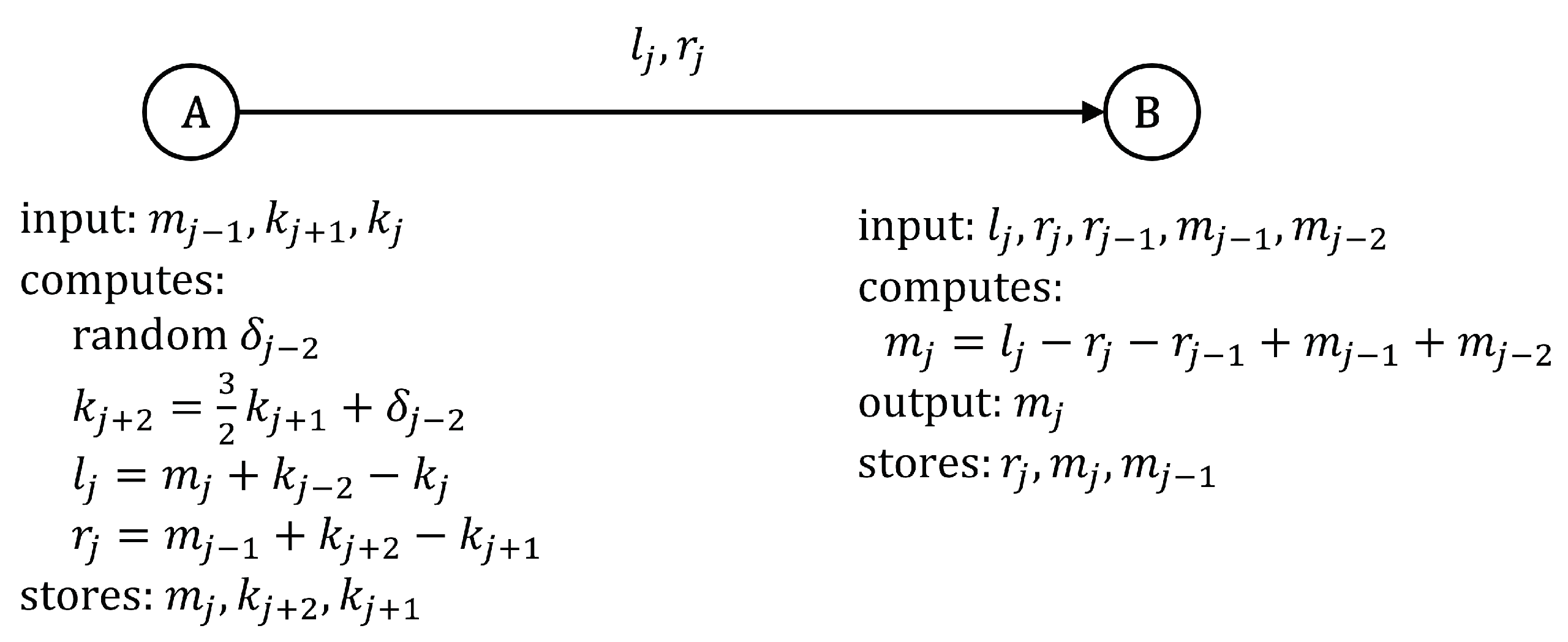
4.2. 3-Encryption
4.3. Perfect Secrecy
- 1.
- Every encryption key must be distinct from any previous key.
- 2.
- The number of available keys is greater than or equal to the number of messages in the system.
- 3.
- Every key is chosen randomly and the probability must be the same for all keys.
- —
- where requires 6 additions and 4 terms to be stored: .
- —
- where requires 4 additions and 3 terms to be stored: .
5. Discussion and Future Work
- 1.
- Digital signature: To avoid analysis by Grover’s quantum search technique, we shall assume that the hash code must be at least 256 bits long. Thus, the size of the private key, , achieves bits. In addition, the size of the public key, reaches bits. These key sizes are really small compared to current public key cryptosystems. Figure 5 in Section 2.3 shows the storage requirements: 1024 bits for Alice, Bob occupies 512 bits, and DB requires 256 bits. The signature process uses three random numbers, five XOR operations, and one hash computation. Finally, signature verification needs four XOR operations, one hash, and one comparison. The main drawback of our method involves the need for a central node, which can introduce delays in the signature process.
- 2.
- Blockchain: In the blockchain system [40], miners calculate and maintain a unified chain of all transactions on the network. In the distributed database, a table entry is 768 bits in size. In contrast, the table entry size is 8192 bits in the HMAC chain and hash chain algorithms. In this scenario, every user calculates and maintains his own independent chain of transactions. The table entry size in the XOR chain introduced here is 768 bits. Similar to blockchain, network nodes compute and store copies of a unified chain of transactions. However, some of the major advantages of our scheme over blockchain are the following: (1) it does not require proof of work (PoW), and (2) it is immune to quantum cryptanalysis. The comparison of such parameters is given in Table 7.
- 3.
- The 3-encryption: Figure 12 in Section 4.2 shows the storage prerequisites for 3-encryption. If we assume that both the message segment and key size are 256 bits, Alice requires 768 bits and Bob needs the same. The encryption process demands the generation of one random number, five (adding) operations, and one multiplication. Decryption takes four (adding) operations. The encryption method holds promise for exceptional execution performance since it does not necessitate numerous rounds of substitution and permutation, unlike the symmetric CBC chained mode. However, as previously stated, our system lacks a data permutation or dispersion mechanism; thus, if a message is repeated in the next round, the previous one can be inferred.
| Blockchain | Hash Chain | HMAC Chain | This Work | |
|---|---|---|---|---|
| Table Size Entry | 768 | 8192 | 8192 | 768 |
| PQ | no | yes | yes | yes |
| PoW | yes | no | no | no |
- 1.
- Keep a distributed copy of the database among the users of the system, which is the approach used by the blockchain system.
- 2.
- Offline operation. The protocol operates without requiring intervention from the central node, which would guarantee the continuity of the system in the event of failures.
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Perfect Secrecy Proof
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Dattani, N.S.; Bryans, N. Quantum factorization of 56153 with only 4 qubits. arXiv 2014, arXiv:1411.6758. [Google Scholar]
- Dridi, R.; Alghassi, H. Prime factorization using quantum annealing and computational algebraic geometry. arXiv 2016, arXiv:1604.05796. [Google Scholar]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Nagaraj, N.; Vaidya, V.; Vaidya, P.G. Re-visiting the One-Time Pad. arXiv 2005, arXiv:cs/0508079. [Google Scholar]
- Damgård, I.; Pedersen, T.B.; Salvail, L. A quantum cipher with near optimal key-recycling. In Proceedings of the Advances in Cryptology–CRYPTO 2005: 25th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2005. Proceedings 25; Springer: Cham, Switzerland, 2005; pp. 494–510. [Google Scholar]
- Baptista, M. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Jakimoski, G.; Kocarev, L. Chaos and cryptography: Block encryption ciphers based on chaotic maps. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 163–169. [Google Scholar] [CrossRef]
- Dachselt, F.; Schwarz, W. Chaos and cryptography. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 1498–1509. [Google Scholar] [CrossRef]
- Nagaraj, N. One-Time Pad as a nonlinear dynamical system. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4029–4036. [Google Scholar] [CrossRef]
- Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Proceedings of the International Algorithmic NUMBER Theory Symposium; Springer: Berlin/Heidelberg, Germany, 1998; pp. 267–288. [Google Scholar]
- Buchmann, J.; Dahmen, E.; Hülsing, A. XMSS-a practical forward secure signature scheme based on minimal security assumptions. In Proceedings of the Post-Quantum Cryptography: 4th International Workshop, PQCrypto 2011, Taipei, Taiwan, 29 November–2 December 2011. Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2011; pp. 117–129. [Google Scholar]
- Bernstein, D.J.; Hopwood, D.; Hülsing, A.; Lange, T.; Niederhagen, R.; Papachristodoulou, L.; Schneider, M.; Schwabe, P.; Wilcox-O’Hearn, Z. SPHINCS: Practical stateless hash-based signatures. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2015; pp. 368–397. [Google Scholar]
- McEliece, R.J. A public-key cryptosystem based on algebraic. Coding Thv 1978, 4244, 114–116. [Google Scholar]
- Niederreiter, H. Knapsack-type cryptosystems and algebraic coding theory. Prob. Contr. Inform. Theory 1986, 15, 157–166. [Google Scholar]
- Matsumoto, T.; Imai, H. Public quadratic polynomial-tuples for efficient signature-verification and message-encryption. In Proceedings of the Advances in Cryptology—EUROCRYPT’88: Workshop on the Theory and Application of Cryptographic Techniques Davos, Switzerland, 25–27 May 1988 Proceedings 7; Springer: Berlin/Heidelberg, Germany, 1988; pp. 419–453. [Google Scholar]
- Ding, J.; Schmidt, D. Rainbow, a new multivariable polynomial signature scheme. In Proceedings of the International Conference on Applied Cryptography and Network Security; Springer: Berlin/Heidelberg, Germany, 2005; pp. 164–175. [Google Scholar]
- Jao, D.; De Feo, L. Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In Proceedings of the Post-Quantum Cryptography: 4th International Workshop, PQCrypto 2011, Taipei, Taiwan, 29 November–2 December 2011. Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2011; pp. 19–34. [Google Scholar]
- Standard, A.E. Federal Information Processing Standards Publication 197. FIPS PUB. 2001; pp. 3–46. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf (accessed on 12 October 2023).
- Campagna, M.; Hardjono, T.; Pintsov, L.; Romansky, B.; Yu, T. Kerberos revisited quantum-safe authentication. In Proceedings of the ETSI Quantum-Safe-Crypto Workshop, Nice, France, 26–27 September 2013; pp. 26–27. [Google Scholar]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef]
- Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Third Round of the Nist Post-Quantum Cryptography Standardization Process; US Department of Commerce, NIST: Gaithersburg, MD, USA, 2022.
- Laboratory, I.T. PQC Standardization Process: Third Round Candidate Announcement. 2020. Available online: https://csrc.nist.gov/news/2020/pqc-third-round-candidate-announcement (accessed on 12 October 2023).
- Chen, L.; Chen, L.; Jordan, S.; Liu, Y.K.; Moody, D.; Peralta, R.; Perlner, R.; Smith-Tone, D. Report on Post-Quantum Cryptography; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016; Volume 12.
- Persichetti, E. NIST Round 3 Finalists. 2020. Available online: https://pqc-wiki.fau.edu/w/Special:DatabaseHome (accessed on 12 October 2023).
- Castryck, W.; Decru, T. An Efficient Key recovery Attack on SIDH (Preliminary Version). Cryptology ePrint Archive 2022. Available online: https://eprint.iacr.org/2022/975 (accessed on 12 October 2023).
- Beullens, W. Breaking Rainbow Takes a Weekend on a Laptop. Cryptology ePrint Archive, Paper 2022/214. 2022. Available online: https://eprint.iacr.org/2022/214 (accessed on 12 October 2023).
- Beullens, W. Improved cryptanalysis of UOV and rainbow. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer International Publishing: Cham, Switzerland, 2021; pp. 348–373. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- PUB, F. Digital Signature Standard (DSS). FIPS PUB. 2000; pp. 186–192. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf (accessed on 12 October 2023).
- Moody, D.; Alagic, G.; Apon, D.C.; Cooper, D.A.; Dang, Q.H.; Kelsey, J.M.; Liu, Y.K.; Miller, C.A.; Peralta, R.C.; Perlner, R.A.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process; US Department of Commerce, NIST: Gaithersburg, MD, USA, 2020.
- Merkle, R.C. Secrecy, Authentication, and Public Key Systems; Stanford University: Stanford, CA, USA, 1979. [Google Scholar]
- Lizama-Pérez, L.A.; Montiel-Arrieta, L.J.; Hernández-Mendoza, F.S.; Lizama-Servín, L.A.; Eric, S.A. Public hash signature for mobile network devices. Ing. Investig. Tecnol. 2019, 20, 1–10. [Google Scholar] [CrossRef]
- Lizama-Perez, L.A. Digital signatures over hash-entangled chains. SN Appl. Sci. 2019, 1, 1568. [Google Scholar] [CrossRef]
- Schneier, B. Description of a new variable-length key, 64-bit block cipher (Blowfish). In Proceedings of the International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 1993; pp. 191–204. [Google Scholar]
- Rogaway, P. Evaluation of Some Blockcipher Modes of Operation. Cryptography Research and Evaluation Committees (CRYPTREC) for the Government of Japan. 2011. Available online: https://www.cs.ucdavis.edu/~rogaway/papers/modes-cryptrec.pdf (accessed on 12 October 2023).
- Bujari, D.; Aribas, E. Comparative analysis of block cipher modes of operation. In Proceedings of the International Advanced Researches & Engineering Congress, Osmaniye, Turkey, 16–18 November 2017; pp. 1–4. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Decentralized Business Review. 2008, p. 21260. Available online: https://assets.pubpub.org/d8wct41f/31611263538139.pdf (accessed on 12 October 2023).
- Johar, S.; Ahmad, N.; Asher, W.; Cruickshank, H.; Durrani, A. Research and applied perspective to blockchain technology: A comprehensive survey. Appl. Sci. 2021, 11, 6252. [Google Scholar] [CrossRef]
- Kearney, J.J.; Perez-Delgado, C.A. Vulnerability of blockchain technologies to quantum attacks. Array 2021, 10, 100065. [Google Scholar] [CrossRef]
- Vujičić, D.; Jagodić, D.; Ranđić, S. Blockchain technology, bitcoin, and Ethereum: A brief overview. In Proceedings of the 2018 17th International Symposium Infoteh-Jahorina (Infoteh), East Sarajevo, Bosnia and Herzegovina, 21–23 March 2018; pp. 1–6. [Google Scholar]
- Paulavičius, R.; Grigaitis, S.; Igumenov, A.; Filatovas, E. A decade of blockchain: Review of the current status, challenges, and future directions. Informatica 2019, 30, 729–748. [Google Scholar] [CrossRef]
- Papageorgiou, O.; Sedlmeir, J.; Fridgen, G.; Vlachos, I.; Kostopoulos, N.; Damvakeraki, T.; Noszek, Z.; Papoutsoglou, I.; Anania, A.; Belotti, M.; et al. Energy Efficiency of Blockchain Technologies; European Union Blockchain Observatory & Forum. 2021. Available online: https://www.eublockchainforum.eu/sites/default/files/reports/Energy%20Efficiency%20of%20Blockchain%20Technologies_1.pdf (accessed on 12 October 2023).
- Fernandez-Carames, T.M.; Fraga-Lamas, P. Towards post-quantum blockchain: A review on blockchain cryptography resistant to quantum computing attacks. IEEE Access 2020, 8, 21091–21116. [Google Scholar] [CrossRef]
- Edwards, M.; Mashatan, A.; Ghose, S. A review of quantum and hybrid quantum/classical blockchain protocols. Quantum Inf. Process. 2020, 19, 184. [Google Scholar] [CrossRef]
- Ruggeri, C. Quantum Key Distribution in Softwarised Networks. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2020. [Google Scholar]
- Ikeda, K. qBitcoin: A peer-to-peer quantum cash system. In Proceedings of the Intelligent Computing: Proceedings of the 2018 Computing Conference, Volume 1; Springer International Publishing: Cham, Switzerland, 2019; pp. 763–771. [Google Scholar]
- Gottesman, D.; Chuang, I. Quantum digital signatures. arXiv 2001, arXiv:quant-ph/0105032. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Feutrill, A.; Roughan, M. A Review of Shannon and Differential Entropy Rate Estimation. Entropy 2021, 23, 1046. [Google Scholar] [CrossRef] [PubMed]
- Martin, K.M. Everyday cryptography. The Australian Mathematical Society; Oxford University Press: Oxford, UK, 2012; pp. 231–234. [Google Scholar]
- Shimeall, T.; Spring, J. Introduction to Information Security: A Strategic-Based Approach; Newnes: Oxford, UK, 2013. [Google Scholar]
- Lizama-Pérez, L.A. Digital signatures over HMAC entangled chains. Eng. Sci. Technol. Int. J. 2021, 32, 101076. [Google Scholar] [CrossRef]
- Krawczyk, H.; Canetti, R.; Bellare, M. HMAC: Keyed-Hashing for Message Authentication. 1997. Available online: https://www.rfc-editor.org/rfc/rfc2104 (accessed on 12 October 2023).
- Yan, B.; Tan, Z.; Wei, S.; Jiang, H.; Wang, W.; Wang, H.; Luo, L.; Duan, Q.; Liu, Y.; Shi, W.; et al. Factoring integers with sublinear resources on a superconducting quantum processor. arXiv 2022, arXiv:2212.12372. [Google Scholar]
- Ehrsam, W.F.; Meyer, C.H.; Smith, J.L.; Tuchman, W.L. Message Verification and Transmission Error Detection by Block Chaining. U.S. Patent 4,074,066, 14 February 1978. [Google Scholar]
- Trappe, W. Introduction to Cryptography with Coding Theory; Pearson Education: London, UK, 2020. [Google Scholar]

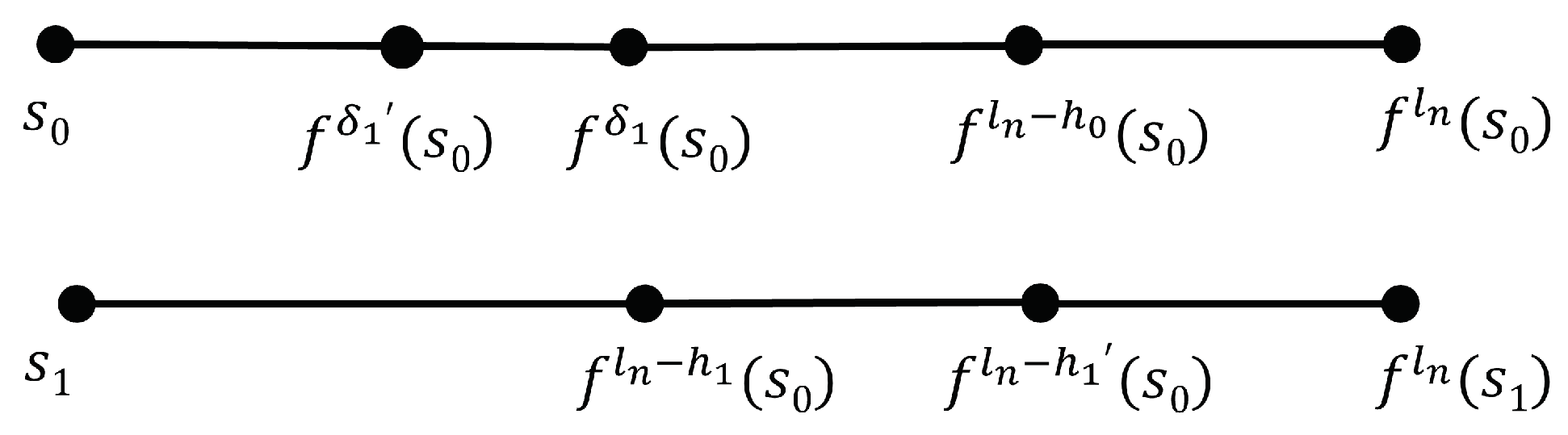
| User | Public Key | Private Keys |
|---|---|---|
| Alice | ||
| Bob |
| Private Key | Public Key |
|---|---|
| Round | ||||||
|---|---|---|---|---|---|---|
| 0 | — | |||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| j |
| Round | ||||
|---|---|---|---|---|
| 0 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| j |
| j | |||||
|---|---|---|---|---|---|
| 0 | — | ||||
| ↙ | |||||
| 1 | |||||
| ↙ | |||||
| 2 | |||||
| ↙ | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ||
| j | |||||
| ↙ |
| Round | ||||
|---|---|---|---|---|
| 0 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| j |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lizama-Pérez, L.A. XOR Chain and Perfect Secrecy at the Dawn of the Quantum Era. Cryptography 2023, 7, 50. https://doi.org/10.3390/cryptography7040050
Lizama-Pérez LA. XOR Chain and Perfect Secrecy at the Dawn of the Quantum Era. Cryptography. 2023; 7(4):50. https://doi.org/10.3390/cryptography7040050
Chicago/Turabian StyleLizama-Pérez, Luis Adrián. 2023. "XOR Chain and Perfect Secrecy at the Dawn of the Quantum Era" Cryptography 7, no. 4: 50. https://doi.org/10.3390/cryptography7040050
APA StyleLizama-Pérez, L. A. (2023). XOR Chain and Perfect Secrecy at the Dawn of the Quantum Era. Cryptography, 7(4), 50. https://doi.org/10.3390/cryptography7040050






