Timing-Attack-Resistant Acceleration of NTRU Round 3 Encryption on Resource-Constrained Embedded Systems
Abstract
:1. Introduction
- A specific solution for the NTRU polynomial multiplier in resource-constrained devices, where the availability of resources and the energy budget are very limited (which is common in the IoT integration framework), which allows for acceleration without generating any security breaches related to timing attacks in the system.
- The design of a highly configurable intellectual property (IP) module to implement an ad hoc serial polynomial multiplier on the programmable logic included in the SoC. The configuration enables the possibility to easily implement different security parameters defined in the NTRU algorithm scheme, as well as different arithmetic units responsible for performing the multiplication operation.
- The design of an interconnection scheme based in an AXI4-Stream protocol that optimizes the bandwidth of communication infrastructures between the processor core and the IP.
- The evaluation of (i) the resources used for each particular solution and comparison with other implementations in the literature; and (ii) the acceleration factors achieved with the proposed implementations using the software implementation of the NTRU algorithm included in the third round of the NIST PQC contest as reference. In addition, a figure of merit called Efficiency is proposed, which enables one to know which implementation achieves the best trade-off between a high acceleration factor and a moderated value of power consumption and area occupation.
2. The NTRU Encryption Scheme
2.1. Mathematical Background
- is the polynomial ;
- is the polynomial ;
- represents the operation modulus q for the coefficients and modulus for the polynomial degree;
- represents the operation modulus q for the coefficients and modulus for the polynomial degree;
- represents the operation modulus 3 for the coefficients and modulus for the polynomial degree.
2.2. Hardware Implementation of Polynomial Multiplication
| Algorithm 1 Accelerating the polynomial multiplication using nonzero elements |
| for do |
| if then |
| for do |
| end for |
| end if |
| end for |
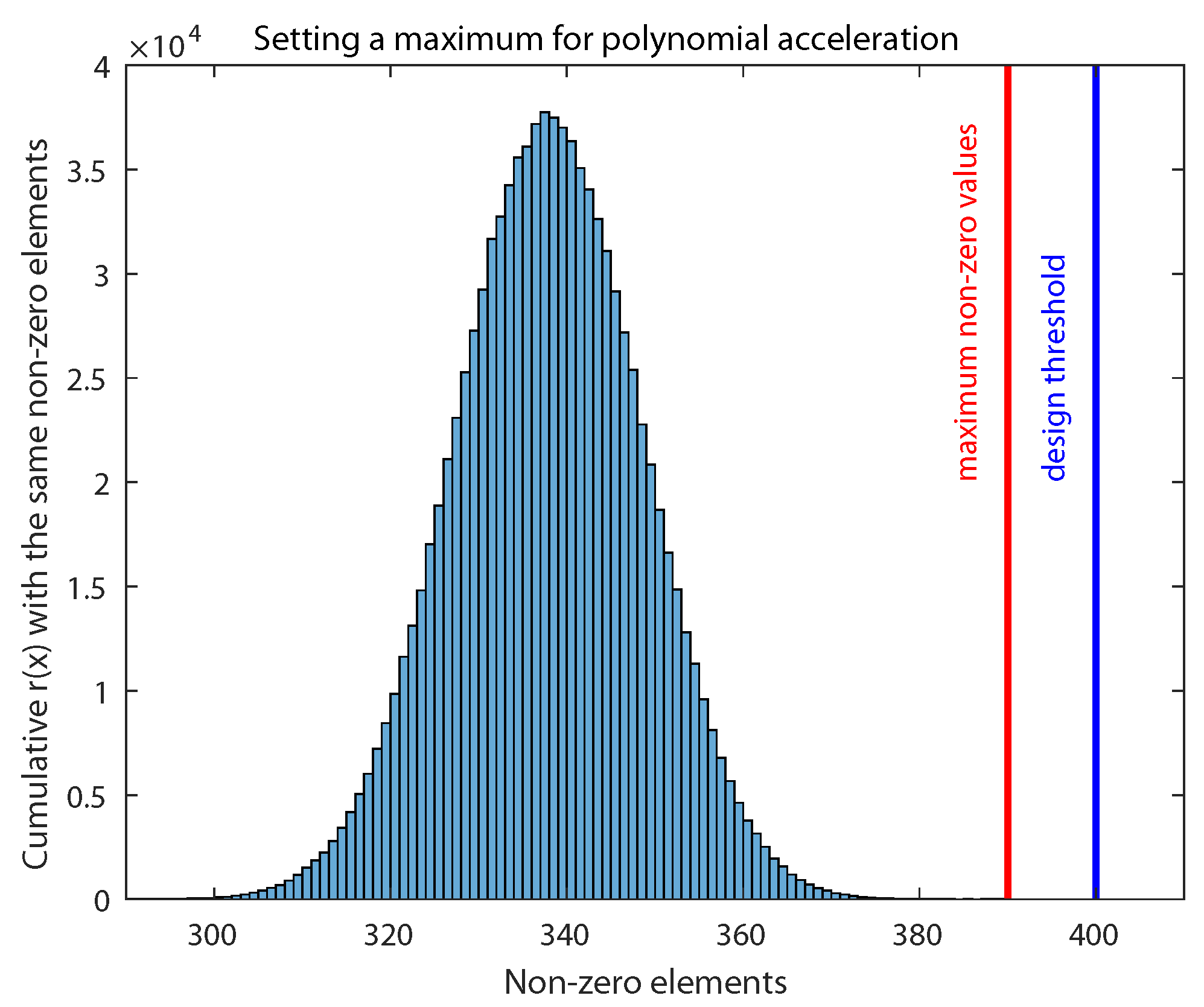
3. Robust Acceleration against Timing Attacks
| Algorithm 2 Accelerating the polynomial multiplication considering nonzero elements and avoiding timing attacks |
| for do |
| if then |
| end if |
| if or ( and ) then |
| for do |
| end for |
| end if |
| end for |
4. IP Module Design and Integration
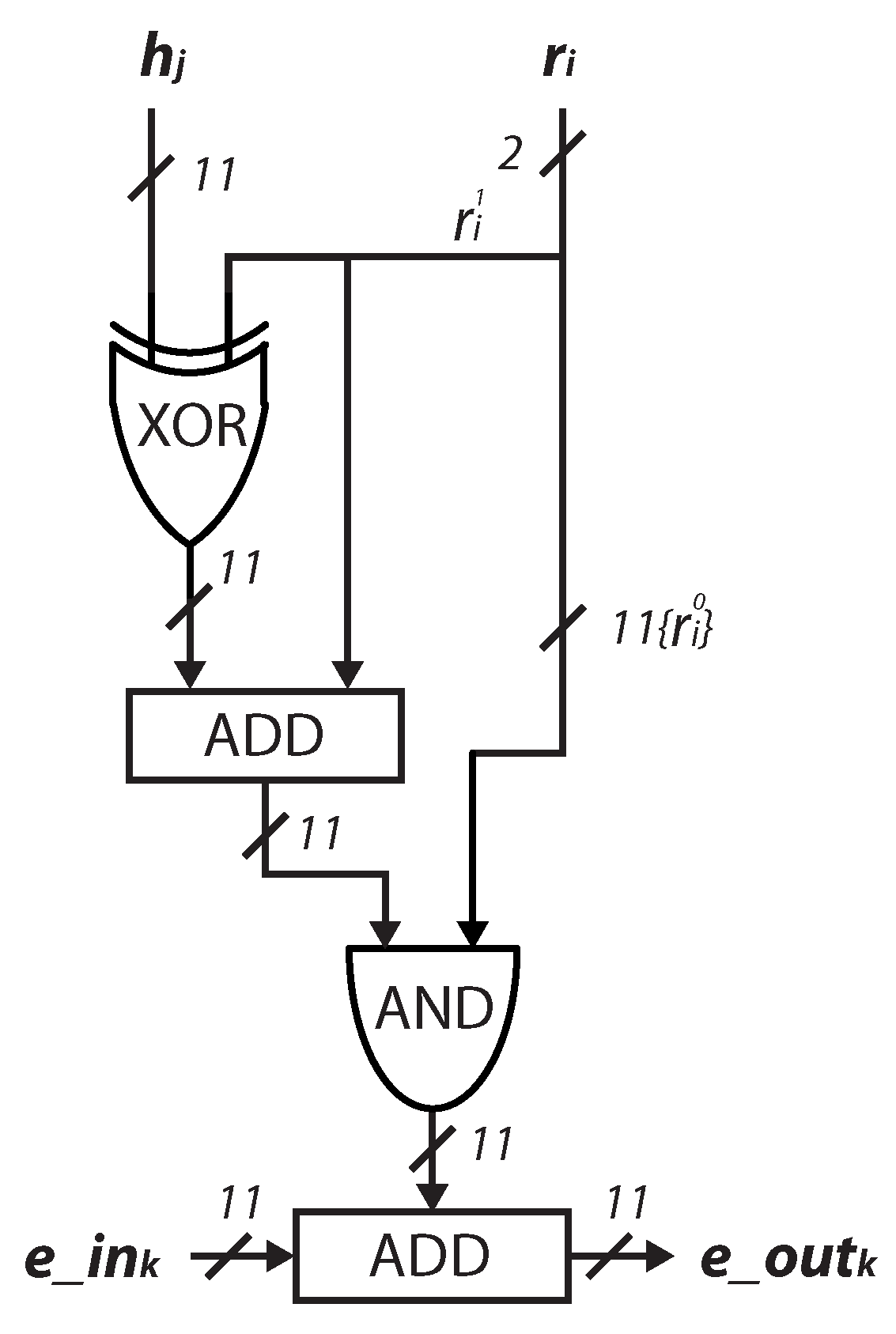
4.1. Design of the Arithmetic Unit
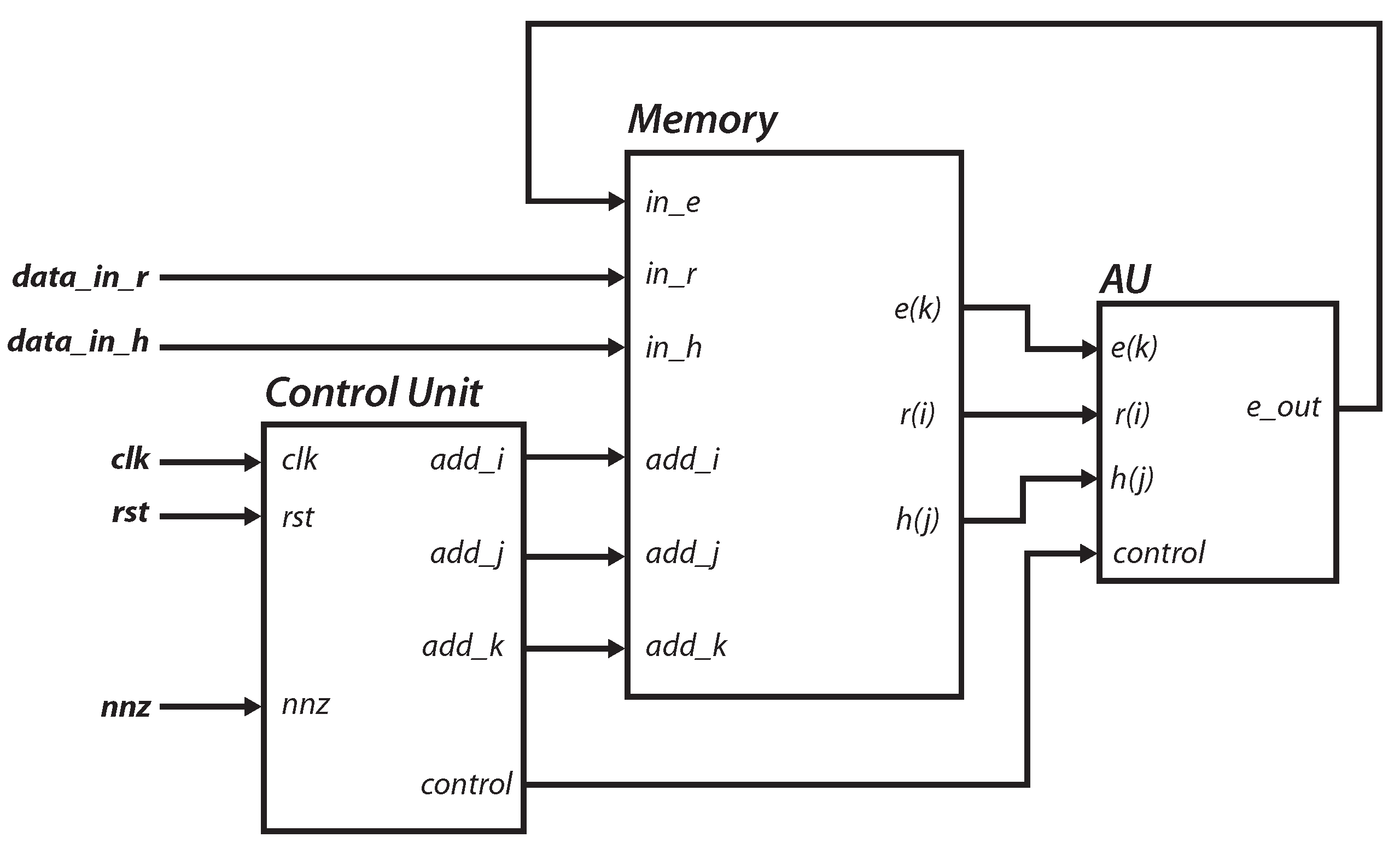
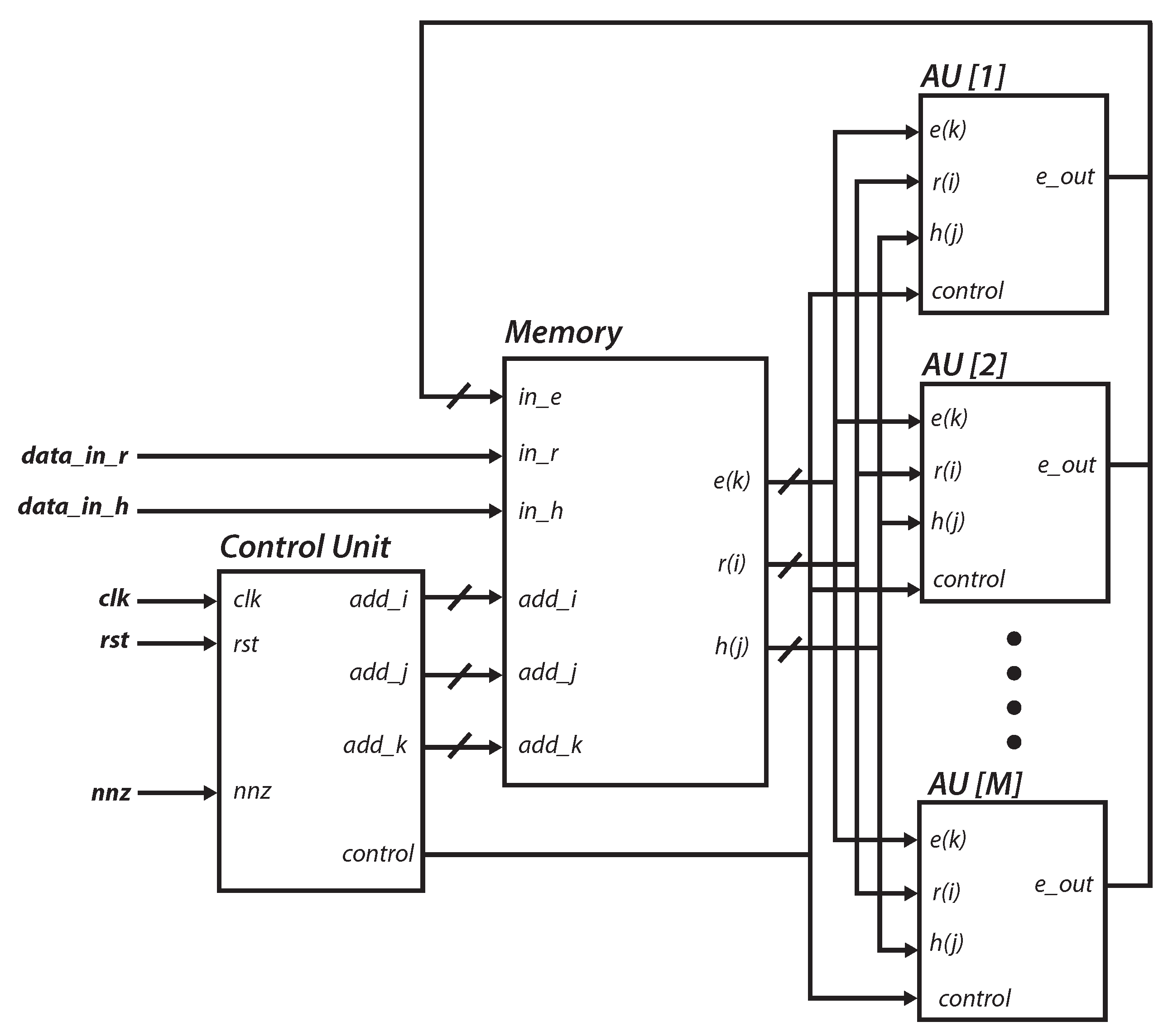
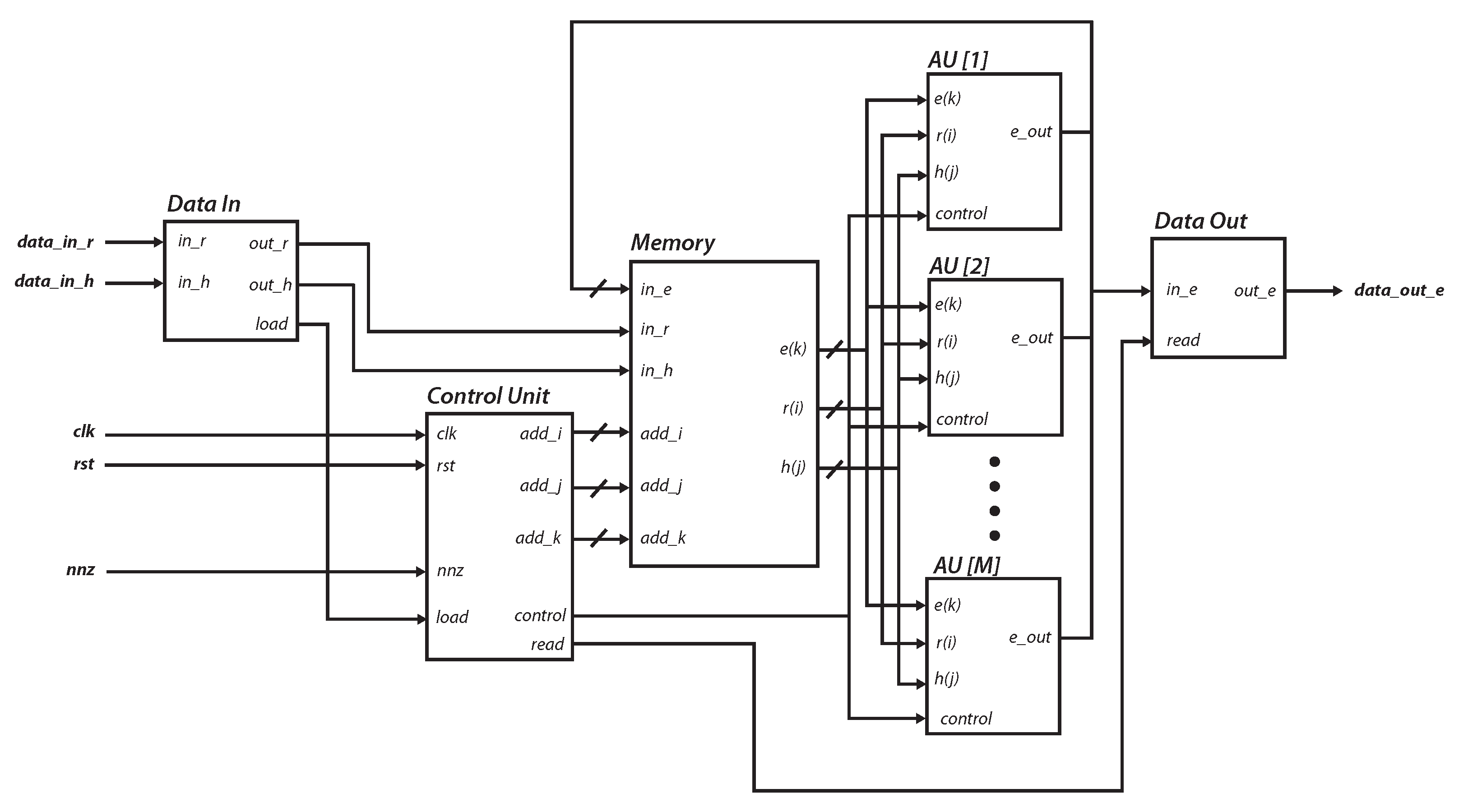
4.2. Core Design
4.3. Parallelizing the Multiplication Process
| Algorithm 3 Parallelizing the polynomial multiplication considering nonzero elements and avoiding timing attacks |
| for do |
| if then |
| end if |
| if or ( and ) then |
| for do |
| ⋮ |
| end for |
| end if |
| end for |
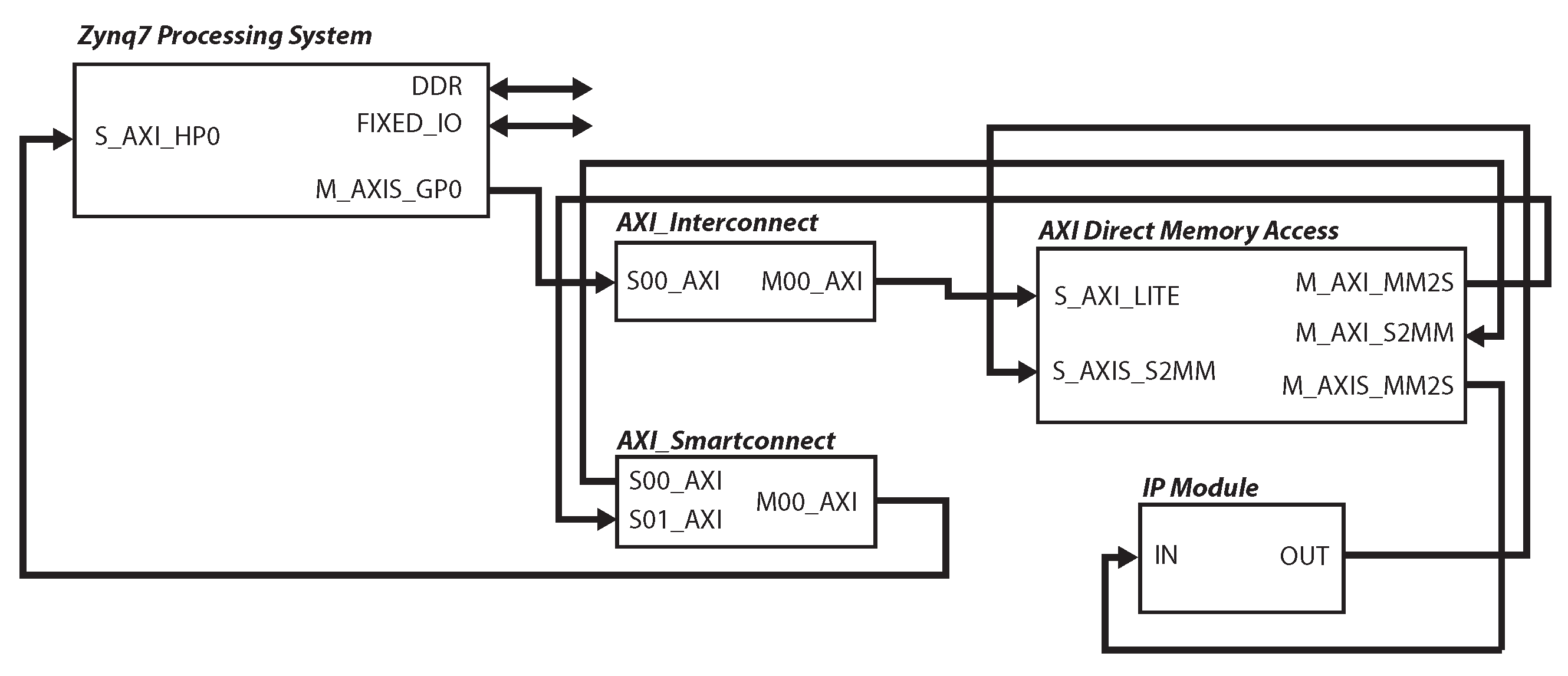
4.4. Embedded System Integration
5. Results
5.1. Resource Consumption
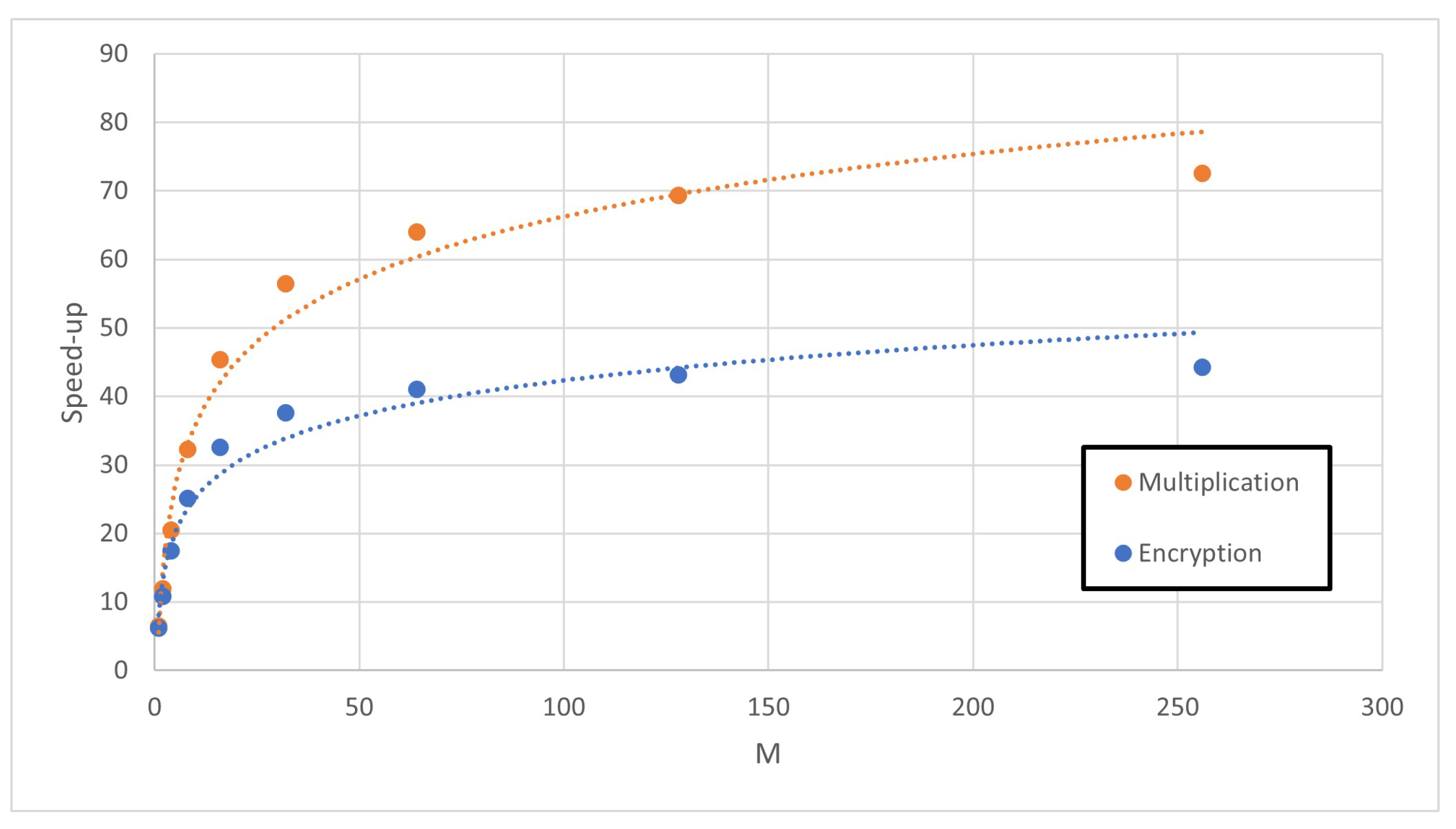
5.2. Analysis of Acceleration Factors
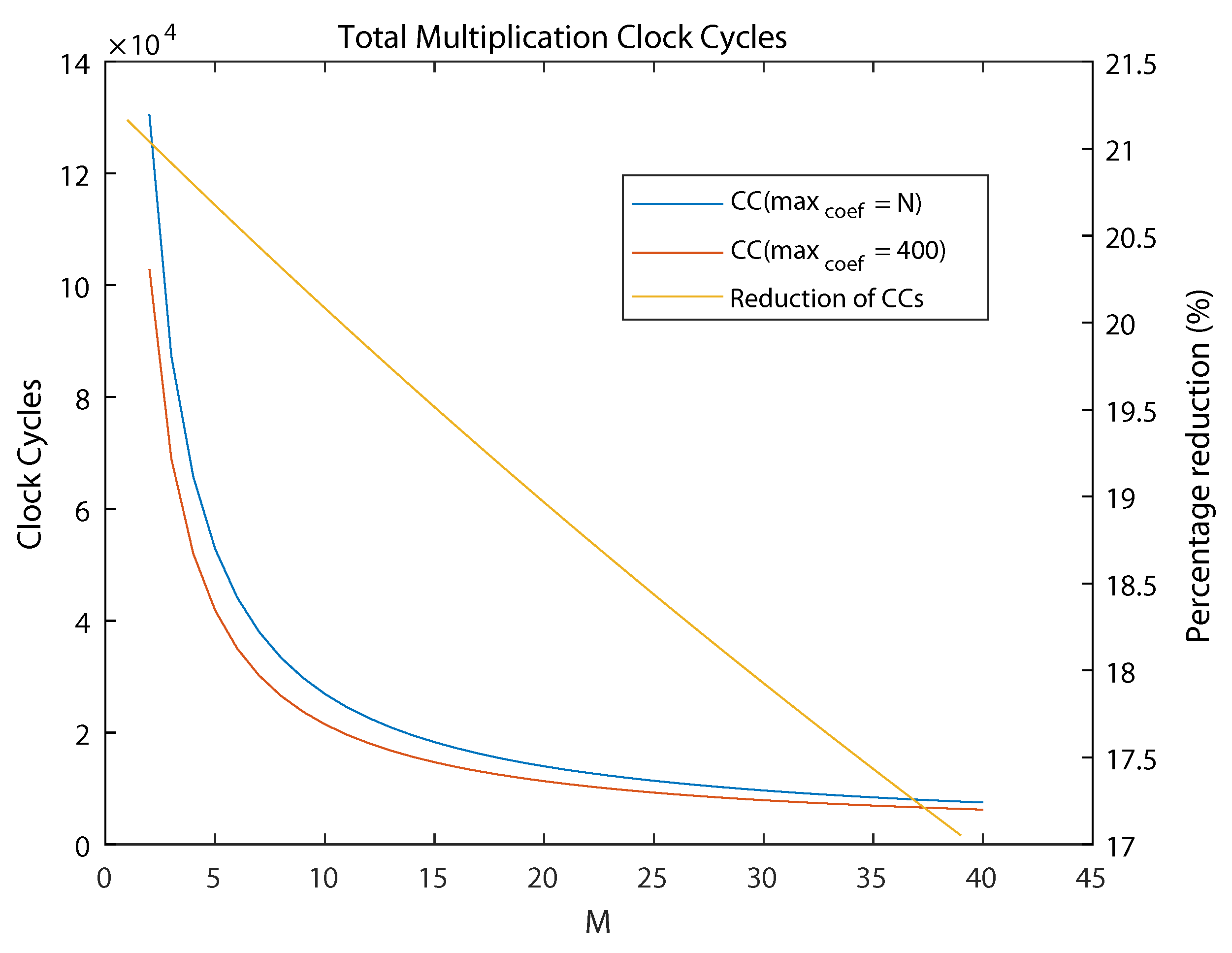
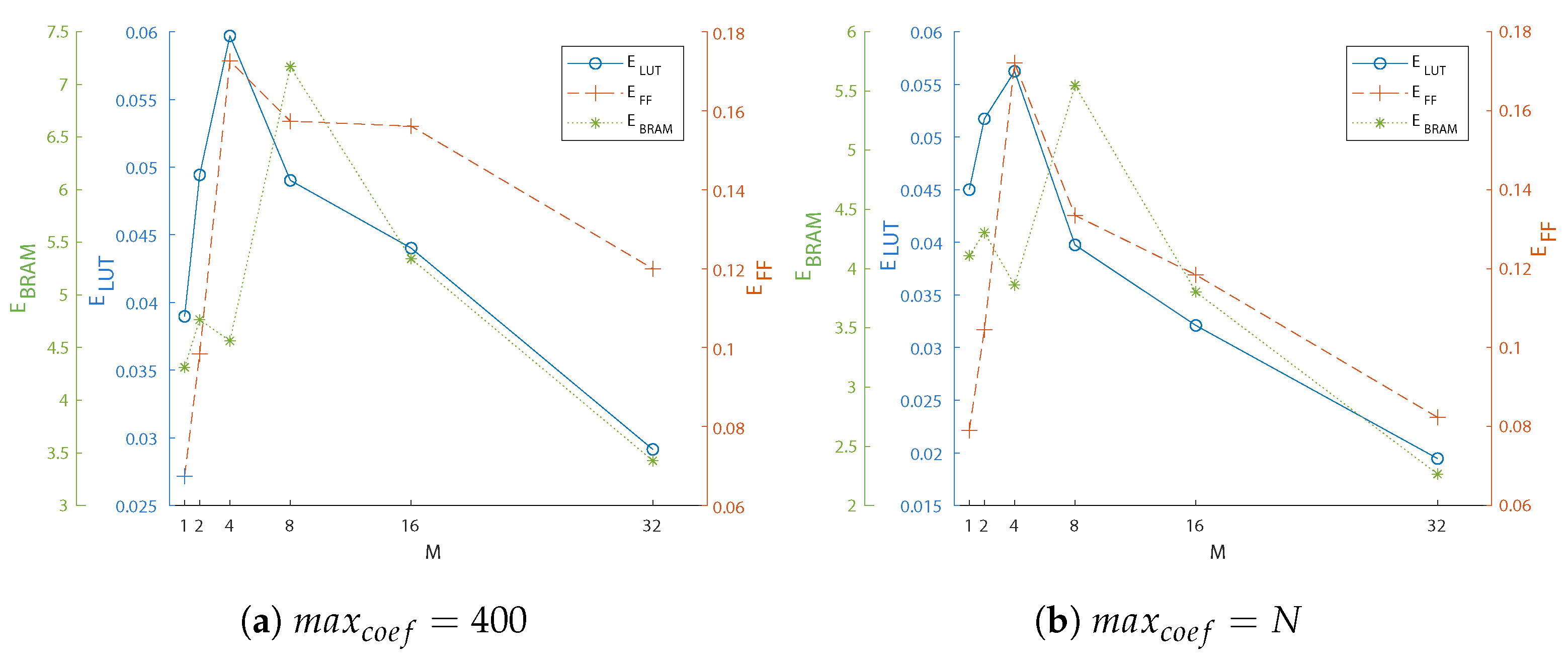
5.3. Optimizing Area and Acceleration
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANSI | American National Standards Institute |
| AU | Arithmetic Unit |
| AXI | Advanced eXtensible Interface |
| BRAM | Block Random Access Memory |
| CC | Clock Cycle |
| DH | Diffie-–Hellman |
| DMA | Direct Memory Access |
| DLP | Discrete Logarithm Problem |
| DSA | Digital Signature Algorithm |
| ECC | Elliptic Curve Cryptography |
| ENISA | European Union Agency for Cybersecurity |
| EU | European Union |
| FF | Flip-Flop |
| FIFO | First-In, First-Out |
| FPGA | Field-Programmable Gate Arrays |
| HDL | Hardware Description Language |
| HLS | High-Level Synthesis |
| HPS | Hoffstein, Pipher, and Silverman |
| HRSS | Hülsing, Rijnveld, Schanck, and Schwabe |
| HW | Hardware |
| IEEE | Institute of Electrical and Electronics Engineers |
| IP | Intellectual Property |
| IoT | Internet-of-Things |
| KEM | Key Encapsulation Mechanism |
| LUT | Look-Up Table |
| NIST | National Institute of Standards and Technology |
| NTRU | N-th-degree Truncated polynomial Ring Unit |
| PKC | Public Key Cryptography |
| PL | Programmable Logic |
| PQ | Post-Quantum |
| PQC | Post-Quantum Cryptography |
| PS | Processing System |
| PYNQ | PYthon Productivity for zyNQ |
| RAM | Random Access Memory |
| RSA | Rivest–Shamir–Adleman |
| RTL | Register-Transfer Level |
| SoC | System-on-Chip |
| SVP | Shortest Vector Problem |
| SW | Software |
| VLSI | Very Large-Scale Integration |
References
- Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- ENISA EUROPA. Available online: https://www.enisa.europa.eu/publications/post-quantum-cryptography-current-state-and-quantum-mitigation (accessed on 21 July 2022).
- NIST. Post-Quantum Cryptography Standardization. Available online: https://csrc.nist.gov/Projects/post-quantum-cryptography (accessed on 21 July 2022).
- Kostalabros, V.; Ribes-González, J.; Farràs, O.; Moretó, M.; Hernandez, C. HLS-Based HW/SW Co-Design of the Post-Quantum Classic McEliece Cryptosystem. In Proceedings of the 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 30 August–3 September 2021; pp. 52–59. [Google Scholar]
- Roy, D.B.; Fritzmann, T.; Sigl, G. Efficient Hardware/Software Co-Design for Post-Quantum Crypto Algorithm SIKE on ARM and RISC-V based Microcontrollers. In Proceedings of the 2020 IEEE/ACM International Conference On Computer Aided Design (ICCAD), San Diego, CA, USA, 30 October–3 November 2020; pp. 1–9. [Google Scholar]
- Dang, V.B.; Farahmand, F.; Andrzejczak, M.; Mohajerani, K.; Nguyen, D.T.; Gaj, K. Implementation and Benchmarking of Round 2 Candidates in the NIST Post-Quantum Cryptography Standardization Process Using Hardware and Software/Hardware Co-design Approaches. In Cryptology ePrint Archive: Paper 2020/795; 2020; Available online: https://eprint.iacr.org/2020/795 (accessed on 21 July 2022).
- IEEE Std 1363.1-2008; IEEE Standard Specification for Public Key Cryptographic Techniques Based on Hard Problems over Lattices. IEEE: New York, NY, USA, 2009; pp. 1–81.
- Lattice-Based Polynomial Public Key Establishment Algorithm for the Financial Services Industry. ANSI X9.98-2010. 2011. Available online: https://webstore.ansi.org/standards/ascx9/ansix9982010r2017 (accessed on 21 July 2022).
- Chen, C.; Hoffstein, J.; Whyte, W.; Zhang, Z. NIST PQ Submission: NTRUEncrypt, a Lattice Based Encryption Algorithm. Tech. Rep., NIST PQC Standardization, Round 1. 2017. Available online: https://ntru.org/resources.shtml (accessed on 21 July 2022).
- Hülsing, A.; Rijneveld, J.; Schanck, J.; Schwabe, P. High-Speed Key Encapsulation from NTRU. In Cryptographic Hardware and Embedded Systems; CHES 2017; Springer International Publishing: Cham, Switzerlamd, 2017; pp. 232–252. [Google Scholar]
- Chen, C.; Danba, O.; Hoffstein, J.; Hulsing, A.; Rijneveld, J.; Schanck, J.M.; Schwabe, P.; Whyte, W.; Zhang, Z. NIST PQ Submission: NTRU, Algorithm Specifications and Supporting Documentation. Tech. Rep., NIST PQC Standardization, Round 3. 2020. Available online: https://ntru.org/resources.shtml (accessed on 21 July 2022).
- Guillen, O.M.; Pöppelmann, T.; Mera, J.M.B.; Bongenaar, E.F.; Sigl, G.; Sepulveda, J. Towards post-quantum security for IoT endpoints with NTRU. In Proceedings of the Conference on Design, Automation & Test in Europe, DATE’17, Lausanne, Switzerland, 27–31 March 2017; pp. 698–703. [Google Scholar]
- Farahmand, F.; Sharif, M.U.; Briggs, K.; Gaj, K. A High-Speed Constant-Time Hardware Implementation of NTRUEncrypt SVES. In Proceedings of the 2018 International Conference on Field-Programmable Technology (FPT), Naha, Japan, 10–14 December 2018; pp. 190–197. [Google Scholar]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Experimental Study of Building Blocks of Lattice-Based NIST Post-Quantum Cryptographic Algorithms. Electronics 2020, 9, 1953. [Google Scholar] [CrossRef]
- Farahmand, F.; Nguyen, D.T.; Dang, V.B.; Ferozpuri, A.; Gaj, K. Software/Hardware Codesign of the Post Quantum Cryptography Algorithm NTRUEncrypt Using High-Level Synthesis and Register-Transfer Level Design Methodologies. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 8–12 September 2019; pp. 225–231. [Google Scholar]
- Camacho-Ruiz, E.; Martínez-Rodríguez, M.C.; Sánchez-Solano, S.; Brox, P. Accelerating the Development of NTRU Algorithm on Embedded Systems. In Proceedings of the 2020 XXXV Conference on Design of Circuits and Integrated Systems (DCIS), Segovia, Spain, 18–20 November 2020; pp. 1–6. [Google Scholar]
- Camacho-Ruiz, E.; Sánchez-Solano, S.; Brox, P.; Martínez-Rodríguez, M.C. Timing-Optimized Hardware Implementation to Accelerate Polynomial Multiplication in the NTRU Algorithm. J. Emerg. Technol. Comput. Syst. 2021, 17, 1–16. [Google Scholar] [CrossRef]
- Sánchez-Solano, S.; Camacho-Ruiz, E.; Martínez-Rodríguez, M.C.; Brox, P. Multi-Unit Serial Polynomial Multiplier to Accelerate NTRU-Based Cryptographic Schemes in IoT Embedded Systems. Sensors 2022, 22, 2057. [Google Scholar] [CrossRef] [PubMed]
- Primas, R.; Pessl, P.; Mangard, S. Single-Trace Side-Channel Attacks on Masked Lattice-Based Encryption. In Cryptology ePrint Archive, Paper 2017/594; 2017; pp. 513–533. Available online: https://eprint.iacr.org/2017/594 (accessed on 21 July 2022).
- Aydin, F.; Aysu, A.; Tiwari, M.; Gerstlauer, A.; Orshansky, M. Horizontal side-channel vulnerabilities of post-quantum key exchange protocols. ACM Trans. Embed. Comput. Syst. (TECS) 2021, 20, 1–22. [Google Scholar] [CrossRef]
- Karimi, E.; Fei, Y.; Kaeli, D. Hardware/Software Obfuscation against Timing Side-channel Attack on a GPU. In Proceedings of the 2020 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), San Jose, CA, USA, 7–11 December 2020; pp. 122–131. [Google Scholar]
- Targhi, E.E.; Unruh, D. Post-Quantum Security of the Fujisaki-Okamoto and OAEP Transforms. In Theory of Cryptography, TCC 2016; Hirt, M., Smith, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9986. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NTRU: A ring-based public key cryptosystem. In Algorithmic Number Theory, ANTS 1998; Buhler, J.P., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1423. [Google Scholar]
- Dang, V.B.; Mohajerani, K.; Gaj, K. High-Speed Hardware Architectures and FPGA Benchmarking of CRYSTALS-Kyber, NTRU, and Saber. In Cryptology ePrint Archive, Paper 2021/1508; 2021; Available online: https://eprint.iacr.org/2021/1508 (accessed on 21 July 2022).
- Bailey, D.V.; Coffin, D.; Elbirt, A.; Silverman, J.H.; Woodbury, A.D. NTRU in constrained devices. In Cryptographic Hardware and Embedded Systems—CHES 2001; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2162. [Google Scholar]
- Atici, A.C.; Batina, L.; Fan, J.; Verbauwhede, I.; Yalcin, S.B.O. Low-cost Implementations of NTRU for pervasive security. In Proceedings of the International Conference on Application-Specific Systems, Architectures and Processors, Leuven, Belgium, 2–4 July 2008. [Google Scholar]
- Kamal, A.A.; Youssef, A.M. An FPGA implementation of the NTRUencrypt cryptosystem. In Proceedings of the International Conference on Microelectronics—ICM, Marrakech, Morocco, 19–22 December 2009. [Google Scholar]
- Zhan, X.; Zhang, R.; Xiong, Z.; Zheng, Z.; Liu, Z. Efficient Implementations of NTRU in Wireless Network. Commun. Netw. 2013, 5, 485–492. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Efficient architecture and implementation for NTRUEncrypt system. In Proceedings of the 2015 IEEE 58th International Midwest Symposium on Circuits and Systems (MWSCAS), Fort Collins, CO, USA, 2–5 August 2015; pp. 1–4. [Google Scholar]
- Liu, B.; Wu, H. Efficient multiplication architecture over truncated polynomial ring for NTRUEncrypt system. In Proceedings of the IEEE International Symposium on Circuits and Systems, Montreal, QC, Canada, 22–25 May 2016. [Google Scholar]
- Braun, K.; Fritzmann, T.; Maringer, G.; Schamberger, T.; Sepúlveda, J. Secure and compact full NTRU hardware implementation. In Proceedings of the IEEE/IFIP International Conference on VLSI and System-on-Chip (VLSI-SoC), Verona, Italy, 8–10 October 2018; pp. 89–94. [Google Scholar]
- Qin, Z.; Tong, R.; Wu, X.; Bai, G.; Wu, L.; Su, L. A Compact Full Hardware Implementation of PQC Algorithm NTRU. In Proceedings of the 2021 International Conference on Communications, Information System and Computer Engineering (CISCE), Beijing, China, 14–16 May 2021; pp. 792–797. [Google Scholar]
- PYNQ—Python Productivity for Zynq. Available online: http://www.pynq.io (accessed on 21 July 2022).
- Brown, N. PYNQ API: C API for PYNQ FPGA Board. Available online: https://github.com/mesham/pynq_api (accessed on 21 July 2022).

| Operation | |
|---|---|
| 00 | |
| 01 | |
| 11 |
| M | LUTs | FFs | BRAM | Clk (MHz) | Latency (s) | |
|---|---|---|---|---|---|---|
| 1 | 166 | 96 | 1.5 | 96.53 | 203,709 | 2110.43 |
| 2 | 241 | 121 | 2.5 | 97.28 | 102,109 | 1049.68 |
| 4 | 344 | 119 | 4.5 | 98.04 | 51,309 | 523.35 |
| 8 | 658 | 205 | 4.5 | 94.43 | 25,709 | 272.25 |
| 16 | 1032 | 291 | 8.5 | 94.43 | 12,909 | 136.70 |
| 32 | 1939 | 471 | 16.5 | 92.94 | 6509 | 70.03 |
| 64 | 4452 | 826 | 32.5 | 86.43 | 3309 | 38.28 |
| 128 | 8668 | 1545 | 64.5 | 79.93 | 1709 | 21.38 |
| 256 | 17,505 | 3017 | 128.5 | 77.77 | 909 | 11.70 |
| NTRU Version | Work | LUT | FF | #CC | Latency (s) | #AU |
|---|---|---|---|---|---|---|
| Round-3 | Our Work | 17,505 | 3017 | 1018 | 11.70 | 256 |
| [32] | 56,218 | 21,406 | 821 | 12.32 | 509 | |
| IEEE-1363.1 | [17] | 29,194 | 19,096 | 245 | 3.23 | 541 |
| [18] | 603 | 90 | 7107 | 71.07 | 8 | |
| [30] | 30,300 | - | 343 | 3.62 | 541 | |
| [31] | 38,240 | - | 541 | - | 541 |
| M | SW | HW | Acc. | HW | Acc. | SW | HW | Acc. | HW | Acc. |
|---|---|---|---|---|---|---|---|---|---|---|
| (s) | (s) | (x) | (s) | (x) | (s) | (s) | (x) | (s) | (x) | |
| 1 | 14,354 | 2219 | 6.47 | 2772 | 5.18 | 14,468 | 2347 | 6.16 | 2900 | 4.95 |
| 2 | 1205 | 11.91 | 1486 | 9.66 | 1334 | 10.76 | 1614 | 8.89 | ||
| 4 | 699 | 20.53 | 842 | 17.05 | 826 | 17.38 | 972 | 14.77 | ||
| 8 | 445 | 32.26 | 509 | 28.20 | 575 | 24.96 | 639 | 22.46 | ||
| 16 | 316 | 45.42 | 350 | 41.01 | 444 | 32.33 | 479 | 29.97 | ||
| 32 | 254 | 56.51 | 271 | 52.97 | 384 | 37.38 | 400 | 35.88 | ||
| 64 | 224 | 64.08 | 231 | 62.14 | 352 | 40.78 | 360 | 39.87 | ||
| 128 | 207 | 69.34 | 209 | 68.68 | 335 | 42.85 | 338 | 42.47 | ||
| 256 | 198 | 72.49 | 199 | 72.13 | 327 | 43.90 | 328 | 43.76 | ||
| Multiplication | Encryption | |||||||||
| M | LUTs | FFs | BRAM | Clk (MHz) | Latency (s) | |
|---|---|---|---|---|---|---|
| 3 | 288 | 125 | 3.5 | 97.09 | 68,109 | 701.50 |
| 5 | 397 | 124 | 5.5 | 96.90 | 40,909 | 422.18 |
| 6 | 443 | 123 | 6.5 | 97.09 | 34,109 | 351.31 |
| 7 | 492 | 124 | 7.5 | 94.43 | 29,309 | 310.38 |
| 9 | 720 | 222 | 5 | 96.53 | 22,909 | 237.33 |
| 10 | 791 | 232 | 5.5 | 96.90 | 20,509 | 211.65 |
| 11 | 859 | 244 | 6 | 93.98 | 18,909 | 201.20 |
| 12 | 907 | 253 | 6.5 | 92.25 | 17,309 | 187.63 |
| 13 | 980 | 266 | 7 | 92.59 | 16,109 | 173.98 |
| 14 | 1043 | 276 | 7.5 | 90.66 | 14,909 | 164.46 |
| 15 | 1104 | 288 | 8 | 90.66 | 13,709 | 151.21 |
| M | SW (s) | HW (s) | Acc. (x) | HW (s) | Acc. (x) |
|---|---|---|---|---|---|
| 3 | 14,354 | 868 | 16.49 | 1045 | 13.69 |
| 5 | 595 | 24.12 | 703 | 20.42 | |
| 6 | 524 | 27.39 | 619 | 23.19 | |
| 7 | 476 | 30.16 | 555 | 25.86 | |
| 9 | 412 | 34.84 | 482 | 29.78 | |
| 10 | 389 | 36.90 | 444 | 32.33 | |
| 11 | 373 | 38.48 | 423 | 33.93 | |
| 12 | 358 | 40.09 | 403 | 35.62 | |
| 13 | 345 | 41.61 | 388 | 36.99 | |
| 14 | 334 | 42.98 | 373 | 38.48 | |
| 15 | 321 | 44.72 | 358 | 40.09 | |
| Max. Eff. | M | LUTs | FFs | BRAM | Acc. (x) | |
|---|---|---|---|---|---|---|
| 400 | LUT | 6 | 443 | 123 | 6.5 | 27.39 |
| FF | 7 | 492 | 124 | 7.5 | 30.16 | |
| BRAM | 9 | 658 | 205 | 4.5 | 32.26 | |
| N | LUT | 4 | 309 | 101 | 4.5 | 17.05 |
| FF | 7 | 465 | 106 | 7.5 | 25.86 | |
| BRAM | 9 | 690 | 204 | 5 | 29.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camacho-Ruiz, E.; Martínez-Rodríguez, M.C.; Sánchez-Solano, S.; Brox, P. Timing-Attack-Resistant Acceleration of NTRU Round 3 Encryption on Resource-Constrained Embedded Systems. Cryptography 2023, 7, 29. https://doi.org/10.3390/cryptography7020029
Camacho-Ruiz E, Martínez-Rodríguez MC, Sánchez-Solano S, Brox P. Timing-Attack-Resistant Acceleration of NTRU Round 3 Encryption on Resource-Constrained Embedded Systems. Cryptography. 2023; 7(2):29. https://doi.org/10.3390/cryptography7020029
Chicago/Turabian StyleCamacho-Ruiz, Eros, Macarena C. Martínez-Rodríguez, Santiago Sánchez-Solano, and Piedad Brox. 2023. "Timing-Attack-Resistant Acceleration of NTRU Round 3 Encryption on Resource-Constrained Embedded Systems" Cryptography 7, no. 2: 29. https://doi.org/10.3390/cryptography7020029
APA StyleCamacho-Ruiz, E., Martínez-Rodríguez, M. C., Sánchez-Solano, S., & Brox, P. (2023). Timing-Attack-Resistant Acceleration of NTRU Round 3 Encryption on Resource-Constrained Embedded Systems. Cryptography, 7(2), 29. https://doi.org/10.3390/cryptography7020029







