Abstract
Searchable encryption technology enables users to access data that has been made publicly encrypted without divulging the original content. The majority of the currently available multi-user certificateless searchable encryption technologies are based on identity-based public key encryption as well as conventional public key cryptosystems. Thus, they are challenged to adapt to the security needs of today’s large-scale network computing environment. As a result, issues such as excessive overhead, poor security, and the inability to handle large-scale applications are unavoidable. In order to address the aforementioned issues, this paper uses the method of combining public key authentication encryption and searchable encryption to propose a certificateless searchable encryption scheme in multi-user circumstances. The stochastic prediction model demonstrates that the scheme can effectively fend off keyword guessing attacks. The proposed algorithm not only performs well in terms of computation but also significantly reduces the amount of computation in simulations.
1. Introduction
Contemporarily, the use of electronic devices is becoming more common in our daily lives [1]. However, there is a significant shortage of storage capacity and computing power for the regular use of these devices. As a result, cloud environments [2] have been developed. Cloud environments can be used by users for computing, storage, and management operations. However, user data may be accessed by cloud servers and unauthorized users without the user’s consent and used for illicit purposes. Therefore, users must encrypt their data before saving it on an untrusted server in order to ensure the security and privacy of their data. However, this poses a challenge for users to retrieve data on cloud servers. The solution to this problem is to download all the encrypted information from the cloud server and then run the data retrieval procedure. As a result, user expenditure and network transmission costs are quite high.
To address the aforementioned issue, Song et al. [3] proposed Searchable Symmetric Encryption (SSE) in 2000. The scheme, however, suffers from the key distribution problem and it is only compatible with one user model. Therefore, for the first time, Boneh et al. [4] developed a searchable encryption scheme called Public Key Encryption Scheme with Keyword Search (PEKS). This scheme is the first searchable encryption scheme that can support multi-user encryption. This model tests a single data receiver and mandates the use of secure channels to deliver trapdoors to the email gateway. Baek et al. [5] first proposed a searchable encryption scheme without a secure channel in 2008. Yong et al. [6] used the ensemble keyword search scheme to construct public key encryption and it was later extended to support multi-user encryption. However, Byun et al. [7] pointed out that the above schemes based on public-key encryption regimes are not resistant to keyword guessing attacks (KGA), and all PEKS schemes mostly have problems with key escrow or certificate management.
In 2003, AI-Riyam et al. [8] proposed a certificateless cryptography (CLC) scheme as a solution to this issue. In this scheme, the public and private keys are both composed of two parts, one by the Key Generation Center (KGC) and one by the user-selected secret value. After the user receives part of the private key, the full private key is calculated and generated according to the secret value selected. With the whole private key, the user can decrypt the ciphertext. The key escrow problem is resolved since KGC cannot compute and generate the user’s entire private key because it only has partial information about the user’s private key. The security of the ciphertext is ensured by the user’s exclusive possession of the entire private key, which is unavailable to other users.
The Certificateless Cryptography with Keyword Search (CLEKS) scheme was first proposed by Peng et al. [9] in 2014. Lu et al. [10] designed a CLEKS scheme that can guarantee user privacy without necessitating the advance pairing of operations with multi-receiver circumstances. Wu et al. [11] proposed a CLEKS scheme that can run on a specific server and that is resistant to internal keyword guessing attacks (IKGA). Yang et al. [12] developed a blockchain-based multi-keyword CLEKS scheme, which proved to be resistant to IKGA under a stochastic prediction machine model. In 2017, Ma et al. [13] proposed an adaptation of the Industrial Internet CLEKS scheme, but the scheme is susceptible to the IKGA.
CLEKS schemes are typically designed for single-receiver applications. To solve the problem, Curtmola et al.’s [14] solution to the issue was to directly extend the single-user scheme to allow multi-users to share the security key for searching files. However, direct application of the single-recipient encryption scheme to a multi-recipient scenario requires encrypting the same keyword associated with the information multiple times using each recipient’s public key separately. As a result, it causes great overhead. The multi-recipient CLEKS encryption scheme can minimize the cost and streamline such a laborious encryption process. Zhang et al. [15] proposed a certificateless certifiable encryption scheme tailored to a multi-user environment in 2020, but the scheme is slightly flawed in terms of efficiency. Recently, in a multi-user system, Mina et al. [16] developed an mCLEKS scheme. However, it is vulnerable to internal keyword guessing attacks, and sending trapdoors to the cloud server requires a secure channel.
The motive of this research is to graph a CLEKS scheme that is appropriate for multi-recipient circumstances without the usage of bilinear pairing. Most of the previous CLEKS schemes rely on pricey bilinear pairing, which is not only extremely ineffective but also considerably increases the overload of the system. A CLEKS scheme without bilinear pairing has a substantially reduced computational cost. In order to cater to multi-environment users, we designed an unpaired CLEKS scheme in this study.
The foremost contributions of this paper are as follows:
(1) A completely multi-user environment-based certificateless searchable encryption scheme is proposed.
(2) Using a random prediction model, it is demonstrated that the approach presented in this study is resistant to keyword guessing assaults.
(3) The results of an efficiency analysis conducted for both computing and communication performance show that the scheme described in this paper has clear advantages.
2. Related Knowledge
2.1. Elliptic Curve
In public key cryptography, elliptic curve groups [17] are of major research significance. Elliptic curve groups were first introduced into public key cryptography by Miller [18] in 1986. The Definition 1 and relevant operations are described as follows.
Let be a finite field of order , where is a prime number, n is a positive integer, , and the algebraic closure on the finite field is . The Weierstrass equation on the finite field is:
where (i = 1, 2, 3, 4, 6). All solutions satisfying the Weierstrass equation on and the infinity point form a curve E. If the Wierstrass equation has three distinct solutions, E is said to be an elliptic curve [19].
Another variant of Equation (1) takes the form:
where Equation (2) has three different solutions only when the discriminant Δ = 4 + 27 ≠ 0. Therefore, the elliptic curve group [19] can be formulated as:
2.2. Mathematically Difficult Problems
Definition 1.
( problem) Suppose G is an elliptic curve group of order and is a prime number. P is a generating element of G. The binary group , where are unknown random numbers, compute .
3. Scheme Model
3.1. System Model
Figure 1 depicts the system model for the certificateless searchable encryption method based on a multi-user environment which contains four main subjects: data owner, multi-user, cloud server, and KGC. Table 1 shows the main symbols and explanations in this scheme.
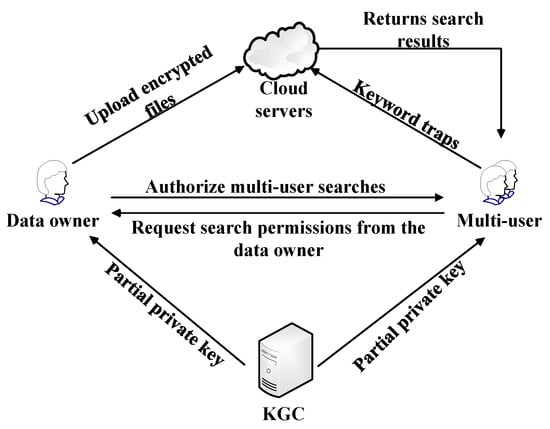
Figure 1.
System model.

Table 1.
Main symbols and explanations.
(1) Data owner: The users have permission to access the data after the keywords and data have been encrypted and transferred to the cloud server.
(2) Multi-user: Users that receive search authority can retrieve data in the cloud based on the corresponding keywords.
(3) Cloud server: accountable for storing the encrypted data that was uploaded by the owner of the data and performing complex ciphertext matching operations.
(4) KGC: Responsible for generating system parameters, system master key, and a portion of the user’s private key.
3.2. Algorithm Model
Formally, the CLEKS scheme in a multi-user environment is composed of the following six algorithms: the system parameter generation algorithm, partial key generation algorithm, user key generation algorithm, keyword encryption algorithm, trapdoor generation, and testing.
Setup: Input the security parameter , and KGC generates the master key and public system parameter .
Partial key generation: Input system parameter , master key , and user U’s identity , and KGC generates the user’s partial private key and partial public key .
User key generation: Enter system parameter , consumer U’s identity and partial public and personal keys (, ) to generate a complete pair of public and private keys ().
Keyword encryption: Input system parameter , keyword , multiple receiver identities and their public keys {} to generate keyword ciphertext C.
Trapdoor generation: Input system parameter , keyword , more than one receiver identities and private key , which will generate the corresponding keyword trapdoor .
Test: Input system parameter , keyword ciphertext and keyword trapdoor , if and correspond to the same keyword, then output 1, otherwise output 0.
3.3. Security Model
In the protection definition of the certificateless cryptosystem [20], there are two kinds of adversaries: , .
The first kind of adversary, , simulates a malicious user. can replace the user’s public key; however, it does not comprehend the system master key and part of the user’s private key.
The second kind of adversary, , simulates a malicious KGC. has to obtain admission to the system master key and part of the user’s private key but does not have the right to replace the user’s public key.
The following defines the random oracles that may be used in the game and offers the protection model of the certificate-free searchable encryption scheme under two different types of adversary attacks. The model is carried out through a game between adversary A and challenger C.
Private-Key-Queries: Adversary is allowed to interrogate the private key of identity , and challenger C sends the private key of the generated pair to adversary A.
Partial-Private-Key-Queries: Allow adversary A to interrogate the partial personal key of identity , and challenger C sends the generated partial private key to adversary . The second type of adversary does not need to make this query.
Replace-Key-Queries: Allows adversary A to perform public key replacement operation. Rival A needs to provide a private key that matches the pseudo-public key . Only adversaries of the first type can perform this query.
Trap-Door-Queries: Enter keyword w and user identity, and challenger C will respond by generating keyword trapdoor . If adversary has already performed public key substitution, challenger C will use the private key submitted by adversary A to generate keyword trapdoor .
A CLEKS scheme based on a multi-user environment must be semantically impervious under an adaptive selection keyword attack (IND-CKA). IND-CKA security can be accomplished between challenger C and adversaries (). This is shown as follows.
System establishment phase: Challenger C first enters a protection parameter λ. The system establishment algorithm is executed to generate the system parameter and the master key s. If the adversary is , Params is sent to the adversary. If the adversary is , both and are provided.
Phase 1: Adversary can make the following prophecy machine queries: Private-Key-Queries, Partial-Private-Key-Queries, Replace-Key-Queries, and Trap-Door-Queries. Adversary can make the following prophecy machine queries: Private-Key-Queries and Trap-Door-Queries.
Challenge phase: Adversary A submits two unqueried pairs of keywords (), and challenger C chooses a random number , computes, and returns the corresponding ciphertext.
Phase 2: The adversary can proceed to make repeated prediction machine queries as in Phase 1, and Challenger C replies to the adversary as in Phase 1.
Guessing phase: Ultimately, as in Phase 2, adversary A offers a guess, , and if , then adversary A wins the game.
4. Specific Construction of the Scheme
4.1. Description of the Scenario
- 1.
- Setup : given a security parameter of as input, the algorithm works as follows.
- (1)
- Generate a cyclic group G of order q on an elliptic curve .
- (2)
- P is chosen as the generating element of G.
- (3)
- Select uniformly and randomly and compute .
- (4)
- Choose three collision-resistant cryptographic hash functions , : and :. The system parameters are { and master key s = x.
- 2.
- Partial key generation: Given params, master key s and U’s identity , the algorithm stochastic selects and calculates partial public key and partial private key .
- 3.
- User key generation: Given params, user U’s identity , partial and partial private keys , the algorithm randomly selects , generates private key ), and generates public key.
- 4.
- Keyword encryption: Given params, keyword , multiple receiver identities, and receiver’s public key , the algorithm stochastic selects and calculates and uses each recipient i’s identity and public key to compute , and the multi-user keyword ciphertext .
- 5.
- Trapdoor generation: Given params, keyword w, U’s identity and his private key , the algorithm calculates keyword trapdoor .
- 6.
- Test: Given params, a keyword ciphertext and a trapdoor , the algorithm checks whether holds. If it holds, output 1; otherwise, output 0.
4.2. Proof of Correctness
Proof.
Suppose the following proof of the correctness of the scheme.
That is, ), so the scheme is right. □
4.3. Proof of Security
Theorem 1.
The scheme achieves IND-CKA (indistinguishability under selective keyword attack) security if the CDH problem is tough under the stochastic predicator system.
Lemma 1 and Lemma 2 can be used to demonstrate the Theorem 1.
Lemma 1.
Assume that , , and are three random oracles. If the adversary is able to break the scheme by a margin of β, there exists an algorithm C that solves the problem with chance .
Proof.
Algorithm B inputs a random instance of the CDH problem: given (), the purpose of B is to calculate by calling as a subroutine. □
System establishment phase: Algorithm B randomly selects an identity as the challenge identity and sets and returns the parameter to adversary .
queries: sustains a list consisting of tuples that are input and the query is responded to. If is contained in the tuples, is output directly. If it does not exist, is randomly selected and returned as the result, and is inserted into the list .
queries: sustains a list consisting of tuples . Input keyword , respond to the query. If the keyword is contained in the tuple , then output directly; if not, then will be randomly selected and returned as the result, and is inserted into the list .
queries: sustains a list consisting of tuples . Input , respond to the query. If is contained in the tuple , output directly; if not, is randomly selected and returned as the result and is inserted into the list .
Phase 1: will perform the following queries:
(1) Partial-Private-Key-Queries: maintains a list initialized as empty, which contains in the user table. When receives a query from adversary for , looks up in the user table and then performs the following operations.
① If , terminates the simulation (this event is represented by ).
② Otherwise, sends (part of the private key generated by KGC).
(2) Private-Key-Queries: sustains a list initialized as empty, and this user table contains when performs private key interrogation on identity . The following operation is executed.
① If , B terminates the simulation (this event is represented by ).
② Otherwise, B sends to .
(3) Replace-Key-Queries: When receives the identity and false public key from , B records the replacement.
(4) Trap-Door-Queries: When performs trap-door interrogation on , perform the following operation.
① If , terminates the simulation (this event is represented by ).
② Otherwise, , or has been replaced. Algorithm generates trapdoor and sends the trapdoor to .
Challenge phase: outputs two different challenge keywords , for the identity . B performs the following operations.
① If , terminates the simulation (this event is denoted by ).
② Otherwise, B stochastic selects and , sets and sets as the challenge ciphertext and sends to , , and .
Phase 2: As in phase 1, continues to initiate a series of queries, and algorithm answers as in phase 1.
Guessing: Ultimately, as in Phase 2, outputs as its answer. If , then wins the game.
Let
Then it is easy to introduce .
Analyze B’s strengths in winning the aforementioned games.
In the guessing phase, the probability that Algorithm gets the correct tuple from the table is , so
Lemma 2.
Suppose that , , and are three random oracles. If adversary A2 is able to attack the solution by a margin of , and there exists an algorithm B with probability that solves the CDH problem by a margin.
Proof.
Algorithm B inputs a random occasion of the CDH problem: given , the purpose of B is to calculate abP by calling as a subroutine. □
Phase 1: will perform the following queries.
(1) Private-Key-Queries: B maintains a list initialized as empty, which contains ( in the user table when performs a private-key interrogation on identity . Perform the following operations.
① If , B terminates the simulation.
② Otherwise, sends to .
(2)Trap-Door-Queries: When performs trap-door interrogation on , perform the following operations.
① If , terminates the simulation.
② Otherwise, or has been replaced. Algorithm B generates trapdoor and sends the trapdoor to .
Challenge phase: As in phase 1, outputs two different challenge keywords , to the identity . do the following operations.
① If , terminates the simulation.
② Otherwise stochastic selects and , sets and sets as the challenge ciphertext and sends to . and .
Conjecture
Let
Then, we can effortlessly obtain .
Likewise, we can derive
5. Efficiency Analysis
In the section that follows, we analyze the effectivity in phrases of both computational price and communication cost, and we evaluate the scheme in this paper with the certificateless searchable encryption scheme based entirely on multi-user surroundings proposed in the literature [13,15].
The experimental environment used in this paper is a HUAWEI laptop with Intel-Core i5 processor, 1.60 GHz CPU, 16 GB RAM, and Windows 10 operation system. It relies on MIRACL library. Table 2 shows the explanation of Notations.

Table 2.
Explanation of Notations.
5.1. Computation Costs
The cost of all encryption operations is added together to determine the algorithm’s computational cost. The approach presented in this study, for instance, necessitates the computation of three scalar multiplications in G and one modulo multiplication in . Therefore, the spending in the encryption phase is 3TSM + TMM. Additionally, the measurement of the ciphertext is computed by calculating the whole range of contained group factors and the hash value. For instance, in the scheme of this paper, the ciphertext size consists of two factors in G. Therefore, its size is 2|G| bits.
The computational cost of the key creation, encryption, trapdoor generation, and checking out algorithms used in this paper’s approach as well as other schemes is shown in Table 3. In this paper’s scheme, the key generation phase spends 49.243 ms, which is about 44% of that of scheme [13] compared with 111.276 ms of literature [13], and is slightly inferior though compared with 49.1384 ms of scheme [15]. However, in the encryption phase, the scheme in this paper spends about 14.94 ms, which is about 21% of scheme [13] and 6.6% of scheme [15] compared with 223.2 ms of scheme [13] and 68.9 ms of [15]. The spending of the scheme in this paper on trapdoor generation is about 19.32 ms compared with 45.1 ms in scheme [13] and 84.2 ms in scheme [15], which is about 42% of scheme [13] and 22% of scheme [15]. The spending of the scheme in this paper in the testing phase is about 22.1 ms, which is about 21% of scheme [13] and 27% of scheme [15] compared with 101.4 ms of scheme [13] and 79.9 ms of scheme [15]. The simulation effect can be seen in Figure 2, where it is evident that the multi-user environment-based CLEKS scheme in this research performs more effectively overall.

Table 3.
Computation costs of compared CLEKS schemes.
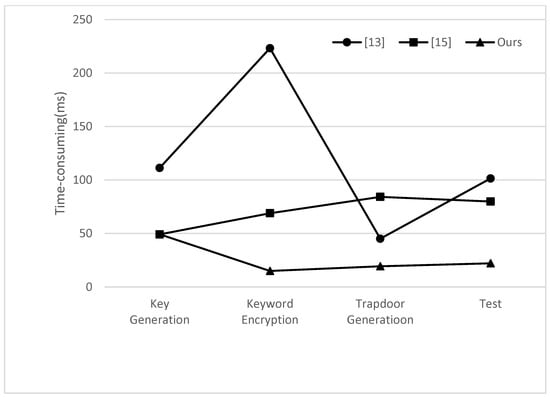
Figure 2.
Computation costs of compared CLEKS schemes.
5.2. Communication Costs
In this paper, the communication cost in terms of both ciphertext (C) size and trapdoor (T) are compared with the other two scheme solutions, and the effects are proven in Table 4.

Table 4.
Communication costs of compared CLEKS schemes.
Table 4 shows that this paper’s scheme communication costs are lower and more effective.
6. Summary
This study provides an effective CLEKS scheme based on multi-user environment to satisfy multi-authorized users employing keywords for ciphertext retrieval and shows that this scheme has IND-CKA security under the random prediction model. Meanwhile, the scheme described in this study has significant computing and communication costs according to the efficiency analysis. Therefore, the scheme presented in this paper is more effective and secure.
Author Contributions
T.F. performed the data collection and review. J.S. conducted the software implementation and wrote the initial draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 61762060) and the Foundation for the Key Research and Development Program of Gansu Province, China (grant number 20YF3GA016).
Data Availability Statement
No data were used to support this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sandhu, A.K. Big Data with Cloud Computing: Discussions and Challenges. Big Data Min. Anal. 2022, 5, 32–40. [Google Scholar] [CrossRef]
- Liu, X.; Lu, T.; Yang, X. Authenticizable Keyword Search Scheme with Privacy Protection. J. Electron. Inf. Technol. 2021, 43, 8. [Google Scholar]
- Song, D.X.; Wagner, D.; Perrig, A. Practical Techniques for Searches on Encrypted Data. In Proceedings of the IEEE Symposium on Security & Privacy, Berkeley, CA, USA, 14–17 May 2000. [Google Scholar]
- Boneh, D.; Crescenzo, G.D.; Ostrovsky, R.; Persiano, G. Public Key Encryption with Keyword Search. In Proceedings of the Advances in Cryptology—EUROCRYPT 2004, Interlaken, Switzerland, 2–6 May 2004; Volume 3027. [Google Scholar]
- Baek, J.; Safiavi-Naini, R.; Susilo, W. Public Key Encryption with Keyword Search Revisited. In Proceedings of the Computational Science and Its Applications—ICCSA 2008, Perugia, Italy, 30 June–3 July 2008. [Google Scholar]
- Yong, H.H.; Lee, P.J. Public Key Encryption with Conjunctive Keyword Search and Its Extension to a Multi-user System. In Proceedings of the International Conference on Pairing-Based Cryptography, Tokyo, Japan, 2–4 July 2007. [Google Scholar]
- Byun, J.W.; Rhee, H.S.; Park, H.A.; Lee, D.H. Off-Line Keyword Guessing Attacks on Recent Keyword Search Schemes over Encrypted Data. In Workshop on Secure Data Management; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless public key cryptography. In Proceedings of the 9th International Conference on the Theory and Application of Cryptology, Taipei, Taiwan, 30 November–4 December 2003. [Google Scholar]
- Peng, Y.; Cui, J.; Peng, C.; Ying, Z. Certificateless Public Key Encryption with Keyword Search. China Commun. 2014, 11, 100–113. [Google Scholar]
- Lu, Y.; Li, J.; Zhang, Y. Privacy-Preserving and Pairing-Free Multirecipient Certificateless Encryption with Keyword Search for Cloud-Assisted IIoT. IEEE Internet Things J. 2020, 7, 2553–2562. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Y.; Ma, M.; Kumar, N.; He, D. Certificateless searchable public key authenticated encryption with designated tester for cloud-assisted medical Internet of Things. Ann. Telecommun. 2019, 74, 423–434. [Google Scholar] [CrossRef]
- Yang, X.; Chen, G.; Wang, M.; Li, T.; Wang, C. Multi-keyword Certificateless Searchable Public Key Authenticated Encryption Scheme Based on Blockchain. IEEE Access 2020, 8, 158765–158777. [Google Scholar] [CrossRef]
- Ma, M.; He, D.; Kumar, N.; Choo, K.K.R.; Chen, J. Certificateless Searchable Public Key Encryption Scheme for Industrial Internet of Things. IEEE Trans. Ind. Inform. 2018, 14, 759–767. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Wen, L.; Wang, H.; Wang, C.F. Searchable symmetric encryption: Improved definitions and efficient constructions. J. Comput. Secur. 2011, 19, 895–934. [Google Scholar]
- Zhang, Y.L.; Wen, L.; Wang, H.; Wang, C.F. Searchable Encryption Scheme without Certificate Authentication in Multi-User Environment. J. Electron. Inf. Technol. 2020, 42, 1094–1101. [Google Scholar]
- Ma, M.; Fan, S.; Feng, D. Multi-user certificateless public key encryption with conjunctive keyword search for cloud-based telemedicine. J. Inf. Secur. Appl. 2020, 55, 102652. [Google Scholar] [CrossRef]
- Qiu, Z.; Meng, X.; Gong, D.; Wei, P.; Huang, Y.; Zhang, P. An Improved elliptic curve group signature scheme. Appl. Math. Prog. 2021, 10, 7. [Google Scholar]
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Proceedings of the Advances in Cryptology—CRYPTO ’85, Santa Barbara, CA, USA, 18–22 August 1985. [Google Scholar]
- Cui, W.; Jia, Z.; Hu, M.; Gong, B.; Wang, L. Signature scheme based on elliptic curve. Comput. Appl. Softw. 2020, 37, 6. [Google Scholar]
- Lin, H.; Gao, F.; Zhang, H.; Jin, Z.; Li, W.; Wen, Q. Public Key Encryption with Equality Test Supporting Flexible Designated Authorization in Cloud Storage. IEEE Syst. J. 2022, 16, 1460–1470. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).