1. Introduction
Security concerns regarding the integrity and privacy of Integrated Circuits (IC) designs are becoming more and more prominent as the IC supply chain becomes globalized and designers outsource fabrication to potentially untrusted foundries. In this process, the threat of the design being revealed to the untrusted parties, insertion of hardware Trojans [
1], or overproduction of the IC are possible. Reverse engineering by end-users using ever-improving IC delayering and imaging techniques [
2] is a growing concern as well.
Logic locking, first introduced in [
3], is based on making the design semi-programmable by inserting additional key inputs into the logic before sending it to the untrusted foundry. Post-fabrication, the circuit will be inoperable and unintelligible without the correct configuration of the key inputs. Besides logic locking,
IC camouflaging and
split-manufacturing are two other ways to partially hide the design of an IC from untrusted end-users or foundries, respectively. IC camouflaging is based on inserting nanodevice structures into the chip that are difficult to disambiguate using conventional microscopy-based reverse engineering by end-users. In split manufacturing, the upper metal layers are fabricated in a trusted facility to hide the design from the foundry. Both methods introduce ambiguity into the design from an attacker’s perspective.
The task of retrieving the original circuit given the ambiguous view by an attacker is typically referred to as circuit deobfuscation/learning in this context. In many real-world scenarios, it is possible for an attacker to access a functional/unlocked instance of the obfuscated circuit and use it as an oracle to obtain correct input-output pairs. Deobfuscation in the presence of such an oracle is referred to as oracle-guided deobfuscation.
In 2015, a generic powerful oracle-guided attack, since termed the SAT attack, was proposed. In the attack, a satisfiability (SAT) solver is used to iteratively mine for input patterns on which to query the oracle, while simultaneously searching for a key that satisfies the observed input-output behavior of the oracle [
4,
5]. The original SAT attack was limited to combinational circuit deobfuscation. If the oracle circuit has uncontrollable flip-flops, a sequential oracle-guided attack is needed. Such attacks were later developed in [
6,
7] using bounded-model-checking (BMC) techniques. Here, the query location and the correct key are mined using a model-checker instead of a SAT solver. This is typically a more computationally intensive process than the combinational case.
Existing oracle-guided sequential attacks assume that there is a single clock signal that is shared by all flip-flops in the obfuscated circuit. Some existing work has targeted timing ambiguous circuits. In [
8] authors introduce timing ambiguous elements into combinational logic leading incorrect keys to create timing violations in fabricated chips. In [
9] incorrect keys lead to much slower sequential performance. Both works, however, remain consistent with the sequential-oracle-guided single-clock threat model and as such can be fed to existing SAT or BMC attacks (even though instances of them might overwhelm said attacks). However, an important case that to the best of our knowledge has not been studied in prior work and does not fit directly into existing attack models, is when the clock signal itself is ambiguous (key-dependent) in some way. In this paper, we explore this case. We present the following contributions:
We discuss several generic schemes for clock obfuscation. These include obfuscating the choice of clock frequency for a flip-flop among a set of multiples of a known or unknown base frequency, plus using dummy clock-ambiguous flip-flops.
We discuss the security of these clock obfuscation schemes in the context of formal notions of functional security.
We discuss how clock obfuscation can take advantage of the inherent clock uncertainty in some asynchronous circuit designs.
We present generic techniques for deobfuscating clock-obfuscated circuits using techniques derived from multi-rate model-checking.
We present experimental deobfuscation runtime data on the ISCAS [
10] sequential benchmark circuits and compare it to traditional XOR/XNOR-based locking.
The paper is organized as follows:
Section 2 presents preliminaries and background.
Section 3 explains different methods of clock obfuscation, and
Section 4 explains how to model and attack clock obfuscated circuits. In the
Section 5, we present the experimental data and discuss our findings. Finally, in
Section 6, we conclude our paper.
2. Preliminaries
Circuit Locking [11]. Formally we can define circuit locking as an algorithm that transforms an original circuit
where
I and
O are the input and output space respectively, to a locked/obfuscated circuit
with
l added key inputs and key space
K. There must exist a correct key
, that when loaded into
will make it functionally equivalent to
:
. The original circuit is chosen from a distribution/family of circuits
, known to the attacker which can be used to capture the attacker’s a priori knowledge of the original circuit
. Changing the key induces a possible obfuscated circuit function space
. The basic goal here is to make it hard for an attacker to recover the unseen original circuit
from the obfuscated circuit
which the attacker can see.
Oracle-Guided (OG) Attacks. In an oracle-guided (OG) attack (or attack model), the attacker, in addition to access to the structure of the obfuscated circuit , has access to a black-box that implements the original circuit , which is called the oracle. The attacker can query this oracle adaptively on chosen points to help identify a correct key for . An attacker with no oracle-access is called an oracle-less attacker (or attack model).
Sequential Oracle-Guided (SOG) Attacks. In the case of a sequential obfuscated circuit, if the attacker has an original functional circuit (oracle), but he for any reason cannot control or observe all the internal state elements (flip-flops or latches) of the oracle [
12,
13] this we refer to as the sequential oracle-guided attack model. The attacker only controls primary inputs and observes primary outputs and has a way to reset the oracle to its known reset state. An unknown reset state of
s bits here can be modeled by
s extra (virtual) key inputs, an extra flip-flop, and some multiplexer logic.
Security Definitions. Formal definitions of security are routinely used in modern cryptography to reason about the security of protocols. A long-overdue effort to use a similar approach in circuit obfuscation has been initiated [
11,
14,
15]. We state the security properties from [
11], as they are used later on in the context of clock obfuscation:
Approximate Functional Secrecy (AFS). A locking scheme is said to be -- secure if the success probability (advantage) of any adversary A that has the locked circuit , and can make up to q chosen adaptive input queries to the oracle of , who has to return an -approximation of , is no more than better than an adversary that makes q queries to the original circuit and randomly guesses the remaining truth-table entries of .
Exact Functional Secrecy (EFS).
-
-
≡
-
-
. i.e.,
is satisfied as soon as the attacker is not able to recover the precise functionality of the original circuit. It turns out that for many families of circuits, an
attacker can disregard the obfuscated circuit
and try to “black-box-learn/approximate” the oracle circuit
with the circuit family
as the a priori function space, making
-
impossible for such families. More relaxed notions of approximation resiliency can avoid this result [
11].
with exponential query complexity on the other hand is satisfiable with comparator logic for many circuit families [
11].
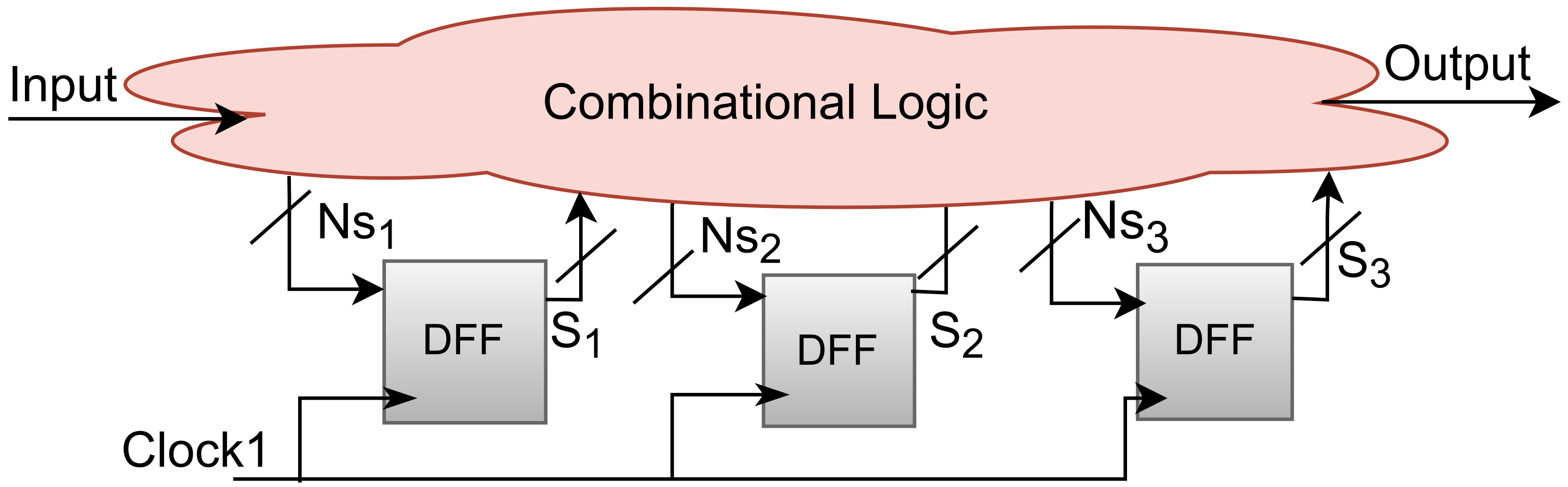
Clock Domain. If a circuit has state elements such as latches or flip-flops then it may have one or more clock signals (see
Figure 1 and
Figure 2). The input and output of the circuit are related to the incoming sequence of the clock signal. The elements of the circuit, which are dependent on a particular clock signal, are in the
domain of that clock. Hence a circuit with multiple clock signals will typically have multiple clock domains.
Clock Sources. A clock signal may come from outside the chip via dedicated clock pins, or be generated internally using an on-chip oscillator. An LC (inductor-capacitor) circuit along with an amplifier can be used to generate periodic signals. Such an on-chip oscillator is constrained by the available device technology (inaccurate R/C (resistor/capacitor) values available, while L components can take up a large on-chip area), whereas an external clock-source can use discrete crystals that produce higher accuracy clock waves.
Setup Time. The input data to a flip-flop needs to be stable for more than a certain amount of time before a clock edge arrives. This time is known as setup time.
Hold Time. The input data to a flip-flop needs to be stable for more than a certain amount of time after a clock edge has arrived. This time is known as hold time.
Combinational SAT Attack. The combinational SAT attack, as presented in [
4,
16] is a generic oracle-guided attack. Given an arbitrary keyed circuit
and an oracle
, it begins by formulating a
miter circuit
. This circuit is converted to a conjunctive normal form (CNF) formula through the Tseitin transform and asserted using a SAT-solver to obtain
.
is called a discriminating-input-pattern (DIP), as it leads to different outputs under two different keys
(uncertainty sampling). The oracle is queried on this DIP
. This input-output (IO) observation will be inconsistent with at least one of
or
and is hence guaranteed to prune the key space. This IO condition
is added back to
M as a constraint and the process is repeated until
is no longer satisfiable. At this point solving
alone is guaranteed to return a functionally correct key as long as
.
Model-Checking Sequential Oracle-Guided Attack. The above SAT-attack cannot be formulated directly for a stateful circuit. However, a solver-based sequential oracle-guided deobfuscation attack can be built with the same paradigm as above [
6,
12]. We first extend the locking model to sequential circuits by defining sequential locking as transforming the sequential original circuit
with
S and
being the current and next state spaces respectively, and
is an
-bit state register, to the obfuscated circuit
for which
is an
- bit state register where a correct key
exists such that for all sequential
traces we have
and
and
. We can assume that
is initialized to zero
. An unknown reset state for
can be modeled with extra virtual key-bits. This allows modeling finite-state-machine (FSM) obfuscation [
17] with the above scheme as well.
Under the above model, the sequential attack can proceed by unrolling the obfuscated sequential circuit up to a given clock cycle bound u. From this we get which takes u inputs and produces u outputs. Since such an unrolled circuit is going to be combinational, it can be directly passed to a combinational SAT attack. The DIP extracted from this unrolled miter will now contain a sequence of input patterns and hence is called a discriminating-input-sequence (DIS). The DIS can be queried on the sequential oracle. An unrolled input-output constraint can then be extracted and appended to the unrolled miter and the process can be repeated.
Once the above process concludes (miter unsatisfiable) for a particular bound
u, the recovered key will be a functionally correct key for up to this round. The attack can terminate early by checking for certain termination conditions, such as the combinational equivalence of the next-state functions, or checking whether the miter is unsatisfiable for an unconstrained reset state. The attack can in fact be modeled entirely using the model-checking problem. Model-checking is the task of (dis)proving properties over sequential transition systems represented by FSMs or stateful circuits. Unrolling a circuit and passing it to a SAT solver is a common fast approach to solving model-checking problems called bounded-model-checking (BMC). Algorithm 1 shows the overall flow of the BMC-based sequential oracle-guided attack.
| Algorithm 1 Given oracle access to sequential circuit and structure of sequential obfuscated circuit return a correct key |
- 1:
functionSeqDecrypt(, as black-box) - 2:
, - 3:
- 4:
- 5:
while !Termination() do - 6:
if Bmc() is then - 7:
- 8:
- 9:
- 10:
- 11:
- 12:
else - 13:
- 14:
end if - 15:
end while - 16:
satisfy with and - 17:
return - 18:
end function
|
3. Clock Obfuscation
In this section we discuss how an ambiguous clock may be created in the view of an oracle-guided attacker. The baseline threat model here is similar to SOG where the attacker lacks full scan-chain access, and additionally is uncertain about the frequency of some the clocks in the designs. Note that a non-SOG/OG/combinational attacker (one with full and immediate state observability) can easily recover clock frequencies by simply observing changes in the state and hence not the focus of our discussion.
We will discuss various technical aspect of this clock obfuscation process ranging from clock sourcing and key-dependent programming to state-element selection, and finally designs that are inherently multi-clock as prime candidates for this form of obfuscation.
3.1. External Clock Sources
In the conventional locking-enhanced supply chain, the key is never shared with an untrusted party as such a party can collaborate with the untrusted foundry to learn the functionality of the original circuit. Instead, the secret key is programmed onto the chip by a trusted party in a trusted facility, and then one has to ensure that the programmed key is nonvolatile/persistent and tamper-resistant. For instance, if the state of key-bits can be recovered via optical/electrical probing the security of locking obviously falls apart [
18].
This also means that placing the key outside the chip is difficult. An off-chip key will need to be transmitted securely to the locked chip. This itself may require encryption and hence another encryption secret key with exactly the same key management issues. Similarly, in the case of clock obfuscation, securing an external source will be very difficult. An attacker can easily probe an external clock signal and record its frequency. Hence except for the case of trusted end-users, clock obfuscation should focus primarily on ambiguating internal clock sources.
Note that regardless of the origin of the clock the attacker can try to bound its upper-frequency limit. The attacker can study the layout and transistor technology of the locked circuit and use timing analysis to get an estimate of the maximum clock frequencies as dictated by setup/hold-time constraints. Finding a minimum clock frequency bound that is larger than zero will be harder if not impossible.
3.2. Internal Key-Programmable Clock Sources
Given that external clocks are hard to obfuscate, the defender has to produce clock ambiguity on-chip which we discuss herein.
The first approach is to use internal key-programmable oscillators. There are a myriad of ways to implement frequency controllable on-chip oscillators. Modern processors require such oscillators to implement dynamic voltage/frequency scaling (DVFS) to reduce power consumption during low-intensity computational periods. For instance, ref. [
8] implements a programmable clock source via a ring oscillator with variable/controllable capacitors inserted in the ring to tune its oscillation frequency.
Since the frequency needs to be programmed on-chip there are some limitations. Typically, digital bits are used to tune such oscillators. This will make it such that for l key bits there will exist at most different possible frequencies. For the purposes of locking, however, it is possible to imagine a chip that has programmable continuous RLC elements that are configured using an external analog voltage/current. In such a setting, it may seem that the number of possible frequencies can become infinite. However, the attacker can use a bounded number of frequency “bins” to place the continuous variable into, capturing the inevitable imprecision in the defender’s configuration process. There is obviously a limit here on the number of different frequency possibilities in the attacker’s view that the defender can create. On-chip oscillators cannot be tuned with infinite precision. Moreover, the infinite precision may not translate into infinite Boolean function possibilities for .
Another approach is to use an external fast master clock, the frequency of which will be known to the attacker (represented by the smallest period T). This fast clock can be slowed down by integer multiples by adding a programmable digital clock divider. A counter circuit can be used to count the number of positive edges on the clock. The value of the counter d is compared to a key vector and a tick is generated in case of a match. The attacker can produce a clock period in addition to the T-period master clock using such logic. The overhead here will be a function of the bit width of and will consist of comparator and counter logic. The maximum possible period (slowest frequency) above zero will be .
3.3. Frequency Fractions
Using the above various clock generation approaches, given the assumption that the number of different clock frequencies in the design is finite, we can model this with t different possible clock frequencies/periods . The relationship between these clocks can vary creating different scenarios that lead to somewhat different threat models:
Integer Multiples of a Single Base Period. The somewhat simplest case here is when includes a single base minimum period T, plus integer multiples of it. e.g., . For instance given a clock-divider with a programmable n-bit division-factor controlled by the n-bit key , we will have .
Integer Multiples of Multiple Base Periods. The more complicated case is when there are multiple base frequencies and their integer multiples. This corresponds to the case where one uses several on-chip controllable oscillators to produce more than one base period and , where and are completely independent. Multiples of these periods can then appear in as well. In this work, we do not directly present a generic deobfuscation algorithm for this case. Such cases will have to be modeled with a single base period alternative.
To transform the multiple base period case to a single base period, one can pick a small single base period and use it to express both and . i.e., and . In a real-world scenario, absent external unknown clock frequencies, and can take a finite number of different values. One can extend this to more than two base periods.
Note that in model checking research, when dealing with multi-rate transition systems, a similar approach is often used [
19]. i.e., a single global minimum step size is used to express the different rates. However, it is possible to imagine truly independent clock rates. Take the case of asynchronous transmitter and receiver logic. Here the frequencies on both sides can be completely independent and the system must perform correctly regardless. Unrolling the circuit to capture its behavior, in this case, is not straightforward. Formal analysis of such fully asynchronous circuits is a topic of ongoing research [
20] and outside the scope of this paper.
Rational Multiples of a Single Base Period. Here
can include non-integer multiples of the base period. i.e.,
. In this paper, we avoid deobfuscating such cases directly. As for the deobfuscation, we will model obfuscated circuits with the multi-rate model-checking [
19] method, we need to convert this non-integer multiples to the case of integer multiples by finding a
that is small enough to express all the periods in
. For instance
, can be used to express
and
. As for the defender he can implement such a setting by using a fast master clock of
and dividing the frequency down to the other periods, or by using
different tunable oscillators that can be tuned in steps of size
.
We will explore these scenarios further in
Section 4.
3.4. State Element Clock Ambiguation
Clock signals are primarily routed to state elements in digital logic. Hence, subsequent to the generation of different clock frequencies, the defender has to create in the view of the attacker an ambiguity in which clock frequency is used for a particular state element.
We can assume that the previous step results in the generation of
t different clock frequencies/periods
. These frequencies can be implemented on a single wire. For instance, a single-ended programmable oscillator or clock-divider will have a single clock signal output that can be programmed to oscillate at different frequencies. By routing this signal to a state element, an ambiguity is immediately created in the attacker’s view on the clock frequency of that particular element. Different clock frequencies can also be implemented on different wires. One can build a fixed (key-independent) clock frequency divider that generates a
-period clock in addition to the
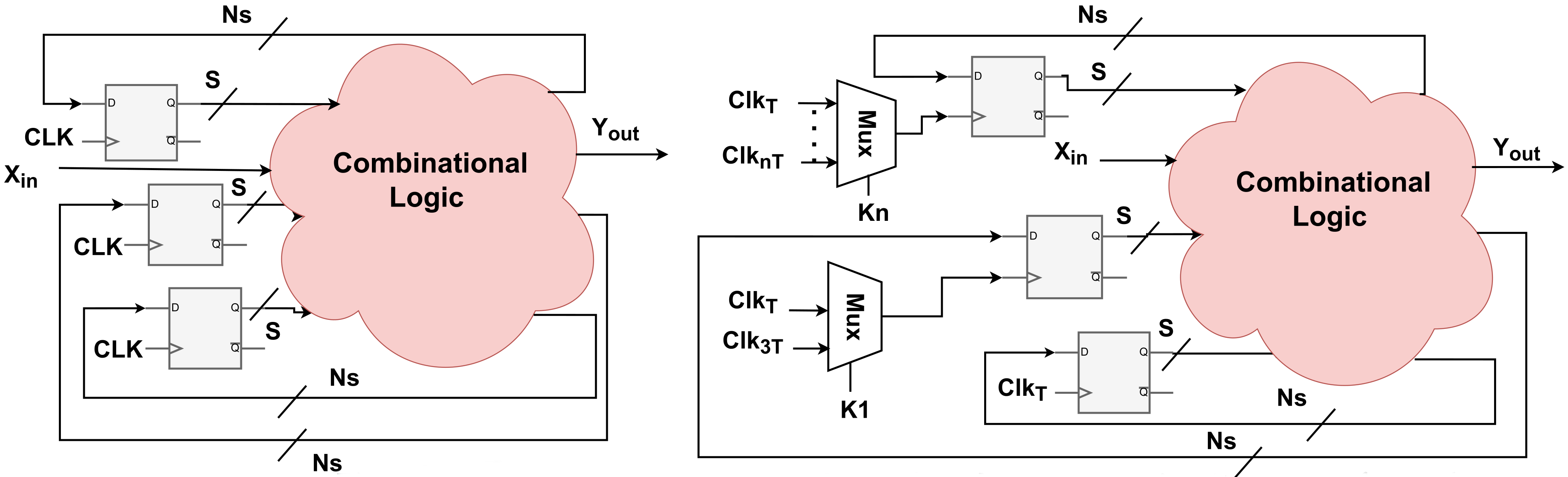
T-period master clock. Then, a key-controlled MUX-gate can be used to select one of the two known frequencies as the clock source of a particular DFF. This is shown in
Figure 3. While this is functionally equivalent to the single-wire case, the hardware overhead may be different. The MUX approach requires both clock signals to be routed to the state element. The single-ended programmable clock on the other hand can take on only a single frequency, meaning that if routed to multiple DFFs, they will all take on the same frequency post-configuration and hence does not lead to DFF-specific ambiguity (captured by virtual keys) in the attacker’s view.
In the functional secrecy paradigm of logic locking, one can model a given ambiguity in the locked circuit with alternative key structures. Given a precise locked circuit netlist , a functional attacker can replace it with as long as the possible function set of is a superset of the possible function set of . We use this approach by introducing virtual key-bits that model the attacker’s ambiguity over the behavior of the circuit in our attacks later on.
3.5. State Element Selection
Once a set of different frequencies is generated one has to select which state elements in the design to obfuscate with what subset of frequencies. The space of possible ways to select state elements here would be prohibitively large. In our experiments on benchmark circuits, we select a random subset of flip-flops and obfuscate them with a choice of different frequencies. However, one can perform the selection to optimize metrics such as area/timing/routing/congestion or security metrics.
One important issue that needs addressing here is that of
Oracle-Less (OL) attacks [
21]. An OL attacker has to determine the frequency of a particular flip-flop by studying the structure of the obfuscated circuit alone. For instance, if the transistor technology and DFF structure dictate a certain setup/hold-time requirement, that can be discerned from the obfuscated circuit layout itself, then the attacker can discard frequency values that are high enough to violate setup/hold-time requirements. i.e., a clock frequency where the period
where
is the setup time and
is the hold time can be removed from the set of possible frequencies for that particular clock. Note that hold-time requirements that are satisfied by adding delay to timing paths do not help in determining the clock frequency beyond the above-discussed point.
Another potential oracle-less vulnerability is the fact that the flip-flops that are closer to one another in the physical layout or the netlist graph are more likely to have the same frequency. The defender can try to alleviate this by ensuring that clusters of nearby flip-flops are clock-obfuscated simultaneously.
One more OL vulnerability in clock obfuscation is the fact that given the distribution of real-world original circuits modules, those with fine-grained multiple clock rates per DFF are less common. This bias in the original circuit space
, means that an attacker will have a non-negligible advantage in correctly recovering the circuit by just assuming that all clocks run at the same frequency. It is better therefore to target clock obfuscation towards circuits that inherently exhibit some sort of clock gating or frequency control. We discuss some of these special cases in
Section 3.7.
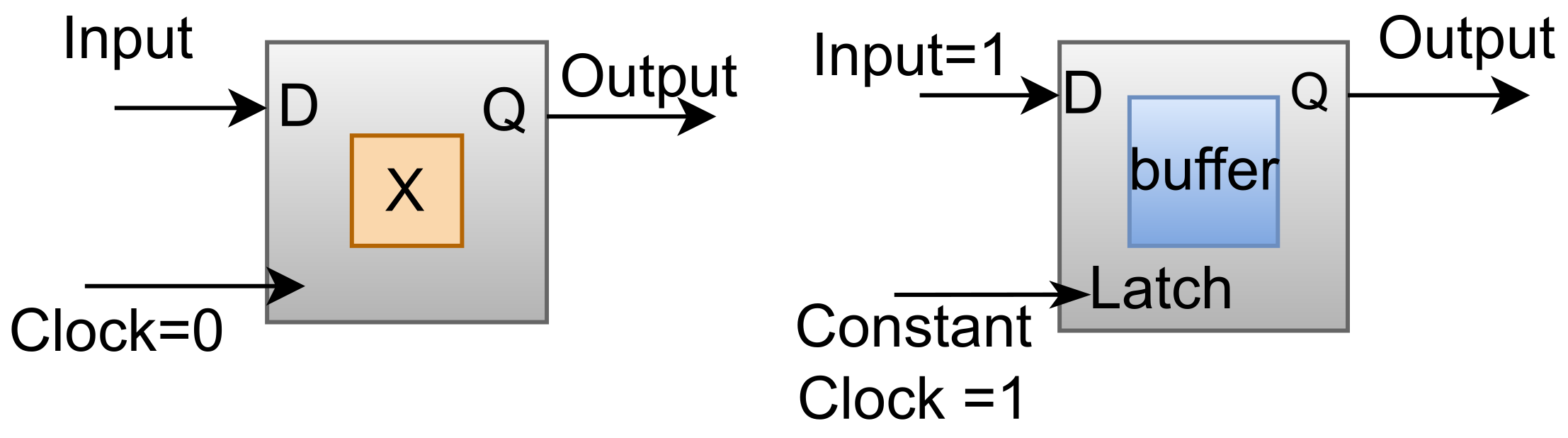
3.6. Dummy (Constant-Clock) State Elements
One can insert a flip-flop in the circuit that has a
constant clock signal:
An edge-sensitive D-flip-flop with a zero clock signal will remain forever in its reset state. This can serve as a constant in the circuit. Constants can be mixed with AND/OR/XOR gates to create “phantom” sequential behavior in the attacker’s view of the circuit.
A level-sensitive latch with an always-on/off clock signal can serve as a buffer/constant. This can be inserted on wires or replace existing buffers/inverters. The above cases can be seen in
Figure 4.
Implication for . Achieving
with exponential security is possible for many combinational circuit classes by inserting for instance detachable comparator logic to the circuit [
11]. A detachable comparator/point-function
can convince the attacker that there may be an activating pattern
k in the input space of the circuit. Since such a comparator can be disabled by setting
, the attacker will have to explore a significant proportion of the input space of the circuit in order to be able to rule out the existence of this activating pattern with high confidence.
A similar phenomenon can happen with dummy clock obfuscated state elements. The attacker suspects that the dummy state element is going to make a transition at some point, ruling out of which requires querying and waiting for a time that is the longest non-infinite potential period of a clock signal in the circuit. Generating a with a clock-divider from a base clock period of will require a comparator of size n but can create with time complexity.
3.7. Inherently Asynchronous Circuits
The attacker’s a priori knowledge of the original circuit is captured in : the original circuit distribution. It is not straight-forward to precisely describe . This is similar to the plaintext distribution problem in cryptography. English text has a distribution, but describing the distribution is not easy. Modern ciphers are designed to not lose their security as the distribution of the plaintext changes. This is not the case unfortunately for circuit locking. A locking scheme can go from information theoretically secure to completely broken by just changing . In the case of clock obfuscation, applying the obfuscation to original circuits that are inherently multi-clocked will ensure that an attacker that simply decides that all state elements are running at the same frequency will be wrong in at least some instances, i.e., instances where the original circuit itself was multi-clocked rather than the clock ambiguity being exclusively artificially introduced via the locking scheme.
We discuss two common asynchronous circuit examples below that can be locked manually with clock obfuscation. This can be extended to other asynchronous circuits.
Digital PLL. Phase-locked loops (PLL) are feedback control systems that adjust the phase of a locally generated signal to match the phase of an input periodic signal automatically. This is done by detecting the difference in phase between the two signals and adjusting the local oscillator based on this difference.
A common PLL design paradigm is to use the following stages: a phase detector measures phase differences between the internal and external signal. A low-pass loop filter filters this difference signal producing a voltage that tunes a voltage-controlled oscillator (VCO). The output of the VCO is then fed back to the phase detector after going through a feedback divider. One can implement the above with analog or mixed-signal components. One common mixed-signal way to design the phase detector is to feed the input and oscillator signals to the clock port on a pair of DFFs. This can allow for clock obfuscation.
In a Digital PLL (DPLL), these blocks can be converted to digital blocks (see
Figure 5). The loop filter is converted to digital loop filter, the phase detector to a time-to-digital converter (TDC), and the VCO to a digitally-controlled oscillator (DCO) [
22].
A TDC block design is shown in
Figure 6. As can be seen, the
timed signal is passed as the clock signal to a series of DFFs capturing a series of consecutively delayed signals. Since this
signal is not the common master clock in the system, it can be obfuscated via key-controlled MUX gates. One has to ensure that the precision of the TDC is not harmed by trying to reduce the mismatch induces by the insertion of MUX gates.
Oracle-less resiliency may be harder to maintain as the TDC block has a very particular structure without additional interconnect and structural obfuscation. Oracle-guided resiliency will depend heavily on the controllability/observability of its input/output in a larger design.
Digital Counter. A digital
n-bit counter can be built with a sequence of DFFs. The frequency of the rising edges on the clock signal that is shared among these DFFs will reduce by half after each stage of DFFs creating a binary counter function at the
outputs. One can use MUX gates here to confuse the attacker in the choice of clocks as seen in
Figure 7. It is also possible to take any sequence of
n DFFs in a design, and use key-controlled MUX gates to create a “potential digital counter” in the attacker’s view among them by creating a scenario where there will exist a key under which the DFFs will act as a counter.
The oracle-less resiliency here will depend on how undiscernible the counter logic can become from the rest of the circuit which will depend on the density and topology of inserted MUX gates. The oracle-guided resiliency for counter logic can increase exponentially, as the last bit (most significant bit) of the counter has exponentially small observability, which can lead to exponentially high query counts or wait times.
4. Clock Deobfuscation
Up until now, we have discussed clock-based obfuscation techniques and their possible implementation in circuit designs. Sequential circuits are considered to be harder than the combinational circuit in the deobfuscation process. As mentioned in preliminaries, the deobfuscation of sequential circuits is possible with the sequential oracle-guided attack with bounded model checking. Here we show that it is possible to adapt these attacks to the case of deobfuscating clock-ambiguous circuits.We use a common technique used in multi-rate model-checking [
19]. The idea here is to try to model the multi-rate semantics with a single-rate model with the same functionality that can then simply be passed to a traditional single-rate model-checking attack.
4.1. Clocks with Known Integer Multiples of a Base Period
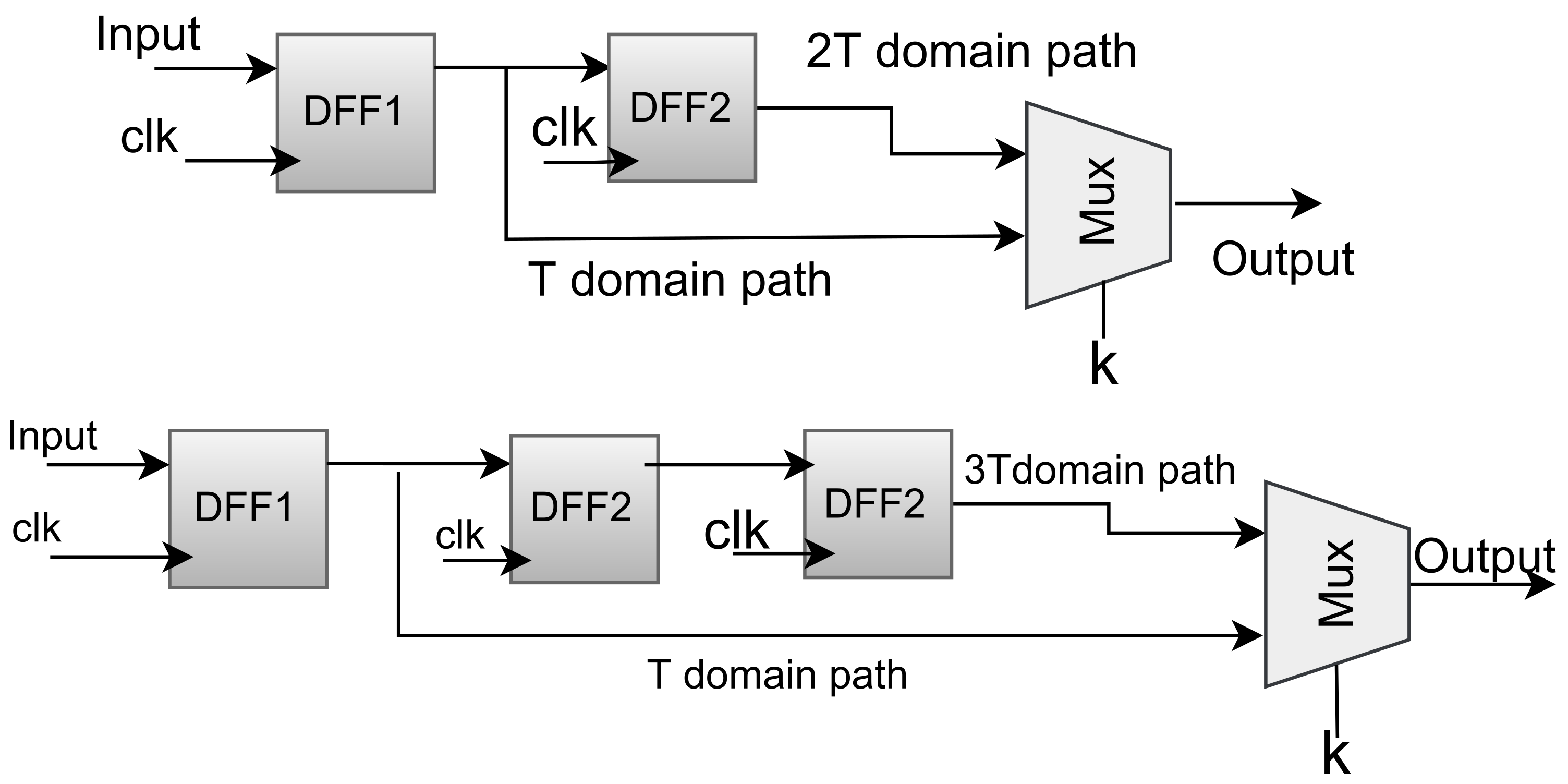
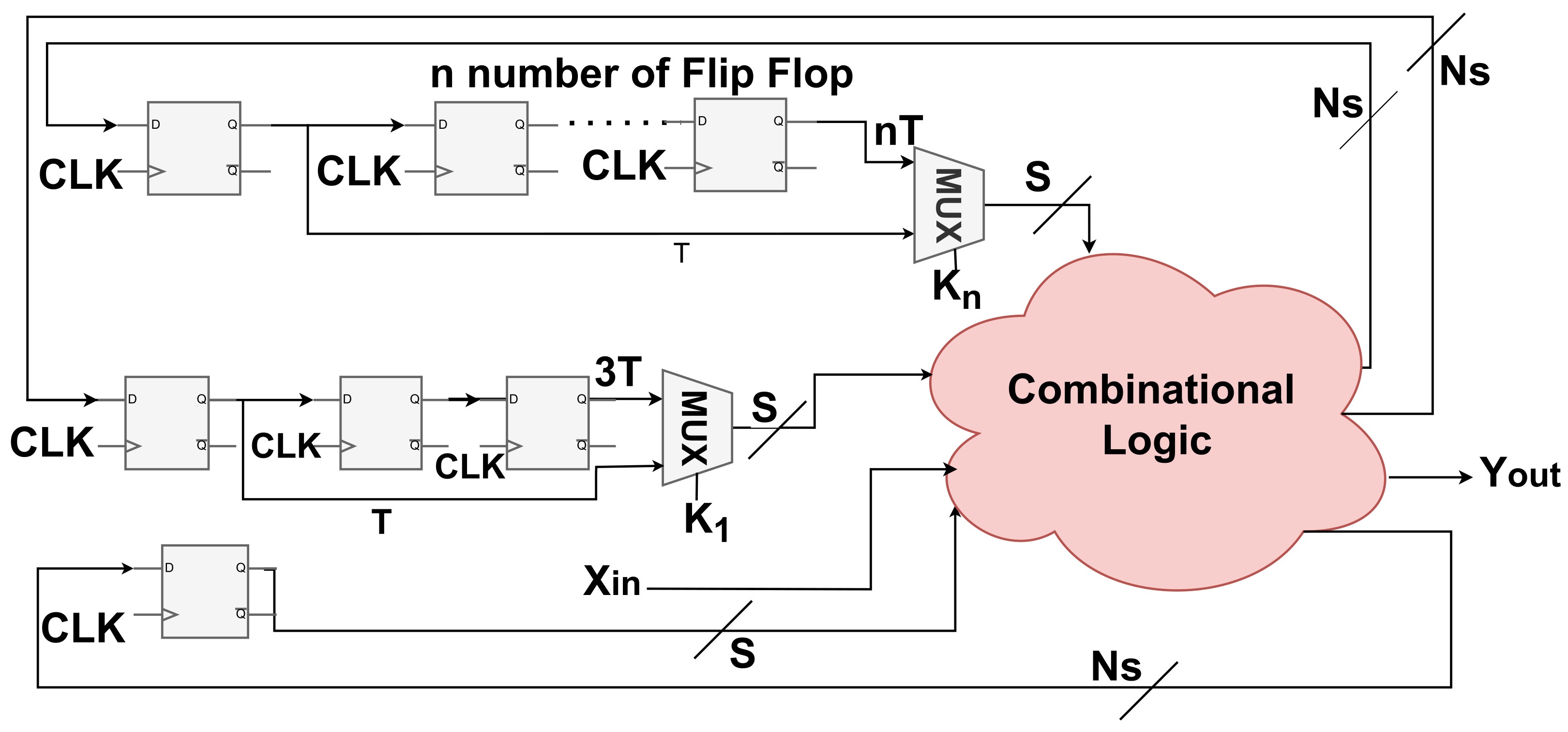
The first and simplest case here is when the attacker is faced with a set of DFFs, where for each DFF the clock signal is a choice among a subset of known multiples of a base period T. For instance, some DFFs will be connected to a clock signal , while for another DFF in the circuit the clock signal is picked using key-controlled MUXs among and . If is generated by a clock-divider from with a public division ratio of 2, then the attacker knows that the DFF can be running at either T or .
Formally speaking, the attacker is given , where will include DFFs, each driven by a clock running at a period given by a key-controlled choice of a subset of , where the are known integers. We begin describing the modeling process by imagining two DFFs running at two different known clock rates. If one DFF is running at a period of while the other DFF is running at a period of T, this simply means that the one running at a faster clock rate (T) will be getting updated twice as often. One can capture this behavior by simply inserting a second “virtual” DFF in the path of the slow DFF. i.e., Given a DFF , will get updated on each tick of which occurs every T seconds. By adding a second DFF we create . Now for the value at s to reach the output at it will take not one but two ticks of . Effectively, ends up getting updated with s at half the rate, i.e., as if it were driven by a clock with half the frequency (twice the period), i.e., .
It is possible to extend this to the case of clocks running at for . For a clock running with a period of , a many back-to-back flip-flops can be inserted to slow down the fast data moving at a period of T, to the data that moves with the a-times slower . These signals can then be used as functional equivalents of a DFF next-state signal that is running at a slower clock.
If the above model is passed to a model checker, it will get unrolled into a combinational circuit in which the state to next-state connections may effectively end up skipping some intermediate unrolled frames. This also means that instead of modifying the sequential circuit by adding slowdown DFFs, one can implement the same behavior as part of the unrolling subroutine of the model-checker. In our experiments however, we avoid this as modifying the internals of the BMC engine is somewhat more difficult than simply inserting slowdown flip-flops in .
With the above technique, we can generate a series of next-state signals each being updated at a fixed integer ratio of the base clock rate. If the clock rate for a particular DFF is known, we can then just select the next-state signal that corresponds to this. However, in the case of deobfuscation, this choice may be unknown for some DFFs. Per our usual arrangement in deobfuscation, we may model this uncertainty/ambiguity using introduced virtual key bits. We create a key-controlled MUX that will select one of the next-state signals that are running at different rates. i.e.,
. If passed to a sequential deobfuscation routine, the value of the virtual key
k learned from the attack represents a choice of which clock rate the particular DFF is running at.
Figure 8 shows this.
4.2. Clocks with Unknown Integer Multiples of a Base Period
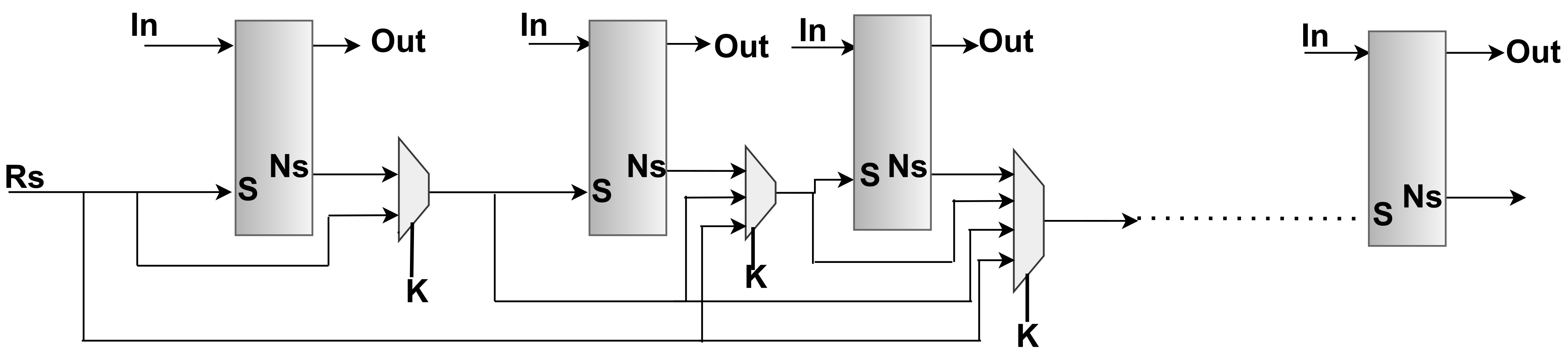
Now we come to the case where the clock choices are integer multiples of a base period , yet the can be unknown to the attacker.
Since the here are still integers and are all greater than 1 (slower versions of the base period T), we can use the slowdown DFFs discussed previously. While we know how many slowdown DFFs to insert for a known multiple of T, for an unknown multiple, we are uncertain about exactly how many to insert, i.e., by how much to slow down the next-state signals. This is a true uncertainty on the side of the attacker. An uncertainty that nonetheless cannot escape being modeled by added virtual key bits.
For a DFF that may be running at an unknown multiple period , we go ahead and slowdown the next-state signal of the DFF by inserting -many slow-down DFFs. Using key-controlled MUX gates we allow the circuit to pick any of the slowed down signals for . If we now set to an integer value that is higher than the maximum expected period multiplier in the attacker’s hypothesis, we will effectively end up modeling clocks that can be arbitrarily slower than the base clock within some reasonable range.
With the above approach, the overhead in the model of the multi-rate circuit grows linearly with . Hence if the attacker can truly expect some clocks in the circuit to be running at exponentially slower than the base period, this can create an exponential blow up in the size of the multi-rate model. This directly ties the slowdown in the multi-rate obfuscation to the resiliency against our proposed attack. This is somewhat analogous to the relationship between observability and query complexity. Slower clocks produce less observable circuits in time.
The attacker can bound the value of by studying the clock source. For instance, if the clock is driven by an n-bit digital clock-divider that can divide the base frequency by up to , then will have to be greater than . If an on-chip LC oscillator is used, the attacker may be able to use the LC variables limit in the given technology or the digital bits used to program them to get an idea of how slow of a signal they can produce.
Note that the unrolled version of the above model of the circuit will include possible updates of next-state in each frame. This can be seen in
Figure 9. Note that for constant dummy DFFs, the possible connection between the next-state in frame
u and the reset state
through the key-controlled MUX captures the possibility of some DFFs never changing from their reset state in
u rounds.
A combination of known and up-to-
clock obfuscation is possible and can be seen in
Figure 10. The single rate equivalent model is seen in
Figure 11.
4.3. Non-Integer Multiples of a Base Period
The clock period choices can be non-integer multiples of a base period, e.g.,
,
. be As we briefly mentioned in
Section 3.3, in this paper we do not directly attack this case. Instead, such cases have to be converted to an integer multiple period equivalent model. This can be done by trying to find the smallest period
, which can be used to describe all the non-integer periods in the circuit.
First, we consider the case where the non-integer periods are known. i.e., . We can first multiply both numbers by a decimal factor to turn them into integers , . We can then take the greatest-common-divisor of and which will be here. We then reverse our early transform by dividing by 10 obtaining . We now take , which allows us to express the other periods , and . This returns us to the known integer multiple case and allows for applying the previous deobfuscation routines.
If the non-integer multiples are unknown, similar to the case of integer multiples we pick an that represents the maximum multiple of the base period that could occur in the circuit and allow for a choice between all slowed down versions of using virtual key bits and MUX gates.
As for identifying
one can follow the same procedure as before. If the clock is generated by a digital clock divider, the maximum
is visible. If the clock is sourced via a fine-grained oscillator, per our discussion in
Section 3.3 the smallest step in the oscillator frequency range can still be taken as
and the attack can proceed.
4.4. Finding the Base Period
As discussed above, in all cases, in order to deobfuscate the circuit with our proposed approach one needs to express the potential clock period choices as multiples of a symbolic base period T.
The oracle-guided attacker, however, needs to have some idea of the concrete value of this symbolic base period too. This is required for trying to make sense of the sequential oracle output behavior. Recall that in the conventional sequential OG attack, the clock period is known to the attacker or the attacker is assumed to have direct control of the clock signal. Hence when querying the sequential oracle, the attacker will restart it, pass the first input pattern to the circuit, tick the clock or wait for period T, read the output, then repeat the process. Even if an output bit is not changing for several input patterns, the attacker knows that the unchanging output bits belong to different frames, simply from knowing/controlling the clock period.
For a clock-ambiguous circuit, however, this may not work. Here, the attacker, not knowing the base period of the clock, will not know precisely how to attribute the different outputs observed on the oracle to the unrolling of the different frames in the model-checking attack. Hence a first step in the attack must be to identify the base period T itself too.
If the locked circuit has an external master clock and there are no frequency boosters in the circuit, the attacker can assume that the fastest clock in the circuit is the external clock. If however, the fastest clock in the circuit is generated internally, the attacker may not directly observe this fast clock’s period T. Instead, the only manifestation of T will be that at rates of where a may be unknown, the output of the circuit may change. The attacker can hence try to measure the time it takes for an output to exhibit change while the inputs are kept the same to identify .
We can in fact devise a miter condition to capture this. This is shown in
Figure 12. The circuit condition
where
is the
t-round unrolled obfuscated circuit’s output at the
uth frame. This condition captures input patterns
x and key patterns
k for which a transition in the output may occur if the internal unknown clock keeps ticking. The attacker can then pass such an input to the oracle and wait for a change in the output and measure the time as an estimate of some multiple of
T. Note that since the key is unknown, this is not guaranteed to happen on the oracle. Thus, the attacker must repeat the process in theory for every possible
x that can satisfy
M. Also keep in mind that, during the attack, if the attacker observes any change at the outputs that occurs at a rate faster than
, the attacker can downgrade his measure of the lowest period
T and restart the attack.
5. Experiments
We present proof-of-concept implementations of the ideas discussed in the paper. We use the sequential ISCAS benchmarks seen in
Table 1. These benchmark circuits are single clock circuits.
For obfuscation, we do not implement the full-fledged multi-clock tape-out-ready circuits with oscillators. Instead, we model the multi-clock obfuscation by inserting slowdown DFFs plus MUX gates following our discussions in
Section 4 using Python scripts to evaluate security. For deobfuscation we pass these multi-rate equivalent model circuits to the open-source sequential deobfuscation tool
neos [
23].
neos is written in C++ and uses the Glucose SAT-solver along with an internal unrolling-based BMC solver for sequential doebfuscation.
We primarily report on deobfuscation runtime. Runtime is collected as the wall clock time for neos excluding the modeling part which is insignificant. Tests are run on a 128-thread dual-CPU EPYC AMD server with 256 GB. Each process is given 2 GB of memory and 30 min of time.
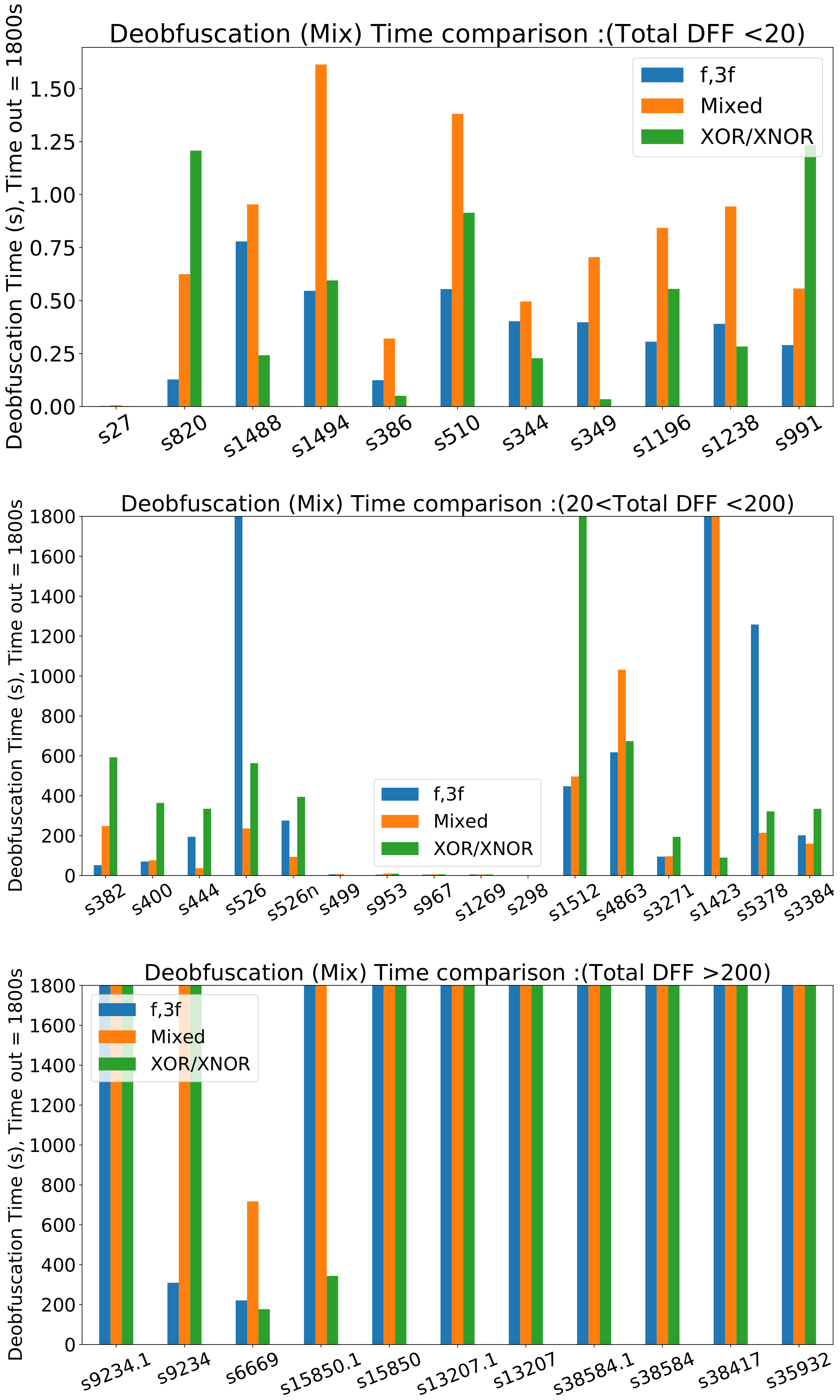
Table 1 and
Table 2 report deobfsucation time for circuits obfuscated with a choice of 2 different known clocks. i.e., a given percentage of the DFFs in the circuit are picked randomly and obfuscated with the 2-choice clock. The clock choices are known integer multiples of the base period (
and
). We observe from the data in
Table 1 and
Table 2 for 2-choice clocks that the majority of benchmarks with less than 240 DFFs can be deobfuscated in the 30-min time window. We also compare this to random XOR/XNOR insertion with a key size the same as the number of DFFs that are clock-obfuscated.
Figure 13 shows the runtime for clock-based obfuscation versus XOR/XNOR, versus a combination of both with twice the key size. As can be seen the runtime of clock-based locking can be in the same range as XOR/XNOR locking. We do not observe a clear winner in terms of SAT-attack time. In both schemes, the runtime tends to increase as the key width increases. In some instances, it can be observed that increasing the DFF clock obfuscation rate may not result in a higher runtime. This could be because in one instance the obfuscated DFFs happened to be inserted in a location that does not produce as much deobfuscation difficulty.
We can also create cases where there are more than 2 clock signals available in the circuit. We tested the benchmarks with 3 choice clock obfuscation.
Table 3 shows the runtime for 3-choice clock deobfuscation. We can present similar observations that we made for the 2-choice obfuscation method.
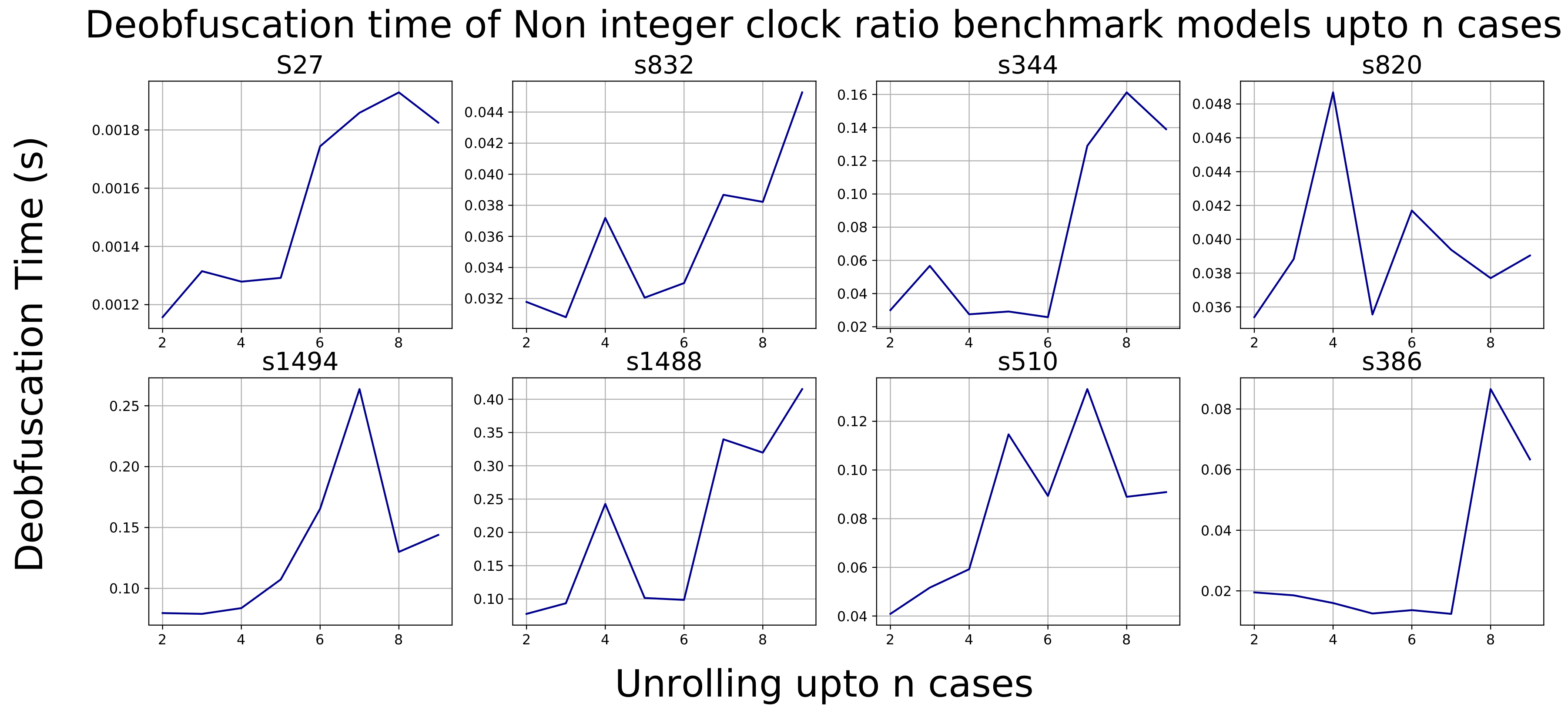
For deobfuscation given unknown multiples of the base period, we present the data in
Figure 14. Here we report the deobfuscation runtime for small circuits that can be attacked in minutes as a function of increasing
.
is the maximum number of rounds that the attacker has to unroll the circuit to capture the unknown multiple
clock behavior where
. As can be seen one can increase the runtime somewhat superlinearly as
increases. An
n-bit clock divider can create an
and lead to exponential blow-up of the deobfuscation circuit model. We verified this results against a simple counter circuit with
n bits.
We also performed a test of dummy flip-flop insertion on a few of the benchmark circuits. As predicted from our theoretical analysis, in these cases, as soon as the sequential output is dependent on the dummy state element, the attack will continue unrolling indefinitely and not terminate, as it suspects that the dummy element could awaken at some unknown clock cycle and input pattern in the future. In some cases, this dependency can fall apart and termination can be reached earlier. This is primarily a function of where the dummy state element happens to be inserted.