Multiverse of HawkNess: A Universally-Composable MPC-Based Hawk Variant
Abstract
:1. Introduction
1.1. A Private Smart Contract Execution
1.2. Our Contributions
How V-zkHawk Is Different from zkHawk
1.3. Existing Private Smart Contract Protocols
- zkay: zkay [21] extends on Ethereum smart contracts to allow users to share encrypted data on the blockchain. This is not an off-chain protocol but rather works on private data on-chain to prove that data are correctly encrypted and that the smart contract executions are correct.
- Arbitrum: Arbitrum [22] uses virtual machines (VMs) to implement smart contracts. Each party can create smart contract functionality by writing a code that the VMs then implement off-chain. Only verifiable digital signatures are needed to ensure that the parties have agreed on the VMs functionality. This ensures that the contract is executed off-chain. Similar to Hawk, Arbitrum also relies on a manager who is one of the parties to monitor the behavior of the VMs. It also relies on an honest majority setting for privacy guarantees.
- Kachina: Kachina [23] is a more recent PSC protocol that models its security in the UC framework. This provides a more private and secure PSC evaluation for Zcash privacy-preserving payment system, but it does not bode well with a dishonest majority in a malicious setting.
- Zether: Zether [24], being a retro-fitted privacy-preserving smart contract protocol for currency, can be utilized only in places such as sealed-bid auctions or crowdfunding. This protocol cannot be utilized in non-monetary smart contract applications such as e-Voting, Rock-Paper-Scissors, etc.
- Shielded Computations in Smart Contracts: Recent work by V. Botta et al. [25] leverages on-chain MPC protocols for executing smart contracts by forking blockchains such as Ethereum. It works for both honest and dishonest majority setting.
- ShadowEth: ShadowEth [26] utilizes the Trusted Execution Environment (TEE) to generate private smart contract evaluations for public blockchains such as Ethereum. It utilizes the Intel SGX [27] hardware enclave to implement the protocol that creates an isolated secure environment running parallel to the OS.
1.4. Outline of the Paper
2. Preliminaries
- ∀,∈ it satisfies the relation =
- ∀←, it satisfies the relation
2.1. Universal Composability
- The protocol πϕ, i.e,
- The protocol π
2.2. Smart Contract
- For all choices of and , one of the following statements is true
- 1.
- 2.
where .
3. Variant zkHawk (V-zkHawk)
3.1. Preprocessing Phase
3.2. Freeze Phase
3.3. Computation Phase
- :
- –
- –
- For all :
- *
- –
- –
- Return
3.4. Finalization Phase
3.5. Financial Penalties for Malicious Parties
4. Ideal Functionalities and UC Security Analysis
4.1. Threat Model
4.2. Security Proof
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations/Symbols
| This notation denotes that a is sampled according to the distribution B | |
| The set of elements | |
| C is a commitment for the value x and randomness r | |
| The distributions and are computationally indistinguishable | |
| Environment | |
| Real World Adversary | |
| Ideal World Simulator | |
| $ | Currency values |
| Party identifiers | |
| Session identifiers | |
| x is an ideal functionality | |
| or | x is a V-zkHawk function |
| P | Set of |
| Symmetric Key for Encryption | |
| EUF-CMA One time Key homomorphic signature scheme |
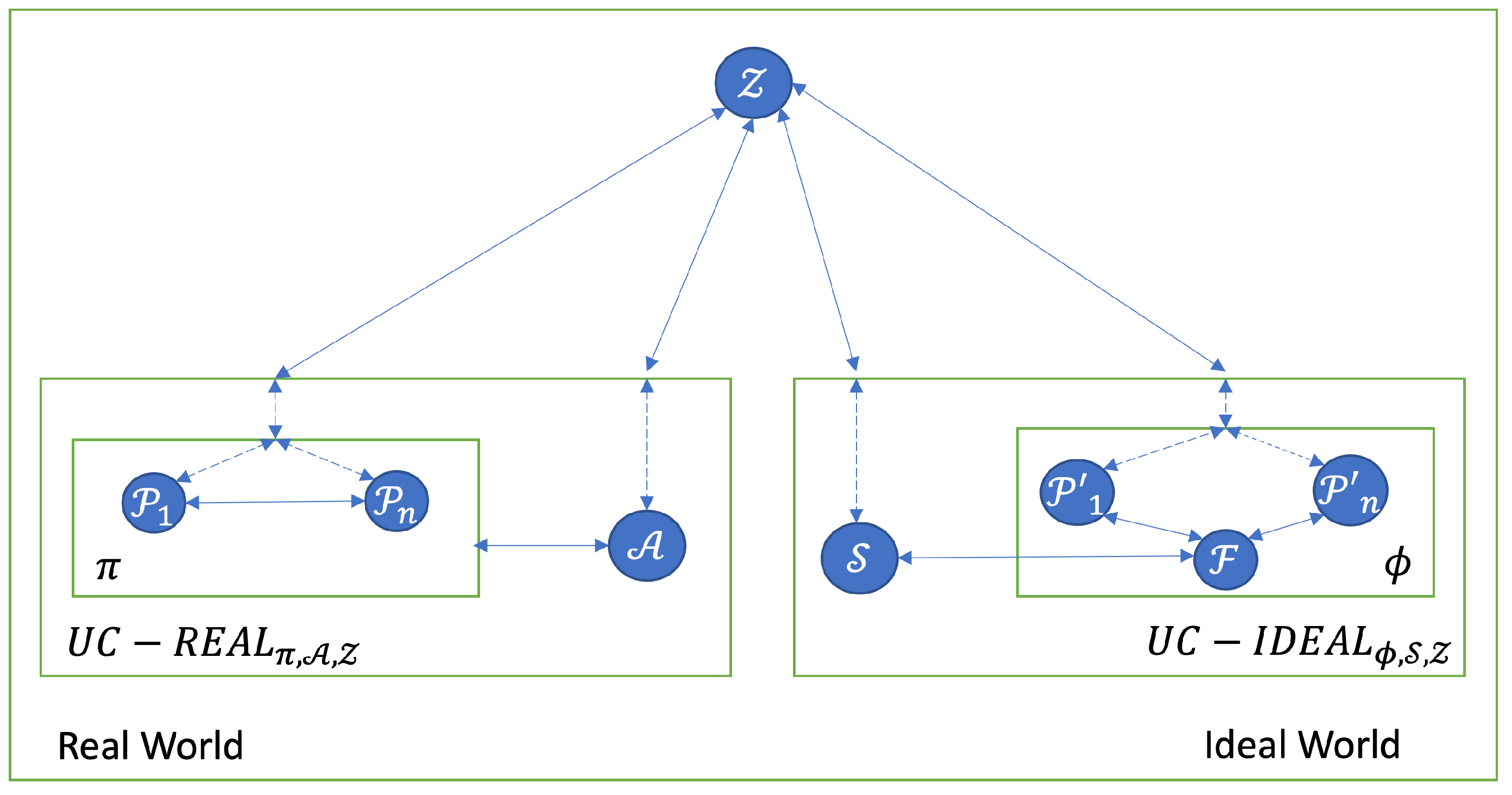
Appendix A. UC Framework
References
- Savelyev, A. Contract law 2.0:‘Smart’contracts as the beginning of the end of classic contract law. Inf. Commun. Technol. Law 2017, 26, 116–134. [Google Scholar] [CrossRef]
- Buterin, V. A Next Generation Smart Contract & Decentralized Application Platform (2013) Whitepaper. Ethereum Foundation. 2013. Available online: https://blockchainlab.com/pdf/Ethereum_white_paper-a_next_generation_smart_contract_and_decentralized_application_platform-vitalik-buterin.pdf (accessed on 23 June 2022).
- Sasson, E.B.; Chiesa, A.; Garman, C.; Green, M.; Miers, I.; Tromer, E.; Virza, M. Zerocash: Decentralized anonymous payments from bitcoin. In Proceedings of the 2014 IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 18–21 May 2014; pp. 459–474. [Google Scholar]
- Groth, J. On the size of pairing-based non-interactive arguments. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Vienna, Austria, 2016; pp. 305–326. [Google Scholar]
- Groth, J. Short pairing-based non-interactive zero-knowledge arguments. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Singapore, 2010; pp. 321–340. [Google Scholar]
- Banerjee, A.; Clear, M.; Tewari, H. Demystifying the Role of zk-SNARKs in Zcash. In Proceedings of the 2020 IEEE Conference on Application, Information and Network Security (AINS), Kota Kinabalu, Malaysia, 17–19 November 2020; pp. 12–19. [Google Scholar]
- Kosba, A.; Miller, A.; Shi, E.; Wen, Z.; Papamanthou, C. Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. In Proceedings of the 2016 IEEE symposium on security and privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 839–858. [Google Scholar]
- Banerjee, A.; Clear, M.; Tewari, H. zkHawk: Practical Private Smart Contracts from MPC-based Hawk. arXiv 2021, arXiv:2104.09180. [Google Scholar]
- Kursawe, K.; Danezis, G.; Kohlweiss, M. Privacy-friendly aggregation for the smart-grid. In Privacy Enhancing Technologies; Springer: New York, NY, USA, 2011; pp. 175–191. [Google Scholar]
- Keller, M. MP-SPDZ: A versatile framework for multi-party computation. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual, 9–13 November 2020; pp. 1575–1590. [Google Scholar]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar] [CrossRef]
- Micali, S.; Goldreich, O.; Wigderson, A. How to play any mental game. In Proceedings of the Nineteenth ACM Symposium on Theory of Computing, STOC, ACM, New York, NY, USA, 1 January 1987; pp. 218–229. [Google Scholar]
- Bogetoft, P.; Christensen, D.L.; Damgård, I.; Geisler, M.; Jakobsen, T.; Krøigaard, M.; Nielsen, J.D.; Nielsen, J.B.; Nielsen, K.; Pagter, J.; et al. Secure multiparty computation goes live. In International Conference on Financial Cryptography and Data Security; Springer: Accra Beach, Barbados, 2009; pp. 325–343. [Google Scholar]
- Damgård, I.; Keller, M.; Larraia, E.; Pastro, V.; Scholl, P.; Smart, N.P. Practical covertly secure MPC for dishonest majority–or: Breaking the SPDZ limits. In European Symposium on Research in Computer Security; Springer: Egham, UK, 2013; pp. 1–18. [Google Scholar]
- Archer, D.W.; Bogdanov, D.; Lindell, Y.; Kamm, L.; Nielsen, K.; Pagter, J.I.; Smart, N.P.; Wright, R.N. From keys to databases—Real-world applications of secure multi-party computation. Comput. J. 2018, 61, 1749–1771. [Google Scholar] [CrossRef] [Green Version]
- Boyle, E.; Gilboa, N.; Ishai, Y. Function secret sharing. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Sofia, Bulgaria, 2015; pp. 337–367. [Google Scholar]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Newport Beach, CA, USA, 8–11 October 2001; pp. 136–145. [Google Scholar]
- Canetti, R.; Fischlin, M. Universally composable commitments. In Annual International Cryptology Conference; Springer: Santa Barbara, CA, USA, 2001; pp. 19–40. [Google Scholar]
- Blum, M.; Feldman, P.; Micali, S. Non-interactive zero-knowledge and its applications. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali; ACM: New York, NY, USA, 2019; pp. 329–349. [Google Scholar]
- Banerjee, A. A Fully Anonymous e-Voting Protocol Employing Universal Zk-SNARKs and Smart Contracts. In International Congress on Blockchain and Applications; Springer: Salamanca, Spain, 2021; pp. 349–354. [Google Scholar]
- Steffen, S.; Bichsel, B.; Gersbach, M.; Melchior, N.; Tsankov, P.; Vechev, M. zkay: Specifying and enforcing data privacy in smart contracts. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 1759–1776. [Google Scholar]
- Kalodner, H.; Goldfeder, S.; Chen, X.; Weinberg, S.M.; Felten, E.W. Arbitrum: Scalable, private smart contracts. In Proceedings of the 27th {USENIX} Security Symposium ({USENIX} Security 18), Baltimore, MD, USA, 15–17 August 2018; pp. 1353–1370. [Google Scholar]
- Kerber, T.; Kiayias, A.; Kohlweiss, M. KACHINA–Foundations of Private Smart Contracts. In Proceedings of the 2021 IEEE 34th Computer Security Foundations Symposium (CSF), IEEE, Dubrovnik, Croatia, 21–24 June 2021; pp. 1–16. [Google Scholar]
- Bünz, B.; Agrawal, S.; Zamani, M.; Boneh, D. Zether: Towards privacy in a smart contract world. In International Conference on Financial Cryptography and Data Security; Springer: Kota Kinabalu, Malaysia, 10–14 February 2020; pp. 423–443. [Google Scholar]
- Botta, V.; Friolo, D.; Venturi, D.; Visconti, I. Shielded computations in smart contracts overcoming forks. In Proceedings of the International Conference on Financial Cryptography and Data Security, Virtual Event, 1–5 March 2021; pp. 73–92. [Google Scholar]
- Yuan, R.; Xia, Y.B.; Chen, H.B.; Zang, B.Y.; Xie, J. Shadoweth: Private smart contract on public blockchain. J. Comput. Sci. Technol. 2018, 33, 542–556. [Google Scholar] [CrossRef]
- Costan, V.; Devadas, S. Intel sgx explained. IACR Cryptol. ePrint Arch. 2016, 2016, 1–118. [Google Scholar]
- Canetti, R.; Dodis, Y.; Pass, R.; Walfish, S. Universally composable security with global setup. In Theory of Cryptography Conference; Springer: Amsterdam, The Netherlands, 2007; pp. 61–85. [Google Scholar]
- Badertscher, C.; Canetti, R.; Hesse, J.; Tackmann, B.; Zikas, V. Universal composition with global subroutines: Capturing global setup within plain UC. In Theory of Cryptography Conference; Springer: Durham, NC, USA, 2020; pp. 1–30. [Google Scholar]
- Feige, U.; Lapidot, D.; Shamir, A. Multiple noninteractive zero knowledge proofs under general assumptions. SIAM J. Comput. 1999, 29, 1–28. [Google Scholar] [CrossRef]
- Groth, J.; Ostrovsky, R.; Sahai, A. New techniques for noninteractive zero-knowledge. J. ACM (JACM) 2012, 59, 1–35. [Google Scholar] [CrossRef]
- Lu, S.; Ostrovsky, R.; Sahai, A.; Shacham, H.; Waters, B. Sequential aggregate signatures and multisignatures without random oracles. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: St. Petersburg, Russia, 2006; pp. 465–485. [Google Scholar]
- Maxwell, G.; Poelstra, A.; Seurin, Y.; Wuille, P. Simple Schnorr multi-signatures with applications to Bitcoin. Des. Codes Cryptogr. 2019, 87, 2139–2164. [Google Scholar] [CrossRef]
- Boneh, D.; Lynn, B.; Shacham, H. Short signatures from the Weil pairing. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Gold Coast, Australia, 2001; pp. 514–532. [Google Scholar]
- Boneh, D.; Gentry, C.; Lynn, B.; Shacham, H. Aggregate and verifiably encrypted signatures from bilinear maps. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Warsaw, Poland, 2003; pp. 416–432. [Google Scholar]
- Johnson, D.; Menezes, A.; Vanstone, S. The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Secur. 2001, 1, 36–63. [Google Scholar] [CrossRef]
- Derler, D.; Slamanig, D. Key-homomorphic signatures: Definitions and applications to multiparty signatures and non-interactive zero-knowledge. Des. Codes Cryptogr. 2019, 87, 1373–1413. [Google Scholar] [CrossRef]
- Canetti, R. Security and Composition of Cryptographic Protocols: A Tutorial. Cryptology ePrint Archive, Report 2006/465. 2006. Available online: https://ia.cr/2006/465 (accessed on 23 June 2022).
- Canetti, R.; Lindell, Y.; Ostrovsky, R.; Sahai, A. Universally composable two-party and multi-party secure computation. In Proceedings of the Thirty-Fourth Annual ACM Symposium on Theory of Computing, Montreal, QC, Canada, 19–21 May 2002; pp. 494–503. [Google Scholar]
- Li, Q.; Cascudo, I.; Christensen, M.G. Privacy-preserving distributed average consensus based on additive secret sharing. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Krawczyk, H. Secret sharing made short. In Annual International Cryptology Conference; Springer: Santa Barbara, CA, USA, 1993; pp. 136–146. [Google Scholar]
- Damgård, I.; Geisler, M.; Krøigaard, M.; Nielsen, J.B. Asynchronous multiparty computation: Theory and implementation. In International Workshop on Public Key Cryptography; Springer: Irvine, CA, USA, 2009; pp. 160–179. [Google Scholar]
- Goldwasser, S.; Lindell, Y. Secure multi-party computation without agreement. J. Cryptol. 2005, 18, 247–287. [Google Scholar] [CrossRef]
- Pedersen, T.P. Non-interactive and information-theoretic secure verifiable secret sharing. In Annual International Cryptology Conference; Springer: Santa Barbara, CA, USA, 1991; pp. 129–140. [Google Scholar]
- Canetti, R. Universally composable signature, certification, and authentication. In Proceedings of the 17th IEEE Computer Security Foundations Workshop, Pacific Grove, CA, USA, 30 June 2004; pp. 219–233. [Google Scholar]
- Boneh, D.; Drijvers, M.; Neven, G. Compact multi-signatures for smaller blockchains. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Brisbane, QLD, Australia, 2018; pp. 435–464. [Google Scholar]
- Laud, P.; Kamm, L. Applications of Secure Multiparty Computation; IOS Press: Amsterdam, The Netherlands, 2015; Volume 13. [Google Scholar]
- Damgård, I.; Ravi, D.; Siniscalchi, L.; Yakoubov, S. Minimizing Setup in Broadcast-Optimal Two Round MPC. Cryptology ePrint Archive, Report 2022/293. 2022. Available online: https://ia.cr/2022/293 (accessed on 23 June 2022).
- Cohen, R.; Garay, J.; Zikas, V. Broadcast-optimal two-round MPC. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Zagreb, Croatia, 2020; pp. 828–858. [Google Scholar]
- Ciampi, M.; Ostrovsky, R.; Waldner, H.; Zikas, V. Round-Optimal and Communication-Efficient Multiparty Computation. Cryptology ePrint Archive, Report 2020/1437. 2020. Available online: https://ia.cr/2020/1437 (accessed on 23 June 2022).
- Garg, S.; Polychroniadou, A. Two-round adaptively secure MPC from indistinguishability obfuscation. In Theory of Cryptography Conference; Springer: Warsaw, Poland, 2015; pp. 614–637. [Google Scholar]
















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banerjee, A.; Tewari, H. Multiverse of HawkNess: A Universally-Composable MPC-Based Hawk Variant. Cryptography 2022, 6, 39. https://doi.org/10.3390/cryptography6030039
Banerjee A, Tewari H. Multiverse of HawkNess: A Universally-Composable MPC-Based Hawk Variant. Cryptography. 2022; 6(3):39. https://doi.org/10.3390/cryptography6030039
Chicago/Turabian StyleBanerjee, Aritra, and Hitesh Tewari. 2022. "Multiverse of HawkNess: A Universally-Composable MPC-Based Hawk Variant" Cryptography 6, no. 3: 39. https://doi.org/10.3390/cryptography6030039
APA StyleBanerjee, A., & Tewari, H. (2022). Multiverse of HawkNess: A Universally-Composable MPC-Based Hawk Variant. Cryptography, 6(3), 39. https://doi.org/10.3390/cryptography6030039





