Side-Channel Attacks on Masked Bitsliced Implementations of AES
Abstract
:1. Introduction
2. Background
2.1. Side-Channel Attacks
2.1.1. Correlation Power Analysis (CPA)
- Traces acquisition: Power consumption traces are acquired for a large set of input plaintexts, encrypted with the same key, generating a set of output ciphertext. Suppose we have n traces available , corresponding to plaintext and ciphertexts . All of these are associated with the input key k. Each trace is a vector composed of a number of samples m. We will later refer to sample j of trace i as .
- Intermediate value selection and computation: Sensitive variables v depend on both the key and the plaintext/ciphertext. The selection is dependent on the encryption algorithm as well. In the current analysis, two scenarios were used: the output of the first key addition (ARK) and the output of the first S-BOX.
- Attack leakage model selection and running: In this paper, we focus on correlation power analysis (CPA) attacks, which rely on generating a hypothetical power consumption. A typical leakage model is based on the Hamming weight, defined as follows:where [20] (i.e., the total number of bits set to 1 of the value x).A second model relies on the Hamming distance between two variables, defined as:We are interested in the correlation between the actual power consumption (recorded in the trace) and the hypothetical power values, which are computed considering all sample points of interest (where the intermediate values should occur). The correlation is computed using Pearson’s correlation coefficient:Essentially, considering that the variable leaks between samples and () and considering a hypothetical consumption h of the variable, then, for each sample j (), we compute the correlation between h and the vector comprised of each trace sample j: , where = (, …, ). However, h does depend on the key.In particular, if we define the subkey () as a byte of the entire key (k), then we would compute the correlations for each , where .
- Identify the correct subkey: the correct key byte () value should correspond to the highest correlation value.
2.1.2. Template Attack
- Traces acquisition on training device: The attacker acquires large datasets of power traces using different plaintext inputs and keys to build a sound model of the power consumption for the target computations [21]. Typical target computations are those operations that combine known input, such as plaintext bytes, with the unknown target key bytes of cryptographic algorithms. A canonical example is the output of the S-BOX in AES, where the power consumption depends on one plaintext byte and one key byte.
- Template generation: The datasets are used to derive a statistical model of the device, eventually applying a compression (or sample selection) [19]. This typically results in a set of mean vectors (one per candidate key byte value) and covariance matrices, known as the template parameters.
- Traces acquisition on victim device: The attacker acquires a relatively small number of power traces on the target device, using different input plaintexts. For the attack to be effective, the training and victim devices should be of the same kind. In a practical attack scenario, the attacker will perform the profiling step in one device (where he can run extensive data acquisition and experimentation), and the attack step on the victim device. However, for evaluation purposes, it is also possible to use the same device in order to attest to the leakage of a particular implementation or to compare different methods of attack or protection.
- Attack setup: The model is applied to the attack traces. The output consists of a list of scores or probabilities for each possible candidate value in the subkey space.
- Identify the correct subkey: The correct subkey value is considered as the one corresponding to the highest probability in the list of scores (or probabilities).
2.2. Masking
Attacks on Masking
- Absolute difference:
- Product combining:
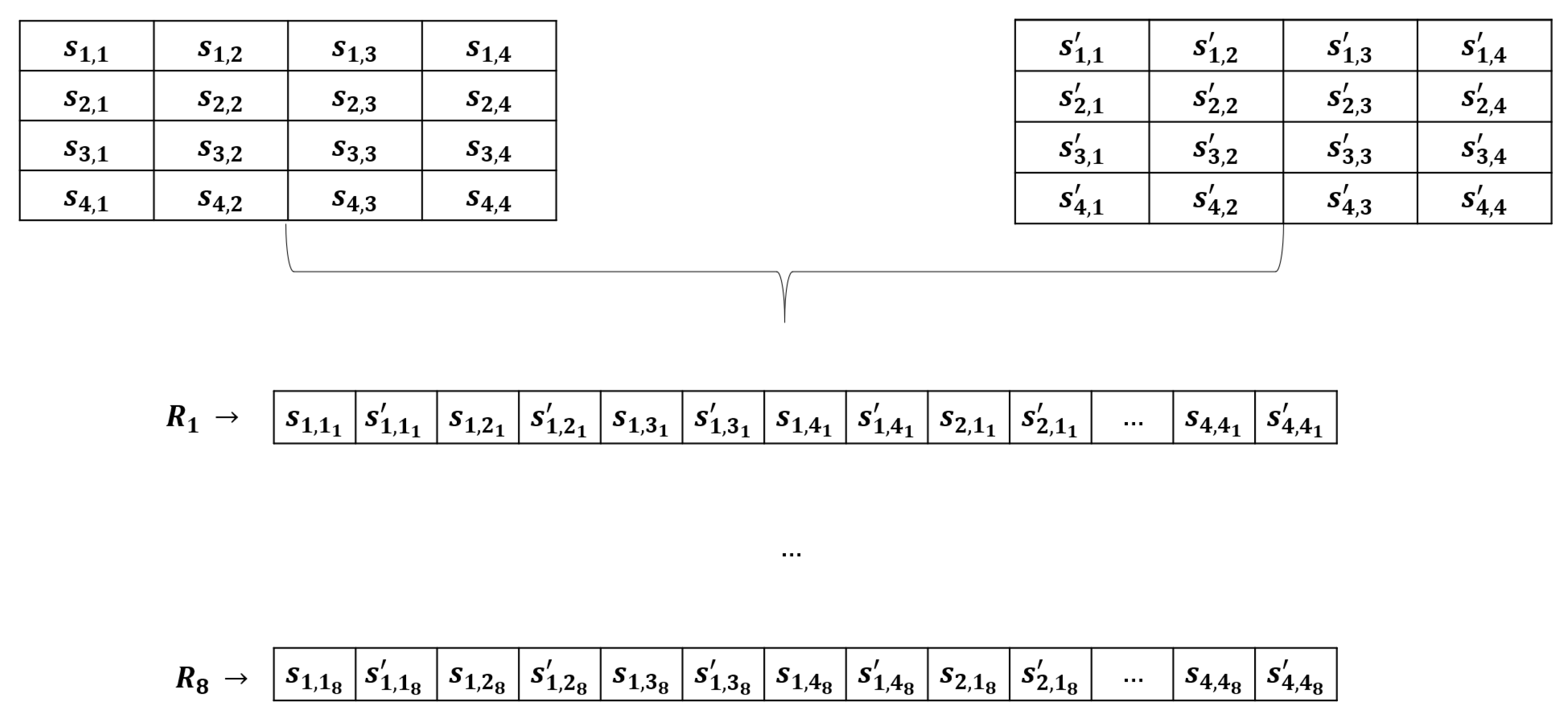
2.3. Bitsliced AES
- AddRoundKey: The key is also converted into the bitsliced representation, considering Equation (9). At this point, in the standard implementation, the state is XORed with the round key where is the current round index. Considering a bitsliced representation, the XOR can be done bit-level-wise, between the corresponding bits.
- ByteSub: This is the only non-linear step of the algorithm. Whereas in the standard implementations, each byte of the state is replaced with the corresponding value mapped by a LUT (S-BOX table), in the bitsliced variant, logic gate operations (XOR, XNOR, AND) are used to implement the S-BOX. As pointed out in both [4,9], several solutions have been proposed for implementing the S-BOX, considering aspects such as performance, throughput, and the architecture targeted. Both articles pinpoint the compact S-BOX implementation described by Canright [30], which is also the one considered in the current study, employing multi-level arithmetic representation.
- ShiftRows: In a standard implementation, each row of the byte array is shifted to the left with a displacement equal to the row index—1.The same convention is valid in the bitsliced approach, by adjusting accordingly the bits in every register.
- MixColumns: This step is applied at the column level and can be seen as a matrix multiplication in . The logic gate described in [4] was implemented in the current setup.
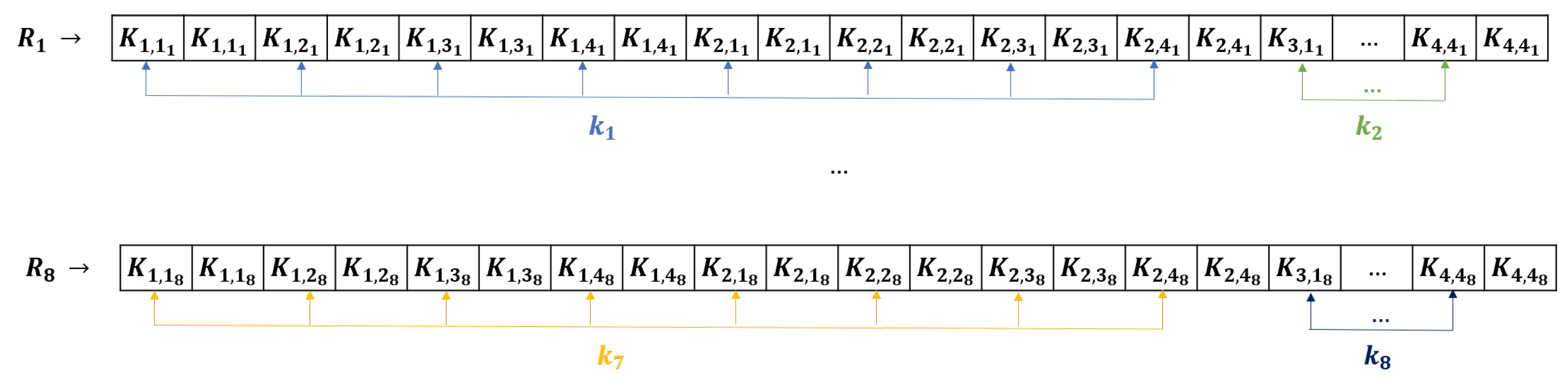
Masked Bitsliced AES
3. Attacks
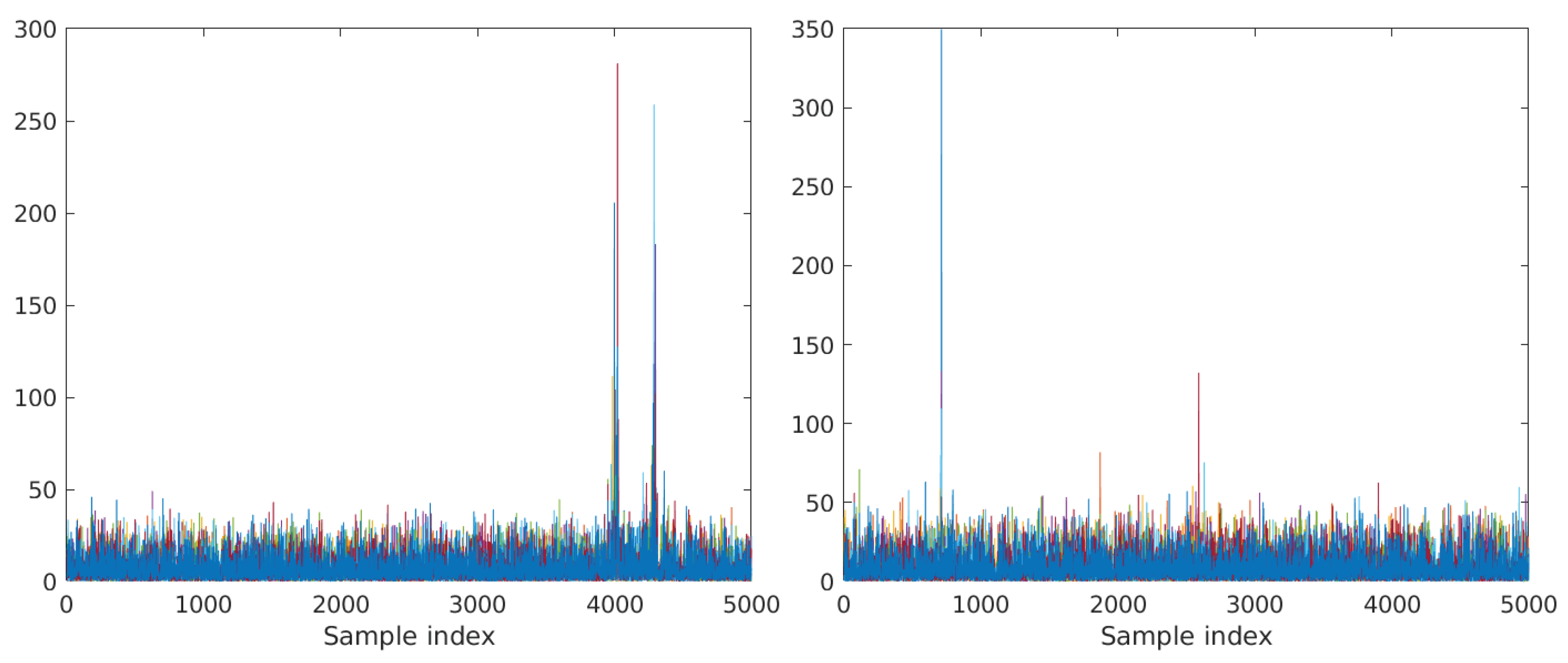
3.1. Reference CPA Attacks on Bitsliced AES
| Algorithm 1 CPA attack on first S-BOX. |
 |
3.2. Alternative CPA Attack
| Algorithm 2 CPA attack on First ARK. |
 |
3.3. Template Attacks on Bitsliced AES
| Byte 1: bit 1 of the first 8 bytes of the first plaintext (first bitsliced reg). |
| Byte 2: bit 1 of the last 8 bytes of the first plaintext (first bitsliced reg). |
| Byte 3: bit 2 of the first 8 bytes of the first plaintext (second bitsliced reg). |
| ... |
| Byte 16: bit 8 of the last 8 bytes of the first plaintext (last bitsliced reg). |
3.4. Prior Work
4. Experimental Setup
4.1. Unprotected Bitsliced Implementation
4.2. Masked Bitsliced Implementation
4.3. Evaluator Attack Scenario
5. Results
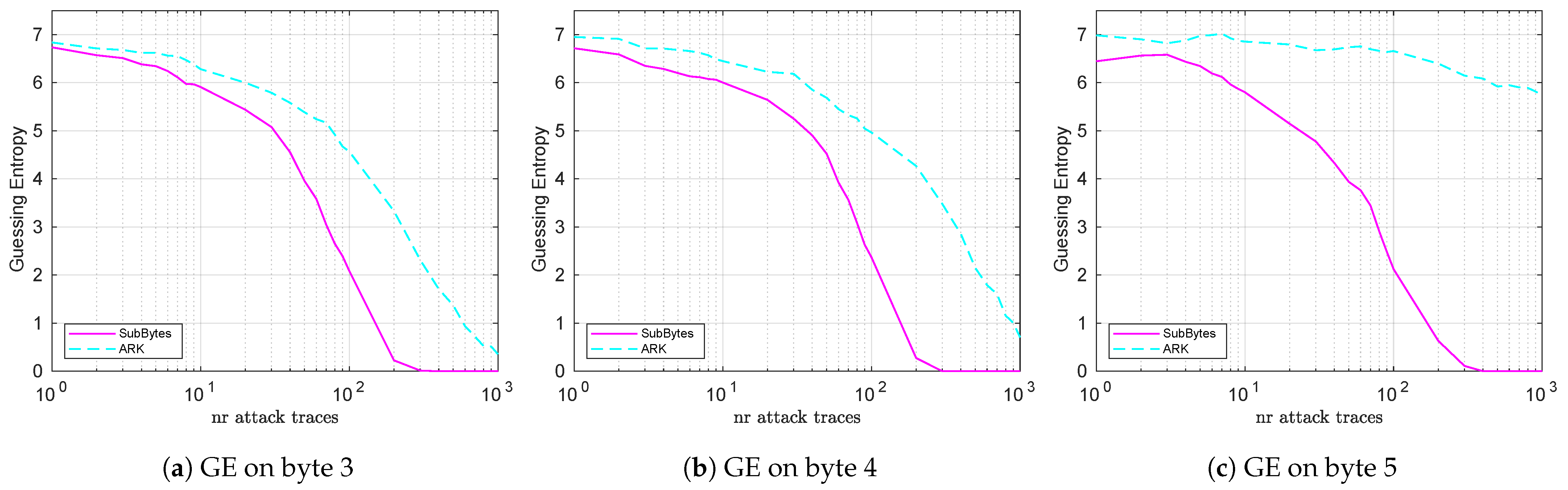
5.1. Attacks on Unprotected Bitsliced Implementations of AES
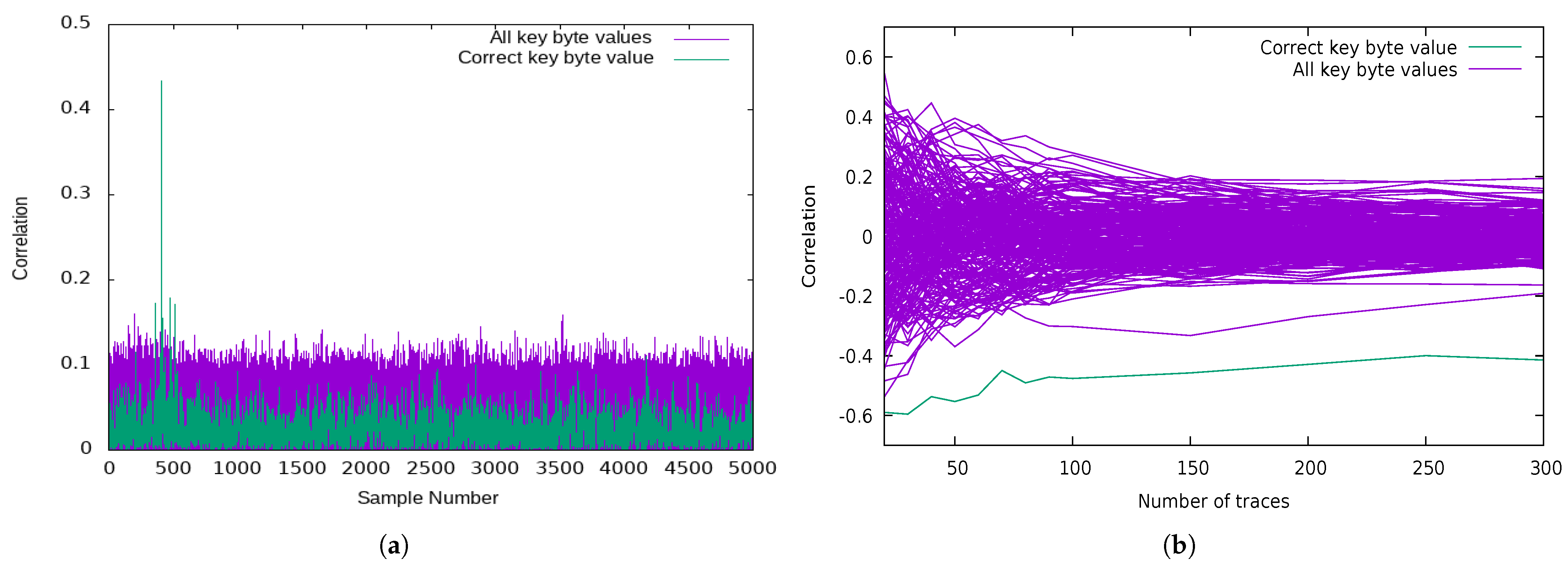
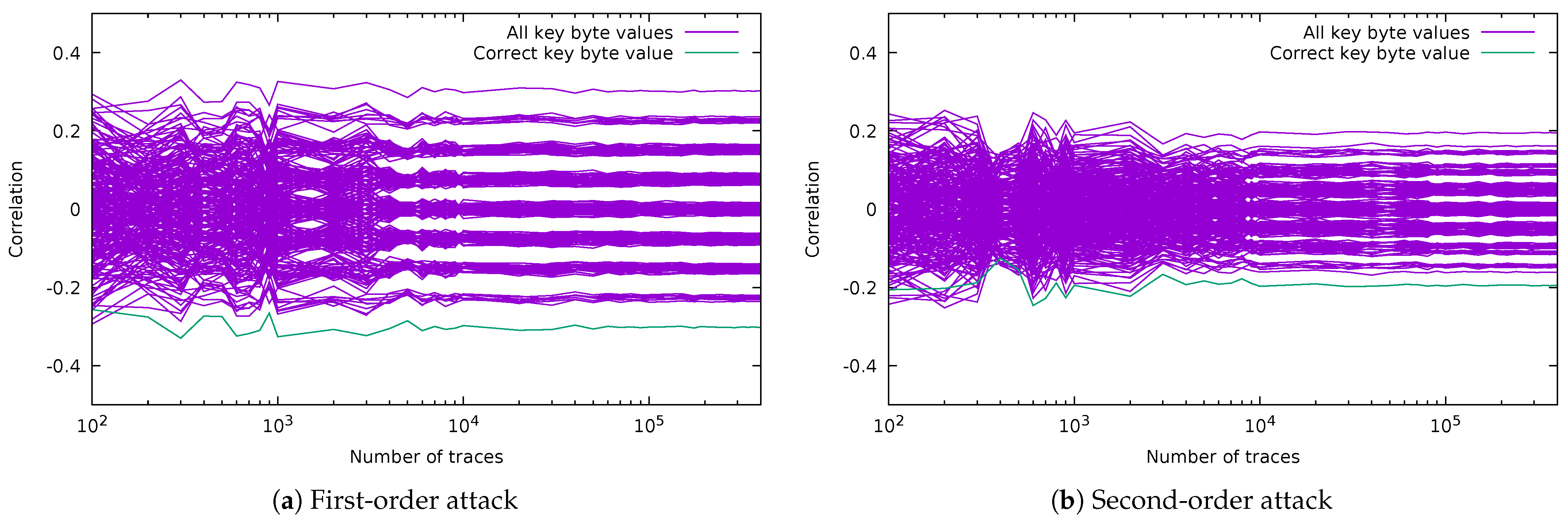
5.1.1. Classic CPA on SubBytes (Targeting 2 Key Bits)
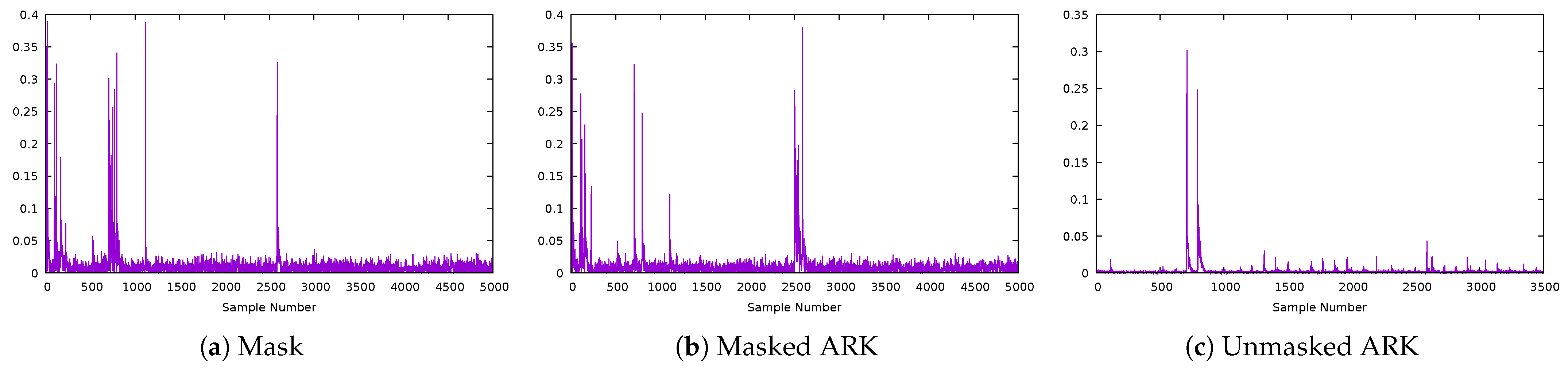
5.1.2. CPA Attacks on ARK (Targeting 8 Key Bits)
5.1.3. Template Attacks
5.2. Attacks on Masked Bitsliced Implementations of AES
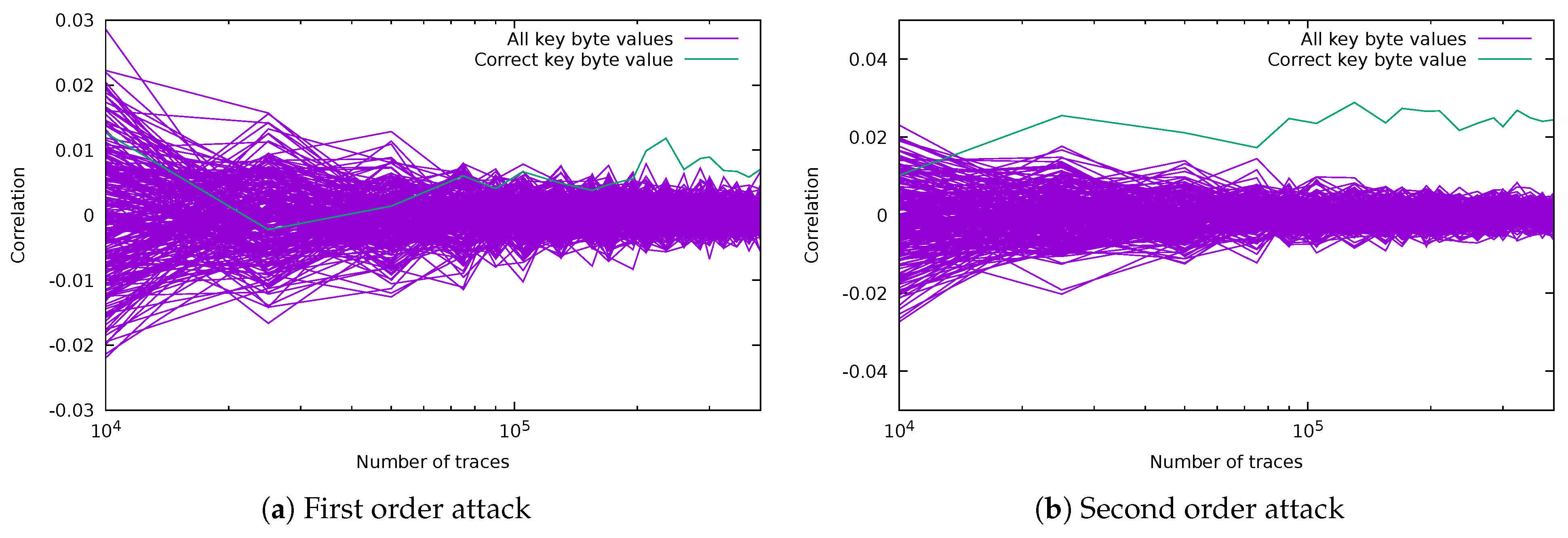
5.2.1. CPA Attack on Masked SubBytes (Targeting 2 Key Bits)
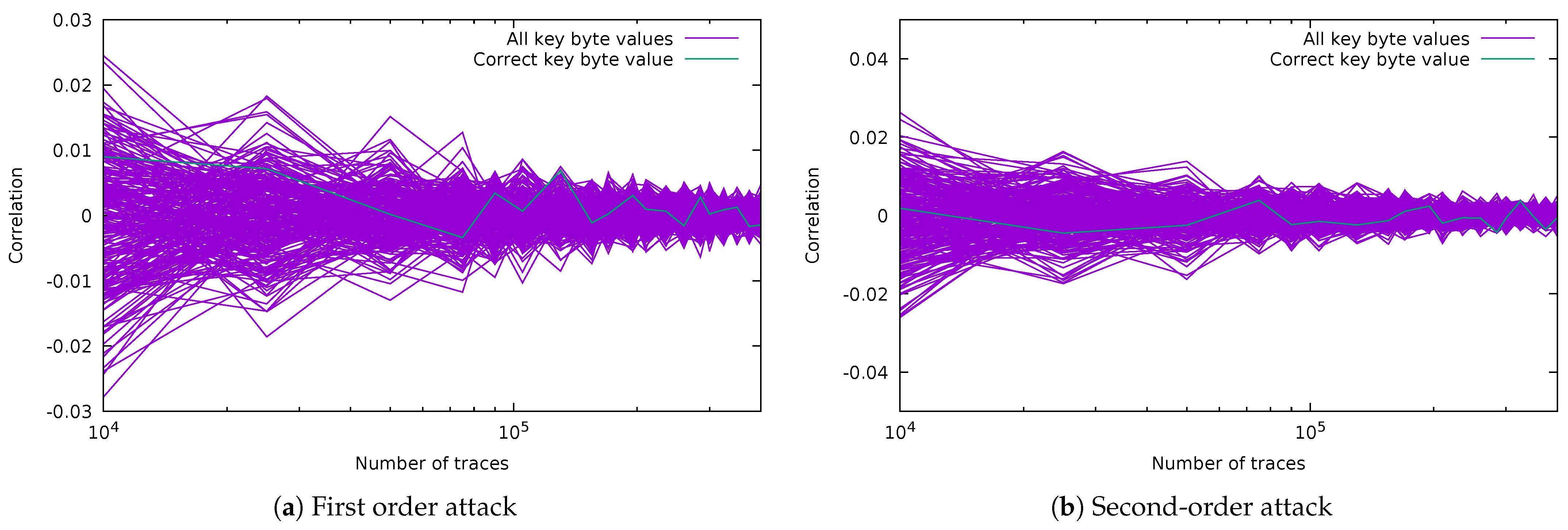
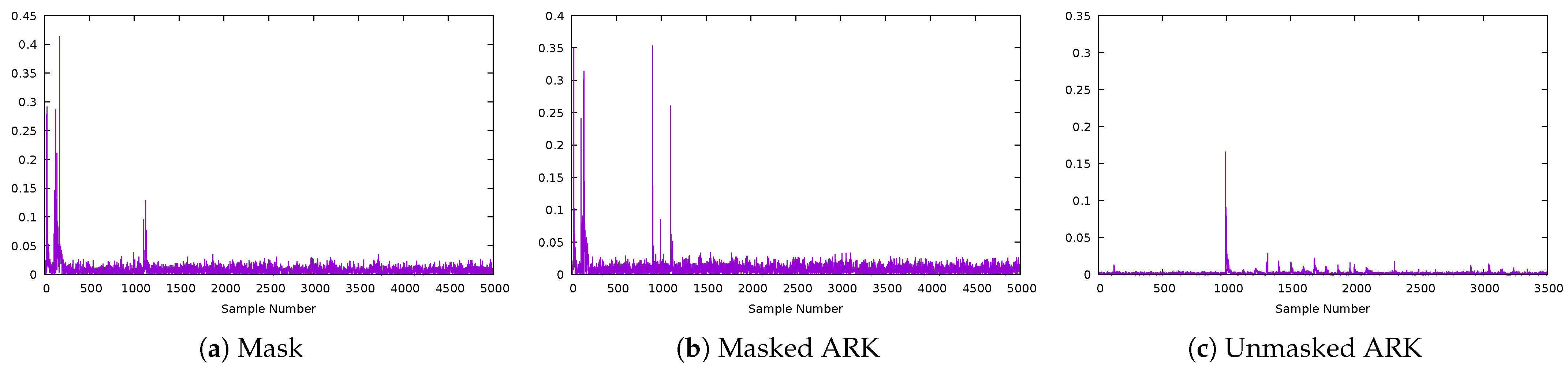
5.2.2. CPA Attacks on Masked ARK (Targeting 8 Key Bits)
5.2.3. Template Attacks
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rijmen, V.; Joan, D. Advanced Encryption Standard. Federal Information Processing Standards Publication 197. 2001; pp. 1–47. Available online: https://nvlpubs.nist.gov/nistpubs/fips/nist.fips.197.pdf (accessed on 3 March 2022).
- Rebeiro, C.; Selvakumar, D.; Devi, A. Bitslice Implementation of AES. In Proceedings of the International Conference on Cryptology and Network Security, Suzhou, China, 8–10 December 2006; pp. 203–212. [Google Scholar]
- Hajihassani, O.; Khalaj Monfared, S.; Khasteh, S.H.; Gorgin, S. Fast AES Implementation: A High-Throughput Bitsliced Approach. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2211–2222. [Google Scholar] [CrossRef]
- Könighofer, R. A Fast and Cache-Timing Resistant Implementation of the AES. In Proceedings of the Cryptographers’ Track at the RSA Conference (CT-RSA 2008), San Francisco, CA, USA, 8–11 April 2008; pp. 187–202. [Google Scholar]
- Mangard, S.; Oswald, E.; Popp, T. Power Analysis Attacks: Revealing the Secrets of Smart Cards; Springer: New York, NY, USA, 2007. [Google Scholar]
- Agrawal, D.; Archambeault, B.; Rao, J.R.; Rohatgi, P. The EM Side—Channel(s). In Cryptographic Hardware and Embedded Systems—CHES 2002; Lecture Notes in Computer Science; Kaliski, B.S., Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2523, pp. 29–45. [Google Scholar]
- Chari, S.; Jutla, C.; Rao, J.; Rohatgi, P. Towards Sound Approaches to Counteract Power-Analysis Attacks. In Advances in Cryptology—CRYPTO’ 99. CRYPTO 1999. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1666, pp. 398–412. [Google Scholar]
- Grosso, V.; Leurent, G.; Standaert, F.X.; Varıcı, K. LS-Designs: Bitslice Encryption for Efficient Masked Software Implementations. In Fast Software Encryption. FSE 2014; Lecture Notes in Computer Science; Cid, C., Rechberger, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 8540, pp. 18–37. [Google Scholar]
- Balasch, J.; Gierlichs, B.; Reparaz, O.; Verbauwhede, I. DPA, bitslicing and masking at 1 GHZ. In Cryptographic Hardware and Embedded Systems—CHES 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9293, pp. 599–619. [Google Scholar]
- Goudarzi, D.; Rivain, M. How Fast Can Higher-Order Masking Be in Software? In Advances in Cryptology—EUROCRYPT 2017; Lecture Notes in Computer Science; Coron, J.S., Nielsen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10210, pp. 567–597. [Google Scholar]
- Longo, J.; De Mulder, E.; Page, D.; Tunstall, M. SoC It to EM: ElectroMagnetic Side-Channel Attacks on a Complex System-on-Chip. In Cryptographic Hardware and Embedded Systems—CHES 2015; Lecture Notes in Computer Science; Güneysu, T., Handschuh, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9293, pp. 620–640. [Google Scholar]
- de Groot, W.; Papagiannopoulos, K.; de La Piedra, A.; Schneider, E.; Batina, L. Bitsliced Masking and ARM: Friends or Foes? In Lightweight Cryptography for Security and Privacy. LightSec 2016; Lecture Notes in Computer Science; Bogdanov, A., Ed.; Springer: Cham, Switzerland, 2017; Volume 10098, pp. 91–109. [Google Scholar]
- Journault, A.; Standaert, F.X. Very High Order Masking: Efficient Implementation and Security Evaluation. In Cryptographic Hardware and Embedded Systems—CHES 2017; Lecture Notes in Computer Science; Fischer, W., Homma, N., Eds.; Springer: Cham, Switzerland, 2017; Volume 10529, pp. 623–643. [Google Scholar]
- Azouaoui, M.; Bronchain, O.; Grosso, V.; Papagiannopoulos, K.; Standaert, F.X. Bitslice Masking and Improved Shuffling: How and When to Mix Them in Software? 2021. Available online: hal.archives-ouvertes.fr (accessed on 22 February 2022).
- Han, J.; Kim, Y.J.; Kim, S.J.; Sim, B.Y.; Han, D.G. Improved Correlation Power Analysis on Bitslice Block Ciphers. IEEE Access 2022, 10, 39387–39396. [Google Scholar] [CrossRef]
- Brier, E.; Clavier, C.; Olivier, F. Correlation Power Analysis with a Leakage Model. In Proceedings of the Cryptographic Hardware and Embedded Systems, Cambridge, MA, USA, 11–13 August 2004; Volume 3156, pp. 16–29. [Google Scholar]
- Chari, S.; Rao, J.R.; Rohatgi, P. Template Attacks. In Cryptographic Hardware and Embedded Systems—CHES 2002; Lecture Notes in Computer Science; Kaliski, B.S., Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2523, pp. 13–28. [Google Scholar]
- Gierlichs, B.; Batina, L.; Tuyls, P.; Preneel, B. Mutual information analysis. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Washington, DC, USA, 10–13 August 2008; pp. 426–442. [Google Scholar]
- Choudary, M.; Kuhn, M. Efficient, Portable Template Attacks. IEEE Trans. Inf. Forensics Secur. 2017, 13, 490–501. [Google Scholar] [CrossRef] [Green Version]
- Prouff, E.; Rivain, M.; Bevan, R. Statistical Analysis of Second Order Differential Power Analysis. IACR Cryptol. ePrint Arch. 2010, 646, 799–811. [Google Scholar] [CrossRef]
- Durvaux, F.; Standaert, F.X.; Veyrat-Charvillon, N. How to Certify the Leakage of a Chip? In Advances in Cryptology—EUROCRYPT 2014; Lecture Notes in Computer Science; Nguyen, P.Q., Oswald, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8441, pp. 459–476. [Google Scholar]
- Goubin, L.; Patarin, J. DES and Differential Power Analysis The “Duplication” Method. In Cryptographic Hardware and Embedded Systems. CHES 1999; Lecture Notes in Computer Science; Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1717, pp. 158–172. [Google Scholar]
- Schramm, K.; Paar, C. Higher Order Masking of the AES. In Topics in Cryptology—CT-RSA 2006; Lecture Notes in Computer Science; Pointcheval, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3860, pp. 208–225. [Google Scholar]
- Coron, J.S.; Prouff, E.; Rivain, M.; Roche, T. Higher-order side channel security and mask refreshing. In Proceedings of the International Workshop on Fast Software Encryption, Singapore, 11–13 March 2013; Volume 8424, pp. 410–424. [Google Scholar]
- Coron, J.S. Higher Order Masking of Look-Up Tables. In Advances in Cryptology—EUROCRYPT 2014; Lecture Notes in Computer Science; Nguyen, P.Q., Oswald, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8441, pp. 441–458. [Google Scholar]
- Rivain, M.; Prouff, E. Provably Secure Higher-Order Masking of AES. In Cryptographic Hardware and Embedded Systems, CHES 2010; Lecture Notes in Computer Science; Mangard, S., Standaert, F.X., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6225, pp. 413–427. [Google Scholar]
- Reparaz, O.; Bilgin, B.; Nikova, S.; Gierlichs, B.; Verbauwhede, I. Consolidating Masking Schemes. In Advances in Cryptology—CRYPTO 2015; Lecture Notes in Computer Science; Gennaro, R., Robshaw, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9215, pp. 764–783. [Google Scholar]
- Messerges, T.S. Using Second-Order Power Analysis to Attack DPA Resistant Software. In Cryptographic Hardware and Embedded Systems—CHES 2000; Lecture Notes in Computer Science; Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1965, pp. 238–251. [Google Scholar]
- Standaert, F.X.; Veyrat-Charvillon, N.; Oswald, E.; Gierlichs, B.; Medwed, M.; Kasper, M.; Mangard, S. The World Is Not Enough: Another Look on Second-Order DPA. In Advances in Cryptology—ASIACRYPT 2010; Lecture Notes in Computer Science; Abe, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6477, pp. 112–129. [Google Scholar]
- Canright, D. A Very Compact Rijndael S-Box; Naval Postgraduate School, Department of Mathematics: Monterey CA, USA, 2004. [Google Scholar]
- Trichina, E. Combinational Logic Design for AES SubByte Transformation on Masked Data. IACR Cryptol. ePrint Arch. 2003, 236, 1–13. [Google Scholar]
- Schindler, W.; Lemke, K.; Paar, C. A Stochastic Model for Differential Side Channel Cryptanalysis. In Cryptographic Hardware and Embedded Systems—CHES 2005; Lecture Notes in Computer Science; Rao, J.R., Sunar, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3659, pp. 30–46. [Google Scholar]
- Choudary, M.O.; Kuhn, M.G. Efficient Stochastic Methods: Profiled Attacks Beyond 8 Bits. In Smart Card Research and Advanced Applications. CARDIS 2014; Lecture Notes in Computer Science; Joye, M., Moradi, A., Eds.; Springer: Cham, Switzerland, 2015; Volume 8968, pp. 85–103. [Google Scholar]
- Standaert, F.X.; Malkin, T.G.; Yung, M. A Unified Framework for the Analysis of Side-Channel Key Recovery Attacks. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2009; pp. 443–461. [Google Scholar]
- Glowacz, C.; Grosso, V.; Poussier, R.; Schüth, J.; Standaert, F.X. Simpler and More Efficient Rank Estimation for Side-Channel Security Assessment. In International Workshop on Fast Software Encryption. FSE 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9054, pp. 117–129. [Google Scholar]
- Mangard, S.; Pramstaller, N.; Oswald, E. Successfully Attacking Masked AES Hardware Implementations. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Edinburgh, UK, 29 August–1 September 2005; pp. 157–171. [Google Scholar]
- Oswald, E.; Mangard, S. Template Attacks on Masking—Resistance Is Futile. In Proceedings of the Cryptographers’ Track at the RSA Conference (CT-RSA 2007), San Francisco, CA, USA, 5–9 February 2007; pp. 243–256. [Google Scholar]
- Papagiannopoulos, K.; Veshchikov, N. Mind the Gap: Towards Secure 1st-Order Masking in Software. In Constructive Side-Channel Analysis and Secure Design. COSADE 2017; Lecture Notes in Computer Science; Guilley, S., Ed.; Springer: Cham, Switzerland, 2017; Volume 10348, pp. 282–297. [Google Scholar]
- O’Flynn, C.; Chen, Z.D. Chipwhisperer: An open-source platform for hardware embedded security research. In Proceedings of the International Workshop on Constructive Side-Channel Analysis and Secure Design, Paris, France, 13–15 April 2014; pp. 243–260. [Google Scholar]
- ChipWhispererLite 32-Bit API. Available online: https://chipwhisperer.readthedocs.io/en/latest/api.html (accessed on 10 January 2021).












| CPA S-BOX/1-2 Bits | CPA ARK/8 Bits | TA Simple | TA Preprocessing | T-Test or MI | |
|---|---|---|---|---|---|
| Mangard et al. [36] | ✓ | ✕ | - | - | - |
| Oswald et al. [37] | - | - | ✕ | ✓ | - |
| Balasch et al. [9] | ✓ | - | - | - | - |
| Groot et al. [12] | ✓ | - | - | - | - |
| Han et al. [15] | ✓ | - | - | - | - |
| Journault et al. [13] | - | - | - | - | ✓ |
| Azouaoui et al. [14] | - | - | - | - | ✓ |
| Current paper | ✓ | ✓ | ✓ | - | - |
| Implementation | Clock Cycles |
|---|---|
| Unmasked implementation | 360,934.3 |
| Masked implementation | 479,084.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rădulescu, A.; Choudary, M.O. Side-Channel Attacks on Masked Bitsliced Implementations of AES. Cryptography 2022, 6, 31. https://doi.org/10.3390/cryptography6030031
Rădulescu A, Choudary MO. Side-Channel Attacks on Masked Bitsliced Implementations of AES. Cryptography. 2022; 6(3):31. https://doi.org/10.3390/cryptography6030031
Chicago/Turabian StyleRădulescu, Anca, and Marios O. Choudary. 2022. "Side-Channel Attacks on Masked Bitsliced Implementations of AES" Cryptography 6, no. 3: 31. https://doi.org/10.3390/cryptography6030031
APA StyleRădulescu, A., & Choudary, M. O. (2022). Side-Channel Attacks on Masked Bitsliced Implementations of AES. Cryptography, 6(3), 31. https://doi.org/10.3390/cryptography6030031





