Computational Analysis of Interleaving PN-Sequences with Different Polynomials
Abstract
:1. Introduction
2. Preliminaries
2.1. Shrinking Generator

2.2. Shifted Versions of the Same PN-Sequence
3. Interleaving PN-Sequences with Different Characteristic Polynomials
4. Comparison with Other Sequence Generators
- 1
- Shrinking generatorGiven two primitive polynomials of degree and , the linear complexity of the shrunken sequence satisfies: and . In this case, the sequence is obtained interleaving shifted versions of the same PN-sequence.If we interleave PN-sequences generated by different primitive polynomials of degree , the linear complexity of the resultant sequence is , which is much higher than that of the SG. Notice that the period and the number of ones remain the same.In the following example, we compare the shrunken sequence and the corresponding t-interleaved with similar parameters. We see that the of the t-interleaved sequence is greater.Example 7.Consider the SG composed of two registers of length and . In this case, the shrunken sequence is made up by interleaving four shifted versions of the same PN-sequence generated by a primitive polynomial of degree 5. The period of the shrunken sequences in this case is and .If we consider again Example 4, we interleave four PN-sequences produced by primitive polynomials of degree 5. The resultant sequence has period 124 (the same as that of the SG with polynomials of degree 3 and 5) and , which is four times higher than that of the SG.
- 2
- t-interleaved sequences with the same polynomialIn [12], the authors analyze the t-interleaved sequences obtained interleaving shifted versions of the same PN-sequence produced by a primitive polynomial of degree L. They determine the period and the linear complexity of the t-interleaved sequences for some particular cases of t. They also study an upper bound for the and the period of t-interleaved PN-sequences. In [21], the authors study different cases of interleaving sequences, analyzing the and the characteristic polynomials of the resultant sequences. The next theorem is a consequence of Theorem 2 in [21] and the results obtained in [12].In the following example, we compare a t-interleaved sequence obtained using one primitive polynomial of degree L with a corresponding t-interleaved sequence, with similar parameters, obtained using t different primitive polynomials of degree L, . We see that the of the t-interleaved sequence with different polynomials is greater.Example 8.Consider any -interleaved sequence obtained with a primitive polynomial of degree 5 and shifted versions of the corresponding PN-sequence. In this case, the period of the sequences is and .Consider the primitive polynomials of degree 5 given in Example 4 and interleave different PN-sequences produced by these polynomials. The resultant sequences have period 124 and . If we compare both types of -interleaved sequence, we have that using different polynomials for the construction provides higher values for the , in this case, four times larger.
5. Statistical Analysis of T-Interleaved Sequences
- Unpredictability: Having k consecutive elements of should not give any information about the next element of the sequence.
- Uniformity: Given any subsequence of , there should be nearly equal number of 1’s and 0’s.
- Independence: Each element of is independent from other elements.
- Golomb’s Randomness Postulates
- (R1)
- In a period of , the number of ones should differ from the number of zeros by at most 1. In other words, the sequence should be balanced.
- (R2)
- In a period of , at least of the all runs of zeroes or ones should have length one, at least should have length 2, at least should have length 3, and so on. Moreover, for each one of these lengths, there should be (almost) equally many gaps and blocks.
- (R3)
- The autocorrelation function should be two valued. That is, for some integer k and for all
5.1. Simple Visual Analysis
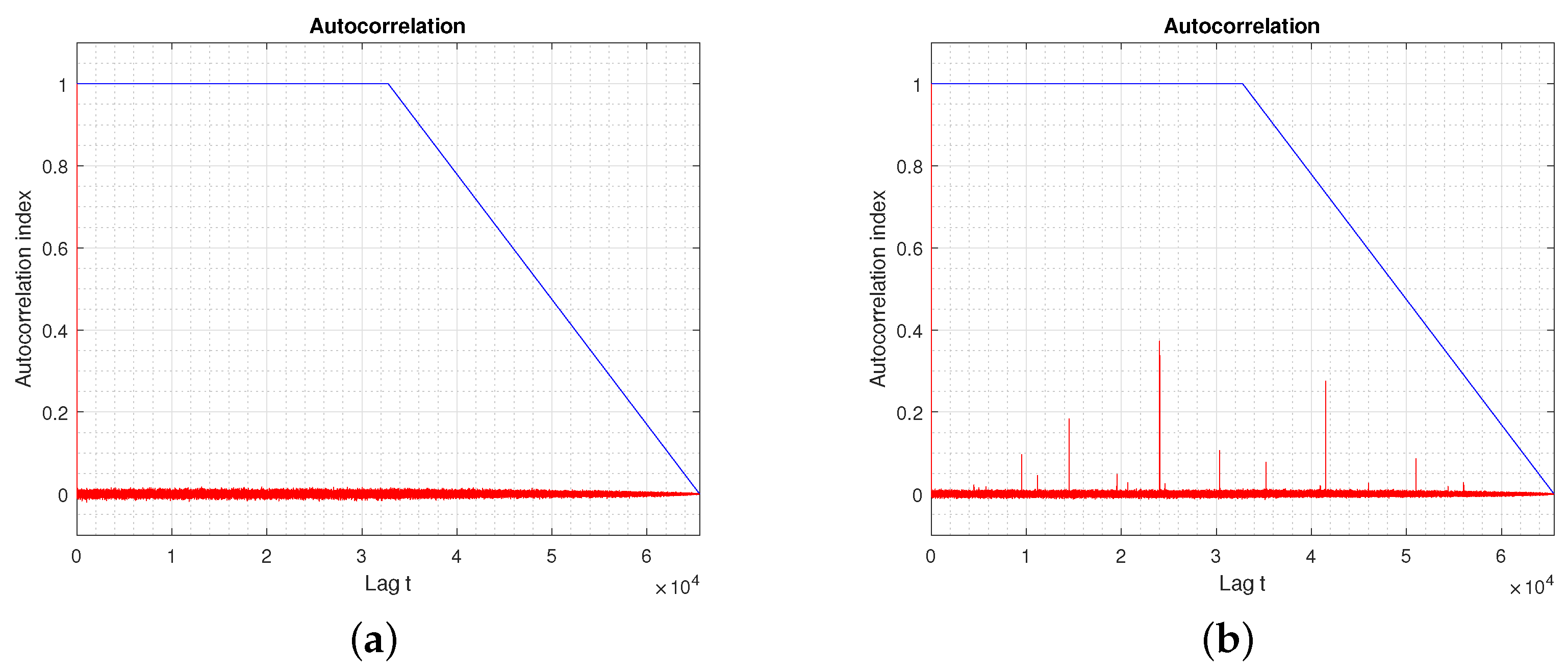
- Autocorrelation
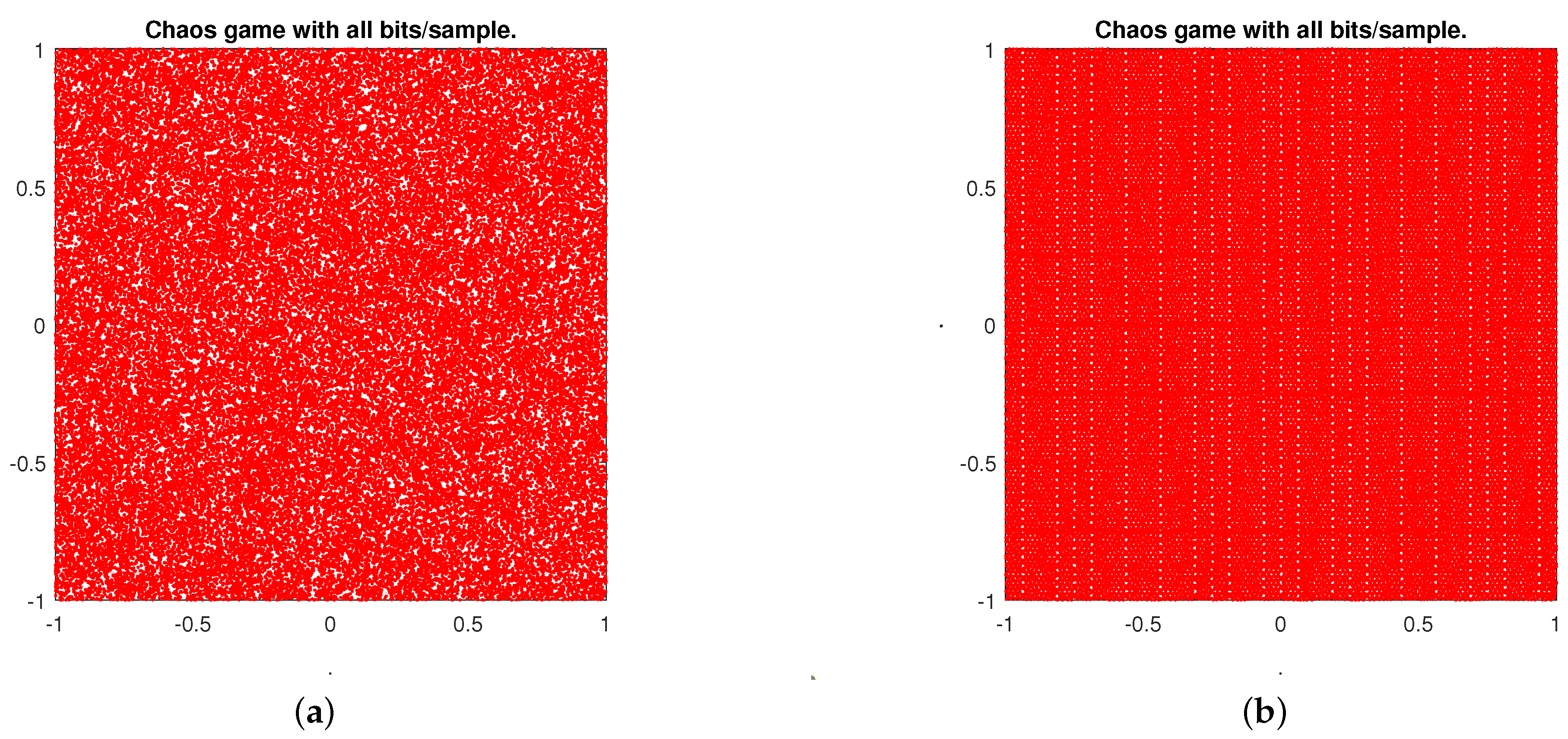
- Chaos Game
- Lyapunov exponent
| Lyapunov Hamming exponent, ideal | = | 4 |
| Lyapunov Hamming exponent, real | = | |
| Absolute desviation from ideal | = | 2.2889 × 10 |
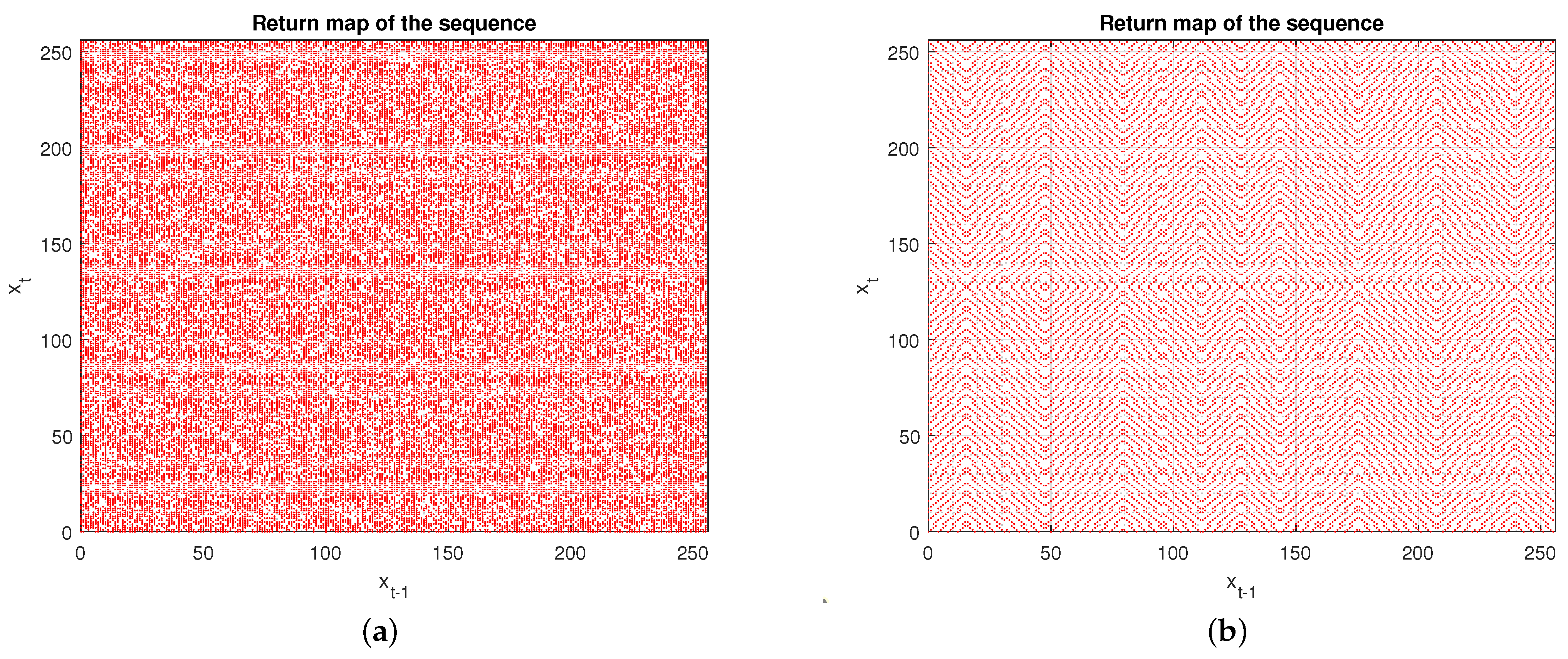
- Return map
5.2. Battery of Statistical Tests
- NISTThe Statistical Test Suite developed by NIST [30] is an excellent and exhaustive document looking at various aspects of randomness in a long sequence of bits. The NIST has documented 15 statistical tests, where FIPS 140-2 package, Maurer’s Universal Test [31] and Lempel–Ziv Compression Test are among them.The Frequency Test, Maurer’s Universal Test and Lempel-Ziv Compression have the standard normal as reference distribution. The rest of the tests have the chi-square as reference distribution. The chi-square and the normal variation is converted into a p-value. If the computed p-value is <0.01, then we conclude that the sequence is non-random. Otherwise, we conclude that the sequence is random.
- FIPS 140-2FIPS 140-2 is an U.S. government computer security standard used to approve cryptographic modules issued by the National Institute of Standards and Technology (NIST). It consists of four statistical random number generator tests: the Monobit Test, The Poker Test, The Runs Test and The Long Runs Test. Moreover, we add the Frequency Test within a block, which can be categorized as a frequency test. If a sequence passes all five tests, there is no guarantee that it was indeed produced by a random bit generator. However, if one of the algorithms fails any of these tests, then the other tests are not even applied, and we can not consider our sequence sufficiently random; and, therefore, our generator is not secure in cryptographic terms.Each test needs a binary sequence of bits. All our sequences have the required length for this analysis.
- FREQUENCY (MONOBIT) TEST: The focus of the test is the proportion of zeros and ones along the whole sequence. The purpose of this test is to determine whether the number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence. The test assesses the closeness of the fraction of ones to ; that is, the number of ones and zeros in a sequence should be about the same. All subsequent tests depend on the approval of this test.
- POKER (SERIAL) TEST: Let m be an integer number such that and let . The sequence is divided into k non-overlapping parts each one of length m, and let be the number of occurrences of the i-th type of sequence of length m, for . The Poker Test determines if each stream of length m appears approximately the same number of times in , as would be expected for a random sequence. Note that for , the Poker Test is equivalent to the Frequency Test.
- RUNS TEST: The incidences of runs (for both consecutive zeros and consecutive ones) of all lengths (≥1) in the sample stream should be counted and stored. The purpose of the Runs Test is to determine if the number of runs of different lengths in the sequence is as expected for a random sequence. In particular, this test determines whether the oscillation between zeros and ones is too fast or too slow.
- LONG RUNS TEST: A long run is defined to be a run of length 26 or more (of either zeros or ones). The focus of this test is the longest run of ones within M-bit blocks. Its purpose is to determine whether the length of the longest run of ones within the sequence is consistent with the length of the longest run of ones that would be expected in a random sequence. Note that one irregularity in the expected length of the longest run of ones implies that there is also an irregularity in the expected length of the longest run of zeros. Therefore, only a test for ones is necessary.
- FREQUENCY TEST WITHIN A BLOCK: The focus of this test is the proportion of ones within M-bit blocks. The purpose is to determine whether the frequency of ones in an M-bit block is approximately , as would be expected under an assumption of randomness. For the block size , this test degenerates to the Frequency (Monobit) test.
Frequency Test is defined to check the first postulate of Golomb. The second postulate of Golomb, about the number of runs in sequences, is analyzed in the Runs Tests. Finally, the third postulate gives information about similarities between the sequence and shifted versions of it. If is a random sequence, the autocorrelation should be constant. - Maurer’s Universal TestThe focus of this test is the number of bits between matching patterns (a measure that is related to the length of a compressed sequence). The purpose of the test is to detect whether or not the sequence can be significantly compressed without loss of information. A significantly compressible sequence is considered to be non-random.
- Lempel–Ziv Compression TestThe focus of this test is the number of cumulatively distinct patterns (words) in the sequence. The purpose is to determine how far the tested sequence can be compressed; it is considered to be non-random if it can be significantly compressed. A random sequence will have a characteristic number of distinct patterns.This test works by reading a sequence of symbols, grouping the symbols into strings, and converting the strings into codes. We get compression because the codes take up less space than the strings they replace. No data are lost when compressing.In Table 3, we present a small sample of the results obtained in the NIST tests here presented. All these values are the average of the results obtained for any sample of t-interleaved sequences studied.
- DiehardDiehard battery of tests [32] is a reliable standard for evaluating the randomness of sequences of pseudo-random number generators. This tool is a powerful instrument for the practical evaluation process of cryptographic primitives. It cannot guarantee if your generator can be considered perfectly random, but if it does not pass the test suite, then it is not suitable for cryptographic applications.Diehard battery [32] consists of 15 different independent statistical tests, some of them repeated but with different parameters:
- BIRTHDAY SPACINGS TEST: Choose random points on a large interval. The spacings between the points should be asymptotically exponentially distributed.
- OPERM5 TEST: Analyze sequences of five consecutive random numbers. The 120 possible orderings should occur with statistically equal probability.
- BINARY RANK TEST FOR MATRICES: The leftmost 31 bits of 31 random integers from the test sequence are used to form a binary matrix over the field . The rank is determined. That rank can be from 0 to 31, but ranks less than 28 are rare, and their counts are pooled with those for rank 28. Ranks are found for 40,000 of such random matrices, and a chi-square test is performed on counts for ranks and ≤28.
- BINARY RANK TEST FOR MATRICES: The rank of a random matrix is identified. Ranks less than 29 are rare. Chi-square tests are performed on the ranks and less than or equal to 29. This is repeated 40,000 times.
- BINARY RANK TEST FOR MATRICES: The rank of a random matrix is identified. Ranks less than 4 are rare. Chi-square tests are performed on the ranks and less than or equal to 4. This is repeated 100,000 times.
- BITSTREAM TEST: Consider each bit as a single letter . In a rolling group of 20 bits, count the number of 20-bit permutations out of 20-bit groups. As there are possible 20-bit permutations, count how many are missing, which should be normally distributed. This test is repeated 20 times.
- OPSO, OQSO and DNA TESTS:
- (a)
- OPSO TEST: This is the overlapping-pairs-sparse-occupancy test. Each set of 5 bits is considered a ’letter’; thus, there are 1024 letters in the ’alphabet’. Two-letter words are taken from each 32-bit integer and are counted. As there are possible two-letter words, the missing words are identified and should be normally distributed.
- (b)
- OQSO TEST: A variant that uses four-letter words.
- (c)
- DNA TEST: A variant where there are only four letters in the alphabet, and each letter is two bits.
- COUNT-THE-1s TEST: A specific byte from each integer is chosen to represent a letter. There are five possible letters, each chosen by counting the number of 1’s in the byte: . The five probabilities are therefore and 37 over 256, respectively. Five integer sequences are selected on a rolling basis, and counts are made on word frequencies. A covariance matrix is formed.
- PARKING LOT TEST: Randomly place unit circles in a square. A circle is successfully parked if it does not overlap an existing successfully parked one. After 12,000 tries, the number of successfully parked circles should follow a certain normal distribution.
- MINIMUM DISTANCE TEST: In a square of size 10,000 × 10,000, randomly select 8000 points. Find the minimum distance between the pairs. The square of this distance should be exponentially distributed with a mean close to . This is repeated for 100 random selections of 8000 points.
- RANDOM SPHERES TEST: Randomly choose 4000 points in a cube of edge 1000. Center a sphere on each point, whose radius is the minimum distance to another point. The smallest sphere’s volume should be exponentially distributed with a certain mean.
- SQUEEZE TEST: Multiply by random floats on until you reach 1. Repeat this 100,000 times. The number of floats needed to reach 1 should follow a chi-square distribution.
- OVERLAPPING SUMS TEST: Generate a long sequence of random floats on . Add sequences of 100 consecutive floats. The sums should be normally distributed with characteristic mean and variance.
- RUNS TEST: Generate a long sequence of random floats on a distribution. Ascending and descending runs should follow a certain covariance matrix. This is repeated 10 times for sequences of length 10,000.
- CRAPS TEST: Play 200,000 games of craps, counting the wins and the number of throws per game. Each count should follow a chi-square distribution.
Note that The Count-The-1s and the OPSO tests are both sometimes known as the Monkey Test. These statistical tests are designed to test the null hypothesis , which states that the input sequence is randomly generated. If the hypothesis is not rejected in all the tests, then it is implied that the input sequences are random. Most of the tests in DIEHARD return a p-value or the KS p-value (given by the Kolmogorov–Smirnov test), which should be uniform on if the input file contains truly independent random bits. It is considered that a bit stream really fails when it obtains p-values of 0 or 1 to six or more places.Testing Diehard battery of tests for a hundred eight-interleaved sequences with different polynomials of degree 24, we say that Diehard does not show any weakness. >From the results of Table 4 of a particular sequence, we can check that all the values are in the appropriate range.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| PRNG | Pseudo-Random Number Generator |
| LFSR | Linear Feedback Shift Register |
| LC | Linear Complexity |
| PN-sequence | Pseudo Noise-sequence |
| SG | Shrinking Generator |
| MAC | Message Authentication Code |
References
- Gallegos-Segovia, P.; Bravo-Torres, J.; Argudo-Parra, J. Internet of things as an attack vector to critical infrastructures of cities. In Proceedings of the 2017 International Caribbean Conference on Devices, Circuits and Systems (ICCDCS), Cozumel, Mexico, 5–7 June 2017; pp. 117–120. [Google Scholar]
- Biryukov, A.; Perrin, L. State of the Art in Lightweight Symmetric Cryptography. Cryptology ePrint Archive, Report 2017/511. 2017. Available online: https://ia.cr/2017/511 (accessed on 3 April 2022).
- Chin, W.; Li, W.; Chen, H. Energy big data security threats in IoT-based smart grid communications. IEEE Commun. Mag. 2017, 55, 70–75. [Google Scholar] [CrossRef]
- Mavromoustakis, C.; Mastorakis, G.; Batalla, J. Internet of Things (IoT) in 5G Mobile Technologies; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- National Institute of Standards and Technology (NIST). NIST Lightweight Cryptography Project. Technology Administration. 2022. Available online: https://csrc.nist.gov/Projects/Lightweight-Cryptography (accessed on 3 April 2022).
- Zia, U.; McCartney, M.; Scotney, B.; Martinez, J.; Sajjad, A. A novel pseudo-random number generator for IoT based on a coupled map lattice system using the generalised symmetric map. SN Appl. Sci. 2022, 4, 48. [Google Scholar] [CrossRef]
- Kietzmann, P.; Schmidt, T.C.; Wählisch, M. A Guideline on Pseudorandom Number Generation (PRNG) in the IoT. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Golomb, S.W. Shift Register-Sequences; Aegean Park Press: Laguna Hill, CA, USA, 1982. [Google Scholar]
- Coppersmith, D.; Krawczyk, H.; Mansour, Y. The shrinking generator. In Advances in Cryptology—CRYPTO’93; Stinson, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; Volume 773, pp. 22–39. [Google Scholar] [CrossRef] [Green Version]
- Cardell, S.D.; Fúster-Sabater, A. Modelling the shrinking generator in terms of linear CA. Adv. Math. Commun. 2016, 10, 797–809. [Google Scholar] [CrossRef] [Green Version]
- Cardell, S.D.; Climent, J.J.; Fúster-Sabater, A.; Requena, V. Representations of Generalized Self-Shrunken Sequences. Mathematics 2020, 8, 1006. [Google Scholar] [CrossRef]
- Cardell, S.D.; Fúster-Sabater, A.; Requena, V. Interleaving Shifted Versions of a PN-Sequence. Mathematics 2021, 9, 687. [Google Scholar] [CrossRef]
- Pichler, F. (Ed.) Linear Complexity and Random Sequences. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1986; Volume 219. [Google Scholar]
- Duvall, P.F.; Mortick, J.C. Decimation of Periodic Sequences. SIAM J. Appl. Math. 1971, 21, 367–372. [Google Scholar] [CrossRef]
- Fúster-Sabater, A.; Caballero-Gil, P. Linear solutions for cryptographic nonlinear sequence generators. Phys. Lett. A 2007, 369, 432–437. [Google Scholar] [CrossRef] [Green Version]
- Lidl, R.; Niederreiter, H. Introduction to Finite Fields and Their Applications; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Mita, R.; Palumbo, G.; Pennisi, S.; Poli, M. Pseudorandom bit generator based on dynamic linear feedback topology. Electron. Lett. 2002, 28, 1097–1098. [Google Scholar] [CrossRef]
- Ali Eljadi, F.M.; Taha Al Shaikhli, I.F. Dynamic linear feedback shift registers: A review. In Proceedings of the 5th International Conference on Information and Communication Technology for The Muslim World (ICT4M), Kuching, Malaysia, 17–18 November 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Peinado, A.; Munilla, J.; Fúster-Sabater, A. Improving the Period and Linear Span of the Sequences Generated by DLFSRs. In Proceedings of the International Joint Conference SOCO’14-CISIS’14-ICEUTE’14, Advances in Intelligent Systems and Computing, Bilbao, Spain, 25–27 June 2014; de la Puerta, J.G., Ferreira, I.G., Bringas, P.G., Klett, F., Abraham, A., de Carvalho, A.C., Herrero, Á., Baruque, B., Quintián, H., Corchado, E., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 299, pp. 397–406. [Google Scholar] [CrossRef]
- Stępień, R.; Walczak, J. Comparative analysis of pseudo random signals of the LFSR and DLFSR generators. In Proceedings of the 20th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES 2013, Gdynia, Poland, 20–22 June 2013; pp. 598–602. [Google Scholar]
- Xiong, H.; Qu, L.; Li, C.; Fu, S. Linear complexity of binary sequences with interleaved structure. IET Commun. 2013, 7, 1688–1696. [Google Scholar] [CrossRef]
- Massey, J.L. Shift-register synthesis and BCH decoding. IEEE Trans. Inf. Theory 1969, 15, 122–127. [Google Scholar] [CrossRef] [Green Version]
- Golomb, S.W.; Parker, M.; Pott, A.; Winterhof, A. In Proceedings of the Sequences and Their Applications—SETA 2008, Lexington, KY, USA, 14–18 September 2008; Volume 5203.
- National Institute of Standards and Technology. FIPS 140-2: Security Requirements for Cryptographic Module. Federal Information Processing Standards Publication; U.S. Department of Commerce: Washington, DC, USA, 2001. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.140-2.pdf (accessed on 3 April 2022).
- Barnsley, M. Fractals Everywhere, 2nd ed.; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Peitgen, H.; Jurgens, H.; Saupe, D. Chaos and Fractals: New Frontiers of Science; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Orúe, A.; Fúster-Sabater, A.; Fernández, V.; Montoya, F.; Hernández, L.; Martín, A. Actas de la XIV Reunión Espanola sobre Criptología y Seguridad de la Información, RECSI XIV. Available online: https://alarcos.esi.uclm.es/DocumentosWeb/2016-RECSI-Moreno.pdf (accessed on 3 April 2022).
- Romera, M. Técnica de Los Sistemas Dinámicos Discretos. Textos Univ. CSIC 1997, 27, 50–58. [Google Scholar]
- Álvarez, G.; Montoya, F.; Romera, M.; Pastor, G. Cryptanalyzing an improved security modulated chaotic encryption scheme using ciphertext absolute value. Chaos Solitons Fractals 2005, 23, 1749–1756. [Google Scholar] [CrossRef] [Green Version]
- National Institute of Standards and Technology (NIST). A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. 2010. Available online: http://csrc.nist.gov/publications/nistpubs800/-22rec1/SP800-22red1.pdf (accessed on 3 April 2022).
- Maurer, U. A universal statistical test for random bit generators. J. Cryptol. 1992, 5, 89–105. [Google Scholar] [CrossRef]
- Marsaglia, G. The Marsaglia Random Number CDROM Including the Diehard Battery of Tests of Randomness. 1995. Available online: https://web.archive.org/web/20160125103112/http://stat.fsu.edu/pub/diehard/ (accessed on 3 April 2022).

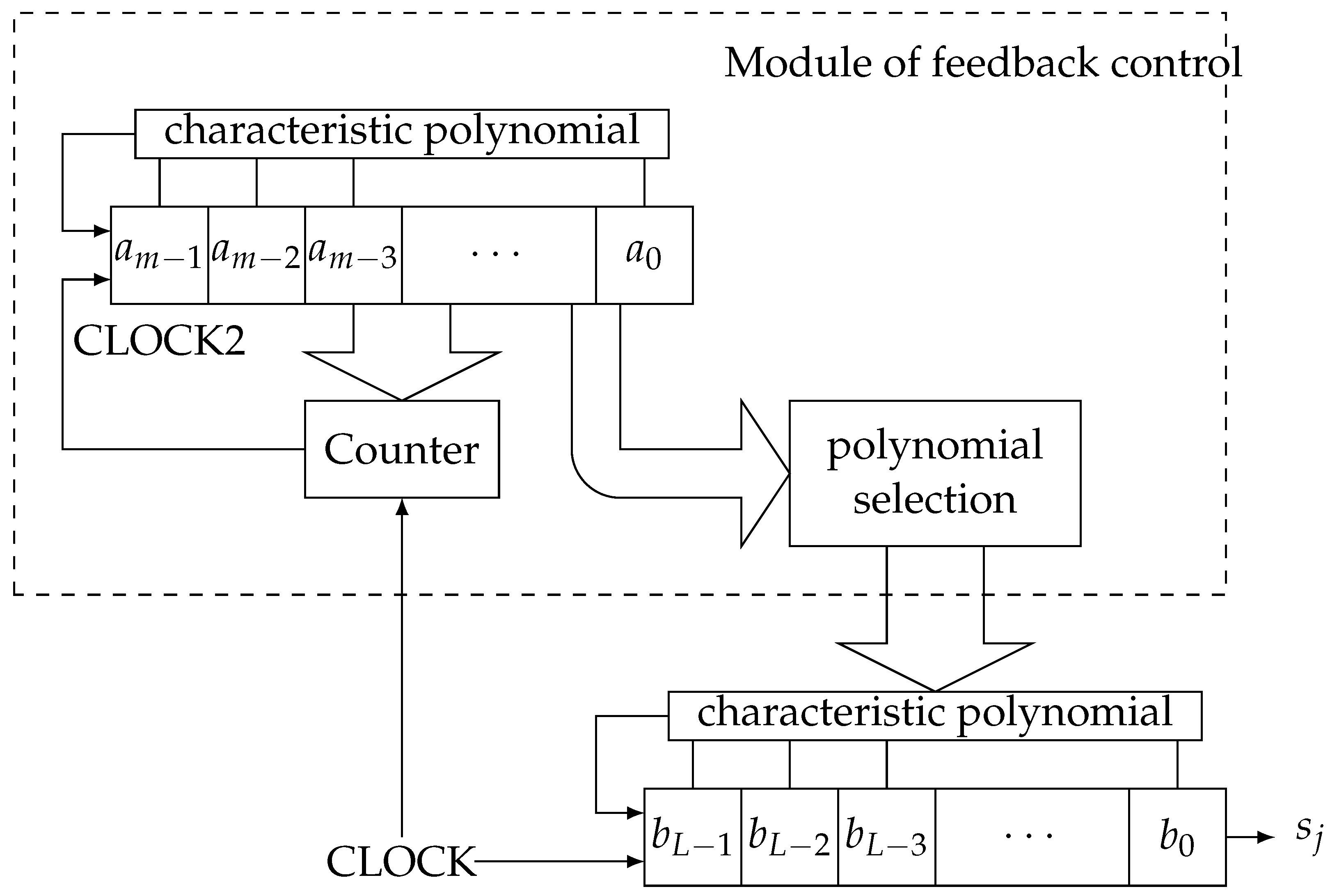
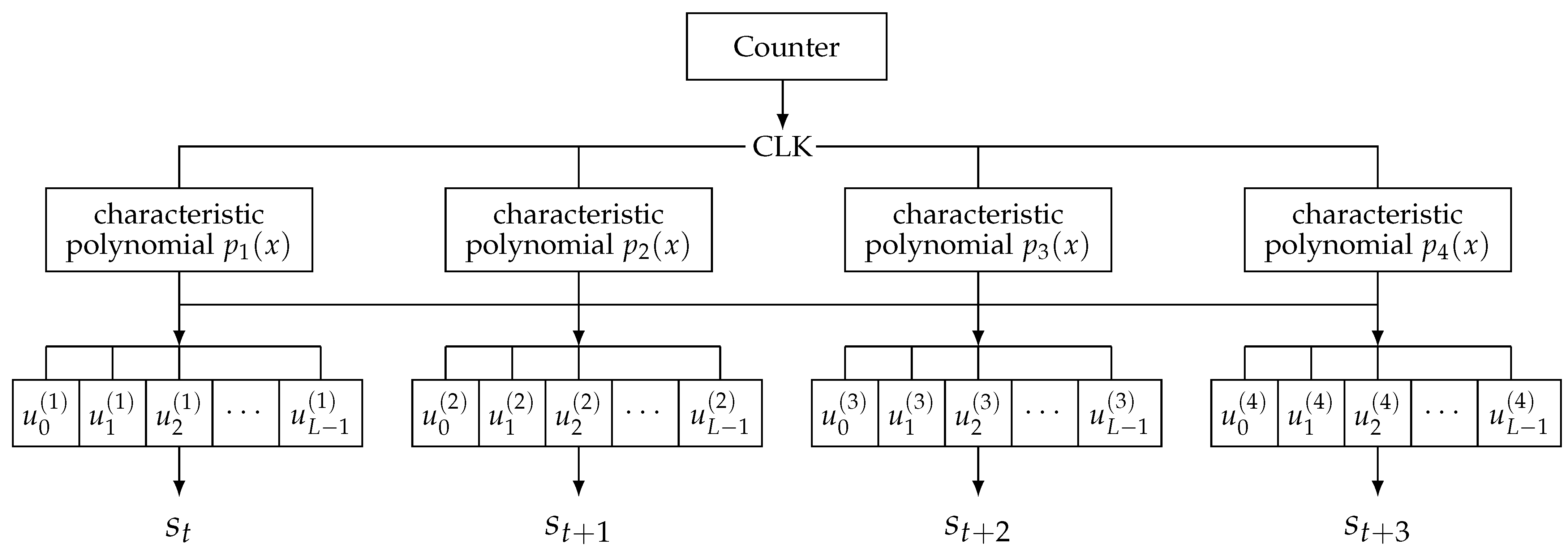
| L | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|
| t | ||||||
| 4 | 80 | 96 | 112 | 128 | 144 | |
| 5 | 125 | 150 | 175 | 200 | 225 | |
| 6 | 180 | 216 | 252 | 288 | 324 | |
| 7 | 245 | 294 | 343 | 392 | 441 | |
| 8 | 320 | 384 | 448 | 512 | 576 | |
| t Different Polynomials | 1 Polynomial | |||
|---|---|---|---|---|
| (8,16) | 1024 | 524,280 | 128 | 524,280 |
| (8,17) | 1088 | 1,048,568 | 136 | 1,048,568 |
| (8,18) | 1152 | 2,097,144 | 144 | 2,097,144 |
| (8,19) | 1216 | 4,194,296 | 152 | 4,194,296 |
| (8,20) | 1280 | 8,388,600 | 160 | 8,388,600 |
| t-Interleaved | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|
| Tests | |||||||
| Monobit | 0.4952 | 0.4740 | 0.0493 | 0.6213 | 0.5592 | 0.9745 | |
| Poker | 0.9083 | 0.2742 | 0.5086 | 0.0488 | 0.9960 | 0.4902 | |
| Runs | 0.5402 | 0.5160 | 0.4629 | 0.5946 | 0.6000 | 0.9840 | |
| Long Runs | 0.5715 | 0.5823 | 0.6785 | 0.8791 | 0.1204 | 0.9719 | |
| Frequency block | 0.4068 | 0.2167 | 0.3672 | 0.7633 | 0.3473 | 0.5089 | |
| Maurer’s | 0.6623 | 0.4129 | 0.2069 | 0.8374 | 0.5539 | 0.4262 | |
| Lempel-Ziv | 0.0931 | 0.9159 | 0.0531 | 0.2314 | 0.9069 | 0.9719 | |
| Test Name | p-Value | Result | Test Name | p-Value | Result |
|---|---|---|---|---|---|
| Birthday spacing | 0.770936 | Pass | OQSO | 0.8197 | Pass |
| 0.747460 | 0.1329 | ||||
| 0.989202 | 0.5293 | ||||
| 0.774785 | 0.6284 | ||||
| 0.576802 | 0.7687 | ||||
| 0.176450 | 0.0969 | ||||
| 0.874796 | 0.7288 | ||||
| 0.139735 | 0.9149 | ||||
| 0.514557 | 0.9812 | ||||
| Overlapping | 0.974948 | Pass | OQSD | 0.7603 | Pass |
| permutations | 0.759794 | 0.6207 | |||
| Binary ranks | 0.752307 | Pass | 0.8554 | ||
| Binary ranks | 0.934338 | Pass | 0.3293 | ||
| Binary ranks | 0.445734 | Pass | 0.0179 | ||
| Bit stream (Monkey tests) | 0.76389 | Pass | 0.7859 | ||
| 0.13337 | 0.4336 | ||||
| 0.67455 | 0.1403 | ||||
| 0.49876 | 0.7540 | ||||
| 0.88496 | 0.3442 | ||||
| 0.96748 | 0.1236 | ||||
| 0.07041 | 0.1888 | ||||
| 0.08609 | 0.8394 | ||||
| 0.67958 | 0.6233 | ||||
| 0.61726 | 0.1351 | ||||
| 0.78081 | 0.4005 | ||||
| 0.61369 | 0.4097 | ||||
| 0.80996 | 0.4941 | ||||
| 0.88405 | 0.8206 | ||||
| 0.35224 | DNA | 0.5756 | Pass | ||
| 0.62968 | 0.7611 | ||||
| 0.53228 | 0.5149 | ||||
| 0.17966 | 0.8418 | ||||
| 0.02605 | 0.9799 | ||||
| 0.16593 | 0.2000 | ||||
| OPSO | 0.8834 | Pass | 0.6843 | ||
| 0.7423 | 0.8916 | ||||
| 0.2625 | 0.2560 | ||||
| 0.5394 | 0.2569 | ||||
| 0.5394 | 0.0096 | ||||
| 0.6175 | 0.2598 | ||||
| 0.2614 | 0.1103 | ||||
| 0.6739 | 0.2117 | ||||
| 0.7986 | 0.5963 | ||||
| 0.6588 | 0.3547 | ||||
| 0.7102 | 0.4503 | ||||
| 0.4069 | 0.5184 | ||||
| 0.8906 | 0.9202 | ||||
| OPSO | 0.4968 | Pass | DNA | 0.0457 | Pass |
| 0.1266 | 0.8440 | ||||
| 0.1259 | 0.9479 | ||||
| 0.8229 | 0.6468 | ||||
| 0.4243 | 0.3536 | ||||
| 0.3429 | 0.6446 | ||||
| 0.6911 | 0.0831 | ||||
| 0.1838 | 0.7538 | ||||
| 0.2961 | 0.7575 | ||||
| 0.2145 | 0.9951 | ||||
| Count-the-1’s (stream of bytes) | 0.476036 | Pass | 0.5849 | ||
| 0.572657 | 0.2852 | ||||
| Count-the-1’s (specific bytes) | 0. | Pass | Parking lot | 0.407931 | Pass |
| 0.453489 | Minimum distance | 0.752286 | Pass | ||
| 0.531694 | 3D Spheres | 0.947691 | Pass | ||
| 0.476337 | Squeeze | 0.990622 | Pass | ||
| 0.115181 | Overlapping sums | 0.276467 | Pass | ||
| 0.238283 | Runs | 0.276783 | Pass | ||
| 0.248038 | 0.893007 | ||||
| 0.170200 | 0.908305 | ||||
| 0.595302 | 0.913183 | ||||
| 0.167417 | Craps | 0.995956 | Pass | ||
| 0.574701 | 105,661 | ||||
| 0.384873 | |||||
| 0.944743 | |||||
| 0.955924 | |||||
| 0.210026 | |||||
| 0.142320 | |||||
| 0.717744 | |||||
| 0.191102 | |||||
| 0.728247 | |||||
| 0.297792 | |||||
| 0.971290 | |||||
| 0.323464 | |||||
| 0.408101 | |||||
| 0.013264 | |||||
| 0.859849 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardell, S.D.; Requena, V.; Fúster-Sabater, A. Computational Analysis of Interleaving PN-Sequences with Different Polynomials. Cryptography 2022, 6, 21. https://doi.org/10.3390/cryptography6020021
Cardell SD, Requena V, Fúster-Sabater A. Computational Analysis of Interleaving PN-Sequences with Different Polynomials. Cryptography. 2022; 6(2):21. https://doi.org/10.3390/cryptography6020021
Chicago/Turabian StyleCardell, Sara D., Verónica Requena, and Amparo Fúster-Sabater. 2022. "Computational Analysis of Interleaving PN-Sequences with Different Polynomials" Cryptography 6, no. 2: 21. https://doi.org/10.3390/cryptography6020021
APA StyleCardell, S. D., Requena, V., & Fúster-Sabater, A. (2022). Computational Analysis of Interleaving PN-Sequences with Different Polynomials. Cryptography, 6(2), 21. https://doi.org/10.3390/cryptography6020021






