Quantum Identity-Based Encryption from the Learning with Errors Problem
Abstract
:1. Introduction
Can we construct a fully secure IBE scheme with which the network security protocol can provide perfect forward secrecy?
1.1. Our Contributions
- Network security protocols with our QIBE scheme provide perfect forward secrecy. The ciphertext is transmitted in the form of a quantum state that is unknown to the adversary, who cannot duplicate the ciphertext. Thus, in security protocols based on QIBE construction, even if the private identity key is threatened, the adversary does not possess the previous ciphertexts of session keys to decrypt, and therefore cannot threaten the security of the previous session keys. Therefore, security protocols based on QIBE construction have perfect forward secrecy.
- The classic KGC system can still be used for QIBE schemes to generate and distribute private identity keys, reducing the cost of implementing this scheme. The classic KGC system can be used because the , algorithms of our scheme are classic, and the master public and secret keys of our scheme are both in the form of classic bits.
1.2. Outline of the Paper
2. Preliminaries
2.1. Quantum Computation
- Addition and subtraction: Cuccaro et al. [20] proposed a quantum addition circuit. The quantum addition achieves the addition of two registers, that is,To prevent overflows caused by the carry, the second register (initially loaded in state ) should be sufficiently large, i.e., if both a and b are encoded on ℓ qubits, the second register should be of size . In the addition circuit, the last carry is the most significant bit of the result and is written in the -th qubit of the second register. As a result of the reversibility of unitary operations, by reversing the addition circuit, i.e., applying each gate of the circuit in the reversed order, the subtraction circuit is obtained. The addition and subtraction circuits are shown in and of Figure 4, respectively. In this paper, a circuit with a bar on the left side represents the reversed sequence of elementary gates embedded in the same circuit with the bar on the right side.In the subtraction circuit, with the input , the output produces when . When , the output is , where the size of the second register is . i.e.,When , the significant qubit, that is, the -th qubit of the second register, which indicates whether an overflow occurred in the subtraction, always contains 1. We denote the addition circuit by when this algorithm takes two ℓ-qubit states and as input. Similarly, we denote the subtraction circuit by when this algorithm takes two ℓ-qubit states and as input. To calculate the addition or subtraction of two ℓ-bit inputs, a total of qubits, Toffoli gates, and CNOT gates are required.
- Addition and subtraction module q: Liu et al. [21] improved Roetteler’s [22] quantum modular addition circuit and reduced the number of quantum gates required. This quantum circuit produceswhere . The simplified form of the addition module q circuit is shown in Figure 4c. The modular subtraction can be obtained by reversing the modular addition circuit, and its bar is on the left-hand side. We denote the modular addition circuit by when this algorithm takes two -qubit states and as input. Similarly, we denote the modular subtraction circuit by when this algorithm takes two -qubit states and as input. To calculate the addition or subtraction module q of two -bit inputs, a total of qubits, Toffoli gates, CNOT gates are required.
- Comparison: Markov et al. [23] constructed a quantum comparison circuit by comparing and based on whether the highest bit of is or . This circuit is obtained by modifying the previous subtraction circuit so that it outputs only the highest bit of . The comparison circuit achieves the comparison of two registers, that isThe simplified form of the quantum comparison circuit is shown in Figure 4e. We denote the comparison circuit by when this algorithm takes two ℓ-qubit states and as input. To compare two ℓ-bit inputs and , a total of qubits, Toffoli gates, and CNOT gates are required.
2.2. Lattices
- a randomised algorithm that, when , outputs a pair such that is close to uniform in and is a basis of , satisfying with overwhelming probability.
- a randomised algorithm that, given a full rank matrix ,a basis of , a vector and , outputs a vector sampled from a distribution close to .
2.3. Classic Identity-Based Encryption
- . The key generation algorithm takes a security parameter as input. It outputs a master public key and a master secret key .
- . The key extraction algorithm takes a master public key , a master secret key , and an identity as input. It outputs a private identity key . We assume that is implicitly included in .
- . The encryption algorithm takes a master public key , an identity , and the message m as input. It outputs a ciphertext .
- . The decryption algorithm takes the master public key , the private identity key , and the ciphertext as input. It outputs the message m. Correctness. For all , all identities , all messages m, and all , we haveSecurity. The security game is defined by the following experiment, which is played by a challenger and an adversary :
- The challenger runs to generate . It gives to the adversary .
- The adversary adaptively requests keys for any identity of its choice. The challenger responds with the corresponding secret key , which it generates by running .
- The adversary submits two messages of equal length, and , and a challenge identity with the restriction that is not equal to any identity requested in the previous phase. The challenger picks , encrypts under by running the encryption algorithm, and sends the ciphertext to the adversary .
- continues to issue key queries for any identity as in step (2) with the restriction that .
- The adversary outputs a guess for .
3. QIBE and Its Construction
3.1. Definition of QIBE
3.2. Our Construction
- (1) It runs to obtain a uniformly random matric and which is a good basis for . (2) Then, it selects a hash function , which maps an identity to a vector. (3) Finally, it outputs and . (4) In summary, .
- : (1) On input , and an identity , it computes and generates such that . It is clear that . (2) In summary, .
- : (1) On input of an identity , , and a bit quantum superposition state , it first computes and chooses a uniformly random , and . (2) Then, it sets and . More procedures are performed as follows:
- ⋆
- Step 1: Taking and as input, it runs and gets
- ⋆
- Step 2: Taking the second register of the above result and x as input, it runs and obtains
- ⋆
- Step 3: Finally, taking the two registers of the above result as input, it runs the unentanglement quantum circuit (which is described in Section 4, and we denote it by ) to obtain(3) In summary, .
- : To decrypt a ciphertext using an identity secret key , it computes . Then, more processes are performed as follows:
- ⋆
- Step 1: Taking and as input, it runs to obtain
- ⋆
- Step 2: Taking the above result and as input, it runs ( is a quantum circuit, which takes two ℓ-qubit quantum states and as input and outputs the absolute value of their subtraction, i.e., ) to obtainPlease refer to Section 4.1 for more information about .
- ⋆
- Step 3: Taking the above result and as input, it runs to obtainNext, the algorithm will unentangle the first and second registers of this quantum state.
- ⋆
- Step 4: Taking the first register of the above result and as input, it runs (The (which is the inverse of ) is a quantum circuit which takes in two ℓ-qubit quantum states and as input and outputs one ℓ-qubit quantum state, i.e., ) to obtainPlease refer to Section 4.1 for more information about the inverse of .
- ⋆
- Step 5: Taking the first register of the above result and as input, it runs to obtain
- ⋆
- Step 6: Taking the second register of the above result and as the input, it runs to obtain
- ⋆
- Step 7: Taking the first register and the third register of the above result as input, it runs to obtainFinally, the algorithm unentangles the second and third registers of the above result.
- ⋆
- Step 8: Taking the third register of the above result and as input, it performs the inverse of the controlled copy circuit to obtainThe quantum state is no longer entangled with other registers and the decryption procedure is completed. In summary,
3.3. Correctness
3.4. Security Proof
- Hash queries: When makes a random oracle query to on , the challenger chooses a random vector and locally stores the tuple , and returns to .
- Identity secret key queries: When queries an identity secret key for , the challenger uses the algorithm , which takes as input to compute and returns to .
- Challenge ciphertext: When the adversary submits two messages and of equal length and a challenge identity with the restriction that is not equal to any identity requested in the previous phase, the challenger picks , and encrypts under by running the encryption algorithm to get , where and and . Then, the ciphertext is sent to .
- Hash queries: When queries the random oracle on , the challenger generates a pair by first sampling and setting . Then, it locally stores the tuple and returns to .
- Identity secret key queries: When makes an identity secret key query for , the challenger uses the algorithm , which takes as input to compute and returns to .
- Challenge ciphertext: The same as that in the .
- Hash queries: When queries the random oracle on , the challenger generates a pair as in the previous game. Then, it locally stores the tuple and returns to .
- Identity secret key queries: When queries an identity secret key for , the challenger retrieves the unique tuple from the local storage and returns .
- Challenge ciphertext: The same as that in the .
- Hash queries: The same as that in the .
- Identity secret key queries: The same as that in the .
- Challenge ciphertext: The same as that in the .
- Hash queries: On ’s -th distinct query to , the challenger does the following: if , then locally stores the tuple and returns to . Otherwise, for , the challenger selects and computes ; then, it locally stores the tuple and returns to .
- Identity secret key queries: The same as that in the .
- Challenge ciphertext: When produces a challenge identity (distinct from all its identity secret key queries) and messages , , assume without loss of generality that already queried on . If , i.e., if the tuple is not in the local storage, then the challenger ignores the output of and aborts the game (we denote this event as ). Otherwise, i.e., if the does not occur (we denote this event as ), the challenger picks and encrypts under by running the encryption algorithm to obtain , where and , and . Then, the ciphertext is sent to the adversary .
- Hash queries: The same as that in the .
- Identity secret key queries: The same as that in the .
- Challenge ciphertext: When produces a challenge identity (distinct from all its identity secret key queries) and messages , , assume without loss of generality that already queried on . If , i.e., if the tuple is not in the local storage, then the challenger ignores the output of and aborts the game. Otherwise, i.e., if the does not occur, the challenger picks and encrypts under using two random vectors to obtain , where and , and . Then, the ciphertext is sent to the adversary .
3.5. Advantages of Our QIBE
- A fundamental fact in quantum information theory is that unknown or random quantum states cannot be replicated [17]. The probability amplitude and corresponding basis state of ciphertext are unknown to the adversary, so the ciphertext is an unknown quantum state and cannot be replicated during transmission. When attempting to attack our QIBE-based network security protocol, an attacker cannot copy and store the ciphertext of the session key, which is encrypted by a private identity key (called a long-term key). Thus, the attacker does not have the quantum ciphertext of the previous session key to decrypt, and the security of the previous session key will not be threatened even if the attacker obtains the long-term key. In other words, all encrypted communications and sessions recorded in the past cannot be retrieved. Therefore, the security protocol based on our QIBE has perfect forward secrecy, which cannot be achieved by the security protocol based on classic IBE.
- In our QIBE scheme, the KGC uses the algorithms and to generate the private identity key when it takes as input a master public key , a master secret key , and an identity . The key observation is that both the input () and the output () of are in the form of classic bits, and so are the input () and the output () of . Therefore, the classic KGC system can still be used in our QIBE scheme to generate and distribute private identity keys, reducing the cost when this scheme is implemented.
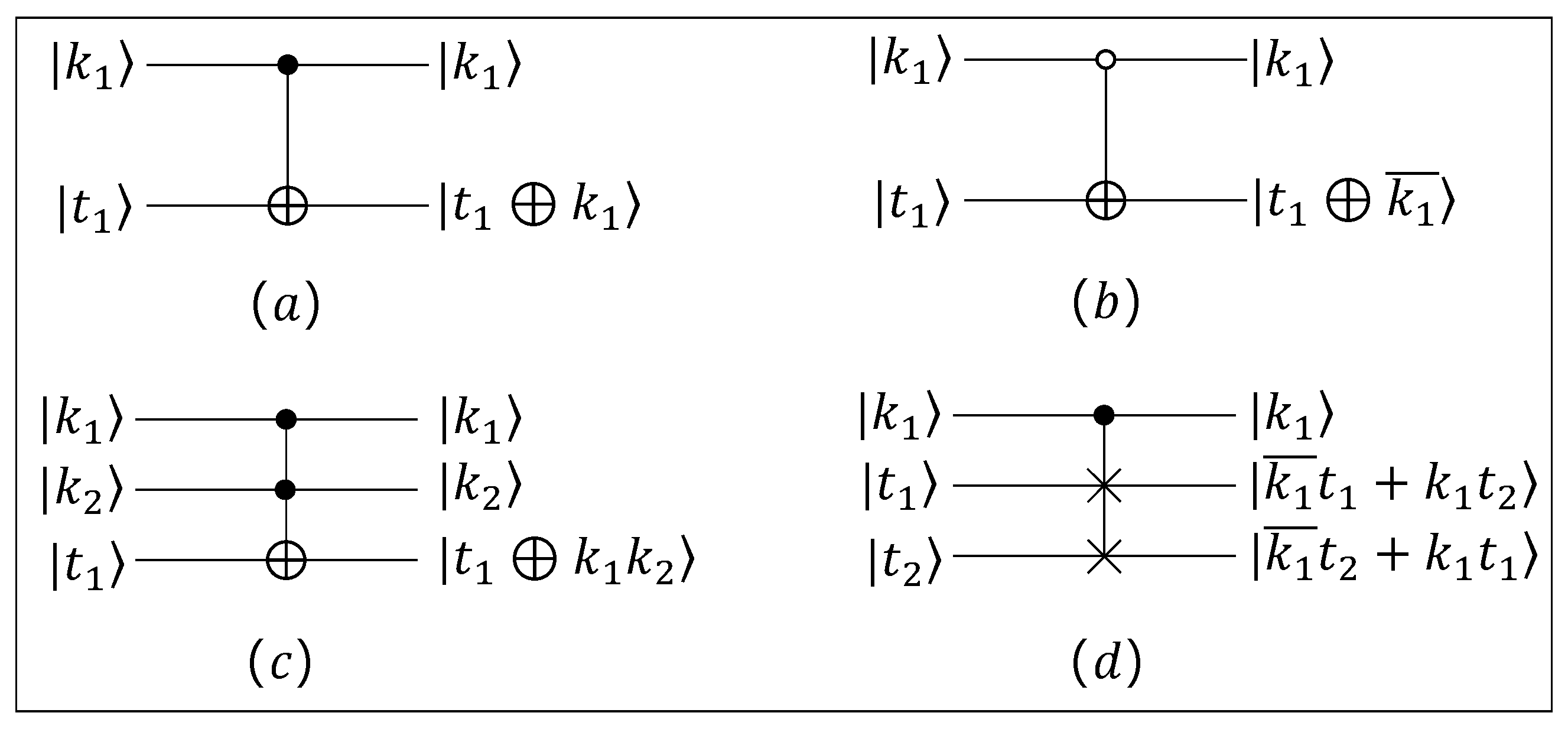
4. Quantum Circuit Realisation
4.1. Quantum Circuit
- On input , and , the initial output where the number 1 is located is , and . This is because only one -combination-CNOT operation is performed.
- The output where the number 2 is located is , and . This is because only one -controlled-NOT variant operation is performed, in which the control bits are and the target bit is . If , the control bits are -qubit , and the target qubit will change to . Otherwise, the control bits are not equal to -qubit , and the target qubit is all the time.
- The final output where the number 3 is located is , and . Only one -combination-CNOT operation is performed, in which the control bits are and the target bits are ; therefore, it can obtain .
4.2. Complexity Analysis
- To encrypt one qubit, a total of qubits, Toffoli gates, and CNOT gates are required.
- To decrypt one ciphertext that encrypts one qubit, a total of qubits, Toffoli gates, and CNOT gates are required.
5. Conclusions and Future Work
- The network security protocol with our QIBE scheme provides perfect forward secrecy. The ciphertext is transmitted in the form of a quantum state that is unknown to the adversary and cannot be copied and stored. Thus, in network security protocols based on our QIBE construction, the adversary cannot have access to any previous quantum ciphertext to decrypt and obtain the previous session key, even if the private identity key is threatened.
- Classic KGC systems still can be used in our QIBE scheme to generate and distribute private identity keys, thus reducing the cost when this scheme is implemented. The classic KGC systems can be used because the master public and secret keys of our scheme are both in the form of classic bits.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Classic IBE Scheme
- (1) It runs to obtain a uniformly random matric and which is a good basis for . (2) Then, it selects a hash function which maps an identity to a vector. (3) Finally, it outputs and . (4) In summary, .
- : (1) On input , and an identity , it computes and generates such that . It is clear that . (2) In summary, .
- : (1) On input of an identity , , and a bit message , it first computes and chooses a uniformly random , and . (2) Then, it computes and , and sets , where . (3) In summary, .
- : (1) To decrypt a ciphertext using an identity secret key , it computes . (2) Then, it computes(3) Furthermore, it treats b as an integer in , and sets if ; otherwise, . (4) Finally, it returns the plaintext m. (5) In summary, .
- : (1) It runs to obtain a uniformly random matric and which is a good basis for . (2) Then, it selects a hash function which maps an identity to a matrix. (3) Finally, it outputs and . (4) In summary, .
- : (1) On input , , and an identity , it computes which is an -matrix. (2) It takes advantage of the algorithm to generate the identity secret key such that is composed of where is the i-th column of . It is easy to see that . (3) In a word, .
- : (1) On input of an identity , , and one n-bit message , it first computes and chooses a uniformly random , and . (2) Then, it computes and , and sets , where . (3) In summary, .
- : (1) To decrypt a ciphertext using an identity secret key , it computes . (2) Then, it computes(3) Furthermore, it treats each coordinate of as an integer in , and sets if , else . (4) Finally, it returns the plaintext . (5) In a word, .
References
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Advances in Cryptology, Proceedings of CRYPTO; Springer: Berlin/Heidelberg, Germany, 1984; Volume 196, pp. 47–53. [Google Scholar]
- Boneh, D.; Franklin, M.K. Identity-Based Encryption from the Weil Pairing. In Advances in Cryptology—CRYPTO 2001; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2139, pp. 213–229. [Google Scholar]
- Boneh, D.; Boyen, X. Efficient Selective-ID Secure Identity-Based Encryption Without Random Oracles. In Advances in Cryptology—EUROCRYPT 2004; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3027, pp. 223–238. [Google Scholar]
- Waters, B. Efficient Identity-Based Encryption Without Random Oracles. In Advances in Cryptology—EUROCRYPT 2005; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3494, pp. 114–127. [Google Scholar]
- Cocks, C.C. An Identity Based Encryption Scheme Based on Quadratic Residues. In Cryptography and Coding, 8th IMA International Conference; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2260, pp. 360–363. [Google Scholar]
- Boneh, D.; Gentry, C.; Hamburg, M. Space-Efficient Identity Based Encryption Without Pairings. In Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS’07), Providence, RI, USA, 21–23 October 2007; pp. 647–657. [Google Scholar]
- Jhanwar, M.P.; Barua, R. A Variant of Boneh-Gentry-Hamburg’s Pairing-Free Identity Based Encryption Scheme. In Information Security and Cryptology; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5487, pp. 314–331. [Google Scholar]
- Joye, M. Identity-Based Cryptosystems and Quadratic Residuosity. In Public-Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9614, pp. 225–254. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the 40th Annual Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]
- Cash, D.; Hofheinz, D.; Kiltz, E.; Peikert, C. Bonsai Trees, or How to Delegate a Lattice Basis. In Advances in Cryptology—EUROCRYPT 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6110, pp. 523–552. [Google Scholar]
- Agrawal, S.; Boneh, D.; Boyen, X. Efficient Lattice (H)IBE in the Standard Model. In Advances in Cryptology—EUROCRYPT 2010; Gilbert, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6110, pp. 553–572. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Xue, R.; Zhang, R. Deterministic Public Key Encryption and Identity-Based Encryption from Lattices in the Auxiliary-Input Setting. In Security and Cryptography for Networks; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7485, pp. 1–18. [Google Scholar]
- Yamada, S. Adaptively Secure Identity-Based Encryption from Lattices with Asymptotically Shorter Public Parameters. In Advances in Cryptology—EUROCRYPT 2016; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9666, pp. 32–62. [Google Scholar]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef] [Green Version]
- Chinese-State-Cryptography-Administration. Chinese SSL VPN Technology Specification. Available online: http://gmbz.org.cn/main/viewfile/20180110021416665180.html (accessed on 1 January 2022).
- Van Oorschot, P.C.; Menezes, A.J.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; American. Assoc. Phys. Teach. 2002, 70, 558–559. [Google Scholar]
- Häner, T.; Jaques, S.; Naehrig, M.; Roetteler, M.; Soeken, M. Improved quantum circuits for elliptic curve discrete logarithms. In International Conference on Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2020; pp. 425–444. [Google Scholar]
- Cuccaro, S.A.; Draper, T.G.; Kutin, S.A.; Moulton, D.P. A new quantum ripple-carry addition circuit. arXiv 2004, arXiv:0410184. [Google Scholar]
- Liu, X.; Yang, H.; Yang, L. CNOT-count optimized quantum circuit of the extended Shor’s algorithm for ECDLP. arXiv 2021, arXiv:2112.11358. [Google Scholar]
- Roetteler, M.; Naehrig, M.; Svore, K.M.; Lauter, K. Quantum resource estimates for computing elliptic curve discrete logarithms. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; pp. 241–270. [Google Scholar]
- Markov, I.L.; Saeedi, M. Constant-Optimized Quantum Circuits for Modular Multiplication and Exponentiation. Quantum Inf. Comput. 2012, 12, 361–394. [Google Scholar] [CrossRef]
- Ajtai, M. Generating Hard Instances of the Short Basis Problem; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1–9. [Google Scholar]
- Alwen, J.; Peikert, C. Generating Shorter Bases for Hard Random Lattices; STACS Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2009; pp. 75–86. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. STOC 2005, 56, 84–93. [Google Scholar]
- Wu, C.; Yang, L. A complete classification of quantum public-key encryption protocols. In Electro-Optical and Infrared Systems; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9648, p. 964818. [Google Scholar]
- Xiang, C.; Yang, L.; Peng, Y.; Chen, D. The classification of quantum symmetric-key encryption protocols. In Quantum and Nonlinear Optics III; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9269, p. 926909. [Google Scholar]
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar]
- Amy, M.; Maslov, D.; Mosca, M.; Roetteler, M. A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 818–830. [Google Scholar] [CrossRef] [Green Version]

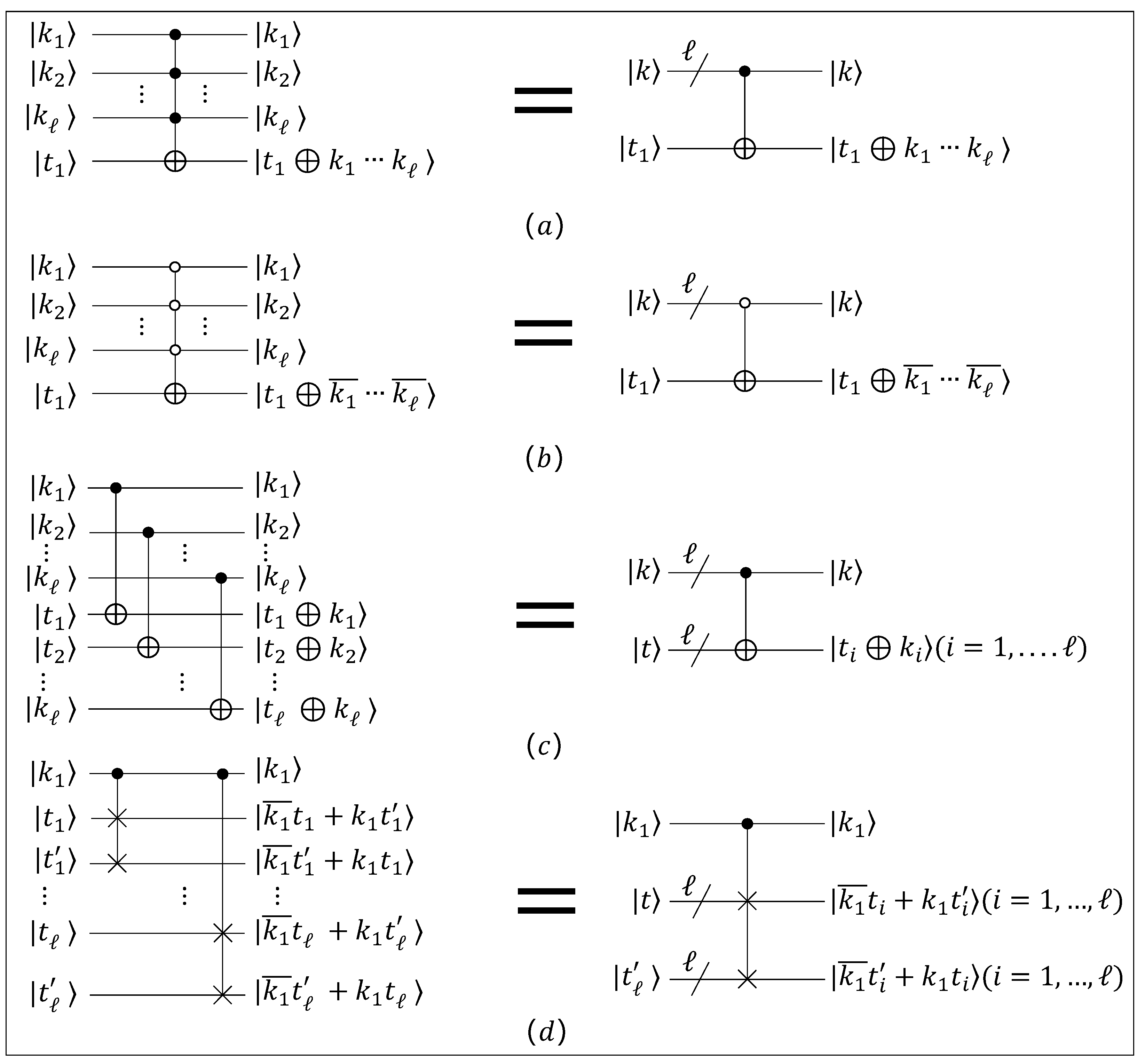

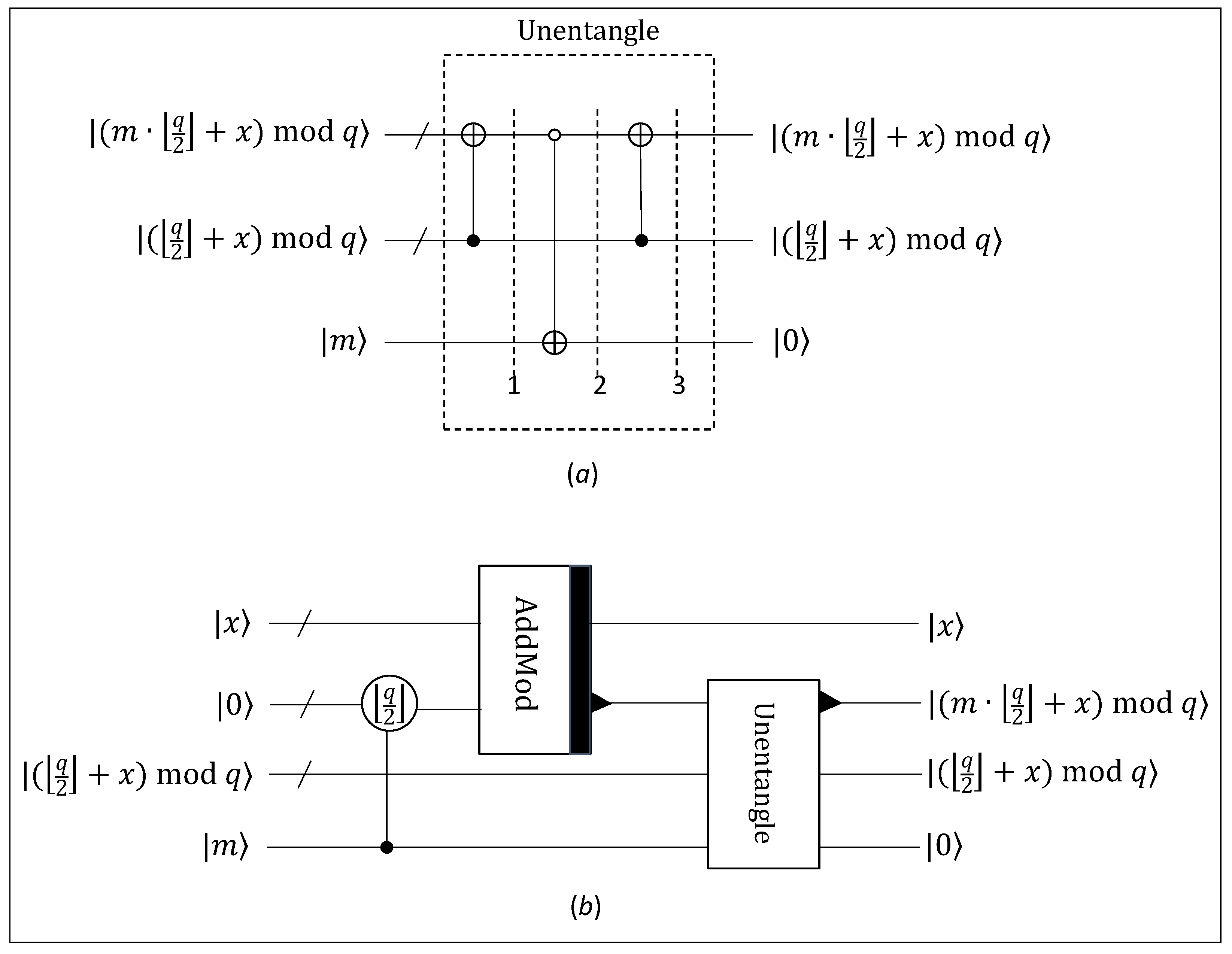


| Quantum Resource | ||
|---|---|---|
| Qubit | ||
| Hadamard gate | ||
| phase gate | ||
| T gate | ||
| CNOT gate |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Yang, L.; Zhang, D.; Liu, X. Quantum Identity-Based Encryption from the Learning with Errors Problem. Cryptography 2022, 6, 9. https://doi.org/10.3390/cryptography6010009
Gao W, Yang L, Zhang D, Liu X. Quantum Identity-Based Encryption from the Learning with Errors Problem. Cryptography. 2022; 6(1):9. https://doi.org/10.3390/cryptography6010009
Chicago/Turabian StyleGao, Wenhua, Li Yang, Daode Zhang, and Xia Liu. 2022. "Quantum Identity-Based Encryption from the Learning with Errors Problem" Cryptography 6, no. 1: 9. https://doi.org/10.3390/cryptography6010009
APA StyleGao, W., Yang, L., Zhang, D., & Liu, X. (2022). Quantum Identity-Based Encryption from the Learning with Errors Problem. Cryptography, 6(1), 9. https://doi.org/10.3390/cryptography6010009






