Variations of QKD Protocols Based on Conventional System Measurements: A Literature Review
Abstract
1. Introduction
2. Literature Review
2.1. Classical Cryptography
2.2. Quantum Cryptography
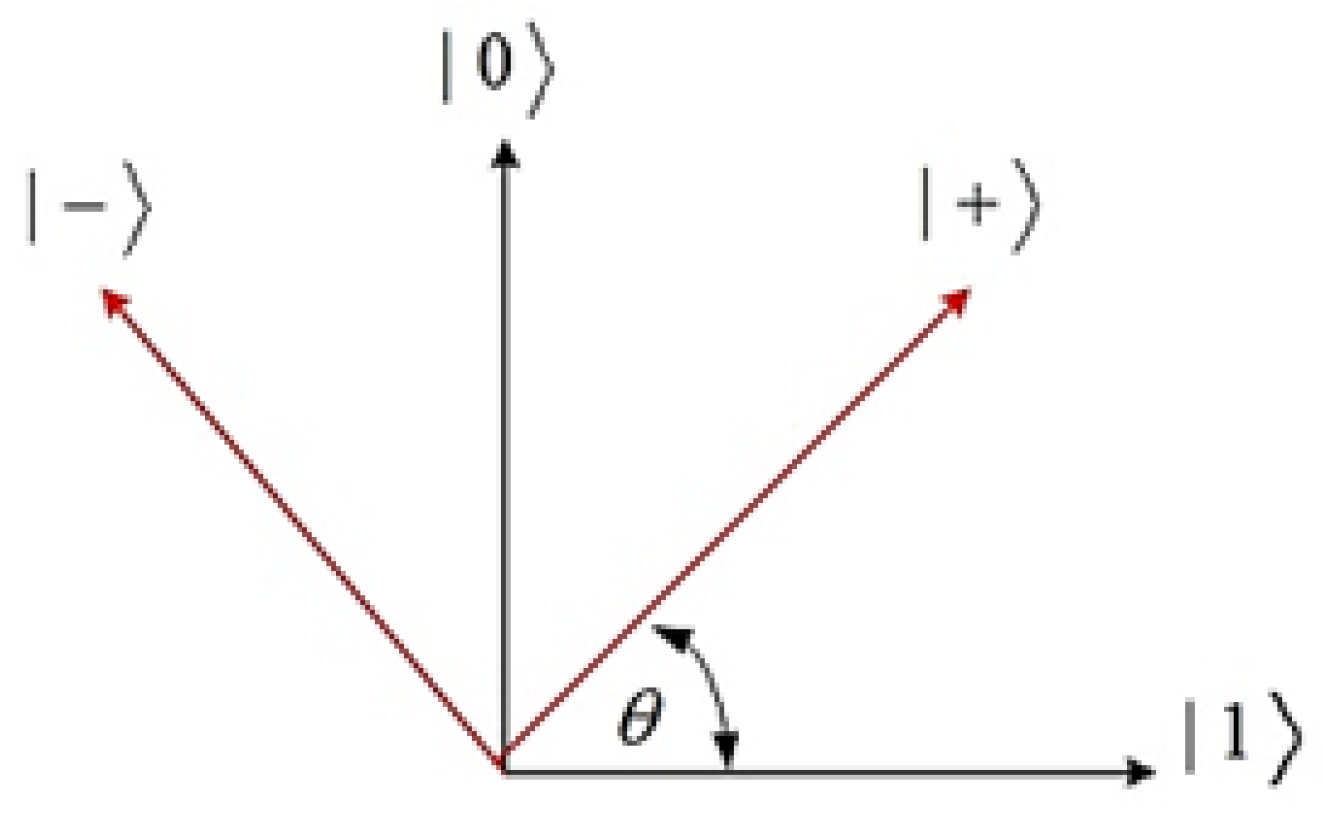
2.2.1. The BBB84 Protocol
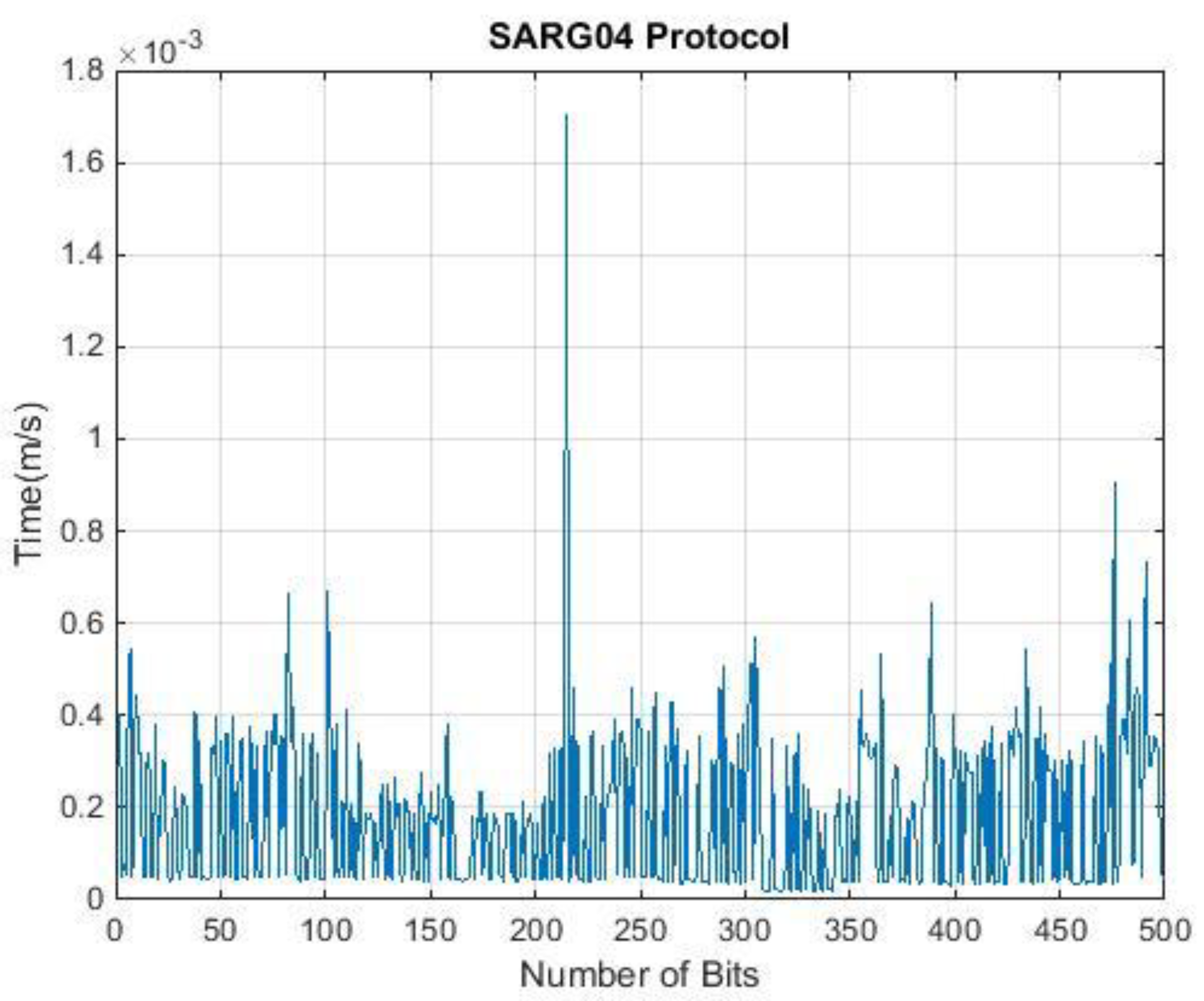
2.2.2. The SARG04 Protocol
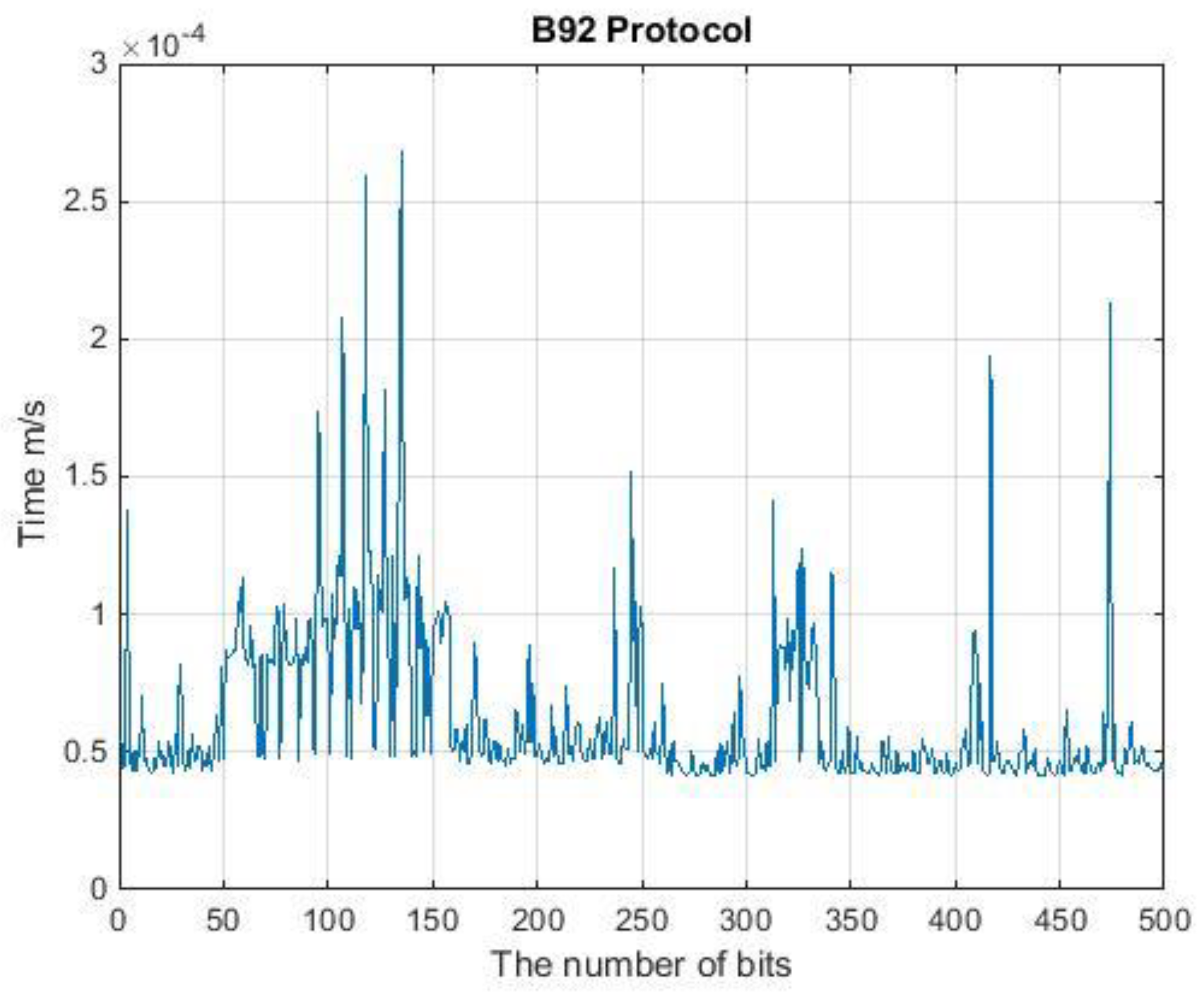
2.2.3. The B92 Protocol
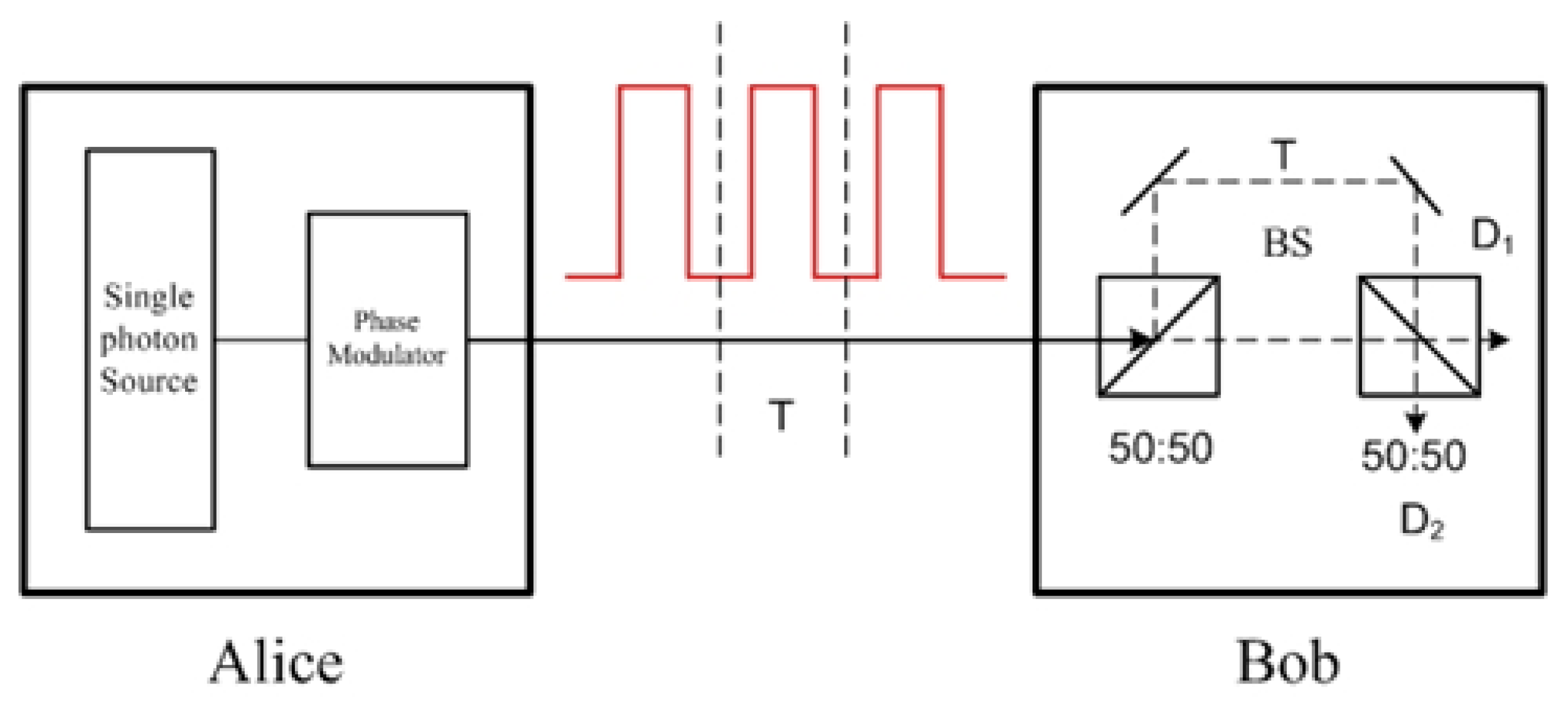
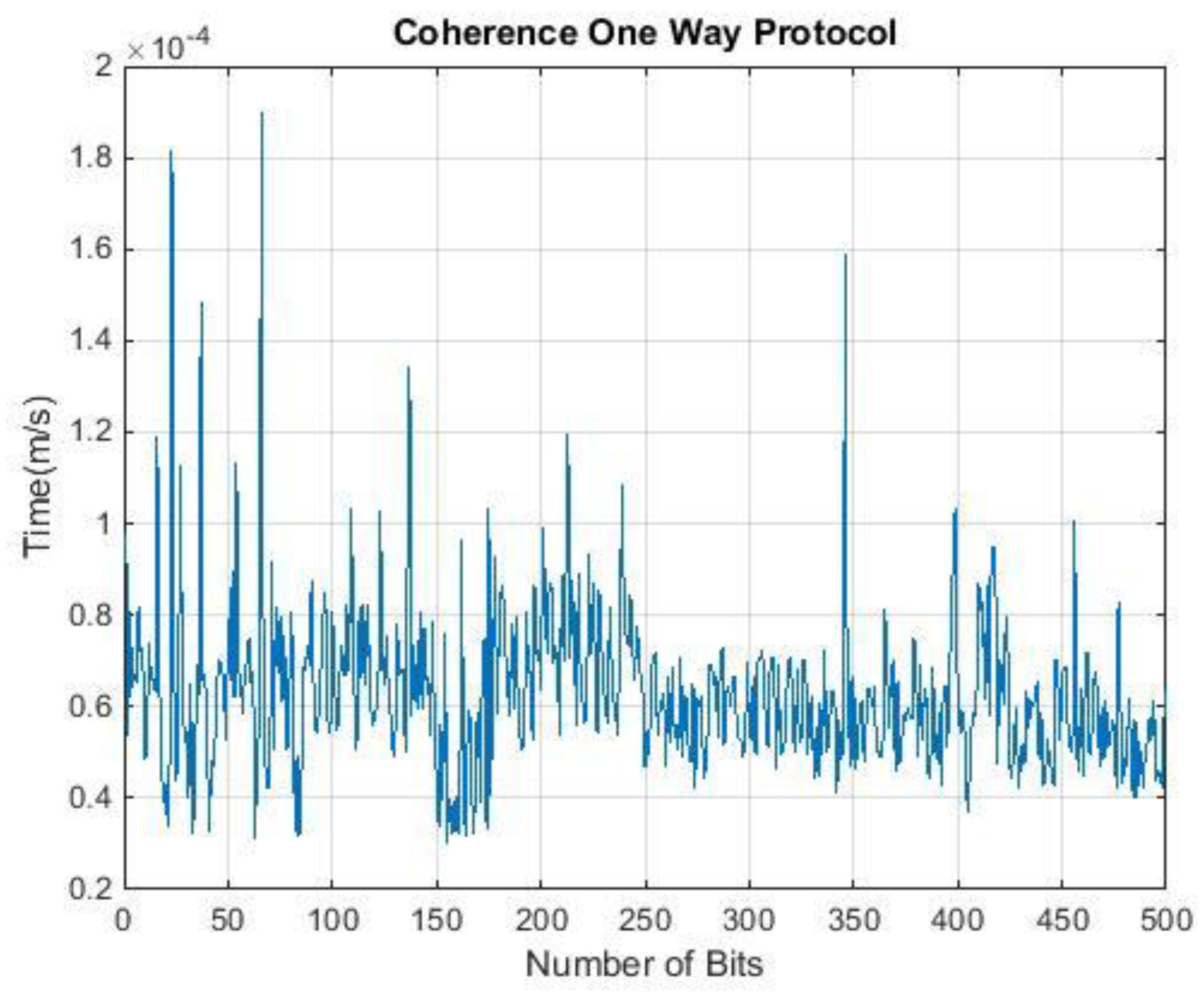
2.2.4. The Coherent One-Way Protocol
2.2.5. The KMB09 Protocol
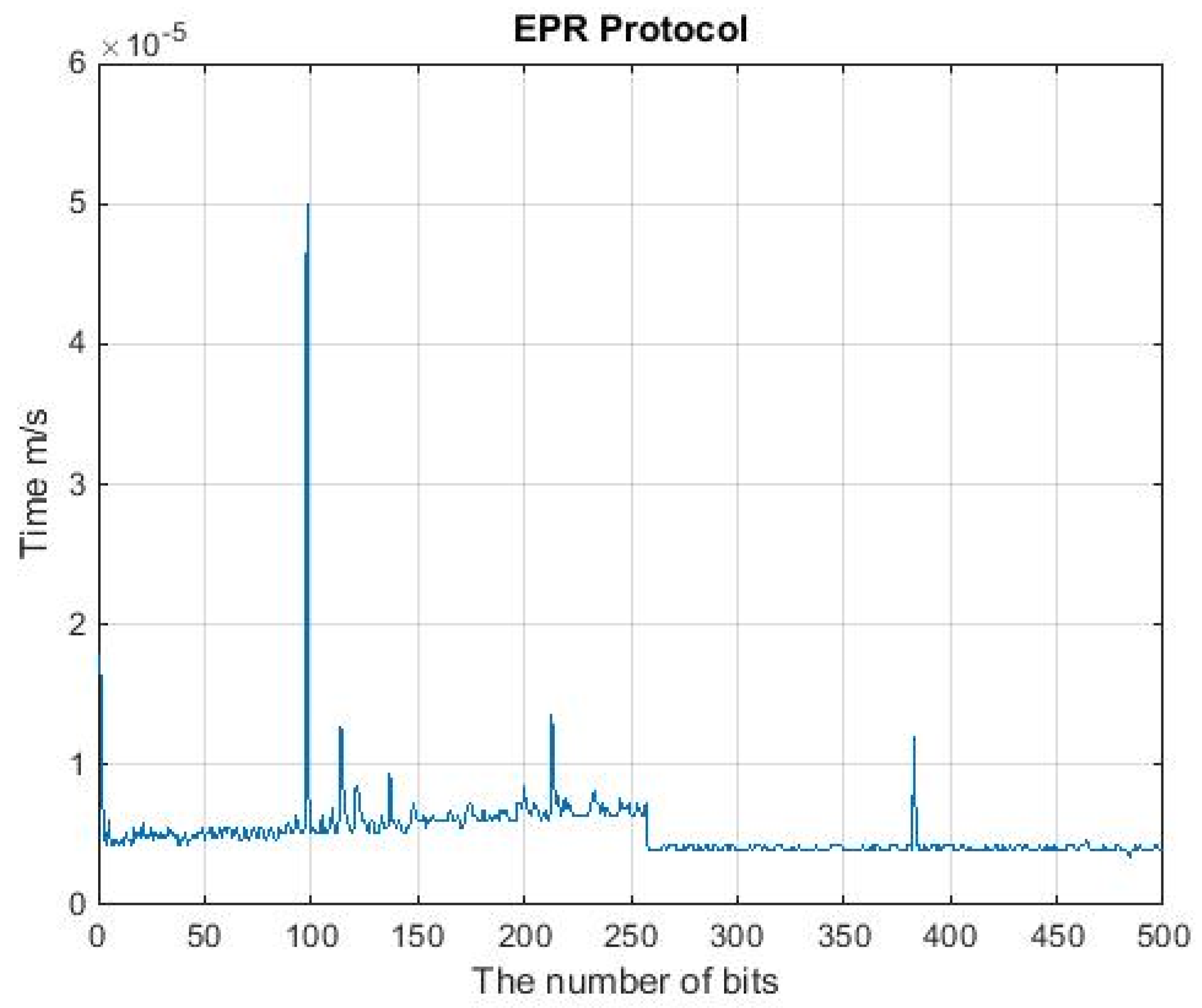
2.2.6. The EPR Protocol
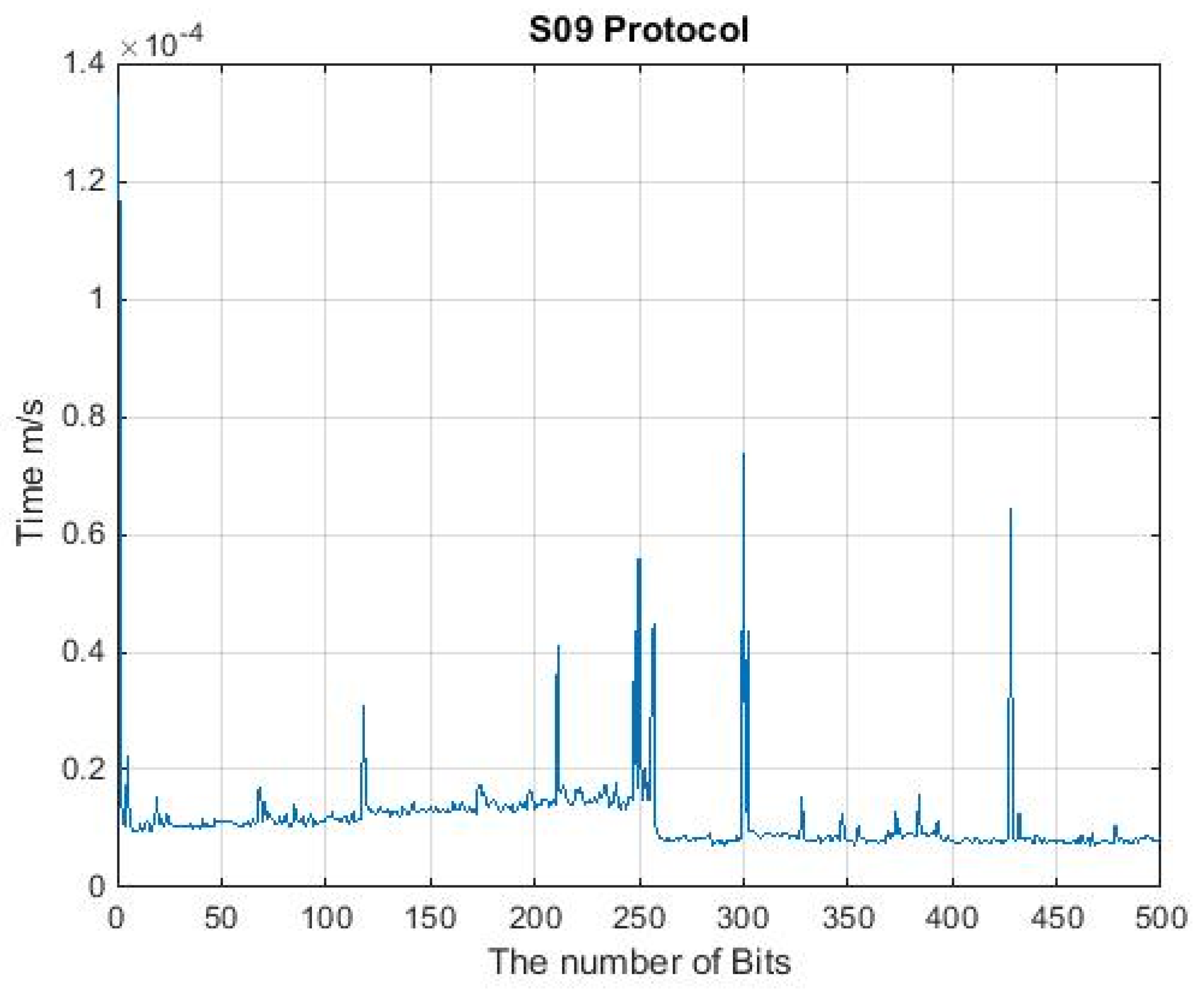
2.2.7. The S09 Protocol
2.2.8. The S13 Protocol
- Quantum part
- -
- Raw key exchange: (as shown in the BB84 protocol).
- -
- Random seed: one of the communicating parties creates a random binary string
- -
- Missing key exchange:
- Alice makes a summation of the random binary string with the binary basis from the first part and obtains a binary basis . Alice then randomly generates another string of binary , where this is an exchanged key with Bob.
- Bob sums each of the sequences sent to him by Alice with the created binary string , where . Thus, the sum becomes a binary string basis . Next, Bob measures the received state , with the correspondence of the basis to generate .
- Classical partAlice and Bob apply function to different binary exchanges in a set of binary strings:
- Asymmetric cryptography:Step 1: Alice sums the binary string created by her in quantum part with a random string of binary values that were created by missing the key exchange .where will be sent to Bob.Step 2: To obtain the public key, Bob encrypts:Step 3: Alice makes a summation to obtain the private string of , which is:and then decrypts the string .
- Private Reconciliation:Step 4: Bob receives the binary sequence after completing the comparison between and by Alice.Step 5: Bob sums the sequence of bases with , where .This is to obtain the private string .Bob then obtains the private string from Alice .
2.2.9. The Differential-Phase-Shift Protocol
3. The QKD Protocols Features Based on Quantum Computing
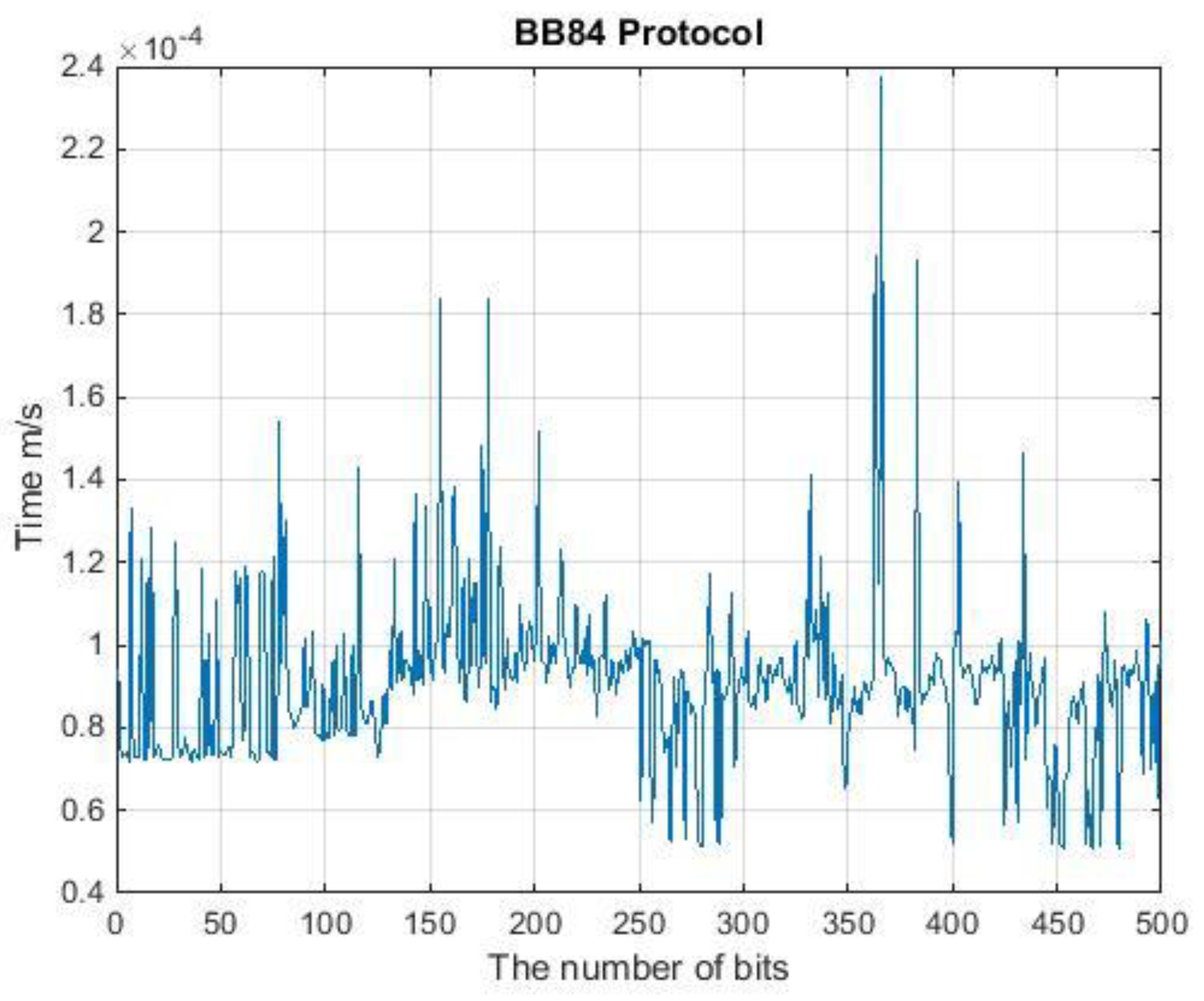
4. Runtime Analysis of QKD Protocols
| Algorithm 1: QKD Protocol | |
| 1. Initiate n Qubits | // prepare a plaintext |
| 2. for: each n → () | // Initiation loop |
| 3. | |
| 4. | // Loop (1) |
| 5. | |
| 6. | // ending the loop |
| 7. Reconciliation phase: | |
| 8. for: 1 → n | // reconciliation loop |
| 9. | // loop (2) |
| 10. use different mechanisms 11. to correct error, | |
| 12. | |
| 13. | //ending the loop |
5. Comparison between QKD Protocols
6. Conclusions
Funding
Conflicts of Interest
References
- Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Wiesner, S. Conjugate coding. ACM Sigact News 1983, 15, 78–88. [Google Scholar] [CrossRef]
- Brassard, G. Brief history of quantum cryptography: A personal perspective. In IEEE Information Theory Workshop on Theory and Practice in Information-Theoretic Security; IEEE: Piscataway, NJ, USA, 2005; Volume 2005, pp. 19–23. [Google Scholar]
- Walk, N.; Ralph, T.C.; Symul, T.; Lam, P.K. Security of post-selection based continuous variable quantum key distribution against arbitrary attacks. In CLEO: Applications and Technology; Optical Society of America: Washingdon, DC, USA, 2011; p. JTuC4. [Google Scholar]
- Oesterling, L.; Hayford, D.; Friend, G. Comparison of commercial and next generation quantum key distribution: Technologies for secure communication of information. In Proceedings of the 2012 IEEE Conference on Technologies for Homeland Security (HST), Waltham, MA, USA, 13–15 November 2012; pp. 156–161. [Google Scholar]
- Possignolo, R.T.; Margi, C.B. A quantum-classical hybrid architecture for security algorithms acceleration. In Proceedings of the 2012 IEEE 11th International Conference on Trust, Security and Privacy in Computing and Communications, Liverpool, UK, 25–27 June 2012; pp. 1032–1037. [Google Scholar]
- Yanofsky, N.S.; Mannucci, M.A. Quantum Computing for Computer Scientists; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in Quantum Cryptography. Adv. Opt. Photon. 2020, 12, 1012. [Google Scholar] [CrossRef]
- Sharbaf, M.S. Quantum cryptography: An emerging technology in network security. In Proceedings of the 2011 IEEE International Conference on Technologies for Homeland Security (HST), Waltham, MA, USA, 15–17 November 2011; pp. 13–19. [Google Scholar]
- Barker, W.C.; Barker, E.B. SP 800-67 Rev. 1. Recommendation for the Triple Data Encryption Algorithm (TDEA) Block Cipher; Citeseer: Princeton, NJ, USA, 2012. [Google Scholar]
- Schneier, B. Description of a new variable-length key, 64-bit block cipher (Blowfish). In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 1993; pp. 191–204. [Google Scholar]
- Patarin, J.; Goubin, L. Asymmetric cryptography with S-Boxes Is it easier than expected to design efficient asymmetric cryptosystems? In Proceedings of the International Conference on Information and Communications Security, Beijing, China, 11–14 November 1997; pp. 369–380. [Google Scholar]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [PubMed]
- Bužek, V.; Hillery, M. Quantum copying: Beyond the no-cloning theorem. Phys. Rev. A 1996, 54, 1844. [Google Scholar] [CrossRef]
- Steege, M. Free-Space Optics: A Viable, Secure Last Mile Solution? Sans Institute: Bethesda, MD, USA, 2002. [Google Scholar]
- Niemiec, M.; Pach, A.R. Management of security in quantum cryptography. IEEE Commun. Mag. 2013, 51, 36–41. [Google Scholar] [CrossRef]
- Cabello, A.; Feito, Á.; Lamas-Linares, A. Bell’s inequalities with realistic noise for polarization-entangled photons. Phys. Rev. A 2005, 72, 052112. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Russell, J. Application of quantum key distribution. In Proceedings of the MILCOM 2008—2008 IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008; pp. 1–6. [Google Scholar]
- Gottesman, D.; Lo, H.-K. From quantum cheating to quantum security. arXiv 2001, arXiv:quant-ph/0111100. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Cao, Z.; Liu, L. Improvement of one quantum encryption scheme. Int. J. Quantum Inf. 2012, 10, 1250076. [Google Scholar] [CrossRef]
- Zhao, S.-M.; Li, F.; Zheng, B.-Y. A proof of security of quantum key distribution in probabilistic clone scheme. In Proceedings of the International Conference on Communication Technology Proceedings, ICCT 2003, Beijing, China, 9–11 April 2003; Voume 2, pp. 1507–1509. [Google Scholar]
- Sharma, R.D.; De, A. A new secure model for quantum key distribution protocol. In Proceedings of the 2011 6th International Conference on Industrial and Information Systems, Kandy, Sri Lanka, 16–19 August 2011; pp. 462–466. [Google Scholar]
- Jouguet, P.; Kunz-Jacques, S. High performance error correction for quantum key distribution using polar codes. arXiv 2012, arXiv:1204.5882. [Google Scholar] [CrossRef]
- Cerf, N.J.; Bourennane, M.; Karlsson, A.; Gisin, N. Security of quantum key distribution using d-level systems. Phys. Rev. Lett. 2002, 88, 127902. [Google Scholar] [CrossRef]
- Kartheek, D.N.; Amarnath, G.; Reddy, P.V. Security in quantum computing using quantum key distribution protocols. In Proceedings of the 2013 International Mutli-Conference on Automation, Computing, Communication, Control and Compressed Sensing (iMac4s), Kottayam, India, 22–23 March 2013; pp. 19–25. [Google Scholar]
- Zeng, G.; Wang, X. Quantum key distribution with authentication. arXiv 1998, arXiv:quant-ph/9812022. [Google Scholar]
- Sharma, A.; Ojha, V.; Lenka, S.K. Security of entanglement based version of BB84 protocol for Quantum Cryptography. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; Volume 9, pp. 615–619. [Google Scholar]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef]
- Scarani, V.; Acin, A.; Ribordy, G.; Gisin, N. Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Phys. Rev. Lett. 2004, 92, 057901. [Google Scholar] [CrossRef]
- ElGamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Stipčević, M. How secure is quantum cryptography? In Proceedings of the 2012 35th International Convention MIPRO, Opatija, Croatia, 21–25 May 2012; pp. 1529–1533. [Google Scholar]
- Ghazali, L.I.A.; Abas, A.F.; Adnan, W.A.W.; Mokhtar, M.; Mahdi, M.A.; Saripan, M.I. Security proof of Improved-SARG04 protocol using the same four qubit states. In Proceedings of the International Conference on Photonics 2010, Langkawi, Malaysia, 5–7 July 2010. [Google Scholar]
- Abushgra, A.A. SARG04 and AK15 Protocols Based on the Run-Time Execution and QBER. In Proceedings of the 2021 IEEE 5th International Conference on Cryptography, Security and Privacy (CSP), Zhuhai, China, 8–10 January 2021; pp. 176–180. [Google Scholar]
- Rass, S.; Schartner, P.; Greiler, M. Quantum coin-flipping-based authentication. In Proceedings of the 2009 IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar]
- Zhou, Y.; Zhou, X.; Gao, J. Scarani-acin-ribordy-gisin decoy-state protocols in quantum key distribution with a heralded single photon source. In Proceedings of the 2009 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 16–19 August 2009; pp. 4–751. [Google Scholar]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Bennett, C.H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 68, 3121. [Google Scholar] [CrossRef] [PubMed]
- Elboukhari, M.; Azizi, M.; Azizi, A. Quantum Key Distribution Protocols: A Survey. Int. J. Univers. Comput. Sci. 2010, 1, 59–67. [Google Scholar]
- Jobez, P.; Timoney, N.; Laplane, C.; Etesse, J.; Ferrier, A.; Goldner, P.; Gisin, N.; Afzelius, M. Towards highly multimode optical quantum memory for quantum repeaters. Phys. Rev. A 2016, 93, 032327. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Zbinden, H.; Stucki, D.; Brunner, N.; Scarani, V. Towards practical and fast quantum cryptography. arXiv 2004, arXiv:quant-ph/0411022. [Google Scholar]
- Stucki, D.; Brunner, N.; Gisin, N.; Scarani, V.; Zbinden, H. Fast and simple one-way quantum key distribution. Appl. Phys. Lett. 2005, 87, 194108. [Google Scholar] [CrossRef]
- Gottesman, D.; Lo, H.-K.; Lutkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. In Proceedings of the International Symposium onInformation Theory, Chicago, IL, USA, 27 June–2 July 200; p. 136.
- Singh, H.; Gupta, D.L.; Singh, A.K. Quantum key distribution protocols: A review. J. Comput. Eng. 2014, 16, 1–9. [Google Scholar] [CrossRef]
- Inoue, K.; Waks, E.; Yamamoto, Y. Differential phase shift quantum key distribution. Phys. Rev. Lett. 2002, 89, 037902. [Google Scholar] [CrossRef]
- Khan, M.M.; Murphy, M.; Beige, A. High error-rate quantum key distribution for long-distance communication. New J. Phys. 2009, 11, 063043. [Google Scholar] [CrossRef]
- Serna, E.H. Quantum key distribution protocol with private-public key. arXiv 2009, arXiv:0908.2146. [Google Scholar]
- Han, Z.-F.; Li, H. Security of practical quantum key distribution system. In Proceedings of the 2011 International Symposium on Intelligent Signal Processing and Communications Systems (ISPACS), Chiang Mai, Tailand, 7–9 December 2011; pp. 1–3. [Google Scholar]
- Khan, M.M.; Xu, J.; Beige, A. Improved Eavesdropping Detection in Quantum Key Distribution. arXiv 2011, arXiv:1112.1110. [Google Scholar]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Abushgra, A.; Elleithy, K. Initiated decoy states in quantum key distribution protocol by 3 ways channel. In Proceedings of the 2015 Long Island Systems, Applications and Technology, Farmingdale, NY, USA, 1 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Hwang, T.; Lee, K.-C. EPR quantum key distribution protocols with potential 100% qubit efficiency. IET Inf. Secur. 2007, 1, 43–45. [Google Scholar] [CrossRef]
- Serna, E.H. Quantum Key Distribution from a random seed. arXiv 2013, arXiv:1311.1582. [Google Scholar]
- Inoue, K.; Waks, E.; Yamamoto, Y. Differential-phase-shift quantum key distribution using coherent light. Phys. Rev. A 2003, 68, 022317. [Google Scholar] [CrossRef]
- Honjo, T.; Uchida, A.; Amano, K.; Hirano, K.; Someya, H.; Okumura, H.; Yoshimura, K.; Davis, P.; Tokura, Y. Differential-phase-shift quantum key distribution experiment using fast physical random bit generator with chaotic semiconductor lasers. Opt. Express 2009, 17, 9053. [Google Scholar] [CrossRef] [PubMed]
- Abushgra, A.; Elleithy, K. Differentiations of QKDPs in Run-Time Execution. p. 12. Available online: Khaledelleithy.org/Conferences/5-%20Differentiations%20of%20QKDPs%20in%20Run-Time%20Execution.pdf (accessed on 10 January 2022).
- Rohde, P.P. Quack! A Quantum Computer Simulator for Matlab; Centre for Quantum Computer Technology, Department of Physics, University of Queensland: Brisbane, Australia, 2005. [Google Scholar]
- Tan, S.M. A quantum optics toolbox for Matlab 5. J. Opt. B Quantum Semiclass. Opt 1999, 1, 161. [Google Scholar] [CrossRef]
- Bruen, A.A.; Forcinito, M.A. Cryptography, Information Theory, and Error-Correction: A Handbook for the 21st Century; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 68. [Google Scholar]







| Symbol | Description |
|---|---|
| Φ | Quantum superposition of n states. |
| Ψ | Quantum superposition of n states. |
| Exclusive OR (digital logical gate). | |
| A | Alice, and usually is the sender. |
| B | Bob, and usually is the receiver. |
| ↑ | A state with a definite value of spin operator. |
| X | The original message that should be shared between Alice and Bob. |
| Ket-notation, where it is a vector v. | |
| Bra-notation, where it is a linear form. | |
| + | Non-orthogonal States. |
| × | Orthogonal States. |
| OTP | One-Time Pad. |
| Qubit | Quantum Bit. |
| QBER | Quantum Bit Error Rate. |
| Bit Number | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Alice’s random bits | 0 | 1 | 1 | 0 | 1 | 1 |
| Alice’s random bases | + | + | × | + | + | + |
| Alice sends | → | ↑ | ↖ | → | ↑ | ↑ |
| Bit Number | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Bob’s random bases | × | + | × | × | + | × |
| Bob observes | ↗ | ↑ | ↖ | ↖ | ↑ | ↗ |
| Bob’s bits | 0 | 1 | 1 | 1 | 1 | 0 |
| Bit Number | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Alice’s random bases | + | + | × | + | + | + |
| Bob’s random bases | × | + | × | × | + | × |
| Agreement | ✓ | ✓ | ✓ | |||
| Shared secret key | 1 | 1 | 1 |
| Bit Number | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Shared secret keys | 1 | 1 | 1 | |||
| Randomly chosen | ✓ | ✓ | ||||
| Shared secret key | 1 | 1 | 1 | |||
| Agreements | ✓ | ✓ | ||||
| Unrevealed secret keys | 1 |
| Bit Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Alice’s random bases | × | × | + | + | × | + |
| Alice’s observations | ↗ | ↖ | → | ↑ | ↗ | → |
| Bob’s random bases | × | + | + | × | × | + |
| Bob’s observations | ↗ | → | → | ↗ | ↗ | → |
| Bit Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Alice’s random bases | × | × | + | + | × | + |
| Public channel | ⇕ | ⇕ | ⇕ | ⇕ | ⇕ | ⇕ |
| Bob’s random bases | × | + | + | × | × | + |
| Agree | ✓ | ✓ | ✓ | ✓ |
| Cases | Quantum Key Distribution Protocols | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| BB84 | B92 | SARG04 | COW | KMB09 | EPR | S09 | S13 | DPS | |
| Properties | Heisenberg | Heisenberg | Heisenberg | Arbitrary | Heisenberg | Entanglement | Kp, Ks | Heisenberg | Arbitrary |
| Number of States | 4 states | 2 States | 4 States | Time slots | 2 states | 2 EPR | Arbitrary states | 4 states | 4 States |
| Detection of presence | QBER | QBER | QBER | Break of coherence | ITER | Bell’s inequality | appending parity bits | Random Seed | Timeslot |
| Polarization | Orthogonal | Non orthogonal | Orthogonal | Arbitrary | Arbitrary | Orthogonal | Bit-Flip Phase-Flip | 2 orthogonal | DPS |
| State Probability | Various | 50% | 50% | Calculated | 50% | Equal | Various | Various | Equal |
| Qubit String | Discrete | Discrete | Discrete | Discrete | Discrete | Discrete | No | Discrete | Discrete |
| Classical channels | Yes | Yes | Yes | Yes | Yes | Yes | No | Yes | Yes |
| Decoy States | No | No | No | Yes | No | No | Yes | No | No |
| Sifting phase | Revealing Bases | Alice = 1 − Bob | Revealing non-orth. state | Revealing times 2k + 1 | Revealing Indices | Bell’s Inequality | No | Revealing Bases | Timeslot |
| Bell’s inequality | No | No | No | No | No | Yes | No | No | No |
| PNS attack | Vulnerable | Vulnerable | better than BB84 | Robust | Robust | N/A | N/A | N/A | Robust |
| IRUD attack | Vulnerable | Vulnerable | Vulnerable | Under Test | Under Test | Vulnerable | N/A | N/A | N/A |
| BS attack | Vulnerable | Vulnerable | Robust | Robust | Robust | Vulnerable | N/A | N/A | Robust |
| DoS attack | Vulnerable | Vulnerable | Vulnerable | Vulnerable | Vulnerable | Vulnerable | N/A | N/A | Robust |
| MAM attack | Vulnerable | Robust | Robust | Robust | Robust | Robust | Robust | N/A | Robust |
| IRA attack | Vulnerable | Vulnerable | Robust | Robust | Robust | Bell’s inequality | Robust | N/A | Robust |
| Authentication | No | No | No | No | No | No | No | Yes [classic] | No |
| QKDP | Input (Qubit) | Output (Qubit) | Time (ms) |
|---|---|---|---|
| BB84 | 500 | 142 | 0.164 |
| B92 | 500 | 119 | 0.177 |
| SARG04 | 500 | 247 | 0.815 |
| KMB09 | 16 | 362 | 0.012 |
| EPR | 500 | 119 | 0.860 |
| DPS | 500 | N/A | Constant |
| S09 | 500 | N/A | 0.927 |
| S13 | 500 | N/A | 0.639 |
| COW | 500 | 126 | 0.686 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abushgra, A.A. Variations of QKD Protocols Based on Conventional System Measurements: A Literature Review. Cryptography 2022, 6, 12. https://doi.org/10.3390/cryptography6010012
Abushgra AA. Variations of QKD Protocols Based on Conventional System Measurements: A Literature Review. Cryptography. 2022; 6(1):12. https://doi.org/10.3390/cryptography6010012
Chicago/Turabian StyleAbushgra, Abdulbast A. 2022. "Variations of QKD Protocols Based on Conventional System Measurements: A Literature Review" Cryptography 6, no. 1: 12. https://doi.org/10.3390/cryptography6010012
APA StyleAbushgra, A. A. (2022). Variations of QKD Protocols Based on Conventional System Measurements: A Literature Review. Cryptography, 6(1), 12. https://doi.org/10.3390/cryptography6010012






