Algorithm of Information Embedding into Digital Images Based on the Chinese Remainder Theorem for Data Security
Abstract
1. Introduction
- A novel ternary logic-based technique of information embedding into digital objects is proposed. The technique allows reducing the number of changes in a digital image that are required to embed a message of a given length. This feature leads to improved effectiveness of the information embedding.
- A novel ternary logic and the Chinese remainder theorem-based algorithm of information embedding is proposed. The ternary logic is implemented through the Chinese remainder theorem. Moreover, the Chinese remainder theorem enables rigorous mathematical tools of the number theory to be used in the task of information embedding effectiveness enhancement. The most prominent features of the proposed algorithm are imperceptibility qualities and an option not to transfer any side information.
- Multiple applications of information embedding techniques are analyzed. The most suitable application for the proposed technique is suggested.
2. Related Works
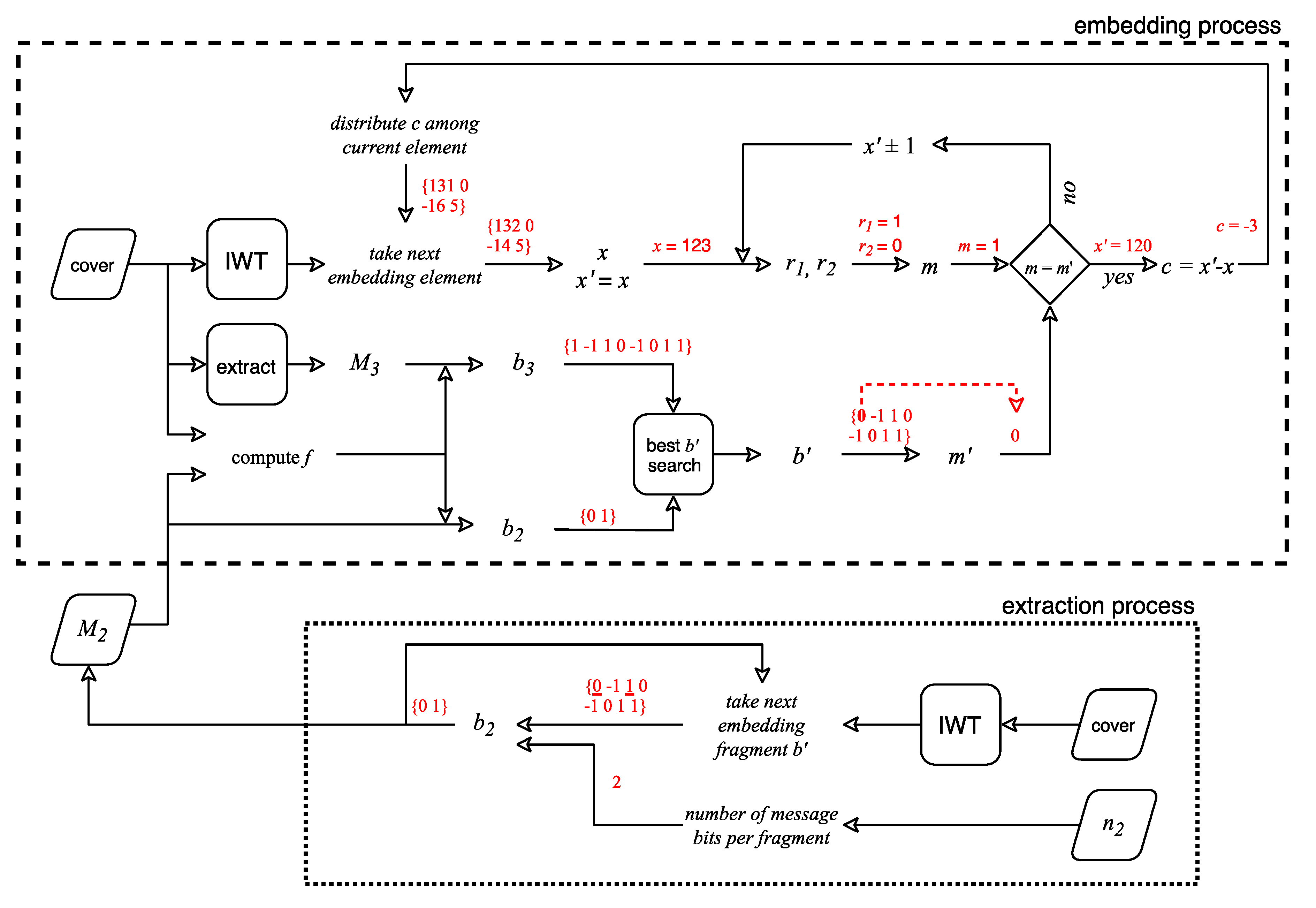
3. Proposed Method
4. Results
4.1. Method Evaluation
4.2. Comparisons with Other Data Hiding Methods
5. Discussion
- (1).
- Both embedding and extraction algorithms are lightweight and could be processed on server and end device. There could be a hidden transmission of end device’s data (sensors reading, end device state and actions, etc.) towards the server and transmission of data and commands that are needed to control the end device from the server towards the end device.
- (2).
- The embedding algorithm is computationally complex while an extraction algorithm is lightweight. In that case, it is challenging to perform the embedding on end devices with low power consumption. Thus, it is better to have a simplex channel between the server and the end device. However, it is still possible to organize a feedback channel if the embedding is performed not on a low-powered device but on a significantly more powerful mobile device that is used as a gateway.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amin, F.; Ahmad, A.; Choi, G.S. Towards trust and friendliness approaches in the social Internet of Things. Appl. Sci. 2019, 9, 166. [Google Scholar] [CrossRef]
- Kadhim, I.J.; Premaratne, P.; Vial, P.J.; Halloran, B. Comprehensive survey of image steganography: Techniques, Evaluations, and trends in future research. Neurocomputing 2019, 335, 299–326. [Google Scholar] [CrossRef]
- Simmons, G.J. The prisoners’ problem and the subliminal channel. In Advances in Cryptology; Springer: Boston, MA, USA, 1984; pp. 51–67. [Google Scholar]
- Anderson, R.J.; Petitcolas, F.A. On the limits of steganography. IEEE J. Selected Areas Commun. 1998, 16, 474–481. [Google Scholar] [CrossRef]
- Johnson, N.F.; Jajodia, S. Exploring steganography: Seeing the unseen. Computer 1998, 31, 26–34. [Google Scholar] [CrossRef]
- Devi, S.; Sahoo, M.N.; Muhammad, K.; Ding, W.; Bakshi, S. Hiding medical information in brain MR images without affecting accuracy of classifying pathological brain. Future Gener. Comput. Syst. 2019, 99, 235–246. [Google Scholar] [CrossRef]
- Parah, S.A.; Ahad, F.; Sheikh, J.A.; Bhat, G.M. Hiding clinical information in medical images: A new high capacity and reversible data hiding technique. J. Biomed. Inform. 2017, 66, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wornell, G.W. Quantization index modulation: A class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inf. Theory 2001, 47, 1423–1443. [Google Scholar] [CrossRef]
- Maniriho, P.; Ahmad, T. Information hiding scheme for digital images using difference expansion and modulus function. J. King Saud Univ.-Comput. Inf. Sci. 2019, 31, 335–347. [Google Scholar] [CrossRef]
- Kumar, R.; Kim, D.-S.; Jung, K.-H. Enhanced AMBTC based data hiding method using hamming distance and pixel value differencing. J. Inf. Secur. Appl. 2019, 47, 94–103. [Google Scholar] [CrossRef]
- Gull, S.; Parah, S.A.; Muhammad, K. Reversible data hiding exploiting huffman encoding with dual images for IoMT based healthcare. Comput. Commun. 2020, 163, 134–149. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, A.; Kumar, M. Information hiding with adaptive steganography based on novel fuzzy edge identification. Def. Technol. 2019, 15, 162–169. [Google Scholar] [CrossRef]
- Evsutin, O.; Kokurina, A.; Meshcheryakov, R.; Shumskaya, O. The adaptive algorithm of information unmistakable embedding into digital images based on the discrete Fourier transformation. Multimed. Tools Appl. 2018, 77, 28567–28599. [Google Scholar] [CrossRef]
- Pu, Y.-F.; Zhang, N.; Wang, H. Fractional-Order Spatial Steganography and Blind Steganalysis for Printed Matter: Anti-Counterfeiting for Product External Packing in Internet-of-Things. IEEE Internet Things J. 2018, 6, 6368–6383. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Abd-El-Atty, B.; Hossain, M.S.; Elmougy, S.; Ghoneim, A. Secure quantum steganography protocol for fog cloud Internet of Things. IEEE Access 2018, 6, 10332–10340. [Google Scholar] [CrossRef]
- Djebbar, F.; Abu-Ali, N. Lightweight noise resilient steganography scheme for Internet of Things. In Proceedings of the 2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Khari, M.; Garg, A.K.; Gandomi, A.H.; Gupta, R.; Patan, R.; Balusamy, B. Securing data in Internet of Things (IoT) using cryptography and steganography techniques. IEEE Trans. Syst. Man Cybern. Syst. 2019, 50, 73–80. [Google Scholar] [CrossRef]
- Meng, R.; Cui, Q.; Zhou, Z.; Fu, Z.; Sun, X. A Steganography Algorithm Based on CycleGAN for Covert Communication in the Internet of Things. IEEE Access 2019, 7, 90574–90584. [Google Scholar] [CrossRef]
- Cui, Q.; Zhou, Z.; Fu, Z.; Meng, R.; Sun, X.; Wu, Q.J. Image steganography based on foreground object generation by generative adversarial networks in mobile edge computing with Internet of Things. IEEE Access 2019, 7, 90815–90824. [Google Scholar] [CrossRef]
- Elhoseny, M.; Ramírez-González, G.; Abu-Elnasr, O.M.; Shawkat, S.A.; Arunkumar, N.; Farouk, A. Secure medical data transmission model for IoT-based healthcare systems. IEEE Access 2018, 6, 20596–20608. [Google Scholar] [CrossRef]
- Kaw, J.A.; Loan, N.A.; Parah, S.A.; Muhammad, K.; Sheikh, J.A.; Bhat, G.M. A reversible and secure patient information hiding system for IoT driven e-health. Int. J. Inf. Manag. 2019, 45, 262–275. [Google Scholar] [CrossRef]
- Weber, A. The USC-SIPI Image Database. Signal and Image Processing Institute of the University of Southern California. 1997. Available online: http://sipi.usc.edu/services/database (accessed on 6 December 2020).
- Chen, Y.-C.; Shiu, C.-W.; Horng, G. Encrypted signal-based reversible data hiding with public key cryptosystem. J. Vis. Commun. Image Represent. 2014, 25, 1164–1170. [Google Scholar] [CrossRef]











| Message Length (kbit) | Embedding Time (Seconds) | Extraction Time (Seconds) |
|---|---|---|
| 16.4 | 6.97 | 2.2 |
| 32.8 | 17.81 | 3.38 |
| 49.2 | 11.39 | 3.48 |
| 65.5 | 17.57 | 2.77 |
| 81.9 | 15.95 | 2.41 |
| 98.3 | 10.34 | 2.38 |
| 114.7 | 7.69 | 2.53 |
| 131.1 | 30.4 | 2.68 |
| 147.5 | 27.32 | 2.65 |
| 163.8 | 27.87 | 3.21 |
| 180.2 | 23.73 | 2.88 |
| 196.6 | 15.35 | 2.46 |
| 213.0 | 12 | 2.28 |
| 229.4 | 9.42 | 2.41 |
| 245.8 | 8.45 | 2.45 |
| 262.1 | 6.16 | 2.2 |
| Average | 15.53 | 2.65 |
| Message Length (kbit) | Without Adaptive Embedding (%) | With Adaptive Embedding (%) |
|---|---|---|
| 16.4 | 4.63 | 3.40 |
| 32.8 | 8.97 | 6.52 |
| 49.2 | 13.45 | 10.12 |
| 65.5 | 16.80 | 17.91 |
| 81.9 | 21.01 | 15.20 |
| 98.3 | 25.22 | 19.00 |
| 114.7 | 29.42 | 24.50 |
| 131.1 | 30.44 | 33.63 |
| 147.5 | 34.35 | 24.80 |
| 163.8 | 38.06 | 27.51 |
| 180.2 | 41.96 | 31.20 |
| 196.6 | 45.69 | 34.56 |
| 213.0 | 49.57 | 39.77 |
| 229.4 | 53.30 | 44.58 |
| 245.8 | 57.17 | 52.89 |
| 262.1 | 60.85 | 60.85 |
| Average | 33.18 | 27.90 |
| Image | Embedding Capacity (bpp) | PSNR [9] (dB) | PSNR Proposed (dB) | Computational Time [9] (Seconds) | Computational Time Proposed (Seconds) |
|---|---|---|---|---|---|
| Elaine | 0.0673 | 56.2007 | 58.034 | 3.738 | 7.1448 |
| Boat | 0.0658 | 56.1899 | 58.77 | 3.122 | 4.9716 |
| Lena | 0.0958 | 54.5336 | 56.871 | 3.721 | 6.277 |
| Peppers | 0.0807 | 55.1808 | 57.82 | 3.622 | 7.4901 |
| Baboon | 0.0389 | 58.2953 | 60.972 | 3.726 | 6.6042 |
| House | 0.1181 | 54.593 | 55.157 | 3.656 | 5.0032 |
| F-16 | 0.1378 | 53.478 | 55.193 | 3.839 | 7.8503 |
| Sailboat | 0.0684 | 56.0315 | 58.583 | 3.718 | 8.181 |
| Average | 0.084 | 55.563 | 57.675 | 3.643 | 6.690 |
| Image | PSNR 0.25 bpp (dB) | PSNR 0.5 bpp (dB) | PSNR 0.75 bpp (dB) | SSIM 0.75 bpp | ||||
|---|---|---|---|---|---|---|---|---|
| [23] | Proposed | [23] | Proposed | [7] | Proposed | [7] | Proposed | |
| Lena | 42.85 | 52.284 | 39.83 | 48.713 | 46.3661 | 46.72 | 0.9869 | 0.9889 |
| F-16 | 42.84 | 52.021 | 39.84 | 48.33 | 46.3658 | 46.42 | 0.9869 | 0.9874 |
| Peppers | 42.85 | 52.356 | 39.83 | 48.814 | 46.3670 | 46.958 | 0.9868 | 0.9907 |
| Sailboat | 42.87 | 52.335 | 39.85 | 48.926 | – | – | – | – |
| Boat | 42.81 | 52.367 | 39.81 | 48.888 | 46.3725 | 47.017 | 0.9894 | 0.9930 |
| Baboon | 42.85 | 52.499 | 39.84 | 49.142 | 46.3707 | 47.268 | 0.9932 | 0.9964 |
| Average | 42.85 | 52.310 | 39.83 | 48.802 | 46.3684 | 46.88 | 0.9886 | 0.9913 |
| Data Security Technique | Cover Media | Application | Difference with the Proposed Method |
|---|---|---|---|
| Fractional-order spatial steganography [14] | Printed matter | Anti-counterfeiting for product external packing | Cover media |
| Secure quantum steganography protocol [15] | Quantum channel | Fog cloud | Cover media |
| Lightweight noise resilient steganography scheme [16] | Audio | Securing communications | Cover media |
| EGC protocol [17] | Digital image/video | Healthcare/protection against data infiltration during transmission over the IoT network | Protocol implementing both cryptography and steganography while the proposed method is focused only on data hiding |
| S-Cycle GAN [18] | Digital image | Covert communications | Cover images are generated while in the proposed method data is hidden in the given images |
| Image Steganography Based on Foreground Object Generation by Generative Adversarial Networks [19] | Digital image | Mobile edge computing | Cover images are generated while in the proposed method data is hidden in the given images |
| Secure medical data transmission model [20] | Digital image | Healthcare | The scheme is tested on significantly lower capacities than the proposed method |
| Reversible data hiding exploiting Huffman encoding with dual images [11] | Digital image | Healthcare | Dual stego images and key are used for extraction while in the proposed method one image suffices |
| A reversible and secure patient information hiding system [21] | Digital image | Healthcare | The closest to ours; not enough data to compare imperceptibility at the same capacity and time complexity with the proposed method |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evsutin, O.; Dzhanashia, K. Algorithm of Information Embedding into Digital Images Based on the Chinese Remainder Theorem for Data Security. Cryptography 2020, 4, 35. https://doi.org/10.3390/cryptography4040035
Evsutin O, Dzhanashia K. Algorithm of Information Embedding into Digital Images Based on the Chinese Remainder Theorem for Data Security. Cryptography. 2020; 4(4):35. https://doi.org/10.3390/cryptography4040035
Chicago/Turabian StyleEvsutin, Oleg, and Kristina Dzhanashia. 2020. "Algorithm of Information Embedding into Digital Images Based on the Chinese Remainder Theorem for Data Security" Cryptography 4, no. 4: 35. https://doi.org/10.3390/cryptography4040035
APA StyleEvsutin, O., & Dzhanashia, K. (2020). Algorithm of Information Embedding into Digital Images Based on the Chinese Remainder Theorem for Data Security. Cryptography, 4(4), 35. https://doi.org/10.3390/cryptography4040035






