Tamper and Clone-Resistant Authentication Scheme for Medical Image Systems
Abstract
1. Introduction
- The state of the art of watermarking, PUFs, and some related works are summarized in Section 2.
- The SUC-creation process is briefly presented in Section 3 to make the paper self-contained.
- Section 4 presents our proposed clone-resistant watermarking approach. The benefits of combining SUC and watermarking are carefully discussed and the proposed system operation scenario and its protocols are presented in detail.
- In Section 5, the threat model and security level of the proposed system are analyzed and evaluated. The performance evaluation of our proposed system is estimated through some experimental results.
- Section 6 concludes the paper.
2. Background Motivation and State of the Art
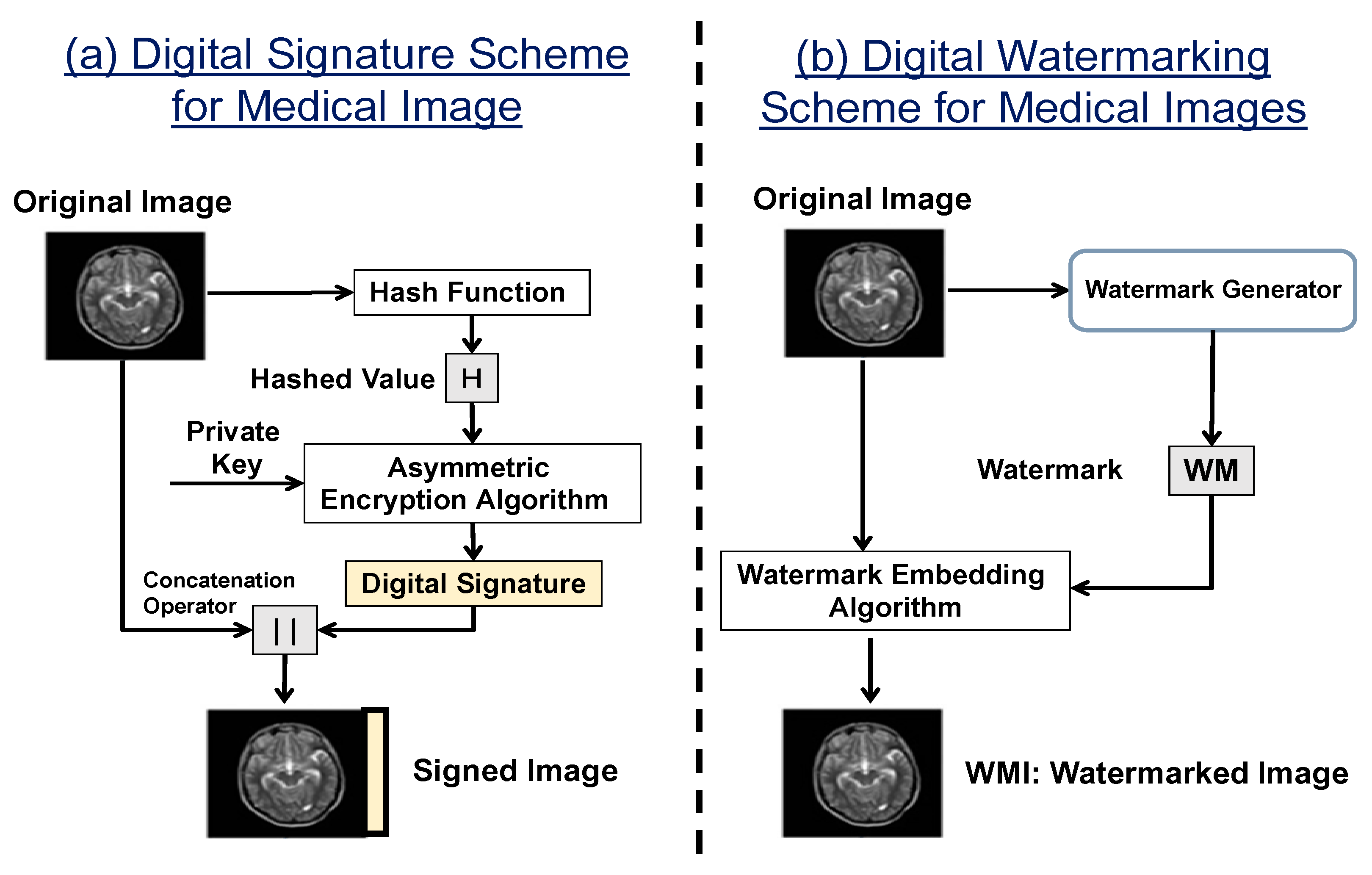
2.1. Combining Watermarking with Cryptographic Primitives
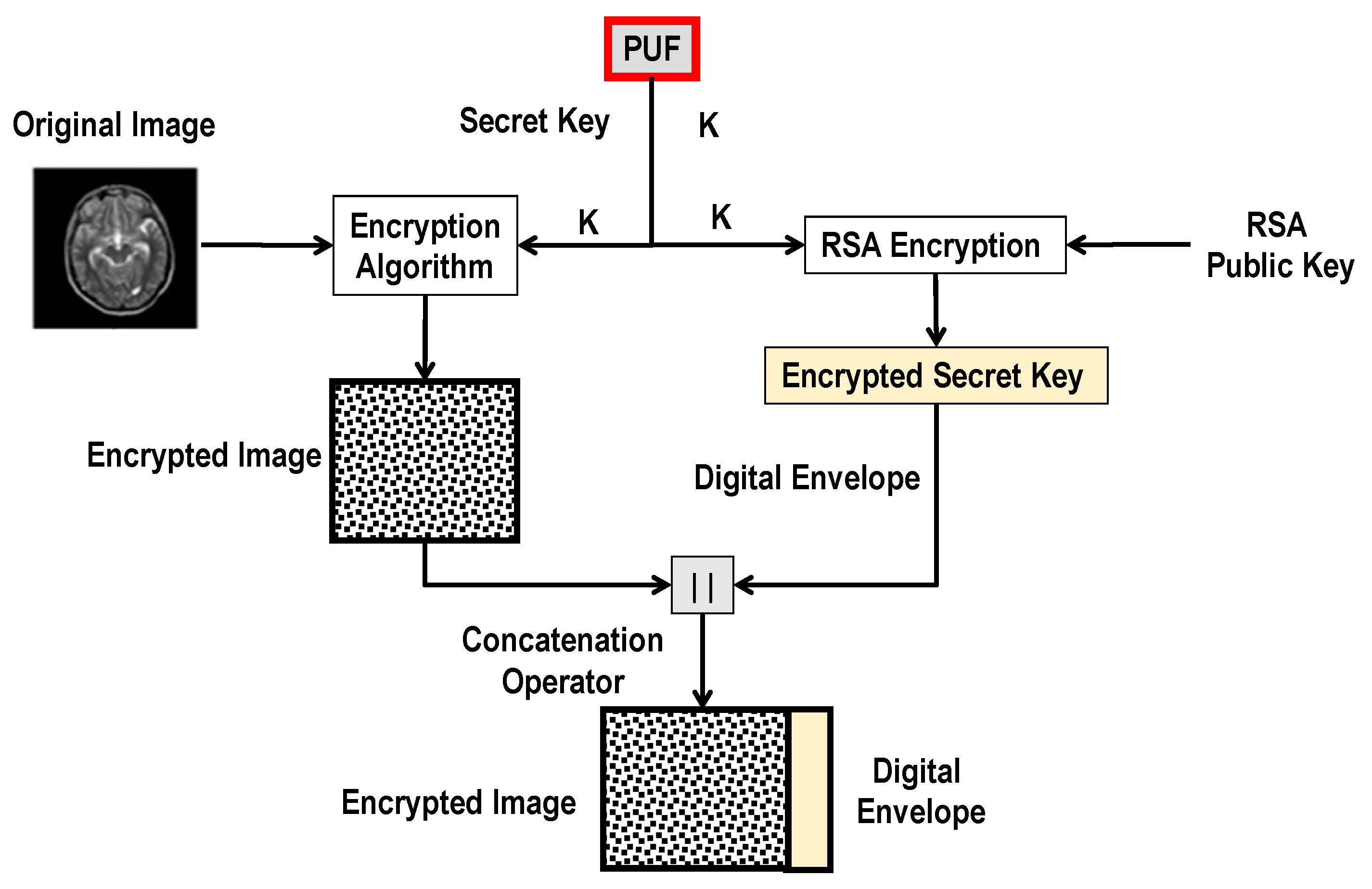
2.2. Unclonable Medical Image Transmission System
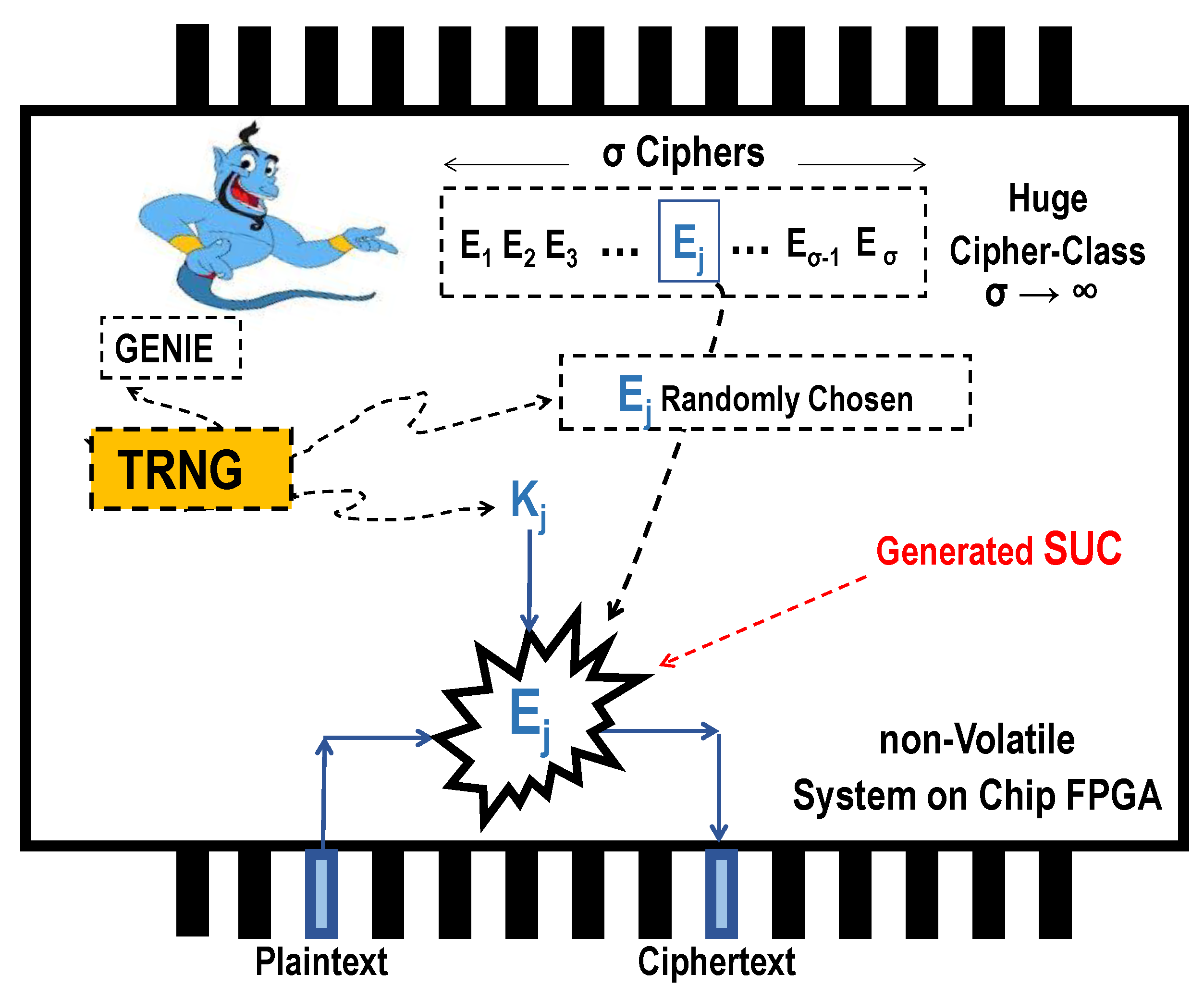
3. The SUC Concept and Its Realization as an Alternative to the PUF
- A non-volatile/flash-based FPGA-fabric.
- Self-reconfigurable FPGA device.
- FPGA with an internal true random number generator (TRNG) meeting the requirements of a NIST standard.
- A cipher-class with large cardinality () is generated.
- A single-event process with the help of the internal TRNG leads to a one-time random choosing of a cipher from the generated class .
- Lastly, all the dashed symbols (entities) are completely eliminated, irreversibly abolished, and fully removed from the chip in Figure 3. What remains inside the chip is just an irreversible, unrepeatable, and unpredictable cipher module as unknown cipher-choice even to the designer himself.
Unknown Ciphers as Clone-Resistant Modules
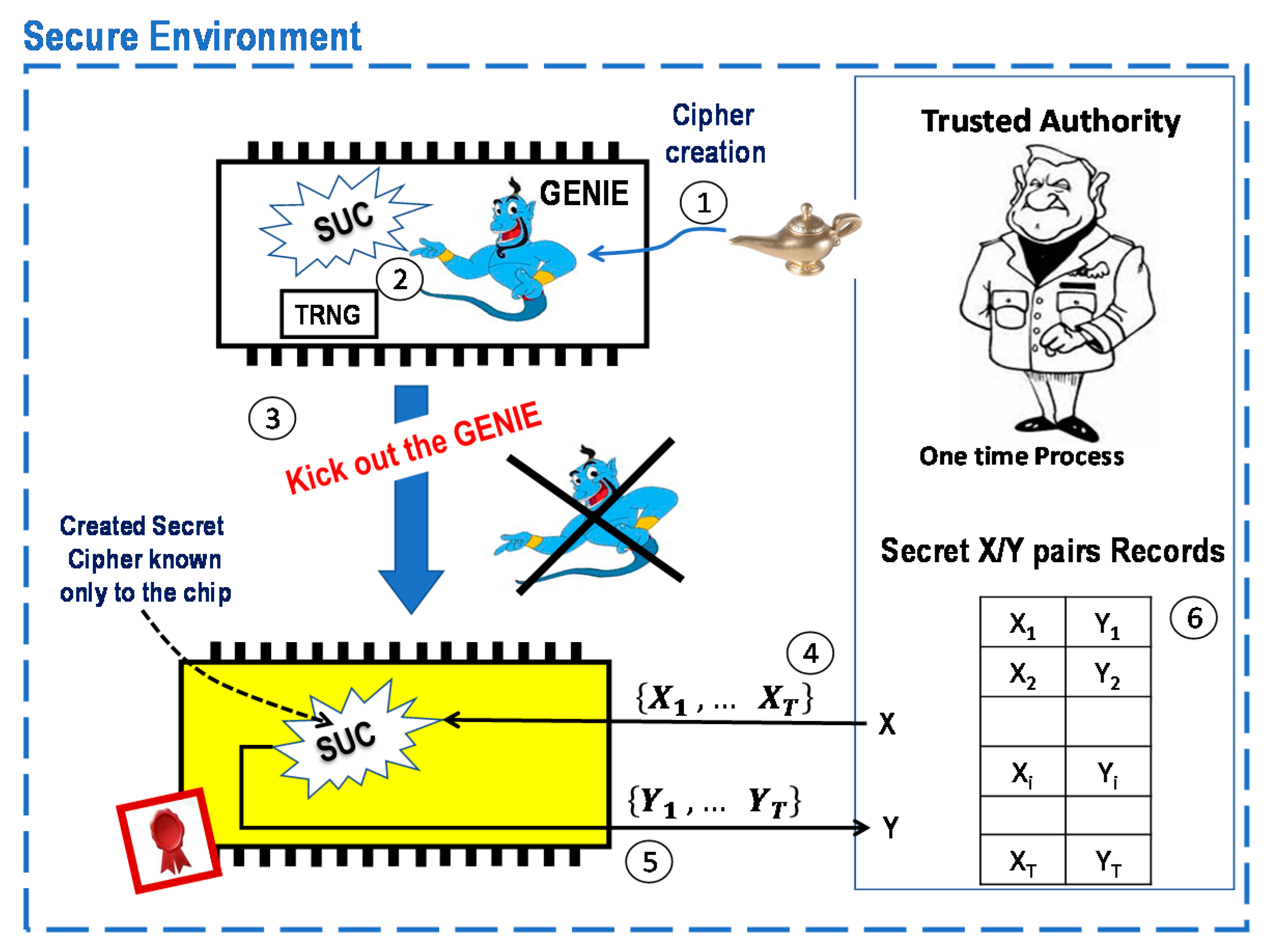
- A software package “GENIE” as an SUC creator is shortly injected by a trusted authority (TA) into a SoC FPGA.
- The GENIE generates/chooses a cipher with the help of an internal unpredictable bit stream from the internal TRNG.
- The GENIE is irreversibly eliminated and completely removed from the SoC FPGA. What remains inside the SoC FPGA is an unchangeable, non-repeatable, and unremovable cipher (SUC) which no one knows.
- 4.
- TA randomly chooses a set of plaintexts out of the 2n possible inputs, where the SUC- input size is n bits input-size.
- 5.
- TA stimulates the SoC with the set of plaintexts to get the corresponding ciphertexts {y1, … yT} using its SUC.
- 6.
- TA stores the resulting SUC T-(xi, yi) pair in a secret pair record for later use.
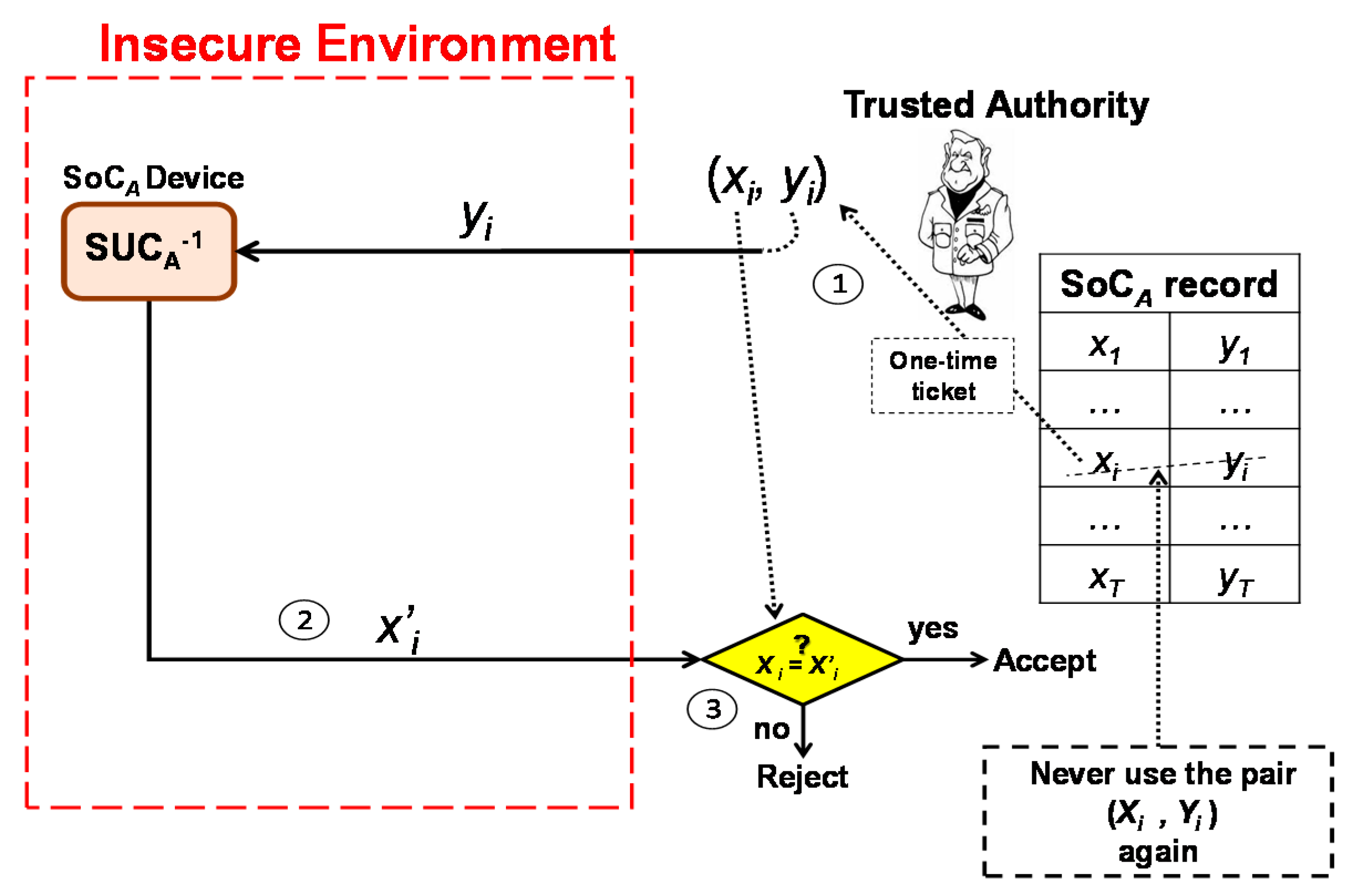
- TA randomly chooses a pair (xi, yi) from the secret records of SoCA. Then, the TA sends yi to SoCA.
- The SoCA device decrypts yi by using its SUCA and sends the plaintext x’i to TA.
- SoCA is authentic when x’i = xi. TA then marks the pair (xi, yi) as a used pair and never uses it again.
4. A Proposed New Secured Unclonable Medical Watermarking Scheme
- (i)
- Medical images are not repeatable and are non-replaceable.
- (ii)
- Medical images are non-splice-able.
- (iii)
- Non-repudiation.
- (iv)
- Provably unique medical images.
- (v)
- Integrity guarantee.
- (vi)
- Authentication.
4.1. The Proposed Medical Image System Architecture
- (i)
- Medical images are not repeatable and are non-replaceable.
- (ii)
- Provably unique medical images.
- (iii)
- Selective authentication privilege.
4.2. The Proposed Embedding and Extraction of Clone-Resistant Watermarking
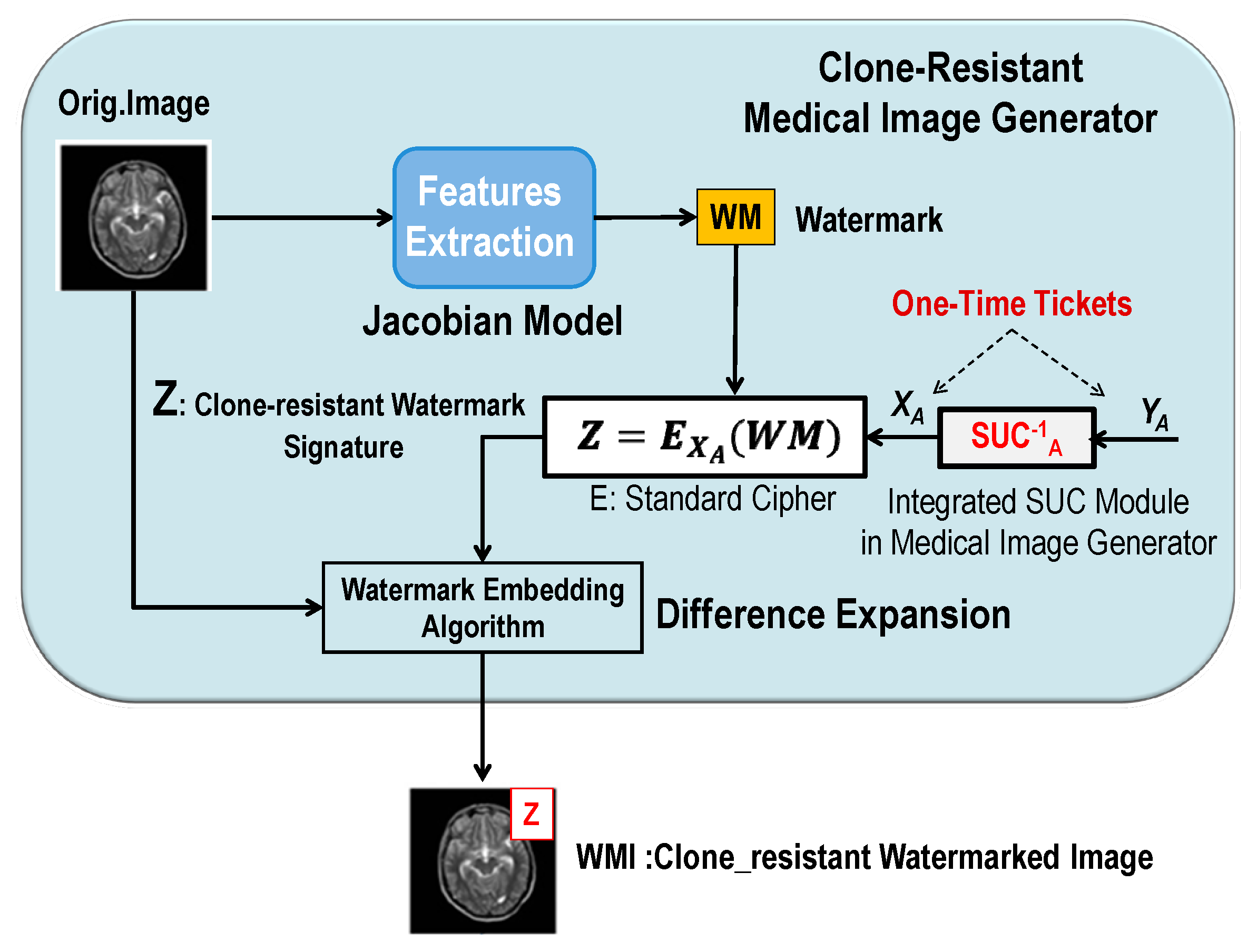
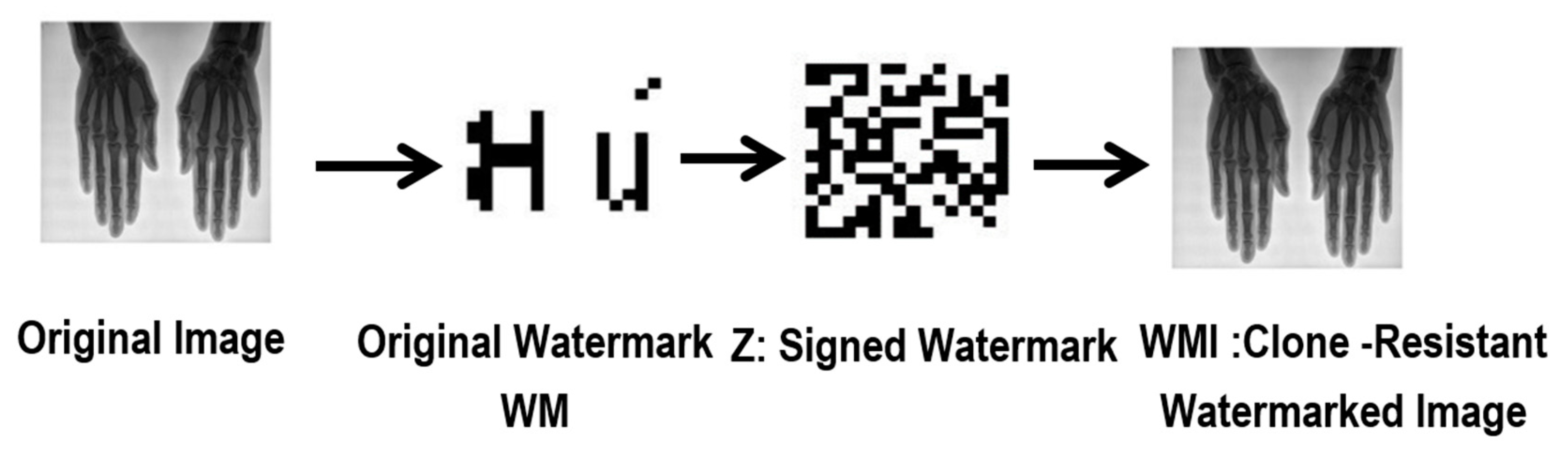
4.2.1. Generating, Signing, and Embedding Watermarks (One-Time Watermark Signature)
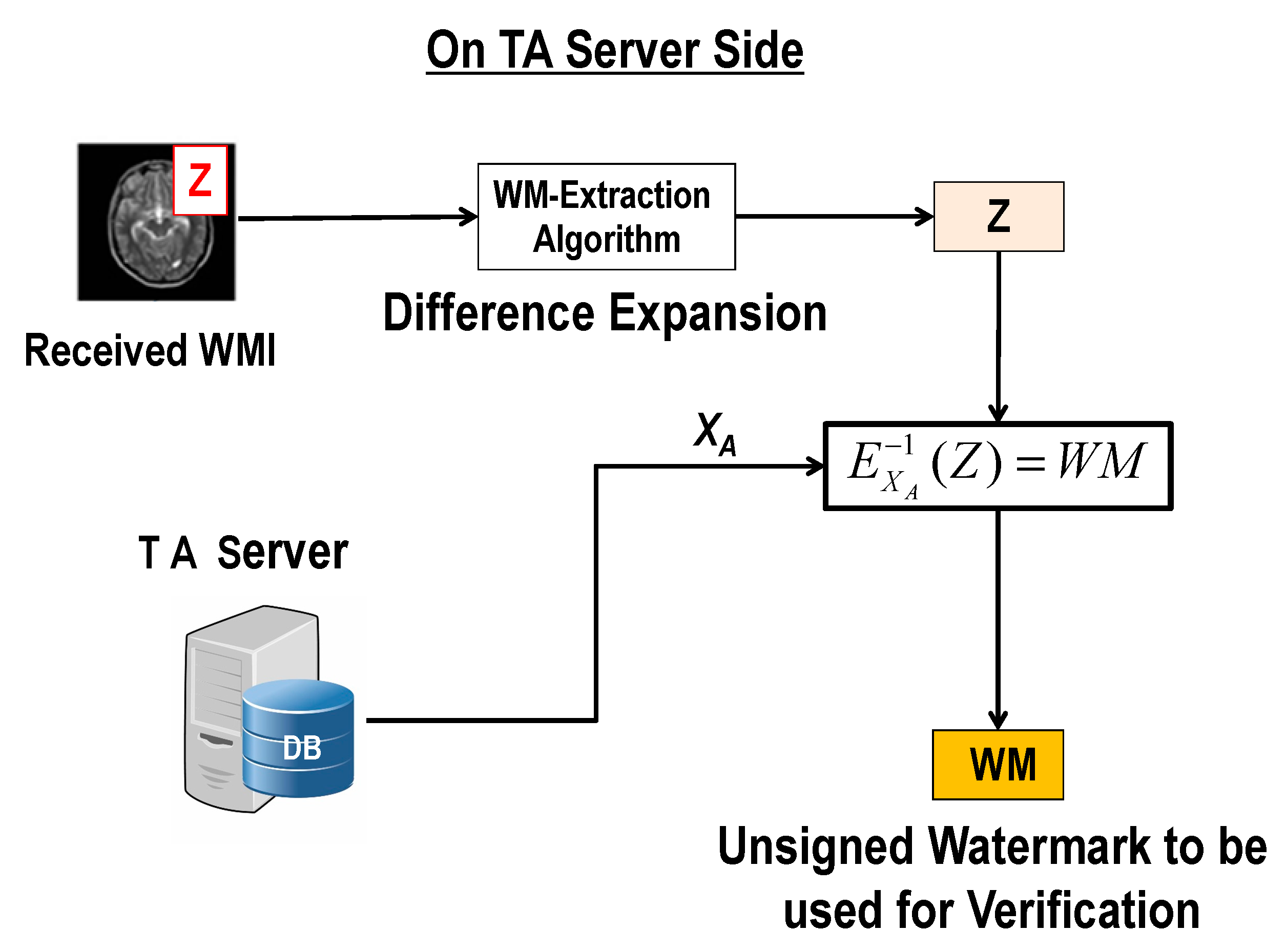
4.2.2. Procedure of Extraction and Verification of the Watermark
4.3. System Analysis: Benefits of Combining SUC and Watermarking
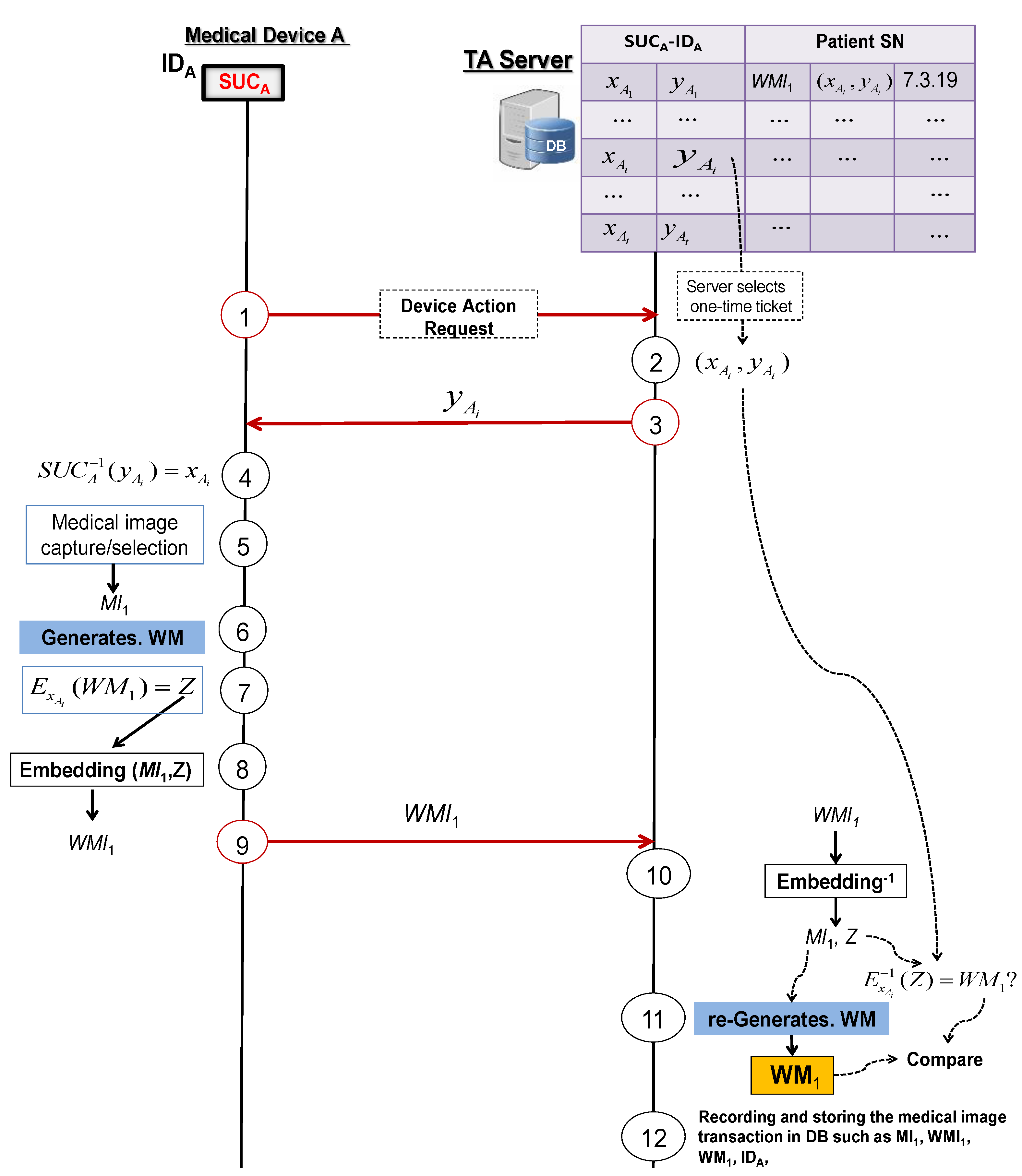
4.3.1. Protocol 1: Secured Logging of a Medical Image Transaction
- Medical device A asks the TA server to start the process of generating a watermarked image.
- The TA server randomly selects a ticket from the medical device A’s secret record in DB.
- The TA server answers with .
- Medical device A computes by using its SUC as .
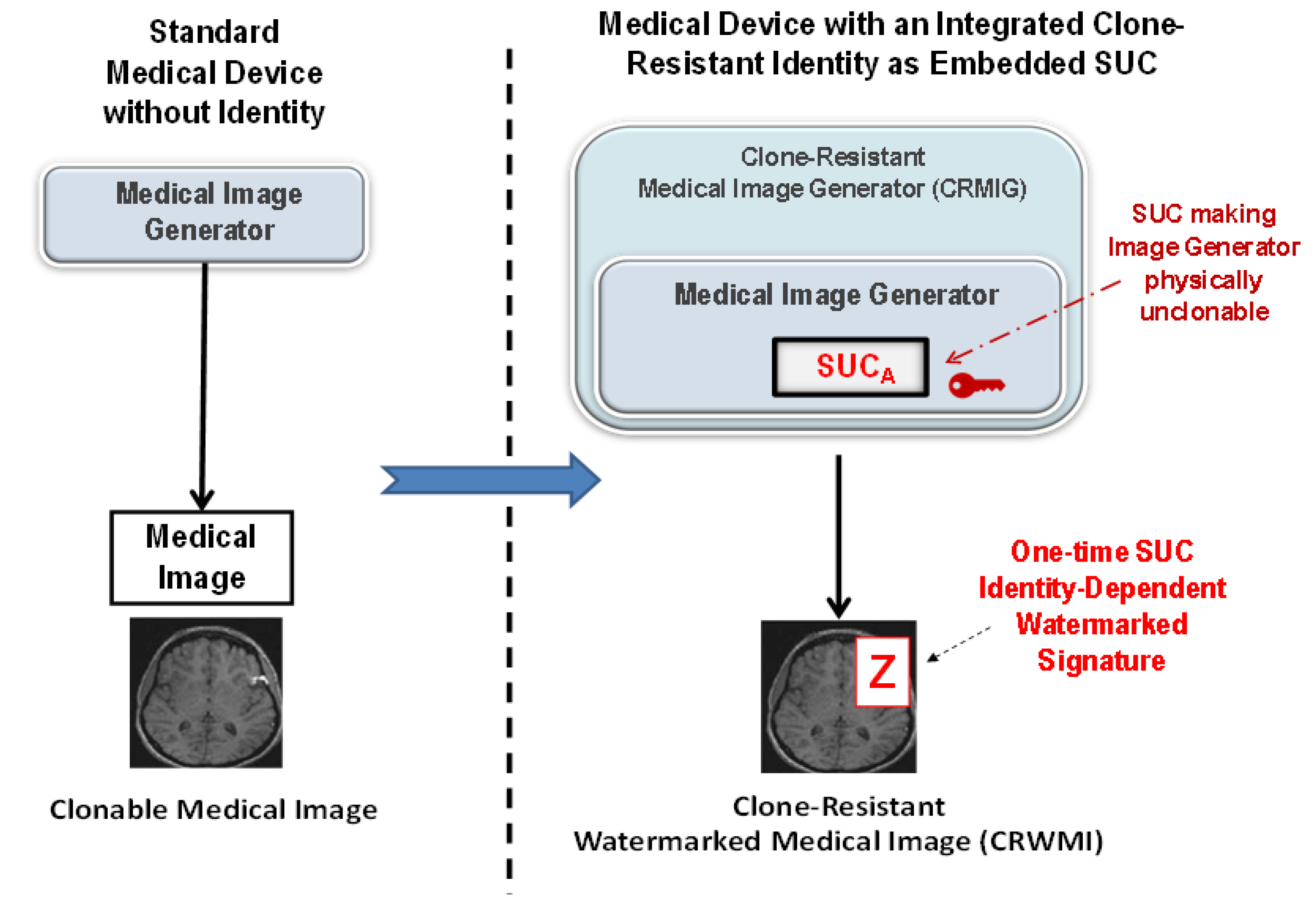
- Medical device A generates or selects a medical image .
- Medical device A generates a watermark from .
- Medical device A signs the generated watermark by using a standard cipher E with the secret key as: .
- Medical device A embeds the signed watermark Z in the original image to generate the clone-resistant medical watermarked image .
- Medical device A sends to the TA server.
- TA server reverses the embedding algorithm to extract Z and to recover the medical image from the received watermarked image and then uses to recover the watermark .
- TA server generates from the recovered medical image and rejects if ≠.
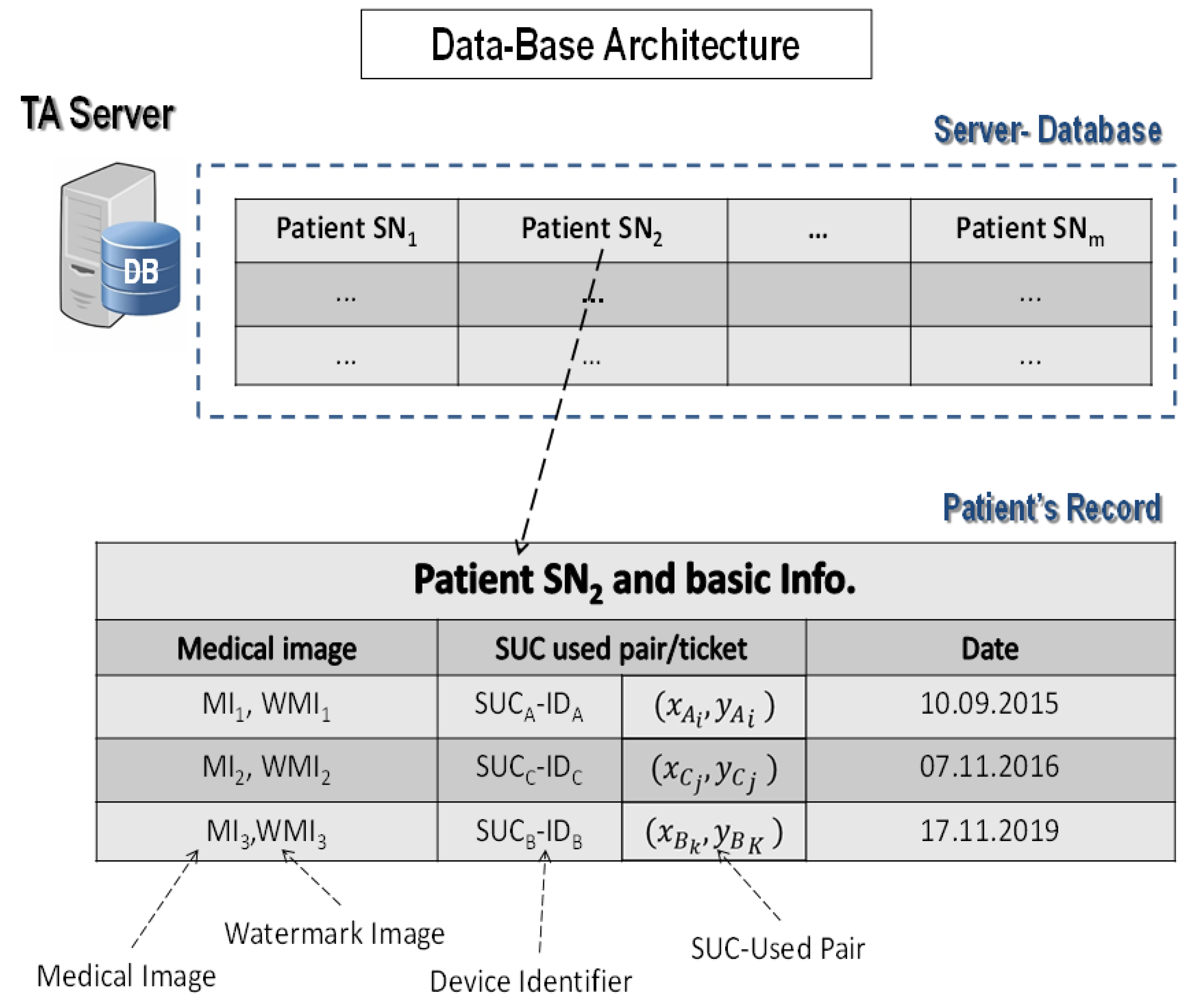
- TA server stores and registers the medical image transaction and , together with the used ticket in DB for later use.
- (i)
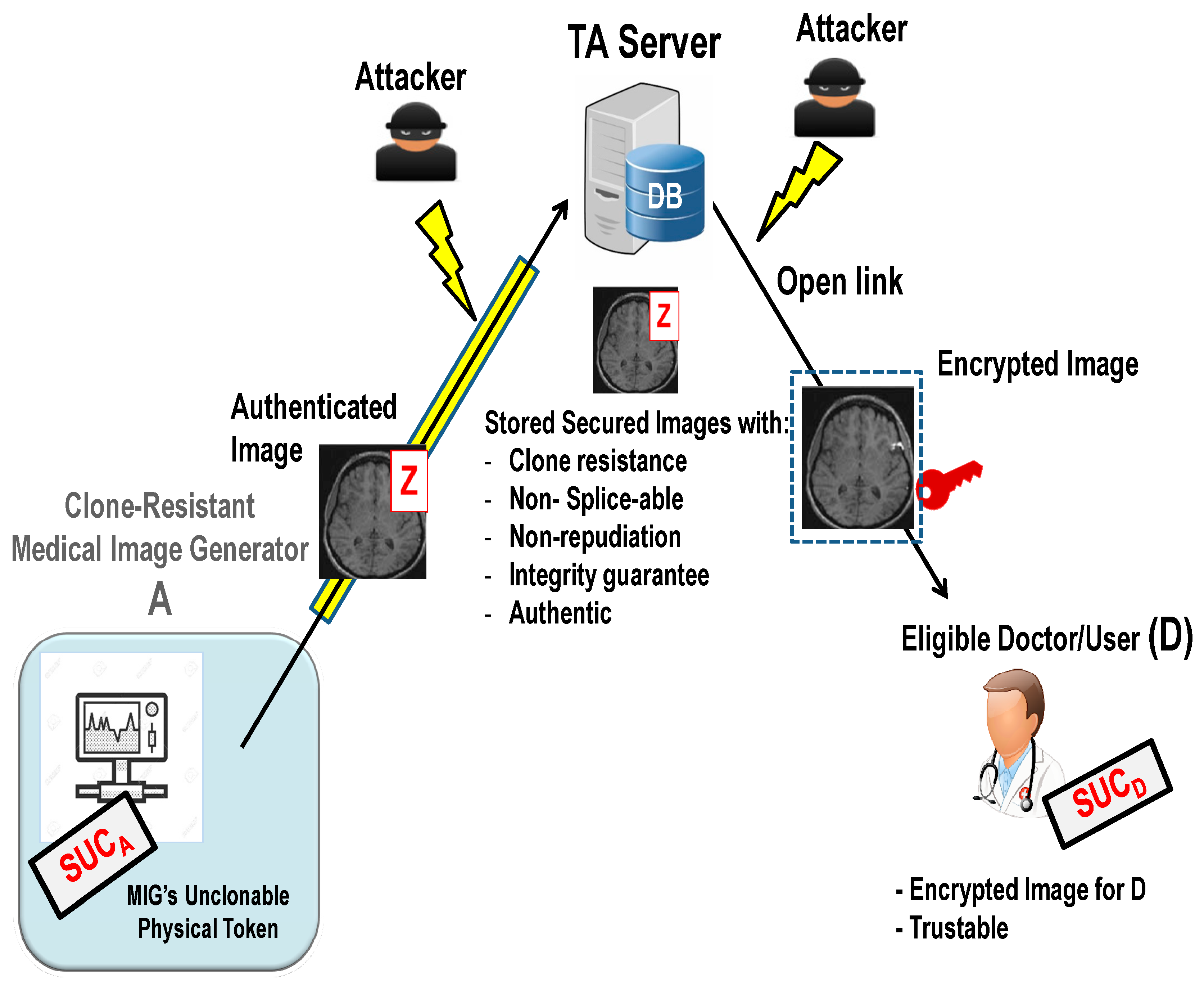
- Medical device A generates a clone-resistant watermarked image by deploying its SUCA.
- (ii)
- The resulting watermarked image is authentic and tamper-resistant.
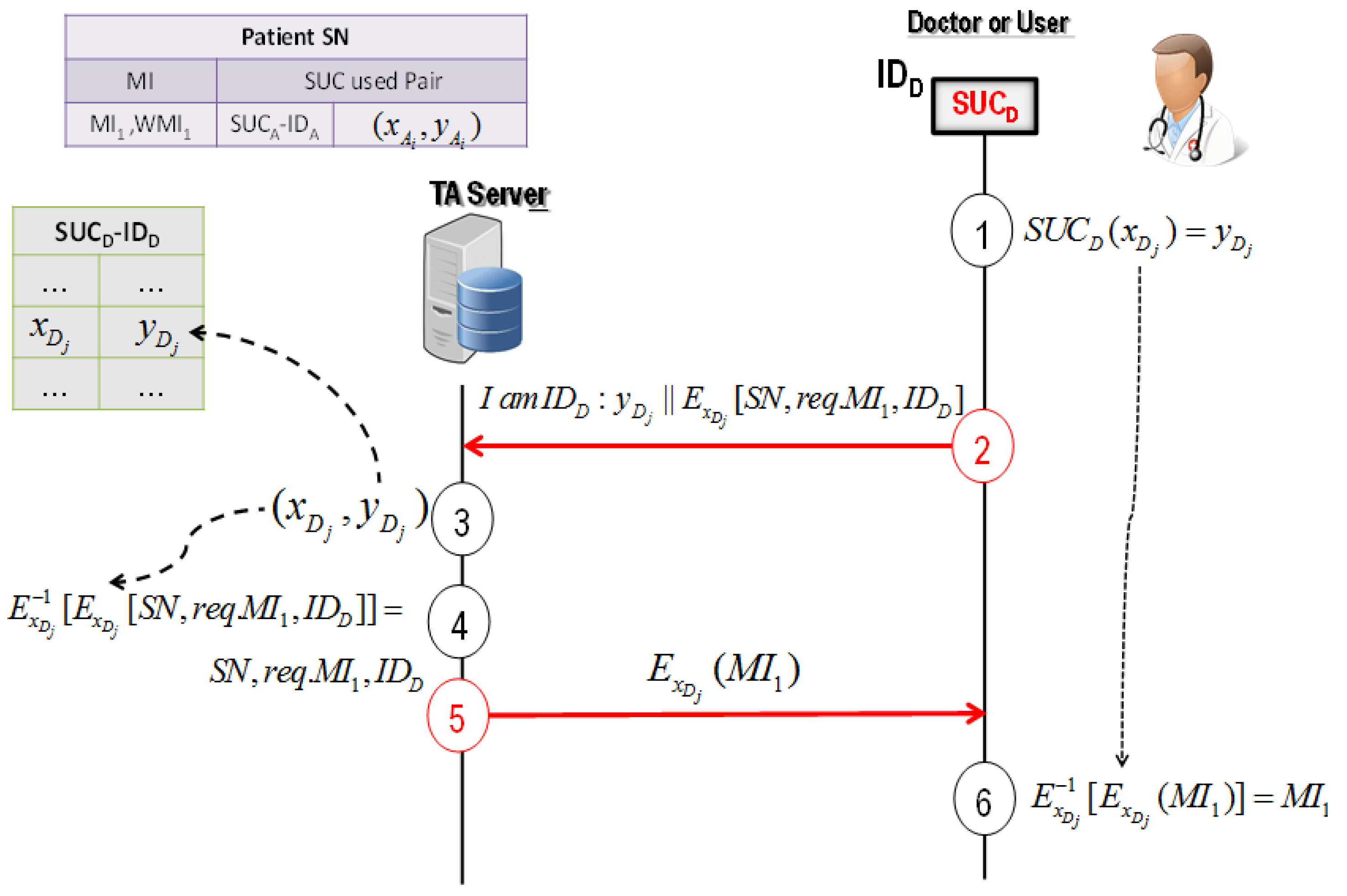
4.3.2. Protocol 2: User-Server Authentication Protocol for Image Verification
- Doctor D randomly selects and computes the corresponding cyphertext by using its SUCD.
- Doctor D asks the TA server to send the required medical image of the patient SN as , where is the request of the medical image and is a public identifier of doctor D.
- TA server uses to determine from the device D’s secret record in DB.
- TA server decrypts the received message . If the decrypted matches the public identifier of doctor D, the TA server registers the request of the medical image and doctor D cannot deny using .
- TA server answers with , where is the medical image.
- Doctor D decrypts the received message: . It should be noted that doctor D cannot generate or predict the signed watermark Z of stored in DB (see Section 5). Therefore, doctor D cannot change and fake .
- (i)
- Doctor D cannot deny using the image generated by medical device A.
- (ii)
- The stored image in the TA server cannot be changed or faked later by doctor D.
- (iii)
- TA server knows undeniably “who and when” a user such as doctor D was using the medical image.
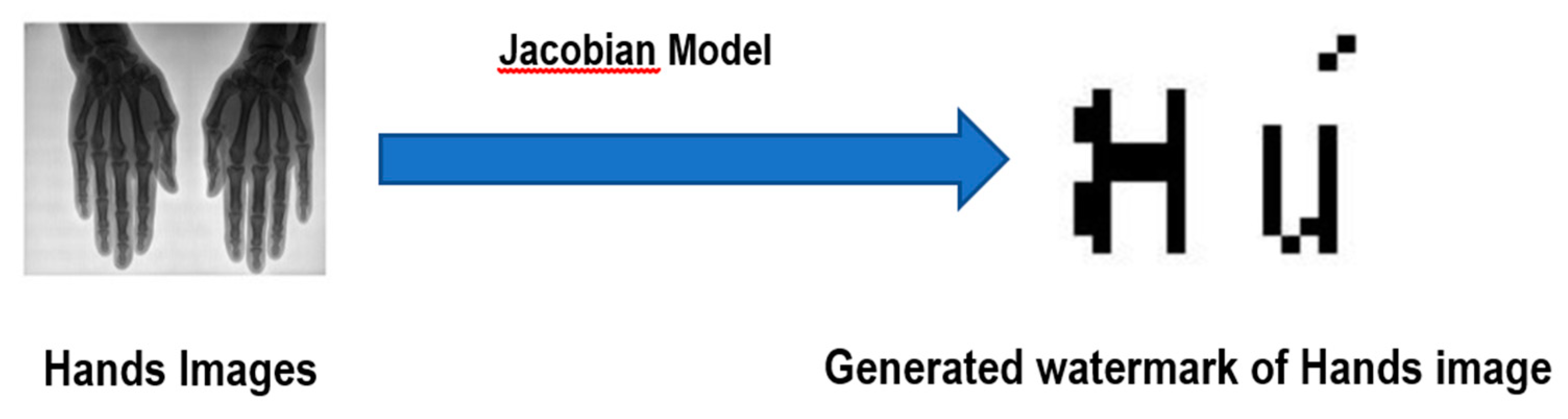
4.4. The Jacobian Model for Generating Watermarks
Watermark Generation Using the Jacobian Model
5. Watermarking Analysis and Security Evaluation
5.1. Security Analysis of the Proposed Protocols
5.1.1. Adversary Model
- Ψ can run any medical device with an integrated SUC.
- Ψ can listen to the transmitted and exchanged messages between the TA server and the medical devices.
- Ψ can exchange messages with the medical devices and the TA server.
5.1.2. Man-in-the-Middle Attack
5.1.3. Tampering Attacks
- Every functioncan be uniquely identified by a specific key.
- Every probabilistic polynomial time (p.p.t.) adversary has a negligible advantage to distinguish between the output ofand a random value.
- The challenger arbitrarily selects one bit .
- The challenger returns , if to ; otherwise, it returns , within time .
5.2. Experimental Results
5.2.1. Imperceptibility Analysis
5.2.2. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Universal Declaration of Human Rights | United Nations. Available online: https://www.un.org/en/universal-declaration-human-rights/index.html (accessed on 8 January 2020).
- Kobayashi, L.O.M.; Furuie, S.S.; Barreto, P.S.L.M. Providing integrity and authenticity in DICOM images: A novel approach. Proc. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 582–589. [Google Scholar] [CrossRef] [PubMed]
- Sittig, D.F.; Wright, A.; Coiera, E.; Magrabi, F.; Ratwani, R.; Bates, D.W.; Singh, H. Current challenges in health information technology-related patient safety. Health Inform. J. 2018, 26, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Coatrieux, G.; Maître, H.; Sankur, B.; Rolland, Y.; Collorec, R. Relevance of watermarking in medical imaging. In Proceedings of the IEEE/EMBS Region 8 International Conference on Information Technology Applications in Biomedicine, ITAB, Arlington, VA, USA, 9–10 November 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 250–255. [Google Scholar]
- Bhunia, S.; Tehranipoor, M. Hardware Security Primitives. In Hardware Security; Elsevier: Amsterdam, The Netherlands, 2019; pp. 311–345. [Google Scholar]
- Tu, Y.S.; Chen, J. A secure and unclonable medical image transmission system by using embedded physical uncloneable function. In Proceedings of the 2016 International Conference on Communication Problem-Solving, ICCP, Taipei, Taiwan, 7–9 September 2016; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2016. [Google Scholar]
- Delvaux, J.; Peeters, R.; Gu, D.; Verbauwhede, I. A Survey on Lightweight Entity Authentication with Strong PUFs. ACM Comput. Surv. 2015, 48, 1–42. [Google Scholar] [CrossRef]
- Adi, W.; Ouertani, N.; Hanoun, A.; Soudan, B. Deploying FPGA self-configurable cell structure for micro crypto-functions. In Proceedings of the 2009 IEEE Symposium on Computers and Communications, Sousse, Tunisia, 5–8 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 348–354. [Google Scholar]
- Adi, W. Clone-Resistant DNA-Like Secured Dynamic Identity. In Proceedings of the 2008 Bio-Inspired, Learning and Intelligent Systems for Security, Edinburgh, UK, 4–6 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 148–153. [Google Scholar]
- Ghadi, M.; Laouamer, L.; Nana, L.; Pascu, A. A novel zero-watermarking approach of medical images based on Jacobian matrix model. Secur. Commun. Netw. 2016, 9, 5203–5218. [Google Scholar] [CrossRef]
- Van Schyndel, R.G.; Tirkel, A.Z.; Osborne, C.F. A digital watermark. In Proceedings of the International Conference on Image Processing, ICIP, Austin, TX, USA, 13–16 November 1994; IEEE Computer Society: Piscataway, NJ, USA, 1994; Volume 2, pp. 86–90. [Google Scholar]
- Chao, H.M.; Hsu, C.M.; Miaou, S.G. A data-hiding technique with authentication, integration, and confidentiality for electronic patient records. IEEE Trans. Inf. Technol. Biomed. 2002, 6, 46–53. [Google Scholar] [CrossRef]
- Nyeem, H.; Boles, W.; Boyd, C. A review of medical image watermarking requirements for teleradiology. J. Digit. Imaging 2013, 26, 326–343. [Google Scholar] [CrossRef]
- Coatrieux, G.; Lecornu, L.; Sankur, B.; Roux, C. A review of image watermarking applications in healthcare. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology, New York, NY, USA, 30 August–3 September 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 4691–4694. [Google Scholar]
- Memon, N.A.; Keerio, Z.A.; Abbasi, F. Dual watermarking of CT scan medical images for content authentication and copyright protection. Commun. Comput. Inf. Sci. 2013, 414, 173–183. [Google Scholar] [CrossRef]
- Bouslimi, D.; Coatrieux, G. A crypto-watermarking system for ensuring reliability control and traceability of medical images. Signal Process. Image Commun. 2016, 47, 160–169. [Google Scholar] [CrossRef]
- Metkar, S.P.; Lichade, M.V. Digital image security improvement by integrating watermarking and encryption technique. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Computing and Control, ISPCC 2013, Shimla, India, 26–28 September 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Dagadu, J.C.; Li, J. Context-based watermarking cum chaotic encryption for medical images in telemedicine applications. Multimed. Tools Appl. 2018, 77, 24289–24312. [Google Scholar] [CrossRef]
- Bouslimi, D.; Coatrieux, G.; Cozic, M.; Roux, C. Combination of watermarking and joint watermarking-decryption for reliability control and traceability of medical images. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC, Chicago, IL, USA, 26–30 August 2014; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2014; pp. 4495–4498. [Google Scholar]
- AlShaikh, M.; Laouamer, L.; Nana, L.; Pascu, A.C. Efficient and robust encryption and watermarking technique based on a new chaotic map approach. Multimed. Tools Appl. 2017, 76, 8937–8950. [Google Scholar] [CrossRef]
- Parah, S.A.; Sheikh, J.A.; Ahad, F.; Loan, N.A.; Bhat, G.M. Information hiding in medical images: A robust medical image watermarking system for E-healthcare. Multimed. Tools Appl. 2017, 76, 10599–10633. [Google Scholar] [CrossRef]
- Singh, A.; Dutta, M.K. A robust zero-watermarking scheme for tele-ophthalmological applications. J. King Saud Univ.–Comput. Inf. Sci. 2017. [Google Scholar] [CrossRef]
- Bouslimi, D.; Coatrieux, G.; Roux, C. A joint encryption/watermarking algorithm for verifying the reliability of medical images: Application to echographic images. Comput. Methods Programs Biomed. 2012, 106, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Chaduvula, S.C.; Dachowicz, A.; Atallah, M.J.; Panchal, J.H. Security in cyber-enabled design and manufacturing: A survey. J. Comput. Inf. Sci. Eng. 2018, 18. [Google Scholar] [CrossRef]
- Zimmermann, P. PGP User’s Guide; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Gassend, B.L.P. Physical Random Functions. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Marchand, C.; Bossuet, L.; Mureddu, U.; Bochard, N.; Cherkaoui, A.; Fischer, V. Implementation and Characterization of a Physical Unclonable Function for IoT: A Case Study With the TERO-PUF. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2018, 37, 97–109. [Google Scholar] [CrossRef]
- Lim, D.; Lee, J.W.; Gassend, B.; Suh, G.E.; van Dijk, M.; Devadas, S. Extracting secret keys from integrated circuits. IEEE Trans. Very Large Scale Integr. Syst. 2005, 13, 1200–1205. [Google Scholar] [CrossRef]
- Gołofit, K.; Wieczorek, P. Chaos-Based Physical Unclonable Functions. Appl. Sci. 2019, 9, 991. [Google Scholar] [CrossRef]
- Adi, W.; Zeitouni, S.; Huang, X.; Fyrbiak, M.; Kison, C.; Jeske, M.; Alnahhas, Z. IP-core protection for a non-volatile Self-reconfiguring SoC environment. In Proceedings of the 2013 IFIP/IEEE 21st International Conference on Very Large Scale Integration (VLSI-SoC), Istanbul, Turkey, 6–9 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 252–255. [Google Scholar]
- Mulhem, S.; Adi, W. New Mathblocks-Based Feistel-Like Ciphers for Creating Clone-Resistant FPGA Devices. Cryptography 2019, 3, 28. [Google Scholar] [CrossRef]
- Mulhem, S.; Mars, A.; Adi, W. Low-Complexity Nonlinear Self-Inverse Permutation for Physically Clone-Resistant Identities. Cryptography 2019, 4, 6. [Google Scholar] [CrossRef]
- Adi, W.; Soudan, B. Bio-Inspired Electronic-Mutation with genetic properties for Secured Identification. In Proceedings of the ECSIS Symposium on Bio-inspired, Learning, and Intelligent Systems for Security, Edunburgh, UK, 9–10 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 133–136. [Google Scholar]
- Mulhem, S.; Mohammad, M.; Adi, W. A New Low-Complexity Cipher Class for Clone-Resistant Identities. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 971–976. [Google Scholar]
- Fekri-Ershad, S. A Review on Image Texture Analysis Methods. arXiv 2018, arXiv:1804.00494. [Google Scholar]
- Bellare, M.; Rogaway, P. Introduction to Modern Cryptography. 2005. Available online: http://almuhammadi.com/sultan/crypto_books/BR.2005.pdf (accessed on 3 July 2020).
- Mulhem, S.; Zarrouk, R.; Adi, W. Security and Complexity Bounds of SUC-Based Physical Identity. In Proceedings of the 2018 NASA/ESA Conference on Adaptive Hardware and Systems (AHS), Edinburgh, UK, 6–9 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 317–322. [Google Scholar]
- Mishra, M.; Adhikary, M.C. Detection of Clones in Digital Images. Int. J. Comput. Sci. Bus. Inform. 2014, 9, 91–102. [Google Scholar]
- Goldreich, O.; Goldwasser, S.; Micali, S. How to construct random functions. J. ACM 1986, 33, 792–807. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Singh, A.K.; Kumar, B.; Saini, J.P. Quantization based multiple medical information watermarking for secure e-health. Multimed. Tools Appl. 2019, 78, 3911–3923. [Google Scholar] [CrossRef]
- Thakur, S.; Singh, A.K.; Ghrera, S.P.; Elhoseny, M. Multi-layer security of medical data through watermarking and chaotic encryption for tele-health applications. Multimed. Tools Appl. 2019, 78, 3457–3470. [Google Scholar] [CrossRef]
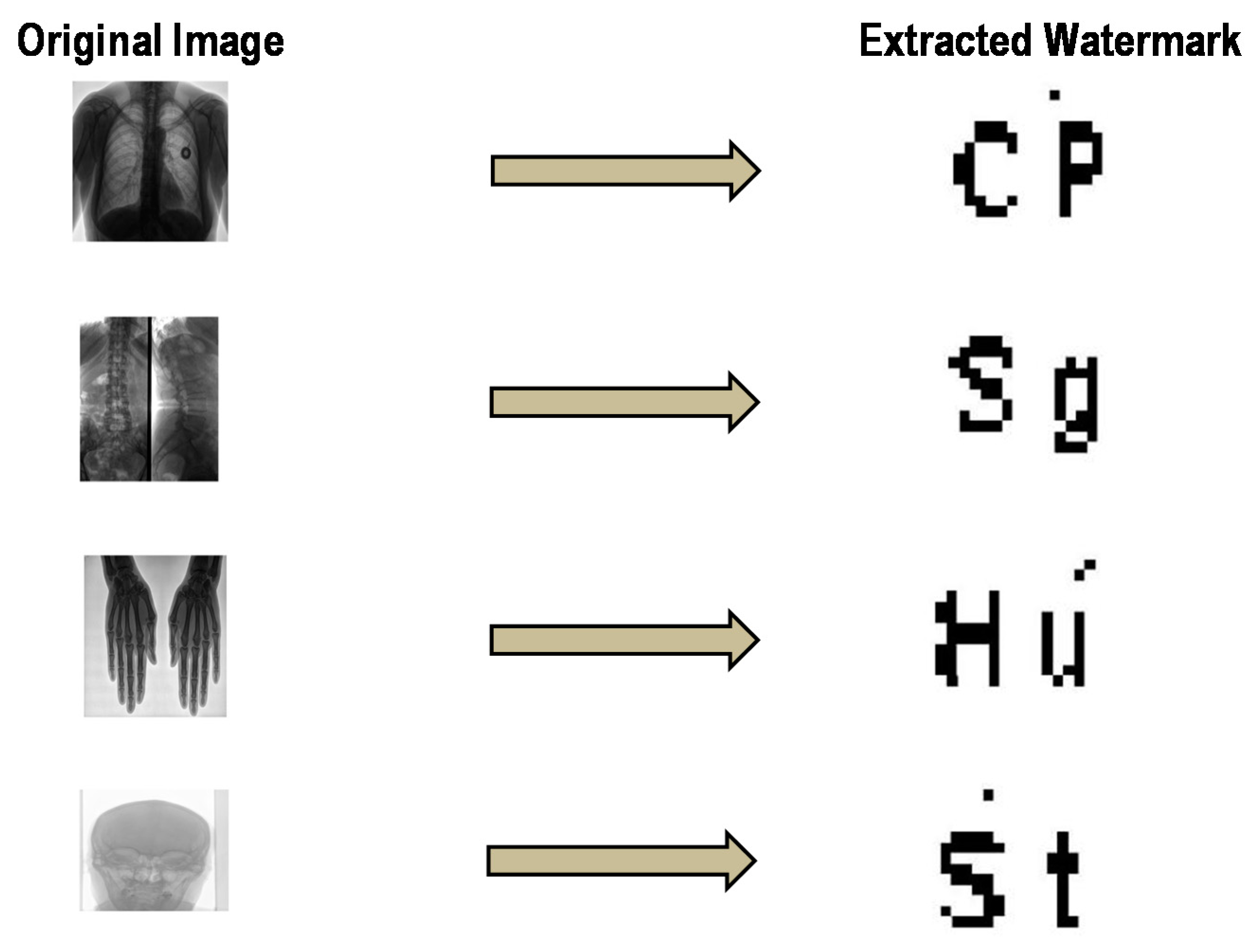

| Image | SSIM | PSNR |
|---|---|---|
| Chest | 0.9861 | 38.15 |
| Tspine | 0.9895 | 37.77 |
| Hands | 0.9997 | 49.52 |
| Skull | 0.9995 | 52.89 |
| Attacks | Average SSIM | Average PSNR |
|---|---|---|
| Median filtering 2 × 2 | 0.9776 | 50.49 |
| Median filtering 3 × 3 | 0.9748 | 54.80 |
| Salt and pepper (0.01) | 0.9820 | 50.69 |
| Average filtering 3 × 3 | 0.9624 | 55.92 |
| Cropping left top corner | 0.9741 | 52.23 |
| Gaussian filtering 3 × 3 | 0.9844 | 50.00 |
| Histogram equalization | 0.9874 | 50.15 |
| Gaussian noise (0.01) | 0.9779 | 53.72 |
| Rotation 1° | 0.9977 | 52.12 |
| Rotation 5° | 0.9906 | 49.99 |
| Rotation 10° | 0.9838 | 55.60 |
| Sharpening | 0.9854 | 57.25 |
| Translate (10) | 0.9782 | 52.85 |
| Blurring | 0.9847 | 57.69 |
| Contrast Enhancement | 0.9999 | 56.96 |
| Scaling | 0.9882 | 52.69 |
| Wiener filtering | 0.9707 | 55.58 |
| Attacks | Average BER | Average NC |
|---|---|---|
| Median filtering 2 × 2 | 0.0080 | 0.9494 |
| Median filtering 3 × 3 | 0.0214 | 0.9427 |
| Salt and pepper (0.01) | 0.0333 | 0.9099 |
| Average filtering 3 × 3 | 0.0203 | 0.9407 |
| Cropping left top corner | 0.0575 | 0.8445 |
| Gaussian filtering 3 × 3 | 0.0172 | 0.9488 |
| Histogram equalization | 0.0918 | 0.4929 |
| Gaussian noise (0.01) | 0.0284 | 0.8980 |
| Rotation 1° | 0.0221 | 0.9881 |
| Rotation 5° | 0.0235 | 0.9260 |
| Rotation 10° | 0.0243 | 0.9226 |
| Sharpening | 0.0047 | 0.9852 |
| Translate (10) | 0.0202 | 0.9287 |
| Blurring | 0.0847 | 0.9904 |
| Contrast Enhancement | 0.0126 | 0.9530 |
| Scaling | 0.0112 | 0.9558 |
| Wiener filtering | 0.0536 | 0.9819 |
| Attacks | Proposed Method | [18] | [40] | [21] | [22] |
|---|---|---|---|---|---|
| Cropping left top corner 25% | 0.0575 | 0 | - | 0.0566 | - |
| Noise attack (0.01) | 0.0284 | 0.1418 | - | - | - |
| Salt and pepper noise (0.01) | 0.0333 | 0.4323 | - | 0.0175 | - |
| Sharpening | 0.0047 | - | 0.0180 | 0.0026 | 0 |
| Histogram equalization | 0.0918 | - | 0.0259 | 0.0080 | - |
| Gaussian filter | 0.0102 | - | 0.0117 | - | - |
| Median filtering 2 × 2 | 0.0080 | - | 0.0027 | 0.0596 | 0.0383 |
| Wiener filtering | 0.0536 | - | - | 0.0488 | 0 |
| Average filtering | 0.0150 | - | - | 0.0654 | - |
| Gaussian noise (0.0001) | 0.0994 | - | - | 0.0800 | - |
| Gaussian noise (0.01) | 0.0284 | - | - | - | 0 |
| Rotation 1° | 0.0221 | - | - | 0.0259 | - |
| Rotation 5° | 0.0235 | - | - | 0.0283 | - |
| Rotation 10° | 0.0243 | - | - | 0.0330 | 0.0597 |
| Blurring | 0.0847 | - | 0.0738 | - | - |
| Contrast Enhancement | 0.0126 | - | 0.0131 | - | - |
| Attacks | Proposed Method | [18] | [40] | [21] | [41] |
|---|---|---|---|---|---|
| Cropping left top corner 25% | 0.8445 | 0.9997 | - | 1 | 0.9966 |
| Noise attack (0.01) | 0.9114 | 0.9589 | - | - | - |
| Salt and pepper noise (0.01) | 0.9099 | 0.9589 | - | - | 0.9758 |
| Sharpening | 0.9852 | - | 0.9018 | 0.9977 | 0.8898 |
| Histogram equalization | 0.4929 | - | 0.8556 | 0.9921 | 0.6038 |
| Gaussian filter | 0.9488 | - | 0.9322 | - | - |
| Median filtering 2 × 2 | 0.9494 | - | - | - | 0.6973 |
| Median filtering 3 × 3 | 0.9427 | - | 0.9845 | 0.9430 | - |
| Wiener filtering | 0.9819 | - | - | 0.9539 | - |
| Average filtering | 0.9407 | - | - | 0.9354 | - |
| Gaussian noise (0.0001) | 0.9856 | - | - | 0.9215 | 0.9979 |
| Gaussian noise (0.01) | 0.9114 | - | - | - | 0.9144 |
| Rotation 1° | 0.9881 | - | - | 0.9728 | 0.9460 |
| Rotation 5° | 0.9260 | - | - | 0.9695 | - |
| Rotation 10° | 0.9226 | - | - | 0.9653 | - |
| Gaussian low pass filter | 0.9488 | - | - | - | 0.5406 |
| Image scaling ×1.1 | 0.9558 | - | - | - | 0.9309 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tayachi, M.; Mulhem, S.; Adi, W.; Nana, L.; Pascu, A.; Benzarti, F. Tamper and Clone-Resistant Authentication Scheme for Medical Image Systems. Cryptography 2020, 4, 19. https://doi.org/10.3390/cryptography4030019
Tayachi M, Mulhem S, Adi W, Nana L, Pascu A, Benzarti F. Tamper and Clone-Resistant Authentication Scheme for Medical Image Systems. Cryptography. 2020; 4(3):19. https://doi.org/10.3390/cryptography4030019
Chicago/Turabian StyleTayachi, Mayssa, Saleh Mulhem, Wael Adi, Laurent Nana, Anca Pascu, and Faouzi Benzarti. 2020. "Tamper and Clone-Resistant Authentication Scheme for Medical Image Systems" Cryptography 4, no. 3: 19. https://doi.org/10.3390/cryptography4030019
APA StyleTayachi, M., Mulhem, S., Adi, W., Nana, L., Pascu, A., & Benzarti, F. (2020). Tamper and Clone-Resistant Authentication Scheme for Medical Image Systems. Cryptography, 4(3), 19. https://doi.org/10.3390/cryptography4030019





