2.1. Bell Polytopes, Realistic Theories and Quantum Correlations
We summarize basic aspects concerning the theoretical description of those statistical correlations, which are typically explored by Bell experiments, within the theoretical framework of (classical) local realistic theories. The constraints imposed on these correlations within the framework of local realistic theories can be described in terms of (generalized) Bell inequalities. Even beyond the scenarios originally considered by J. S. Bell [
1], for each multipartite measurement setup the structure of these correlations is described by a corresponding polytope, the so-called Bell polytope. Characteristic features of these polytopes have been explored, for example, in Refs. [
9,
14,
15,
16].
Let us consider a typical N-partite Bell-type experiment in which N parties perform a joint measurement on a physical system shared between them. For this purpose, each of these parties selects a physical variable (observable) from a finite set of possible physical variables (observables), say . This selection can be described formally by an N-tuple (input) with , . Thus, in an N-partite spin experiment, for example, each party measures the spin of a many-particle system consisting of at least N spin particles generally in a different direction. Depending on the choices of these physical variables each of these parties observes a measured value. All these measured values define an N-tuple of measured values (output) . In the following we assume that these measured values form a finite discrete set , i.e., with .
If we describe such an
N-partite Bell-type experiment within the general framework of a classical realistic theory without any further constraint, such as a locality requirement, we can distinguish between two types of theoretical descriptions, namely a deterministic one and a statistical one. In a deterministic realistic description, there exists a transfer function
F (or state) which relates each value of the input variable (choice of physical variable) with a unique value of the output variable (result of the measurement), i.e.,
Within the framework of a statistical realistic theory the state of the physical system, i.e.,
F, is described by a random variable characterized by a normalized probability distribution
with
. This probability distribution
generates conditional probability distributions
by the relation
with
for
and zero otherwise. These conditional probabilities describe the probability that the choice of the physical variables
yields a joint measurement result
of all the
N parties involved. They define a probability polytope with vertices
F [
10] characterizing a (classical) statistical realistic theory. If the parties involved in such a Bell-type correlation experiment are pairwise space-like separated, the input of any party cannot influence the output of any other party due to the finite speed of light in vacuum. This locality constraint is equivalent with the requirement that each party has its own transfer function, i.e.,
so that for this locality constraint the conditional probabilities characterizing a statistical theory are of the form
These conditional probabilities define a probability polytope with vertices
characterizing a (classical) statistical local realistic theory [
10].
There are two different ways to describe the probability polytope of a (classical) statistical realistic theory mathematically, either by a vertex representation or by a half-space representation. For any given experimental setup, the vertex representation of the associated probability polytope is defined in terms of the relevant transfer functions [
9,
10,
15]. The half-space representation of such a probability polytope is defined by inequalities, which in the case of a locality constraint are called generalized Bell inequalities. Whereas the vertex representation can be constructed in a systematic way, in general its conversion to the corresponding half-space representation constitutes a hard mathematical problem which can typically be solved only for very small numbers of parties, numbers of observables and measurement results. In view of these problems, the exploration of generalized Bell inequalities for multipartite scenarios is still an active field of research. In the following we use the term ‘Bell inequality’ for any inequality, which divides the probability space in such a way that the full probability polytope of a statistical local realistic theory, i.e., its Bell polytope, is inside the half-space defined by this inequality. Of particular interest will be those inequalities, which are also facets of the relevant Bell polytope. Clearly, a violation of such a Bell inequality by a quantum system shared between
N parties proves that these statistical correlations cannot be described within the framework of a statistical local realistic theory. In particular, entangled quantum states may exhibit such characteristic quantum features. Apart from very simple physical systems it is still a largely open question which violations of Bell inequalities describing local realistic correlations are possible by quantum theory.
2.2. Bell Experiments with Imperfect Detection
In the following we explore correlations of local realistic theories in the presence of imperfections concerning the measurements involved. In particular, generalizing recent investigations we concentrate on imperfect detection of measurements in the additional presence of dark counts of detectors in bipartite and tripartite scenarios.
Putting the problem into perspective let us concentrate on one of the simplest possible generalizations with imperfect detection, namely a bipartite scenario, i.e., , in which each party selects one of two inputs randomly, i.e., and in which for each of the parties four different outcomes are possible, i.e., . Physically speaking these four exclusive measurement results (outputs), namely , are supposed to represent the no-detection event (∅), the possibly ideal measurement results 1 and 2 and the dark count event (). To realize such a scenario, it is necessary that each party has two detectors available which can detect the exclusive measurement results 1 and 2. In a typical Bell experiment measuring polarization states of photons, for example, this would require that each party uses two photon detectors which detect two orthogonal photon polarizations. If only one photon has been sent to a party and if none of these two photon detectors of this party clicks, the event ∅, i.e., no photon present, is registered. If both detectors click a dark count () is taking place.
We model each of the two imperfect detectors of each party by two (statistically) independent parameters, namely
and
. These parameters are assumed to be identical for all detectors involved. The parameter
is the probability that a particle is detected provided a particle has been sent to the party. The parameter
is the probability that a dark count is produced. Correspondingly, for each party the conditional probabilities transforming ideal outputs with potential measurement results
into the actually observed imperfect outputs
are given by
Here, is the probability to measure the result a in the system with imperfect detectors, if the measurement would have resulted in the value in the ideal system with perfect detection. Therefore, the four exclusive events have the following physical meanings:
A: no particle is detected, and no dark count takes place in both detectors,
B: no particle is detected by the detector which should have registered it in the ideal case and a dark count takes place in the other detector,
C: either the particle is detected by one of the detectors and a dark count takes place in the other detector or the particle is not detected, and dark counts take place in both detectors,
D: either the particle is detected, and no dark count takes place or the particle is not detected and a dark count takes place in the detector in which the particle should have been registered.
Within this detection model the observed bipartite conditional probabilities
are related to the corresponding ideal (unobserved) bipartite conditional probabilities
by
with
and
. This model for imperfect detection can be viewed as the subsequent application of a perfectly working inner box, which creates ideal correlations without errors, and of an outer box so that losses and dark counts are introduced for each party separately. Thus, a party (observer) has only access to the inputs and outputs of the outer box, while classical or quantum physics restricts the possible correlations created by the inner box.
2.3. Required Detector Parameters for Loophole-Free Bipartite Bell Tests
To perform a Bell test successfully, a Bell inequality must be violated using some quantum setup. Thus, we need to find a probability distribution P, which (a) lies outside the Bell polytope, and (b) can be achieved by quantum correlations. Here, P denotes the vector of all conditional probabilities characterizing the experimental setup under investigation.
To check condition (a), we use a linear program as in [
10]. Given all vertices
of the Bell polytope by evaluating all the possible combinations of transfer functions for the parties, the probabilities
obtained by a convex combination of these vertices, i.e.,
, with
and
, are also part of the Bell polytope. In the bipartite case considered in this section and for ideal conditional probabilities
, the conditional probabilities
observed with imperfect detectors are computed using the detector model. Using a convex sum of the vertices
, the linear program then finds the point in the Bell polytope which is closest to
P. It returns the distance between that point and
P with respect to the 1-norm. For probabilities
, which lie outside the Bell polytope for ideal detectors, i.e.,
and
, we can now find critical detector parameters. To do this,
is fixed and the detection probability
is decreased (or vice versa) until the distance of
P to the Bell polytope reaches 0. Once this happens, no violation of any Bell inequality is possible with these detector parameters and the given
. However, there might be some other
, that, for the same detector parameters, result in a probability distribution
P which still is well outside the Bell polytope.
This brings us back to condition (b), namely which
are we allowed to use when trying to find the
that stays outside of the Bell polytope for the worst possible detector parameters? To answer this, we use a hierarchy of semidefinite programs (SDP) [
13] as described in Materials and Methods. In short, the program maximizes a linear objective function on the probabilities while following mathematical restrictions arising from quantum theoretical principles. In our case, the objective function is the left hand side of a Bell inequality of the form
. In the following, we will choose
, which is always possible using
. For each order of the hierarchy, the SDP returns an upper bound for the quantum value on this inequality, as probabilities might be viable, which lie outside of the possible quantum correlations. The results of SDP are conjectured to be identical with the possible quantum correlations only in the limit of infinite order of the hierarchy or in special cases, e.g., a finite-dimensional quantum system and a correspondingly high order of the hierarchy, see [
13].
With SDP we can find the amount of violation of a Bell inequality by quantum theory for given detector parameters and we also obtain the responsible conditional probability
. As the chosen Bell inequality may not be optimal, we use these probabilities to find an optimized inequality. To this end, we compute the Bell inequality which is maximally violated by
, obtained from
and from fixed detector parameters, by solving the linear program
The first constraint limits the values of the weights within the Bell inequality, as the optimal value would go to infinity otherwise. The second constraint makes sure that only inequalities are considered, which leave every vertex and thus the whole Bell polytope in the feasible half-space. In this sense, it is still a Bell inequality, although this algorithm typically does not return a facet of the polytope. To get a facet with this method, P must be chosen very close to the surface of the polytope, by increasing the detector inefficiency or the dark count probability.
Using several starting points and detector efficiencies it turns out that in our model the most robust inequalities are all equivalent to the Clauser–Horne (CH) inequality [
17]
They are equivalent in the sense that they only differ by a relabeling of the parties, of the inputs or outputs or by instances of
. Here, the no-signaling condition is used, making it possible to write
as the result of one party cannot depend on the input chosen by the other party. The inequality is also equivalent to the well-known Clauser–Horne–Shimony–Holt (CHSH) inequality [
18] if the additional outputs created by detector errors are subsumed in one of the original outputs. This implies a lifting of the original inequality to a scenario with more possible results per measurement (here from 2 outputs to 4), without additional changes to the inequality [
19].
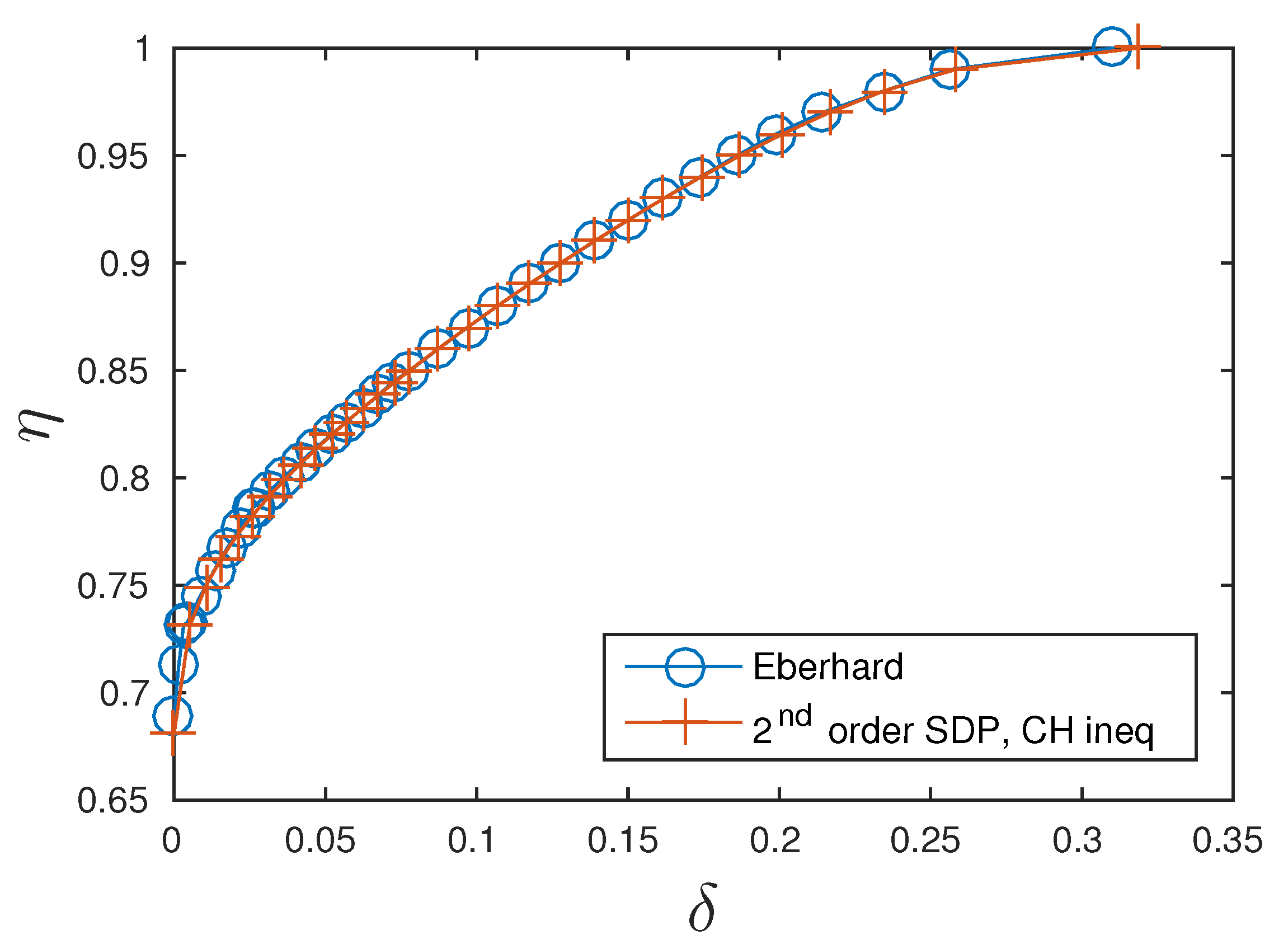
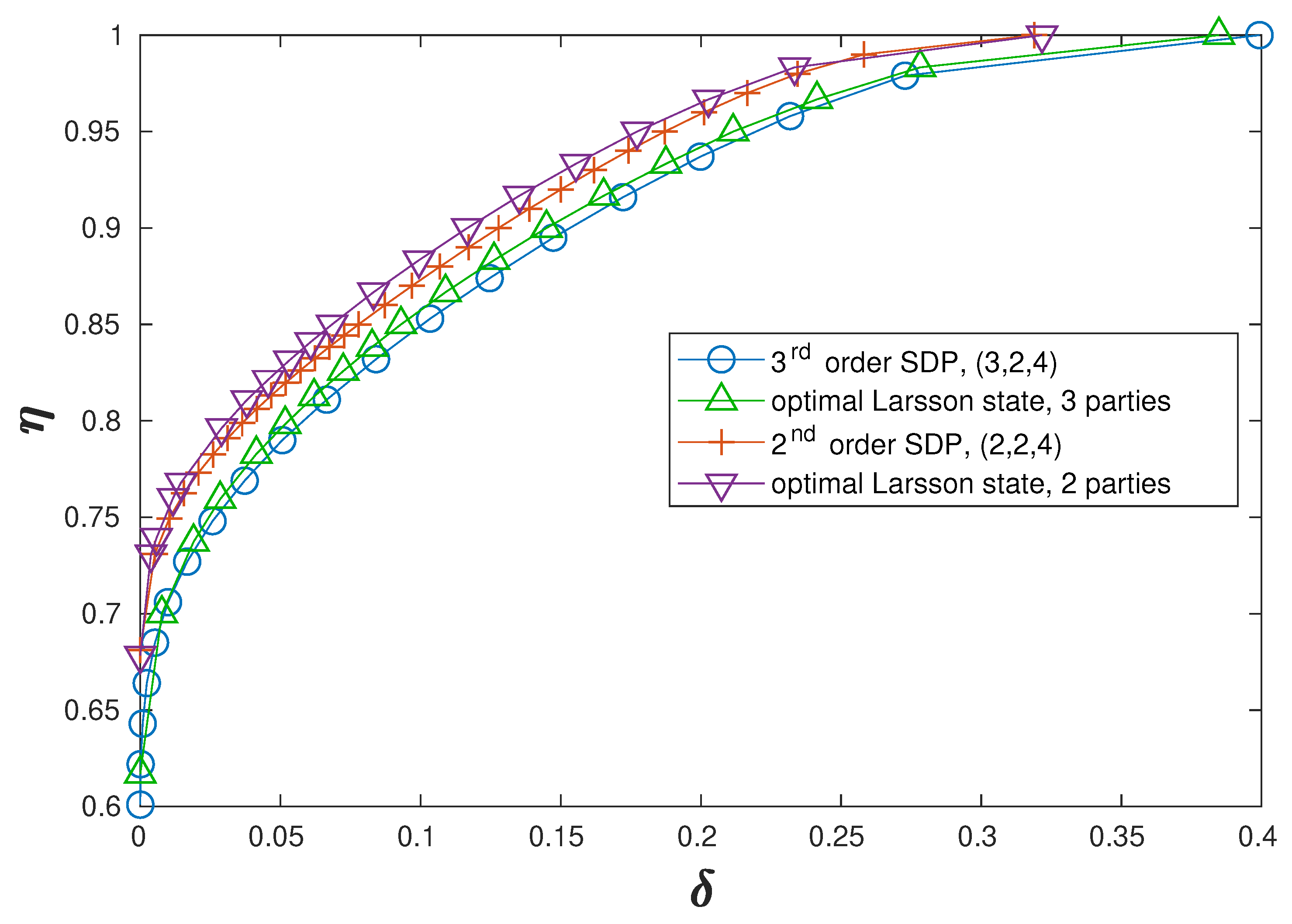
The hierarchy of semidefinite programs yields improving lower bounds for necessary detector efficiencies by giving better and better upper estimates for the possible quantum correlations with each order of the hierarchy. However, this method does not tell us if and how these quantum correlations can be created experimentally. However, using the CH inequality, we find that the step from 2nd to 3rd order SDP does not change the results for the necessary detector parameters. This implies that the obtained probabilities, and thus detector parameters, are identical to the ones possible by quantum physics. These lower bounds on the detector parameters necessary for a successful Bell test are shown as the red crosses in
Figure 1.
To find an upper bound on the detector parameters, we take the quantum states and measurements proposed by Eberhard [
7] for bipartite scenarios. These define several probability distributions
. As previously described, we vary
and
to obtain
and we use our linear program to check at which point these correlations are no longer outside the Bell polytope. As there are specific instructions on how to create the needed probabilities experimentally, they definitely can be reached by quantum systems and the resulting upper bounds on the detector efficiencies are shown as the blue circles in
Figure 1.
As the upper and lower bounds are identical up to numerical precision, they represent the critical detector parameters for a successful Bell test, i.e., a violation of a Bell inequality, in this bipartite scenario.