1. Introduction
Cryptography techniques have been utilized in different areas. In this era, due to progress in computer and communication technology have facilitated mankind to transfer important personal data through the long-distance channels. The concerns that are related to secrecy of transfer data is a big problem. Cryptology provides the solution of all such requirements in modern day communication systems. The symmetric (private) and asymmetric (public) key cryptography are two most trusted cryptographic models for secure communication. Both methodologies have several benefits and drawbacks as well.
Symmetric key cryptography algorithms have two types. These types are block ciphers and stream ciphers. The concept of block cipher was introduced by C. Shannon. Block ciphers, like DES, advanced encryption standard (AES), and international data encryption algorithm (IDEA), play an important role in multimedia security. The substitution box and permutation box are the two most indispensable parts of a secure block cipher. The role of substitution box is to make the relationship between the secret key and the ciphertext as complex as possible. Permutation box induces diffusion in the system.
2. Related Work
In literature, different researchers worked in this aspect. The construction of AES [
1] is based on the composition of inversion map and affine transformation. In 2007 Cui and Cao presented the APA S-box [
2]. In the construction of affine-power-affine S-box, the composition of affine surjection, power function, and again affine surjection are used. This model of S-box improves algebraic complexity as compared to AES. In 2008 Minh-Triet Tran, Doan-Khanh Bui and Anh-Duc Duong proposed Gray S-box [
3]. It was obtained that AES includes an additional transformation based on the binary gray code. This S-box has similar properties to AES. In addition, it is more secure against algebraic and interpolation attacks in comparison to AES. In 2009, Kim and Phan suggest Skipjack S-box [
4]. This S-box is a Feistel network that is based on 32 rounds. This scheme uses the 80-bit key for encryption or decrypts 64-bit blocks. Later, Iqtadar et al. in [
5] proposed chaos based S-boxes. Also, in [
6,
7,
8,
9,
10,
11,
12,
13,
14] different S-boxes are constructed utilizing different algebraic structures and chaotic maps. These S-boxes have strong algebraic analysis but weak statistical analysis [
13]. In [
14] Iqtadar et use permutations of
on Liu S-box to attain 40,320 S-boxes, but there are p- boxes that were obtained from S-boxes and a different author using group action on Galois field by linear fractional transformation.
A substitution box is a mapping . This mapping map input bits to output bits. Substitution box is signified in matrix from a rectangular and square matrix. Substitution box of dimension with has two categories. In first category, every input has a distinctive output. Second category involves those substitution boxes where several inputs may have the same output and all possible output are not existing in S-box. An S-box of dimension , which is one-to-one and onto is said to be bijective S-box. This S-box maps each input to a distinct output and all possible outputs are included in the S-box. The existence of bijective S-boxes may imply that and these S-boxes are also renowned as reversible S-boxes. Reversible S-boxes are very significant in symmetric key cryptosystems.
Most of the work that is related to S-boxes is based on affine transformations and linear fractional transformations [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26]. In both cases, we have some constraints on coefficients of affine transformations and linear fractional transformations. Also, for diffusing property chaotic maps [
27], permutations on S-box entries and binary gray code are used. The motivations behind the present work are to obtain a scheme free of constraints, to generate large number of highly nonlinear S-boxes and the S-boxes having the diffusing property as well. This work is unique in the aspect of constructing a large number of highly non-linear substitution permutation boxes (S-p-boxes).
3. Preliminaries
Group is a non-empty set with an associative binary operation having the properties of unique identity and each member of the set has unique inverse. For instance, a set of rational number under multiplication is a group.
Symmetric Group is also an example of group. It is the group of all possible permutations on a set of n members with the binary operation of composition of functions.
A polynomial is said to be irreducible over a unitary commutative ring if it is non-unit in and if we write it as then one of , is unit in .
Galois field
is a field that has order
, where
is prime and
is a positive integer. Suppose that
be the
degree polynomial, which is primitive irreducible over the prime field
where
is prime. For primitive root
of the polynomial
, we define Galois field, as follows
For instance,
, we have following Galois field.
here
1 +
+
,
has eight elements.
Let
be the primitive irreducible root of
here, the coefficient belongs to
and −1 in
is equal to 1.
Similarly,
is constructed and we computed it computationally.
where
1 +
+
+
+
is a primitive irreducible polynomial.
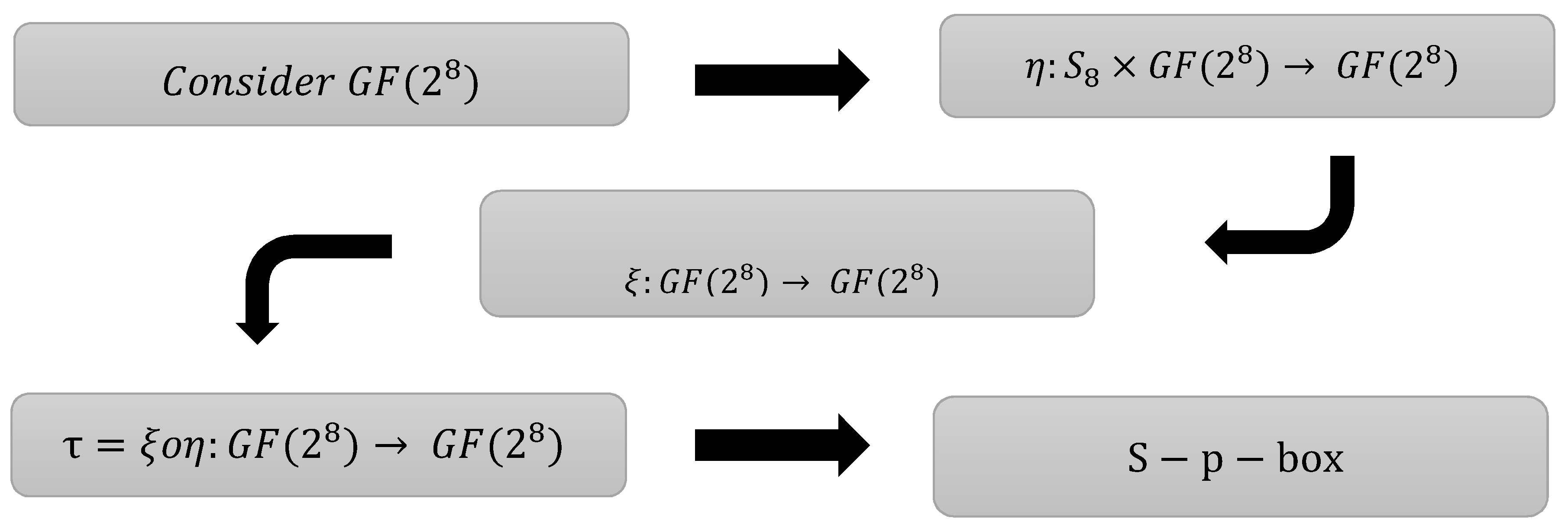
4. Design for Proposed S-p-Boxes
The design of the suggested S-p-box is dependent on the composition of action of symmetric group
on to Galois field
and inversion map. The action of
on
is defined as:
The construction of S-p-boxes has four steps:
Step 1: Construct Galois field
Step 2: Define action of the symmetric group
, defined by
here, a fixed
is utilized in the design of a single S-p-box. This phase of design will kill the structure of Galois field and induced diffusion.
Step 3: Define inversion map
by
Step 4: Define composition map
by
This composition gives us the desired S-p-box. We pick a specific permutation, and using this permutation, we permute according to the defined action in the Galois field (in
Table 1) in step 2. In the third step, each member of Galois field is mapped to its inverse. Following the same procedure, we get 40,320 highly nonlinear S-p-boxes. The method is explained below by a simple example by constructing a small S-box and with the similar method, an S-box of dimension
is constructed. The computational scheme is presented in
Figure 1. It notable that, in this construction, zero is always mapped on zero and the remaining numbers are mapped on a different number according to the permutations.
In
Table 1, Galois field
is constructed. We choose
to explain the procedure by a small example. We select
.
In step 1, as
is constructed in
Table 1.
In step 2 (
Table 2),
In step 3 (
Table 3), the resulting form which is again a
is mapped on there inverses.
Hence, the S-box obtained is of dimension
The S-p-box presented in
Table 4 is designed using a permutation
. Similarly, for each permutation of
, we can get an S-p-box. These S-p-boxes depend on permutation. For each permutation of
, we have a new S-p-box that is different from other S-p-boxes. Accordingly, permutation can be used as a key for the unique S-p-boxes. The inverse S-p-box is obtained by using reverse procedure.
5. Algebraic Analysis and Simulation Results
In order to judge the utility of proposed S-box for any cryptosystem, we generally used standard algebraic analysis. This analysis includes bit independence criterion, nonlinearity, strict avalanche criterion, and differential and linear approximation probability. The comparison of proposed S-p-box is also made with some classical S-boxes and presently constructed S-boxes. The proposed S-p-box fulfills all of the optimal values of standard algebraic analysis. Detail of these analyses is discussed below.
5.1. Nonlinearity
Nonlinearity measures the minimum distance between the set of all n-variable affine functions and an n-variable Boolean function
. Mathematically, it is defined as
where
is the maximum absolute value in the Walsh-Hadamard transform vector.
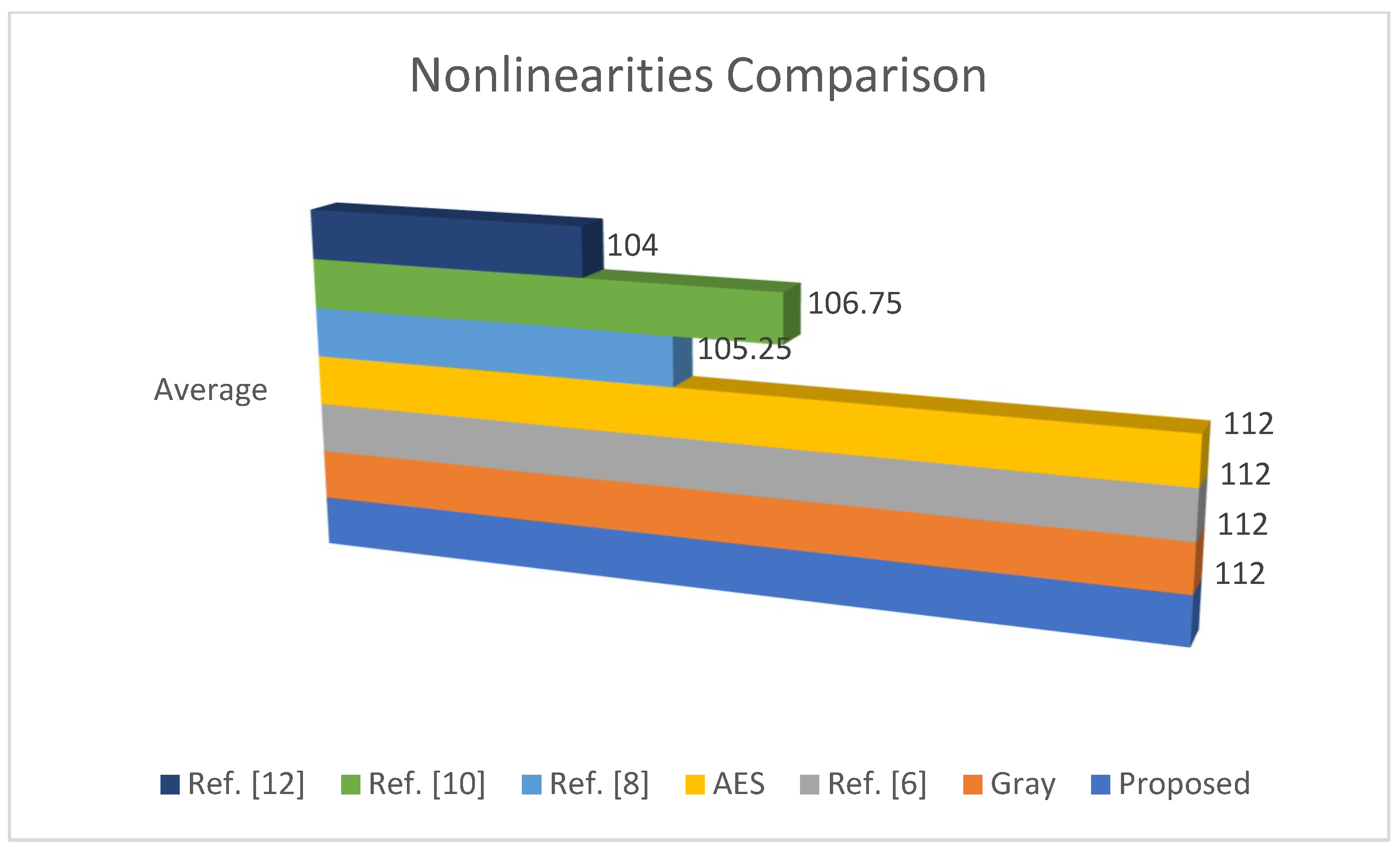
Non-linearity of newly suggested S-p-box is 112 and a comparison is made with some classic as well, as recently constructed S-boxes is shown in
Table 5. The graphical representation is shown in
Figure 2. Here, it is noteworthy that, following the similar method, 40,320 highly non-linear S-p-boxes are obtained. The non-linearity of proposed S-p-box has a superior value than Ref. [
8], Ref. [
10], and Ref. [
12], and it has equal value to AES, Ref. [
6], and Gray.
5.2. Strict Avalanche Criterion
A Boolean function
such that for every
satisfies the expression
Known as strict avalanche criterion. In other words, strict avalanche criterion (SAC) measures how much the output bits altered when a single change in input bits is made.
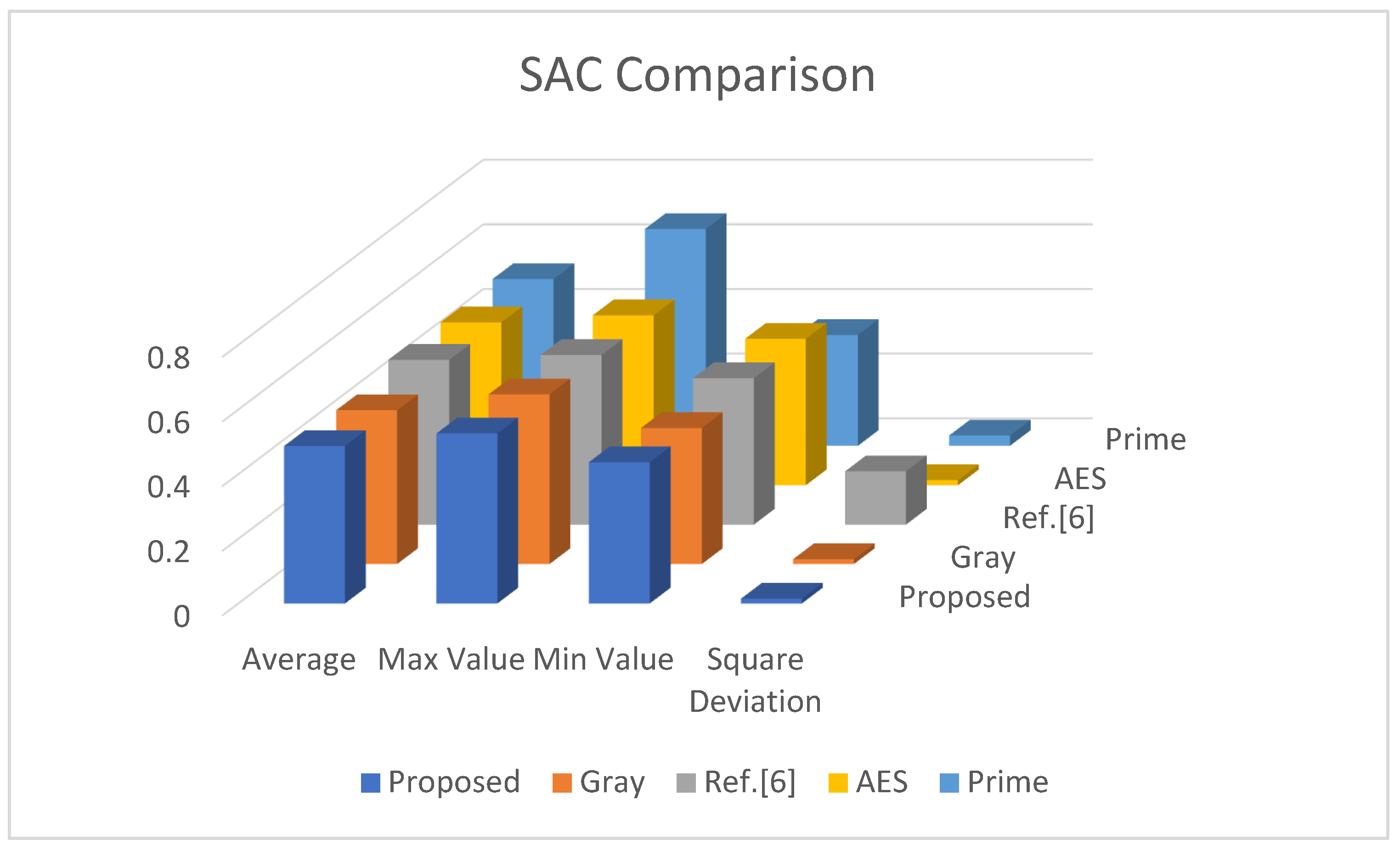
An S-box fulfills SAC criterion if an alteration in one bit in the input bit can cause an avalanche change in the output bits that is nearly half of the output bits must be altered. The comparison of overall SAC analysis of proposed S-p-box with AES and Gray is shown in
Table 6,
Table 7 and
Table 8, while the average outcomes are shown in
Table 9 and graphical representation of analysis comparison is described in
Figure 3. It can be observed from
Table 9 that the proposed S-p-box has attained a maximum value = 0.526, minimum value = 0.437, average value = 0.487, and square deviation = 0.015. These outcomes are better than the Gray S-box.
5.3. Bit Independence Criterion
Bit independence criterion (BIC) investigated those input bits that continue unaltered. The modification of unaltered input bits and the avalanche vectors’ independent performance of pairwise variables are the assets of this criterion. In the symmetric cryptosystem, BIC is an effective property as, by increasing independence between bits, it is almost impossible to predict and recognize the pattern of the system [
11].
The outcomes of nonlinearity are presented in
Table 10. The bits, which are generated by eight constituent functions, are compared with each other for the purpose to measure the independence characteristics. The correlation due to the alteration in input bit and the corresponding alteration in output bits is calculated. Initially,
and
bits are kept fixed and
bit is changed from 1 to n after that j and k are altered.
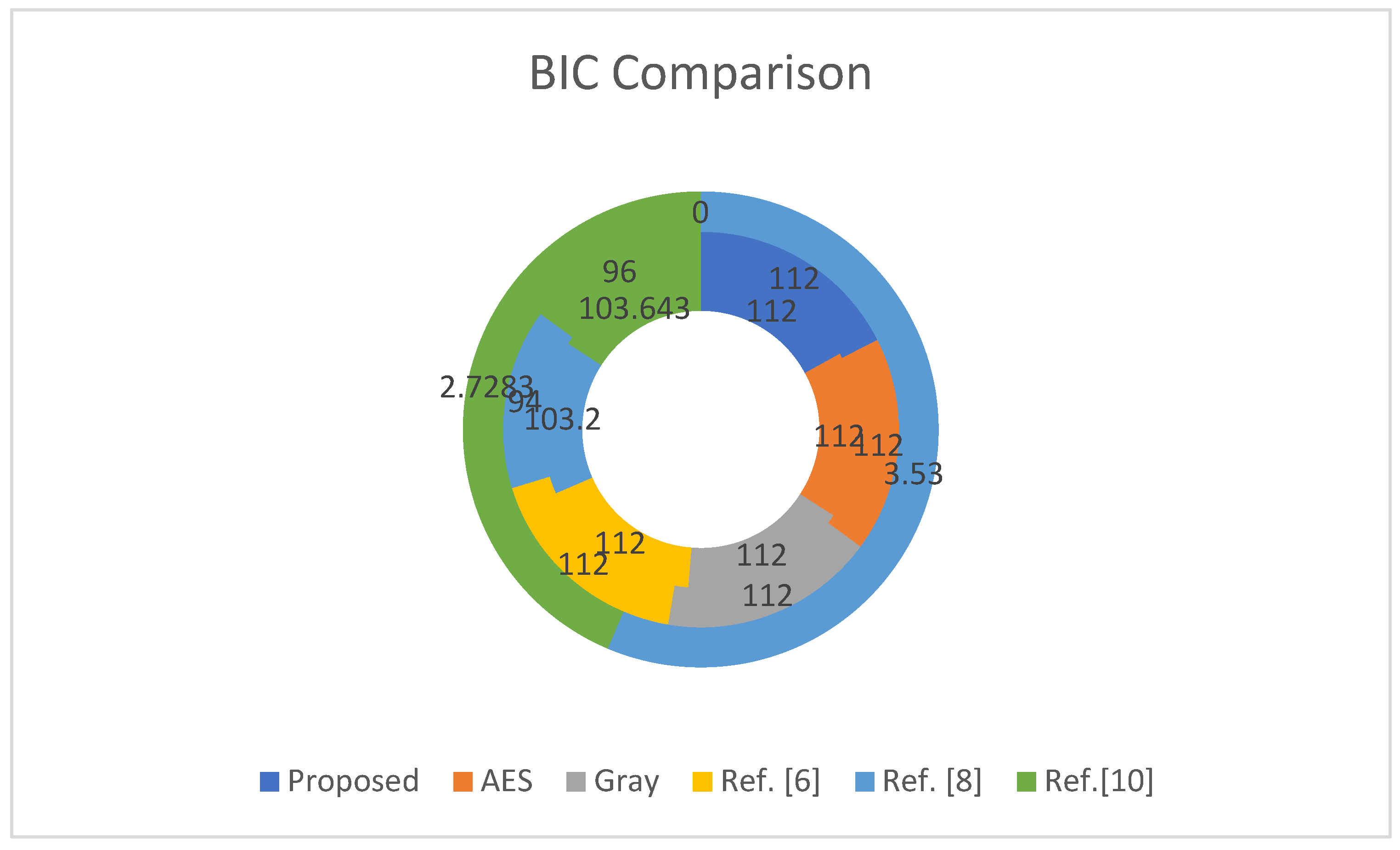
BIC analysis performed on different S-boxes and their comparison with the proposed S-box is shown in
Table 11. It can be observed that BIC analysis of proposed S-box has a minimum value = 112, average value = 112, and square deviation = 0. These outcomes are comparatively excellent when compared to Ref. [
8] and Ref. [
10]. Graphical representations of outcomes are presented in
Figure 4.
5.4. Linear Approximation Probability
Linear approximation probability measures the imbalance of the incident. This analysis is convenient in enumerating the supreme value of the discrepancy of an event between input and output. The two masks,
and
, are applied to the parity of the input bits and output bits, respectively.
where
is all possible inputs and
is a number of the input element.
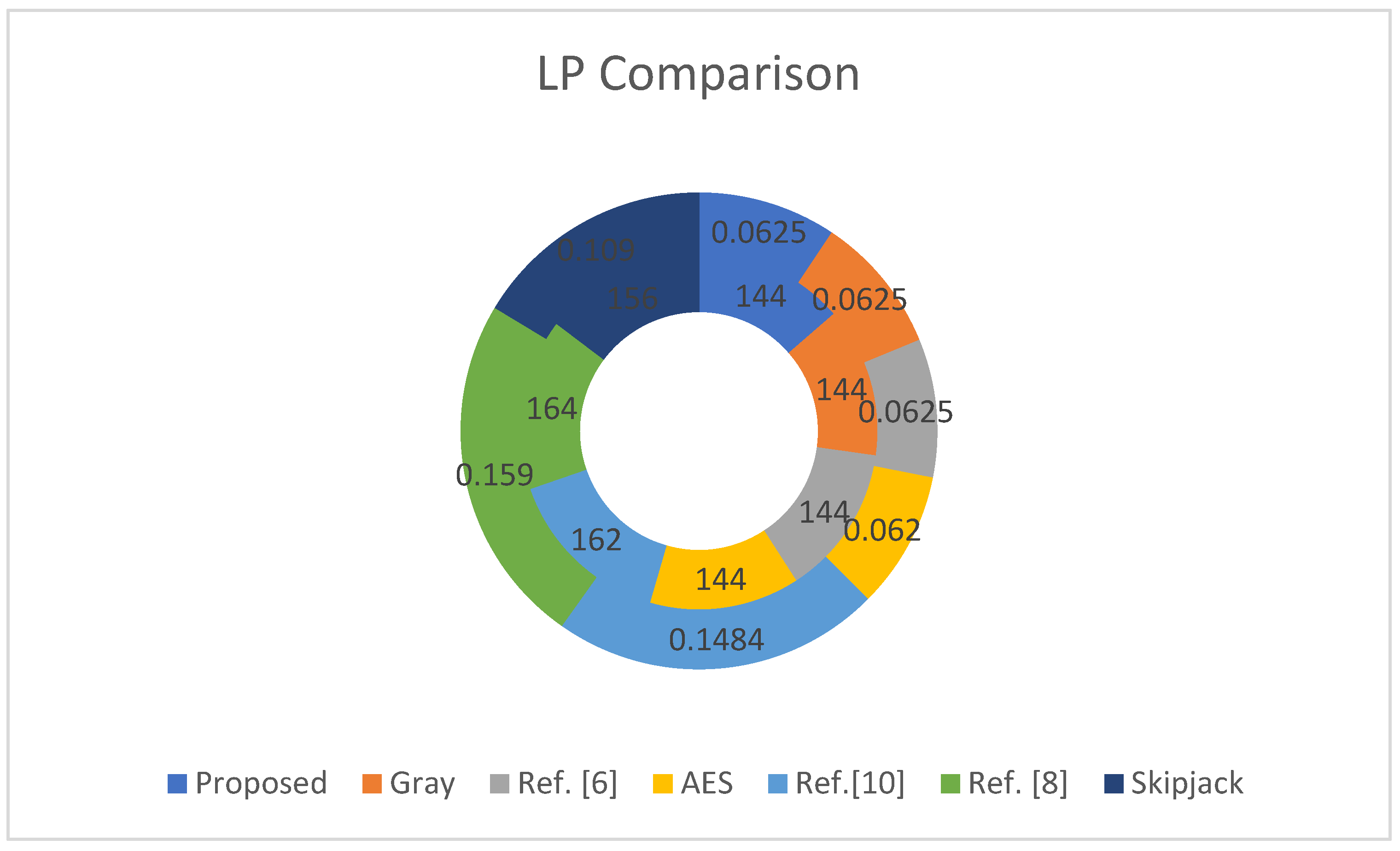
In
Table 12, linear probability (LP) analysis is presented and a comparison with selected S-boxes is also shown. The maximum value of linear approximation of the proposed S-box is 144, which demonstrates that the proposed S-p-box has strong resisting ability against linear attacks. In
Figure 5, a graphical representation of the suggested S-p-box with some selected S-boxes is presented. LP analysis of the proposed S-p-box is better than Ref. [
8], Ref. [
10], and Skipjack, while its Max LP is the same as AES, Gray, and Ref. [
6].
5.5. Differential Approximation Probability
Differential approximation probability guaranteed uniform mapping. For every change in the input, there must be a unique change in output. These features of differential approximation probability guarantee uniform mapping probability for every input bit i.
where
is the input differential and
is the output differential.
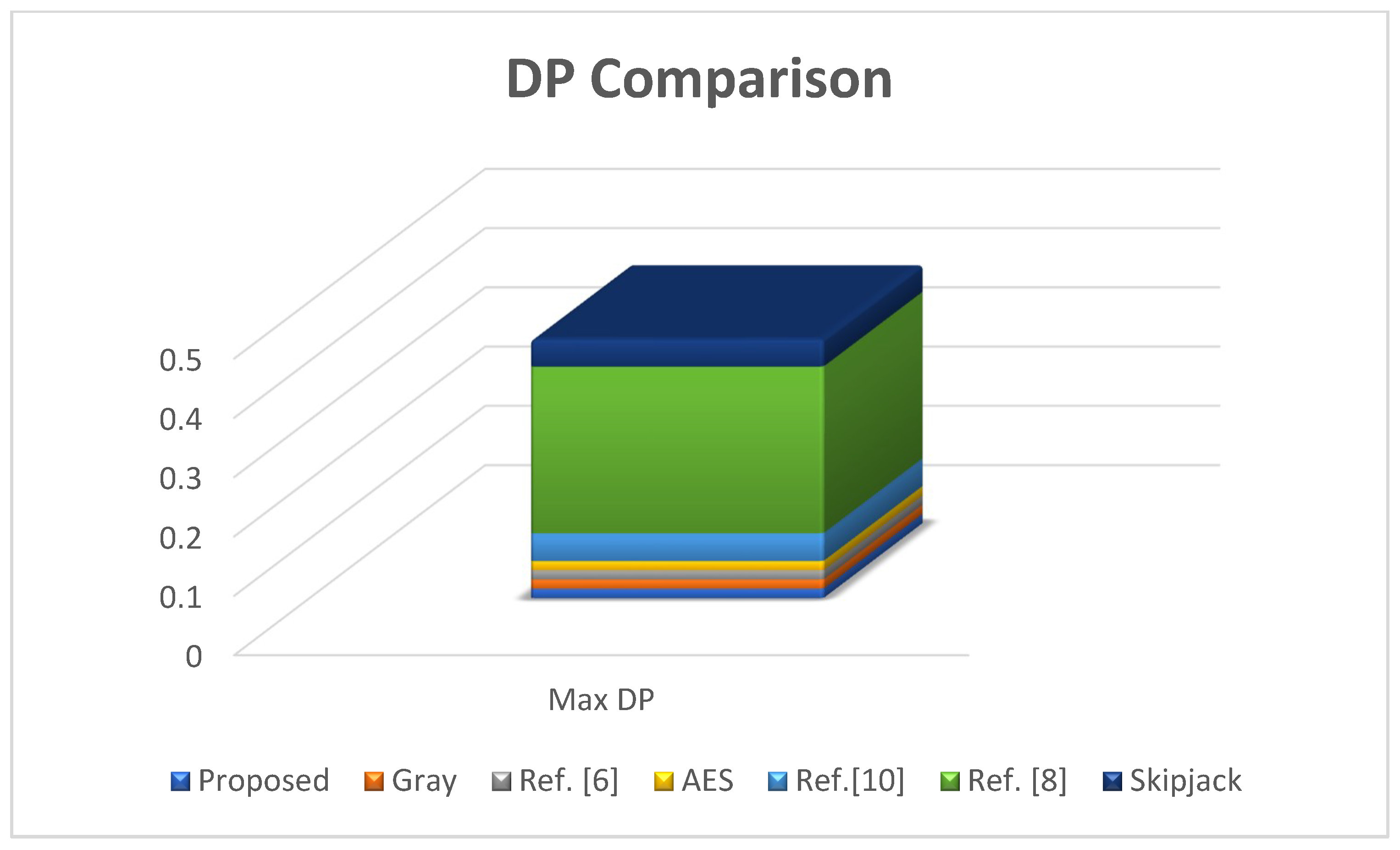
The proposed S-p-box has maximum differential probability is 0.015625, which is comparable to the S-boxes that are present in
Table 13. These S-boxes include Ref. [
6], Ref. [
8], Ref. [
10], AES, Gray, and skipjack. The performance of proposed S-p-box is better than Ref. [
8], Ref. [
10], and skipjack.
Figure 6 represents the graphical representation of differential approximation probability analysis.
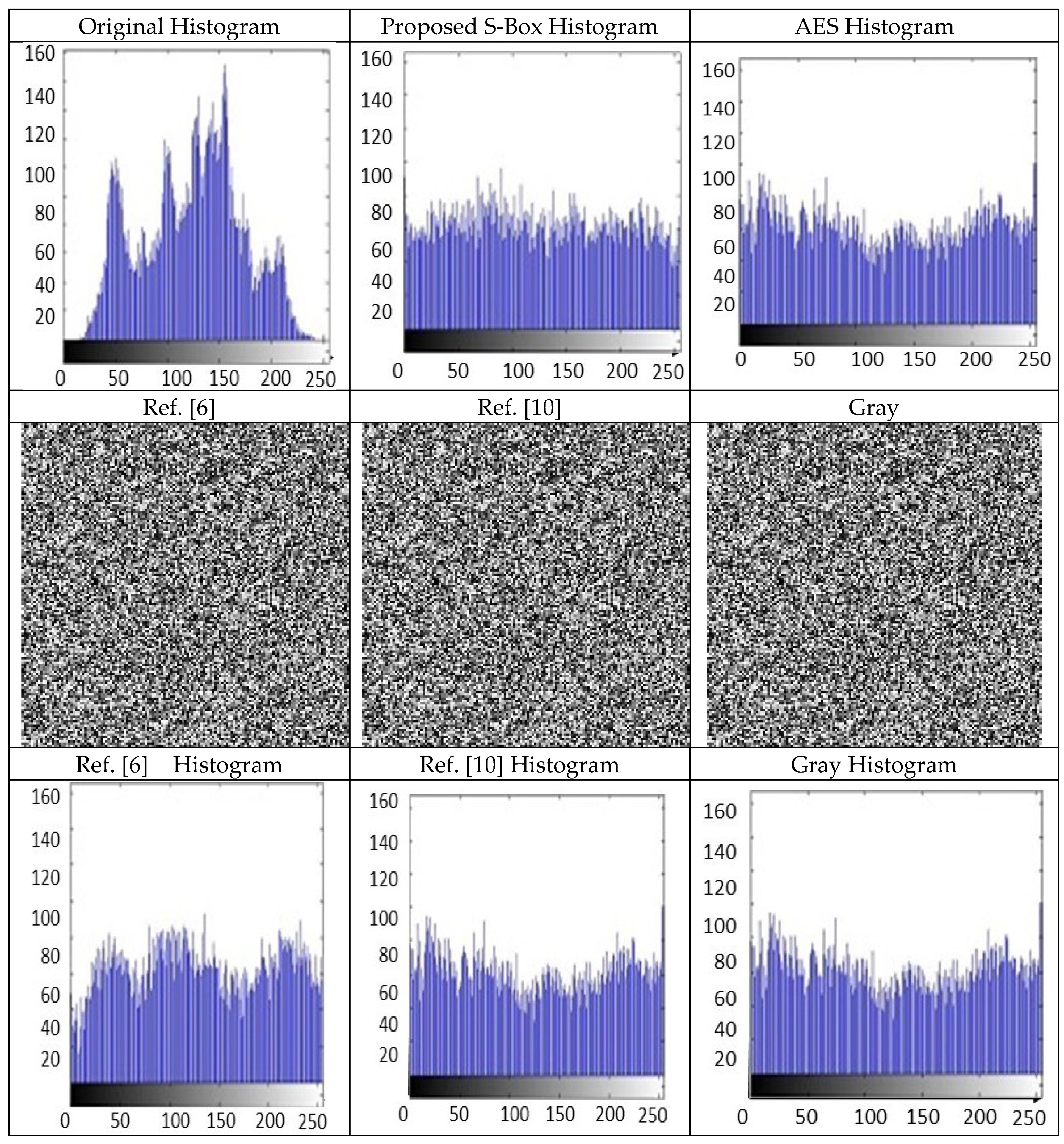
6. Statistical Analysis
Statistical analyses are judged through majority logic criteria (MLC). MLC decides the suitability of an S-box for the encryption procedure of a specific type of data. In this criterion, a test image is encrypted using S-box by substituting the pixel values. This process is just testing of S-box suitability in the encryption process. This is not itself an encryption scheme. In this criterion, statistical analysis is applied on the original data and encrypted data. It measures the statistical properties. During the procedure of encryption, data is used and during this utilization of data produces alterations in the original data. The outcomes of several statistical analyses, which include contrast analysis, entropy analysis, energy analysis, correlation analysis, mean of absolute deviation analysis, and homogeneity analysis, which defines the appropriateness of S-box in encryption applications. This criterion is a decider, its analysis described whether the S-box is suitable for encryption applications or not [
13].
Figure 7 shows that the image encryption sample image of Lena by using the proposed S-p-box and their corresponding histogram, respectively. The outcomes of statistical analysis of proposed S-p-box and a comparison with AES, Ref. [
6], Ref. [
10] and Gray are shown in
Table 14. In
Table 14, AES and Ref. [
6] are the most suitable for encryption and the proposed S-p-box has a better outcome than both, according to the majority logic criterion. The MLC analysis of proposed S-p-box showed that this S-p-box is more diffusing and better for any cryptosystem as compared to the best S-boxes in the literature. The proposed S-p-box is confusing as well as diffusing, which differentiate it from all other S-boxes constructed so far in literature. The majority logic criterion suggests that the proposed S-p-box has excellent image encryption properties.
7. Conclusions
A simple and innovative method is suggested for the construction of S-p-boxes in an unconstraint system as compared to linear fractional and affine transformation. The proposed S-p-box has an additional property of diffusion as well. S-p-box is constructed using the composition of the action of symmetric group on Galois field and inversion map. Due to this scheme, 8! highly nonlinear S-p-boxes are obtained. To judge the strength and efficiency of S-p-box, we apply nonlinearity analysis, strict avalanche analysis, bit independence analysis, and linear and differential approximation probability analysis. Suitability of S-p-box in image encryption application is measured by MLC analysis and its diffusing capability proves its superiority in image encryption application. It is further summarized that the suggested scheme of the proposed S-p-box has all the desired cryptographic properties and it is useable in any cryptosystem.