1. Introduction
Today’s environment of large and high-speed centralized cloud-based computing is expanding into tomorrow’s smaller and lightweight edge-based computing, which will consist of billions of devices in the “Internet of Things” (IoT). IoT devices are both resource-constrained, especially in terms of power and energy, and particularly vulnerable to exploitation and compromise, since they are more likely to be physically accessible by an adversary.
Authenticated ciphers, such as AES-GCM, are well-suited for lightweight edge devices in the IoT, since they combine the functionality of confidentiality, integrity, and authentication services, and can potentially provide more efficient integration of disparate cryptographic components, such as block ciphers and keyed hashes [
1].
Input and output fields, and computational processes of authenticated ciphers, are introduced in [
2], and are summarized below:
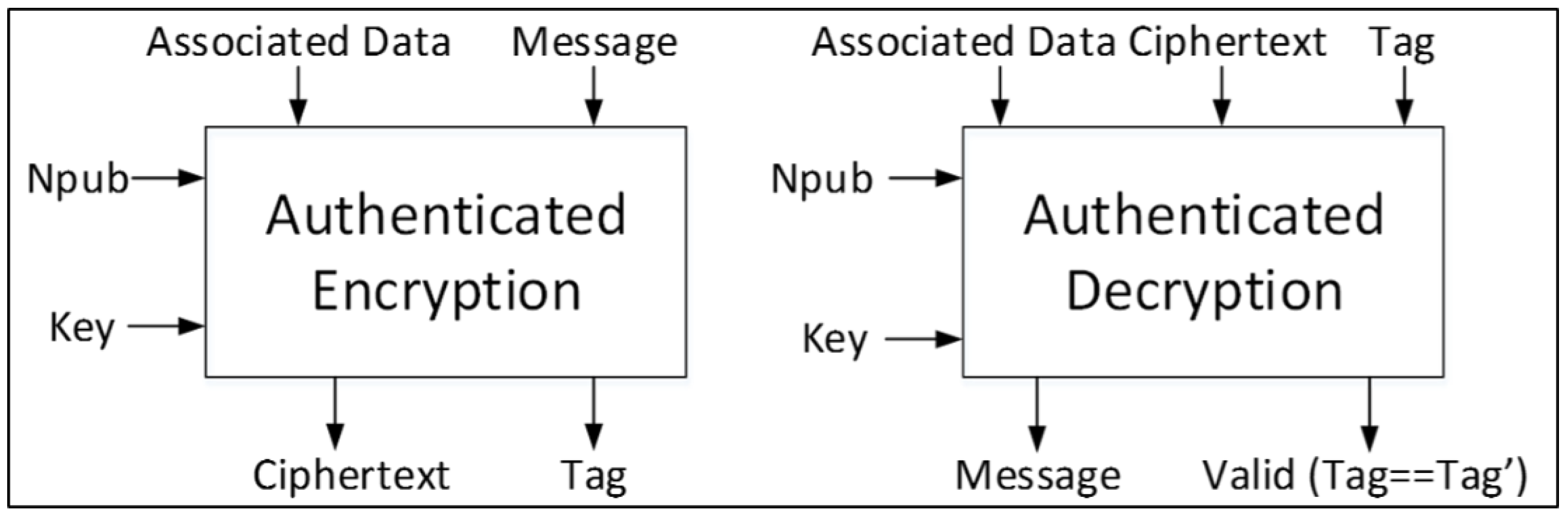
—An input field to authenticated encryption consisting of to be encrypted to , which is an output from authenticated encryption.
—An output from authenticated encryption, and input to authenticated decryption, which consists of data to be decrypted to .
(Associated Data)—Data accompanying that will not be encrypted, but contains ancillary information such as header or protocol information.
—A public message number; usually a nonce (number used once).
—A secret key, used for encryption and decryption to ensure confidentiality, and used in keyed hash functions to ensure integrity and authenticity.
—A function of all blocks of , , , and , which is produced at the conclusion of message encryption, and provides a value which is used by the recipient to verify integrity and authenticity.
During authenticated decryption,
, forwarded from the module performing authenticated encryption, is compared to
, computed by the module performing authenticated decryption, as a function of
,
,
, and
. If
=
, then the authentication is considered valid, and
is released. A notional authenticated cipher is shown in
Figure 1.
Cryptographic algorithms, which are either well-researched or endorsed by government standardization organizations (e.g., NIST), are generally secure against cryptanalysis or brute-force attacks, given currently available computing power. However, cryptography is implemented in physical devices, which are subject to information leakage, and which can be exploited through so-called side-channel attacks, such as Differential Power Analysis (DPA), through which an attacker can often recover sensitive information.
Several competitions and standardization efforts are evaluating authenticated cipher candidates worldwide to determine the most optimal algorithms for various applications, including lightweight cryptography suitable for the IoT. One of these efforts is the Competition for Authenticated Encryption: Security, Applicability, and Robustness (CAESAR), which has evaluated a large number of candidate authenticated ciphers over the last four years, in order to ultimately select a final portfolio of ciphers that offer advantages over AES-GCM, and are suitable for widespread adoption [
3]. Beginning in Round 3, the CAESAR committee identified use-cases for which candidates would be evaluated. One of these use cases is for lightweight applications, for which desired characteristics include “natural ability to protect against side-channel attacks” [
4].
Another example is the NIST Lightweight Cryptography (LWC) Standardization Process, which is a multi-year effort to examine categories of lightweight cryptographic algorithms (including authenticated ciphers) in order to choose eventual U.S. federal standards. The NIST LWC standardization process takes into account candidate ciphers’ abilities to be protected against side-channel attacks. Additionally, the NIST LWC standardiztion process emphasizes the desire for third-party analysis, i.e., analysis by researchers other than the authors of cipher submissions [
5].
Given the widespread interest in developing and standardizing authenticated ciphers, it is useful to examine implementations of authenticated ciphers with specified lightweight use-cases to compare resistance of unprotected and protected implementations to DPA, as well as their costs of protection. However, to date, there has been no study of the side-channel resistance of a large group of authenticated ciphers, implemented using the same methodology and same test equipment, and no study of their comparative costs of protection against DPA.
In this work, we demonstrate a methodology for determining vulnerabilities of authenticated ciphers to DPA, and evaluating the effectiveness of DPA countermeasures. We use an existing Test Vector Leakage Assessment (TVLA) methodology (i.e.,
t-test, further discussed in “Materials and Methods”) [
6,
7], and upgrade the Flexible Open-source workBench fOr Side-channel analysis (FOBOS) [
8], to perform TVLA on authenticated ciphers. The FOBOS interface with the victim cipher implementation is standardized by leveraging the CAESAR Hardware Applications Programming Interface (API) for Authenticated Ciphers, which was adopted by the CAESAR committee in May 2016 [
9,
10]. Additionally, our use of the CAESAR Hardware API Development Package, available at [
11] enables a repeatable and exportable test methodology for all CAESAR candidates.
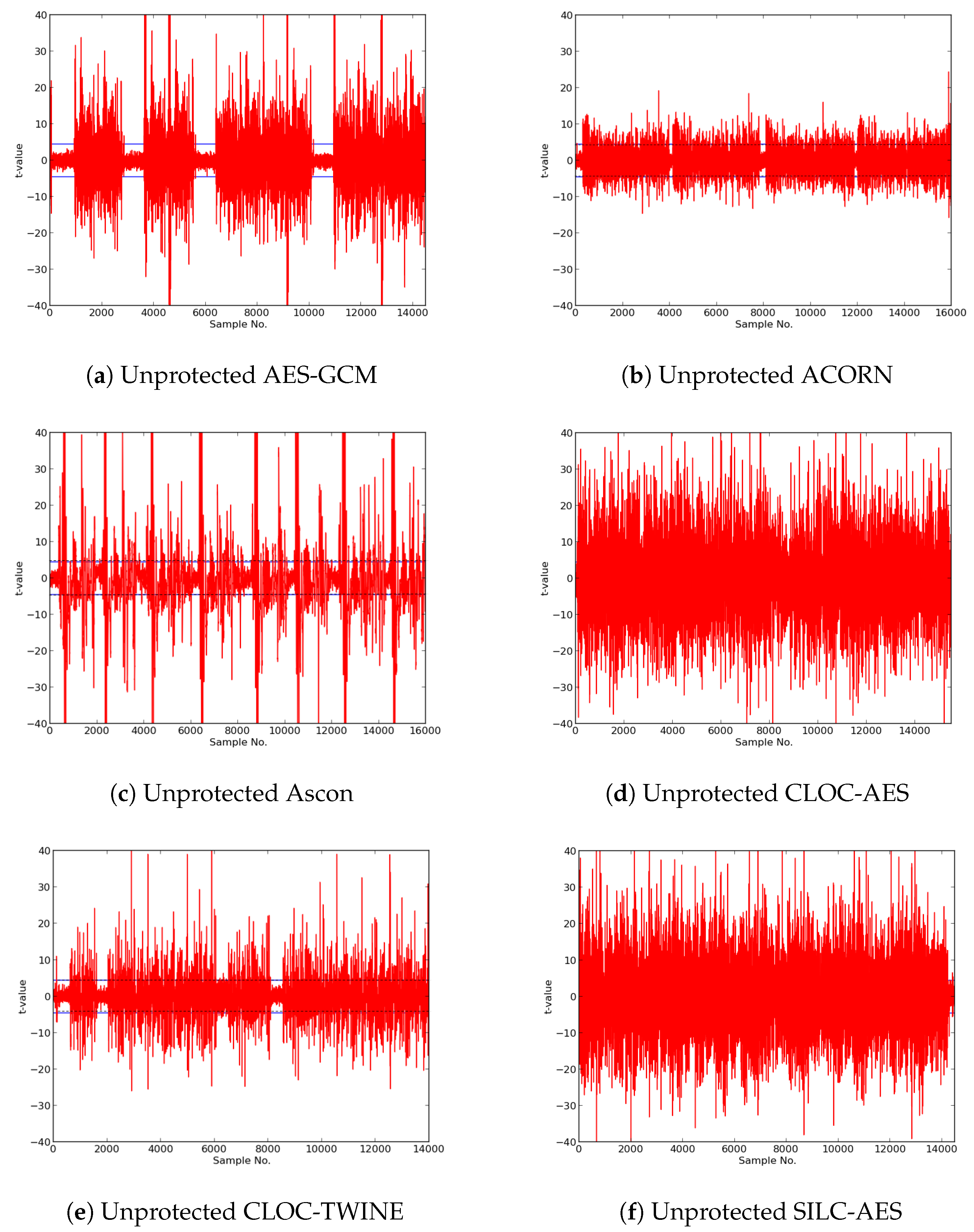
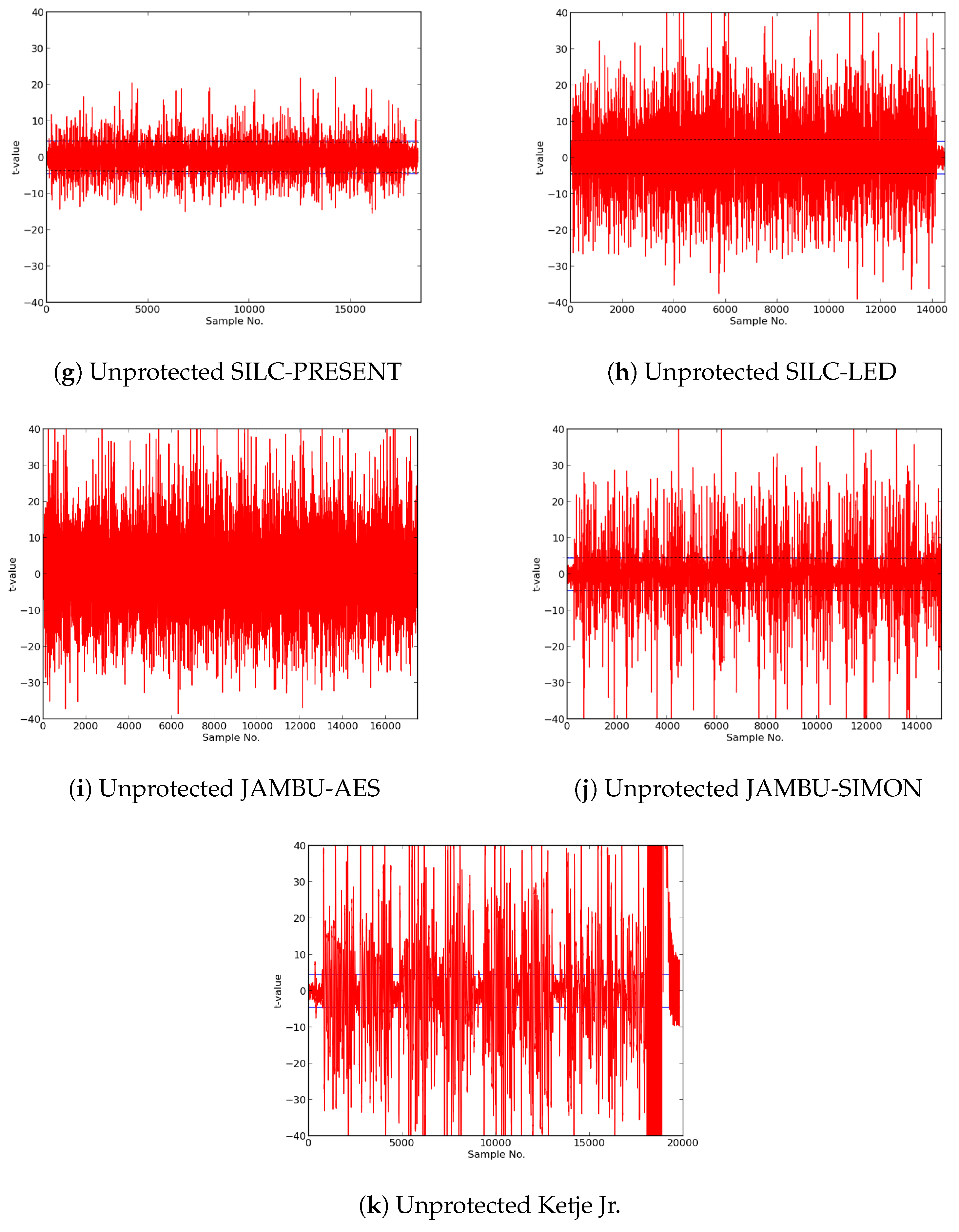
Using the augmented FOBOS, we demonstrate
t-tests on unprotected implementations of the CAESAR Round 3 variants of the ACORN, Ascon, CLOC-SILC, JAMBU, and Ketje families of authenticated ciphers, described in [
12,
13,
14,
15,
16], respectively. We choose these ciphers since their authors have specified an intended lightweight use case for their respective ciphers. We additionally analyze an existing defacto authenticated cipher standard AES-GCM, described in [
17], for purposes of comparison. We use register transfer level (RTL) VHDL implementations of AES-GCM, Ascon, CLOC-AES, JAMBU-AES, and SILC-AES available at [
18], ACORN at [
19], CLOC-TWINE, SILC-PRESENT, and SILC-LED at [
20], JAMBU-SIMON available at [
21], and Ketje Jr. available at [
22]. The authenticated ciphers investigated in this research, including relevant characteristics, are summarized in
Table 1.
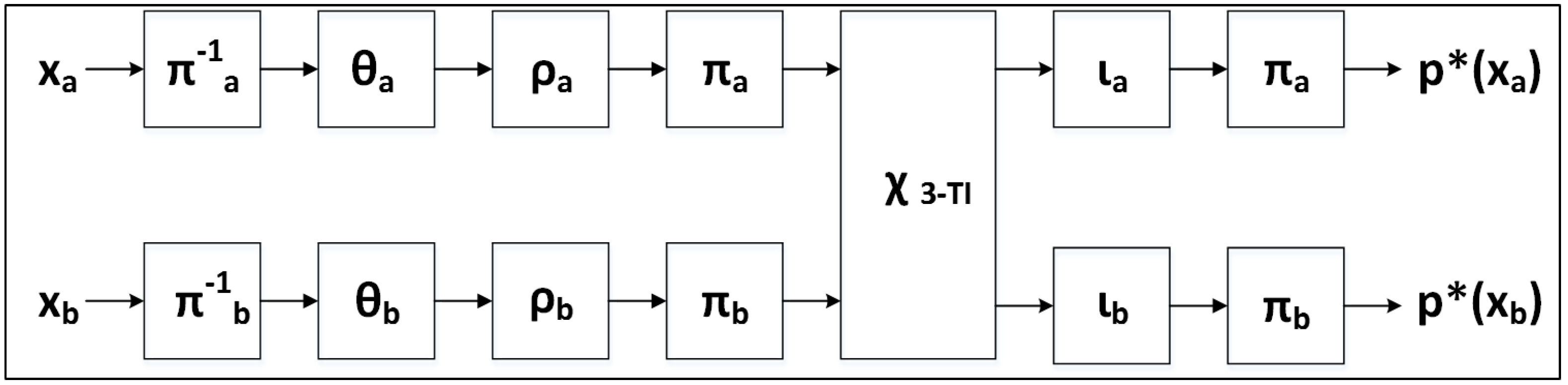
After demonstrating vulnerabilities of the unprotected cipher implementations to DPA, we seek to employ countermeasures to mitigate vulnerabilities. Although there are several types of DPA countermeasures, including algorithmic and non-algorithmic countermeasures, we limit our research to one particular algorithmic countermeasure called threshold implementations (TI).
TI, introduced in [
23], involve the separation of sensitive data into “shares”. Computations are subsequently performed on individual shares, in order to prevent an adversary from being able to simultaneously have access to all sensitive data. TI are based on the concepts of secret sharing and multi-party communications, where the communications of a single party do not provide sufficient information to reveal the contents of an entire message [
23,
24,
25].
TI are designed to provide security in CMOS technologies which are subject to glitches, where multiple level transitions per clock cycle can be observed by an attacker and correlated to recover sensitive data [
26]. In order to be provably secure against power analysis in the presence of glitches, algorithmic countermeasures constructed using TI should adhere to the following three properties, as discussed in [
23]:
Non-completeness. Every function is independent of at least one share of each of the input variables. Defined formally, if
, and
x and
y are divided into
n shares, then
Since does not depend on and , it cannot leak information about or .
Correctness. The sum of the output shares gives the desired output. Formally,
where
Uniformity. A realization of sharing is uniform if for all distributions of the inputs x and y, the output distribution preserves the input distribution.
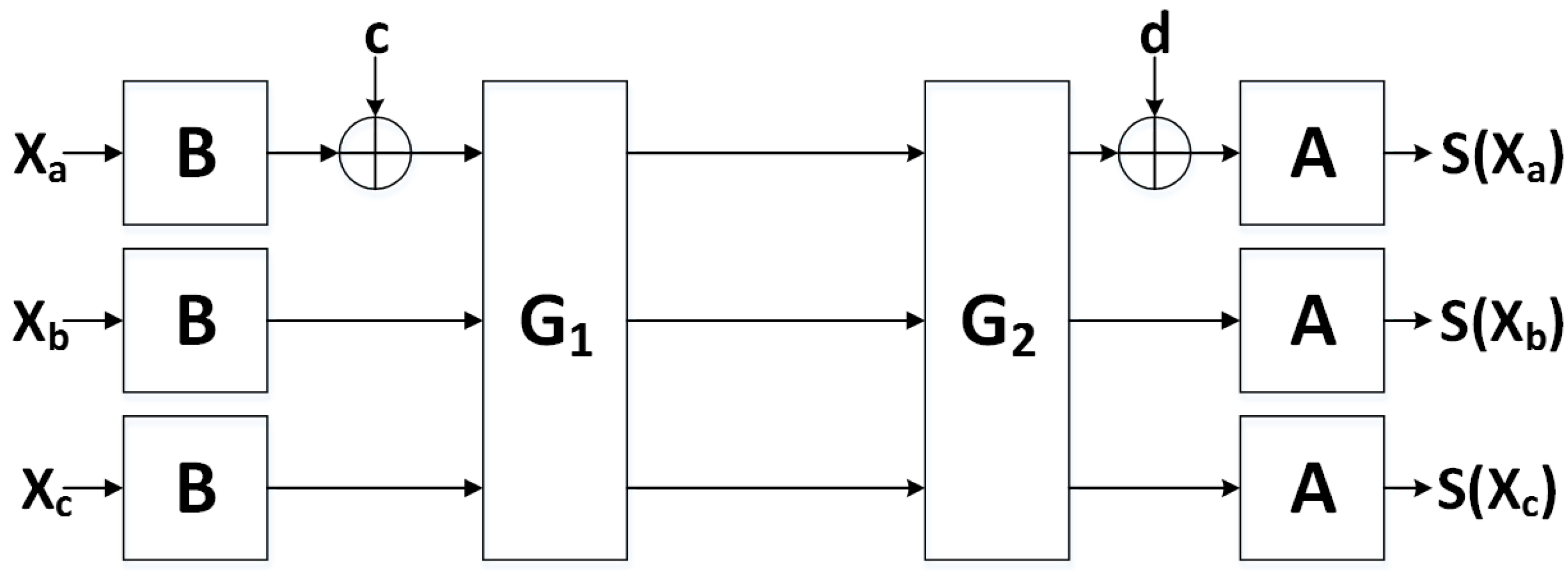
A nonlinear second-degree algebraic function, such as
(e.g., a 2-input
and gate), can be shared using three TI shares, since
shares are required to share a function of degree
d. However, as discussed in [
27,
28], achieving TI sharings which are simultaneously non-complete and uniform is not trivial. The uniformity property can be achieved by supplying fresh random bits (e.g., “resharing” or “remasking” randomness); however, this requires augmenting an implementation with a source of randomness, which must either be imported into the device, or generated internally at run-time. Thus, the engineer must make a decision whether to use fewer TI shares, which increases the amount of required additional randomness, or more TI shares, which results in more required logic.
Although TVLA has been used to show vulnerabilities in block ciphers, and to confirm the effectiveness of countermeasures to DPA (e.g., [
29,
30]), it has not previously been used to demonstrate improved resistance for a large group of authenticated ciphers. In this research, we enhance the methodology of [
30] to provide the first documented methodology suitable for analyzing side-channel resistance, and evaluating the effectiveness of countermeasures against side-channel attacks (SCA), for a large number of authenticated ciphers (i.e., 11 cipher variants in this research). Our methodology uses a free and open-source SCA test bench (FOBOS), published specification for the CAESAR Hardware API for Authenticated Ciphers, associated Development Package, and publicly-available source codes for the unprotected cipher implementations in this research. As such, it should be possible for other researchers to either duplicate, or improve upon these results.
Having established a baseline of identically protected implementations of authenticated ciphers, we compare unprotected and protected implementations in terms of FPGA resources in the Spartan-6 FPGA (LUTs and slices), maximum frequency (MHz), throughput (Mbps), throughput-to-area (TP/A) ratio (Mbps/LUT), power (mW), and energy per bit (E/bit) (nJ/bit), in order to determine absolute and relative costs of protection.
The key contributions of this work are as follows:
While it is well-known that the implementation of countermeasures against DPA is costly in terms of resources and performance, comparison between multiple ciphers often occurs using ambiguous metrics, performed by diverse research groups, and operating on different hardware and test architectures. This work presents a methodology for the comparison of the costs of protection against 1st order DPA which are suitable for adaptation across all authenticated ciphers, and could assist evaluation and standardization committees in selection of the best candidates.
This work performs a large-scale analysis of 10 CAESAR candidate authenticated ciphers, with comparison to a defacto standard of AES-GCM, which provides implementation data to support evaluation of CAESAR Final Round candidates, and provides early support to the NIST Lightweight Cryptography Standardization Project.
In addition to providing a large-scale comparison of protected implementations of authenticated ciphers, this research provides analysis and insights of the structures of individual ciphers which could spur further research into improved DPA protection techniques.
3. Discussion
For both the unprotected and protected implementations, ACORN is the smallest in terms of LUTs, followed by JAMBU-AES and JAMBU-SIMON. CLOC-AES and SILC-AES are larger than JAMBU-AES, since the CLOC and SILC implementations at [
18] instantiate two AES cores, whereas JAMBU-AES uses only one. AES-GCM (with one AES core) is nearly the size of SILC-AES (with two AES cores), since the AES-GCM
multiplier compares in size to the 8-bit pipelined AES core. Ketje Jr. and Ascon are relatively large due to their full-width basic-iterative architectures.
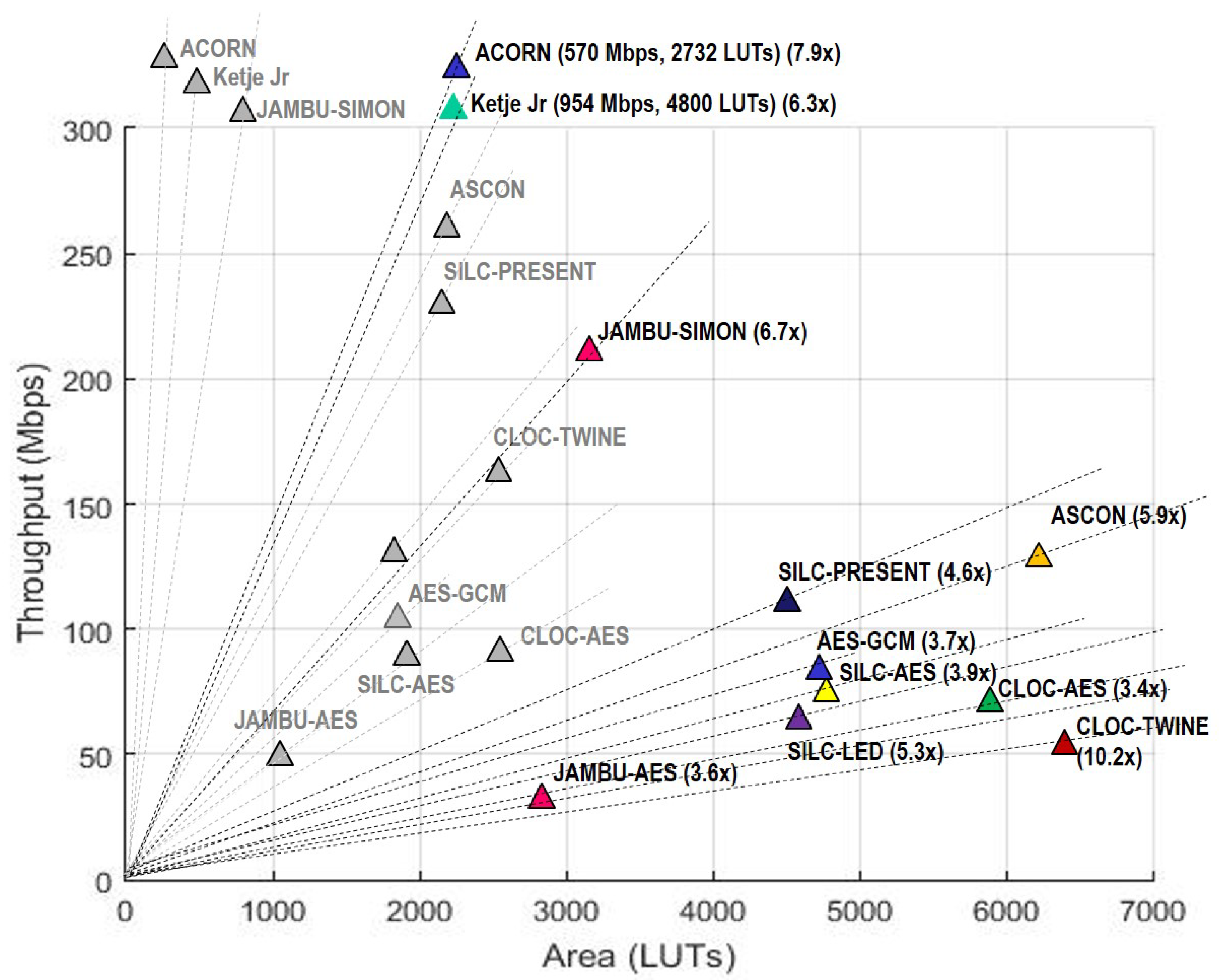
In terms of throughput, Ketje Jr. is highest among both unprotected and protected implementations, followed by ACORN and JAMBU-SIMON. However, ACORN has the highest TP/A ratio, followed by Ketje Jr. and SIMON-JAMBU, for both unprotected and protected implementations.
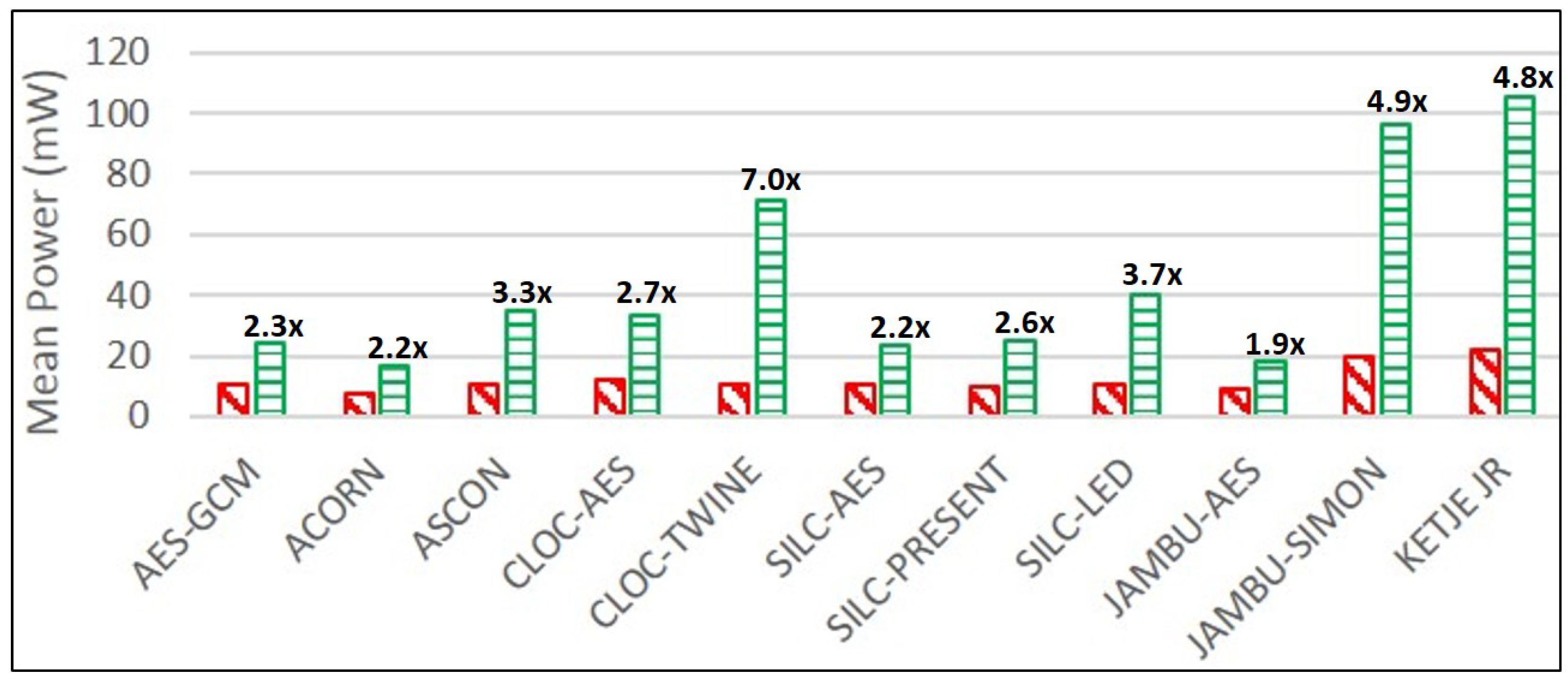
ACORN, followed by JAMBU-AES and SILC-PRESENT, have the lowest mean power consumption, as measured on the Spartan-6 FPGA at 10 MHz. For protected versions, ACORN uses the lowest mean power, followed by JAMBU-AES and SILC-AES.
Protected implementations resistant to DPA are generally not “constant-power” implementations. However, a minimal difference between and is desirable, from both an engineering standpoint, and for reducing potential vulnerability to power analysis attacks. Ascon, JAMBU-AES, and ACORN have the lowest difference between and , while SILC-AES, Ketje Jr.; and CLOC-TWINE have the greatest difference.
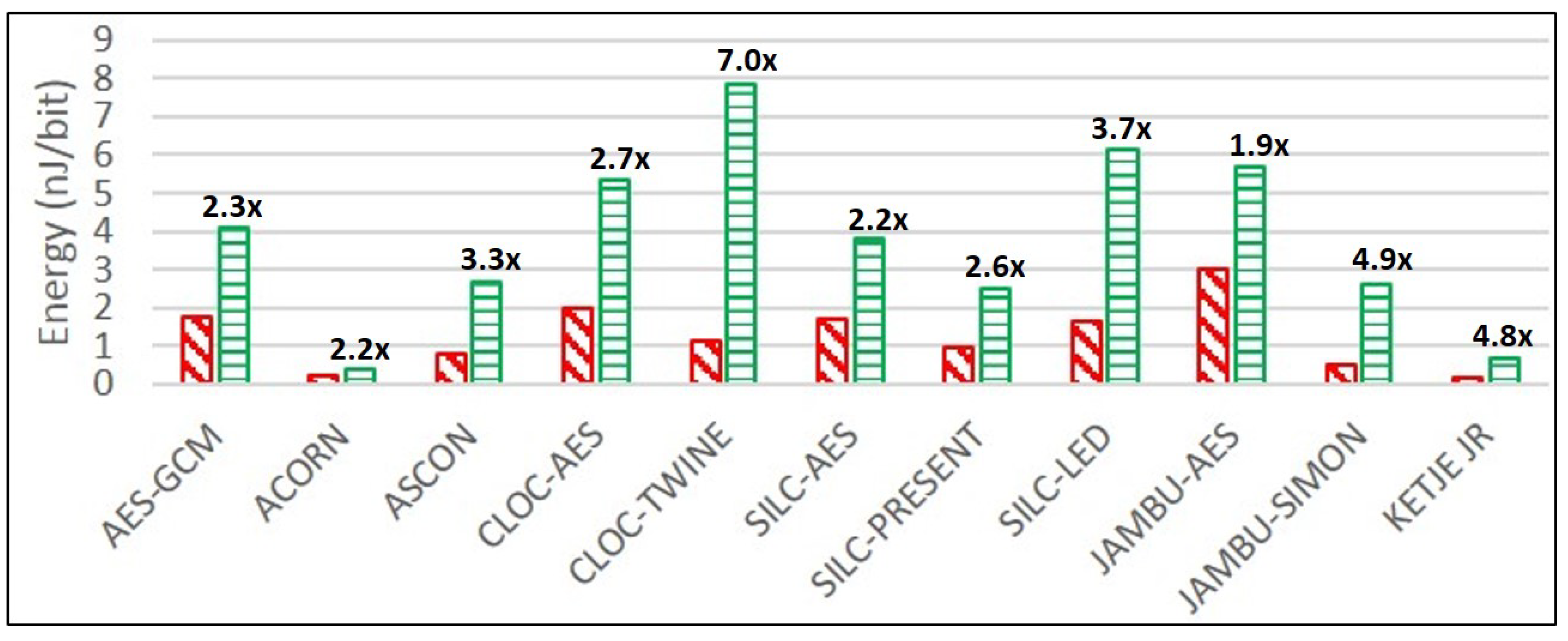
Ketje Jr. is the most energy-efficient of the unprotected cipher implementations, followed by ACORN and JAMBU-SIMON. For protected ciphers, ACORN is the most efficient, followed by Ketje Jr. and SILC-PRESENT.
The average number of LUTs increases by a factor of 3.1, and the throughput decreases by a factor of 1.8, when comparing unprotected to protected implementations. The reduction in throughput results from a 1.8 factor decrease in average maximum frequency, which is due to increase in critical path and routing congestion in the protected versions. The average TP/A ratio of the protected implementations decreases by a factor of 5.6 compared to the unprotected versions. The average power and E/bit of protected implementations increase by a factor of 3.4 compared to unprotected implementations. However, the growth factor for area, and reduction factors for TP and TP/A ratios (respectively) for individual protected cipher versions vary widely. In terms of area (LUTs), protected versions of SILC-PRESENT, CLOC-AES, and SILC-LED have the lowest growth factors over unprotected versions, while ACORN, CLOC-TWINE, and Ketje Jr. have the highest growth factors. The reason for high area growth factors is a combination of architecture required for protection against DPA, and additional required randomness. For example, the high growth factor in ACORN is due to the addition of a PRNG capable of sourcing 120 random bits per clock cycle, the size of which is comparable to the area of the protected ACORN not including the PRNG.
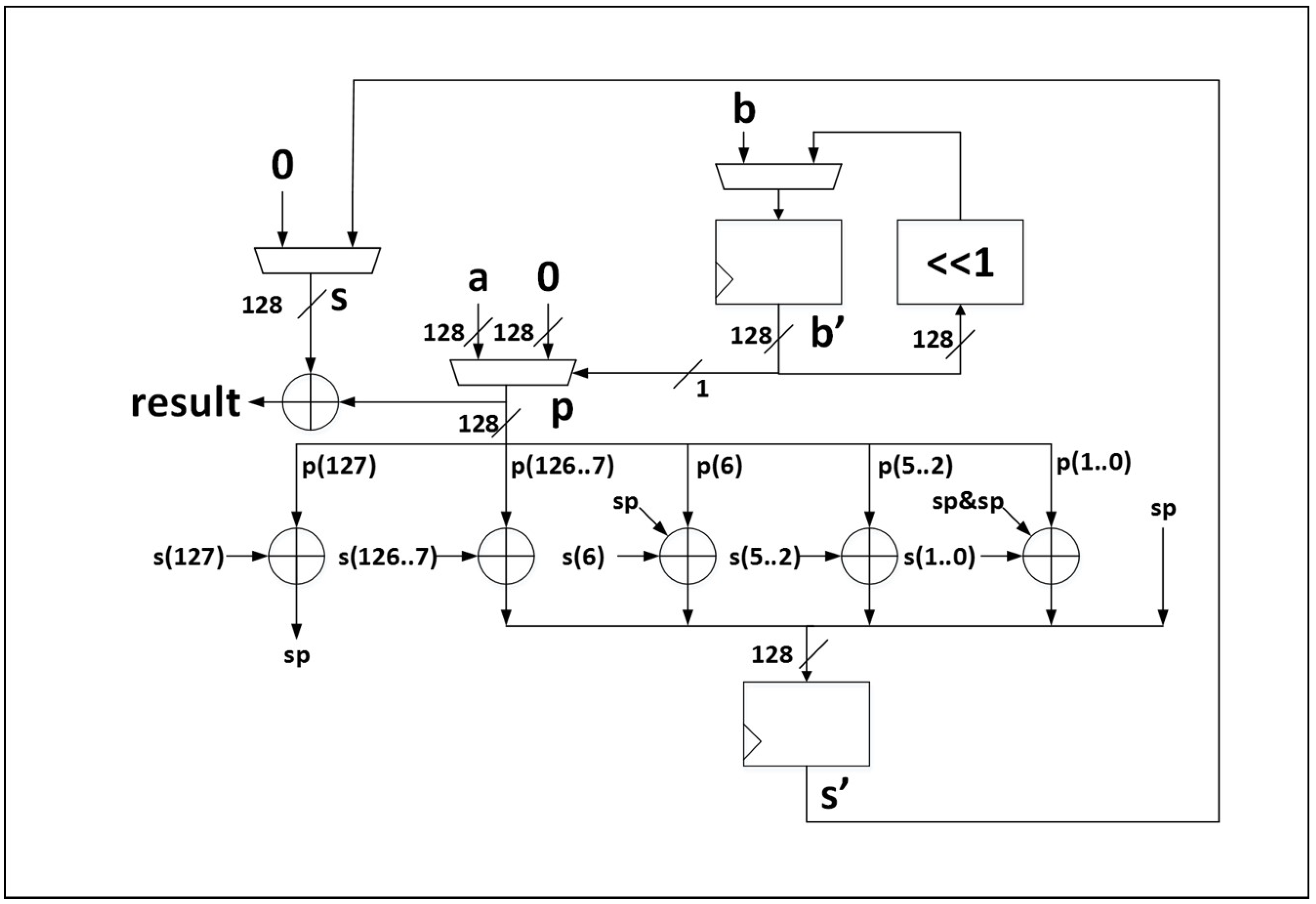
In terms of throughput, the lowest reduction ratios for protected cipher implementations are for JAMBU-AES, CLOC-AES, and AES-GCM, while the highest reduction ratios are for CLOC-TWINE, JAMBU-SIMON, and SILC-LED. Since architectures for protected and unprotected versions are analogous, this means that DPA protection most negatively affects the combination of critical path and routing congestion for CLOC-TWINE, JAMBU-SIMON and SILC-LED, and least affects JAMBU-AES, CLOC-AES, and AES-GCM. If we expand lowest reduction cost to fourth place, we note that SILC-AES and ACORN have nearly equivalent costs. This shows that the 8-bit pipelined AES core itself has a relatively low cost of protection against DPA.
In terms of throughput-to-area (TP/A) ratio, the lowest reduction ratios for protected cipher implementations are CLOC-AES, JAMBU-AES and AES-GCM, and the highest reduction ratios are CLOC-TWINE, ACORN, and JAMBU-SIMON. If we expand highest reduction ratios to four places, Ketje. Jr. has the next highest reduction cost. This shows that the best three overall performing protected ciphers (Ketje Jr.; ACORN, and JAMBU-SIMON) also have the highest relative protection costs. CLOC-TWINE has the highest ratio, indicating that either our protection of the TWINE primitive, or implementation of the protected 3-share CLOC-TWINE, is sub-optimal and could be improved.
JAMBU-AES, ACORN, and SILC-AES have the lowest growth ratios in power and energy consumption comparing protected to unprotected implementations, while CLOC-TWINE, JAMBU-SIMON, and Ketje Jr. have the highest growth ratios. This is a positive result for ACORN, since the highest performing protected cipher implementation (in terms of TP/A ratio) also has a very low growth in power consumption, at least at 10 MHz. While we have already noted the possibly sub-optimal DPA protection used in CLOC-TWINE, the high power and energy growths of JAMBU-SIMON and Ketje Jr. are explained by the use of architectures optimized for TP/A ratio (i.e., full-width datapath with basic iterative architectures), since the additional overhead of TI-protected modules results in the use of more than five times the additional computations in the same clock cycle compared to unprotected versions.
Table 5 ranks all authenticated ciphers in this study, in terms of absolute and relative costs of protections, as described above.
In general, comparison with results from previous research is difficult because there are very few reports on comparative costs of DPA protection of authenticated ciphers. An exception is [
43], where the authors construct several unprotected and DPA-protected versions of the Ascon authenticated cipher, and synthesize results in ASIC technologies. Although implementation areas (i.e., gate equivalents) are not directly comparable to FPGA results, we can examine the relative increases in area for the protected implementations. Additionally, the authors of [
43] use the same protection methodologies used in our research—a 3-share threshold implementation, which facilitates fair comparison.
In [
43], the authors produce one version of Ascon called Ascon-
fast. This version has a 64-bit datapath, and computes one round in 59 clock cycles. As such, it is similar to our protected version which has a 64-bit datapath, and computes one round in 49 clock cycles. The authors observe a 3.83 factor increase in area in the protected implementation, which compares to our observation of a 3.11 factor growth in the protected implementation. One notable observation is that the authors of two different Ascon implementations (i.e., [
43] and this work) have both observed a relatively high cost of protection for analogous Ascon architectures. In contrast, the authors of [
43] observe only a 2.45 factor cost of protection in the serialized version Ascon-
x-low-area, which completes one round in 512 clock cycles.
Although not directly comparable, one can examine costs of our 3-share TI-protected authenticated cipher implementations versus costs for 3-share TI-protected block cipher implementations. Studies of the protection costs of several block ciphers are published in [
29,
30], in which results for the AES, SIMON, and PRESENT block ciphers can be loosely compared to authenticated ciphers in our research using the same primitives, such as the CLOC-SILC and JAMBU families, as well as AES-GCM.
The resulting matrix of comparisons of area growth factors for protected implementations is shown in
Table 6. Of note, the average area growth factor of all protected AES implementations, including block ciphers and authenticated ciphers, is 2.53, which is less than the average observed cost of 3.1 for all authenticated ciphers in this research. Since protected AES implementations in [
29,
30], and all of this research, use a similar TI-protection strategy leveraging 8-bit datapaths and field inversions in Tower Fields, one can infer that this TI-protection technique is relatively efficient.
In this research, we examine implementations of CAESAR Round 3 candidate authenticated ciphers which are fully (or nearly-fully) compliant with the CAESAR HW API for Authenticated Ciphers [
9,
10]. The version of ACORN at [
19] enables a close-to-optimal protection against DPA using threshold implementations, since it uses a small datapath width (i.e., 8 bits), and has a maximum of two cascaded
and gates in its nonlinear state update computation path. In general, however, the implementations available at [
18,
20,
21,
22] are not optimized for TI protection. Specifically, they have either large datapath widths (e.g., 128 bits for AES-based ciphers, 64 bits for Ascon, SILC-PRESENT, SILC-LED, CLOC-TWINE, etc.), basic iterative architectures with multiple nonlinear operations performed in parallel (e.g., Ascon, CLOC-SILC cipher variants, Ketje Jr.), or even unrolled architectures with multiple rounds completed in a single cycle (e.g., JAMBU-SIMON).
While the above choices of architecture provide optimal throughput-to-area (TP/A) ratios, they are suboptimal when attempting TI-protection. Some reasons include:
Wide datapaths with multiple TI-protected gates in the same clock cycle lead to a large growth of resources (which increase quadratically in order of protection), and large power consumption, which is not optimal for IoT devices.
Multiple cascaded nonlinear computations, occurring in the same clock cycle, increase the probability of enabling power correlations based on glitch transitions in CMOS logic, which have the potential to leak sensitive information [
26].
The amount of randomness (measured in random bits per clock cycle) required for resharing from two to three TI shares, or required to meet the TI uniformity property, increases with wide datapaths and with basic iterative or unrolled architectures. This increases the required output of either an internal randomness source (such as a PRNG), or external randomness provided through an interface.
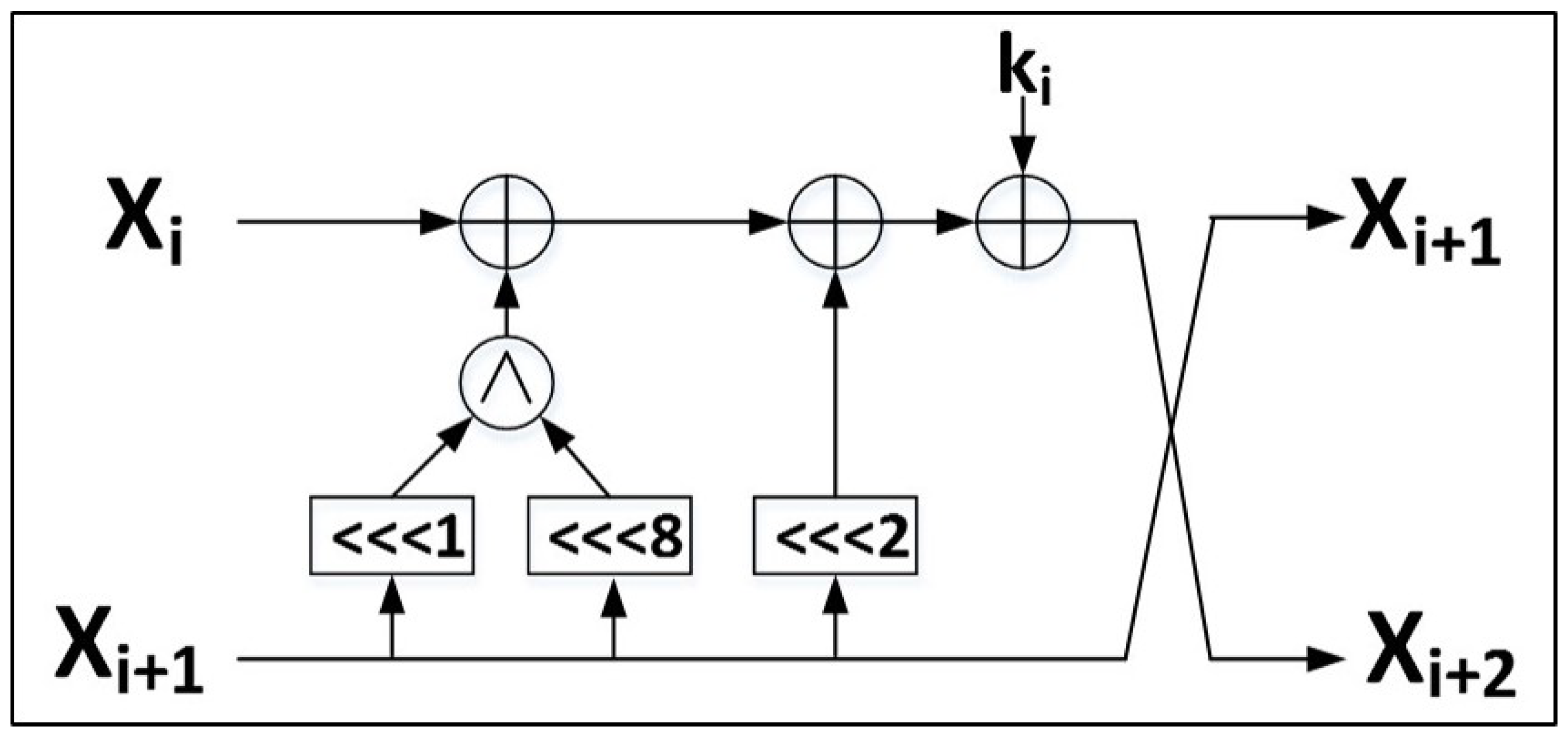
Therefore, authenticated ciphers, optimized for TI protection, should be constructed with small internal datapaths (e.g., 8 or 16 bits), and with a maximum of one logic level of nonlinear functions (e.g., and) conducted in a single clock cycle, which could result in pipelined or folded (e.g., multi-cycle) architectures. This approach has been fully adopted for modification of AES-based ciphers (i.e., reduced datapath and pipelined architecture), and partially adopted for ACORN and Ascon (e.g., multi-cycle architectures). However, these techniques should be investigated for all authenticated cipher candidates, and is left to future research.
Future research could include investigation of additional pairs of authenticated ciphers, investigation of cipher versions which are optimized for protection against DPA, and measurement of power and energy at higher frequencies, i.e., closer to actual maximum operating frequencies. The use of attack-based testing methods (such as Correlation Power Analysis) to quantify improved resistance of protected versions to DPA (including higher orders of DPA) could provide additional insight into the relative costs of protection of the subject ciphers. Additionally, the techniques in this research could be adapted to investigate costs of protection for future cryptographic competitions, such as for post-quantum resistant public key cryptography.
4. Materials and Methods
Our research leverages methods and methodologies applied for comparing costs of DPA resistance for block ciphers, described in [
30], but expanded to apply to authenticated ciphers.
Differential Power Analysis (DPA) is used to analyze differences between observed power measurements, and power based on hypothetical contents of a sensitive intermediate variable, according to a power model. However, determining the correct power model is time consuming, can require extensive trial and error, and can be completely invalidated by changes in the associated architecture [
30,
44,
45].
One method of analyzing cryptographic implementations for information leakage is introduced in [
6,
7] and further described in [
46], and is called the Test Vector Leakage Assessment (TVLA). This methodology uses common statistical methods such as the Welch’s
t-test to determine whether two distributions are different from one another. Advantages of this leakage assessment methodology are that it locates information leakage without having to conduct a more time-consuming DPA attack, is a “black-box” testing approach, in that it does not require extensive internal knowledge of the implementation, and can quickly assess the effectiveness of countermeasures. However, it cannot be used to recover a secret key, or provide immediate information about the difficulty of a prospective DPA attack.
In TVLA, a confidence factor
t is calculated as
where
and
are means of distributions
and
(to be subsequently defined),
and
are standard deviations, and
and
are the cardinality of the distributions, or the number of samples.
Assuming a normally distributed probability density function (pdf) , a probability of accepting a null hypothesis p is calculated as . We start with distributions and , and assume the null hypothesis, i.e., that we are unable to distinguish between and . We designate a “threshold”, e.g., , beyond which we reject the null hypothesis. If we exceed this threshold during a t-test involving and , we reject the null hypothesis, and conclude that the device is leaking information.
In our research, we use the so-called “fixed versus random”
t-test, where we preselect some “fixed” input data
D (which for authenticated ciphers consists of a test vector including
,
, and
), and randomly interleave the feeding of
D, or random data, to the algorithm [
7,
46].
In order to conduct a fixed versus random t-test, we instantiate the cipher on a physical device (e.g., FPGA or microcontroller), isolate external noise sources, monitor changes in voltage or current that occur in response to varying input, capture data from thousands of repetitive traces, and perform offline statistical analysis to diagnose vulnerabilities.
In order to avoid noise and corrupted analysis, we wish to prevent external I/O during trace collection. Additionally, we require test vectors, such as
and
, which reflect a fixed-versus-random methodology, are suitable for thousands of repetitions, and are available at the cipher module at the start of every trigger event. These conditions are easily met for the typical block cipher, where there are only a few (e.g., 16) bytes each of
and
for every trace event. These few bytes of data are stored in the cipher module itself prior to trigger, or in a thin-veneer of buffers on the test board. Additionally, the cipher-test architecture interface is typically trivial, consisting of (for example),
m-bit
,
n-bit
,
p-bit
ports, clock, and control signals. Likewise, the only protocol events for block cipher operations are typically “start” and “done”. As a result, it is usually easy for cipher developers to send their designs to a “power analysis test shop”, and assume that the tester will be able to adapt the block cipher to their test architecture. The above assumptions, however, do not hold for authenticated ciphers. In order to detect all possible leakage in an authenticated cipher, one should test a variety of sequences of operations, including key initialization,
and
processing, authenticated encryption and decryption, and
generation and verification. This requires a test vector potentially thousands of bytes long, interlaced with protocol that describe the entire range of permitted authenticated cipher operations. A sample authenticated cipher test vector is shown in
Figure 21.
This long test vector must be provided to the victim board (but remain outside the cipher) prior to the trigger event. In contrast to the block cipher, long test vectors will arrive and depart the cipher unit during the trace event, but should not enter or exit the victim board during the event. Additionally, an authenticated cipher must have a more-complex external interface to encompass the range of possible operations. It is not reasonable to expect that a laboratory engineer could adapt each individual custom-designed authenticated cipher interface to a power analysis test bench, and, if so, the expense in time and resources would preclude performing a large-scale analysis of DPA-resistance of multiple authenticated ciphers.
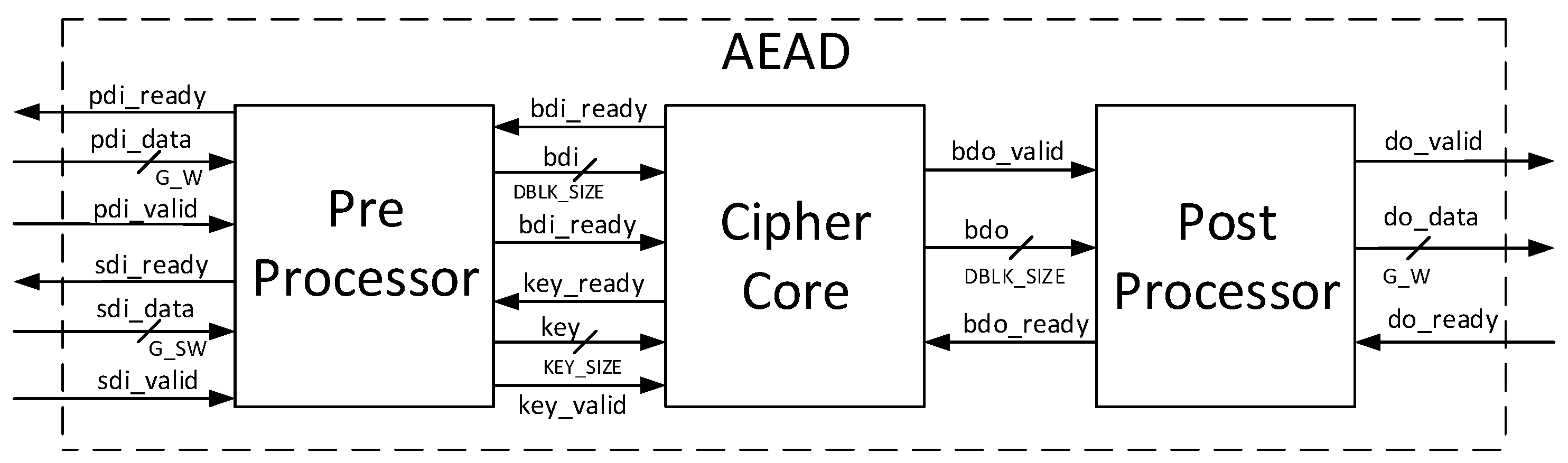
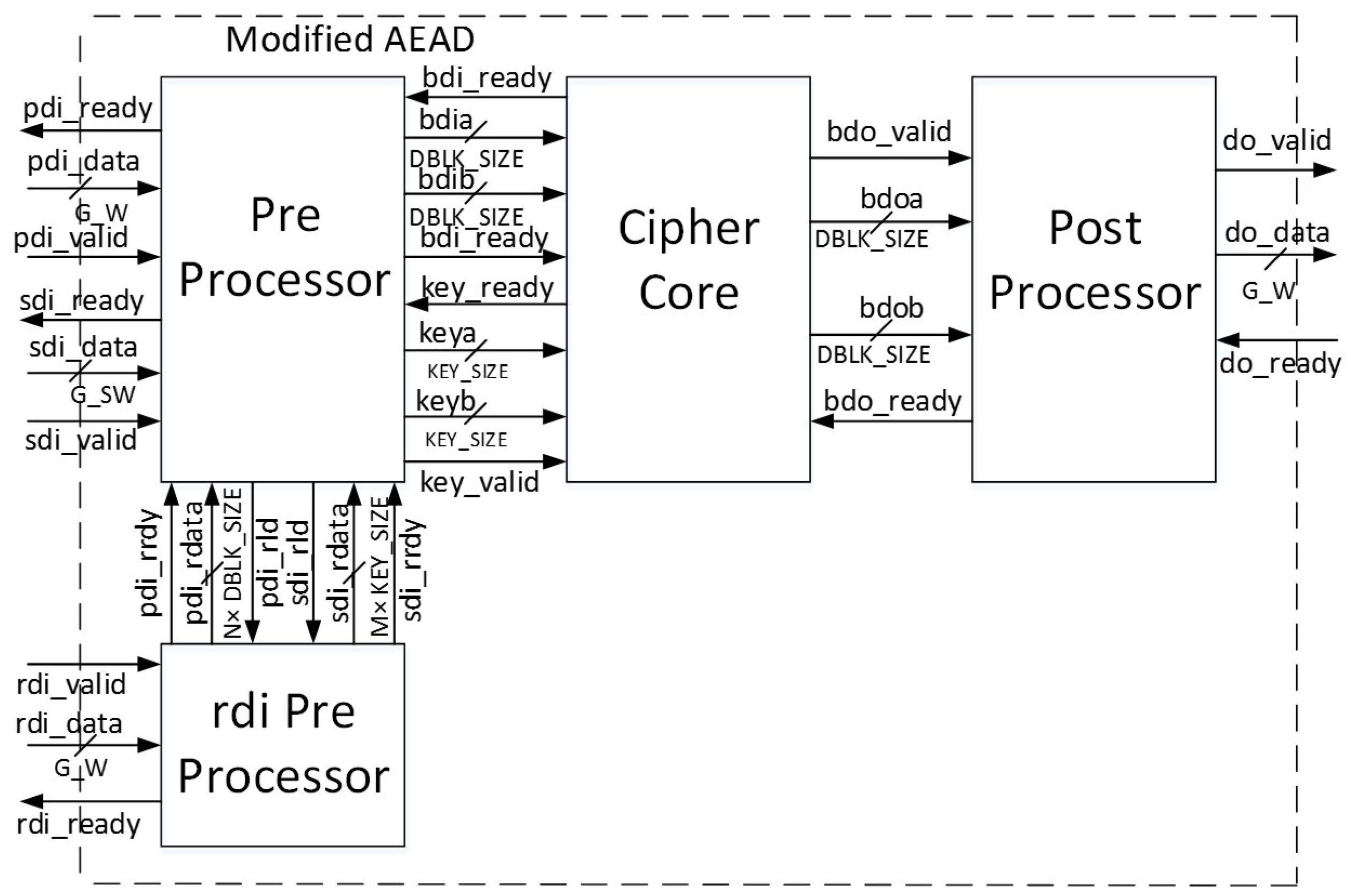
The adoption by the CAESAR Committee of the CAESAR HW API for Authenticated Ciphers enables the definition of an interface which is applicable to all CAESAR-candidate authenticated ciphers, and is readily compatible with our DPA test bench and benchmarking processes. This API, available at [
9,
10], includes a protocol for all required authenticated cipher operations, as summarized above. The API also specifies an AXI-compatible external interface, shown in
Figure 11, and further described in [
41]. Additionally, the Development Package for the CAESAR HW API contains a test vector generator,
aeadtvgen.py, which facilitates construction of deterministic and comprehensive test vectors required for our power analysis [
11].
We adapt the Flexible Open-source Workbench for Side-channel analysis (FOBOS) to perform TVLA for side-channel leakage detection on authenticated ciphers. FOBOS is designed to measure resistance to power analysis side-channel attack (SCA) and evaluate the effectiveness of countermeasures [
8]. It is trigger-activated, captures power analysis data in a specified window using an oscilloscope, and stores data offline for post-run analysis in a personal computer (PC). FOBOS uses separate control and victim boards, where the control board interfaces with host personal computer and external peripheral devices, and the victim board instantiates the device under test (DUT).
In our instance of FOBOS, the oscilloscope used is the Agilent Technologies DSO6054A (Santa Clara, CA, USA), and the control and victim boards are the Digilent Nexys-3 (Seattle, WA, USA) with Xilinx Spartan 6 FPGA. However, the components of FOBOS are built in a modular fashion so that the entire experimental setup can easily be adapted for different control and victim FPGA boards, oscilloscopes, and attack techniques.
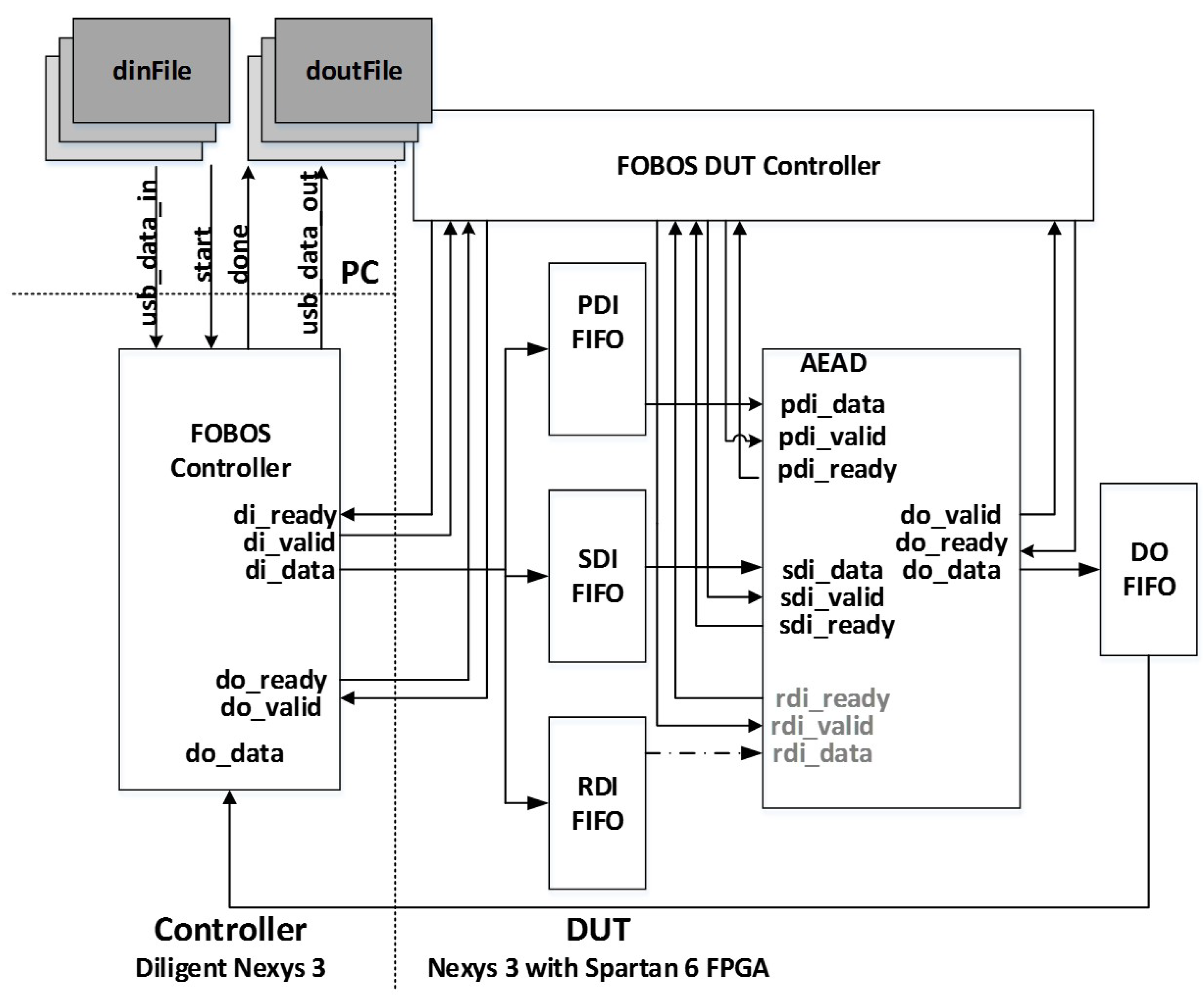
For authenticated ciphers, the FOBOS DUT victim wrapper is configured with separate FIFOs (First-in, First-out) corresponding to the data ports prescribed in [
9], including public data interface
pdi, secret data interface
sdi, and data output
do. A fourth FIFO is aligned to the random data interface
rdi, which augments [
9] to provide random data necessary for initial masking of public and secret data in protected ciphers. The FOBOS architecture, updated for authenticated ciphers, is shown in
Figure 22. The baseline FOBOS software suite, including acquisition and offline side-channel analysis packages, is coded in Python and is available for download at [
8].
The procedure for performing t-tests on authenticated ciphers using FOBOS is summarized below:
The test vector dinFile.txt, created by aeadtvgen.py, is pre-formatted using a FOBOS parsing utility. It contains thousands of consecutive vectors of randomly-interleaved fixed or “random” data, where random data is substituted for all instances of , , , , and . The test vectors are wrapped in a layer of FOBOS-specific protocol, which determines their FIFO address on the victim board.
Two separate bitstreams, FOBOS Controller (control board), and FOBOS DUT (which contains FOBOS DUT wrapper and victim cipher) are instantiated in hardware.
The acquisition process dataAcquisiton.py is run from the PC. Each vector is loaded by the FOBOS Controller into FOBOS DUT. FOBOS Controller provides an oscilloscope trigger upon completion of test vector loading. Power measurements, sensed by a current probe and measured in the oscilloscope, are sent to the PC for offline analysis. Data output (e.g., ) from each trace is accumulated in doutFile.txt. Output data, although not used in the non-specific t-test, is valuable for ensuring proper cipher operation.
At the completion of all traces, the tester performs offline analysis on traces, stored in.npy format [
47]. A utility routine “splits” the collected power traces into two distributions
and
, according to a “fixed-versus-random” metafile created during test vector generation. The tester then runs the
t-test utility on distributions
and
, which generates a two-dimensional display of samples (corresponding to the time domain on the
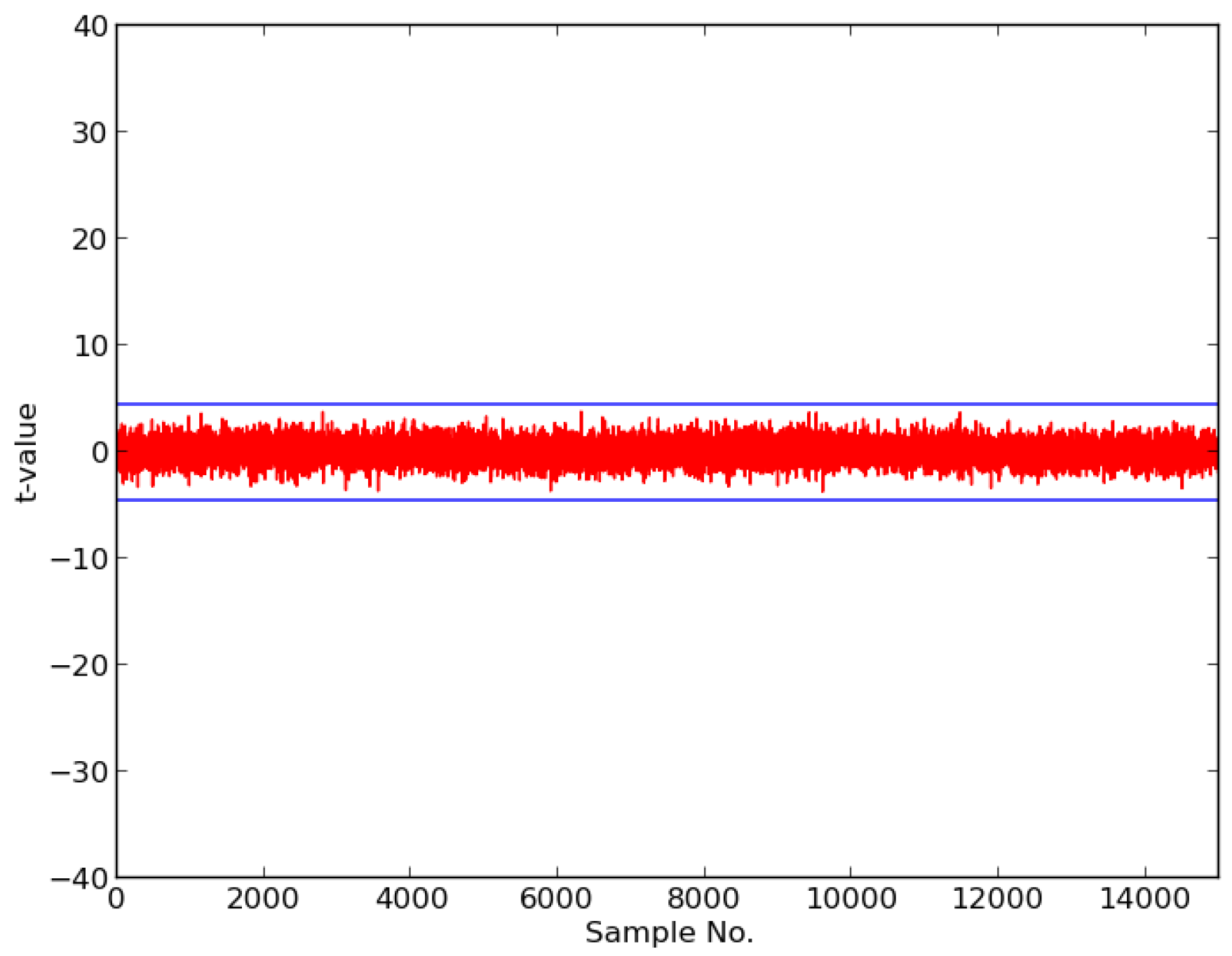
x-axis), and t-values, where sustained and repeatable results of
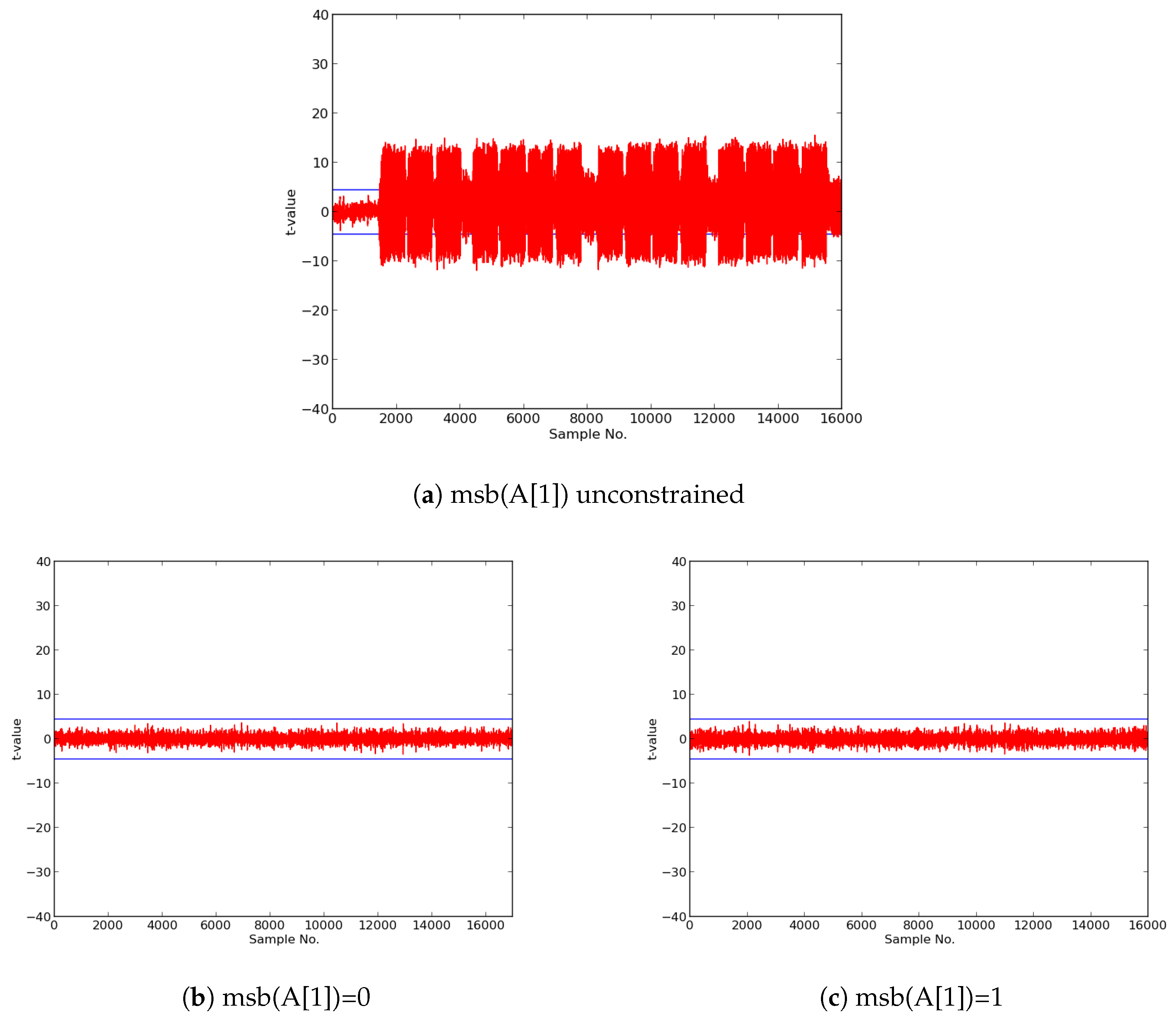
are considered a sign of vulnerability to DPA leakage.
We adapt the FOBOS architecture to measure power consumed by the Spartan-6 1.2V bus, e.g., , by measuring current through a 1 shunt resistor. Measured current is amplified by a TI INA225 amplifier (Dallas, TX, USA), collected by the attached oscilloscope, and transferred to a host computer for post-acquisition power computation.
Power measurements are recorded at discrete time intervals corresponding to sample rate. Between 10 and 100 traces (using various test vectors of up to 2000 bytes each) are used to generate power traces. The power measurements contain a combination of static and dynamic power at each sample, where dynamic power sourced by accounts for about 95% of total dynamic power, according to Xilinx Power Analyzer (XPA) simulations. The victim board itself, including hardware outside the DUT but instantiated in the DUT wrapper, accounts for some static and dynamic power usage, which results in some error in power measurement. However, this error is expected to be nearly constant across all evaluated authenticated cipher candidates, so that the relative difference between observed power is accurate.
During post-analysis, mean power () is computed by averaging instantaneous power measurements over the entire time domain, while maximum power () is estimated by sampling the highest peaks during each trace. E/bit (nJ/bit) is then estimated as , where TP (throughput) is the throughput of an authenticated encryption of a long message.
5. Conclusions
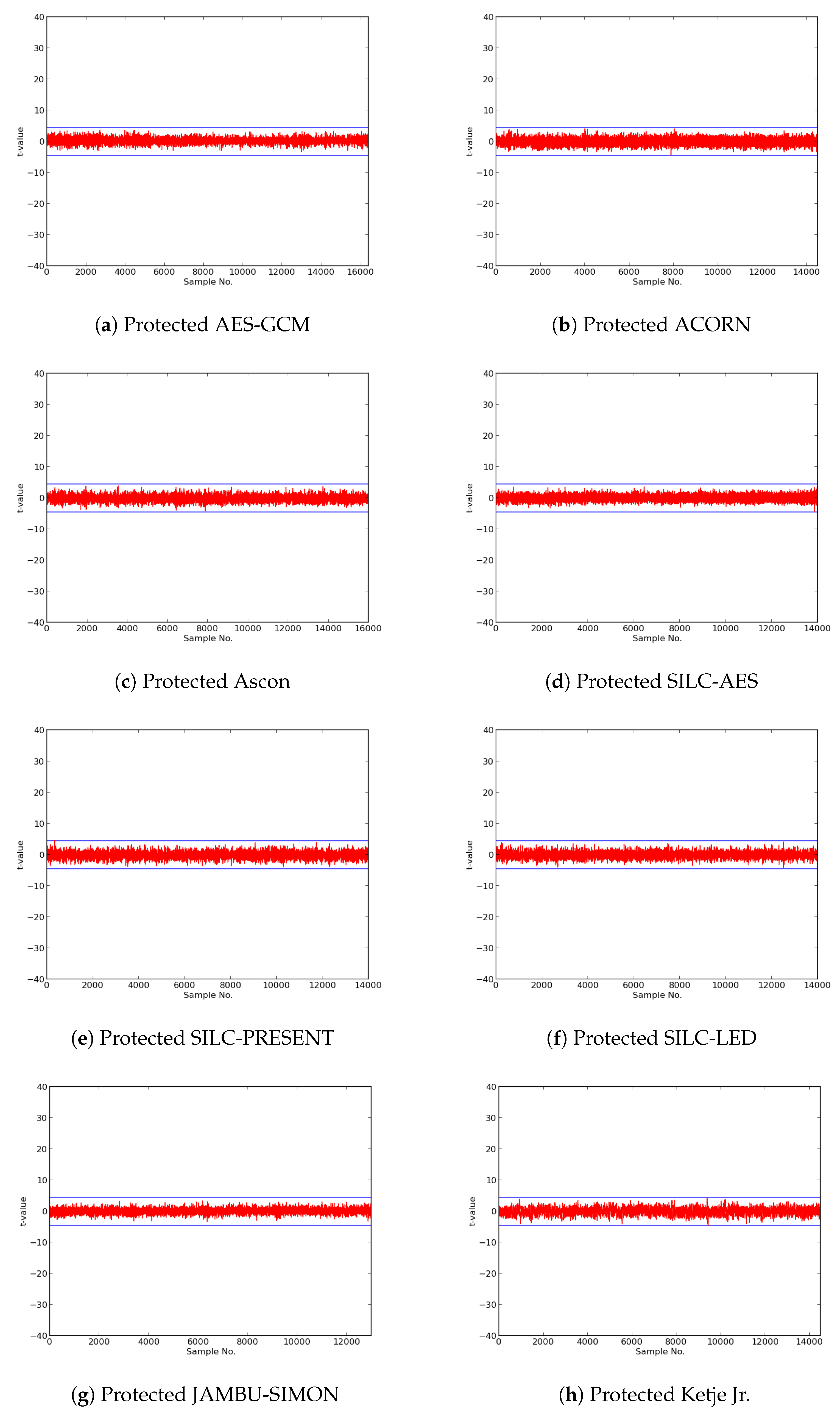
In this research, we expanded the Test Vector Leakage Assessment (TVLA) methodology to enable comprehensive large-scale analysis of authenticated ciphers, in order to determine resistance to DPA side-channel attack, and to verify effectiveness of countermeasures against DPA. Our methodology, which leverages the Flexible Open-source workBench fOr Side-channel analysis (FOBOS) test bench, CAESAR Hardware API for Authenticated Ciphers, and related Development Package, confirms that unprotected implementations of AES-GCM, ACORN, Ascon, CLOC (AES and TWINE), SILC (AES, PRESENT, and LED), JAMBU (AES and SIMON), and Ketje Jr., in the Spartan-6 FPGA, have significant information leakage and are likely vulnerable to DPA.
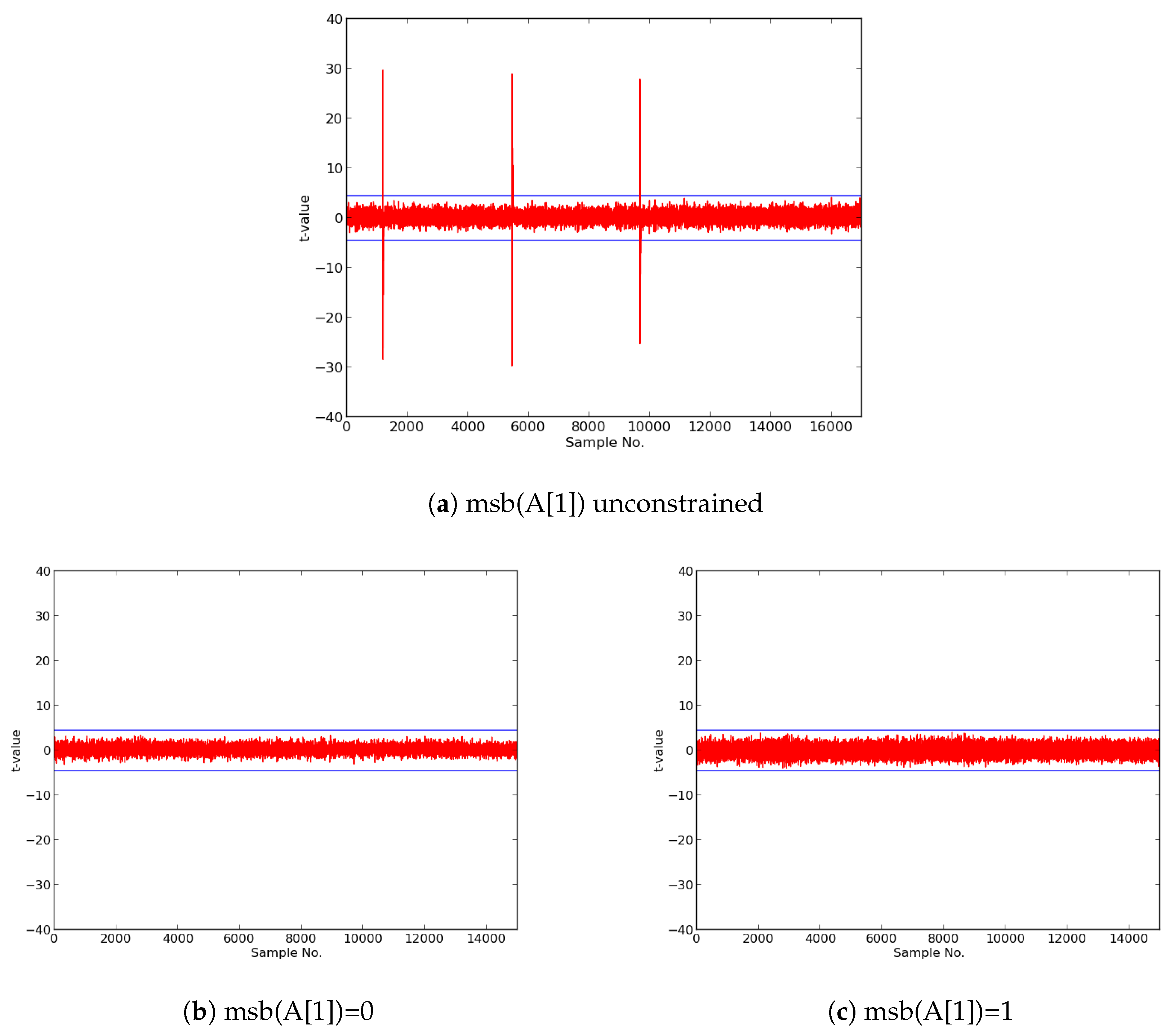
We then constructed protected implementations of all above ciphers, and verified their improved resistance to 1st order DPA using TVLA as implemented on FOBOS. In the case of the CLOC authenticated cipher (i.e., CLOC-AES and CLOC-TWINE), we demonstrated leakage due to a data-dependent conditional decision in the CLOC specification. Although CLOC-AES and CLOC-TWINE protected implementations did not pass a t-test with generic test vectors, we use modified test vectors to demonstrate that conditionally-protected CLOC authenticated cipher implementations achieved improved resistance to 1st order DPA.
Our results showed that ACORN had the lowest area of the protected cipher implementations, followed by JAMBU-AES and JAMBU-SIMON. Likewise, ACORN had the highest throughput-to-area (TP/A) ratio, followed by Ketje Jr. and JAMBU-SIMON. ACORN was also the most energy efficient of the protected implementations (i.e., used the lowest energy per bit), followed by Ketje Jr. and SILC-PRESENT, according to our evaluations on the Spartan-6 FPGA at a fixed frequency of 10 MHz.
Given our large-scale analysis of multiple protected implementations of authenticated ciphers, we are able to generally characterize costs of protection against 1st order DPA. The area of protected implementations increased by an average factor of 3.1, the throughput decreased by a factor of 1.8, and the TP/A ratio decreased by a factor of 5.6, when comparing protected to unprotected implementations. The energy per bit of protected implementations increased by an average factor of 3.4 compared to unprotected implementations.
SILC-PRESENT had the lowest relative growth in area, while JAMBU-AES had the lowest reduction in throughput, and CLOC-AES had the lowest reduction in TP/A ratio, when comparing protected to unprotected cipher versions. JAMBU-AES had the lowest growth in power and energy per bit.
Our results and repeatable methodologies demonstrated in this research can be used to experimentally develop improved algorithmic side-channel protection techniques for existing and future cipher specifications.