Provably Secure Covert Communication on Blockchain

Abstract

Blockchain is a public open ledger that provides data integrity in a distributed manner. It is the underlying technology of cryptocurrencies and an increasing number of related applications, such as smart contracts. The open nature of blockchain together with strong integrity guarantees on the stored data makes it a compelling platform for covert communication. In this paper, we suggest a method of securely embedding covert messages into a blockchain. We formulate a simplified ideal blockchain model based on existing implementations and devise a protocol that enables two parties to covertly communicate through the blockchain following that model. We also formulate a rigorous definition for the security and covertness of such a protocol based on computational indistinguishability. Finally, we show that our method satisfies this definition in the random oracle model for the underlying cryptographic hash function.

1. Introduction

Covert communication channels are designed to protect the relationship between the transmitter and the receiver by hiding the fact that secret communication is taking place in the first place. Such channels can be used, for example, in military communication or in the presence of an authoritarian government. Secure covert communication can be implemented as a combination of cryptography and steganography. Cryptography ensures that the communicated message stays private while steganography is used to hide the fact that there is encrypted communication. However, steganography requires a medium. It requires that there is a channel where innocuous communication is taking place and both the transmitter and the receiver have access to that channel. In addition, the channel needs to be reliable so that the receiver gets the transmitted message with high probability and it has not been manipulated with.

The blockchain technology was first introduced as the underlying mechanism for cryptocurrency in Bitcoin [1] as an open decentralized method of providing trust. Blockchain is a public distributed ledger implemented as a continuously growing chain of blocks that is designed to provide authenticity of the data without any centralized parties. Its integrity is ensured collaboratively by the majority of the nodes participating in the blockchain network. Therefore, data recorded into a blockchain is inherently resilient to manipulation, since manipulation would require the adversary to control a large fraction of the nodes. Since its introduction, blockchain technology has attracted a lot of interest in various applications, such as smart contracts enabled by Ethereum [2], Internet of Things [3], healthcare [4] and medical data management [5]. Typically, blockchain networks, such as those underlying cryptocurrencies, are free for anyone to join. This openness together with strong integrity guarantees on the stored data make blockchains an interesting platform for implementing covert communication channels.

There are three main advantages of blockchain compared to other cover mediums: (1) it is anonymous and free to join, meaning that the communication parties have free access, (2) submitted data cannot be altered and, in particular, the integrity guarantees are not provided by any centralized party, but the consensus of the entire network, and (3) published data cannot be removed, meaning that no authority can apply censorship to already published data. Since the blockchain is immutable, alteration of the covert messages is virtually impossible and the embedding of covert information is free to be fragile. This is not the case, for example, for images on an image board.

In this paper, we suggest a method of submitting covert messages through a blockchain considered as a payment platform. Due to the immutable nature of the blockchain, the sender’s ability to embed into it is limited. However, since everybody is free to submit payments into the chain, we apply those payments to convey encrypted messages to a receiver. We start by providing a model for the blockchain, called a simplified ideal blockchain, where irrelevant technical details have been abstracted away. We then devise $\mathsf{BLOCCE}$, a method of embedding and extracting reliably into a blockchain following this model by submitting payments and show that the method is reliable and runs in expected polynomial time excluding the time spent waiting for new blocks to appear into the chain. Based on the provable security of stegosystems, we then formulate a definition of secure covert communication on a blockchain based on the hardness of distinguishing the payload containing payments from random payments. Finally, we prove that our method satisfies this definition. The embedding rate of our method is rather inefficient and it is considered in a simplified model. Therefore, our proposal can be seen more as a proof-of-concept scheme than a practical scheme that is ready to be implemented. However, our proposal is the first to achieve a covert channel over a public blockchain with provable security.

The paper is organized as follows. Section 2 explains the preliminaries for the rest of the paper such as the utilized cryptographic primitives and steganography. In Section 3, we describe our model of a simplified ideal blockchain. The suggested method is explained in detail in Section 4 and its security is studied and proved in Section 5. Finally, Section 6 and Section 7 provide the discussion on future work and the conclusion, respectively.

Related Work

To the best of our knowledge, there are no suggestions implementing provably secure covert channels on a blockchain. However, there are methods and services that systematically insert arbitrary data into a blockchain [6]. The insertion can be based on either the input scripts, that unlock funds for the transaction, or the output scripts that specify the receiver of the unlocked funds. Depending on the transaction type (coinbase transactions that generate new currency or normal ones that make payments) deviations from the standard payment templates enable users to insert a message into the blockchain. This can be achieved, for example, by using dead conditional branches in an input script or replacing receiver public keys or script hashes with arbitrary data. Especially, methods manipulating the receiver address bear similarities to the one suggested in this paper. However, none of the existing methods address the covertness and privacy of the inserted data, which is the main motivation of our proposal. See [6] for a recent survey on existing blockchain data insertion methods and [7] for the methods that are used to detect and thwart them.

Our work is also related to the wider topic of privacy of blockchain based applications. Privacy was not an inherent property of the original Bitcoin design [1]. In fact, due to its open and public nature, there are several threats to the privacy of blockchain users [8]. However, there are several suggestions in the literature that attempt to address these issues by improving the anonymity, for example, by unlinking payments from their origin [9], using zero-knowledge proofs [10] or blind signatures [11]. There are also suggestions that use blockchain as a medium for secure communication. Typically, these suggestion apply encryption to protect the stored application data. For example, atrusted blind escrow service with encrypted data using a blockchain was suggested in Ref. [12]. In Ref. [13], an energy trading platform with bi-directional encrypted message streams was suggested. A decentralized data storage based on blockchain with end-to-end encryption for the internet of things was suggested in [14]. In order to provide a tamper-proof media transaction framework, blockchain technology was combined with digital watermarking of the media in [15].

2. Preliminaries

2.1. Notation

Let $\mathcal{D}$ be a probability distribution. A random variable V that is distributed according to $\mathcal{D}$ is denoted by $V\sim \mathcal{D}$. If an element u is sampled from a probability distribution $\mathcal{D}$, we denote $u\leftarrow \mathcal{D}$. The uniform probability distribution on a set X is denoted by $U\left(X\right)$. For probabilistic algorithms, we apply the standard notation [16]. When an algorithm $\mathsf{A}$ is run with an input x and it outputs y, we denote $y\leftarrow \mathsf{A}\left(x\right)$. Algorithms can be given access to oracles. Oracles are considered as “black boxes” that can compute, for example, functions or other algorithms. An algorithm $\mathsf{A}$ with oracle access to an oracle $\mathsf{O}$ is denoted by ${\mathsf{A}}^{\mathsf{O}}$. We assume that the time complexity of calling an oracle and receiving its answer is constant time $O\left(1\right)$.

The length of a string $\sigma ={\sigma }_1{\sigma }_2\dots {\sigma }_n\in {\{0,1\}}^n$ is denoted by $\left|\sigma \right|=n$. The least significant bit (LSB) of $\sigma ={\sigma }_1{\sigma }_2\dots {\sigma }_n$ is ${\sigma }_n$. The binary string of length s consisting solely of ones is denoted by $1^s$ and is often used as a security parameter for cryptographic primitives. A function $ϵ:\mathbb{N}\to \mathbb{R}$ is negligible if for every $k\in \mathbb{N}$ there $n^{\prime }\in \mathbb{N}$ such that $\left|ϵ\left(n\right)\right|\le n^{-k}$ for every $n\ge n^{\prime }$.

2.2. Cryptographics Primitives

Our method is based on the perceived randomness of the outputs of a hash function. Let ${\{0,1\}}^{\ast }$ denote the set of all finite-length strings over $\{0,1\}$ together with the empty string (Kleene closure). We follow the random oracle model where a cryptographic hash function $H:{\{0,1\}}^{\ast }\to {\{0,1\}}^n$ is modeled as a random oracle. For each input string $m\in {\{0,1\}}^{\ast }$, the output $H\left(m\right)$ is independently and uniformly randomly selected (and fixed for subsequent queries with the same input) from ${\{0,1\}}^n$.

A symmetric encryption scheme $\mathsf{SE}=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$, where $\mathsf{Gen}$ is a key generation algorithm that on input a security parameter $1^s$ outputs a secret key $k\leftarrow \mathsf{Gen}(1^s)$, $\mathsf{Enc}$ is an encryption algorithm that on input a key k and a plaintext message m outputs a ciphertext $c\leftarrow \mathsf{Enc}(k,m)$ and $\mathsf{Dec}$ is a decryption algorithm that on input a key k and a ciphertext message c outputs a plaintext message m such that $m\leftarrow \mathsf{Dec}(k,c)=\mathsf{Dec}(k,\mathsf{Enc}(k,m))$.

Algorithm 1 Pseudorandom Ciphertext Experiment
1:	procedure$\mathsf{PRC}\_{\mathsf{EXP}}_{\mathsf{A}}^{\mathsf{SE}}$ ($1^s$)
2:	$k\leftarrow \mathsf{Gen}\left(1^s\right)$
3:	$(m,S)\leftarrow {\mathsf{A}}_1^{{\mathsf{Enc}}_k}\left(1^s\right)$	▹ S is internal state information of $\mathsf{A}$
4:	$b\leftarrow U(\{0,1\})$
5:	if $b=1$ then
6:	$c\leftarrow \mathsf{Enc}(k,m)$	▹ Use the actual encryption
7:	else
8:	$c\leftarrow U({\{0,1\}}^{|\mathsf{Enc}(k,m)|})$	▹ Use a random string
9:	end if
10:	$b^{\prime }\leftarrow {\mathsf{A}}_2^{{\mathsf{Enc}}_k}(c,S)$
11:	if $b=b^{\prime }$ then
12:	return 1	▹ $\mathsf{A}$ guessed correctly
13:	else
14:	return 0	▹ $\mathsf{A}$ did not guess correctly
15:	end if
16:	end procedure

A symmetric encryption scheme $\mathsf{SE}$ has pseudorandom ciphertexts under a chosen plaintext attack if a probabilistic polynomial time adversary is unable to distinguish the ciphertext message $c\in {\{0,1\}}^n$ from a uniformly random string $\sigma \in {\{0,1\}}^n$ even if he was able to choose the plaintext message. Formally, a polynomial time adversary $\mathsf{A}=({\mathsf{A}}_1,{\mathsf{A}}_2)$ is run in two stages ${\mathsf{A}}_1$ and ${\mathsf{A}}_2$ and is given oracle access to ${\mathsf{Enc}}_k$, the encryption algorithm under a random secret key k. First, ${\mathsf{A}}_1$, is run with oracle access to ${\mathsf{Enc}}_k$ and it outputs a cleartext message m together with its internal state information S that it may need in the second phase. Then, based on a coin toss, the second phase ${\mathsf{A}}_2$ is run with either the correct encryption of the chosen plaintext message or a completely random string from the ciphertext space (together with the state information). This pseudorandom ciphertext experiment is defined in Algorithm 1.

The encryption scheme $\mathsf{SE}$ has pseudorandom ciphertexts under a chosen plaintext attack if the success advantage,

$${\mathbf{Adv}}_{\mathsf{A},\mathsf{SE}}^{\mathsf{PRC}}\left(s\right)=\left|\frac{1}{2}-Pr\left[\mathsf{PRC}\_{\mathsf{EXP}}_{\mathsf{A}}^{\mathsf{SE}}\left(1^s\right)=1\right]\right|,$$

is negligible for every probabilistic polynomial time adversary $\mathsf{A}$. For an example of a cryptosystem with pseudorandom ciphertexts see for example [17].

A digital signature scheme is a public key authentication mechanism that enables a user to sign messages so that anybody can later verify the authenticity of that signature. A digital signature scheme $\Sigma =(\mathsf{Gen},\mathsf{Sign},\mathsf{Verify})$ consists of three algorithms such that $\mathsf{Gen}$ on input the security parameter $1^s$ outputs a private and public key pair $(s_k,p_k)\leftarrow \mathsf{Gen}\left(1^s\right)$, $\mathsf{Sign}$ outputs a digital signature $\sigma \leftarrow \mathsf{Sign}(s_k,m)$ of a message m computed using the private key $s_k$ and $\mathsf{Verify}$ verifies the signature $\sigma$ by outputting $1\leftarrow \mathsf{Verify}(p_k,m,\sigma )$ if and only if $\sigma$ is a valid signature for m. A digital signature scheme should be existentially unforgeable meaning that no adversary should be able to generate valid signatures for any message m without the private key $s_k$. For details, see for example [18].

2.3. Steganography

We follow the terminology of Hopper et al. [19], where Alice tries to convey a hidden message to Bob. The communication channel from Alice to Bob is modeled as a probability distribution on bit sequences. Each of the communication bits is augmented with a monotonically increasing timestamp. Communication on the channel is viewed as sampling from this distribution, possibly adaptively bit-by-bit. That is, a channel distribution $\mathcal{C}$ produces elements of the form

$$(b_1,t_1),(b_2,t_2),\dots ,(b_n,t_n),$$

where $b_i\in \{0,1\}$ and $t_i\le t_{i+1}$ for every $i\in \{1,2,\dots ,n\}$. Let $\mathcal{H}$ denote a channel history of bits drawn from the channel. We denote by ${\mathcal{C}}_{\mathcal{H}}$ the channel distribution conditioned on the history $\mathcal{H}$ of already sampled bits together with their timestamps.

Definition 1.

A stegosystem $\mathsf{\Pi }=(\mathsf{Embed},\mathsf{Extract})$ with security parameter s on a channel $\mathcal{C}$ consists of two probabilistic algorithms such that

1. 

The embedding algorithm $\mathsf{Embed}$ takes as input a secret key $k\in {\{0,1\}}^{n_k}$, a hiddentext message $m\in {\{0,1\}}^{\ast }$ and a channel history $\mathcal{H}\in {\{0,1\}}^{\ast }\times \mathbb{R}$ and returns a stegotext message $c\in {\{0,1\}}^{\ast }$.

2. 

The extraction algorithm $\mathsf{Extract}$ takes as input a secret key $k\in {\{0,1\}}^{n_k}$ and a stegotext message $c\in {\{0,1\}}^{\ast }$ and outputs a hiddentext message $m\in {\{0,1\}}^{\ast }$.

In our investigation, the channel history $\mathcal{H}$ that is given as input to $\mathsf{Embed}$ and the stegotext c given as input to $\mathsf{Extract}$ will be replaced by access to the blockchain. That is, in our investigation, the blockchain represents the channel history.

Definition 2.

The reliability of a stegosystem $\mathsf{\Pi }=(\mathsf{Embed},\mathsf{Extract})$ with messages of length n is the probability

$$\underset{m\in {\{0,1\}}^n,\mathcal{H}}{min}Pr\left[\mathsf{Extract}(k,\mathsf{Embed}(k,m,\mathcal{H}))\right].$$

To be useful, we require that the stegosystem has high reliability for hiddentext messages of some length. That is, there is $n\in \mathbb{N}$ such that for hiddentext messages of length n, the reliability is reasonably high (for example 2/3) meaning that messages can be reliably embedded and extracted.

We also need to stegosystem to be secure. The security is modeled using a chosen hiddentext attack by giving an adversary $\mathsf{A}$ access to the channel $\mathcal{C}$ through a sampling oracle M and to an additional oracle which is either ${\mathsf{\Pi }}_k$ that outputs stegotexts embedded by the stegosystem $\mathsf{\Pi }$ under a random key k or an oracle O that outputs random elements of ${\mathcal{C}}_{\mathcal{H}}$ for the current history $\mathcal{H}$ each with probability 1/2 [20]. The adversary is free to choose the hidden message m and needs to distinguish which of these sets of two oracles it was given. If the advantage of distinguishing between these cases,

$$\left|Pr\left[{\mathsf{A}}^{M,{\mathsf{\Pi }}_k}\left(1^s\right)=1\right]-Pr\left[{\mathsf{A}}^{M,O}\left(1^s\right)=1\right]\right|,$$

where s is the security parameter, is negligible for any adversary, then the stegosystem is secure. For details, see [20].

3. A Simplified Blockchain Model

We shall start by describing our model for the blockchain. In order to clarify our disposition, we apply a simplified model that abstracts away technical details that are irrelevant for our investigation. For example, in practice, consensus can be reached with several different mechanisms, such as proof-of-work or proof-of-stake. However, for our method, we do not need to know the working details of the implementation as long as immutability is guaranteed. Our model is similar to the idealized public ledger model from [21]. The simplified ideal blockchain $\mathcal{B}=(C,\Sigma ,H,\mathsf{Read},\mathsf{Submit})$ consists of a chain of blocks C, an existentially unforgeable [18] digital signature scheme $\Sigma$, a cryptographic hash function H that is modeled as a random oracle and two oracles $\mathsf{Read}$ and $\mathsf{Submit}$ that can be used to read and write data to the blockchain. We shall describe these components in detail below.

For privacy reasons, payment addresses should be used only once for each payment. While it is technically possible, address re-use is generally considered bad practice since it may lead to identity exposure (For Bitcoin, see for example (https://en.bitcoin.it/wiki/Address_reuse)). Typically, the pseudonyms (that is, the addresses) in a blockchain are made to look like random. For example, in Bitcoin and Ethereum the address is computed by hashing the public key. In the random oracle model, the hash function outputs random strings. That is, for any public key $p_k^{\left(i\right)}$, the corresponding address $a^{\left(i\right)}=H(p_k^{\left(i\right)})$ is a random string.

The simplified ideal blockchain contains

• Payee identities. In order to join the systems, an individual i generates a private and public key pair $(s_k^{\left(i\right)},p_k^{\left(i\right)})$ using a digital signature scheme $\Sigma$. When paying, individuals are represented by their public keys $p_k^{\left(i\right)}$.
• Recipient addresses. Payments to an individual i are sent to a one-time address $a^{\left(i\right)}\in {\{0,1\}}^n$ that the recipient can publish after hashing her public key: $a^{\left(i\right)}=H(p_k^{\left(i\right)})$. Each payment address appears only once in a payment and a new private and public key pair $(s_k^{\left(i\right)},p_k^{\left(i\right)})$ is generated to receive additional payments.
• Money. The blockchain records the amount of money ${\mu }^{\left(i\right)}$ that is associated to an address $a^{\left(i\right)}$ and, consequently, to a public key $p_k^{\left(i\right)}$.
• Initial status of the blockchain. The initial total amount of money is distributed among a finite set of L individuals represented by their addresses $a^{\left(1\right)},a^{\left(2\right)},\dots ,a^{\left(L\right)}$. An amount of money ${\mu }^{\left(i\right)}\ge 0$ is associated to each of these addresses and the initial status of the blockchain

  $$C_0=\left((a^{\left(1\right)},{\mu }^{\left(1\right)}),(a^{\left(2\right)},{\mu }^{\left(2\right)}),\dots ,(a^{\left(L\right)},{\mu }^{\left(L\right)})\right)$$

  is public knowledge and the first block of the chain.
• Payments. Let $p_k^{\left(i\right)}$ and $p_k^{\left(j\right)}$ be two distinct public keys. A valid payment P of amount μ from a user i to a user j is a tuple

  $$P=(p_k^{\left(i\right)},a^{\left(j\right)},\mu ,t,\sigma ),$$

  where $a^{\left(j\right)}=H(p_k^{\left(j\right)})$ is the address of user j, $\mu$ is the amount of payment such that $\mu \le {\mu }^{\left(i\right)}$, t is a unique identifier or a timestamp for the payment and $\sigma$ is a digital signature,

  $$\sigma =\mathsf{Sign}(s_k^{\left(i\right)},(p_k^{\left(i\right)},a^{\left(j\right)},\mu ,t)).$$

  Once the payment is published in the blockchain, ${\mu }^{\left(i\right)}$ and ${\mu }^{\left(j\right)}$ are (implicitly) updated accordingly.
• The ideal chain of blocks. For the simplified ideal blockchain, all published payments are valid and are published in a tamper-proof chain C of payment blocks

  $$C=(C_0,C_1,C_2,\dots )$$

  where $C_0$ is the initial status of the blockchain and the block $C_{i+1}$ consists of all of the valid payments submitted to the blockchain after the publication of block $C_i$. In the ideal system, a new block appears after a finite and fixed amount of time.

Note that users are free to join the system by generating their own private and public key pairs $(s_k,p_k)$. Any address generated from a public key appearing as the recipient of a payment is valid even if it has never appeared in the blockchain before. In practice, addresses are substrings of the digest $H(p_k^{\left(i\right)})$ in order to make then of a manageable length. However, for simplicity, we use the whole digest. For our proofs to work, it is imperative that a unique address is generated for every payment.

To enable access to the blockchain, in our model the users are given oracle access to oracles $\mathsf{Read}$ and $\mathsf{Submit}$ which can be used to read the contents of the blockchain block by block and to submit new payments. These are defined as

• $\mathsf{Read}\left(i\right)$ on input the block number $i\in {\mathbb{N}}_{\ge 0}$ outputs the block $C_i$ from the chain $(C_0,C_1,C_2,\dots ,C_{i-1},C_i,C_{i+1},\dots )$ if it has appeared already. If the last block that has appeared is $C_{i^{\prime }}$ where $i^{\prime }<i$, $\mathsf{Read}$ outputs ⊥ indicating error.
• $\mathsf{Submit}\left(P\right)$ on input a payment $P=(p_k^{\left(i\right)},a^{\left(j\right)},\mu ,t,\sigma )$ verifies that the payment is valid and saves it to be published in the next block to appear. If the payment is invalid, it is discarded.

4. The Suggested $\mathsf{BLOCCE}$ Scheme

In this section, we give a detailed description of our method called $\mathsf{BLOCCE}=({\mathsf{Gen}}_{\mathsf{BLOCCE}},\mathsf{Embed},\mathsf{Extract})$ (Blockchain Covert Channel). We first give a general overview of the scheme. Then we describe the embedding and extraction procedures in detail. Finally, we show that embedding runs in expected polynomial time (exluding the time spent waiting for new blocks to appear on the chain) and that the method is reliable.

4.1. General Overview of $\mathsf{BLOCCE}$

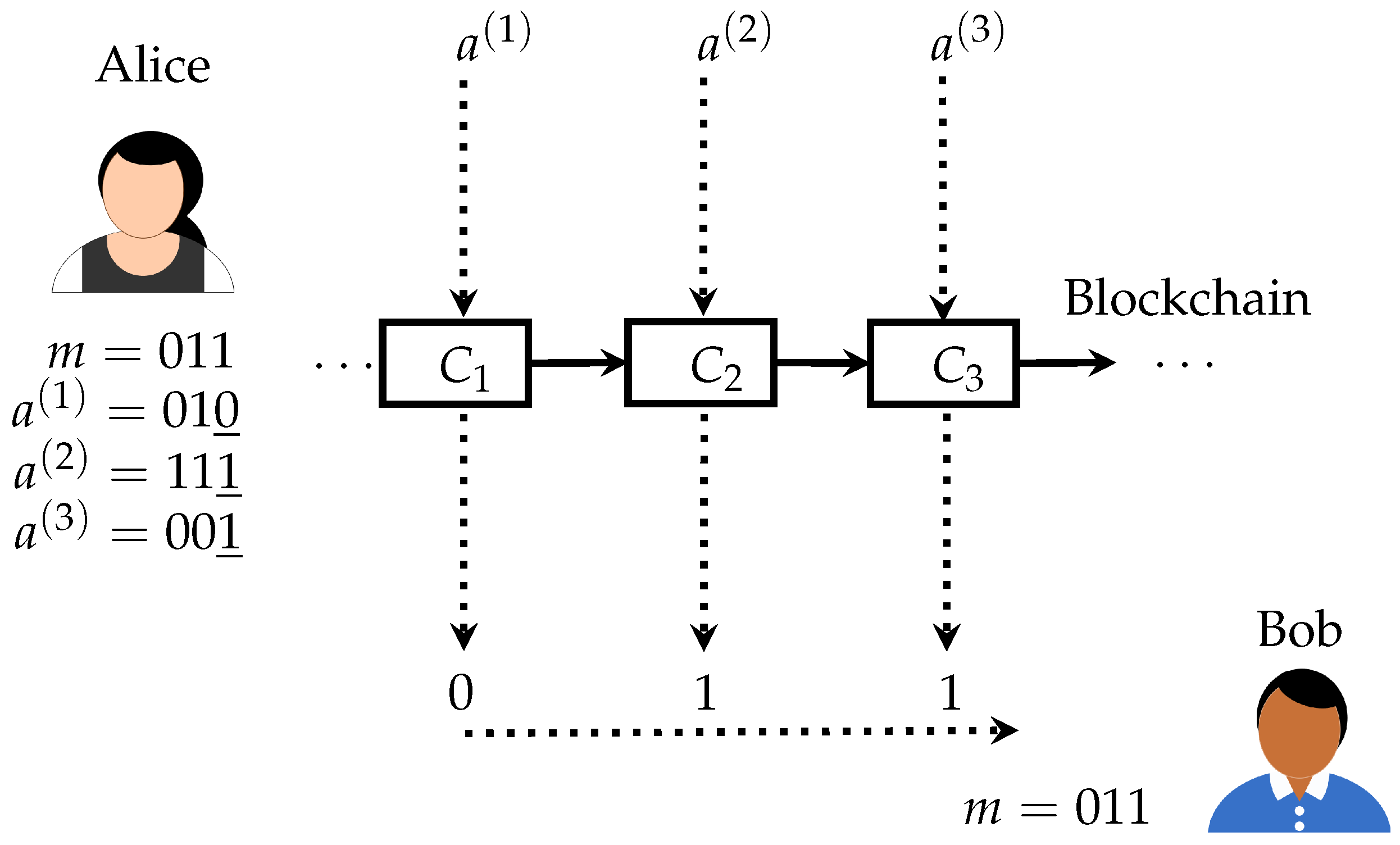
In our scenario, Alice attempts to convey a hidden message to Bob through the blockchain, while the adversary attempts to detect any such communication. Contrary to traditional steganography, Alice has no ability to alter the “covertexts” (that is, the blocks) stored in the blockchain due to the consensus mechanism. However, Alice has complete control on the payments she submits to the chain. In addition, the consensus mechanism will protect these payments from the possible modification attempts of the adversary. We will apply these payments and, in particular, the payment addresses to convey a hidden message to Bob. For simplicity, we shall send one bit for each block appearing in the chain. The general overview of the scheme is the following:

• Alice generates a number of private and public key pairs

  $$(s_k^{\left(1\right)},p_k^{\left(1\right)}),(s_k^{\left(1\right)},p_k^{\left(1\right)}),\dots ,(s_k^{\left(n\right)},p_k^{\left(n\right)})$$

  and generates the payment addresses $a^{\left(1\right)},a^{\left(2\right)},\dots ,a^{\left(n\right)}$ corresponding to these keys.
• Alice generates payments (of small amounts) from her own account to these addresses and, depending on the hiddentext message m, orders them such that the least significant bits (LSBs) of the payment addresses form m.
• Alice submits the payments in the correct order to the blockchain.
• Bob reads the blockchain for payments made by Alice and reads the hiddentext message from the LSBs of the payment addresses.

Note that Alice does not lose any money by running the scheme excluding the possible transaction costs, since she controls the generated key pairs $(s_k^{\left(i\right)},p_k^{\left(i\right)})$. While the transaction costs for certain blockchain implementations using the proof-of-work paradigm may be significant, there are also blockchains with other consensus mechanisms that do not require transaction costs. The scheme has been depicted in a simplified form in Figure 1.

4.2. Embedding Into the Blockchain

In this section, we give a detailed description of the embedding algorithm. For simplicity, we assume that Alice sends exactly one payment to the blockchain for each published block. This means that we are able to embed at most one bit for each published block. It would be possible to embed multiple bits, but it would complicate the formulation of the method. The embedding of a single bit simplifies our disposition and makes it more clear for the reader. For the same reason, we assume that the length of the hidden text is fixed and known to both Alice and Bob. We would not need to make such an assumption, but it greatly simplifies the description of the algorithms, as well as makes the discussion more clear.

Let $\mathcal{B}=(C,\Sigma ,H,\mathsf{Read},\mathsf{Submit})$ be a simplified ideal blockchain, where $\Sigma =({\mathsf{Gen}}_{\Sigma },\mathsf{Sign},\mathsf{Verify})$ and let the security parameter employed by the blockchain implementation be $1^s$. Let $H:{\{0,1\}}^{\ast }\to {\{0,1\}}^n$. Let also $\mathsf{SE}=({\mathsf{Gen}}_{\mathsf{SE}},\mathsf{Enc},\mathsf{Dec})$ be a symmetric encryption scheme that has pseudorandom ciphertexts under the chosen plaintext attack and suppose that the security parameter $1^s$ is used for key generation. We note that it is crucial that an encryption scheme with pseudorandom ciphertexts is used. The argument of the security later in Section 5 is based the pseudorandomness of the ciphertexts. It should be noted that the utility of such encryption schemes in the construction of steganographic algorithms has been already observed in the literature [17,22].

Algorithm 2 Embedding Algorithm
1:	procedure$\mathsf{Embed}$($(k,\lambda ),m,\mathcal{B}$)
2:	$c\leftarrow \mathsf{Enc}(k,m)$
3:	Concatenate $c^{\prime }=\lambda \left|\right|c$
4:	Set $N=|c^{\prime }|$
5:	Interpret $c^{\prime }$ as a bit representation $c_1^{\prime }{c}_2^{\prime }\dots c_N^{\prime }\in {\{0,1\}}^N$
6:	$i=1$
7:	while $i\le N$ do
8:	Generate unseen $(s_k,p_k)\leftarrow {\mathsf{Gen}}_{\Sigma }\left(1^s\right)$
9:	$a\leftarrow H(p_k^{\left(i\right)})$
10:	Interpret a as a bit representation $a_1{a}_2\dots a_n\in {\{0,1\}}^n$
11:	if $a_n=c_i^{\prime }$ then
12:	$\mu \leftarrow {\mathcal{M}}_{\mathcal{H}}$
13:	Generate a unique identifier t for the payment
14:	$\sigma \leftarrow \mathsf{Sign}(s_k^{\left(A\right)},(p_k^{\left(A\right)},a,\mu ,t))$
15:	$\mathsf{Submit}(p_k^{\left(A\right)},a,\mu ,t,\sigma )$
16:	Wait for the blockchain to publish a new block
17:	Update $\mathcal{H}$
18:	$i\leftarrow i+1$
19:	end if
20:	end while
21:	end procedure

In the following, let the private and public key pair of Alice be $(s_k^{\left(A\right)},p_k^{\left(A\right)})$. Let $\mathcal{H}$ denote the history of payments Alice has made through the blockchain. We denote by ${\mathcal{M}}_{\mathcal{H}}$ the probability distribution on the amount of money in a payment of Alice conditioned on the history $\mathcal{H}$. It is important that the payments are made according to this distribution to prevent the adversary from detecting the communication. For any consequent payments, we assume that $\mathcal{H}$ is updated with the most recent payment and ${\mathcal{M}}_{\mathcal{H}}$ is the resulting probability distribution on the amount of money. For clarity, we also assume that Alice does not run out of money.

On input a security parameter $1^s$, the key generation algorithm ${\mathsf{Gen}}_{\mathsf{BLOCCE}}$ outputs a secret key of the form $(\lambda ,k)$, where $\lambda$ is a uniformly random message start indicator such that $\lambda \in {\{0,1\}}^{n_{\lambda }},n_{\lambda }\in \mathbb{N},$ that will enable Bob to detect the start of the hidden message and k is an encryption key $k\leftarrow {\mathsf{Gen}}_{\mathsf{SE}}\left(1^s\right)$. The length $n_{\lambda }$ of the message start indicator will play a role in the consideration of the reliability of the extraction. We assume that the concatenated length of the message start indicator $\lambda$ together with the ciphertext $c\leftarrow \mathsf{Enc}(k,m)$ are known to both Alice and Bob and let us denote this length by $N=n_{\lambda }+\left|c\right|$, where $\left|c\right|$ is the length of the ciphertext c. Embedding is described in Algorithm 2.

Note that since the algorithm waits for a new block to be published after the submission of a payment, only a single payment from $p_k^{\left(A\right)}$ is ever included into a single block. This will help Bob to extract the message.

4.3. Extraction

Extraction is straightforward. Bob will read the blocks from the chain and scans for any transactions made by Alice. Once Bob detects the secret message start indicator $\lambda$, he can read the encrypted hidden message. Since there is a single payment from $p_k^{\left(A\right)}$ for each block, the message can be gathered in the correct order. Extraction is described in Algorithm 3.

Algorithm 3 Extraction Algorithm
1:	procedure$\mathsf{Extract}$($(\lambda ,k),\mathcal{B}$)
2:	$i=1$
3:	$j=1$
4:	while have not found $\lambda$ yet do                        ▹ Scan for $\lambda$
5:	$C=\mathsf{Read}\left(j\right)$
6:	if $C=\perp$ then
7:	Wait until a block appears and read it: $C=\mathsf{Read}\left(j\right)$
8:	end if
9:	for any payment $P\in C$ do
10:	if P is from $p_k^{\left(A\right)}$ then
11:	Extract address a from P and get the LSB $a_n$
12:	Scan if we have found the entire $\lambda \in {\{0,1\}}^{n_{\lambda }}$
13:	end if
14:	end for
15:	$j\leftarrow j+1$
16:	end while
17:	$i=1$                    ▹ Now reading the encrypted hidden message
18:	while $i\le N-n_{\lambda }$ do
19:	$C=\mathsf{Read}\left(j\right)$
20:	if $C=\perp$ then
21:	Wait until a block appears and read it: $C=\mathsf{Read}\left(j\right)$
22:	end if
23:	for any payment $P\in C$ do
24:	if P is from $p_k^{\left(A\right)}$ then
25:	Extract address a from P and get the LSB $a_n$
26:	$c_i\leftarrow a_n$
27:	$i\leftarrow i+1$
28:	end if
29:	end for
30:	$j\leftarrow j+1$
31:	end while
32:	Compile $c=c_1{c}_2\dots c_{N-n_{\lambda }}$
33:	$m\leftarrow \mathsf{Dec}(k,c)$
34:	output m
35:	end procedure

The variables used in $\mathsf{Embed}$, $\mathsf{Extract}$ and the following proofs have been collected into

Table 1. Used variables and notations.

Variable	Explanation
H	hash function
$(s_k,p_k)$	private and public key pair for the digital signature scheme
$(s_k^{\left(A\right)},p_k^{\left(A\right)})$	Alice’s keypair
k	secret key for symmetric encryption
$\lambda$	message start indicator
$n_{\lambda }$	length of $\lambda$
m	hiddentext message
c	$c\leftarrow \mathsf{Enc}(k,m)$
$c^{\prime }$	concatenation $c^{\prime }=\lambda \left|\right|c$
N	total number of embedded bits $N=|c^{\prime }|$
$a,a^{\left(i\right)}$	address computed by hashing a public key
$\mathcal{H}$	the history of payments Alice has made through the blockchain
${\mathcal{M}}_{\mathcal{H}}$	distribution on the amount of money in Alice’s payment conditioned on the history of payments $\mathcal{H}$
$\mu$	payment amount
t	unique payment identifier
$\sigma$	digital signature
$C,C_i$	block in the blockchain
P	payment
$L_A$	total number of payments made by Alice

for easy reference.

4.4. Computational Complexity and Correctness

We shall now show that the embedding can be done in expected polynomial time excluding the time spent waiting for new blocks to appear. That is, we consider here the computational complexity theoretic notion of “time”, which is the number of computational steps needed for the algorithm to finish its task. Then, we show that the method is correct. That is, for a fixed $N\in \mathbb{N}$ and for any payload $(\lambda ,c)\in {\{0,1\}}^N$, Alice can embed it into the blockchain and Bob is able to extract it with high reliability.

Let us first establish the computational complexity of the embedding algorithm.

Proposition 1.

Suppose that $\mathsf{Submit}$ and $\mu \leftarrow {\mathcal{M}}_{\mathcal{H}}$ run in $O\left(1\right)$ for any payment history $\mathcal{H}$. Let $c_E$ be the computational complexity of the encryption algorithm $\mathsf{Enc}$, $c_t$ be the complexity of generating a unique identifier for a payment, $c_{{\mathsf{Gen}}_{\Sigma }}$ be the complexity of the digital signature key generation ${\mathsf{Gen}}_{\Sigma }$, $c_H$ be the complexity of computing the hash of a public key and $c_{\sigma }$ be the complexity of generating a signature for a payment. $\mathsf{Embed}$ runs in expected time of

$$O(c_E(N-n_{\lambda })+N·(2c_{{\mathsf{Gen}}_{\Sigma }}+2c_H+c_t+c_{\sigma })),$$

where N is the number of embedded bits and $n_{\lambda }$ is the length of the message start indicator.

Proof. 

Let $m\in {\{0,1\}}^{N-n_{\lambda }}$ be arbitrary. First, Alice runs a single encryption of m which takes $c_E(N-n_{\lambda })$ steps. The while-loop is repeated for until i reaches the total number of embedded bits N. Now, i is updated whenever the LSB $a_n$ of $a=H(p_k^{\left(i\right)})$ is equal to $c_i^{\prime }$. Suppose that the while-loop ends in a total of M iterations. Let $A_v$ denote the random variable on $\{0,1\}$ such that $A_v=1$ whenever $a_n$ obtained from the call to H in the v-th while-loop iteration equals $c_i^{\prime }$ and $A_v=0$ otherwise. Since H is a random oracle, $A_1,A_2,\dots$ are independent and distributed according to the Bernoulli distribution with probability 1/2.

Let now I denote the random variable corresponding to i. We have $I={\sum }_{v=1}^M{A}_v$, where M is the number of calls we had to make to H. That is, I is distributed according to the binomial distribution $\mathsf{Bin}(M,1/2)$ that has the expected value of $M/2$. Since we need to match N values, we expect the while-loop to run $M=2N$ times. In each of the loop iterations, we run ${\mathsf{Gen}}_{\Sigma }$. Finally, lines 12–18 are repeated exactly N times. ☐

Note that $\mathsf{Embed}$ has to wait for a new block to be generated by the blockchain for each of the bits. Therefore, the actual time spent embedding depends also on the blockchain implementation. Even though the computational complexity of embedding is low (virtually close to the complexity of the applied encryption algorithm), for certain blockchains with inefficient block generation the actual time spent embedding can be long. For example, if the block generation takes time T which is significantly greater than the time needed to encrypt m, the time to embed N bits takes time $N·T$ since the majority of the time is spent waiting for new blocks. The same is naturally true for extraction.

Next, we prove that $\mathsf{BLOCCE}$ is reliable provided that the length of the message start indicator $\lambda$ is large enough.

Proposition 2.

$\mathsf{BLOCCE}$ on a simplified ideal blockchain $\mathcal{B}$ with a suitably long message start indicator λ is correct and reliable. That is, for messages of any length, Bob receives Alice’s message with the reliability of at least

$$1-(L_A-n_{\lambda }+1)·2^{-n_{\lambda }}$$

where $L_A$ is the total number of payments Alice has submitted into the blockchain and $n_{\lambda }$ is the length of the message start indicator λ.

Proof. 

By our assumptions, the simplified ideal blockchain is tamper-proof meaning that the adversary is unable to prevent Alice’s submissions from appearing on the chain. Therefore, we may assume that Bob receives every block submitted by Alice. For simplicity, let us assume that all of the message has already appeared on the chain if it has been sent.

Suppose that Alice transmitted m. Let us first show that the scheme is correct, whenever Bob has detected the correct message start indicator $\lambda$. We shall later show that this happens with high probability. By the description of $\mathsf{Embed}$, Alice submits the ciphertext c directly after $\lambda$ by submitting a single bit for each new block. Since the blockchain is tamper-proof, Bob receives all of these blocks and, by the description of $\mathsf{Extract}$, extracts the correct c. Finally, Bob decrypts c to obtain the correct hidden message m.

Let us now show that the method is reliable. That is, let us show that Bob is able to detect the correct message start indicator $\lambda$ with high probability. By the description of $\mathsf{Extract}$, Bob first scans the blockchain for all of the payments from $p_k^{\left(A\right)}$, extracts the LSB $a_n$ of each address a and scans for the appearance of $\lambda \in {\{0,1\}}^{n_{\lambda }}$. There are two ways that the extraction can fail:

• The LSBs of the addresses of the payments Alice has made before transmitting $(\lambda ,c)$ accidentally form $\lambda$ that Bob misinterprets as the start of the hidden message.
• Alice has not submitted any message, but the LSBs of the addresses of her payments form $\lambda$.

These two cases are similar, but provided that Alice has submitted the same number of payments in both cases, in the latter the reliability is lower. To see this, we observe that in the first case, we are trying to find a false match for $\lambda$ in the subchain of blocks that appeared before the true match for $\lambda$, while in the latter case, we have the whole blockchain to search for the false match. Therefore, we can restrict ourselves to the second case. By our assumptions, Alice submits exactly one payment for each published block. We now have to derive a upper bound on the probability of these payments forming $\lambda$. Now, H is a random oracle and both $\lambda$ and the addresses are sampled from the uniform distribution.

Let $\alpha ={\alpha }_1{\alpha }_2\dots {\alpha }_{L_A}\in {\{0,1\}}^{L_A}$ be the string of LSBs of the addresses extacted (in order) from all of Alice’s payments recorded into the blockchain (thus far). Let $A_1,A_2,\dots ,A_{L_A}$ denote the random variables corresponding to the choise of ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{L_A}$ each chosen independently and uniformly at random from $\{0,1\}$. We derive an upper bound for the probability of hitting $\lambda$,

$$Pr\left[\lambda \mathrm{substring} \mathrm{of} \alpha \right].$$

We observe that $\lambda$ can appear in any starting position $i\in \{0,1,\dots ,L_A-n_{\lambda }\}$ in which case we have $\lambda ={\alpha }_{i+1}{\alpha }_{i+2}\dots {\alpha }_{i+n_{\lambda }}$. Therefore, we estimate $Pr\left[\lambda \mathrm{substring} \mathrm{of} \alpha \right]$ with sum of the probabilities $Pr\left[A_{i+1}{A}_{i+2}\dots A_{i+n_{\lambda }}=\lambda \right]$ for $i\in \{0,1,\dots ,L_A-n_{\lambda }\}$. This sum over-counts, since for large $L_A$, $\lambda$ can appear in multiple positions. However, we are only interested in deriving an upper bound. We have,

$$\begin{array}{ccc}\hfill Pr\left[\lambda \mathrm{substring} \mathrm{of} \alpha \right]& \le & \sum _{i=0}^{L_A-n_{\lambda }}Pr\left[A_{i+1}{A}_{i+2}\dots A_{i+n_{\lambda }}=\lambda \right]\hfill \\ & =& \sum _{i=0}^{L_A-n_{\lambda }}\prod _{j=1}^{w}Pr\left[A_{i+j}={\lambda }_j\right]\hfill \\ & =& \sum _{i=0}^{L_A-n_{\lambda }}{2}^{-n_{\lambda }}=(L_A-n_{\lambda }+1)·2^{-n_{\lambda }}.\hfill \end{array}$$

Therefore, the reliability of $\mathsf{BLOCCE}$ is at least

$$1-Pr\left[\lambda \mathrm{substring} \mathrm{of} \alpha \right]\ge 1-(L_A-n_{\lambda }+1)·2^{-n_{\lambda }}.$$

 ☐

Interestingly, the reliability depends essentially only on the length of the message start indicator. Note that we have assumed that Alice has submitted a single bit for each block. If multiple bits are embedded into a single block, Proposition 2 needs to be updated accordingly. Finally, the result also assumes that addresses are not reused.

5. Security

In this section, we consider the security of $\mathsf{BLOCCE}$. Following the notions of security for a stegosystem [20], we derive a security definition for the blockchain based covert channel by modeling a chosen hiddentext attack of a probabilistic polynomial time adversary on $\mathsf{BLOCCE}$. We start by listing our assumptions. We then proceed to the formulation of a security definition called payment indistinguishability that requires the adversary to distinguish the payload containing payments from random. Finally, we show that $\mathsf{BLOCCE}$ satisfies this definition.

5.1. Assumptions

Our security proofs are based on a simplified ideal blockchain $\mathcal{B}$. In particular, we assume that digital signatures are existentially unforgeable and the applied cryptographic hash function is modeled as a random oracle. There are three participants in our scenario:

• Alice represents the transmitter of our scheme and is known through her (payee identity) public key $p_k^{\left(A\right)}$. She has agreed with the recipient Bob beforehand on a secret key $(\lambda ,k)\in {\{0,1\}}^{n_{\lambda }}\times {\{0,1\}}^{n_k}$ that is not known to anyone else. She attempts to send a confidential message m to Bob through the simplified ideal blockchain $\mathcal{B}$. Both Alice and Bob know the total amount of embedded bits N. Finally, Alice is aware of her “normal” distribution of payment amounts ${\mathcal{M}}_{\mathcal{H}}$ given her history of payments $\mathcal{H}$ and is able to sample from it.
• Bob represents the recipient of our scheme. He expects a confidential message from Alice through the blockchain, knows the public key $p_k^{\left(A\right)}$ of Alice, as well as the secret key $(\lambda ,k)$ and the total number of embedded bits N.
• The adverary attempts to detect the presence of covert communication on the blockchain. We assume that the adversary knows Alice and her public key $p_k^{\left(A\right)}$. The warden also has complete access to the blockchain $\mathcal{B}$ through the oracles $\mathsf{Read}$ and $\mathsf{Submit}$. The job of the adversary is to distinguish the secret communication payments from regular payments.

5.2. Payment Indistinguishability

We apply a computational indistinguishability based approach for the security definition. In particular, we define a scenario, where the adversary has to distinguish the payments containing the hidden message from a set of random payments. To formalize this into a rigorous security definition, we can apply a chosen hiddentext attack described in Section 2.3. We model the situation by defining the following payment distinguishing experiment against a stegosystem $\mathsf{\Pi }$ in which the adversary $\mathsf{A}$ attempts to distinguish between the scenarios where it is either given a set of randomly generated addresses or a set of addresses containing the conceiled message each with probability 1/2.

We give the adversary full control to choose the hiddentext message m and to observe the blockchain. However, we do not give the adversary the power to block Alice from sending payments to the blockchain or to prevent Bob from observing the blockchain. We also do not give him access to the private keys generated by Alice or to the secret key $(\lambda ,k)$ shared between Alice and Bob. Note that since the digital signature scheme is unforgeable, this means that the adversary cannot masquerade as Alice and forge messages into the blockchain.

The probabilistic polynomial time adversary $\mathsf{A}=({\mathsf{A}}_1,{\mathsf{A}}_2)$ is modeled in two stages ${\mathsf{A}}_1$ and ${\mathsf{A}}_2$. In the first stage, it is given access to the full block history of the blockchain through the oracle $\mathsf{Read}$, the ability to submit payments through the oracle $\mathsf{Submit}$, as well as the public key $p_k^{\left(A\right)}$ of Alice. In the first stage, the job of the adversary is to output a hiddentext message m that Alice is required to send to Bob. In the experiment, a coin is then tossed and, based on the outcome, either the stegosystem $\mathsf{\Pi }$ is applied to send m into the blockchain or a set of random valid payments from Alice is generated. In the second stage, ${\mathsf{A}}_2$ is invoked with oracle access to the blockchain and it eventually outputs a bit trying to distinguish whether the blockchain contained the hidden message or just a set of random valid payments. As with the pseudorandom ciphetext experiment, a string storing the internal state information S of the adversary is also passed from ${\mathsf{A}}_1$ to ${\mathsf{A}}_2$.

The rigorous definition of the payment distinguishing experiment is the following.

Algorithm 4 Payment Distinguishing Experiment
1:	procedure$\mathsf{PAY}\_\mathsf{DIST}\_{\mathsf{EXP}}_{\mathsf{A}}^{\mathsf{\Pi },\mathcal{B}}$($1^s$)
2:	$(s_k,p_k)\leftarrow {\mathsf{Gen}}_{\Sigma }\left(1^s\right)$
3:	$(m,S)\leftarrow {\mathsf{A}}_1^{\mathsf{Read},\mathsf{Submit}}(p_k)$ ▹ S is internal state information of the adversary that can be passed to the second stage
4:	$(\lambda ,k)\leftarrow {\mathsf{Gen}}_{\mathsf{\Pi }}\left(1^s\right)$
5:	$b\leftarrow U(\{0,1\})$
6:	if $b=1$ then                   ▹ Actual message is sent to the blockchain
7:	$\mathsf{Embed}((\lambda ,k),m,\mathcal{B})$
8:	else                     ▹ Random payments are sent to the blockchain
9:	$n_{\lambda }\leftarrow \left|\lambda \right|$
10:	$N\leftarrow |\mathsf{Enc}(k,m)|+n_{\lambda }$              ▹ $\mathsf{Enc}$ is the encryption scheme used by $\mathsf{\Pi }$
11:	Generate N random addresses $a_i$ for $i\in \{1,2,\dots ,N\}$
12:	Simulate $\mathsf{Embed}$ to generate payments to $a_i$
13:	Submit payments to blockchain one-by-one as $\mathsf{Embed}$ does
14:	end if
15:	$b^{\prime }\leftarrow {\mathsf{A}}_2^{\mathsf{Read},\mathsf{Submit}}(p_k,S)$
16:	if $b=b^{\prime }$ then
17:	return 1                            ▹ $\mathsf{A}$ guessed correctly
18:	else
19:	return 0                          ▹ $\mathsf{A}$ did not guess correctly
20:	end if
21:	end procedure

Definition 3.

Let $\mathsf{\Pi }=(\mathcal{B},{\mathsf{Gen}}_{\mathsf{\Pi }},\mathsf{Embed},\mathsf{Extract})$ be a blockchain stegosystem based on a simplified ideal blockchain $\mathcal{B}=(C,\Sigma ,H,\mathsf{Read},\mathsf{Submit})$ and let $\mathsf{A}=({\mathsf{A}}_1,{\mathsf{A}}_2)$ be a two stage probabilistic polynomial time adversary. The payment distinguishing experiment is defined by Algorithm 4.

We also define the advantage of an adversary in detecting the hidden message based on the payment distinguishing experiment.

Definition 4.

The payment detection advantage of an adversary $\mathsf{A}$ on a blockchain stegosystem Π on a simplified ideal blockchain $\mathcal{B}$ is

$${\mathbf{Adv}}_{\mathsf{A},\mathsf{\Pi },\mathcal{B}}^{\mathsf{PAY}\_\mathsf{DETECT}}\left(s\right)=\left|\frac{1}{2}-Pr\left[\mathsf{PAY}\_\mathsf{DIST}\_{\mathsf{EXP}}_{\mathsf{A}}^{\mathsf{\Pi },\mathcal{B}}\left(1^s\right)=1\right]\right|.$$

If the payment detection advantage of the adversary is significantly greater that 0, then, in practice, the adverasry is able to detect the conceiled message. For a secure system, we want this advantage to be negligible.

Definition 5.

The blockchain stegosystem Π securely embeds into the blockchain $\mathcal{B}$ if for every probabilistic polynomial time adversary $\mathsf{A}$, there is a negligible function ϵ such that

$${\mathbf{Adv}}_{\mathsf{A},\mathsf{\Pi },\mathcal{B}}^{\mathsf{PAY}\_\mathsf{DETECT}}\left(s\right)\le ϵ\left(s\right)$$

for every $s\ge 1$.

5.3. Security Proof of $\mathsf{BLOCCE}$

We shall now show that $\mathsf{BLOCCE}$ securely embeds into the blockchain. In particular, we derive an algorithm that reduces the problem of distinguishing the ciphertexts of the encryption scheme $\mathsf{SE}$ used by $\mathsf{BLOCCE}$ to the problem of distinguishing the payments made with $\mathsf{BLOCCE}$. Since $\mathsf{SE}$ is assumed to have pseudorandom ciphertexts, this shows that there is no adversary that succeeds in the payment distinguishing experiment with non-negligible advantage.

Proposition 3.

$\mathsf{BLOCCE}$ securely embeds into a simplified ideal blockchain $\mathcal{B}$. For every probabilistic polynomial time adversary $\mathsf{A}$ there is a probabilistic polynomial time adversary ${\mathsf{A}}^{\prime }$ such that

$${\mathbf{Adv}}_{{\mathsf{A}}^{\prime },\mathsf{SE}}^{\mathsf{PRC}}\left(s\right)={\mathbf{Adv}}_{\mathsf{A},\mathsf{BLOCCE},\mathcal{B}}^{\mathsf{PAY}\_\mathsf{DETECT}}\left(s\right)\le ϵ\left(s\right),$$

where $\mathsf{SE}$ is the encryption scheme used in $\mathsf{BLOCCE}$ and ϵ is a negligible function.

Proof. 

Let $\mathsf{A}=({\mathsf{A}}_1,{\mathsf{A}}_2)$ be any two-stage probabilistic polynomial time algorithm considered as an adversary against $\mathsf{BLOCCE}$. We need to show that there is a negligible function $ϵ$ such that

$${\mathbf{Adv}}_{\mathsf{A},\mathsf{BLOCCE},\mathcal{B}}^{\mathsf{PAY}\_\mathsf{DETECT}}\left(s\right)\le ϵ\left(s\right).$$

Suppose that there was an adversary $\mathsf{A}$ that succeeds with a non-negligible advantage. Based on such an adversary, we shall construct a probabilistic polynomial time algorithm ${\mathsf{A}}^{\prime }$ that applies $\mathsf{A}$ to achieve a high ciphertext distinguishing advantage for the symmetric encryption scheme $\mathsf{SE}$. In particular, we show that the ciphertext distinguishing advantage is at least the advantage of $\mathsf{A}$ in the payment distinguishing experiment. Since, by the assumptions, $\mathsf{SE}$ has pseudorandom ciphertexts (see Section 4.2), and thus the ciphertext distinguishing advantage is negligible for every adversary, we get the claim.

For this, let ${\mathsf{A}}^{\prime }=({\mathsf{A}}_1^{\prime },{\mathsf{A}}_2^{\prime })$ be a two-stage adversary, that applies $\mathsf{A}=({\mathsf{A}}_1,{\mathsf{A}}_2)$, given below. In the description, we need to save the status information S that ${\mathsf{A}}_1$ outputs in order to invoke ${\mathsf{A}}_2$ in the later state. In addition, since we are emulating a payment distinguishing experiment, we also need to initialize a blockchain and to maintain its state. Therefore, we store the state and internal information of the blockchain into an information string $S^{\prime }$ for a coherent second stage ${\mathsf{A}}_2^{\prime }$.

The adversary ${\mathsf{A}}^{\prime }=({\mathsf{A}}_1^{\prime },{\mathsf{A}}_2^{\prime })$ is described in Algorithms 5 and 6.

Algorithm 5 First Stage of the Adversary ${\mathsf{A}}^{\prime }$
1:	procedure${\mathsf{A}\prime }_1^{{\mathsf{Enc}}_k}$($1^s$)
2:	Initialize a blockchain $\mathcal{B}$
3:	$(s_k,p_k)\leftarrow {\mathsf{Gen}}_{\Sigma }\left(1^s\right)$
4:	$(m,S)\leftarrow {\mathsf{A}}_1^{\mathsf{Read},\mathsf{Submit}}\left(p_k\right)$    ▹ Answers the queries according to the specification of $\mathcal{B}$
5:	$S^{\prime }\leftarrow$ state and internal information of $\mathcal{B}$
6:	output $(m,(S,S^{\prime },p_k,s_k))$
7:	end procedure

Algorithm 6 Second Stage of the Adversary ${\mathsf{A}}^{\prime }$
1:	procedure${\mathsf{A}\prime }_2^{{\mathsf{Enc}}_k}$($c,(S,S^{\prime },p_k,s_k)$)
2:	Initialize a blockchain $\mathcal{B}$ according to the state $S^{\prime }$
3:	$(\lambda ,k)\leftarrow {\mathsf{Gen}}_{\mathsf{BLOCCE}}\left(1^s\right)$
4:	Embed $\lambda \left|\right|c$ into $\mathcal{B}$ by simulating $\mathsf{Embed}$
5:	$b^{\prime }\leftarrow {\mathsf{A}}_2^{\mathsf{Read},\mathsf{Submit}}(p_k,S)$
6:	output $b^{\prime }$
7:	end procedure

If $\mathsf{A}$ is probabilistic polynomial time, so is ${\mathsf{A}}^{\prime }$. Suppose that ${\mathsf{A}}^{\prime }$ was run in an $\mathsf{PRC}\_\mathsf{EXP}$ experiment. Let D denote the random variable corresponding to the experiment coin toss (b of $\mathsf{PRC}\_\mathsf{EXP}$ line 4) such that $D=1$ if ${\mathsf{A}}^{\prime }$ was given the correct $c\leftarrow \mathsf{Enc}(k,m)$ under a random key k and $D=0$ if it was given a random $c\leftarrow U({\{0,1\}}^{N-n_{\lambda }})$. Depending on D, we have the following two cases:

• Suppose first that $D=1$ and ${\mathsf{A}}^{\prime }$ was given the correct $c\leftarrow \mathsf{Enc}(k,m)$. Then ${\mathsf{A}}^{\prime }$ embeds $\lambda \left|\right|c$ into the blockchain which follows the payment distinguishing experiment for $\mathsf{A}$ for the case $b=1$. Since ${\mathsf{A}}_2^{\prime }$ outputs the same bit $b^{\prime }$ as ${\mathsf{A}}_2$ we have

  $$Pr\left[{\mathsf{A}}^{\prime } \mathrm{succeeds} \mathrm{in} \mathsf{PRC}\_\mathsf{EXP}|D=1\right]=Pr\left[\mathsf{A}\mathrm{succeeds}|D=1\right].$$
• Suppose now that $D=0$ and c is a uniformly random string. By the description of ${\mathsf{Gen}}_{\mathsf{BLOCCE}}$, $\lambda$ is also uniformly random, meaning that a uniformly random string $\lambda \left|\right|c$ gets embedded into the blockchain. By the description of the payment distinguishing experiment, this is equal to the case $b=0$ and

  $$Pr\left[{\mathsf{A}}^{\prime } \mathrm{succeeds} \mathrm{in} \mathsf{PRC}\_\mathsf{EXP}|D=0\right]=Pr\left[\mathsf{A}\mathrm{succeeds}|D=0\right].$$

We have established that ${\mathsf{A}}^{\prime }$, which we constructed to be an adversary to distinguish the ciphertexts of $\mathsf{SE}$ from random, succeeds in its experiment if and only if $\mathsf{A}$ succeeds in its own payment distinguishing experiment. Therefore,

$$Pr\left[\mathsf{PRC}\_{\mathsf{EXP}}_{{\mathsf{A}}^{\prime }}^{\mathsf{SE}}\left(1^s\right)=1\right]=Pr\left[\mathsf{PAY}\_\mathsf{DIST}\_{\mathsf{EXP}}_{\mathsf{A}}^{\mathsf{BLOCCE},\mathcal{B}}\left(1^s\right)=1\right].$$

By the definition of advantage,

$${\mathbf{Adv}}_{{\mathsf{A}}^{\prime },\mathsf{SE}}^{\mathsf{PRC}}\left(s\right)={\mathbf{Adv}}_{\mathsf{A},\mathsf{BLOCCE},\mathcal{B}}^{\mathsf{PAY}\_\mathsf{DETECT}}\left(s\right).$$

By the definition of $\mathsf{BLOCCE}$ (see Section 4.2), the applied symmetric encryption scheme $\mathsf{SE}$ has pseudorandom ciphertexts under a chosen plaintext attack, and there is a negligible function $ϵ$ such that ${\mathbf{Adv}}_{{\mathsf{A}}^{\prime },\mathsf{SE}}^{\mathsf{PRC}}\left(s\right)\le ϵ\left(s\right)$ for every $s\ge 1$ (see Section 2.2). Since $\mathsf{A}$ was any two-stage probabilistic polynomial time adversary and

$${\mathbf{Adv}}_{\mathsf{A},\mathsf{BLOCCE},\mathcal{B}}^{\mathsf{PAY}\_\mathsf{DETECT}}\left(s\right)={\mathbf{Adv}}_{{\mathsf{A}}^{\prime },\mathsf{SE}}^{\mathsf{PRC}}\left(s\right)\le ϵ\left(s\right),$$

we have the claim and $\mathsf{BLOCCE}$ securely embeds into a simplified ideal blockchain. ☐

6. Discussion and Future Work

To simplify our investigations, we restricted ourselves to the embedding of a single bit for each block. For many applications, such as Bitcoin, the time to publish a new block is counted in minutes instead of seconds. Therefore, the throughput of our scheme is low. However, it is easy to increase the number of embedded bits per block. One way to do it would be to match multiple LSBs of the address. However, in such a case, the expected computation time for embedding grows exponentially in the number of bits, since the bits are drawn from the random oracle. Proposition 2 would also need to be updated accordingly. It is more efficient to submit several payments into the same block. In such a case, the ordering of the message bits have to be ensured, for example, by using the unique payment identifier t or the public payer keys.

Our method requires the user to distribute the message bits over several payments. For many contemporary blockchains that apply the proof-of-work paradign for it consensus mechanism the transaction costs may be significant for larger hidden messages. However, there are newer consensus mechanisms that aim to address the energy usage issue of the proof-of-work paradigm to improve block generation efficiency and to ultimately possibly remove transaction costs in certain applications. Such mechanisms include proof-of-stake, distributed proof-of-stake and byzantine fault tolerance based mechanisms. For example, at the moment, Ethereum is planning on moving to the prove-of-stake paradigm. While there will be high transaction costs in certain use cases of blockchain, we believe that, in many applications, transaction costs will not be an issue and our method will prove to be useful.

Performance of our method can be also increased by pre-computing a list of L addresses, where L is significantly greater than N, the total length of the embedded message. Since the LSBs of these generated addresses are random, approximately one half will be ones and the rest zeros. Once Alice is ready to embed the payload $(\lambda ,c)$, she can pick the addresses in order from the pre-generated list. This approach would also mitigate the computational complexity of the embedding of multiple bits into a single payment. Furthermore, addresses to embed $\lambda$ can be pre-computed immediately after the key $(\lambda ,k)$ has been agreed on. However, we leave these considerations for future work.

It should be noted that it is important that the hidden message is first encrypted using an encryption scheme $\mathsf{SE}$ that has pseudorandom ciphertexts. If it is not the case, the adversary is able to detect the non-random nature of the LSBs of the addresses in Alice’s payments. For the same reason, the underlying blockchain should not allow the reuse of addresses. In addition to being a privacy risk [23,24,25], it would render the payment indistinguishability approach to the security inapplicable. For such systems, we would need to formulate a security definition that is based on the probability distribution of “normal” payments of Alice and the payload containing payments should be indinstinguishable from this distribution. We leave these considerations also for future work.

In this paper, we have not implemented BLOCCE in practice. Instead, we have considered it in the simplified ideal blockchain model that abstracts away details that are not relevant for the theoretical investigations. For example, the network is completely abstracted away in the simplified model. However, the details, such as the network, are relevant when considering a practical implementation of the scheme. We leave it as future work to investigate the secure implementation of BLOCCE using an existing blockchain such as Ethereum.

7. Conclusions

We suggest the first provably secure method called $\mathsf{BLOCCE}$ of implementing a covert communication channel over a blockchain. Our proofs are shown in the random oracle model, where the cryptographic hash function used by the blockchain is modeled as a random oracle. We formulate a simplified ideal blockchain that models the blockchain implementations underlying existing cryptocurrencies. Based on this model, we suggest a method of embedding a single bit for each block using payments submitted to the blockchain. We show that the method is reliable and runs in expected polynomial time. The method can be generalized to embed multiple bits to increase the throughput. To model the security of covert channels on a blockchain, we formulate the notion of payment indistinguishability, where the transmitted hidden message should be computationally indistinguishable from random payments. Finally, we show that $\mathsf{BLOCCE}$ satisfies this definition.