Sequential Hashing with Minimum Padding
Abstract
:1. Introduction
1.1. Background
1.2. Our Contribution
1.3. Related Work
1.4. Organization
2. Preliminaries
2.1. Notations
2.2. Collision Resistance and Preimage Resistance
2.3. Indifferentiability from Random Oracle
3. Proposed Scheme
4. Collision Resistance
- (i)
- Suppose that one of and uses and the other uses . Assume that uses and uses without loss of generality. If , then one finds a collision pair for F. If and , then one finds a collision pair for F or a preimage of for F. If and , then one finds a collision pair for F or a preimage of for F. If and , then one finds a collision pair or a -pseudo-collision pair for F.
- (ii)
- Suppose that both of and uses a same permutation. If , then one finds a collision pair for F. If and , or and , then one finds a collision pair for F or a preimage of for F. If and , then one finds a collision pair or a preimage of for F.
5. Indifferentiability from Random Oracle
5.1. In the Random Oracle Model
5.2. In the Ideal Cipher Model
6. Application to Sponge Construction
6.1. Scheme
6.2. IRO in the Ideal Permutation Model
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Dang, Q.H. Secure Hash Standard (SHS); FIPS PUB 180-4; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012.
- Merkle, R.C. One Way Hash Functions and DES. In Advances in Cryptology—CRYPTO 89, Proceedings of the 9th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, CA, USA, 20–24 August 1989; Brassard, G., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1990; Volume 435, pp. 428–446. [Google Scholar]
- Damgård, I. A Design Principle for Hash Functions. In Advances in Cryptology—CRYPTO 89, Proceedings of the 9th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, CA, USA, 20–24 August 1989; Brassard, G., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1990; Volume 435, pp. 416–427. [Google Scholar]
- Bellare, M.; Canetti, R.; Krawczyk, H. Keying Hash Functions for Message Authentication. In Advances in Cryptology—CRYPTO 96, Proceedings of the 16th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; Koblitz, N., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1109, pp. 1–15. [Google Scholar]
- Hirose, S.; Park, J.H.; Yun, A. A Simple Variant of the Merkle-Damgård Scheme with a Permutation. In Advances in Cryptology—ASIACRYPT 2007, Proceedings of the 13th International Conference on the Theory and Application of Cryptology and Information Security, Kuching, Malaysia, 2–6 December 2007; Kurosawa, K., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4833, pp. 113–129. [Google Scholar]
- Hirose, S.; Yabumoto, A. A Tweak for a PRF Mode of a Compression Function and Its Applications. In Innovative Security Solutions for Information Technology and Communications, Proceedings of the 9th International Conference, SECITC 2016, Bucharest, Romania, 9–10 June 2016; Bica, I., Reyhanitabar, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 10006, pp. 103–114. [Google Scholar]
- Bagheri, N.; Gauravaram, P.; Knudsen, L.R.; Zenner, E. The suffix-free-prefix-free hash function construction and its indifferentiability security analysis. Int. J. Inf. Secur. 2012, 11, 419–434. [Google Scholar] [CrossRef] [Green Version]
- Nandi, M. Characterizing Padding Rules of MD Hash Functions Preserving Collision Security. In Information Security and Privacy, Proceedings of the 14th Australasian Conference, ACISP 2009, Brisbane, Australia, 1–3 July 2009; Boyd, C., Nieto, J.M.G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5594, pp. 171–184. [Google Scholar]
- Coron, J.S.; Dodis, Y.; Malinaud, C.; Puniya, P. Merkle-Damgård Revisited: How to Construct a Hash Function. In Advances in Cryptology—CRYPTO 2005, Proceedings of the 25th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14-18 August 2005; Shoup, V., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3621, pp. 430–448. [Google Scholar]
- Maurer, U.M.; Renner, R.; Holenstein, C. Indifferentiability, Impossibility Results on Reductions, and Applications to the Random Oracle Methodology. In Theory of Cryptography, Proceedings of the First Theory of Cryptography Conference, TCC 2004, Cambridge, MA, USA, 19-21 February 2004; Naor, M., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2951, pp. 21–39. [Google Scholar]
- Chang, D.; Lee, S.; Nandi, M.; Yung, M. Indifferentiable Security Analysis of Popular Hash Functions with Prefix-Free Padding. In Advances in Cryptology—ASIACRYPT 2006, Proceedings of the 12th International Conference on the Theory and Application of Cryptology and Information Security, Shanghai, China, 3–7 December 2006; Lai, X., Chen, K., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4284, pp. 283–298. [Google Scholar]
- Chang, D.; Nandi, M. Improved Indifferentiability Security Analysis of chopMD Hash Function. In Fast Software Encryption, Proceedings of the 15th International Workshop, FSE 2008, Lausanne, Switzerland, 10–13 February 2008; Nyberg, K., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5086, pp. 429–443. [Google Scholar]
- Bellare, M.; Ristenpart, T. Multi-property-preserving hash domain extension and the EMD transform. In Advances in Cryptology—ASIACRYPT 2006, Proceedings of the 12th International Conference on the Theory and Application of Cryptology and Information Security, Shanghai, China, 3–7 December 2006; Lai, X., Chen, K., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4284, pp. 299–314. [Google Scholar]
- Kelsey, J. Public Comments on the Draft Federal Information Processing Standard (FIPS) Draft FIPS 180-2, Secure Hash Standard (SHS), 2001. Available online: http://www.cs.utsa.edu/∼wagner/CS4363/SHS/dfips-180-2-comments1.pdf (accessed on 9 June 2018).
- Dworkin, M.J. Recommendation for Block Cipher Modes of Operation: The CMAC Mode for Authentication; NIST Special Publication 800-38B; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005.
- Black, J.; Rogaway, P. A Block-Cipher Mode of Operation for Parallelizable Message Authentication. In Advances in Cryptology—EUROCRYPT 2002, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Amsterdam, The Netherlands, 28 April–2 May 2002; Knudsen, L.R., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2332, pp. 384–397. [Google Scholar]
- Nandi, M. Fast and Secure CBC-Type MAC Algorithms. In Fast Software Encryption, Proceedings of the 16th International Workshop, FSE 2009, Leuven, Belgium, 22–25 February 2009; Dunkelman, O., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5665, pp. 375–393. [Google Scholar]
- Sarkar, P. Domain extender for collision resistant hash functions: Improving upon Merkle-Damgård iteration. Discret. Appl. Math. 2009, 157, 1086–1097. [Google Scholar] [CrossRef]
- Bertoni, G.; Daemen, J.; Peeters, M.; Assche, G.V. Sufficient conditions for sound tree and sequential hashing modes. Int. J. Inf. Secur. 2014, 13, 335–353. [Google Scholar] [CrossRef]
- Bertoni, G.; Daemen, J.; Peeters, M.; Assche, G.V. Sakura: A Flexible Coding for Tree Hashing. In Applied Cryptography and Network Security, Proceedings of the 12th International Conference, ACNS 2014, Lausanne, Switzerland, 10–13 June 2014; Boureanu, I., Owesarski, P., Vaudenay, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8479, pp. 217–234. [Google Scholar]
- Bertoni, G.; Daemen, J.; Peeters, M.; Van Assche, G. Sponge Functions. In Proceedings of the ECRYPT Hash Workshop 2007, Barcelona, Spain, 24–25 May 2007. [Google Scholar]
- Dworkin, M.J. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; FIPS PUB 202; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015.
- Guo, J.; Peyrin, T.; Poschmann, A. The PHOTON Family of Lightweight Hash Functions. In Advances in Cryptology—CRYPTO 2011, Proceedings of the 31st Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Rogaway, P., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6841, pp. 222–239. [Google Scholar]
- Bogdanov, A.; Knezevic, M.; Leander, G.; Toz, D.; Varici, K.; Verbauwhede, I. spongent: A Lightweight Hash Function. In Cryptographic Hardware and Embedded Systems—CHES 2011, Proceedings of the 13th International Workshop, Nara, Japan, 28 September–1 October 2011; Preneel, B., Takagi, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6917, pp. 312–325. [Google Scholar]
- Bertoni, G.; Daemen, J.; Peeters, M.; Van Assche, G. Duplexing the Sponge: Single-Pass Authenticated Encryption and Other Applications. In Selected Areas in Cryptography, Proceedings of the 18th International Workshop, SAC 2011, Toronto, ON, Canada, 11–12 August 2011; Miri, A., Vaudenay, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7118, pp. 320–337. [Google Scholar]
- Rogaway, P.; Shrimpton, T. Cryptographic Hash-Function Basics: Definitions, Implications, and Separations for Preimage Resistance, Second-Preimage Resistance, and Collision Resistance. In Fast Software Encryption, Proceedings of the 11th International Workshop, FSE 2004, Delhi, India, 5–7 February 2004; Roy, B.K., Meier, W., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3017, pp. 371–388. [Google Scholar]
- Bellare, M.; Rogaway, P. The Security of Triple Encryption and a Framework for Code-Based Game-Playing Proofs. In Advances in Cryptology—EUROCRYPT 2006, Proceedings of the 25th Annual International Conference on the Theory and Applications of Cryptographic Techniques, St. Petersburg, Russia, 28 May–1 June 2006; Vaudenay, S., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4004, pp. 409–426. [Google Scholar]
- Quisquater, J.; Girault, M. 2n-Bit Hash-Functions Using n-Bit Symmetric Block Cipher Algorithms. In Advances in Cryptology—EUROCRYPT ’89, Proceedings of the Workshop on the Theory and Application of of Cryptographic Techniques, Houthalen, Belgium, 10–13 April 1989; Quisquater, J.J., Vandewalle, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1989; Volume 434, pp. 102–109. [Google Scholar]







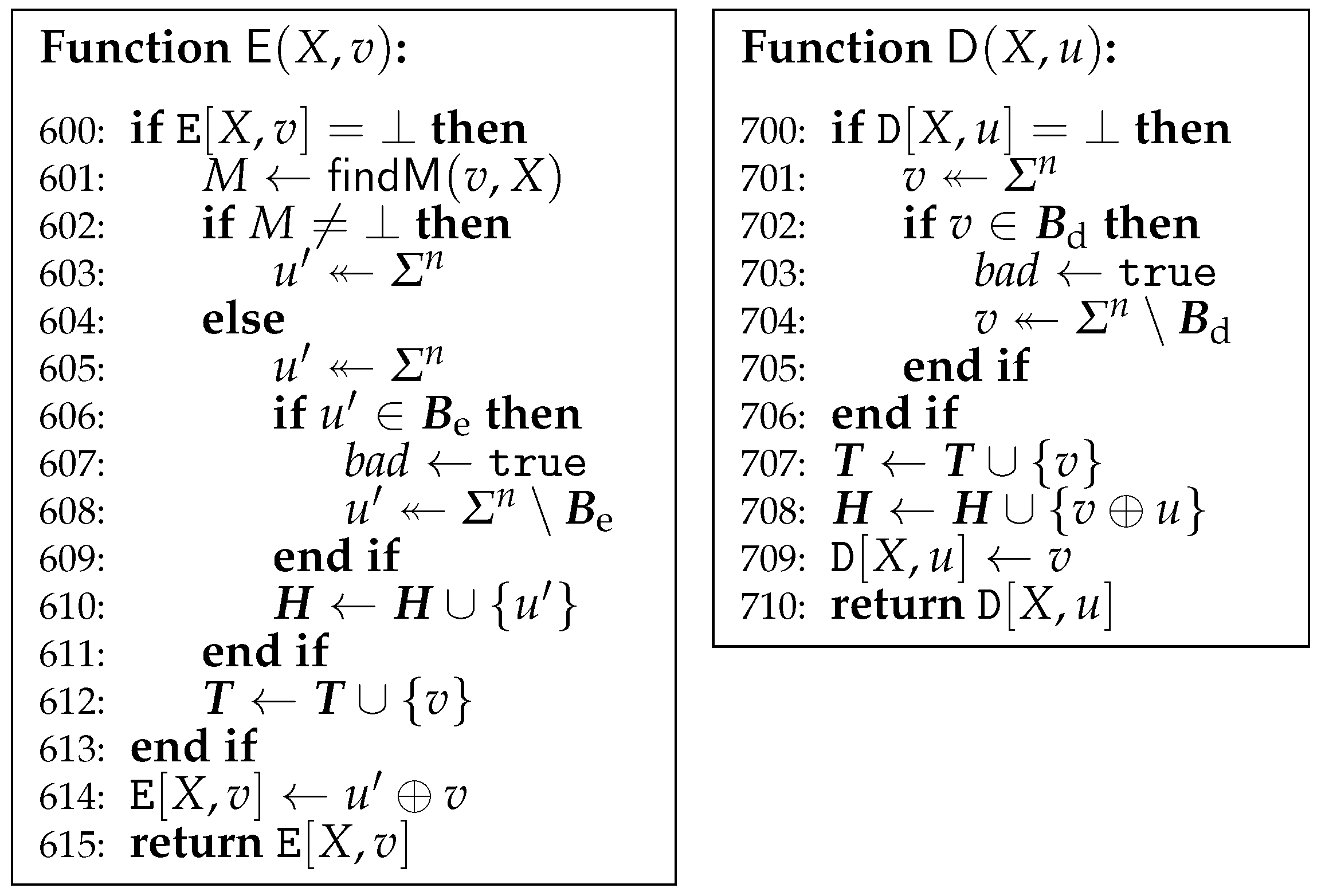
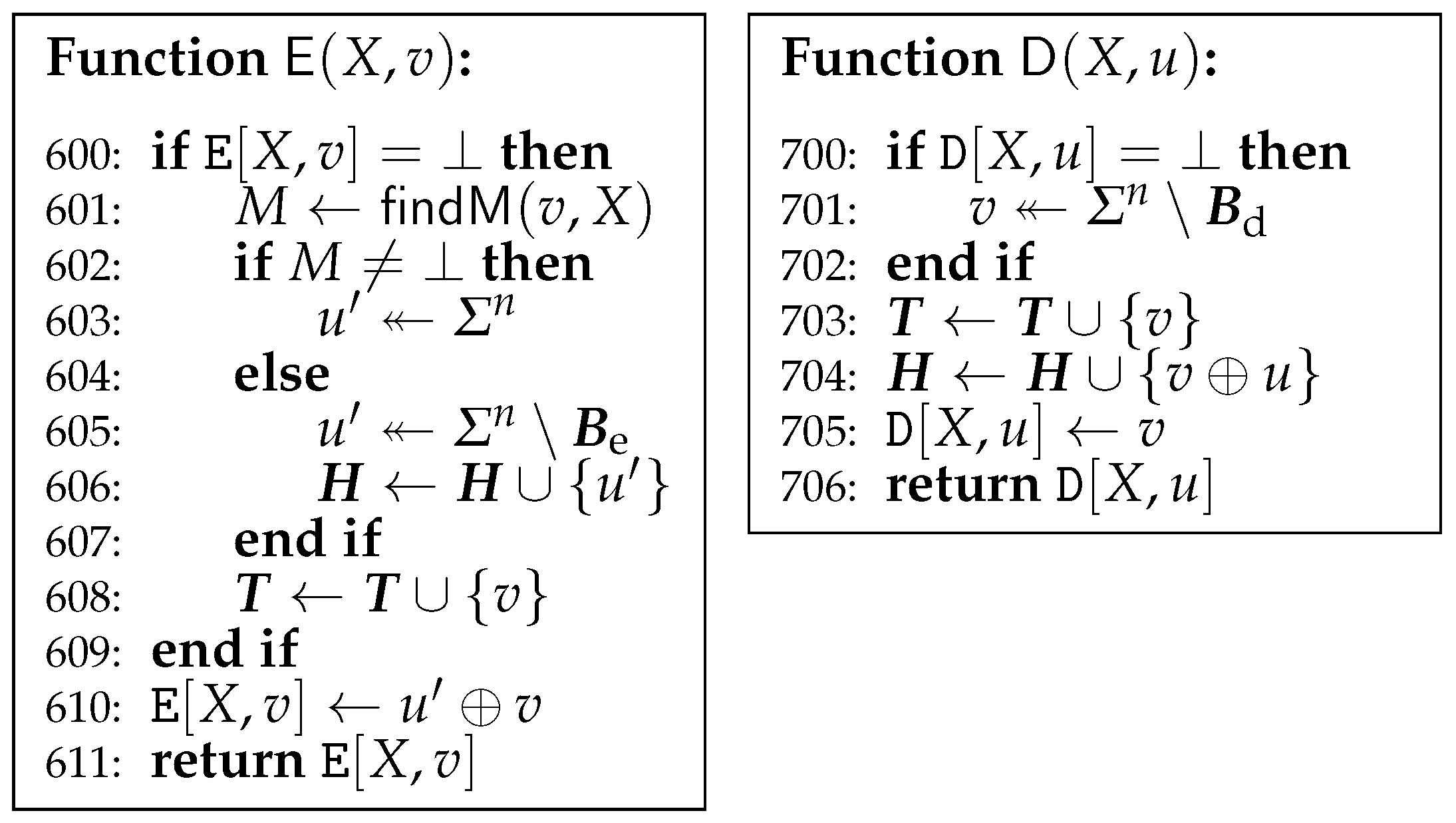

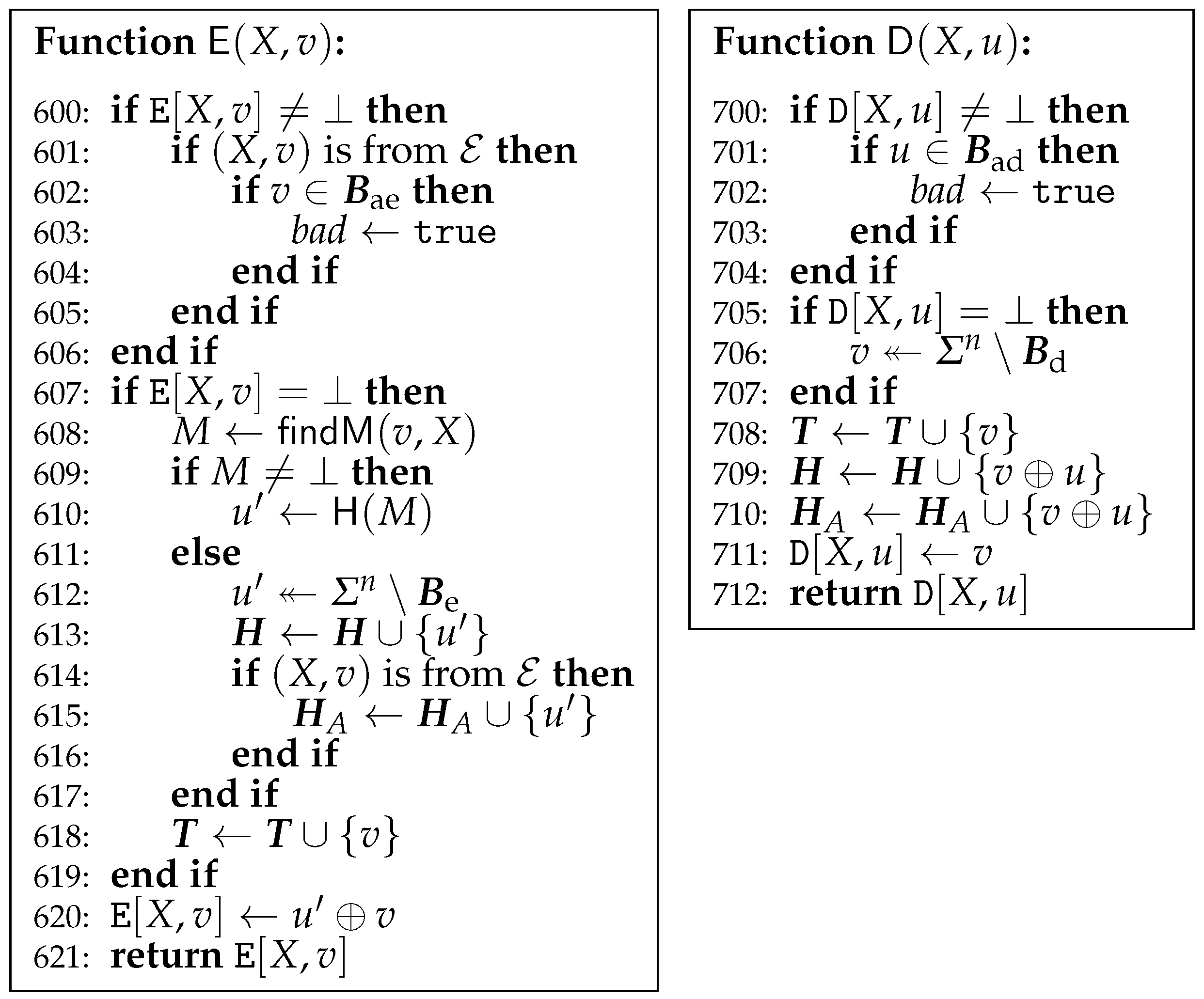









© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirose, S. Sequential Hashing with Minimum Padding. Cryptography 2018, 2, 11. https://doi.org/10.3390/cryptography2020011
Hirose S. Sequential Hashing with Minimum Padding. Cryptography. 2018; 2(2):11. https://doi.org/10.3390/cryptography2020011
Chicago/Turabian StyleHirose, Shoichi. 2018. "Sequential Hashing with Minimum Padding" Cryptography 2, no. 2: 11. https://doi.org/10.3390/cryptography2020011



