Performance Analysis of Secure and Private Billing Protocols for Smart Metering

Abstract

Traditional utility metering is to be replaced by smart metering. Smart metering enables fine-grained utility consumption measurements. These fine-grained measurements raise privacy concerns due to the lifestyle information which can be inferred from the precise time at which utilities were consumed. This paper outlines and compares two privacy-respecting time of use billing protocols for smart metering and investigates their performance on a variety of hardware. These protocols protect the privacy of customers by never transmitting the fine-grained utility readings outside of the customer’s home network. One protocol favors complexity on the trusted smart meter hardware while the other uses homomorphic commitments to offload computation to a third device. Both protocols are designed to operate on top of existing cryptographic secure channel protocols in place on smart meters. Proof of concept software implementations of these protocols have been written and their suitability for real world application to low-performance smart meter hardware is discussed. These protocols may also have application to other privacy conscious aggregation systems, such as electronic voting.

1. Introduction

1.1. Motivation

Ever more objects are designed to be connected to each other and to the Internet as part of the “Internet of Things”. Predictions indicate that 50 billion of these devices will be online by 2025 [1]. As part of this trend, utility supply is in the process of upgrading to use network-connected meters which allow frequent consumption measurements to be taken automatically. The network of these meters is called the “Smart Grid”.

As discussed in a survey of smart metering [2], one advantage of these regular measurements is to improve load monitoring and forecasting so that utility resellers can make more profitable contracts with utility producers and so that utility providers can make better decisions about how to maintain their infrastructure. Another use is to detect network leakage and fraud. The regular consumption measurements can be used automatically to bill customers depending on complex tariffs, such as varying the cost of a utility depending upon the time at which it was used. For these reasons, smart meter roll-out has been mandated by governments in the E.U., U.K., and United States [2].

However, the transmission of these fine-grained consumption measurements has raised significant opposition from both privacy advocates and ordinary consumers [3]. For example, fine-grained household power consumption data make it easy to spot religious activities, such as fasting and nighttime prayer. As another example, a burglar could use these measurements to ensure that a target property is not occupied at the time of a break-in. For similar reasons, law enforcement agencies are interested in utility consumption data. Utility consumption measurements were first used by law enforcement in West Germany in the 1970s, where police used energy consumption records to locate a Red Army safe house [2]. Very high frequency electricity consumption readings have been used to identify the TV program being watched on several TV models from different manufacturers [4].

In general, there have been two responses to privacy concerns: the most widespread of these has been regulatory solutions. For example, in the U.K. Smart Energy Code [5], parties to the energy grid are required only to access the information they are authorized to use, and this authorization is only assigned to those parties who most need it. However, regulation is a weak guarantee because compromised or malicious parties may not abide by the regulation. A stronger privacy guarantee is given by technical solutions, such as the cryptographic protocols put forward in this paper and others (see Section 1.2).

One downside of the technical solutions is that they often require smart meters to carry out complicated cryptographic calculations, which necessitate more expensive smart meter hardware. Furthermore, controlling the distribution of meter readings reduces the flexibility of the smart metering system.

This paper outlines two cryptographic protocols. One protocol is intended to represent the simplest possible approach to the problem. The other protocol improves upon Jawurek et al. [3] using more conservative parameters in the commitment scheme and a more performant public-key signature scheme called “Ed25519”. Each of these protocols addresses different tradeoffs between technical complexity and smart meter cost. These billing protocols are intended to run over an authenticated and confidential communication channel, such as Transport Layer Security TLS. Both protocols were implemented as part of this work. The protocol implementations were written as software libraries which may be included into other projects (see Section 4.3). The main contribution of this paper is to investigate the performance of these protocol implementations on a variety of hardware and to consider their suitability for real deployment.

Section 2 describes the smart meter billing security specification and the two protocols designed to solve this challenge. Section 3 explains how the protocols meet the security specification. Section 4 discusses the performance of these existing implementations and evaluates the implementation’s suitability for use in a real world smart meter deployment. Section 5 concludes the paper.

1.2. Related Work

Firstly, in [6], additional consumption is added as noise to a consumer’s bills. This noise prevents fine-grained billing from revealing information about the consumer and is proven to be differentially private; however, the paper also finds that the expected financial cost of this added consumption is extremely high. The financial cost may be partially mitigated using a more complex protocol to allow some billing rebates for the fake consumption; however, the rebates are only sufficient to make privacy economical for a few days per year. A similar approach is presented in [7], where both additive and subtractive noise are added to energy consumption using a rechargeable battery. The approach in [7] also achieves differential privacy and should be economical for houses already using energy storage systems. Other works using rechargeable batteries include [8,9,10]. Energy forecasting may still be improved under these noise-based systems because the utility consumption after noise adjustment can be safely studied by utility providers. However, the use of differential privacy may greatly reduce the value of these measurements to data brokers and advertising companies.

Another approach to fine-grained billing privacy is to side-step the need for differential privacy by never supplying utility companies with fine-grained usage data [3,11]. Instead, aggregate longer period bills are calculated locally and only these are sent to utility providers, therefore providing no privacy loss when compared to traditional billing. Zero knowledge proof techniques are used to assure utility providers that these bills are calculated honestly per their price specification. However, withholding usage information prevents utility providers from gaining any improved forecasting information and from selling the consumption measurements. This problem may be solved by also using protocols designed to report temporally accurate billing information while keeping the identity of the meter anonymous as proposed in [12,13,14].

Aside from fine-grained billing, a different proposed use for smart meters is to aggregate usage in an area to search for fraud, leaks in the utility system, and real-time system monitoring. Several privacy-preserving protocols are given in [15]. In these protocols, consumption aggregates are computed amongst all the meters in an area, in such a way as to ensure that the utility company learns only the aggregate and can also trust that the total was computed honestly.

Finally, several protocols [16,17] have been proposed using attested Trusted Platform Module TPMs to achieve smart meter security goals. The authors in [17] combine this technique with the anonymous identity protocols (discussed previously) using remote anonymous attestation to verify that providers can trust that they are communicating with a trusted TPM without revealing the identity of the TPM. A similar approach is taken in this paper, where smart meters are assumed to use tamper-resilient hardware (a TPM). However, this paper does not address the problem of attesting the smart meter software and configuration data.

In [3], Jawurek et al. propose a protocol very similar to the three-party protocol described in this paper. However, Jawurek et al. [3] does not contrast the three-party protocol with the much simpler two-party protocol and does not consider the protocol’s performance on smart meter hardware.

Homomorphic encryption has been similarly applied to Electronic Voting Protocols [18].

1.3. Pedersen Commitments Background

The next section briefly reviews Pedersen commitments. For more information on Pedersen commitments see [19,20].

Commitments are often used to claim knowledge of some data without revealing the data. For example, in a puzzle competition, a participant may publish a commitment to the solution of a puzzle so that if challenged later, the participant can prove that they knew the solution of the puzzle at the time at which they published the commitment. Doing so will not reveal the solution to the puzzle to other participants until the time at which the commitment is opened.

To protect against situations in which the data being committed to has low entropy (one attack against such a system could learn which data was committed to by trying to compute a commitment to all possible values for the data and checking which one had the same value as the one which was published. The addition of a sufficiently long random salt makes this attack computationally infeasible because there would be too many possible inputs to exhaustively test), commitments are usually derived from both this data and some random material. Opening a commitment is performed by revealing the data committed to and any other information (such as the random salt) which is required to compute the commitment. Any observer may then compute a commitment using this data to check that the result is the same as the commitment previously published.

The functional requirements for a commitment system lead to two important properties for commitments (for formal definitions see [19]):

(a) A commitment scheme is said to be computationally binding if nobody can find more than one valid opening to the same commitment without performing excessive (impossible on modern hardware) computation.

(b) A commitment scheme is said to be computationally concealing if observers only learn a negligible amount about the data which was committed to using non-excessive computation on the commitment.

In the usage of commitments in this protocol, two further properties are required (where commit(x) is a commitment on x):

(a) The commitment is additively homomorphic: an efficient operation ⊕ exists such that

$$\mathrm{commit}(x)\oplus \mathrm{commit}(y)=\mathrm{commit}(x+y)$$

(b) The commitment is multiplicatively homomorphic: an efficient operation ⊗ exists such that

$$\mathrm{commit}(x)\otimes y=\mathrm{commit}(x\times y).$$

The proof of concept implementation uses Pedersen commitments [20] defined as follows:

• q is a 256-bit random prime;
• p is a large (2048–4094 bit) prime of the form $n\times q+1$ such that $q$ generates a subgroup of p;
• g and h are random members of the subgroup of ${ℱ}^{\ast }$ of order $q$;
• x is the data to be committed to (an integer modulo $q$); and
• r is the random salt (an integer modulo p). Note: r is usually picked from the set of integers modulo q so that computation can remain within this subgroup; however, during the protocol, values for r become too large for this and so the more expensive computations across the whole of the group generated by p are allowed.

  $${\mathrm{commit}}_r(x)≔h^x{g}^r (\mathrm{mod} p)$$

This scheme is computationally binding (so long as the committer does not know the discrete logarithm of h to the base g) and information theoretically concealing [19].

Additive homomorphism can be achieved by multiplying commitments:

$$\begin{array}{c}{\mathrm{commit}}_{r_1}(x_1)\oplus {\mathrm{commit}}_{r_2}(x_2)≔{\mathrm{commit}}_{r_1}(x_1)·{\mathrm{commit}}_{r_2}(x_2)\hfill \\ =(h^{x_1}{g}^{r_1})·(h^{x_2}{g}^{r_2}) (\mathrm{mod} p)= h^{x_1+x_2}{g}^{r_1+r_2} (\mathrm{mod} p)\hfill \\ ={\mathrm{commit}}_{r_1+r_2}(x_1+x_2).\hfill \end{array}$$

Similarly, multiplicative homomorphism can be achieved using exponentiation:

$$\begin{array}{c}{\mathrm{commit}}_r(x)\otimes y≔{({\mathrm{commit}}_r(x))}^y={(h^x{g}^r)}^y (\mathrm{mod} p)\hfill \\ =h^{xy}{g}^{ry} (\mathrm{mod} p)={\mathrm{commit}}_{ry}(xy).\hfill \end{array}$$

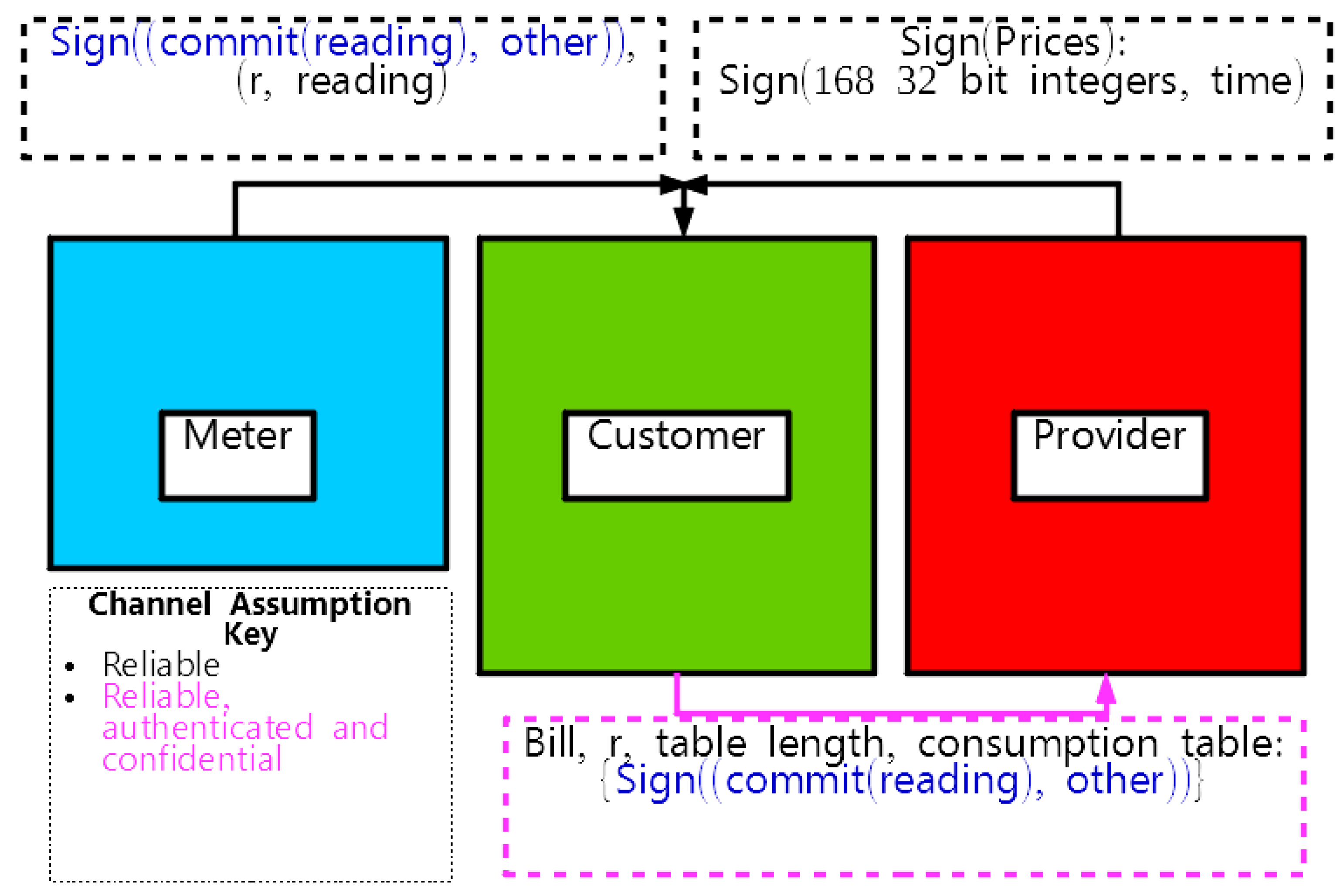
2. Smart Meter Billing

2.1. Security Specification

These protocols are intended to provide time of use pricing without incurring the privacy loss inherent in giving utility companies fine-grained utility consumption information.

2.1.1. Adversaries

We model threats from the following adversaries, all of whom are assumed to be polynomially bounded in computation. Here, we list the attacks we consider.

• Malicious customer
  • Attempts to modify the smart meter to produce incorrect readings.
  • Attempts to modify outputted bills before they are transmitted to the utility provider.
  • Attempts to prevent transmission of bills to the utility provider.
  • Attempts to change the prices input to the smart meter.
• Malicious utility provider
  • Attempts to de-aggregate fine-grained utility readings.
• Malicious third-party
  • Attempts to snoop the bill total off the wire (using passive or active attacks).
  • Attempts to change the pricing information used by the customer.
  • Attempts to de-aggregate fine-grained utility readings.

The following threats are not considered in this protocol:

• A malicious utility provider disclosing the bill total to the malicious third party.
• Hardware and firmware malware embedded in the smart meter either during manufacture or firmware updates: causing the smart meter to act maliciously.
• Attempts by the utility provider to over-charge customers (this is only unmet in the simple protocol. In the three-party protocol, the user gets a signed copy of the smart meter readings and so these could be used as evidence against the utility provider so long as the smart meter does not collude alongside the utility provider).

2.1.2. Required Security Properties

As there is some repetition in these adversarial threats, they have been combined into the following system requirements:

• R1: Do not allow the utility provider (or any third party) to learn utility consumption measurements with any more temporal granularity than they learn in the traditional utility billing system (threats 2a and 3c).
• R2: Do not leak the bill amount to any third party (threat 3a).
• R3: Utility providers must be able to verify that they receive the correct bill amount (threats 1a–c).
• R4: Only the utility provider can change prices (threats 1d and 2b).

2.1.3. Assumptions

To meet these required security properties, the following assumptions will be made:

• A1: The smart meter is tamper resistant and is trusted by all parties.
• A2: The utility provider trusts its own servers to operate correctly.
• A3: Unless otherwise specified, all communications in these protocols are to be performed over a reliable, confidential, and authenticated channel.
• A4: (Specific to the three-party protocol). The customer trusts the “customer” device.

2.2. Simple Protocol

This section outlines the operation of the simple billing protocol.

(1) The smart meter records readings into its own memory.

(2) If a price change is necessary, the provider sends a signed copy of the new price information to the smart meter.

(3) On receiving new pricing information, the smart meter verifies the signature. If the signature is incorrect, the smart meter discards the message. If the signature is correct, then the new pricing information is stored. An acknowledgement of the pricing information is sent back to the utility provider.

(4) At the end of a billing period, the smart meter calculates the bill and deletes the readings.

(5) The smart meter concatenates the aggregate bill with a unique timestamp and signs the pair. This signed pair is transmitted to the utility provider.

(6) The provider verifies the signature on the bill. If it is valid and the timestamp matches this billing period, the bill is charged to the customer by the provider. If the signature was invalid, the message is discarded.

(7) If the provider receives no valid bill for a billing period then this is reported to human operators so that appropriate action may be taken.

2.3. Three-Party Protocol

This section outlines the operation of the three-party billing protocol.

This protocol depends upon the usage of additively and multiplicatively homomorphic commitments. For this purpose, Pedersen Commitments over the set of integers modulo a prime have been used. Pedersen Commitments were reviewed in Section 1.3.

The three parties in the protocol are shown in Figure 1. These are the tamper-resistant smart meter, a proxy device hereby called the “customer hardware”, and the utility provider’s server. The customer hardware may be a hardware device purchased and operated by the customer, such as a smart phone (as suggested in [11]) or a utility communication hub, such as that used in the U.K.’s smart utility system [5]. It may be any device which the customer is willing to trust with their utility readings and which is equipped with a reliable communication channel with both the smart meter and the server. The customer hardware does not have to be trusted by the utility provider but is trusted by the customer (A4).

(1) When the smart meter makes a reading, it first calculates a commitment to the reading. This commitment is then concatenated to the “other” pricing information. For time of use billing, this is the time of the measurement. This time must be unique within the life of the signing key, otherwise a malicious customer could use lower readings from a previous billing cycle. The commitment-other tuple is signed by the smart meter. Finally, this signed tuple is sent to the customer hardware along with the salt used for the commitment and the clear-text reading.

(2) On receiving this message from the smart meter, the customer hardware verifies the signature in the message. If the signature is valid, the message is stored by the customer hardware. If the signature is invalid, the message is discarded.

(3) If a price change is necessary, the provider sends a signed copy of the new price information to the customer hardware.

(4) On receiving new pricing information, the customer hardware verifies the signature. If the signature is incorrect it discards the message. If the signature is correct, the new pricing information is stored.

(5) At the end of the billing period, the customer hardware calculates the bill using its stored readings and prices. The salts of each reading are combined (in the same way as the readings are combined when calculating the bill) to calculate the salt $\overline{r}$ for the bill’s verification. The bill, $\overline{r}$, and all the signed tuples from the meter are sent to the utility provider.

(6) On receiving this billing information, the provider’s server must verify that the bill was calculated honestly by the customer hardware. First, the server should verify all the signatures from the smart meter to ensure that none of the meter readings or times were forged by the customer. The server should also check that all of the expected time measurements (and no others) are present in the billing information. This check prevents the customer from replaying measurements from earlier billing cycles and from omitting some readings. Next, the server should calculate a commitment to the received bill using the salt $\overline{r}$ which was sent previously. Finally, the utility provider can ensure the bill was calculated honestly from the meter readings by using the homomorphic commitments from the smart meter to calculate its own commitment to the final bill and then ensuring that this matches the expected commitment which it had already calculated. The specifics of this step are given in Theorem 1 in the following section.

3. Security Analysis

Lemma 1.

For $N>1$ readings: $R=\{r_1,r_2,\dots ,r_N\}$; corresponding to prices $P=\{p_1,p_2,\dots ,p_N\};$ leading to bill $b={\sum }_{i=1}^N{r}_i{p}_i$: a malicious computationally bounded utility provider cannot work backwards from $P$ and $b$ to discover $R$, where $r_i,p_i,b\in \mathit{Z}/p\mathit{Z}$ (i.e., the finite group in which the commitments are computed).

Proof. 

Solving $b={\sum }_{i=1}^N{r}_i{p}_i$ for an unknown $r_i$, a known total $b,$ and known coefficients $p_i$ is an example of solving a system consisting of one linear equation with $N$ unknowns. Therefore, the system is underdetermined with $N-1$ degrees of freedom and so does not have a unique solution. Each degree of freedom represents an unbound variable which could have any value in $\frac{Z}{pZ}$. Therefore, there will be $p^{(N-1)} possible$ solutions. $p$ is very large and so this aggregate bill represents a negligible amount of information.□

Lemma 2.

The utility provider does not learn any finer-grained billing information from the aggregate bill than they did under the traditional billing system.

Proof. 

By Lemma 1, this aggregate bill does not reveal the smart meter’s fine-grained consumption measurements. The aggregate bill is transmitted at most as often as bills under the traditional system and so it cannot itself be used as a relatively fine-grained measurement.□

Lemma 3.

A pair (data, unique timestamp) which was signed by A, using a private key known only to A, and using an ideal asymmetric signature algorithm cannot be modified by a malicious party M while on transit to B. Assume also that a failed transmission of the message can be detected. The output of A must be trusted by B.

Proof 

• The output of A is trusted by B and so collusion between A and M is beyond the scope of this game. Therefore, signatures made by A are trusted by B.
• M cannot replay old legitimate messages because the unique timestamp would no longer match what was expected by B.
• M cannot forge messages with either the data or timestamp modified because these are both covered by the signature, and forging a signature under an ideal public key signature algorithm is computationally infeasible.
• If M prevents the transmission of the data, this absence will be noticed by B because it knows to expect the message.

Hence, if B receives a message with a valid signature and the expected timestamp, it can trust that the data has not been modified and if B did not receive the message this can be detected.□

3.1. R1: Reading Privacy

3.1.1. Simple Billing Protocol

Corollary 1.

The utility provider does not learn any finer-grained billing information than they did under the traditional billing system.

Proof. 

Only the aggregate bill is transmitted to the utility provider. Apply Lemma 2.□

3.1.2. Three-Party Billing Protocol

Corollary 2.

The utility provider does not learn any finer-grained billing information than they did under the traditional billing system.

Proof. 

The aggregate bill, the salt for the aggregate bill, and commitments to the meter readings are transmitted to the utility provider.

• Applying Lemma 2, the aggregate bill is not an issue.
• The salt for the aggregate bill is the sum of all the salts on the individual commitments weighted by the prices. Therefore, by Lemma 2, this aggregate salt reveals no more information about the salts for individual commitments than the bill reveals about the individual readings.
• Pedersen commitments are information theoretically concealing [19], and so the series of commitments do not reveal information about the readings they commit to.□

3.2. R2: Security from Eavesdroppers

Corollary 3.

The aggregate bill cannot be eavesdropped by a third-party adversary under either protocol.

Proof. 

The protocols are assumed to operate over a confidential and authenticated channel (A2). A passive eavesdropper cannot read the bill in transit because the channel is confidential (encrypted). An active attacker cannot perform a man in the middle attack to obtain unencrypted data, because the channel is authenticated. Old messages cannot be replayed because the channel is authenticated. Security against these and similar attacks follow from the definition of a confidential and authenticated channel.□

3.3. R3: Bill Correctness

3.3.1. Simple Billing Protocol

Corollary 4.

No user can alter their bill without alerting the utility provider (assuming an ideal public key signature algorithm).

Proof. 

Apply Lemma 3 to the signed bill and timestamp the pair transmitted from the smart meter (party A) to the utility provider (party B), with M as a malicious user and using the utility provider’s expectation that it will receive a bill for a billing period to detect a failed message transmission. This assignment is valid because the utility provider trusts the smart meter (A1) and its own computation (A2).□

3.3.2. Three-Party Billing Protocol

Theorem 1.

No user can alter their bill without alerting the utility provider (assuming an ideal public key signature algorithm).

Proof 

• The signed commitment and timestamp pairs from the smart meter are trusted by the utility provider (Lemma 3 applied to the signed bill and timestamp pair transmitted from the smart meter (party A) to the utility provider (party B), with M as a malicious user and using the utility provider’s expectation that it will receive a bill for a billing period to detect a failed message transmission. This assignment is valid because the utility provider trusts the smart meter (A1) and its own computation (A2)).
• These commitments can be combined using the homomorphic operations as follows to obtain a commitment to the bill:

  $$\begin{array}{c}({\mathrm{commit}}_{r_1}(x_1)\otimes p_1)\oplus ({\mathrm{commit}}_{r_2}(x_2)\otimes p_2)\oplus ({\mathrm{commit}}_{r_3}(x_3)\otimes p_3)\oplus \dots \hfill \\ \oplus ({\mathrm{commit}}_{r_N}(x_N)\otimes p_N)\hfill \\ ={\mathrm{commit}}_{\overline{r}}({{\displaystyle \sum }}_{i=1}^N{x}_i{p}_i)={\mathrm{commit}}_{\overline{r}}(\mathrm{bill}).\hfill \end{array}$$
• If a commitment on the aggregate bill sent by the user is computed using the salt sent by the user, and it matches the signature generated from the trusted commitments, then the aggregate bill sent by the user must have been calculated honestly because Pedersen commitments are computationally binding [19].□

3.4. R4: Price Changes

3.4.1. Simple Billing Protocol

Corollary 5.

Only the utility provider can change prices.

Proof 

• After sending pricing information, the utility provider will expect a price acknowledgement response. Therefore, the utility provider can detect if the prices never made it to the smart meter.
• The price updates are signed by the utility provider. Apply Lemma 3 with A as the utility provider, B as the smart meter, a failed transmission detected as in the previous step, and a trust relationship between A and B supplied by A1. Using this lemma, the pricing information cannot be forged by a third party.□

3.4.2. Three-Party Billing Protocol

Theorem 2.

Only the utility provider can change prices.

Proof 

• If the user chooses to calculate the bill from its own fabricated prices, then either the bill will be different or the fabrication will be irrelevant and pointless.
• If the calculated bill is not computed correctly according to the prices on the utility provider’s server, then this can be detected when the bill is verified (Theorem 1).
• The price updates are signed by the utility provider. Apply Lemma 3 with A as the utility provider, B as the user device, a failed transmission detected as in the previous step, and a trust relationship between A and B supplied by A1. Using this lemma, the pricing information cannot be forged by a third party.□

4. Implementation and Evaluation

This section discusses the existing proof of concept implementation of these protocols and evaluates its suitability for real world deployment.

4.1. Existing Implementation

The protocol implementations were split into three parts: a repository containing the billing protocol-level software, a repository implementing a confidential and authenticated secure channel as required for the billing protocols, and a repository containing cryptographic primitives used in the other two repositories. They can be found as follows:

• Implementations of the smart meter billing protocols may be found at https://github.com/tblah/project-billing.
• The Secure Channel protocol may be found at https://github.com/tblah/project-net.
• Some cryptographic primitives used in these protocols are implemented at https://github.com/tblah/project-crypto, but most used the widely reviewed implementations in Libsodium through the SodiumOxide language bindings [21]. The integer exponentiation implementation in the GNU Multiple Precision Arithmetic Library GMP was used to implement the commitment scheme.

Standard practice in the development of software for embedded systems is to write in C. Contrary to this, the protocol implementations were written in Rust. Rust [22] is a modern systems programming language which uses compile-time checks to ensure that code is memory safe and so incurs no run-time overhead to prevent memory safety issues. This feature is very important for secure software because a large proportion of software security vulnerabilities (particularly in C programs) occur because of memory safety issues; such as buffer overflow attacks [23]. Also, when Rust software is multithreaded these same compile-time checks help to avoid data race conditions.

The protocols were implemented as software libraries to ease their integration into other projects. For additional consideration of this, see Section 4.3 on the barriers to the integration of this software into a real product.

4.2. Performance Analysis

To compare the performance of both protocols, the compute time of the most expensive operation on the smart meter has been benchmarked on three platforms (

Table 1. Computation Time of Asymmetric Primitives.

Operation	Platform	Average Time Taken (ms)
Commitment	Raspberry Pi B+ (700 MHz BCM2835)	71,000 ± 1000
Commitment	Novena (1.2 GHz Freescale iMX6)	25,790 ± 30
Commitment	Desktop Computer (Intel i5-3570k)	1140 ± 70
Ed25519 Signature	Raspberry Pi B+ (700 MHz BCM2835)	2.2 ± 0.3
Ed25519 Signature	Novena (1.2 GHz Freescale iMX6)	0.67 ± 0.07
Ed25519 Signature	Desktop Computer (Intel i5-3570k)	0.05 ± 0.04

). Additionally, the worst-case transmission sizes are given in

Table 2. Message Size per Protocol Operation.

Protocol	Operation	Type	Worst-Case Size in Implementation (Bytes)	Theoretical Minimum Size (Bytes)
Three-Party	Meter Reading	Local	2490	1048
Three-Party	Change Prices (168 32-bit prices)	Receive from remote	808	688
Three-Party	Send Bill (168 measurements)	Send to remote	211,923	89,232
Simple	Change Prices (168 32-bit prices)	Receive from remote	808	688
Simple	Send Bill	Send to remote	16	16

.

The performance measurements in Table 1 were taken over 6 runs of 50 iterations (300 total). Each run used different cryptographic key material. All computers in the test were running Debian 9 “Stretch” up to date as of 12 August 2017 The benchmark software was compiled using nightly Rust as of the same day. The sizes of input data were matched to those used in the protocols.

The data sizes given in Table 2 do not include the additional overhead added by the secure channel (A3).

Table 3. Required Computations per Protocol Operation.

Protocol	Operation	Required Operations
Three-Party	All Meter Readings in a cycle.	Smart Meter: N Ed25519 signatures. N Pedersen Commitments.
		Customer: N Ed25519 signature verifications.
Three-Party	Change Prices	Utility Provider: 1 Ed25519 signature.
		Customer: 1 Ed25519 signature verification.
Three-Party	Send Bill	Utility Provider: N Ed25519 signature verifications. 1 Pedersen Commitment. Homomorphic combination of N commitments into a bill commitment (N modulo exponentiations and N modulo multiplications).
Simple	Change Prices	Utility Provider: 1 Ed25519 signature.
		Smart Meter: 1 Ed25519 signature verification.
Simple	Send Bill	Smart Meter: 1 Ed25519 signature.
		Utility Provider: 1 Ed25519 signature verification.

breaks down the number and type of cryptographic operations for each protocol stage. In Table 3, N refers to the number of readings in a billing period. For example, using hourly measurements with monthly billing would set N = 744. Note that Pedersen Commitments consist of two modulo exponentiation operations.

As can be seen in Table 3, the Smart Meter needs to perform a Pedersen Commitment for each measurement. The measurements in Table 1 indicate that this could be very costly.

The Utility Provider also must perform a significant number of modular exponentiation operations when verifying that the bill was sent; however Table 1 indicates that such operations are far less costly on desktop and server hardware. Furthermore, modern server computers use multiple processing cores (and sometimes multiple central processing units (CPUs), each with multiple cores), and so several bills could be processed at once. If billing was batch processed, then a single modest server could easily handle thousands of customers.

In summary, these measurements show that very fine-grained billing (on the order of 1 s billing intervals) would only be practical using the simple protocol due to both compute intensity and bandwidth requirements. However, a Raspberry Pi B+ with very limited bandwidth would be more than sufficient for hourly billing periods using either protocol. Performance on a microcontroller would likely be significantly worse than on the Raspberry Pi but may still be sufficient for hourly billing using the three-party protocol. The simple protocol looks unlikely to experience performance issues.

4.3. Barriers to Integration in A Real Product

Many Smart Meters are designed with cheap microcontrollers [24]. These microcontrollers have limited data-processing capability and cannot run general purpose operating systems such as GNU + Linux.

The first problem is the performance of smart meter readings in the three-party protocol. As found in the previous section, this may take too long on some microcontrollers to allow billing to reach the frequency specified by utility providers.

The second problem is that the proof of concept implementations were written for a hosted environment. Depending upon the microcontroller used and software licensing requirements, adapting the proof of concept implementations to work on un-hosted smart meter systems could require substantial work.

Finally, the proof of concept implementations were written for demonstration purposes and so the implementation of the provider’s server in the three-party protocol lacks the tests to ensure that consumption measurements are not being replayed or removed, which were not included because forcing a particular number of commitments to particular hours would have made the demonstration impractical. These tests would not be difficult to add to the three-party protocol implementation.

As shown in Section 3, both protocols meet the requirements in Section 2. The simple signing protocol meets these requirements with acceptable performance when implemented using Ed25519 signatures. The three-party protocol may not achieve sufficient performance to be useful in a real-world application, but less performance-sensitive applications exist for similar blind addition and multiplication proofs; for example, electronic voting. The performance measurements in Section 4.2 make it clear that a three-party protocol has no advantage over the simpler signing protocol within the requirements studied in this paper.

Similar work in [3] concluded more positively about the performance of Pedersen Commitments on smart meters. Firstly, Jawurek et al. used smaller primes. It is the opinion of the author that this is not appropriate for smart meters because they are very costly to replace after they have been deployed and so the useful lifetime of their cryptography should be maximized. Secondly, performance measurements were made on an Intel(R) Core(TM) i5-M540 CPU operating at 2.53 GHz, which is a significantly more powerful processor than those included in modern smart meters.

5. Conclusions and Future Work

5.1. Conclusions

Privacy respecting fine-grained billing is an important problem in smart grids. This paper listed two smart meter billing protocols which solve this problem and analyzed their performance characteristics on a variety of hardware. This analysis found that cryptographic primitives, such as integer exponentiation modulo a prime (which are used in many protocols intended for the smart grid), may take too much time to compute on the microcontrollers used in TPMs for application to high frequency problems, such as very fine-grained billing.

5.2. Future Work

Specific to the problems addressed in this paper, more mathematical work would be useful to search for alternative commitment systems for the three-party protocol to replace Pedersen Commitments with an alternative with better performance on microcontrollers.

More generally, billing is only one proposed usage for smart meters. Another reason for their deployment is the improvements to utility supply forecasting, which their fine-grained measurements could facilitate. Protocols (such as those outlined in this paper) which prevent clear text readings from leaving the home networks of customers will prevent this functionality: if utility providers only learn monthly consumption totals, they will have no more ability to forecast demand than they do currently. One approach would be to combine protocols such as those in this paper with anonymous smart grid protocols.