Abstract
Computers are used in our everyday activities, with high volumes of users accessing provided services. One-factor authentication consisting of a username and a password is the common choice to authenticate users in the web. However, the poor password management practices are exploited by attackers that disclose the users’ credentials, harming both users and vendors. In most of these occasions the user data were stored in clear or were just processed by a cryptographic hash function. Password-hashing techniques are applied to fortify this user-related information. The standardized primitive is currently the PBKDF2 while other widely-used schemes include Bcrypt and Scrypt. The evolution of parallel computing enables several attacks in password-hash cracking. The international cryptographic community conducted the Password Hashing Competition (PHC) to identify new efficient and more secure password-hashing schemes, suitable for widespread adoption. PHC advanced our knowledge of password-hashing. Further analysis efforts revealed security weaknesses and novel schemes were designed afterwards. This paper provides a review of password-hashing schemes until the first quarter of 2017 and a relevant performance evaluation analysis on a common setting in terms of code size, memory consumption, and execution time.
1. Introduction
Attackers exploit the poor password management practises [1,2], exposing high volumes of user-related data [3,4]. Such attack announcements [5] cause considerable economic losses to the software vendor [6]. As the simple use of secure hash functions is not adequate either, specialized password-hashing schemes (PHS) are suggested, such as PBKDF2 [7], Bcrypt [8], and Scrypt [9]. A study in mobile application security (i.e., on iOS and BlackBerry) reveals that most popular applications provide low password protection [10]. The vast majority of them simply hash the user data with SHA2 or MD5 while only a small number of them utilizes PBKDF2.
However, the progress in dedicated hardware devices and parallel computing [11] enables computational feasible cracking [12,13]. Attacks on ASICs, FPGAs, and GPUs are now benefited with a significant boost in disclosing the user information by testing many candidate passwords in parallel. The most common PHS choices of PBKDF2 and Bcrypt offer little protection as they are susceptible in parallel cracking [14,15,16].
Memory-hard PHSs are proposed as a countermeasure against such attacks. In parallel platforms, the memory utilization by the parallel cores is bounded, as all components must gain access to it. In dedicated hardware, the memory resources are considered expensive. The cracker is constrained when a memory-demanding PHS is analysed as the volume of parallel password-guesses is limited. Thus, the legitimate user determines the memory requirements and the hash iterations to deploy secure and robust schemes. Scrypt implements this approach [17], deriving the parallel password scrambling not much faster than performing it on single-core CPUs. Nevertheless, memory-hard PHSs are vulnerable to other types of attacks. A spy process, running on the same device as the PHS, can, in some cases, gather the memory-access pattern by measuring cache-timings [18]. This information enables and greatly speeds up parallel attacks with low memory for each core. As a huge block of memory is allocated to compute the password-hash, it later becomes a “garbage” when the PHS computations are completed. In garbage-collector attacks [19], the attacker obtains the secret data, by collecting the memory content after the PHS termination.
The low variety of available solutions derived, in 2013, to the announcement of the Password Hashing Competition (PHC) [20]. Initially, 24 more secure PHSs were proposed, with an overview presented in [21]. Nine of them were further examined in the next round, in 2014, based on security, simplicity, efficiency, and the extra features that they provided. In 2015, the winner and four other finalists with special recognition were announced based on more precise security analysis and performance evaluation.
The competition advanced our knowledge in password-hashing and enhanced a trend of memory-hard functions, applied by the winner and most of the honourable finalists. After the competition, the inner primitives of the winning design and the most popular finalists were better analysed, revealing some weaknesses. A problem was found in building secure data-independent memory-hard functions [22,23,24,25]. The affected PHC schemes were revisited and addressed the aforementioned issues. A new scheme, called Balloon [24], was also proposed to counter the security issues that arise. The Internet Engineering Task Force (IETF) [26] is now considering the latest version of the winner for formal standardization.
This paper reviews the three mainstream solutions for password-hashing (PBKDF2, Bcrypt, Scrypt), the nine PHC finalists and their latest versions, and the newer Balloon scheme, also providing a relevant benchmark analysis. Implementations of totally 19 PHSs are evaluated on the same platform, with the results being summarized on a unitary table. Section 2 presents the background theory regarding password-hashing, its security perspectives and applications. Section 3 details the three mainstream PHSs. Section 4 analyses the PHC results and the nine finalists. Section 5 discusses the password-hashing status after the PHC and describes the Balloon scheme. Section 6 describes the evaluation process and the methods that are used. Section 7 concludes this work.
2. Background Theory
This section is referred to the background theory of password-hashing, its usage, and application settings.
2.1. Passwords
A password constitutes a user-memorable secret [27] that consists of a few printable characters. Passwords are the common choice in computer systems for user authentication [28,29,30]. The system stores the user’s identity and password for every account. Then, the user logins this data to authenticate himself and access the service [31,32,33].
Another utilization of passwords is the generation of cryptographic keys. The Key-Derivation Functions (KDF) [34] derive one or more cryptographic keys that are based on an input password. Cryptographic keys are applied by encryption/decryption functions and KDFs are mainly utilized for the encryption of session data [35,36].
The ordinary option for user-login services [27] are user-originated secrets of eight characters long (8 bytes based on ASCII encoding). These passwords often exhibit low entropy and are susceptible to attacks. The exhaustive-search method tests all the different character combinations and tries to discover the actual password for an examined account. The attacker, then, accesses the account, similar with its legitimate user. The user-drawn graphical passwords [37,38] may also suffer from low entropy, as they provide 4–5 bytes of security on average [39,40].
The ordinary choice to provide protection against such attacks is key stretching. Cryptographic hash functions [41,42] constitute a security primitive type that parses input of arbitrary size and outcomes a digest of fixed length. In the password-hashing domain, the password is parsed to a hash function which results an output of fixed length, which then acts as the password. Some attacks become computational infeasible as the result is longer than the original secret (e.g., 32 or 64 bytes). The hash function is iterated a few times in order to further fortify the hashed password. Thus, an attack is slowed down by a factor of , where n represents the iterations’ count and m represents the output length in bits. However, the user is also slowed down. The key stretching parameters are bounded by the user’s tolerance to compute a robust hash password.
If many users possess the exact same passphrase, the hash results will be the same too. When one of these passwords is exposed, the credentials of all users might be disclosed. Similarly, as one user can apply the same secret in many accounts or use the same login platform (i.e., the Facebook social login platform) for many applications [43], the disclosure of one of these accounts raises concerns about the security of the rest involving services. Thus, a salt parameter is utilized (a small value, usually consisting of 8 random bytes). During the creation of a new account, a random salt is generated which is concatenated with the passphrase during hashing. The same secret produces different hashes for different accounts and the correlation of simple hashed passwords that are generated by the same passphrase is prevented. Ordinary, the salt is kept along with the hashed secret, in plaintext. The authentication operation parses the salt and the password of a login procedure, and compares the result with the stored password hash value to validate the user. Figure 1 illustrates this basic PHS setting.

Figure 1.
PHS generic scheme.
As the user-related information is kept as the service end, the provider might wish to upgrade the security level (i.e., increase the hash size or the iterations of the PHS). Client-independent update (CIU) of the hash password increases the security of the stored information without any knowledge regarding the passphrase or the user’s involvement. CIU permits the seamless operation of the service and retains the user’s convenience, becoming an imperative property of future PHSs.
The server load can become unmanageable in popular applications with high volume of users that gain access simultaneously. The total effort can be balanced by server relief (SR) techniques that are performed between clients and servers. Part of the password-hashing computations are performed by the clients (e.g., the first hashing iterations) while the final steps and the user verification are performed by the server.
2.2. PHS Security and Threat Model
Implementing a secure PHS is not a trivial task. There are several security issues that must be considered during the designing phase.
First of all, the PHS must be cryptographically secure and offer the security properties of:
- Preimage resistance,
- Second preimage resistance, and
- Collision resistance
Additionally, the scheme should avoid other cryptographic weaknesses such as those present in (some) Merkle-Damgard constructions, like length extension attacks and partial message collisions.
Except for these cryptographic features, the scheme must defend against time-memory trade-off (TMTO) and lookup table attacks [44]. Mechanisms should be embodied that would render it computational infeasible to perform precomputed lookup table generation, like rainbow tables.
Defense against CPU-optimized crackers is also vital. A robust PHS should be CPU-hard and require significant amounts of CPU processing, in such a way that it cannot be optimized away through either software or hardware. For example, multi-core CPU optimized cracking should offer minimal speed-up benefits to the attacker in contrast to those intended for validation by the legitimate user.
Similar considerations should be taken into account regarding hardware-optimized crackers. The PHS must be memory-hard and require significant amounts of RAM in order to be infeasible to get overcome by TMTO attacks. Thus, optimized cracking on GPU, FPGA, and ASIC should not benefit the attacker against the legitimate validation of the targeted application.
Typically, attackers test high volumes of candidate passwords simultaneously, which is costly when huge amounts of CPU and memory are required for each try. On the other hand, an ordinary application processes only one password and the PHS consumption is configured based on the service’s resources.
However, memory-demanding hashing can enable side-channel attacks, if the attacker can gain access to the memory of the targeted device. Cache-timing attacks are commonly used to exploit Scrypt [18]. Garbage-collector attacks [19] constitute an instance of a memory leak, relevant to PHS security. In the main attack case, the adversary gains access to the device’s memory after the termination of the PHS while in the case of weak garbage-collector attacks the secret (or a value that is produced from it based on an efficient function) is maintained in the memory and is not overwritten for a significant time-gap during the running time of the PHS. If the scheme is vulnerable to garbage-collector attacks, it is likely to significantly reduce the effort of password cracking.
The PHC further highlighted the next design questions:
- Input-dependent, input-independent, or hybrid memory addressing? In input-dependent indexing the timing information enables very fast password-searching and can be exploited by side-channel attacks. On the other hand, in input-independent indexing the read addresses in memory are known beforehand, deriving the time-space tradeoff attacks quite straightforward as the cracker can precompute the missing block when it is needed.
- Is it better to fortify the result by passing over the memory more times, or fill higher amounts of memory and being vulnerable to time-space tradeoffs? As there were no general tradeoff tools to analyze the two defence strategies against these vulnerabilities or unified metrics that could estimate the cost for an attacker, it was difficult to give a concrete answer.
- Which are the proper strategies to compute the input-independent addresses? Different approaches that were considered secure were eventually found vulnerable to attacks.
- What is the proper size for a single block of memory? The spacial locality of modern cache memories makes slower, in terms of cycles per byte, the reading of small and randomly-placed blocks. On the other hand, the small amount of available long registers derives inefficient the processing of larger blocks.
- Which are the features of the proper internal compression function when large blocks are used? Can lightweight functions that implement simple mixing being used or do we need cryptographically secure functions? Several of the candidate schemes simply adopted iterative constructions, contributing against the appliance of cryptographically secure compression functions.
- When multiple CPU cores are available, which is the proper strategy to utilize them? Parallel hash function invocations without any interaction can be exploited by simple tradeoff attacks.
2.3. Applications
PHSs and KDFs can be applied in general purpose services on mainstream systems, web services, and embedded applications. The different domains exhibit diverse properties that a PHS must conformed to.
General purpose services process low volumes of infrequent login requests. The involved devices (e.g., PCs) possess adequate computational resources, and the highest protection level becomes their main target. The PHS and KDF primitives are important and the security is enhanced by tools that detect widely-used passphrases or low-entropy secrets [45,46].
On the other hand, web services must be able to process thousands of login requests simultaneously. The authentication information for all these users is stored in the server, which must serve high volumes of parallel sessions. Successful attacks at the server-end disclose mounts of data for many clients, including the passphrases. The typical user possesses a small number of low-entropy secrets which are used in many web services [47,48]. Online dictionary attacks with login histories are also applicable here [49]. Thus, security issues arise not only for the vulnerable applications but for other services as well which are used by exposed clients. This fact was a main concern for PHC and rendered password-hashing as a main goal for web services. A service provider can further enhance security against analysis of stolen data by applying CIU methods in order to periodically fortify the protection level based on the attackers’ increasing computational capabilities and the technology evolution. Nevertheless, the overall login procedure must be retained fast enough to conform to the user’s tolerance and the communication protocol timings. The total computational requirements of processing a single login request have to permit the uninterrupted service of many users while avoiding DoS attacks. This balance among security and performance can be contributed by SR procedures that establish a good tradeoff between the server and the clients.
Embedded systems are deployed in a wide variety of applications including Internet-of-Things setting and cyber-physical systems [50,51,52,53,54]. The installed devices are resource-constrained in nature, leading to lightweight implementations with small size and low production cost [55,56,57,58,59,60]. The security becomes a prominent part of the whole functionality [61]. Defence mechanisms should provide lightweight designs with low demands on memory and processing. Sensors or other ultra-constrained devices [62,63,64,65] can grant only a few bytes or KBs of memory to achieve a moderate security level [66,67]. In contrast to web services, embedded devices ordinary store a limited volume of authentication-related data. Session key-derivation is important, as the most common interaction includes device-to-device short-term communication (e.g., in wireless sensor networks) [68,69,70]. Real-time specification checking and built-in memory safety methods [71,72,73,74] are responsible for protecting the embedded applications against garbage-collector attacks [19].
3. Mainstream Password-Hashing Schemes
The ordinary choice for implementing password protection are hash-based schemes. Keyed-hash message authentication codes (HMACs) and cryptographic hash functions that process the password and produce one or more secret keys, constitute the main mean to materialize KDFs. The current solutions of PHSs and KDFs for mainstream applications include PBKDF2, Bcrypt, and Scrypt.
3.1. PBKDF2
Password-Based Key Derivation Function 2 (PBKDF2) [7] is the only standardized scheme (RSA Laboratories’ Public-Key Cryptography Standards (PKCS) series (PKCS #5 v2.0) [75] and the RFC 2898 [76]). TrueCrypt, OpenOffice, and CCMP of WPA2 embody the scheme for password-related operations. PBKDF2 uses pseudo-random functions (PRF), commonly implemented by HMACs. The ordinary internal hash option for the HMAC is the function SHA-256 [77]. The password and the salt are parsed as inputs to the scheme. The salt hardens attacks with precomputed data, like dictionary (test hundreds of likely possibilities to figure out the passphrase) [18] or rainbow-table attacks (capability of utilizing tables with precomputed hashes) [19,78]. Its typical size is 8 bytes.
At first, the HMAC processes the password and the salt. Then, the data is processed several times to produce the derived key. The recommended minimum number of iterations is 1000, but, as the standard was established in 2000, it is not considered adequate today. In each iteration, the HMAC parses the password and the last HMAC result. Then, the HMAC results are XORed. The outcome of the XOR operation in the last round is the final hash. Figure 2 illustrates the PBKDF2 PHS.
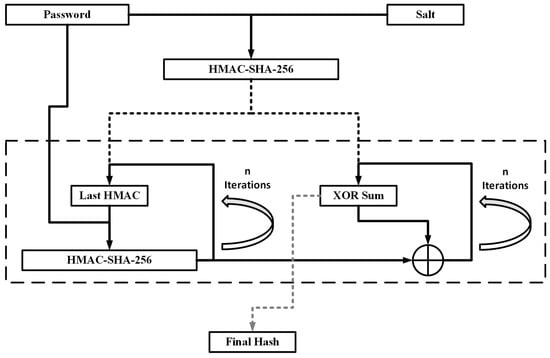
Figure 2.
PBKDF2 PHS with n iterations.
One drawback is the efficient hardware-based cracking, as it can be developed as a compact hardware implementation with low requirements in RAM. Thus, cheap brute-force attacks are feasible on GPUs, FPGAs, and ASICs. GPU and FPGA attacks are presented in [14]. The fastest attacks can find out around the 65% of ordinary passphrases in about one week. Attacks on multi-FPGA systems crack about 245,000 passwords per second [15].
3.2. Bcrypt
Bcrypt [8] is adopted by the BSD operating system as the default PHS. It utilizes the Blowfish [79] block cipher and, by default, is parses 56 bytes long passwords and results 24 bytes long hashes. The number of iterations is a power of 2, which raises as the attacker’s computational power is increased to provide sufficient protection against brute-force attacks. A salt value of 16 bytes harden attacks that are based on rainbow-tables.
At first, the expensive Blowfish key schedule (EksBlowfishSetup) is initialized by a cost parameter, the salt and the Blowfish encryption key. This function stores into the cipher’s S-boxes and subkeys the number. Totally, 18 subkeys are used which are derived, based on the encryption key. The permutation-array (P-array) stores all these subkeys and are XORed with the encryption key. The first element of the P-array () are XORed with the relevant 32 bits of the encryption key, the next P-array element () is XORed with the next 32 bits of the key, and so forth. The key is utilized in cyclic manner, when all its bits have been used, and restarts using bits from the initial position. The current state of key-scheduling encrypts the 64 initial bits of the salt. The subkeys and are then substituted by the encryption result, which is then XORed with next 64-bits of the salt. The outcome is further encrypted with the new key-scheduling state and the ciphertext substitutes the subkeys and . The result is again XORed with the initial salt bits and the next encryption result substituting the subkeys and . The salt is also processed in a cyclic manner and this procedure continues until all P-array entries have been substituted. Then, it proceeds in substituting the entries of the S-box in a similar approach. The process outputs the new key schedule when the two last entries ( and ) of the last S-box are substituted. This expansion operation is repeated times. In each iteration the aforementioned process is performed two times, expanding blocks of zeros and the internal state by the salt and the key respectively.
Then, a magic value, 24 bytes long, is encrypted 64 times by the cipher in ECB mode of operation (BlowfishEncryptECB). Blowfish’s encryption is a Feistel network of 16-rounds and uses large key-dependent S-boxes. The concatenation of the salt, the cost, and the result of the encryption constitutes the final outcome. Figure 3 illustrates the Bcrypt PHS.
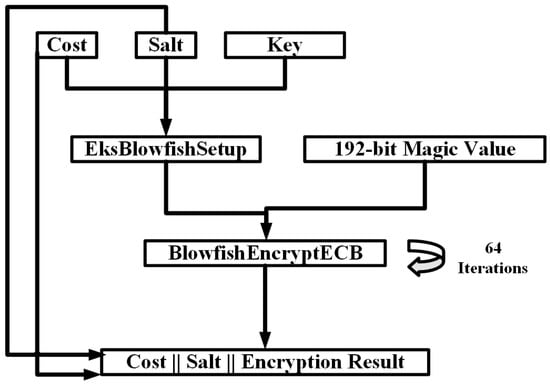
Figure 3.
Bcrypt PHS.
The scheme consumes 4KB of RAM and is slightly better in countering parallel cracking [9] than PBKDF2. Nevertheless, the low memory consumption enables efficient FPGA attacks. In [16], several energy-efficient and low-cost cracking settings are presented. The cheapest attack achieves 1207 cracks per second with 99$ cost while the best attack finds out 20,583 passwords per second.
3.3. Scrypt
IETF examined, in 2012, the Scrypt [9] as an Internet Draft, announcing an informational RFC [80]. The scheme processes an arbitrarily large volume of memory and forms a memory-hard PHS. As main internal components, Scrypt uses the stream cipher Salsa [81] and the PBKDF2. Other building blocks of the scheme include the ROMix, BlockMix, SMix, and MFcrypt functions. ROMix computes a large number of random values, and then, accesses them randomly in order to ensure that they are all stored in RAM. In order to implement a memory-hard ROMix a hash function must be internally utilized that satisfies some design criteria, like uniform distribution of output values, difficulty in iterating the hash function quickly and no significant internal parallelism. BlockMix utilizes the version Salsa20/8 of the cipher to build this functionality and it is embodied by the ROMix functions of Scrypt. The SMix is composed of one or several ROMix functions and forms the mixing function of Scrypt. The number of ROMix functions, called parallelization parameters – p, represents the time and space costs. MFcrypt is the key-derivation function of the scheme. It applies the mixing function SMix and the PBKDF2 with an HMAC that uses the SHA-256 hash function. Figure 4 illustrates the internal software components of Scrypt.
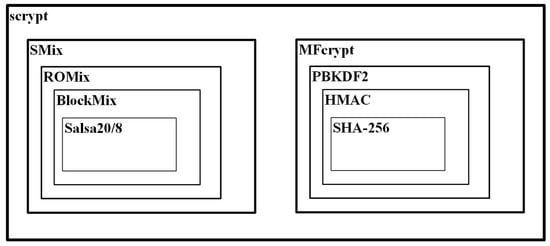
Figure 4.
Scrypt software components.
At first, MFcrypt parses the password and the salt. Then, the output is stored in the array B and is mixed by the SMix. Each ROMix of the SMix processes a relevant block of B. The ROMix’s data is parsed to the BlockMix and the Salsa cipher. The result all ROMixs along with the password are processed by the MFcrypt, which produces the final hash. Figure 5 illustrates the Scrypt PHS.
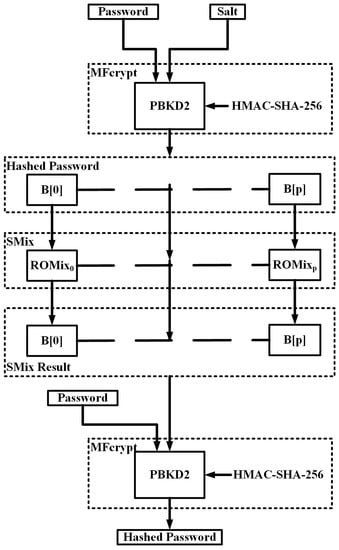
Figure 5.
Scrypt PHS.
In comparison with PBKDF2 and Bcrypt, Scrypt is the most resistant KDF to memory-related vulnerabilities. Brute-force attacks on hardware platforms require 4000 and 20,000 times higher cost than in Bcrypt and PBKDF2 respectively [9].
Attacks on GPUs are reported in [17]. When Scrypt takes about 1–10 ms to compute a legitimate password, the cracking attack discloses 42,650–2333 hashes per second (H/s) respectively. For higher computation settings, requiring 100–1000 ms, the attack’s effectiveness is greatly decreased to 49.06–0.37 H/s. However, DoS attacks on servers can exploit the demands for high memory consumption while handling frequent authentication requests. Scrypt is also vulnerable to garbage-collector [19] and cache-timing [18] attacks.
4. The Password Hashing Competition
The Password Hashing Competition (PHC) [20] evaluated 24 novel schemes [82] based on security, flexibility, and performance. PHC advanced our knowledge in implementing efficient and secure password-hashing. Nine schemes pass successfully the evaluation process of the first round.
All submissions are publicly available with no patent constraints. For input, they require at least:
- Passwords of any size between 0 and 128 bytes, regardless of the encoding
- Salt values of 16 bytes
- Output length of 32 bytes
- One or more cost parameters to configure time (t_cost) and/or memory demands (m_cost)
The schemes were assessed based on security, simplicity, and provided functionality.
4.1. Evaluation Criteria
The main security features that are now indispensable for a state-of-the-art PHS include collision resistance, immunity to length extension, and random-looking output [20]. The candidate scheme must limit the attacker’s benefit from optimized parallel cracking deployments (e.g., FPGA, ASIC, GPUs, or multi-core CPUs), and counter the current set of password-hashing analysis and attacks e.g., time-memory tradeoffs and cryptanalytic attacks). It also must be resilient to side-channel attacks (i.e., leakages and timing attacks) and the attacker must not be able to deduce any information about the password’s length. The attacker model where a server is partially or fully compromised must be taken into account.
Regarding the design aspects, a new algorithm must be sound and easy to understand and examined (e.g., symmetric and modular) in order to ease the security analysis and, therefore, enhance the acceptability of the scheme. The PHC should be simple to implement, integrate in current applications, test, and debug. While novel and original candidates are desirable, the utilization of components from known primitives can be also applied in a limited degree. Documentation for the algorithm and the software implementation should be sufficient and of good quality.
Despite the main password-hashing operation, a candidate should function as a robust KDF, with CIU and SR also being considered important. The interactivity of the cost parameters for memory and time must be effective enough, while an attacker must not be able to surpass the anticipated benefits. Application-specific designs are also evaluated (e.g., client login, web authentication, embedded systems, or key-derivation).
4.2. Finalists
The nine candidates that were finally selected among the first 24 schemes are: Argon [83]/ Argon2 [84], Battcrypt [85], Catena [19,86], Lyra2 [87], MAKWA [88], Parallel [89], POMELO [90], Pufferfish [91], and Yescrypt [92]. Except from MAKWA and Parallel, all other finalists constitute memory-hard PHSs. The finalists exhibit high diversity, which is beneficial as the different PHSs cover a wide range of application settings (e.g., web services, KDF). Argon2 was the final winner. Special recognition was given for four other finalists (Catena, Lyra2, MAKWA, Yescrypt). Catena follows an agile framework approach and is resistant to side-channel attacks. Lyra2 has an elegant sponge-based design and constitutes an alternative approach to side-channel protection. MAKWA presents unique delegation features and factoring-based security. Yescrypt offers a rich feature set and can easily replace Scrypt to existing systems. Battcrypt, Parallel, POMELO, and Pufferfish attract less attention for the final selection process.
4.2.1. Argon/Argon2
Optimized for security, efficiency, and clarity, Argon is a safe and memory-hard hash function. It operates as PHS, KDF, and for any other memory-demanding operation. A significant penalty is imposed on the execution time for any decrease of the available memory by the attacker, safeguarding against tradeoff vulnerabilities. A reduced version of the AES [93] block cipher’s round function with 5 iterations and a fixed-size key of 128-bit is used by Argon along with block permutation and XORs. A t-byte permutation is applied, with the efficiency being linear to the time and memory costs. Argon implements CIU and SR at the server.
The version Argon2 won the competition. It summarized the latest features for the memory-hard designing of password-hashing functions. The original Argon could impose computational penalties on any memory-reducing configuration and was recommended for the highest tradeoff resilience and guaranteed prohibitive time. Argon2 was proposed for high performance and easy scale to arbitrary number of parallel computing units.
Argon2’s design is simple and streamlined, aiming the efficient operation of multiple computing units and the highest rate of memory filling, while countering tradeoff attacks. Two variants are proposed which can fill in a fraction of second around 1 GB of RAM. Argon2d is faster with data-dependent memory indexing. It is appropriate for cryptocurrencies or environments where side-channel timing are not applicable. In Argon2i the memory is parsed more times to enhance resilience to tradeoff attacks, thus, this version is slower than Argon2d. The memory addressing is data-independent, which makes Argon2i more preferable for PHS and KDF operations. Security analysis is detailed in [84,94].
Initially, the password and the salt are hashed, along with other parameters. The memory is organized as a two-dimensional array, referred to as B. The size is determined by a cost parameter, called parallelism degree p, where the rows are equal with p and columns are the total number of memory blocks divided by p. The columns are then divided over 4 slices to enable block computation parallelism. The memory array is filled with a compression function, which takes as input an indexing function. For Argon2i, the indexing is password and salt independent while for Argon2d the indexing is password-dependent. A third hybrid variant of Argon2id [84] is also proposed that combines the two approaches with some indexing being performed by data-dependent functions and the rest indexing being performed by data-independent functions. The compression function utilizes the hash function’s internal permutation process. Segments of the same slice can be computed in parallel. The operation iterates for a variable number of passes. After the final iteration, the memory elements of the last column are XORed. The result is hashed to obtain the final outcome. Figure 6 illustrates the Argon2 PHS for a single pass.
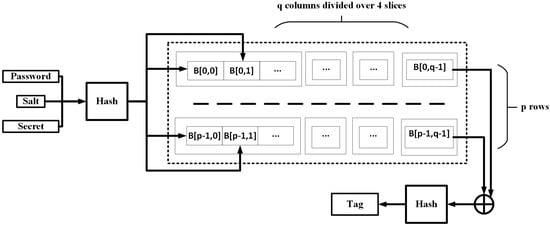
Figure 6.
Argon2 PHS for a single pass.
For the reference implementation, Blake2b [95] is chosen as the hash function and its variant BlaMka [87] as the compression function. BlaMka’s suitability for the password-hashing domain was highlighted during the PHC and it was introduced by Lyra2. Argon2 can use up to threads in parallel.
However, after further analysis, the winning version of PHC was found vulnerable to practical attacks when low-cost parameters were applied [22,23,24,25]. The memory blocks that were produced by Argon2i after the second pass were replacing the blocks of formerly rounds instead of overwriting them. Thus, a time gap elapsed between the last time that a block was used and the moment that it was overwritten. The attacker could compute, with no increment in computational time, the single-pass Argon2i and save more than a factor of four in space.
The scheme was revisited and effectively countered the attack. The overwriting operation was replaced with XOR, which produced a low performance overhead. This strategy was applied only to the vulnerable single-pass Argon2i. The remaining versions, where multiple passes process the data, were secure as the blocks are maintained in memory until the overwriting operation. The current 1.3 version is considered for standardization under IETF [26].
4.2.2. Battcrypt
Battcrypt (Blowfish All The Things) targets server-side services and constitutes a simplified version of Scrypt. For password-hashing, the Blowfish block cipher and the SHA-512 hash function are utilized. The CBC mode of operation of Blowfish is applied as it is slow on GPUs, is well-studied, and is implemented in PHP. Battcrypt’s security is retained even if Blowfish is found vulnerable to attacks.
The plain passwords are used only once. At first, the password and the salt are hashed two times by the SHA-512. The result is called key. The key is utilized for the initialization of the Blowfish cipher and the data. The memory is initialized by encrypting the data with the Blowfish in CBC mode. Then, Blowfish overwrites times the internal state, based on indices that re password-dependent. The result along with the key are hashed two times, producing the final hash.
The m_cost parameter configures the memory consumption and the t_cost parameter determines the processing time. The approach is suitable for web applications with small memory amounts being processed at each hash upgrade. The scheme is slower on GPUs than on CPUs. Battcrypt can parallelize on CPU two or three calculations of the underlying block cipher that could approximately double the speed. It can also implements SR and CIU, if the configuration parameters (i.e., t_cost, m_cost, output size) and the salt are publicly available.
The scheme is more efficient than Bcrypt as it executes around 0.752% to 1.726% less Blowfish blocks [85]. Under the same PHP environment, it performs two times more processing work than Bcrypt [85].
However, Battcrypt was found vulnerable to weak garbage-collector attacks when an attacker had access to the target machine memory (the secret is maintained in internal memory and is not overwritten) [96]. The key value is used in three phases for initializing the Blowfish, initializing the internal state, and the production of the final hash, where it is overwritten for the first time. The main effort of Battcrypt is given in the processing phase. The time-window of one iteration of the outer loop last long enough for an adversary with known salt to launch an attack.
4.2.3. Catena
Catena targets multiple application settings, like multi-core CPUs, embedded systems, and user-database backup. The design is a composed cryptographic operation that utilizes a cryptographic hash function, and the algorithm is easy to understand and simple to understand. The scheme is instantiated by a cryptographic hash function and implements the graph-based structure -Bit-Reversal Graph (BRG), where represents the number of stacks of the inner structure (t_cost), the garlic g is the memory cost (m_cost), and . Figure 7, illustrates the Catena’s BRG component, where are the graph’s edges.
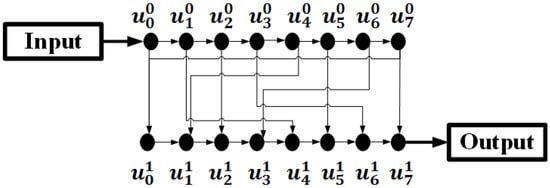
Figure 7.
An (8, 1) Bit-Reversal Graph.
The version of Catena v3 was submitted for the final evaluation. State-of-the-art results regarding memory-hard PHS were embodied for the memory-initialization process and the internal functions for memory-hard processing, randomization, and compression. The new version introduced two instantiations with different memory-hard functions. Catena-Dragonfly was based on BRG and Catena-Butterfly utilizes a stack of -Double-Butterfly Graphs (DBG). Catena-Dragonfly overwrites the internal memory times at minimum and Catena-Butterfly makes at minimum passes.
The defender can choose any strong hash function to initiate the PHS. A reduced round variant of Blake2b, called Blake2b-1 [19], is proposed as the underlying hash function.
Thorough security analysis is provided with proofs, with the reference submission being well-documented. The pebble-game approach [19] is used for to examine time-memory tradeoffs. The offered security properties include indistinguishability from random, resilience to side-channel attacks, lower bounds on the time-memory tradeoffs, and preimage security. Password scrambling on ASICs, FPGAs, and GPUs is penalized with high computational demands. Theoretic effective attacks under realistic parameters on the data-independent memory-hard primitives are presented in [23].
It implements CIU by raising the m_cost and t_cost values. For the SR functionality, the client computes most of the processing, with the server performing the last iteration. Catena also operates as a keyed password-hashing module by XORing the result of the unkeyed version with the hash of the the cryptographic key, the user ID, and the m_cost.
4.2.4. Lyra2
Lyra2, the updated version of Lyra, uses the new trend of hash functions with sponge structure. The Blake2b and BlaMka hash functions were selected for the reference implementation in a duplex sponge structure. The software implementation is simple and strictly sequential to prevent parallel attacks.
The internal state consists of a large matrix, called M, that is maintained in RAM during the processing phase. The m_cost parameter determines the matrix’s size by defining the number of rows R and columns C. Moreover, the optional parameter basil is applied as an extra salt and prevents collisions of ordinary salt and password combinations.
At setup, the memory matrix is initialized. The state S of the sponge hash function is initialized by absorbing the salt and the password. Then, the hash function fills the matrix’s rows by squeezing and duplexing the contents of the previous rows. Starting from the last element of each row, the function parses the context of the current element and the element of the opposite position in the next row. Figure 8, illustrates the memory read and write operations during setup.
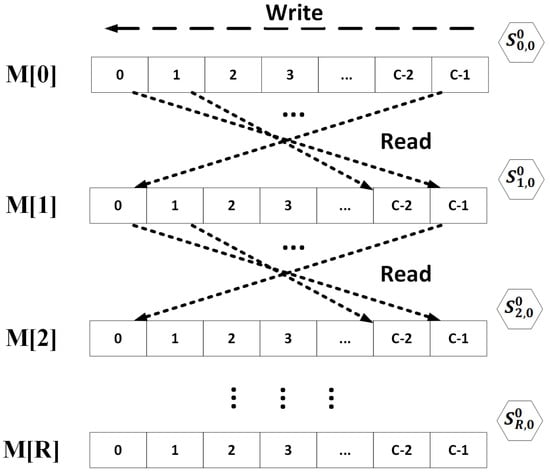
Figure 8.
Lyra2 setup phase.
A time consuming procedure, called wandering phase, overwrites memory data. The t_cost parameter determines the volume of matrix elements that are overwritten. Each half of the matrix visitation loop increases depth by one. An inverted tree-like dependence graph is constructed during the execution process. The hash function absorbs the last column that is visited and squeezes the final hash.
Thorough analysis is presented in the reference submission. The scheme tries to maintain the internal state in RAM during processing, prevent parallel attacks, and make non-invertible the key that is derived.
The performance is improved when the memory matrix is stored in the volatile memory. Lyra2 is an alternative version that enables the multi-core processing for the defender, increasing the attacker’s cost. Security analysis for Lyra2 is also provided [87].
4.2.5. MAKWA
MAKWA applies modular squaring to implement PHS and KDF functionality. The algorithm operates on big numbers, like the asymmetric cipher RSA [97]. Nonetheless, when a trusted entity knows the factors of the modulus, MAKWA does not need to compute the prime factors, avoiding the computational demanding processing. The scheme uses the NIST standardized HMAC_DRBG with SHA-256 [98] as a deterministic KDF. The memory consumption level is fixed, with the cost parameters affecting only the processing time. MAKWA’s strength is derived by a high number of squarings modulo a composite integer n. The password is processed two times during the initialization phase of the scheme’s state, which is further processed in the work phase by squarings modulo n. Figure 9 illustrates the MAKWA PHS.
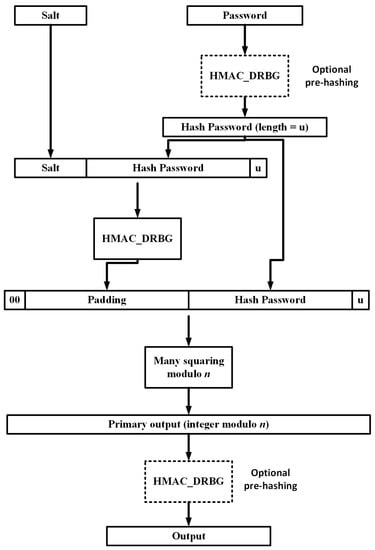
Figure 9.
MAKWA PHS.
Delegation is one of the main operations of MAKWA and is based on the private key procedure of RSA and the blind signatures. The SR functionality implements this feature, offloading the bulk of processing cost to an external untrusted entity. Other operations that are supported by MAKWA include password escrow and offline hash upgrade.
The security claims of MAKWA are based on the relevant analysis on RSA regarding the feasibility of launching attacks on ASICs, FPGAs, and CPUs. The scheme accomplishes the design goals and is resilient to these attacks. Optimization results on GPU and CPU are reported in [99].
4.2.6. Parallel
Parallel password based key derivation function (PPBKDF) is proposed for low-memory setting. It is optimized for parallel execution and is not a memory-hard scheme. The design is compact with constant and low memory requirements. Parallel has a simple design and remains as collision resistant as the internal hash function. The reference submission uses the SHA-512 and offers CIU and SR.
The password and the salt are hashed twice, producing a key parameter. For each sequential round, the working memory is initialized with zeros. Then, it is processed by data-independent rounds which can be executed in parallel. In each iteration the data is hashed with the two loop counters and the key. At the end of each sequential round the key is updated by double hashing the key and the working memory, and is truncated for the next round. When all rounds are finished the key is further truncated, producing the final hash. Figure 10 illustrates the Parallel PHS.
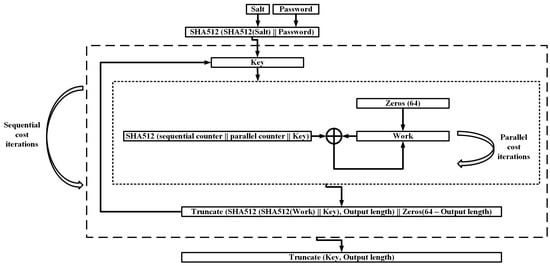
Figure 10.
Parallel PHS.
The attacker-defender ratio (password scrambling results on parallel cores to relevant results on a single core) is considered 1 with any benefits for the attacker, benefiting the defender too. However, the key value is not overwritten at the processing procedure and Parallel is found vulnerable to weak garbage-collector attacks when the attacker has access to the target machine memory [96].
4.2.7. POMELO
POMELO’s design is simple and the implementation is easy. POMELO functions on 8-byte words and utilizes three state update functions , , and , where S is the internal state and i and j are the memory access indices. H constitutes a simple non-linear feedback function, with F, and G implementing simple random memory access over data. The three functions safeguard the scheme against single instruction multiple data (SIMD), low memory, and preimage exploits. The t_cost value configures the computational complexity and the m_cost parameter adjusts the memory size. The password is used only during the initialization of the internal state and is overwritten times on average, countering garbage-collector attacks. The scheme remains efficient even when a significant amount of memory is reserved and retains security against cracking by GPUs or dedicated hardware. Also, the deployment of CIU is straightforward.
However, POMELO produces lower randomness properties. The H function implements random-memory indexing that is based on the password, which enables cache-time attacks [96]. As a result it does not function as a KDF. This main disadvantage restricts its selection once compared with the rest schemes. POMELO 2 [90] enhances randomness and enables the implementation of a secure POMELO-KDF. It derives keys of arbitrary length from a password and a salt by iterating POMELO.
4.2.8. Pufferfish
Pufferfish is built upon is inspired by Bcrypt and uses HMAC-SHA-512 and Blowfish. The extended version of the cipher is utilized which operates on 8-byte words and uses password-dependent and dynamic S-boxes of arbitrary size. This extension is embodied on Bcrypt with minimum changes in the scheme. Pufferfish also implements KDF and SR functionality and offers variable-length output.
At the generation phase of the password-hash, the main processing memory is a two-dimensional array of elements of 512-bits long that is accessed in a regular basis. The password is hashed at the beginning and the result is overwritten times. Moreover, the state word that contains the password hash is overwritten times, providing protection against garbage-collector adversaries. The m_cost value raises the memory consumption by KB while the t_cost value raises the complexity by iterations.
In comparison with Bcrypt, the scheme is faster on CPUs and slower in GPUs. Moreover, Pufferfish inherits the GPU resistance of Bcrypt.
The security features of the extended cipher version have not been validated. Nevertheless, Pufferfish remains secure as long as HMAC and SHA-512 remain unbroken.
4.2.9. Yescrypt
Yescrypt resembles Scrypt, improving the protection level. It operates as KDF and offers CIU and SR. The scheme provides more choices for parallel programming at instruction and thread level. The reference implementation supports OpenMP [100] and applies SIMD. Yescrypt extends the ROMix algorithm by using the Scrypt’s random-read lookup table (RAM) that writes the memory elements in a sequential manner, along with an optional read-only lookup table (ROM) that is pre-filled. For processing, the scheme can use a custom pwx-form algorithm instead of the Salsa20/8 in Scrypt or even inter-mix these two components.
The processing time can be raised without increasing the memory consumption. The security analysis resembles the relevant results on the underlying components of PBKDF2, HMAC, and SHA-256, like in Scrypt. The scheme fortifies protection against attacks on ASICs, FPGAs, and GPUs.
Security analysis is reported in [92,96]. When the attacker can gain access to the system’s memory, Yescrypt is vulnerable to weak and mainstream garbage-collector attacks under specific input parameters [96].
The overall functionality is managed via bit flags. When no flag is specified, the mode of operation is compatible with Scrypt and the scheme is vulnerable to the relevant attacks. The flag YESCRYPT_RW changes the memory management strategy from write once, read many to read-write, and overwrites, at least partially, the lookup table in RAM using random-memory accesses. Thus, the scheme may be vulnerable to garbage-collector attacks if the whole memory is not overwritten. The flag YESCRYPT_WORM enhances the Scrypt compatibility mode by enabling pre- and post-hashing. A minimal version of the scheme is called before the full Yescrypt and if the setted parameters (the ratio of memory size and the number of threats running in parallel) overwrite the password significantly fast, the scheme is resistant against garbage-collector attacks.
5. The Day after the PHC
This section discusses the status of the password-hashing domain after the PHC. The security level is improved and the danger of parallel cracking attacks is reduced. However, security analysis reveals several weaknesses. The PHC finalists are revisited and a new scheme is also proposed.
5.1. Resistance to Parallel Cracking Attacks
As aforementioned in the introductory sections above, dedicated hardware devices enable efficient password-cracking attacks, deriving the common solutions insecure. PHC tended to counter these issues. All finalists harden attacks on dedicated hardware by design.
Table A1 summarizes the GPU measurements of several password-hashing schemes that are referred in the literature. Efficient attacks on simple hashing schemes, like the ones that utilize only SHA1, SHA2, SHA3 or HMAC, can achieve 794–113 MH/s. The standardized scheme PBKDF2 increases security with 424–219 KH/s and Bcrypt reduces further the attack rate to 2.8 KH/s.
When the memory-hard Scrypt is applied with sufficient memory consumption, the parallel attack can be limited to 0.37 H/s. The winner Argon2 can achieve up to 0.04 H/s while Lyra2, which is one of the most efficient memory-hard finalists, reduces the guessing time of parallel GPU attacks to 0.0018 H/s.
As is evident, the memory-hard schemes can drastically slow down attackers and the PHC proposals can provide even higher security. Similar results can be found for other platforms that enable parallel cracking, like FPGAs and ASICs [14,15,16].
5.2. Acceptability and Security Issues
After the completion of the PHC and the announcement of the winner, Argon2 attracted all the attention as the state-of-the-art scheme for password-hashing. Several designers started developing the scheme in different programming languages and platforms, such as C++/C#, Java, Ruby, Python, and Nodejs. Most implementations were offered through cryptographic libraries [101] or are provided by password management tools [46].
On the other hand, the rest PHC schemes sank into oblivion and, in most cases, no implementations were further developed except from the competition’s reference ones. Among them, only Lyra2 was implemented in Nodejs [102] and Catena was deployed on embedded systems with constrain computational capabilities [103].
Meanwhile, Argon2 was submitted for standardization to IETF and further security analysis were conducted [26]. The results soon revealed weaknesses on the winner that enabled practical attacks, especially for the Argon2i variant [22,23,24,25]. Some of these studies concerned the designing of secure memory-hard functions and the results may also effected some of the other finalists, like Catena [23].
Thus, a newer scheme, named Balloon, was proposed that offered the proper resistance to these attacks [24]. The scheme is detailed in the subsection below.
The fact that Argon2 has been revisited several times since its selection, concerns about its early adaptation. As aforementioned, the scheme was revisited and enhanced protection, overcoming the Balloon security [25]. Thus, Argon2 is still considered the state-of-the-art scheme since it overcame the security issues, as it is mentioned in the subsection below.
5.3. Balloon PHS
Balloon is a data-independent memory-hard PHS that provides higher security than the first version of Argon2i. Balloon is based on random sandwich graphs [22,104]. The t_cost parameter determines the number of rounds of computation and can be increased to enhance security without affecting the memory requirements. The m_cost parameter indicates the number of fixed-sized blocks of the hash function’s working space, as in Scrypt.
Balloon utilizes a standard cryptographic hash function, like Blake2b or BlaMka, as a subroutine. The working space is a large memory buffer divided into contiguous fixed-sized blocks (same size with the hash function output). The scheme operates in three steps. At first, the memory is filled up with pseudo-random bytes that are generated by repeatedly invoking the hash function over the password and the salt. In the second step, a mixing operation is performed t_cost times over the pseudo-random bytes in memory. The m_cost represents the total size of the buffer in memory. The content of a block i is the hash result of the block (i-1) mod m_cost. In the third step, the last block of the buffer is extracted, representing the final hash result.
The scheme is easy to implement. It is efficient and matches or outperforms the fastest relevant PHC schemes, like Argon2i and Catena, when the same hash function is utilized.
Balloon can provide second-preimage and collision resistance in a straightforward manner. The analysis in [25] shows that the latest version of Argon2 significantly upgrades security and provides better resistance to the attack than Balloon.
6. Materials and Methods
In this section, the examined PHS are evaluated based on the general functionality that they offer and a common test-bed suite. The most appropriate of them are proposed for different application settings.
6.1. General Features
The general properties and the main features of the examined PHSs are analysed in this subsection. Table A2 (see Appendix B) sums up the attributes of the three mainstream PHSs, the nine PHC finalists, and Balloon in terms of the core cryptographic components, the internal memory demands as recommended by their designers, the offered functionality, and the latest attack and cryptanalysis results.
The core cryptographic components for a PHS include hash functions and symmetric ciphers. SHA512 and SHA1 are the most commonly utilized hash functions that are used by four and three schemes respectively. The hash functions BlaMka and Blake2b are adopted by two PHSs and SHA256 is chosen in on scheme. Blowfish and AES block ciphers are used in three and one scheme respectively, while the Salsa stream cipher is utilized by two schemes. The PHC proposals depend on the well-studied AES, Blowfish, Salsa, SHA256, SHA512, Blake2b, and SHA1.
Regarding the internal state demands, four PHSs can consume less resources than Bcrypt (4KB) and only three PHSs consume high amounts of memory as Scrypt (about 1 GB). MAKWA, Parallel, and Yescrypt have neglectable demands. The internal states for Balloon, Battcrypt, Catena, and Pufferfish require a few KBs-MBs to operate with Argon/Argon2, Lyra2, and POMELO being able to process GBs of data.
Two of the main targets of PHC include the PHS and KDF operations. While a finalist, POMELO is not a KDF and does not offer SR. The rest finalists implement PHS, KDF, and SR. Argon/Argon2, Battcrypt Catena, Lyra2, Parallel, POMELO, and Yescrypt provide CIU, while MAKWA also supports password escrow and offline hash upgrade. Balloon works only as PHS and KDF.
6.2. Results—Software Benchmark
The software benchmark is performed on a PC running the 64-bit version of Windows 8.1 Pro with Intel Core i7 at 2.10 GHz CPU and 8 GB RAM. PBKDF2, Bcrypt, Scrypt, the nine PHC finalists, and Balloon are executed on cygwin. The C implementations of PBKDF2 by CyaSSL [105], Bcrypt by openwall [106], and Scrypt-1.1.6 by Tarsnap [107] are installed. For the PHC schemes, the submitted reference and optimized implementations [82] are examined. For Balloon the reference implementation is included. The schemes are assessed over the same benchmark suite for hashing 1000 passwords, measuring the code size, memory consumption, and processing time. Table A3 (see Appendix C) details the benchmark results, using the default values for password, salt, and output size, and the indicative t_cost and m_cost values as reported by each scheme. In real settings, these parameters are determined by the user (e.g., the password length) or the application designer (e.g., the salt and the output sizes). Nevertheless, the default values reflect to some design considerations of the scheme designers and they are included for completeness. Also, the default sizes that are proposed by most schemes intuitively indicate the minimum options that should be supported by a feature application.
The password length is determined by the user and affects the entropy of the hash outcome. In Balloon and the majority of the finalists (eight PHSs), the default password length is 8 bytes as in Scrypt. Bcrypt sets the password to 12 bytes and PBKDF2 to 24 bytes. Argon/Argon2 use 32 byte passwords, which is the longest proposal.
A randomly produced salt obstructs the correlation of hashed passwords that are derived from the same secret. By default, Battcrypt uses the shortest salt that is 4 bytes long. Balloon and PBKDF2 double the salt to 8 bytes. Most of the finalists (seven PHSs) apply 16 byte salts as Bcrypt. Argon/Argon2 and Scrypt utilize the longest 32 bytes salt.
The initial input passphrase is stretched in all schemes. The final result is safeguarded from vulnerabilities on low-entropy or short secret values by longer output hashes. On the other hand, the processing for producing large hashing outcomes slows down the user. Bcrypt outputs 54 bytes hashed passwords with Argon/Argon2 and Balloon resulting 32 bytes. The rest PHC schemes output 64 bytes, similarly with Scrypt and PBKDF2.
The PHC introduces the cost parameters for time and memory (t_cost and m_cost) in order to configure the different schemes. No specific norm is imposed for assigning specific cost values. Thus, each candidate adopts its own convention based on its design structure, with the range values varying from one scheme to another.
The segment of the consistent memory that is required for a software implementation is defined by the size of the executable code. PBKDF2, Bcrypt, Battcrypt, Catena, and Yescrypt are appropriate for constrained devices (low requirements in RAM with less than 36KB of ROM) as they exhibit the most lightweight implementations. Argon/Argon2, Lyra2, MAKWA, Parallel, POMELO, and Pufferfish produce moderate code sizes (67–110 KB). Scrypt results large code sizes followed by Balloon and the optimized implementation of Pufferfish that produce the largest implementations (398–430 KB).
The processing time and the RAM usage determine the runtime requirements of a software implementation. The execution time and RAM space are derived by the input parameters that are indicated by the designers of each scheme for secure and efficient operation. Thus, for example, some schemes are not suggested for low memory consumption or fast processing due to security issues while others are not proposed for high memory usage due to low performance.
The not RAM-hard PHSs are PBKDF2, Parallel, and MAKWA. PBKDF2 and Parallel need neglected RAM with MAKWA requiring low RAM levels as Bcrypt. From the rest RAM-hard PHSs, Battcrypt, Lyra2, and Pufferfish require low to moderate memory. Yescrypt also takes low to moderate RAM (44 KB–16.46 MB) along with ROM-hard primitives. Balloon operates with moderate memory consumption settings. Argon/Argon2 and POMELO can operate with low to high RAM settings while Catena consumes moderate to high RAM.
Speed is affected by the processing capabilities of the system and constitutes a main feature for choosing software implementations. The computational time that it is required to produce a password’s hash has to conform to the defender’s tolerance and the communication protocol’s thresholds.
MAKWA, Parallel, and Yescrypt need a few ms to produce the outcome, followed by Bcrypt and Scrypt that require moderate timings (a few secs). The remaining PHSs, provide higher degree of adaptability. Battcrypt, Catena, Lyra2, and POMELO takes low to moderate timings while Argon/Argon2, Balloon, PBKDF2, and Pufferfish support the full range from low to high execution time.
6.3. Discussion
In this section, the properties of the three mainstream PHSs, the PHC schemes, and the newer Balloon are analysed. The examined PHSs cover a high variety of different settings and alternative designs. These PHSs are compared in terms of provided functionality and performance. Then, the least competitive solutions are indicated and the most secure and suitable primitives are proposed for different application environments.
As with the design diversion, Argon/Argon2, Balloon, Battcrypt, Catena, Lyra2, POMELO, Pufferfish, and Yescrypt prefix RAM-hardness. From these schemes, only Argon/Argon2, Lyra2, and POMELO process high volumes of memory, like Scrypt. The non RAM-hard schemes are MAKWA and Parallel. MAKWA consumes a constant amount of memory and operates on big number computations like RSA. Parallel imposes computational hardness and is more efficient than the related PBKDF2.
Argon/Argon2, Battcrypt, Catena, Lyra2, Parallel, and Yescrypt implement the full functionality of PHS, KDF, SR, and CIU. MAKWA and Pufferfish provide PHS, KDF, and SR while Balloon offers PHS and KDF operations. POMELO is the only finalist that can not function as a secure KDF and supports only PHS and CIU.
The most well-documented PHSs in terms of security are Catena and Lyra2 while Argon/Argon2, Balloon, and MAKWA are also analysed. Battcrypt, Parallel, and Yescrypt do not provide proofs for the claimed security. The protection level for Pufferfish is not fully validated while POMELO does not support the KDF operation as it produces lower randomness properties.
The code size of the examined PHSs is depicted in Figure 11. Bcrypt, Battcrypt, Catena, PBKDF2, and Yescrypt result the most lightweight implementations (less than 18 KB RAM and less than 36 KB ROM) and are appropriate for constrained embedded devices, like sensors. Argon/Argon2, Lyra2, MAKWA, Parallel, POMELO, and Pufferfish produce moderate code sizes with Scrypt taking about the double code resources. The optimized Pufferfish exhibits a large code-footprint for slightly better speed than the reference version and Balloon exhibits the largest code size.
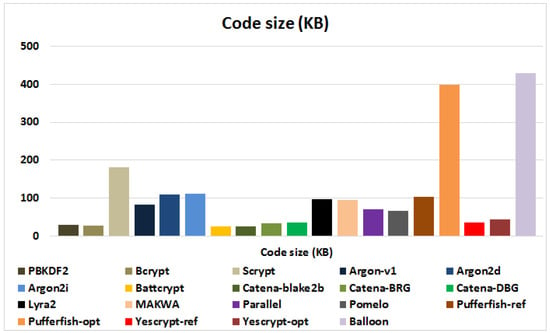
Figure 11.
The code size of PBKDF2, Bcrypt, Scrypt, the nine PHC finalists, and Balloon.
The most efficient schemes are recorded based on the processing time that is needed for similar amounts of memory. The speed to memory measurements of the finalists are depicted in Figure 12 for different levels of RAM usage (Table A2). The most efficient memory-hard schemes are Lyra2, Yescrypt, Catena-BRG, Balloon, Argon2i, and Argon2d, followed by Catena, POMELO, Battcrypt, Argon, and Pufferfish. The most efficient non RAM-hard scheme is Parallel, followed by MAKWA.
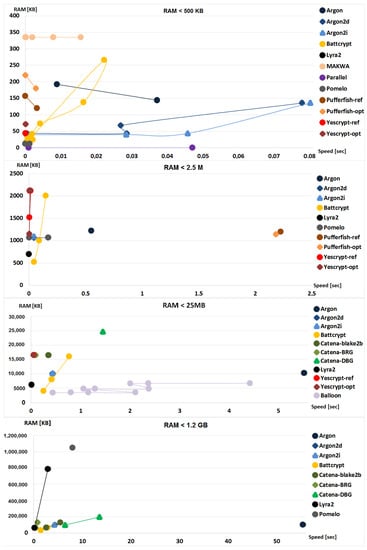
Figure 12.
PHS—Speed to RAM comparison.
Here, the core drawbacks for some of the finalists are summarized based on the security-related results and the analysis above. PBKDF2 and Bcrypt are exploited by low-cost parallel password crackers. Scrypt is vulnerable to cache-timing attacks with relative concerns regarding weak garbage-collector attacks affecting Battcrypt and Parallel as well as some configuration settings of Yescrypt. POMELO can not function as KDF due to low randomness properties—a main design goal for PHC—which obstructed its final selection. Similarly, as Pufferfish’s security features are not fully validated, security concerns arise.
For typical RAM-hard schemes, Argon2, Lyra2, Catena, Yescrypt, Balloon, and Battcrypt are the best choices. They are efficient PHSs and KDFs based on speed and memory consumption. This makes them suitable for general purpose applications. Moreover, the three Argon2, Lyra2, and Catena implement the full functionality and are documented and well-analysed. Argon2 and Lyra2 function well on the web domain and offer server-side implementations. Battcrypt resembles Scrypt’s operation and targets server-side applications. Catena and Yescrypt produce low memory usage and code sizes, making them appropriate for constraint environments and embedded devices. Yescrypt can also replace Scrypt to existing systems. Lyra2 can operate on high amounts of memory more efficiently than Scrypt and can be deployed by applications for hashing hard-disk files or database backups.
Parallel is one of the fastest PHSs and the most appropriate non RAM-hard proposal for web services and general applications. The scheme takes advantage of the computational capabilities of modern CPUs and is optimized for parallel execution while implementing the full functionality. MAKWA uses similar amounts of memory as Bcrypt and it is two to four magnitudes faster. The security is better analysed and documented than Parallel and the scheme can replace Bcrypt in general password-hashing environments.
7. Conclusions
The maintenance of user passwords is an important factor related to the provided security of a service. Security breaches on popular services have revealed high volumes of user information, damaging the providers’ credibility. The poor password-hashing practices and the limited robust solutions led the international cryptographic community to conduct the Password Hashing Competition (PHC). The result was a small portfolio of novel and secure proposals for password-hashing and key-derivation. This paper provides a comparative analysis among the currently available solutions until the first quarter of 2017. Password-hashing schemes are reviewed with software implementations of totally 19 schemes being evaluated under a common platform. The general properties of each scheme are analysed and a benchmark analysis is held. The best schemes that excel are notified, in terms of the overall security and efficiency, and are mapped in different types of application settings. For RAM-hard solutions, Argon2, Lyra2, Catena, Yescrypt, Balloon, and Battcrypt are the best choices. For non RAM-hard schemes, MAKWA and Parallel are suggested.
Acknowledgments
This work was funded by the General Secretarial Research and Technology (G.S.R.T.), Hellas under the Artemis JU research program nSHIELD (new embedded Systems arcHItecturE for multi-Layer Dependable solutions) project. Call: ARTEMIS-2010-1, Grand Agreement No: 269317.
Conflicts of Interest
The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| Battcrypt | Blowfish All The Things |
| BRG | Bit-Reversal Graph |
| CIU | Client-Independent Update |
| DBG | double-butterfly graphs |
| EksBlowfishSetup | Expensive Blowfish key schedule |
| H/s | Hashes per second |
| HMAC | Keyed-Hash Message Authentication Code |
| KDF | Key Derivation Function |
| PBKDF2 | Password-Based Key Derivation Function 2 |
| PPBKDF | Parallel password based key derivation function |
| PRF | Pseudo-Random Function |
| PHC | Password Hashing Competition |
| PHS | Password-Hashing Scheme |
| PKCS | Public-Key Cryptography Standards |
| SIMD | Single Instruction Multiple Data |
| SR | Server relief |
Appendix A. This Appendix Summarizes the GPU Results of Several PHSs

Table A1.
GPU measurements.
Table A1.
GPU measurements.
| PHS | Hashes per Second (H/s) | GPU Model |
|---|---|---|
| SHA1 [108] | 794,600,000.00 | ATI HD 6870 |
| HMAC-SHA1 [108] | 395,210,000.00 | ATI HD 6870 |
| SHA2 [109] | 290,000,000.00 | NVIDIA GRID K520 |
| SHA3 [110] | 113,116,250.00 | NVIDIA GeForce GTX580 |
| PBKDF2-SHA1 [108] | 424,780.00 | ATI HD 6870 |
| PBKDF2-SHA2 [14] | 219,480.00 | NVIDIA Tesla C2070 |
| Bcrypt [108] | 2868.00 | NVIDIA GeForce GTX480 |
| -||- | 319.37 | NVIDIA GeForce GTX480 |
| -||- | 33.73 | NVIDIA GeForce GTX480 |
| -||- | 2.71 | NVIDIA GeForce GTX480 |
| Scrypt [108] | 42,650.00 | NVIDIA GeForce GTX480 |
| -||- | 2333.00 | NVIDIA GeForce GTX480 |
| -||- | 49.06 | NVIDIA GeForce GTX480 |
| -||- | 0.37 | NVIDIA GeForce GTX480 |
| Argon2 [111] | 2.64 | AMD Radeon HD 7900 |
| -||- | 0.70 | AMD Radeon HD 7900 |
| -||- | 0.04 | AMD Radeon HD 7900 |
| Lyra2 [112] | 2688.00 | NVIDIA Tesla K20X |
| -||- | 300.00 | NVIDIA Tesla K20X |
| Lyra2 [113] | 0.018 | NVIDIA GeForce GTX TITAN |
| -||- | 0.0018 | NVIDIA GeForce GTX TITAN |
Appendix B. This Appendix Summarizes the General Features of the Examined PHSs

Table A2.
PHS details.
Table A2.
PHS details.
| PHS | Cryptographic Primitives | Internal Memory | Functionality | Security Analysis/Attacks |
|---|---|---|---|---|
| PBKDF2 | PRF (HMAC-SHA1) | negl. | PHS, KDF | GPU and FPGA attacks [14], multi-FPGA attacks [15] |
| Bcrypt | Blowfish | 4 KB | PHS, KDF | Attacks in several low-cost parallel platforms [16] |
| Scrypt | PBKDF2 HMAC, Salsa20/8 | 1 GB | PHS, KDF | Security analysis [9], Attacks on GPUs [17], Cache-timing attacks [18], Garbage-collector attacks [19] |
| Balloon | Blake2b | 1 MB–32 MB | PHS, KDF | Security analysis [9,25] |
| Argon | AES128 | 1 KB–1 GB | PHS, KDF, SR, CIU | Security analysis [83] |
| Argon2d | BlaMka | 200 MB–4 GB | PHS, KDF, SR, CIU | Security analysis [84], effective attacks [22,23,24,25] |
| Argon2i | BlaMka | 1 GB–6 GB | PHS, KDF, SR, CIU | Security analysis [84], effective attacks [22,23,24,25] |
| Battcrypt | Blowfish-CBC, SHA512 | 128 KB–128 MB | PHS, KDF, SR, CIU | Security claims [85], weak garbage-collector [96] |
| Catena | Blake2b/SHA512 | 8 MB | PHS, KDF, SR, CIU | Security analysis [19], effective attacks [23] |
| Catena-DBG | Blake2b/SHA512 | 4 MB | PHS, KDF, SR, CIU | Security analysis [19], effective attacks [23] |
| Catena-BRG | Blake2b/SHA512 | 128 MB | PHS, KDF, SR, CIU | Security analysis [19], effective attacks [23] |
| Lyra2 | Blake2b / BlaMka | 400 MB–1 GB | PHS, KDF, SR, CIU | Security analysis [87] |
| MAKWA | HMAC_DRBG, SHA256 | 335 KB | PHS, KDF, SR, offline hash upgrade, password escrow | Security analysis [88], Optimization on GPU and CPU [99] |
| Parallel | SHA512 | negl. | PHS, KDF, SR, CIU | Security claims [89], weak garbage-collector [96] |
| POMELO | - | 8 KB, 256 GB | PHS, CIU | Security analysis [90] |
| Pufferfish | Blowfish, HMAC-SHA512 | 4 KB–16 KB | PHS, KDF, SR | Security claims [91] |
| Yescrypt | Scrypt | 3 MB (RAM), 3 GB (ROM) | PHS, KDF, SR, CIU | Security claims [92], garbage-collector and weak garbage-collector [96] |
Appendix C. This Appendix Includes the Evaluation Results for the Examined PHSs

Table A3.
Software implementations of PBKDF2, Bcrypt, Scrypt, the nine PHC finalists, and Balloon.
Table A3.
Software implementations of PBKDF2, Bcrypt, Scrypt, the nine PHC finalists, and Balloon.
| PHS | Password | Salt | Output | t_cost | m_cost | ROM | RAM | CPU |
|---|---|---|---|---|---|---|---|---|
| (bytes) | (bytes) | (bytes) | (KB) | (KB) | ||||
| PBKDF2 | 24 | 8 | 64 | 1000 | 0 | 30 | 0 | 0.002024 |
| PBKDF2 | 24 | 8 | 64 | 2048 | 0 | 30 | 0 | 0.004150 |
| PBKDF2 | 24 | 8 | 64 | 4096 | 0 | 30 | 0 | 0.008141 |
| PBKDF2 | 24 | 8 | 64 | 10,000 | 0 | 30 | 0 | 0.019386 |
| PBKDF2 | 24 | 8 | 64 | 1,000,000 | 0 | 30 | 0 | 1.908592 |
| PBKDF2 | 24 | 8 | 64 | 16,777,216 | 0 | 30 | 0 | 32.969576 |
| Bcrypt | 12 | 16 | 54 | 12 | 0 | 27 | 492 | 2.668653 |
| Scrypt | 8 | 32 | 64 | 5 | 0 | 182 | 450,656 | 2.837654 |
| Balloon | 8 | 8 | 32 | 8 | 1,048,576 | 430 | 3384 | 0.443758 |
| Balloon | 8 | 8 | 32 | 10 | 1,048,576 | 430 | 3428 | 0.807338 |
| Balloon | 8 | 8 | 32 | 20 | 1,048,576 | 430 | 3432 | 1.328957 |
| Balloon | 8 | 8 | 32 | 40 | 1,048,576 | 430 | 3440 | 2.20058 |
| Balloon | 8 | 8 | 32 | 8 | 2,359,296 | 430 | 4716 | 1.175839 |
| Balloon | 8 | 8 | 32 | 10 | 2,359,296 | 430 | 4728 | 1.364459 |
| Balloon | 8 | 8 | 32 | 20 | 2,359,296 | 430 | 4730 | 2.315945 |
| Balloon | 8 | 8 | 32 | 8 | 4,194,304 | 430 | 6504 | 2.017822 |
| Balloon | 8 | 8 | 32 | 10 | 4,194,304 | 430 | 6588 | 2.358291 |
| Balloon | 8 | 8 | 32 | 20 | 4,194,304 | 430 | 6648 | 4.446284 |
| Argon | 32 | 32 | 32 | 3 | 2 | 82 | 192 | 0.008917 |
| Argon | 32 | 32 | 32 | 254 | 1 | 82 | 144 | 0.037167 |
| Argon | 32 | 32 | 32 | 236 | 10 | 82 | 172 | 0.285078 |
| Argon | 32 | 32 | 32 | 56 | 100 | 82 | 244 | 0.674987 |
| Argon | 32 | 32 | 32 | 3 | 1000 | 82 | 1216 | 0.551141 |
| Argon | 32 | 32 | 32 | 3 | 10,000 | 82 | 10,172 | 5.520845 |
| Argon | 32 | 32 | 32 | 3 | 100,000 | 82 | 100,168 | 55.457062 |
| Argon2d | 32 | 32 | 32 | 3 | 2 | 110 | 44 | 0.000524 |
| Argon2d | 32 | 32 | 32 | 254 | 1 | 110 | 44 | 0.028593 |
| Argon2d | 32 | 32 | 32 | 236 | 10 | 110 | 68 | 0.026851 |
| Argon2d | 32 | 32 | 32 | 56 | 100 | 110 | 136 | 0.077891 |
| Argon2d | 32 | 32 | 32 | 3 | 1000 | 110 | 1064 | 0.043209 |
| Argon2d | 32 | 32 | 32 | 3 | 10,000 | 110 | 10,112 | 0.434536 |
| Argon2d | 32 | 32 | 32 | 3 | 100,000 | 110 | 100,064 | 4.325295 |
| Argon2i | 32 | 32 | 32 | 3 | 2 | 111 | 40 | 0.000522 |
| Argon2i | 32 | 32 | 32 | 254 | 1 | 111 | 40 | 0.028412 |
| Argon2i | 32 | 32 | 32 | 236 | 10 | 111 | 44 | 0.045702 |
| Argon2i | 32 | 32 | 32 | 56 | 100 | 111 | 136 | 0.080158 |
| Argon2i | 32 | 32 | 32 | 3 | 1000 | 111 | 1088 | 0.042961 |
| Argon2i | 32 | 32 | 32 | 3 | 10,000 | 111 | 10,112 | 0.431438 |
| Argon2i | 32 | 32 | 32 | 3 | 100,000 | 111 | 100,064 | 4.194904 |
| Battcrypt | 8 | 4 | 64 | 0 | 0 | 27 | 18 | 0.000310 |
| Battcrypt | 8 | 4 | 64 | 1 | 0 | 27 | 18 | 0.000394 |
| Battcrypt | 8 | 4 | 64 | 1 | 1 | 27 | 30 | 0.000760 |
| Battcrypt | 8 | 4 | 64 | 1 | 2 | 27 | 42 | 0.001987 |
| Battcrypt | 8 | 4 | 64 | 1 | 3 | 27 | 74 | 0.004286 |
| Battcrypt | 8 | 4 | 64 | 1 | 4 | 27 | 138 | 0.016476 |
| Battcrypt | 8 | 4 | 64 | 1 | 5 | 27 | 266 | 0.022355 |
| Battcrypt | 8 | 4 | 64 | 1 | 6 | 27 | 520 | 0.045729 |
| Battcrypt | 8 | 4 | 64 | 1 | 7 | 27 | 1000 | 0.091153 |
| Battcrypt | 8 | 4 | 64 | 1 | 8 | 27 | 2000 | 0.149327 |
| Battcrypt | 8 | 4 | 64 | 1 | 9 | 27 | 4000 | 0.254832 |
| Battcrypt | 8 | 4 | 64 | 1 | 10 | 27 | 8000 | 0.418654 |
| Battcrypt | 8 | 4 | 64 | 1 | 11 | 27 | 16,000 | 0.766934 |
| Battcrypt | 8 | 4 | 64 | 1 | 12 | 27 | 32,000 | 1.472502 |
| Battcrypt | 8 | 4 | 64 | 1 | 13 | 27 | 64,000 | 2.853102 |
| Battcrypt | 8 | 4 | 64 | 2 | 1 | 27 | 25 | 0.001090 |
| Battcrypt | 8 | 4 | 64 | 3 | 1 | 27 | 25 | 0.001630 |
| Battcrypt | 8 | 4 | 64 | 4 | 1 | 27 | 25 | 0.002192 |
| Catena–blake2b | 8 | 16 | 64 | 3 | 18 | 25 | 16,384 | 0.353742 |
| Catena–blake2b | 8 | 16 | 64 | 3 | 20 | 25 | 65,596 | 2.619238 |
| Catena–blake2b | 8 | 16 | 64 | 3 | 21 | 25 | 128,484 | 5.461030 |
| Catena–Dragonfly | 8 | 16 | 64 | 3 | 18 | 34 | 16,496 | 0.093241 |
| Catena–Dragonfly | 8 | 16 | 64 | 3 | 20 | 34 | 65,764 | 0.379892 |
| Catena–Dragonfly | 8 | 16 | 64 | 3 | 21 | 34 | 131,428 | 0.797481 |
| Catena–Butterfly | 8 | 16 | 64 | 3 | 18 | 35 | 24,668 | 1.450987 |
| Catena–Butterfly | 8 | 16 | 64 | 3 | 20 | 35 | 98,448 | 6.402041 |
| Catena–Butterfly | 8 | 16 | 64 | 3 | 21 | 35 | 196,852 | 13.508681 |
| Lyra2 | 8 | 16 | 64 | 5 | 5 | 98 | 44 | 0.000084 |
| Lyra2 | 8 | 16 | 64 | 5 | 100 | 98 | 696 | 0.001463 |
| Lyra2 | 8 | 16 | 64 | 5 | 1000 | 98 | 6104 | 0.015104 |
| Lyra2 | 8 | 16 | 64 | 5 | 10,000 | 98 | 60,128 | 0.159651 |
| Lyra2 | 8 | 16 | 64 | 5 | 131,071 | 98 | 787,416 | 2.916398 |
| MAKWA | 8 | 16 | 64 | 0 | 0 | 95 | 335 | 0.000096 |
| MAKWA | 8 | 16 | 64 | 10 | 0 | 95 | 335 | 0.000132 |
| MAKWA | 8 | 16 | 64 | 100 | 0 | 95 | 335 | 0.000273 |
| MAKWA | 8 | 16 | 64 | 1000 | 0 | 95 | 335 | 0.002035 |
| MAKWA | 8 | 16 | 64 | 4000 | 0 | 95 | 335 | 0.007838 |
| MAKWA | 8 | 16 | 64 | 8192 | 0 | 95 | 335 | 0.015621 |
| Parallel | 8 | 16 | 64 | 0 | 0 | 71 | 0 | 0.001000 |
| Parallel | 8 | 16 | 64 | 0 | 10 | 71 | 0 | 0.001018 |
| Parallel | 8 | 16 | 64 | 10 | 0 | 71 | 0 | 0.047020 |
| Parallel | 8 | 16 | 64 | 10 | 10 | 71 | 0 | 0.047051 |
| POMELO | 8 | 16 | 64 | 0 | 0 | 67 | 12 | 0.000031 |
| POMELO | 8 | 16 | 64 | 0 | 7 | 67 | 1064 | 0.003537 |
| POMELO | 8 | 16 | 64 | 0 | 17 | 67 | 1,048,648 | 7.951508 |
| POMELO | 8 | 16 | 64 | 7 | 0 | 67 | 12 | 0.001270 |
| POMELO | 8 | 16 | 64 | 7 | 7 | 67 | 1064 | 0.171375 |
| POMELO | 8 | 16 | 64 | 20 | 0 | 67 | 12 | 8.504152 |
| Pufferfish–ref | 8 | 16 | 64 | 0 | 0 | 103 | 156 | 0.000057 |
| Pufferfish–ref | 8 | 16 | 64 | 6 | 2 | 103 | 120 | 0.003359 |
| Pufferfish–ref | 8 | 16 | 64 | 6 | 10 | 103 | 1192 | 2.225718 |
| Pufferfish–ref | 8 | 16 | 64 | 10 | 10 | 103 | 1188 | 38.341005 |
| Pufferfish–ref | 8 | 16 | 64 | 6 | 11 | 103 | 2236 | 19.884300 |
| Pufferfish–opt | 8 | 16 | 64 | 0 | 0 | 398 | 220 | 0.000055 |
| Pufferfish–opt | 8 | 16 | 64 | 6 | 2 | 398 | 180 | 0.002980 |
| Pufferfish–opt | 8 | 16 | 64 | 6 | 10 | 398 | 1140 | 2.183917 |
| Pufferfish–opt | 8 | 16 | 64 | 10 | 10 | 398 | 1132 | 37.668099 |
| Yescrypt-ref | 8 | 16 | 64 | 0 | 0 | 36 | 44 | 0.000094 |
| Yescrypt-ref | 8 | 16 | 64 | 0 | 7 | 36 | 1516 | 0.004173 |
| Yescrypt-ref | 8 | 16 | 64 | 0 | 8 | 36 | 2112 | 0.007209 |
| Yescrypt-ref | 8 | 16 | 64 | 1 | 8 | 36 | 2112 | 0.008901 |
| Yescrypt-ref | 8 | 16 | 64 | 2 | 8 | 36 | 2112 | 0.012088 |
| Yescrypt-ref | 8 | 16 | 64 | 3 | 8 | 36 | 2112 | 0.015313 |
| Yescrypt-ref | 8 | 16 | 64 | 0 | 11 | 36 | 16,448 | 0.058253 |
| Yescrypt-opt | 8 | 16 | 64 | 0 | 0 | 44 | 72 | 0.000116 |
| Yescrypt-opt | 8 | 16 | 64 | 0 | 7 | 44 | 1148 | 0.003296 |
| Yescrypt-opt | 8 | 16 | 64 | 0 | 8 | 44 | 2124 | 0.005796 |
| Yescrypt-opt | 8 | 16 | 64 | 1 | 8 | 44 | 2124 | 0.006885 |
| Yescrypt-opt | 8 | 16 | 64 | 2 | 8 | 44 | 2124 | 0.009448 |
| Yescrypt-opt | 8 | 16 | 64 | 3 | 8 | 44 | 2124 | 0.011544 |
| Yescrypt-opt | 8 | 16 | 64 | 0 | 11 | 44 | 16,460 | 0.046733 |
References
- Farcasin, M.; Chan-tin, E. Why we hate IT: Two surveys on pre-generated and expiring passwords in an academic setting. In Security and Communication Networks; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Furnell, S. An assessment of website password practices. Comput. Secur. 2007, 26, 445–451. [Google Scholar] [CrossRef]
- Richmond, S.; Williams, C. Millions of Internet Users Hit by Massive Sony PlayStation Data Theft, the Telegraph. London, 26 April 2011. Available online: http://www.telegraph.co.uk/technology/news/8475728/Millions-of-internet-users-hit-by-massive-Sony-PlayStation-data-theft.html (accessed on 28 January 2017).
- Finkle, J.; Saba, J. LinkedIn Suffers Data Breach—Security Experts, Reuters. June 2012. Available online: http://in.reuters.com/article/2012/06/06/linkedin-breach-idINDEE8550EN20120606 (accessed on 28 January 2017).
- Cavusoglu, H.; Cavusoglu, H.; Raghunathan, S. Efficiency of Vulnerability Disclosure Mechanisms to Disseminate Vulnerability Knowledge. IEEE Trans. Softw. Eng. 2007, 33, 171–185. [Google Scholar] [CrossRef]
- Telang, R.; Wattal, S. An Empirical Analysis of the Impact of Software Vulnerability Announcements on Firm Stock Price. IEEE Trans. Softw. Eng. 2007, 33, 544–557. [Google Scholar] [CrossRef]
- Kaliski, B. RFC 2898—PKCS #5: Password-Based Cryptography Specification Version 2.0; Technical Report; IETF: Fremont, CA, USA, 2000. [Google Scholar]
- Provos, N.; Mazieres, D. A Future-Adaptable Password Scheme. In Proceedings of the USENIX Annual Technical Conference, Monterey, CA, USA, 6–11 June 1999; pp. 81–92. [Google Scholar]
- Percival, C. Stronger Key Derivation via Sequential Memory-Hard Functions. In Proceedings of the BSD Conference, Ottawa, ON, Canada, 8–9 May 2009. [Google Scholar]
- Belenko, A.; Sklyarov, D. “Secure Password Managers” and “Military-Grade Encryption” on Smartphones: Oh, Really, 3rd ed.; Hack to Ergo Sum (HES); Elcomsoft Co. Ltd.: Moscow, Russia, 2012. [Google Scholar]
- Fan, D.-R.; Li, X.-W.; Li, G.-J. New Methodologies for Parallel Architecture. J. Comput. Sci. Technol. 2011, 26, 578–587. [Google Scholar] [CrossRef]
- Orman, H. Twelve Random Characters: Passwords in the Era of Massive Parallelism. IEEE Int. Comput. 2013, 17, 91–94. [Google Scholar] [CrossRef]
- Kim, J.W.; Seo, J.; Hong, J.; Park, K.; Kim, S.-R. High-speed parallel implementations of the rainbow method based on perfect tables in a heterogeneous system. Softw. Pract. Exper. 2015, 45, 837–855. [Google Scholar] [CrossRef]
- Durmuth, M.; Guneysu, T.; Kasper, M.; Paar, C.; Yalcin, T.; Zimmermann, R. Evaluation of Standardized Password-Based Key Derivation against Parallel Processing Platforms. In LNCS; Springer: Berlin, Germany, 2012; pp. 716–733. [Google Scholar]
- Abbas, A.; Voss, R.; Wienbrandt, L.; Schimmler, M. An efficient implementation of PBKDF2 with RIPEMD-160 on multiple FPGAs. In Proceedings of the 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS), Hsinchu, Taiwan, 16–19 December 2014; pp. 454–461. [Google Scholar]
- Malvoni, K.; Designer, S.; Knezovic, J. Are Your Passwords Safe: Energy-Efficient Bcrypt Cracking with Low-Cost Parallel Hardware. In Proceedings of the 8th USENIX Workshop on Offensive Technologies (WOOT’14), San Diego, CA, USA, 19 August 2014. [Google Scholar]
- Durmuth, M.; Kranz, T. On Password Guessing with GPUs and FPGAs. In Proceedings of the International Conference on PASSWORDS 2014, Trondheim, Norway, 8–10 December 2014. [Google Scholar]
- Forler, C.; Lucks, S.; Wenzel, J. Memory-Demanding Password Scrambling. In LNCS, Proceedings of the ASIACRYPT, Kaohsiung, Taiwan, 7–11 December 2014; Springer: Berlin, Germany, 2014; Volume 8874, pp. 289–305. [Google Scholar]
- Forler, C.; Lucks, S.; Wenzel, J. The Catena Password Scrambler, PHC Submission. 15 May 2014. Available online: https://www.uni-weimar.de/de/medien/professuren/mediensicherheit/research/catena/ (accessed on 28 January 2017).
- Cryptographic Competition: Password Hashing Competition (PHC). 25 April 2013. Available online: https://password-hashing.net/ (accessed on 28 January 2017).
- Forler, C.; List, E.; Lucks, S.; Wenzel, J. Overview of the Candidates for the Password Hashing Competition and their Resistance against Garbage-Collector Attacks; Cryptology ePrint Archive; Report 2014/881; Springer: Berlin, Germany, 2014. [Google Scholar]
- Alwen, J.; Serbinenko, V. High parallel complexity graphs and memory-hard functions. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing (STOC’15), Portland, OR, USA, 14–17 June 2015; pp. 595–603. [Google Scholar]
- Alwen, J.; Blocki, J. Efficiently Computing Data-Independent Memory-Hard Functions; Cryptology ePrint Archive; Report 2016/115; Springer: Berlin, Germany, 2016. [Google Scholar]
- Boneh, D.; Corrigan-Gibbs, H.; Schechter, S. Balloon hashing: A memory-hard function providing provable protection against sequential attacks. In Proceedings of the ASIACRYPT, Hanoi, Vietnam, 4–8 December 2016. [Google Scholar]
- Alwen, J.; Blocki, J. Towards Practical Attacks on Argon2i and Balloon Hashing; Cryptology ePrint Archive; Report 2016/759; Springer: Berlin, Germany, 2016. [Google Scholar]
- Biryukov, A.; Dinu, D.; Khovratovich, D. The Memory-Hard Argon2 Password Hash and Proof-of-Work Function, IETF, Draft-Irtf-Cfrg-Argon2-01. 22 September 2016. Available online: https://tools.ietf.org/html/draft-irtf-cfrg-argon2-01 (accessed on 28 January 2017).
- Bonneau, J.; Schechter, S. Towards reliable storage of 56-bit secrets in human memory. In Proceedings of the 23rd USENIX Conference on Security Symposium (SEC’14), San Diego, CA, USA, 20–22 August 2014; pp. 607–623. [Google Scholar]
- Vaidya, B.; Park, J.H.; Yeo, S.-S.; Rodrigues, J.J.P.C. Robust one-time password authentication scheme using smart card for home network environment. Comput. Commun. 2011, 34, 326–336. [Google Scholar] [CrossRef]
- Mannan, M.; van Oorschot, P.C. Leveraging personal devices for stronger password authentication from untrusted computers. J. Comput. Secur. 2011, 19, 703–750. [Google Scholar] [CrossRef]
- Lee, S.; Han, K.; Kang, S.-K.; Kim, K.; Ine, S.R. Threshold Password-Based Authentication Using Bilinear Pairings. In Proceedings of the First European PKI Workshop: Research and Applications (EuroPKI 2004), Samos Island, Greece, 25–26 June 2004; pp. 350–363. [Google Scholar]
- Chen, L.; Lim, H.W.; Yang, G. Cross-Domain Password-Based Authenticated Key Exchange Revisited. ACM Trans. Inf. Syst. Secur. 2014, 16, 15. [Google Scholar] [CrossRef]
- Acar, T.; Belenkiy, M.; Kupcu, A. Single password authentication. Comput. Netw. Int. J. Comput. Telecommun. Netw. 2013, 57, 2597–2614. [Google Scholar] [CrossRef]
- HSU, F.; Chen, H.; Machiraju, S. WebCallerID: Leveraging cellular networks for Web authentication. J. Comput. Secur. 2011, 19, 869–893. [Google Scholar] [CrossRef]
- NIST: Recommendation for Password-Based Key Derivation, NIST Special Publication 800-132. December 2010. Available online: http://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-132.pdf (accessed on 28 January 2017).
- Zheng, M.-H.; Zhou, H.-H.; Li, J.; Cui, G.-H. Efficient and provably secure password-based group key agreement protocol. Comput. Stand. Interfaces 2009, 31, 948–953. [Google Scholar] [CrossRef]
- Liao, Y.-P.; Wang, S.-S. A secure dynamic ID based remote user authentication scheme for multi-server environment. Comput. Stand. Interfaces 2009, 31, 24–29. [Google Scholar] [CrossRef]
- Catuogno, L.; Galdi, C. Analysis of a two-factor graphical password scheme. Int. J. Inf. Secur. 2014, 13, 421–437. [Google Scholar] [CrossRef]
- Liu, X.-Y.; Gao, H.-C.; Wang, L.-M.; Chang, X.-L. A vision based graphical password. J. Integr. Des. Process Sci. 2010, 14, 43–52. [Google Scholar]
- Van Oorschot, P.C.; Thorpe, J. On predictive models and user-drawn graphical passwords. ACM Trans. Inf. Syst. Secur. 2008, 10. [Google Scholar] [CrossRef]
- Van Oorschot, P.C.; Thorpe, J. Exploiting predictability in click-based graphical passwords. J. Comput. Secur. 2011, 19, 669–702. [Google Scholar] [CrossRef]
- Sklavos, N. Towards to SHA-3 Hashing Standard for Secure Communications: On the Hardware Evaluation Development. IEEE Lat. Am. Trans. 2012, 10, 1433–1434. [Google Scholar] [CrossRef]
- Sklavos, N.; Koufopavlou, O. Implementation of the SHA-2 hash family standard using FPGAs. J. Supercomput. 2005, 31, 227–248. [Google Scholar] [CrossRef]
- Kontaxis, G.; Polychronakis, M.; Markatos, E.P. Minimizing information disclosure to third parties in social login platforms. Int. J. Inf. Secur. 2012, 11, 321–332. [Google Scholar] [CrossRef]
- Oechslin, P. Making a faster cryptanalytical time-memory trade-Off. Adv. Cryptol. 2003, 2729, 617–630. [Google Scholar]
- Shay, R.; Bertino, E. A comprehensive simulation tool for the analysis of password policies. Int. J. Inf. Secur. 2009, 8, 275–289. [Google Scholar] [CrossRef]
- Reichl, D. KeePass Password Safe. Version 2.35. 2017. Available online: http://keepass.info/ (accessed on 28 January 2017).
- Florencio, D.; Herley, C. A large scale study of web password habits. In Proceedings of the 16th International Conference on World Wide Web (WWW 2007), Banff, AB, Canada, 8–12 May 2007; pp. 657–666. [Google Scholar]
- Zhao, R.; Yue, C. Toward a secure and usable cloud-based password manager for web browsers. Comput. Secur. 2014, 46, 32–47. [Google Scholar] [CrossRef]
- Van Oorschot, P.C.; Stubblebine, S. On countering online dictionary attacks with login histories and humans-in-the-loop. ACM Trans. Inf. Syst. Secur. 2006, 9, 235–258. [Google Scholar] [CrossRef]
- Patel, A.; Nordin, R.; Al-Haiqi, A. Beyond ubiquitous computing: The Malaysian HoneyBee Project for Innovative Digital Economy. Comput. Stand. Interfaces 2014, 36, 844–854. [Google Scholar] [CrossRef]
- Chaurasia, B.K.; Verma, S. Secure pay while on move toll collection using VANET. Comput. Stand. Interfaces 2014, 36, 403–411. [Google Scholar] [CrossRef]
- Fysarakis, K.; Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C. RtVMF—A secure Real-time Vehicle Management Framework with critical incident response. IEEE Pervasive Comput. Mag. 2016, 15, 22–30. [Google Scholar] [CrossRef]
- Fysarakis, K.; Hatzivasilis, G.; Askoxylakis, I.G.; Manifavas, C. RT-SPDM: Real-time Security, Privacy & Dependability Management of Heterogeneous Systems. In LNCS, Proceedings of the International Conference on Human Aspects of Information Security, Privacy and Trust (HCI International 2015), Los Angeles, CA, USA, 2–7 August 2015; Springer: Berlin, Germany, 2015; Volume 9190, pp. 619–630. [Google Scholar]
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C. Real-time management of railway CPS. In Proceedings of the 5th EUROMICRO/IEEE Workshop on Embedded and Cyber-Physical Systems (ECYPS 2017), Bar, Montenegro, 11–15 June 2017. [Google Scholar]
- Fournaris, A.P.; Sklavos, N. Secure embedded system hardware design—A flexible security and trust enhanced approach. Comput. Electr. Eng. 2014, 40, 121–133. [Google Scholar] [CrossRef]
- Fournaris, A.P.; Kitsos, P.; Sklavos, N. Embedded Computing Systems: Applications, Optimization, and Advanced Design. In Security and Cryptographic Engineering in Embedded Systems (Chapter 21); IGI Global: Hershey, PA, USA, 2013; pp. 420–438. [Google Scholar]
- Hatzivasilis, G.; Floros, G.; Papaefstathiou, I.; Manifavas, C. Lightweight Authenticated Encryption for Embedded On-Chip Systems. Inf. Secur. J. Glob. Perspect. 2016, 25, 1–11. [Google Scholar] [CrossRef]
- Hatzivasilis, G.; Fysarakis, K.; Papaefstathiou, M.C. A review of lightweight block ciphers. J. Cryptogr. Eng. 2017, 7, 1–44. [Google Scholar] [CrossRef]
- Manifavas, C.; Hatzivasilis, G.; Fysarakis, K.; Papaefstathiou, I. A survey of lightweight stream ciphers for embedded systems. Secur. Commun. Netw. 2015, 9, 1226–1246. [Google Scholar] [CrossRef]
- Hatzivasilis, G.; Gasparis, E.; Theodoridis, A.; Manifavas, C. ULCL: An Ultra-Lightweight Cryptographic Library for embedded systems. In Proceedings of the Measurable security for Embedded Computing and Communication Systems (MeSeCCS 2014), Lisbon, Portugal, 7–9 January 2014; pp. 11–18. [Google Scholar]
- Fysarakis, K.; Hatzivasilis, G.; Rantos, K.; Papanikolaou, A.; Manifavas, C. Embedded systems security challenges. In Proceedings of the Measurable security for Embedded Computing and Communication Systems (MeSeCCS 2014), Lisbon, Portugal, 7–9 January 2014; pp. 1–10. [Google Scholar]
- Roman, R.; Alcaraz, C.; Lopez, J.; Sklavos, N. Key Management Systems for Sensor Networks in the Context of the Internet of Things. Comput. Electr. Eng. 2011, 37, 147–159. [Google Scholar] [CrossRef]
- Hatzivasilis, G.; Papaefstathiou, G.; Fysarakis, A.I.G. SecRoute: End-to-End Secure Communications for Wireless Ad-hoc Networks. In Proceedings of the 22nd IEEE Symposium on Computers and Communications (ISCC 2017), Heraklion, Greece, 3–6 July 2017. [Google Scholar]
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C. ModConTR: A Modular and Configurable Trust and Reputation-based system for secure routing. In Proceedings of the 11th ACS/IEEE International Conference on Computer Systems and Applications (AICCSA’2014), Doha, Qatar, 10–13 November 2014; pp. 56–63. [Google Scholar]
- Hatzivasilis, G.; Manifavas, C. Building trust in ad hoc distributed resource-sharing networks using reputation-based systems. In Proceedings of the 16th Panhellenic Conference on Informatics (PCI 2012), Piraeus, Greece, 5–7 October 2012; pp. 416–421. [Google Scholar]
- Manifavas, C.; Hatzivasilis, G.; Fysarakis, K.; Rantos, K. Lightweight cryptography for embedded systems—A comparative analysis. In LNCS, Proceedings of the 8th International Workshop on Data Privacy Management and Autonomous Spontaneous Security, Egham, UK, 12–13 September 2013; Springer: New York, NY, USA, 2013; Volume 8247, pp. 333–349. [Google Scholar]
- Regan, G.; Caffery, F.M.; Daid, K.M.; Flood, D. Medical device standards’ requirements for traceability during the software development lifecycle and implementation of a traceability assessment model. Comput. Stand. Interfaces 2013, 36, 3–9. [Google Scholar] [CrossRef]
- Dini, G.; Savino, I.M. LARK: A Lightweight Authenticated ReKeying Scheme for Clustered Wireless Sensor Networks. ACM Trans. Embed. Comput. Syst. 2011, 10, 41. [Google Scholar] [CrossRef]
- Dong, Q.; Liu, D. Using Auxiliary Sensors for Pairwise Key Establishment in WSN. ACM Trans. Embed. Comput. Syst. 2012, 11, 59. [Google Scholar] [CrossRef]
- Chung, H.-R.; Ku, W.-C.; Tsaur, M.-J. Weaknesses and improvement of Wang et al.’s remote user password authentication scheme for resource-limited environments. Comput. Stand. Interfaces 2009, 31, 863–868. [Google Scholar] [CrossRef]
- Wu, G.; Shu, F.; Wang, M.; Chen, W. Requirements specifications checking of embedded real-time software. J. Comput. Sci. Technol. 2002, 17, 56–63. [Google Scholar] [CrossRef]
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C. Software Security, Privacy and Dependability: Metrics and Measurement. IEEE Softw. 2016, 33, 46–54. [Google Scholar] [CrossRef]
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C.; Papadakis, N. A reasoning system for composition verification and security validation. In Proceedings of the 6th IFIP International Conference on New Technologies, Mobility & Security (NTMS 2014), Dubai, UAE, 30 March–2 April 2014; pp. 1–4. [Google Scholar]
- Dhurjati, D.; Kowshik, S.; Adve, V.; Lattner, C. Memory safety without garbage collection for embedded applications. ACM Trans. Embed. Comput. Syst. 2005, 4, 73–111. [Google Scholar] [CrossRef]
- RSA Laboratories: PKCS #5: Password-Based Cryptographic Standard. Version 2.0. 2000. Available online: http://www.emc.com/emc-plus/rsa-labs/standards-initiatives/pkcs-5-password-based-cryptography-\standard.htm (accessed on 28 January 2017).
- Kaliski, B. RSA Laboratories: PKCS #5: Password-Based Cryptography Specification Version 2.0, IETF, RFC2898. September 2000. Available online: http://tools.ietf.org/html/rfc2898 (accessed on 28 January 2017).
- NIST: Secure Hash Standard, FIPS 180-2. April 1995. Available online: http://csrc.nist.gov/publications/fips/fips180-2/\fips180-2.pdf (accessed on 28 January 2017).
- Avoine, G.; Junod, P.; Oechslin, P. Characterization and Improvement of Time-Memory Trade-Off Based on Perfect Tables. ACM Trans. Inf. Syst. Secur. 2008, 11. [Google Scholar] [CrossRef]
- Schneier, B. Description of a New Variable-Length Key, 64-Bit Block Cipher (Blowfish). In LNCS, Proceedings of the Fast Software Encryption, Cambridge Security Workshop, Cambridge, UK, 9–11 December 1993; Springer: London, UK, 1994; Volume 809, pp. 191–204. [Google Scholar]
- Percival, C.; Josefsson, S. The Scrypt Password-Based Key Derivation Function, IETF. 18 May 2016. Available online: https://tools.ietf.org/html/draft-josefsson-scrypt-kdf-05 (accessed on 28 January 2017).
- Bernstein, D.J. The Salsa20 Family of Stream Ciphers, eSTREAM Project. 2007. Available online: http://cr.yp.to/papers.html#salsafamily (accessed on 28 January 2017).
- Password Hashing Competition (PHC): Candidates. 31 March 2014. Available online: https://password-hashing.net/candidates.html (accessed on 28 January 2017).
- Biryukov, A.; Khovratovich, D. Argon v1: Password Hashing Scheme. 8 April 2014. Available online: https://www.cryptolux.org/images/0/0c/Argon-v1.pdf (accessed on 28 January 2017).
- Biryukov, A.; Dinu, D.; Khovratovich, D. Argon2. 3 March 2016. Available online: https://www.cryptolux.org/images/0/0d/Argon2.pdf (accessed on 28 January 2017).
- Thomas, S. Battcrypt (Blowfish All the Things), PHC Submission. 16 February 2014. Available online: https://password-hashing.net/submissions/specs/battcrypt-v0.pdf (accessed on 28 January 2017).
- Lucks, S.; Wenzel, J. Catena Variants—Different Instantiations for an Extremely Flexible Password-Hashing Framework. In LNCS, Proceedings of the 9th International Conference on Passwords, London, UK, 7–9 December 2015; Springer: Berlin, Germany, 2015; Volume 9551, pp. 95–119. [Google Scholar]
- Simplicio, M.A.; Almeida, L.C.; Andrade, E.R.; Santos, P.C.F.; Barreto, P.S.L.M. Lyra2: Password Hashing Scheme with Improved Security against Time-Memory Trade-Offs; Cryptology ePrint Archive; Report 2015/136; Poli-USP: São Paulo, Brazil, 2015. [Google Scholar]
- Thomas, P. The MAKWA Password Hashing Function, PHC Submission. 22 April 2015. Available online: http://www.bolet.org/makwa/makwa-spec-20150422.pdf (accessed on 28 January 2017).
- Thomas, S. Parallel, PHC Submission. 16 February 2014. Available online: https://password-hashing.net/submissions/\specs/Parallel-v1.pdf (accessed on 28 January 2017).
- Hongjun, W. POMELO: A Password Hashing Algorithm (Version 2), PHC Submission. 13 April 2015. Available online: http://www3.ntu.edu.sg/home/wuhj/research/pomelo/POMELO-v2-2015-04-13.pdf (accessed on 28 January 2017).
- Gosney, J. The Pufferfish Password Hashing Scheme, PHC Submission. 31 January 2015. Available online: https://github.com/epixoip/pufferfish (accessed on 28 January 2017).
- Peslyak, A. Yescrypt—A Password Hashing Competition Submission, PHC Submission. 31 January 2015. Available online: https://password-hashing.net/submissions/specs/yescrypt-v2.pdf (accessed on 28 January 2017).
- NIST: Advanced Encryption Standard, FIPS-197. November 2001. Available online: http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf (accessed on 28 January 2017).
- Biryukov, A.; Dinu, D.; Khovratovich, D. Fast and Tradeoff-Resillient Memory-Hard Functions for Crytocurrencies and Password Hashing; Cryptology ePrint Archive; Report 2015/430; Springer: Berlin, Germany, 2015. [Google Scholar]
- Aumasson, J.-P.; Neves, S.; Wilcox-O’Hearn, Z.; Winnerlein, C. BLAKE2: Simpler, Smaller, Fast as MD5. In LNCS, Proceedings of the 11th International Conference on Applied Cryptography and Network Security, Banff, AB, Canada, 25–28 June 2013; Springer: New York, NY, USA, 2013; Volume 7954, pp. 119–135. [Google Scholar]
- Forler, C.; List, E.; Lucks, S.; Wenzel, J. Overview of the candidates for the password hashing competition and their resistance against garbage-collector attacks. In LNCS, Proceedings of the International Conference on Passwords (PASSWORDS’14), Trondheim, Norway, 8–10 December 2014; Springer: Berlin, Germany, 2014; Volume 9393, pp. 3–18. [Google Scholar]
- RSA Laboratories: PKCS #1: RSA Cryptography Standard Version 2.2. 2012. Available online: http://www.emc.com/emc-plus/rsa-labs/pkcs/files/h11300-wp-pkcs-1v2-2-rsa-cryptography-\standard.pdf (accessed on 28 January 2017).
- NIST: Recommendation for Random Number Generation Using Deterministic Random Bit Generators (Revised), NIST Special Publication 800-90A. January 2012. Available online: http://csrc.nist.gov/publications/nistpubs/800-90A/SP800-90A.pdf (accessed on 28 January 2017).
- Thomas, P. Optimizing MAKWA on GPU and CPU; Cryptology ePrint Archive; Report 2015/678; Springer: Berlin, Germany, 2015. [Google Scholar]
- Chandra, R.; Menon, R.; Dagum, L.; Kohr, D.; Maydan, D.; McDonald, J. Parallel Programming in OpenMP. 2000. Available online: http://lib.mdp.ac.id/ebook/Karya%20Umum/Parallel_Programming_in_OpenMP.pdf (accessed on 28 January 2017).
- Sodium Crypto Library: Libsodiom Version 1.0.11. 2016. Available online: https://download.libsodium.org/doc/ (accessed on 28 January 2017).
- Simplicio, M.A.; Almeida, L.C.; Andrade, E.R.; Santos, P.C.F.; Barreto, P.S.L.M. Node-Multi-Hashing with Lyra2reV2. 2015. Available online: https://github.com/upgradeadvice/node-multi-hashing (accessed on 28 January 2017).
- Hatzivasilis, G.; Papaefstathiou, I.; Manifavas, C.; Askoxylakis, I. Lightweight password hashing scheme for embedded systems. In LNCS, Proceedings of the 9th WG 11.2 International Conference on Information Security Theory and Practice (WISTP), Heraklion, Greece, 24–25 August 2015; Springer: Berlin, Germany, 2015; Volume 9311, pp. 249–259. [Google Scholar]
- Alwen, J.; Chen, B.; Kamath, C.; Kolmogorov, V.; Pietrzak, K.; Tessaro, S. On the complexity of Scrypt and proofs of space in the parallel random oracle model. In LNCS, Proceedings of the 35th Annual International Conference on Advances in Cryptology—EUROCRYPT, Vienna, Austria, 8–12 May 2016; Springer: Berlin, Germany, 2016; Volume 9666, pp. 358–387. [Google Scholar]
- CyaSSL: Pwdbased.c. wolfSSL, CyaSSL 3.2.0. 2014. Available online: https://www.wolfssl.com/wolfSSL/Source/output/\wolfcrypt/src/pwdbased.c.html (accessed on 28 January 2017).
- Garcia, R. Bcrypt. Openwall, Solar Designer. Available online: https://github.com/rg3/bcrypt (accessed on 28 January 2017).
- Tarsnap: Scrypt-1.1.6. Tarsnap Online Backups for the Truly Paranoid. January 2010. Available online: http://www.tarsnap.com/scrypt/scrypt-1.1.6.tgz (accessed on 28 January 2017).
- Durmuth, M.; Kranz, T. On Password Guessing with GPUs and FPGAs. In LNCS, Proceedings of the International Conference on Passwords (PASSWORDS’14), Cambridge, UK, 7–9 December 2015; Springer: Berlin, Germany, 2015; Volume 9393, pp. 19–38. [Google Scholar]
- Aggarwal, A.; Chaphekar, P.; Mandrekar, R. Cryptanalysis of Bcrypt and SHA-512 using Distributed Processing over the Cloud. Int. J. Comput. Appl. 2015, 128, 13–16. [Google Scholar] [CrossRef]
- Papaefstathiou, I.; Bilanakos, A.; Fysarakis, K.; Hatzivasilis, G.; Manifavas, C. An efficient anti-malware intrusion detection system implementation, exploiting GPUs. In Proceedings of the International Conference on Advanced Technology & Sciences (ICAT 2014), Antalya, Turkey, 12–15 August 2014; pp. 1–9. [Google Scholar]
- Bielec, A. PHC: Argon2 on GPU. Openwall. 2015. Available online: http://www.openwall.com/lists/john-dev/2015/08/16/6 (accessed on 28 January 2017).
- Andrade, E.R.; Simplicio, M.A.; Barreto, P.S.L.M.; Santos, P.C.F. Lyra2: Efficient password hashing with high security against time-memory trade-offs. IEEE Trans. Comput. 2016, 65, 3096–3108. [Google Scholar] [CrossRef]
- Simplicio, M.A.; Almeida, L.C.; Andrade, E.R.; Santos, P.C.F.; Barreto, P.S.L.M. The Lyra2 Reference Guide, PHC Submission. 15 January 2015. Available online: https://password-hashing.net/submissions/specs/Lyra2-v3.pdf (accessed on 28 January 2017).
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).