1. Introduction
For more than 40 years, philosophical theology has flourished in a way comparable only to the attention it received in the Middle Ages [
1]. Surprisingly, this has taken place in analytic philosophy, in which the Russellian view on analysis constituted a harsh environment for metaphysics to flourish. According to Russell, given a proper analysis, philosophical problems will either turn out to be merely pseudo-problems, or a formal technical matter of logic [
2] (p. 33). Anselm’s ontological argument served as a prime example; it could now, according to Russell, be conclusively dismissed as a logical fallacy based on a technical matter concerning the concept of existence [
3] (p. 786–787). The state of affairs in analytic philosophy in 1950 is evident from Wolterstorff’s recollections when he entered the ranks of professional philosophers. Still in the grip of logical positivism, there was only very little room for philosophical theology [
1] (p. 156). The common perception, not merely within analytic philosophy, but also among theistic philosophers, can be gleaned from Plantinga’s Analytic Philosophy and Christianity (1963) [
4]. Then, “many Christians darkly mistrust analytic philosophy, suspecting that it is either a danger to the faith or a trivial waste of time”. [
4] (p. 17). We can add Bertrand Russell’s own reflections to these personal accounts. He did not share the theistic perspective of Wolterstorff or Plantinga, but when he, in 1945, looked back on a lifetime of philosophy, speculating on the impact of Rousseau on theology, he saw very little hope of being able to discuss theology with theologians like Aquinas. One would have to do with theologians in the tradition of Rousseau, even though Russell held Aquinas’ theology in higher regard than that inspired by Rousseau [
2] (p. 694). Russell would “prefer the ontological argument, the cosmological argument, and the rest of the stock-in-trade, to the sentimental illogicity that has sprung from Rousseau”. Russell’s judgment on the ontological argument was also affirmed by Arthur Prior’s teacher from 1935 to 1947, J.N. Findlay, who, following Russell, had concluded that modern logic had proven it to be an absurd falsehood to claim that God exists necessarily [
5]. Considering this, it is worthwhile to ponder what happened in analytic philosophy that can account for the flourishing of philosophical theology. Wolterstorff has done this [
1] and provides two major explanations. First, “the emergence of a widespread skepticism concerning all attempts to specify general conditions for the thinkable and the assertible”, and second, “the collapse of consensus concerning epistemological theory, in particular, consensus concerning any theory which implies that theistic beliefs are rational only if they are rationally grounded in certitudes”. In addition to these, Wolterstorff also points to the fact that there actually were some “philosophers who thought it important to capitalize on the opportunity offered by this lifting of constraints—to capitalize on it by actually developing philosophical theology”. Here, Wolterstorff is clearly envisioning theistic philosophers, and points to the sociological fact that many American philosophers are theists. When we assess the strength of these coarse-grained explanations, we should do so from a more fine-grained perspective from philosophers who welcomed and actively contributed to the change. To the historical evidence from Wolterstorff, Plantinga, and Russell should be added that of Arthur Norman Prior (1914–1969). Prior’s development of tense-logic marked a significant turning point for philosophical theology. It compelled analytic philosophy to reconsider metaphysics and challenged the prevailing anti-metaphysical view on ‘analysis’. Moreover, Prior’s exploration of quantified tense-logic revealed that modern logic’s dismissal of the ontological argument as a mere fallacy about existence was premature. Tense-logic underscored how modern logic had failed to appreciate the strength of medieval logic, an oversight Prior aimed to rectify. His analysis of quantified tense-logic not only corrected this but also hinted at underlying assumptions in tense-logic that medieval logicians, with their theological mindset, would have embraced. Crucially, Prior’s examination of future contingency led to his important analysis of divine omniscience in
Formalities of Omniscience (1962) [
6], which stands out as one of the earliest and most influential contributions to philosophical theology in analytic philosophy. Prior’s contribution to the resurgence of philosophical theology causes us to question the explanatory weight given by Wolterstorff to the philosophers working from an explicit theist perspective. Prior was not aiming at defending important theistic propositions. In fact, his work was part of a journey away from his Christian convictions which suggests that the resurgence of philosophical theology has a much wider base in modern philosophy than assumed by Wolterstorff.
2. A.N. Prior’s Invention of Tense-Logic
The year 1954 was important for Arthur Norman Prior, because in that year he invented tense-logic. It began, however, on a bad note. January had only just begun when Mary Prior fell ill with tuberculosis which led to a long admission to the Sanatorium in Christchurch. The first we hear about tense-logic is, thus, in a letter to Mary on June 6 where he writes the following:
“This afternoon also whacked out some stuff on this Time business—a short thing for Analysis cracking at Jack’s idea that the flow of time is an illusion; and the beginning of a long thing on ‘The Syntax of Time Distinctions’, which is going to be a classic. I’m waiting to hear from the Phil. Quarterly about the Diodorus thing; if they take it, I’ll shoot the big thing over to the Journal of Computing Systems; if they don’t I’ll shoot Diodorus over to the JCS and tell them the big thing’s coming”.
‘Jack’ was the nickname for Prior’s good friend J.J.C. Smart (1920–2012). The correspondence between Jack and Prior had gone on since 1951, and in June 1954, Jack was on his way to New Zealand to participate in the Second Philosophical Congress in Victoria, which was held in August 1954. Prior’s letter not only reflects the importance of his friendship with Jack, but also raises the question: Why was he aware of the importance his discovery of tense-logic would have? It was apparently so clear to him that he knew
The Syntax of Time Distinctions would become a classic. It also did, though in another way than envisioned by him. After some considerations in June and July, Prior decided to present it as his presidential address to the Philosophical Congress. Besides Jack Smart, Gilbert Ryle also participated in the congress and was instrumental in inviting Prior to give the John Locke Lectures at Oxford University in 1956. Here, despite many warnings by Smart [
8], Prior decided to present his ideas on tense-logic, later published as
Time and Modality (1957) [
9] to the philosophical community in Oxford. This book became the real classic. Prior’s introduction to
Time and Modality makes it clear that he considered his invention of tense-logic to be important beyond the topic itself. What he had discovered, in tense-logic, was a formal way to get logic to take the metaphysics of time seriously, by taking tenses seriously. However, he was also aware that this had wider implications which he expressed in the introduction:
These lectures are the expression of a conviction that formal logic and general philosophy have more to bring to one another than is sometimes supposed.
Tense-logic is, as the name implies, a logic of tenses. It adds to the traditional propositional calculus a future tense
F for ‘it will be’, and a past tense operator
P for ‘it has been’. With these, we can construct such propositions as
Fp, and
Pp as the future or past tense of the simple present tense
p. Like the modal operators for necessity and possibility, there are two strong operators
G (will always) and H (has always),
G ≡ ¬
F¬ and
H ≡ ¬
P¬. In the minimal tense-logic Kt we have the following axioms:
Tense-logic assumes quantification over moments of time such that we can add a metric n for ‘units of time’. Hence,
F(
n)
p takes us
n moments of time into the future at which
p holds, and vice versa for
P(
n)
p. As we shall see, with these operators, Prior could provide a formidable challenge to the then-prevailing view on the relationship between logic and philosophy that, as he anticipated, would demonstrate that logic and general philosophy have more to bring to one another than it was then commonly assumed. We have indeed strong evidence for Prior’s experience of the common assumptions from his correspondence with J.J.C Smart. When he, towards the end of June 1954, had written to Smart about his idea of tense-logic, he received a reply that seems to have made him even more determined to make tense-logic the topic of his presidential address. Furthermore, Smart, by referring to Quine’s discussion of Strawson’s
Introduction to Logical Theory (1953) [
10], provided a perfect way for Prior to demonstrate how his invention of tense-logic could force analytic philosophy to take tenses seriously. In [
10], Strawson argued that formal logic has its limits and used tenses as an example of something that formal logic was not able to adequately make sense of. Against this view, Quine argued that Strawson failed to take modern logic seriously if he cannot see that it must be tenseless [
11]. Smart, knowing that Prior was fond of Quine, referred to this discussion in a letter to Prior on the 30th of July where he also made it clear that he (1) did not believe in any metaphysical difference between the past and the future and (2) did not consider Prior’s application of tense-logic to the problem of determinism a serious argument:
I don’t feel the problem of Diodorus as a live one. Why shouldn’t we say that what has happened might not have happened? Of course, the universe is deterministic and if by ‘impossible’ we don’t mean ‘ruled out by the laws of nature’ but (rather eccentrically) ‘ruled out by the laws of nature + initial conditions’ then what happens is ‘necessary’ and what doesn’t happen is ‘impossible’. But ‘past’ and ‘future’ doesn’t come into the matter—they only date events w.r.t. the moment we are at present discussing the matter in. I don’t believe in any metaphysical difference between past and future—in fact I believe the assertion of such difference can be refuted. And here I have Quine on my side—cf his article on Strawson in Mind. But I only mention this because you are a friend of Willard’s.
From Smart’s reply to Prior, we can see why Prior was only strengthened in his belief that he, with the invention of tense-logic, had found something that would be of great value to his overall project: to get analytic philosophy to take general philosophy seriously. First, the reference to Quine’s and Strawson’s discussion only convinced him of the great value tense-logic would have as an analytic tool that would be hard to dismiss ‘as not being an analysis’. Indeed, as Prior demonstrated in
The Syntax of Time Distinction (1958) [
13], one could, for metaphysical reasons, choose a tenseless logic instead of a tensed logic, but there is no formal reason to not take tenses seriously. Indeed, he argued that
If there is to be any ‘interpretation’ of our calculi in the metaphysical sense, it will probably need to be the other way round; that is, the 1-calculus should be exhibited as a logical construction out of the PF calculus rather than vice versa.
The Syntax of Time Distinctions, therefore, opens with a reference to Quine’s and Strawson’s discussion:
Modern exact logicians commonly operate with ‘propositions’ in the second (timelessly true) sense, while ancient and medieval logicians had in mind ‘propositions’ of the first (‘tensed’) sort. It should be emphasised, however, that there are no grounds of a purely logical character for the current preference, and that ‘propositions’ in the ancient and medieval sense lend themselves as readily to the application of contemporary logical techniques and procedures as do ‘propositions’ in the modern sense. (At this point Strawson, who regards it as a limitation of modern methods that they cannot cope with ‘propositions’ in the ancient and medieval sense, and Quine, who objects to the use of such ‘propositions’ in logic because modern methods cannot handle them, would seem to be equally in error).
Prior’s invention of tense-logic demonstrated the direction he desired philosophy to take, concerning the nature of time in particular, but for philosophy in general. Philosophers should argue their case instead of dismissing the metaphysical discussions with the then-prevalent view that somehow one had failed to make a correct analysis if one’s analysis has philosophical, if not downright, metaphysical implications. Prior had, in fact, experienced this first hand earlier the same year when his analysis of necessary existence was rejected by the journal
Analysis with just that argument (see [
14]). The rejection by
Analysis seems to have had quite an impact. As late as August of the same year, Mary wrote to Arthur because she had thought about the whole thing concerning Arthur’s thoughts on necessary existence:
I’ve been thinking about your necessary existence thing and drawing morals from it. It seems to me to be a paradigm of philosophical argument. I mean the argument against has a philosophical rigour which objections like ‘what Q. could that answer?’ just haven’t. It would be rash to claim that to any philosopher it is clear that the argument is no good because there are people who’ll object to logic itself! But its [sic] clear that to most philosophers of whatever school and its [sic] good to see a philosopher dealing w. an argument as an argument, and not simply brushing it up in order to secure his own particular ‘school’ against an-other. To be interested in ‘what is’ instead of ‘what ism,’ wh. is the curse. And that is what logical formulation can do so well—get philosophy into a common language and clear from the language of the cliques. … So much ‘philosophical’ argument con-sists of changing the subject instead of arguing it out and I think Berkeley and Hume did try to argue out specific problems.
Mary’s suggestion concerning logical formulation indicates how well read she was on the matters her husband worked with, and her view on the matter comes close to the one Prior later expressed. He did this in
Past,
Present and Future (1967) [
16].
The logician must be rather like a lawyer—not in Toulmin’s sense (see [Toulmin 1958]), that of reasoning less rigorously than a mathematician—but in the sense that he is there to give the metaphysician, perhaps even the physicist, the tense-logic that he wants, provided that it be consistent. He must tell his client what the consequences of a given choice will be (e.g., that without denseness, infinity, and linearity you don’t get the Hamblin reductions), and what alternatives are open to him; but I doubt whether he can, qua logician, do more.
Prior’s invention of a logical formulation for tenses is the core of his philosophical discussions concerning the nature of time: tensed or tenseless; the relationship between time and existence; and finally, the question of future contingency. It is fundamentally different from the view of Russell and the logicians who, following him, in logic saw a method to get rid of philosophical problems. This is the first reason Prior thought
The Syntax of Time Distinctions [
13] would be a classic. And it would have a strong influence on the resurgence of philosophical theology. Prior’s discussion of time and existence in [
15] and later in [
16] questioned the certitude displayed by Russell and Findlay in their treatment of the ontological argument concerning the grasp of modern logic on the concept of existence. On the contrary, Prior argued that we do not have existence “tied up and pub in a bag” [
17] (p. 61). This view was based on his thorough analysis of the Barcan formulae [
14]. While Ruth Barcan Marcus (1921–2012) had already formulated what is known as the Barcan formulae in 1946, it was not until Prior’s work on quantified tense-logic that the metaphysical implications of the formulae first became visible [
18] (p. 66). Prior’s discussion of quantified tense-logic openly drew in not just the medieval logic, that took tenses seriously, but also the medieval theology of thinkers who had absolutely no problem with the sempiternal implications one is left with when we quantify over individuals that do not exist, but once did or in the future will. I have discussed these points elsewhere [
14]; here I will only point to Cohen’s review of
Time and Modality, which rejected Prior’s idea of tense-logic:
If we insist on having a ‘tense-logic’ we must assume that some form of discourse is sempiternal; and perhaps such an assumption would have seemed a commonplace to many theologically-minded ancient and medieval logicians. Or, if we reject any such assumption, we must also reject the idea of ‘tense-logic’ and fall back on the timeless truth—evaluations of ordinary logic. What we can be sure about is that ‘it is not good logic’ to try and have it both ways, as Professor Prior seems to do—to adopt a ‘tense-logic’ but to repudiate the sempiternity-assumptions.
Prior had introduced a logic which suggested a discourse that would have seemed commonplace to the theology-minded logicians and judging from Massey’s assessment of Prior’s project, in 1969, Prior was spearheading a revolution together with a “dedicated band of revolutionaries” [
20]. The impact of this movement already began in Oxford. Prior’s work in Britain—including his John Locke Lectures and subsequent colloquiums and visits around the country—“helped to revitalize British logic” [
21] (p. 6). The impact of Prior’s work can be sensed in a letter from his friend, Georg Henrik von Wright, to whom Prior, at the beginning of 1966, had sent an early manuscript of
Past,
Present and Future (1967) [
16].
What I have seen of your work, however, makes it clear that it is important both as a major original contribution to the subject and as a very useful survey of all the work that has been done. It must be very satisfying to you to know that you started this new and exciting branch of logical study. It is still only in its beginnings and I am sure it will have a great future.
To summarize these points. The discovery of tense-logic was important for the revival of philosophical theology because it fundamentally challenged the paradigm of analysis that then dominated analytic philosophy in which logical analysis would cleanse philosophical problems out of philosophy as pseudo-problems or turn them into a matter of logic. Furthermore, the discovery would challenge the then-prevalent view on existence which caused Russell, and Prior’s own teacher, J.N. Findlay, to think that modern logic had demonstrated that the ontological argument rested upon a fallacious treatment of the concept of existence. A more fine-grained look at Prior’s correspondence with Smart and Mary Prior from 1954 shows us that he was aware of the importance this discovery would have, not just for the metaphysics of time, but for philosophy in general. Finally, his discovery and discussion of quantified tense-logic would openly invite modern logicians and philosophers into a discussion of the medieval theories concerning reference to non-existing individuals. Even the opponents of tense-logic, such as Cohen, were aware that the sempiternal discourse assumed in quantified tense-logic was more at home with medieval theology-minded thinkers than the more modern-minded thinkers.
3. Tense-Logic and Future Contingency
Prior’s discussion on time and existence was important for the resurgence of philosophical theology but is eclipsed by his work on future contingency. Prior had, in June 1954, not only written
The Syntax of Time Distinctions (1958) [
13], but also,
Diodorean Modality (1955) [
23]. His work on Diodorus Chronos’ famous Master argument remains central to the discovery and development of tense-logic. The current discussion of future contingency in modern logic is still a discussion in which the syntax (tense-operators), semantics (branching time), and the two major systems developed by Prior constitute the overarching framework surrounding the discussions—the Peircean system named after C.S. Peirce and the Ockham system named after William of Ockham [
24]. The master argument introduced into analytic philosophy a formal treatment of the ancient problem, thereby demonstrating the futility of the contempt shown by modern logic toward ancient and medieval logic. As with Prior’s treatments of the philosophical problems pertaining to time and existence, his discussion of future contingency was a demonstration ad oculus that Russell’s view on analysis was wrong. A genuine philosophical analysis does not have to reveal philosophical problems to be pseudo-problems. On the contrary, tense-logic allows for a more rigorous treatment of the problems by embedding them in a formal language. Accepting Prior’s operator approach to the formalization of tenses makes it clear that tensed realism presents us with a trilemma in which the following three propositions cannot all be true:
- (1)
Every proposition about the past is necessary.
- (2)
An impossible proposition cannot follow from a possible.
- (3)
There is a proposition which is possible even though it is not true and will remain false.
Formalizing the past tense with the operator
P, the future tense with
F, and possibility with ◇ where ◇ ≡ ¬◻¬, with ◻ for necessity, we can put 1–3 into the following symbolic form:
To show that 1–3 entails a contradiction, we must make some assumptions about time. Prior suggested that the following, where
H is a strong past operator equivalent to ¬
P¬
p, and was likely assumed in the ancient argument:
With D1–D5 we can now prove the contradiction:
Equations (6) and (7) follow from D3, 8 from (6) and D5, (9) from (8) and D1, (10) from (9) and ◻ ≡ ¬◇¬, (11) from D2, and (12) from D4 and (11). Finally, (13) follows from (10) and (12).
Since 13 is a contradiction of 7, it is evident that the analysis of the Diodorean dilemma, contrary to the then-prevalent assumptions of analytic philosophy, presents us with a genuine philosophical problem concerning time and modality. That these problems have metaphysical importance was apparent to Prior and fundamentally motivated his attempt to spell out an alternative to William of Ockham’s medieval solution to the problem. Prior’s Ockhamism is a semantics of branching time where time is treated as a temporal structure (TIME, <) in which TIME is the set of temporal moments, and < is a partial ordering of the members of TIME. Chronicles are defined as linear and maximal subsets of TIME, constituting the branches on which propositions are true at various moments. Truth is, in this context, a function π, defined on TIME x Φ, where Φ is the set of atomic propositional symbols from which the propositional expressions of the system can be constructed. Thus, for any pair (t,q) of a temporal moment and a propositional constant of the logical language, a truth-value π(t,q) is given as either 0 (false) or 1 (true) (see [
25]). With this semantics, we can lay down the following truth-conditions:
t, c╞ q if q is a propositional constant with π(t,q) = 1
t, c╞ ~φ if it is not the case that t, c╞ φ
t, c╞ Fφ if there is a t’∈ c with t < t’, such that t’, c╞ φ
t, c╞ Pφ if there is a t’∈ c with t’ < t, such that t’, c╞ φ
t, c╞ ◇φ if there is a t∈ c such that t, c╞ φ
While such a truth-condition for F makes it possible to avoid the contradiction, by rejecting D1, it comes with problematic entailments from a general philosophical perspective.
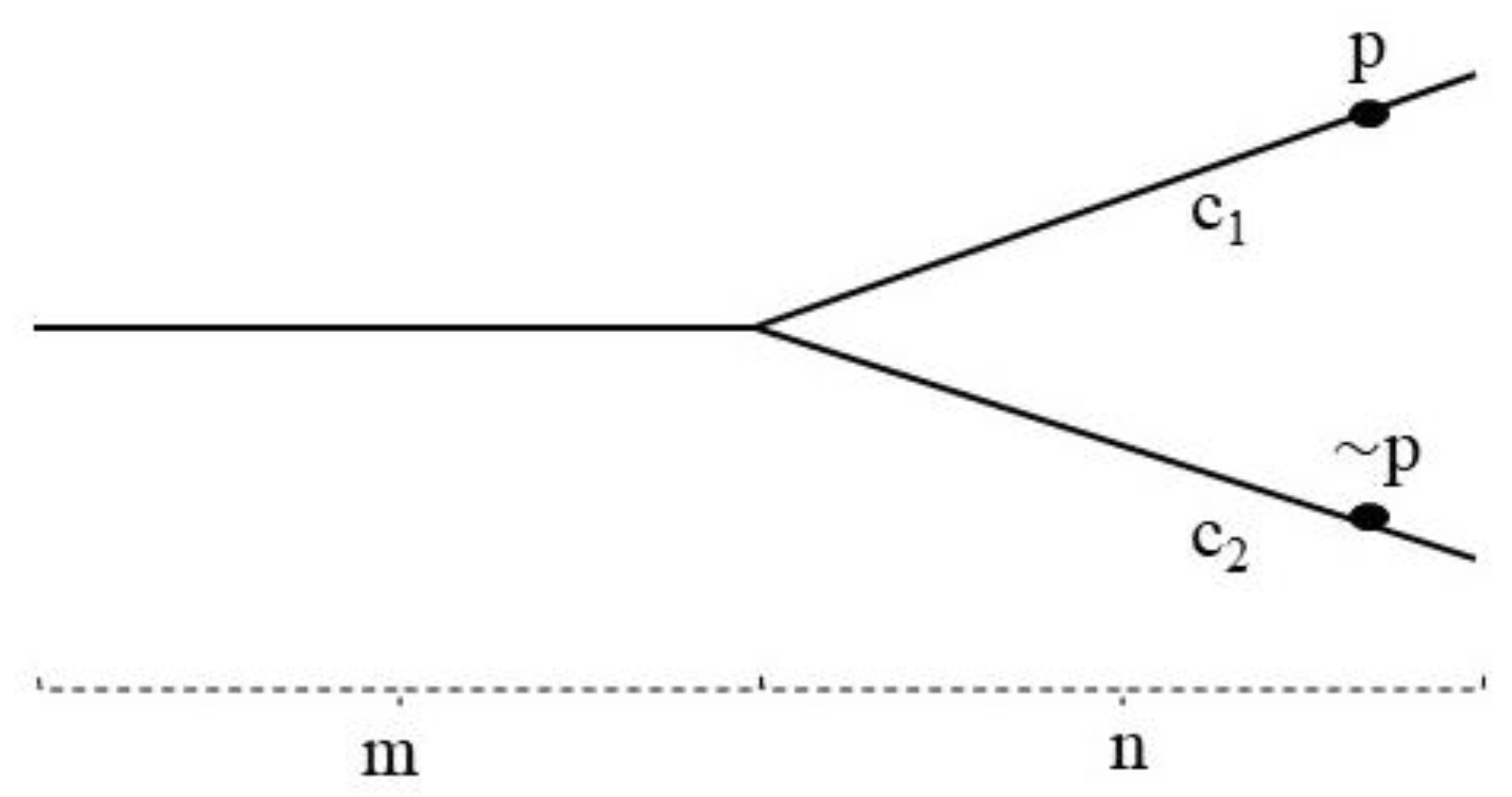
From
Figure 1, we can see that
F(
n)
p entails ◇
F(
n)
p and vice versa, i.e., they are logically equivalent. The assumption of the truth-conditions for F is simply that it holds true relative to a chronicle. It is simply not possible to express propositions about the actual true future. Since tense-logic is, at its core, a commitment to tensed realism, this is problematic. We hold commitments, have beliefs, and make promises about what will actually be the case in the future which assumes more than Prior’s Ockhamism is capable of making sense of. Furthermore, propositions about the future entail propositions about the past and those will be just as open, relative to a chronicle, as the future ones. Prior found both consequences highly problematic and therefore preferred the Peircean system which can be considered a subset of Ockham in which F
Peirce = ◻F
Ockham. This means that to avoid determinism, Peircean must also reject D4. The metaphysical consequences of this are, like the Ockham system, also quite high. It means that whatever happens was not going to be the case! Prior was aware of this and discussed it in [
16]. Philosophers drawn by intuitions like Prior’s concerning future contingency still work on these problems [
26]. More importantly, philosophers and logicians working on Prior’s Ockhamism were quick to point out that Prior’s version does not square well with that of William of Ockham [
27] who clearly distinguish between an actual, possible and a necessary truth-value of future contingent propositions [
28]. Since this view corresponds to our natural language intuition concerning future contingency, quite apart from any theistic beliefs, one way or another, an investigation of semantics for this view has been the center of much attention. A significant development in this discussion, for our study, is Belnap and Green’s investigation of the idea of a thin red line [
29] to pick out the actual true future. In fact, it is evident that Prior, already in 1966, was aware of the need for richer semantics than the one now known as Prior’s Ockhamism. In [
30], and in an unpublished manuscript [
31], Prior developed a system in which it is possible it is possible to refer to the actual future, on “a designated line”. In [
31], which could have been teaching notes or an early draft of [
16,
29], he writes that this designated line could be “picked out in red”. In [
30], he provides the following requirements for truth on the designated line:
“The actual assignment to F(n)a at x gives it the value assigned to a at the distance n to the right of x along the designated line. If x is not on the designated line, F(n)a has no actual assignment there”.
While we do not know why Prior in [
16] dropped this idea, the subsequent early discussion of Prior’s Ockhamism made it clear that it is more difficult to spell out the truth-conditions for an actual future than Prior assumed in 1966 [
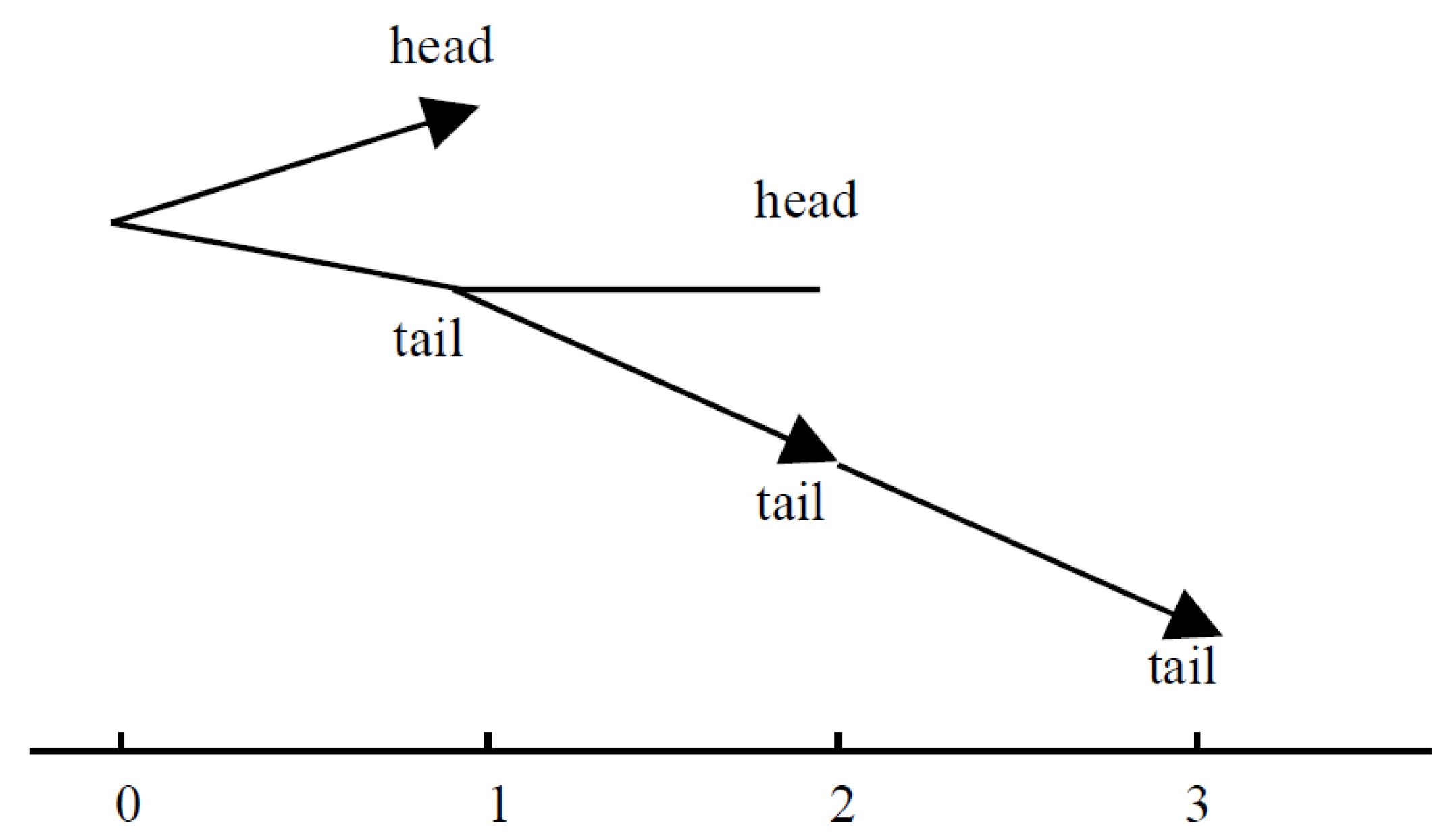
32]. Belnap and Green’s important discussion of this idea refers to the natural language example of tossing a coin.
The coin will come up heads. It is possible, though, that it will come up tails, and then later it will come up tails again (though at this moment it could come up heads), and then, inevitably, still later it will come up tails yet again.
Using the idea of designating a future branch as the actual true future, it is evident that the example given by Belnap and Green implies that it must also be present in a counterfactual true future, which Prior’s truth-conditions appear not to have allowed for (
Figure 2).
While Belnap and Green have argued against the logical tenability of such semantics, subsequent developments have made it clear that these challenges can indeed be met [
33]. Quite interestingly, the modeling of this solution turns out to provide us with another suggestion as to why Prior did not include the model in [
16]. It turns out that such a model is compatible with the late medieval Jesuit Luis de Molina’s view of the future [
34]. Recent discoveries in Prior’s letters to Mary written during the war make it clear that Prior had undertaken a large study of Molina’s theory of Scientia Media. On 29 April 1945, Prior wrote to Mary that he considered Molina’s theory “the Jesuit version of Edwards’ doctrine of the will” [
35] (p. 1). Molina’s theory suggests that God foreknows the true future, not only on what simply will be the case, on the thin red line, but also on the thin red line, from counterfactual futures. The truths foreknown are simply truths that God, logically prior to the moment of creation, foreknows as what creatures would do in various moments where they exercise their free will. Prior finds this theory fallacious because it postulates an initial condition where God is not sovereign. In the letter to Mary, he writes the following:
“Is another God somewhere, one whom we haven’t heard about & of whom it is advisable not to speak? Maybe this other God is not a person—maybe what our God has to contend with is just “the void”; but there’s something sinister even about that. Particularly when it leads the Jesuits to describe God as being forced by this unnamed power to resort to “scheming”. It means this: God does not trust His creatures; because they are not His creatures only, but have been given form partly by the unnamed Unknown. So instead of trusting us, He juggles with us, & turns us into weapons with which He keeps the Unknown at bay.
It is indeed likely that Prior was aware of the Molinistic implications it would have to introduce a designated line for the actual future. However that may be, the subsequent development of the discussion of future contingency underlines the theological background of Prior’s development and discussion of the Ockham system. It is not difficult to find opponents who, like Prior, disagree with the Molinist view on future contingency, but many of these also agree with Belnap that “our tendency to believe that there is a thin red line is powerful” [
29] (p. 366). The reason is, as MacFarlane points out, that “the intuitions behind The Thin Red Line is strong”. [
36] (p. 211). Indeed, [
26] (p. 56) goes so far as to admit that “it is the Ockhamist model (the thin red line) that is implicit in ordinary discourse”. These admissions provide a demonstration of how tense-logic facilitates a flourishing of philosophical theology. The intuitions behind Molinism are those that motivate tensed realism in the first place. Indeed, if we, like Prior, consider our commitment to natural language so fundamental, that we become tensed realists, then what reason do we have to reject Molinism as the best account of future contingency? Another argument is provided by the fact that Prior’s development of Ockhamist models on future contingency relates to his analysis of omniscience. Sometime in 1960, or 1961, judging from his introduction in
Papers on Time and Tense [
37], Prior presented
Formalities of Omniscience [
6] on a philosophical conference at Spode House, Staffordshire. Subsequently, it was published in
Philosophy in April 1962 and has had a significant influence on the philosophical theology that a decade later would begin to flourish, to use Wolterstorff’s timeline. Members of the Cracow circle had, before Prior, worked on philosophical theology in the analytic tradition.
1 Prior was influenced by Polish logic, especially the Lvov-Warshaw School where, as pointed out by Rybaříková “metaphysics was never expelled” [
38] However, Prior’s work stands out for its influence on the discussions that would ensue concerning divine foreknowledge. Indeed, as Hasker points out, Prior’s article, and Nelson Pike’s, published 3 years later, constitute the beginning of the modern discussion of divine foreknowledge and human free will [
39]. Prior’s article is, however, not just important for being published 3 years before Pike’s, but also because it constitutes a significant step in Prior’s later development of his Ockhamist system. In fact, Prior’s comments on the philosophical motivations for Ockhamism in [
30] and [
16] make it clear that they are a further development of Prior’s discussion, and rejection, of Ockham’s ideas of God’s foreknowledge in [
6]. The article is, as Hasker points out, an “excellent exegesis” of Aquina’s treatment of a counterargument, to his own position in
De Veritate, Question 2, Article 12 on ‘Whether God knows future contingents’. In fact, judging from Prior’s early reflections in a letter to Mary on 2 August 1954, one could be forgiven for believing that he developed tense-logic to analyze the problem of omniscience.
Gave, I thing, a very good lecture to Stage III tonight, about medieval & modern views of time, with a fine proof that the logical conclusions of Thomism is Spinozism. If God sees the world spread out before Him in a timeless present, the world is spread out in a timeless present, & is an eternal object & so can be no more be God’s creation than the number 4 can. That was roughly it.—All this arose in the first place, of course, out of my time-calculus, & it’s {2} relation & contrast with the sort of time-calculus in which you translate (A)’It has been the case that Socrates is sitting down’ into (B) ‘For some time t, t is before t0 and Socrates is sitting down at t’, where t0 is some impersonal dating of the time at which the statement happens to my mind. (B) is physicist’s talk; & it is also, on the Thomist view, how God sees the fact of Socrates having sat down. And oddly, (A) is how the fact in question appears in medieval logic, though (B) is how it appears in medieval theology.
Since tense-logic clearly made it possible for Prior to undertake a logical analysis of the problem of omniscience and this problem indeed seems to have been central to the very development of tense-logic, it is an exception to Wolterstorff’s view that the resurgence of philosophical theology was precipitated by a rejection of foundationalists meta-epistemological assumptions. While Prior’s discovery of tense-logic, and the use of it to analyze and discuss the problem of future contingency and determinism had meta-epistemological consequences, it was not predicated upon a meta-epistemological treatment of foundationalism. Tense-logic comes with meta-epistemological consequences, however, because it ultimately rests upon tensed realism. While he also provided an argument for it, he called his commitment to tensed realism a philosophical creed:
So far, then, as I have anything that you could call a philosophical creed, its first article is this: I believe in the reality of the distinction between past, present, and future. I believe that what we see as a progress of events is a progress of events, a coming to pass of one thing after another, and not just a timeless tapestry with everything stuck there for good and all.
Had Prior, however, rested his view on time on an epistemological theory, he would most likely have encountered the same cold reception his treatment of the possibility of necessary existence had received from
Analysis in February 1954 (see [
14]). The key challenge was Russell’s view on ‘analysis’ which had become the center of what Skorupski calls the ‘Analytic School’, defined as “a distinctive school of twentieth-century philosophy which focused on the idea that the analysis of language is basic to philosophy as such: basic, however in a particular way—as the route by which traditional philosophical questions can be revealed as pseudo-problems” [
42] (p. 299). By spelling out a logic of time and using it to highlight problems pertaining to existence and future contingency, Prior did much to help analytic philosophy back to the realism it all began with, albeit a tensed realism. When the meta-epistemological discussions on philosophical neutrality began, Prior’s development of tense-logic already constituted an argument for an alternative view on time grounded on one’s basic commitment to realism—tensed or tenseless. These meta-epistemological discussions were no doubt important for the flourishing of philosophical theology, but they did not begin with a theory on meta-epistemology. It began with the fact that logic does not have to be tenseless. The medieval and ancient view on logic became a live option. It questioned the assumption that modern logic constitutes a break with medieval logic. Contrary to the ‘Analytic School’, tense-logic demonstrated that we face genuine philosophical problems concerning future contingency if we take tenses seriously in modern logic, which openly invited the medieval work on this problem into the discussion. Analytic theology, defined as “the activity of approaching theological topics with the ambitions of an analytic philosopher and in a style that conforms to the prescriptions that are distinctive of analytic philosophic discourse” [
43] (p. 7) stands out as a natural development of the discussions ensued by Prior’s formalization of tenses and the application of this formal tool to discussions in analytic philosophy concerning time and existence and future contingency.