Uncharted Aspects of Human Intelligence in Knowledge-Based “Intelligent” Systems
Abstract
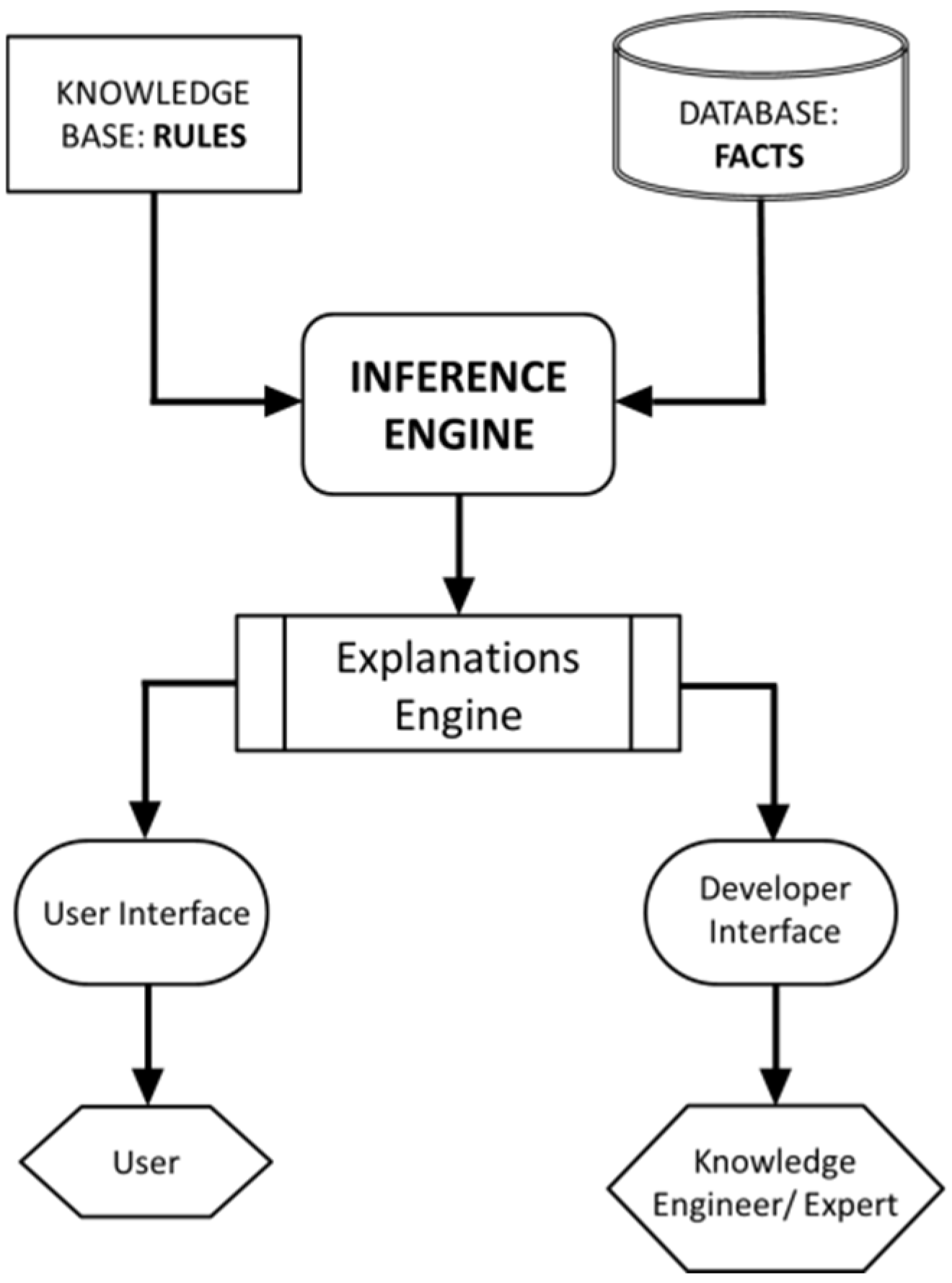
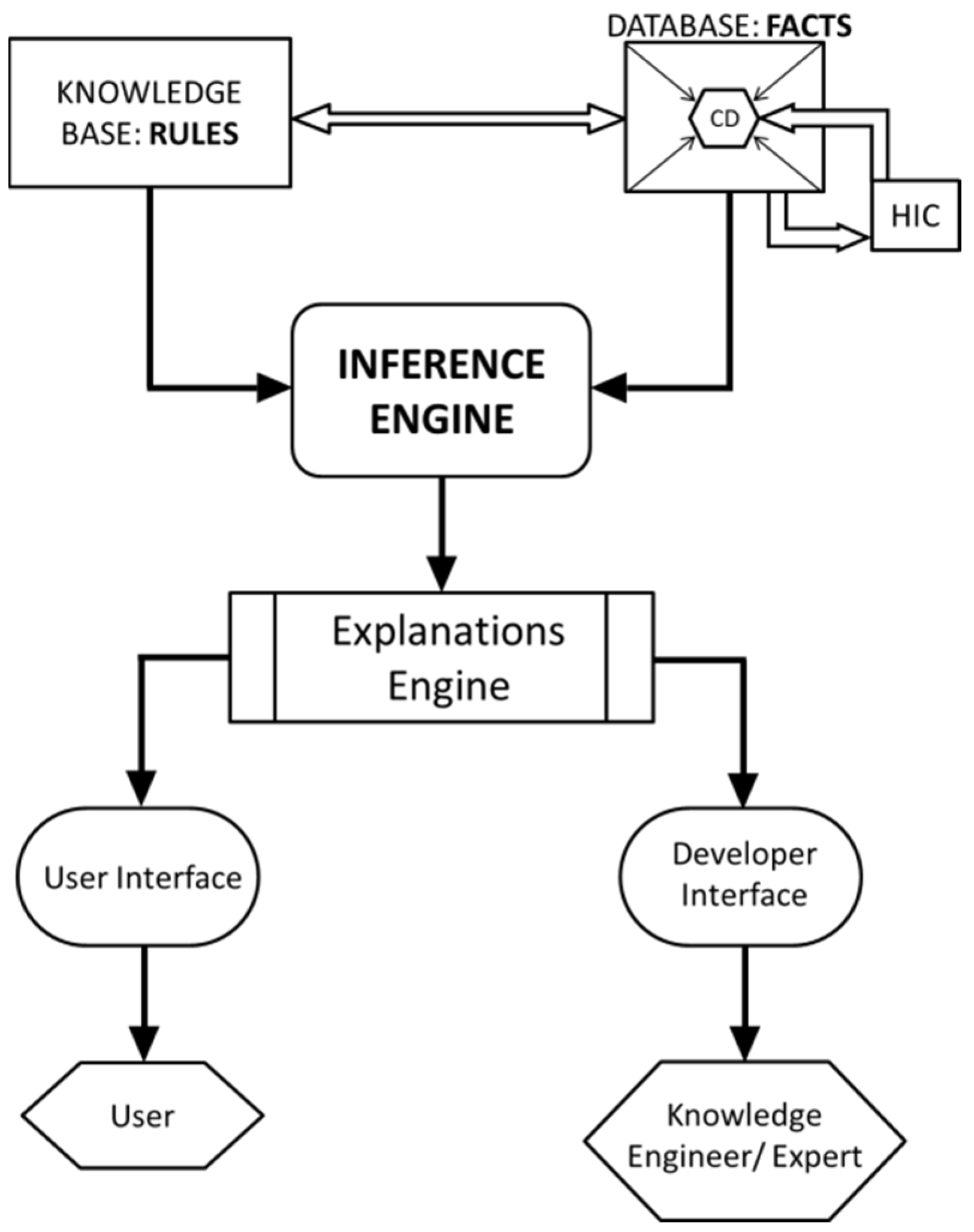
1. Introduction
2. Aspects of Intelligence
2.1. Production Rules and Inductive Inference Systems
2.2. Uncertainty
2.3. Organization
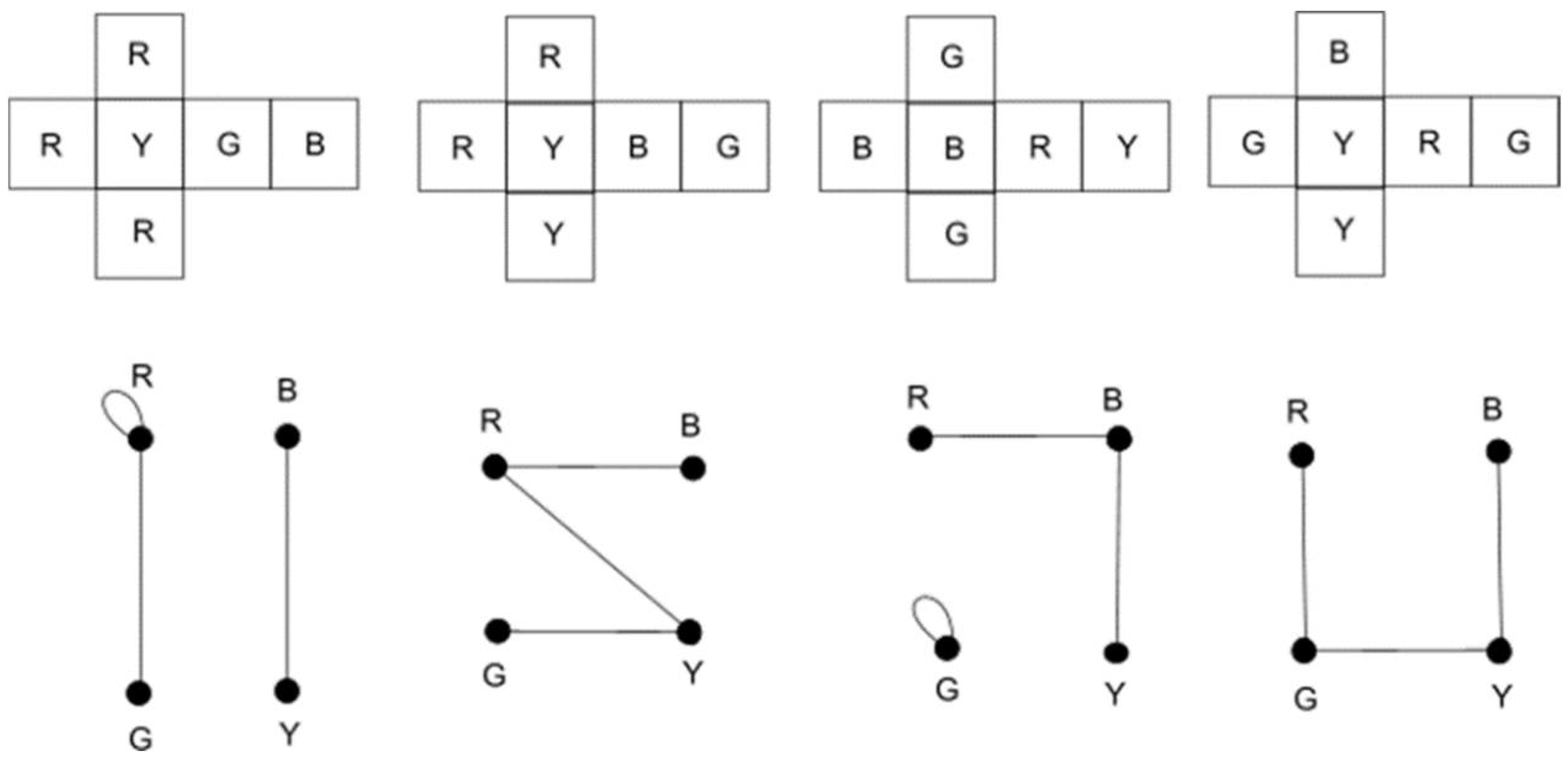
2.4. Ambiguity
2.5. Adaptation
3. Five Missing Key Aspects of Intelligence in KBISes
3.1. Representational Plasticity
3.2. Functional Dynamism
3.3. Domain Specificity
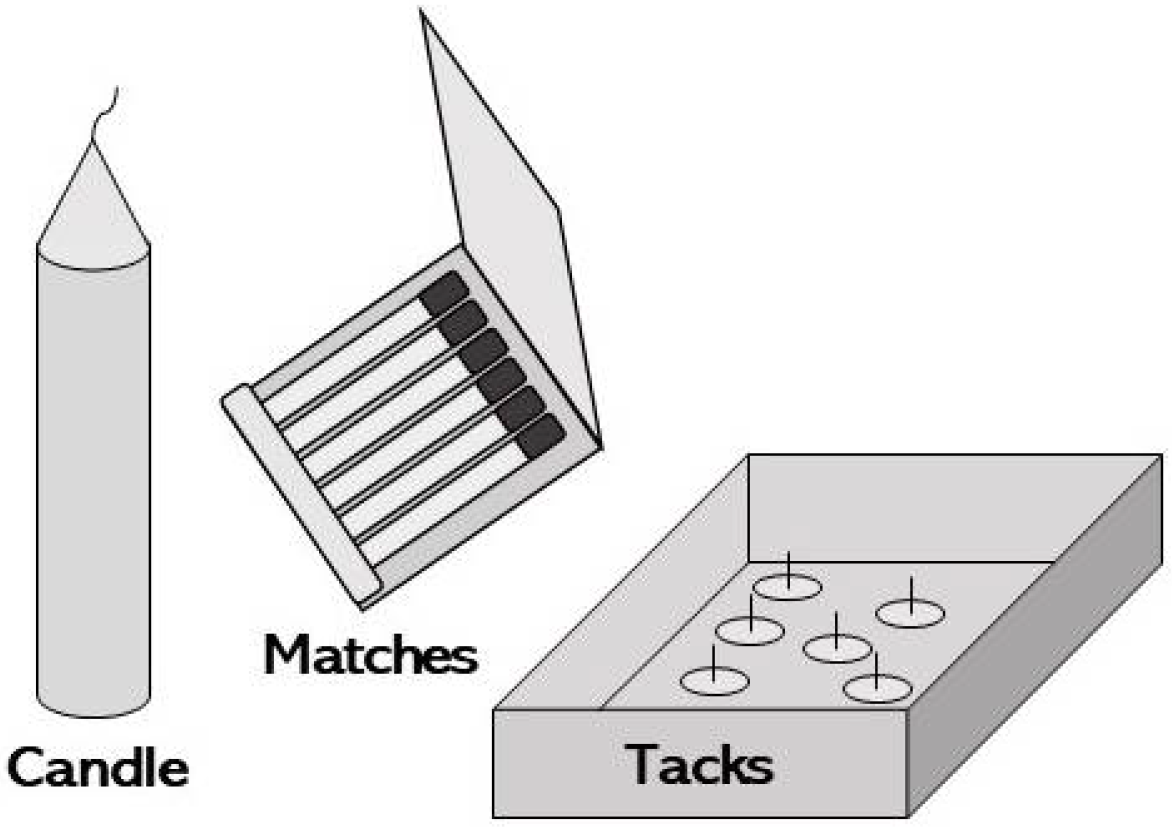
3.4. Creativity
3.5. Concept Learning
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–137. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics; Spartan Books: Kingussie, Scotland, 1962. [Google Scholar]
- Shin, C.; Park, S. Memory and neural network based expert system. Expert Syst. Appl. 1999, 16, 145–155. [Google Scholar] [CrossRef]
- Hatzilygeroudis, I.; Prentzas, J. Integrating (rules, neural networks) and cases for knowledge representation and reasoning in expert systems. Expert Syst. Appl. 2004, 27, 63–75. [Google Scholar] [CrossRef]
- Mukerjee, A.; Deshpande, J.M. Application of artificial neural networks in structural design expert systems. Comput. Struct. 1993, 54, 367–375. [Google Scholar] [CrossRef]
- Shepard, R.N.; Hovland, C.I.; Jenkins, H.M. Learning and memorization of classifications. Psychol. Monogr. Gen. Appl. 1961, 75, 1–42. [Google Scholar] [CrossRef]
- Newell, A.; Simon, H.A. Computer Simulation of Human Thinking. Science 1961, 134, 2011–2017. [Google Scholar] [CrossRef]
- Newell, A.; Simon, H.A. Human Problem Solving; Prentice Hall: Hoboken, NZ, USA, 1972. [Google Scholar]
- Buchanan, B.; Sutherland, G.; Feigenbaum, E.A. Heuristic DENDRAL: A program for generating explanatory hypotheses in organic chemistry. In Machine Intelligence; Edinburgh University Press: Edinburgh, UK, 1969. [Google Scholar]
- Feigenbaum, E.A.; Buchanan, B.G.; Lederberg, J. On generality and problem solving: A case study using the dendral program. In Machine Intelligence 6; Meltzer, B., Michie, D., Eds.; Edinburgh University Press: Edinburgh, UK, 1971; pp. 165–190. [Google Scholar]
- Shortliffe, E.H. Mycin: Computer-Based Medical Consultations; Elsevier Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Firebaugh, M. Artificial Intelligence: A Knowledge-Based Approach; Boyd & Fraser: Boston, MA, USA, 1988. [Google Scholar]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; W.H. Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Sun, R. Anatomy of the Mind: Exploring Psychological Mechanisms and Processes with the Clarion Cognitive Architecture; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Vigo, R. Musings on the utility and challenges of cognitive unification: Review of Anatomy of the Mind, Ron Sun. Rensselaer Polytechnic Institute (2016). Cogn. Syst. Res. 2018, 51, 14–23. [Google Scholar] [CrossRef]
- Cerone, N.; McCalla, G. Artificial intelligence: Underlying assumptions and basic objectives. J. Am. Soc. Inf. Sci. 1984, 35, 280–288. [Google Scholar] [CrossRef]
- Lucas, P.; Van Der Gaag, L. Principles of Expert Systems; Addison-Wesley Longman Publishing: Boston, MA, USA, 1991. [Google Scholar]
- Wilson, B.G.; Welsh, J.R. Small knowledge-based systems in education and training: Something new under the sun. Educ. Technol. 1986, 26, 7–13. [Google Scholar]
- Medsker, L. Hybrid Neural Network and Expert Systems; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Waterman, D.A. A Guide to Expert Systems; Addison-Wesley: Boston, MA, USA, 1986. [Google Scholar]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Judgment under Uncertainty: Heuristics and Biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Quillian, M.R. Semantic Memory—Unpublished Doctoral Dissertation; MIT: Cambridge, MA, USA, 1966. [Google Scholar]
- Rao, A.S.; Georgeff, M.P. BDI agents: From theory to practice. In Proceedings of the First International Conference on Multi-agent Systems, San Francisco, CA, USA, 12–14 June 1995; AAAI Press: Palo Alto, CA, USA, 1995. [Google Scholar]
- Anderson, J.R. Cognitive Psychology and Its Applications; W.H. Freeman: New York, NY, USA, 1985. [Google Scholar]
- Nosofsky, R.M. An exemplar-model account of feature inference from uncertain categorizations. J. Exp. Psychol. Learn. Mem. Cogn. 2015, 41, 1929–1941. [Google Scholar] [CrossRef]
- Vigo, R. The GIST of concepts. Cognition 2013, 129, 138–162. [Google Scholar] [CrossRef]
- Vigo, R. Mathematical Principles of Human Conceptual Behavior: The Structural Nature of Conceptual Representation and Processing; Routledge: London, UK; Taylor & Francis: London, UK, 2015. Original work published 2014. [Google Scholar]
- Vigo, R.; Doan, C.A.; Zhao, L. Classification of three-dimensional integral stimuli: Accounting for a replication and extension of Nosofsky & Palmeri (1996) with a dual discrimination model. J. Exp. Psychol. Learn. Mem. Cogn. 2022. [Google Scholar] [CrossRef]
- Medsker, L.; Leibowitz, J. Design and Development of Expert Systems and Neural Computing; Macmillan: New York, NY, USA, 1994. [Google Scholar]
- Bowers, J.S.; Davis, C.J. Bayesian just-so stories in psychology and neuroscience. Psychol. Bull. 2012, 138, 389–414. [Google Scholar] [CrossRef] [PubMed]
- Tversky, A.; Kahneman, D. Causal Schemes in Judgements under Uncertainty; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Shortliffe, E.H.; Buchanan, B.G. A model of inexact reasoning in medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
- Walley, P. Measures of uncertainty in expert systems. Artif. Intell. 1996, 83, 1–58. [Google Scholar] [CrossRef]
- Baroni, P.; Vicig, P. An uncertainty interchange format with imprecise probabilities. Int. J. Approx. Reason. 2005, 40, 147–180. [Google Scholar] [CrossRef][Green Version]
- Capotorti, A.; Formisano, A. Comparative uncertainty: Theory and automation. Math. Struct. Comput. Sci. 2008, 18, 57–79. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, C.; Leung, H. Information sharing between heterogeneous uncertain reasoning models in a multi-agent environment: A case study. Int. J. Approx. Reason. 2001, 27, 27–59. [Google Scholar] [CrossRef]
- Mauá, D.D.; Antonnuci, A.; de Campos, C.P. Hidden Markov models with set-valued parameters. Neurocomputing 2016, 180, 94–107. [Google Scholar] [CrossRef]
- Núñez, R.C.; Scheutz, M.; Premaratne, K.; Murthi, M.N. Modeling uncertainty in first-order logic: A Dempster-Shafer theoretic approach. In Proceedings of the 8th International Symposium on Imprecise Probability: Theories and Applications, Compiègne, France, 2–5 July 2013. [Google Scholar]
- Zaffalon, M.; Miranda, E. Conservative Inference Rule for Uncertain Reasoning under Incompleteness. J. Artif. Intell. Res. 2009, 34, 757–821. [Google Scholar] [CrossRef]
- Liu, Z.N. Human-simulating intelligent PID control. Int. J. Mod. Nonlinear Theory Appl. 2017, 6, 74–83. [Google Scholar] [CrossRef][Green Version]
- Minsky, M.L. A Framework for Representing Knowledge; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Taylor, D. Object-Oriented Information Systems; John Wiley: Hoboken, NZ, USA, 1992. [Google Scholar]
- Touretzky, D.S. The Mathematics of Inheritance Systems; Morgan Kaufmann: Burlington, MA, USA, 1986. [Google Scholar]
- Anderson, J.R. The adaptive nature of human categorization. Psychol. Rev. 1991, 98, 409–429. [Google Scholar] [CrossRef]
- Gruber, T.R. A translation approach to portable ontology specifications. Knowl. Acquis. 1993, 5, 199–220. [Google Scholar] [CrossRef]
- Frické, M. Classification, facets, and metaproperties. J. Inf. Archit. 2010, 2, 43–65. [Google Scholar]
- Pujara, J.; Miao, H.; Getoor, L.; Cohen, W. Knowledge graph identification. In Proceedings of The Semantic Web—ISWC 2013; Springer: Berlin, Germany, 2013. [Google Scholar]
- Trott, M. Interval arithmetic in the Mathematica Guidebook for Numerics; Springer-Verlag: Berlin, Germany, 2006; pp. 54–66. [Google Scholar]
- Yager, R.R.; Zadeh, L.A. An Introduction to Fuzzy Logic Applications in Intelligent Systems; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kandel, A. Fuzzy Expert Systems; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Dubois, D.; Pride, H.; Yager, R.R. Fuzzy Rules in Knowledge-Based Systems; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Kohout, L.J.; Bandler, W. Fuzzy relational products in knowledge engineering. In Fuzzy Approach to Reasoning and Decision Making; Springer Science and Business Media: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Munakata, T.; Jain, Y. Fuzzy systems: An overview. Commun. ACM 1994, 37, 69–76. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Set Theory—And Its Applications, 4th ed.; Kluwer Academic Publishers: Amsterdam, Netherlands, 2001. [Google Scholar]
- Adlassnig, K.P. Fuzzy Set Theory in Medical Diagnosis. IEEE Trans. Syst. Man, Cybern. 1986, 16, 260–265. [Google Scholar] [CrossRef]
- Adlassnig, K.P. Update on CADIAG-2: A fuzzy medical expert system for general internal medicine. In Progress in Fuzzy Sets and Systems; Janko, W.H., Roubens, M., Zimmermann, H.-J., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1990; pp. 1–6. [Google Scholar]
- Hovy, E. Generating natural language under pragmatic constraints. J. Pragmat. 1987, 11, 689–719. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural language processing (almost) from scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Mendel, J.M. Advances in type-2 fuzzy sets and systems. Inf. Sci. 2007, 177, 84–110. [Google Scholar] [CrossRef]
- Tavana, M.; Hajipour, V. A practical review and taxonomy of fuzzy expert systems: Methods and applications. Benchmarking Int. J. 2019, 27, 81–136. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Zarandi, M.F.; Türkşen, I.; Kasbi, O.T. Type-2 fuzzy modeling for desulphurization of steel process. Expert Syst. Appl. 2007, 32, 157–171. [Google Scholar] [CrossRef]
- Zarandi, M.F.; Rezaee, B.; Turksen, I.; Neshat, E. A type-2 fuzzy rule-based expert system model for stock price analysis. Expert Syst. Appl. 2009, 36, 139–154. [Google Scholar] [CrossRef]
- Zarinbal, M.; Zarandi, M.F. Type-2 fuzzy image enhancement: Fuzzy rule based approach. J. Intell. Fuzzy Syst. 2014, 26, 2291–2301. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Part III Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Liu, H.; Singh, P. ConceptNet: A practical commonsense reasoning tool-kit. BT Technology Journal 2004, 22, 211–216. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Macmillan College Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Patel, M.; Ranganathan, N. IDUTC: An intelligent decision-making system for urban traffic-control applications. IEEE Trans. Veh. Technol. 2001, 50, 816–829. [Google Scholar] [CrossRef]
- Bagloee, S.A.; Asadi, M.; Patriksson, M. Minimization of water pumps’ electricity usage: A hybrid approach of regression models with optimization. Expert Syst. Appl. 2018, 107, 222–242. [Google Scholar] [CrossRef]
- Sharaf-El-Deen, D.A.; Moawad, I.F.; Khalifa, M.E. A new hybrid case-based reasoning approach for medical diagnosis systems. J. Med. Syst. 2014, 38, 9. [Google Scholar] [CrossRef] [PubMed]
- Sharaf-El-Deen, D.A.; Moawad, I.F.; Khalifa, M.E. A breast cancer diagnosis system using hybrid case-based approach. Int. J. Comput. Appl. 2013, 72, 14–19. [Google Scholar]
- Zhou, Q.; Yan, P.; Liu, H.; Xin, Y. A hybrid fault diagnosis method for mechanical components based on ontology and signal analysis. J. Intell. Manuf. 2017, 30, 1693–1715. [Google Scholar] [CrossRef]
- Sahin, S.; Tolun, M.; Hassanpour, R. Hybrid expert systems: A survey of current approaches and applications. Expert Syst. Appl. 2012, 39, 4609–4617. [Google Scholar] [CrossRef]
- Allen, C.; Wallach, W. Wise machines? On the Horizon 2011, 19, 251–258. [Google Scholar] [CrossRef]
- Sterling, L.; Shapiro, E. The Art of Prolog: Advanced Programming Techniques; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Awodey, S. Category Theory; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- French, R.M. Why representation modules don’t make sense. In Proceedings of the 1997 International Conference on New Trends in Cognitive Science: International Conference on New Trends in Cognitive Science; Riegler, A., Peschl, M., Von Stein, A., Eds.; Austrian Society for Cognitive Science: Vienna, Austria; pp. 158–163.
- Beineke, L.W.; Wilson, R.J. Introduction to Graph Theory. Am. Math. Mon. 1974, 81, 679. [Google Scholar] [CrossRef]
- Demers, F.N.; Malenfant, J. Reflection in logic, functional and object oriented programming: A short comparative study. In Proceedings of the IJCAI’95 Workshop on Reflection and Metalevel Architectures and their Applications in AI, Montreal, QC, Canada, 21 August 1995; pp. 29–38. [Google Scholar]
- Gay, S.; Gesbert, N.; Ravara, A.; Vasconcelos, V.T. Modular session types for objects. Log. Methods Comput. Sci. 2015, 11, 1–76. [Google Scholar] [CrossRef]
- Gay, S.; Vasconcelos, V.T.; Ravara, A.; Gesbert, N.; Caldeira, A. Modular session types for distributed object-oriented programming. In Proceedings of the 37th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL’10), Madrid, Spain, 17–23 January 2010; ACM: New York, NY, USA, 2010. [Google Scholar]
- McCarthy, J.; Hayes, P. Some philosophical problems from the standpoint of artificial intelligence. In Machine Intelligence; Meltzer, B., Ed.; Edinburgh University Press: Edinburgh, UK, 1969; Volume 4, pp. 463–502. [Google Scholar]
- Morgenstern, L. The problem with solutions to the frame problem. In The Robot’s Dilemma Revisited: The Frame Problem in Artificial Intelligence; Ablex Publishing Company: New York, NY, USA, 1996; pp. 99–133. [Google Scholar]
- Kruschke, J.K. Models of attentional learning. In Formal Approaches in Categorization; Pothos, E.M., Willis, A.J., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 120–152. [Google Scholar]
- Duncker, K. On problem solving (translated by L.S. Lees). Psychol. Monogr. 1945, 58, 270. [Google Scholar]
- Knoblich, G.; Ohlsson, S.; Raney, G.E. An eye movement study of insight problem solving. Mem. Cogn. 2001, 29, 1000–1009. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, C.A.; Simon, H.A. In search of insight. Cogn. Psychol. 1990, 22, 374–419. [Google Scholar] [CrossRef]
- Forbus, K.D.; Gentner, D.; Markman, A.B.; Ferguson, R.W. Analogy just looks like high level perception: Why a domain-general approach to analogical mapping is right. J. Exp. Theor. Artif. Intell. 1998, 10, 231–257. [Google Scholar] [CrossRef]
- Chalmers, D.J.; French, R.M.; Hofstadter, D. High-level perception, representation, and analogy: A critique of artificial intelligence methodology. J. Exp. Theor. Artif. Intell. 1992, 4, 185–211. [Google Scholar] [CrossRef]
- Alvarez, J.; Abdul-Chani, M.; Deutchman, P.; DiBiasie, K.; Iannucci, J.; Lipstein, R.; Zhang, J.; Sullivan, J. Estimation as analogy-making: Evidence that preschoolers’ analogical reasoning ability predicts their numerical estimation. Cogn. Dev. 2017, 41, 73–84. [Google Scholar] [CrossRef]
- Thibodeau, P.H.; Flusberg, S.J.; Glick, J.J.; Sternberg, D.A. An emergent approach to analogical inference. Connect. Sci. 2013, 25, 27–53. [Google Scholar] [CrossRef]
- Yuan, A. Domain-general learning of neural network models to solve analogy task: A large-scale simulation. In Proceedings of the 39th Annual Meeting of the Cognitive Science Society, London, UK, 16–29 July 2017; Cognitive Science Society: Seattle, WA, USA, 2017. [Google Scholar]
- Feldman, J. A catalog of Boolean concepts. J. Math. Psychol. 2003, 47, 75–89. [Google Scholar] [CrossRef]
- Aiken, H.H. Synthesis of Electronic Computing and Control Circuits; Harvard University Press: Harvard, UK, 1951. [Google Scholar]
- Vigo, R.; Wimsatt, J.; Doan, C.A.; Zeigler, D.E. Raising the bar for theories of categorisation and concept learning: The need to resolve five basic paradigmatic tensions. J. Exp. Theor. Artif. Intell. 2021. [Google Scholar] [CrossRef]
- Thagard, P.; Stewart, T.C. The AHA! experience: Creativity through emergent binding in neural networks. Cogn. Sci. 2011, 35, 1–33. [Google Scholar] [CrossRef]
- Boden, M.A. The Creative Mind: Myths and Mechanisms; Routledge: London, UK, 2004. [Google Scholar]
- Koestler, A. The Act of Creation: A Study of the Conscious and Unconscious in Science and Art; Dell: New York, NY, USA, 1967. [Google Scholar]
- Mednick, S. The associative basis of the creative process. Psychol. Rev. 1962, 69, 220–232. [Google Scholar] [CrossRef]
- Fauconnier, G.; Turner, M. The Way We Think: Conceptual Blending and the Mind’s Hidden Complexities; Basic Books: New York, NY, USA, 2003. [Google Scholar]
- Eppe, M.; Maclean, E.; Confalonieri, R.; Kutz, O.; Schorlemmer, M.; Plaza, E.; Kühnberger, K.-U. A computational framework for conceptual blending. Artif. Intell. 2018, 256, 105–129. [Google Scholar] [CrossRef]
- Hofstadter, D.R. Fluid Analogies Research Group. Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought; Basic Books: New York, NY, USA, 1995. [Google Scholar]
- Vigo, R. A dialog on concepts. Think 2010, 9, 109–120. [Google Scholar] [CrossRef]
- Schwering, A.; Krumnack, U.; Kühnberger, K.-U.; Gust, H. Syntactic principles of heuristic-driven theory projection. Cogn. Syst. Res. 2009, 10, 251–269. [Google Scholar] [CrossRef]
- Guhe, M.; Pease, A.; Smaill, A.; Martinez, M.; Schmidt, M.; Gust, H.; Kühnberger, K.-U.; Krumnack, U. A computational account of conceptual blending in basic mathematics. Cogn. Syst. Res. 2011, 12, 249–265. [Google Scholar] [CrossRef]
- Hedblom, M.M.; Kutz, O.; Neuhaus, F. Image schemas in computational conceptual blending. Cogn. Syst. Res. 2016, 39, 42–57. [Google Scholar] [CrossRef]
- Kutz, O.; Bateman, J.; Neuhaus, F.; Mossakowski, T.; Bhatt, M. E pluribus unum: Formalisation, use-cases, and computational support for conceptual blending. In Computational Creativity Research: Towards Creative Machines; Atlantis Thinking, Machines; Besold, T., Schorlemmer, M., Smaill, A., Eds.; Atlantis Press: Amsterdam, The Netherlands, 2015; Volume 7. [Google Scholar]
- Besold, T.R.; Robere, R. When almost is not even close: Remarks on the approximability of HDTP. In Proceedings of the Artificial General Intelligence—6th International Conference, AGI 2013, Beijing, China, 31 July–3 August 2013; Lecture Notes in Computer Science. Kuhnberger, K., Rudolph, S., Wang, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7999, pp. 11–20. [Google Scholar]
- Vigo, R.; Doan, C.A.; Basawaraj; Zeigler, D.E. Context, structure, and informativeness judgments: An extensive empirical investigation. Mem. Cognit. 2020, 48, 1089–1111. [Google Scholar] [CrossRef]
- Vigo, R. Towards a law of invariance in human concept learning. In Proceedings of the 33rd Annual Conference of the Cognitive Science Society, Boston, MA, USA, 20–23 July 2011; Carlson, L., Hölscher, C., Shipley, T., Eds.; Cognitive Science Society: Seattle, WA, USA, 2011; pp. 2580–2585. [Google Scholar]
- Vigo, R. Representational information. Inf. Sci. 2011, 181, 4847–4859. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vigo, R.; Zeigler, D.E.; Wimsatt, J. Uncharted Aspects of Human Intelligence in Knowledge-Based “Intelligent” Systems. Philosophies 2022, 7, 46. https://doi.org/10.3390/philosophies7030046
Vigo R, Zeigler DE, Wimsatt J. Uncharted Aspects of Human Intelligence in Knowledge-Based “Intelligent” Systems. Philosophies. 2022; 7(3):46. https://doi.org/10.3390/philosophies7030046
Chicago/Turabian StyleVigo, Ronaldo, Derek E. Zeigler, and Jay Wimsatt. 2022. "Uncharted Aspects of Human Intelligence in Knowledge-Based “Intelligent” Systems" Philosophies 7, no. 3: 46. https://doi.org/10.3390/philosophies7030046
APA StyleVigo, R., Zeigler, D. E., & Wimsatt, J. (2022). Uncharted Aspects of Human Intelligence in Knowledge-Based “Intelligent” Systems. Philosophies, 7(3), 46. https://doi.org/10.3390/philosophies7030046




