Emergence and Evidence: A Close Look at Bunge’s Philosophy of Medicine
Abstract
1. Introduction
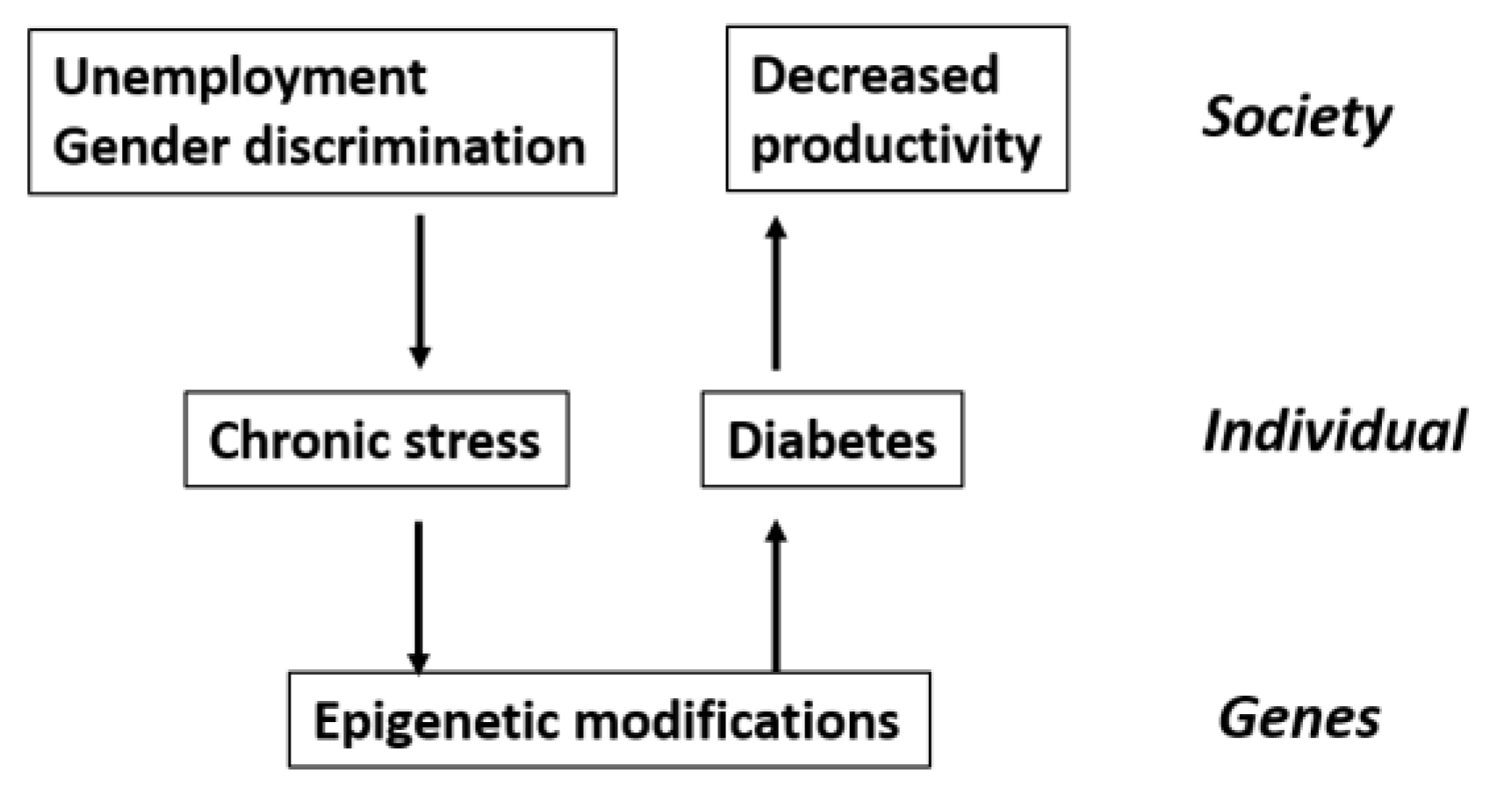
2. Systemism, Emergence and Medicine
2.1. Background
The mass of E. coli can be described by describing one E. coli and then saying “grow 109 of them”, [while] describing a fruit fly requires describing all of its cell types and their interactions in chemistry, space and time.
2.2. Bunge’s Ontological Systemism
- (S1) Everything, whether concrete or abstract, is a system or an actual or potential component of a system;
- (S2) Systems have systemic (emergent) features that their components lack.
The conceptual or empirical analysis of a concrete system, from atom to body to society, consists in identifying its composition, environment, structure, and mechanism. These components may be schematically defined as follows:
3. Bunge’s Epistemology
- (S3) All problems should be approached in a systemic rather than in a sectorial fashion;
- (S4) All ideas should be put together into systems (theories); and
- (S5) The testing of anything, whether idea or artifact, assumes the validity of other items, which are taken as benchmarks, at least for the time being.
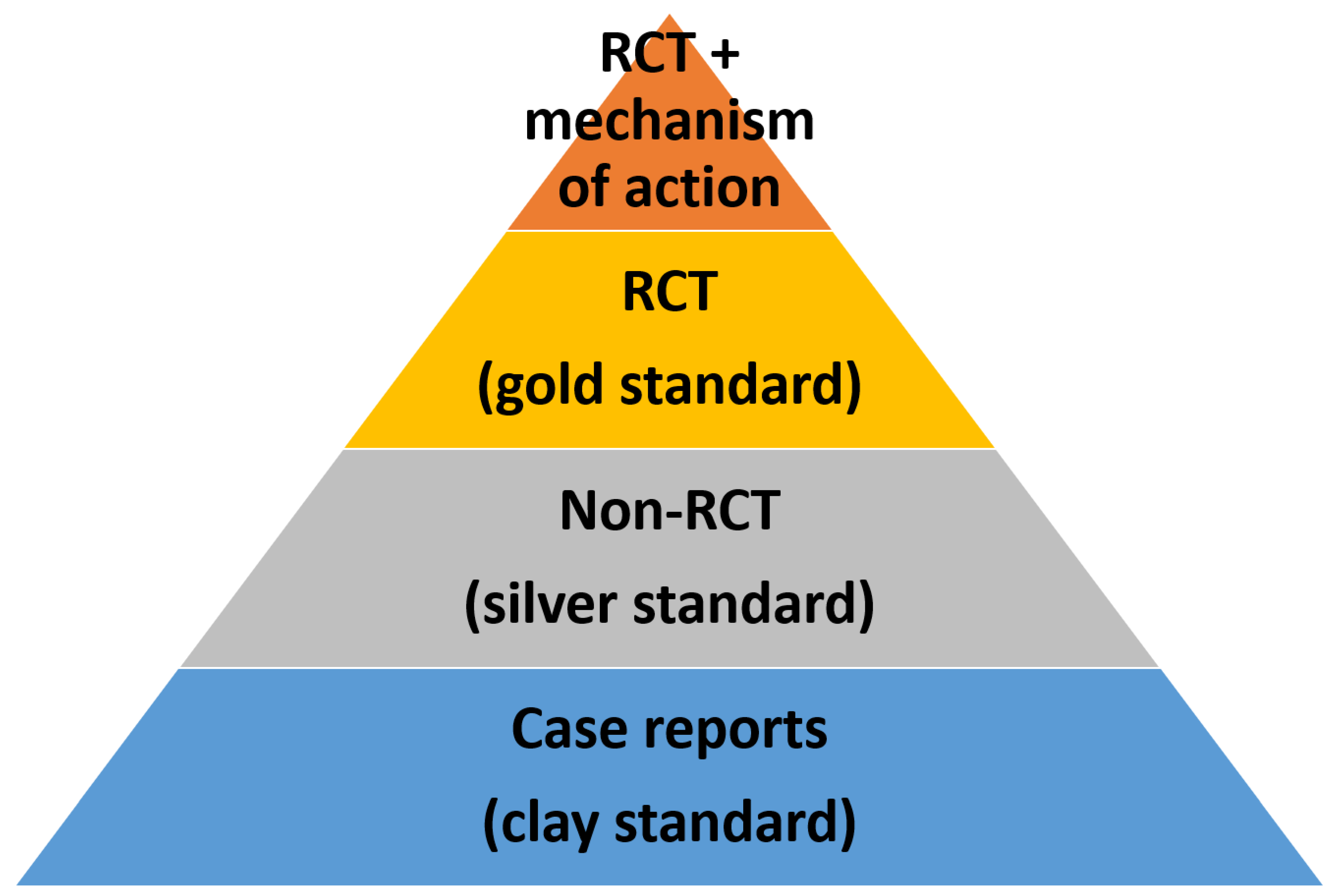
[O]nly RCTs allow researchers to find out whether a medical treatment is effective. (If preferred, this method is used to find out whether propositions of the form “This therapy is effective” are true or false.)[1] (p. 143)
The aim of an experiment, contrary to that of an observation or a measurement, is to garner empirical data relevant to a hypothesis, to test it and find out its degree of factual (or empirical) truth (true, true within such an error, or false). When there is a theory (hypothetico-deductive system of propositions) referring to the same facts, the hypothesis that undergoes an empirical test can also be assigned a theoretical truth value. In both cases, the truth in question is factual, not formal or mathematical.[1] (p. 131)
A datum becomes evidence when confronted with a hypothesis: in this case it either confirms or weakens the hypothesis to some extent.[1] (p. 28)
4. A Critique of Bunge’s Medical Philosophy
- Humans are open systems
- (C1) The confirmation of hypotheses is inherently stochastic and must be distinguished from the notion of objective truth; only comparisons between hypotheses in light of background knowledge and their ability to explain the observed data are objective
- (C2) RCTs are neither necessary nor sufficient to establish the truth of a causal claim
- (C3) Testing of causal hypotheses requires taking into account background knowledge and the context within which an intervention is applied
4.1. Evidence and Confirmation as Separate Concepts
Variations in regularity are generally specified probabilistically or stochastically, as random processes occurring in the ontic domain. Probability is a measure of the likelihood of an event occurring. The re-conceptualization of stochastic event regularities using the concepts of probability, might be styled ‘whenever event x, then on average event y’.[33]
It is natural to assume that the “propensity” of a model to generate a particular sort or set of data represents a causal tendency on the part of natural objects being modeled to have particular properties or behavioral patterns and this tendency or “causal power” is both represented and explained by a corresponding hypothesis.
It is well known that HIV infection is a necessary cause of AIDS: no HIV, no AIDS. In other words, having AIDS implies having HIV, though not the converse. Suppose now that a given individual b has been proved to be HIV-positive. A Bayesian will ask what is the probability that b has or will eventually develop AIDS. To answer this question, the Bayesian assumes that the Bayes’ theorem applies, and writes down this formula: P(AIDS|HIV) = P(HIV|AIDS). P(AIDS)/P(HIV), where an expression of the form P(A) means the absolute (or prior) probability of A in the given population, whereas P(A|B) is read (or interpreted) as “the conditional probability of A given (or assuming) B.”
If the lab analysis shows that b carries the HIV, the Bayesian will set P(HIV) = 1. And, since all AIDS patients are HIV carriers, he will also set P(HIV|AIDS) = 1. Substituting these values into Bayes’ formula yields P(AIDS|HIV) = P(AIDS). But this result is false, since there are persons with HIV but no AIDS. What is the source of this error? It comes from assuming tacitly that carrying HIV and suffering from AIDS are random facts, hence subject to probability theory. The HIV-AIDS connection is causal, not casual; HIV infection is only a necessary cause of AIDS. In conclusion, contrary to what Bayesians (and rational-choice theorists) assume, it is wrong to assign probabilities to all facts. Only random facts, as well as facts picked at random, have probabilities.
4.2. RCTs and the Truth Claim
The gold standard or “truth” view does harm when it undermines the obligation of science to reconcile RCTs results with other evidence in a process of cumulative understanding.
For example, since the mid-20th century, it has been known that lung cancer and smoking are strongly correlated, but only laboratory experiments on the action of nicotine and tar on living tissue have succeeded in testing (and confirming) the hypothesis that there is a definite causal link underneath the statistical correlation: we now know definitely that smoking may cause lung cancer.
4.3. RCTs and Background Knowledge
The bird infers, on repeated evidence, that when the farmer comes in the morning, he feeds her. The inference serves her well until Christmas morning, when he wrings her neck and serves her for dinner. Though this chicken did not base her inference on an RCT, had we constructed one for her, we would have obtained the same result that she did. Her problem was not her methodology, but rather that she did not understand the social and economic structure that gave rise to the causal relations that she observed.
It seems that an alternative realistic perspective on this question [whether antioxidant vitamins can prevent cardiovascular disease] is again ignored in favour of what purports to be an unassailable scientific observation of the results from RCTs. Here, once more, the effect of ignoring differences in mechanisms and contexts may be to close down research in this area prematurely.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bunge, M. Medical Philosophy: Conceptual Issues In Medicine, 1st ed.; World Scientific Publishing Co Pte Ltd.: Singapore, 2013; ISBN 9814508942. [Google Scholar]
- Howick, J. The Philosophy of Evidence-Based Medicine, 1st ed.; John Wiley & Sons Ltd.: Oxford, UK, 2011; ISBN 978-1-4051-9667-3. [Google Scholar]
- Thompson, R.P.; Upshur, R.E.G. Philosophy of Medicine, 1st ed.; Routledge: New York, NY, USA, 2017; ISBN 978-0-415-50109-5. [Google Scholar]
- Parkkinen, V.P.; Wallmann, C.; Wilde, M.; Clarke, B.; Illari, P.; Kelly, M.P.; Norell, C.; Russo, F.; Shaw, B.; Williamson, J. Evaluating Evidence of Mechanisms in Medicine: Principles and Procedures, 1st ed.; Springer International Publishing AG: Cham, Switzerland, 2018; ISBN 978-3-319-94609-2. [Google Scholar]
- Gillies, D. Causality, Probability, and Medicine, 1st ed.; Routledge: New York, NY, USA, 2019; ISBN 978-1-138-82930-5. [Google Scholar]
- Ahn, A.C.; Tewari, M.; Poon, C.-S.; Phillips, R.S. The Limits of Reductionism in Medicine: Could Systems Biology Offer an Alternative? PLoS Med. 2006, 3, e208. [Google Scholar] [CrossRef] [PubMed]
- Ahn, A.C.; Tewari, M.; Poon, C.-S.; Phillips, R.S. The Clinical Applications of a Systems Approach. PLoS Med. 2006, 3, e209. [Google Scholar] [CrossRef] [PubMed]
- Kesić, S. Systems biology, emergence and antireductionism. Saudi J. Biol. Sci. 2016, 23, 584–591. [Google Scholar] [CrossRef] [PubMed]
- Walach, H.; Loughlin, M. Patients and agents—Or why we need a different narrative: A philosophical analysis. Philos. Ethics Humanit. Med. 2018, 13, 13. [Google Scholar] [CrossRef] [PubMed]
- Schoenfeld, J.D.; Ioannidis, J.P.A. Is everything we eat associated with cancer? A systematic cookbook review. Am. J. Clin. Nutr. 2013, 97, 127–134. [Google Scholar] [CrossRef]
- Cofnas, N. Methodological problems with the test of the Paleo diet by Lamont et al. (2016). Nutr. Diabetes 2016, 6, e214. [Google Scholar] [CrossRef]
- Bains, W.; Schulze-Makuch, D. The Cosmic Zoo: The (Near) Inevitability of the Evolution of Complex, Macroscopic Life. Life 2016, 6, 25. [Google Scholar] [CrossRef]
- Bunge, M. Emergence and the Mind. Neuroscience 1977, 2, 501–509. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. An outline of general system theory. Br. J. Philos. Sci. 1950, 1, 134–165. [Google Scholar] [CrossRef]
- Bunge, M. Systemism: The alternative to individualism and holism. J. Socio Econ. 2000, 29, 147–157. [Google Scholar] [CrossRef]
- Bunge, M. Mechanism and Explanation. Philos. Soc. Sci. 1997, 27, 410–465. [Google Scholar] [CrossRef]
- Bunge, M. How does it work? The search for explanatory mechanisms. Philos. Soc. Sci. 2004, 34, 182–210. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. Basic concepts in quantitative biology of metabolism. Helgoländer Wiss. Meeresunters. 1964, 9, 5–37. [Google Scholar] [CrossRef]
- Djulbegovic, B.; Guyatt, G.H. Progress in evidence-based medicine: A quarter century on. Lancet 2017, 390, 415–423. [Google Scholar] [CrossRef]
- Miles, A.; Bentley, P.; Polychronis, A.; Grey, J. Evidence-based medicine: Why all the fuss? This is why. J. Eval. Clin. Pract. 1997, 3, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Welsby, P.D. Reductionism in medicine: Some thoughts on medical education from the clinical front line. J. Eval. Clin. Pract. 1999, 5, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Sniderman, A.D.; LaChapelle, K.J.; Rachon, N.A.; Furberg, C.D. The necessity for clinical reasoning in the era of evidence-based medicine. Mayo Clin. Proc. 2013, 88, 1108–1114. [Google Scholar] [CrossRef]
- Klement, R.J.; Bandyopadhyay, P.S.; Champ, C.E.; Walach, H. Application of Bayesian evidence synthesis to modelling the effect of ketogenic therapy on survival of high grade glioma patients. Theor. Biol. Med. Model. 2018, 15, 12. [Google Scholar] [CrossRef]
- Worrall, J. What Evidence in Evidence-Based Medicine? Philos. Sci. 2002, 69, S316–S330. [Google Scholar] [CrossRef]
- Goldenberg, M.J. On evidence and evidence-based medicine: Lessons from the philosophy of science. Soc. Sci. Med. 2006, 62, 2621–2632. [Google Scholar] [CrossRef]
- Urbach, P. The value of randomization and control in clinical trials. Stat. Med. 1993, 12, 1421–1431. [Google Scholar] [CrossRef] [PubMed]
- Deaton, A.; Cartwright, N. Understanding and misunderstanding randomized controlled trials. Soc. Sci. Med. 2018, 210, 2–21. [Google Scholar] [CrossRef] [PubMed]
- Stegenga, J. Down with the Hierarchies. Topoi 2014, 33, 313–322. [Google Scholar] [CrossRef]
- Walach, H.; Falkenberg, T.; Fønnebø, V.; Lewith, G.; Jonas, W.B. Circular instead of hierarchical: Methodological principles for the evaluation of complex interventions. BMC Med. Res. Methodol. 2006, 6, 29. [Google Scholar] [CrossRef] [PubMed]
- Anjum, R.L.; Copeland, S.; Rocca, E. Medical scientists and philosophers worldwide appeal to EBM to expand the notion of ‘evidence’. BMJ Evid.-Based Med. 2018. [Google Scholar] [CrossRef] [PubMed]
- Clarke, B.; Gillies, D.; Illari, P.; Russo, F.; Williamson, J. Mechanisms and the Evidence Hierarchy. Topoi 2014, 33, 339–360. [Google Scholar] [CrossRef]
- Lawson, T. Abstraction, tendencies and stylised facts: A realist approach to economic analysis. Camb. J. Econ. 1989, 13, 59–78. [Google Scholar]
- Brannan, M.J.; Fleetwood, S.; O’Mahoney, J.; Vincent, S. Critical Essay: Meta-analysis: A critical realist critique and alternative. Hum. Relat. 2017, 70, 11–39. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.S.; Brittan, G.G. Acceptibility, evidence, and severity. Synthese 2006, 148, 259–293. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.S.; Brittan, G., Jr.; Taper, M.L. Belief, Evidence, and Uncertainty: Problems of Epistemic Inference, 1st ed.; Springer International Publishing: Basel, Switzerland, 2016; ISBN 978-3-319-27770-7. [Google Scholar]
- Aronson, J.L. A Realist Philosophy of Science, 1st ed.; The Macmillan Press Ltd.: London, UK, 1984; ISBN 978-1-349-17380-8. [Google Scholar]
- Mingers, J. Systems Thinking, Critical Realism and Philosophy: A Confluence of Ideas, 1st ed.; Routledge: New York, NY, USA, 2014; ISBN 978-0415519533. [Google Scholar]
- Iftikhar, H.; Saleem, M.; Kaji, A. Metformin-associated Severe Lactic Acidosis in the Setting of Acute Kidney Injury. Cureus 2019, 11, e3897. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference, and Learning Algorithms, 3rd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bailer-Jones, C.A.L. Practical Bayesian Inference. A Primer for Physical Scientists; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-316-64221-4. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Klement, R.J. Beneficial effects of ketogenic diets for cancer patients: A realist review with focus on evidence and confirmation. Med. Oncol. 2017, 34, 132. [Google Scholar] [CrossRef] [PubMed]
- Anzala, O.; Sanders, E.J.; Kamali, A.; Katende, M.; Mutua, G.N.; Ruzagira, E.; Stevens, G.; Simek, M.; Price, M. Sensitivity and specificity of HIV rapid tests used for research and voluntary conunselling and testing. East Afr. Med. J. 2008, 85, 500–504. [Google Scholar] [PubMed]
- Subramanian, S.V.; Kim, R.; Christakis, N.A. The “average” treatment effect: A construct ripe for retirement. A commentary on Deaton and Cartwright. Soc. Sci. Med. 2018, 210, 77–82. [Google Scholar] [CrossRef]
- Bovens, L.; Hartmann, S. Bayesian Epistemology, 1st ed.; Oxford University Press: New York, NY, USA, 2003; ISBN 978-0199270408. [Google Scholar]
- Claveau, F.; Grenier, O. The variety-of-evidence thesis: A Bayesian exploration of its surprising failures. Synthese 2019, 196, 3001–3028. [Google Scholar] [CrossRef]
- Pearl, J.; Mackenzie, D. The Book of Why: The New Science of Cause and Effect, 1st ed.; Basic Books: New York, NY, USA, 2018; ISBN 978-0465097609. [Google Scholar]
- Russo, F.; Williamson, J. Interpreting causality in the health sciences. Int. Stud. Philos. Sci. 2007, 21, 157–170. [Google Scholar] [CrossRef]
- Claveau, F. The Russo-Williamson Theses in the social sciences: Causal inference drawing on two types of evidence. Stud. Hist. Philos. Sci. Part C Stud. Hist. Philos. Biol. Biomed. Sci. 2012, 43, 806–813. [Google Scholar] [CrossRef]
- Kossoff, E.H.; Zupec-Kania, B.A. Optimal clinical management of children receiving the ketogenic diet: Recommendations of the International Ketogenic Diet Study Group. Epilepsia Open 2018, 3, 175–192. [Google Scholar] [CrossRef]
- Fowler, J.F. 21 Years of biologically effective dose. Br. J. Radiol. 2010, 83, 554–568. [Google Scholar] [CrossRef]
- Klement, R.J.; Allgäuer, M.; Andratschke, N.; Blanck, O.; Boda-Heggemann, J.; Dieckmann, K.; Duma, M.; Ernst, I.; Flentje, M.; Ganswindt, U.; et al. Bayesian Cure Rate Modeling of Local Tumor Control: Evaluation in Stereotactic Body Radiotherapy for Pulmonary Metastases. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 841–849. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A. Benefits and limitations of randomized controlled trials: A commentary on Deaton and Cartwright. Soc. Sci. Med. 2018, 210, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Challenging the hegemony of randomized controlled trials: A commentary on Deaton and Cartwright. Soc. Sci. Med. 2018, 210, 60–62. [Google Scholar] [CrossRef] [PubMed]
- Connelly, J. Realism in evidence based medicine: Interpreting the randomised controlled trial. J. Health Organ. Manag. 2004, 18, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Wilde, M.; Parkkinen, V.P. Extrapolation and the Russo—Williamson thesis. Synthese 2019, 196, 3251–3262. [Google Scholar] [CrossRef]
- Tsang, E.W.K. Case studies and generalization in information systems research: A critical realist perspective. J. Strateg. Inf. Syst. 2014, 23, 174–186. [Google Scholar] [CrossRef]
- Mingers, J. A critique of statistical modelling in management science from a critical realist perspective: Its role within multimethodology. J. Oper. Res. Soc. 2006, 57, 202–219. [Google Scholar] [CrossRef]
| 1 | Bunge makes no further distinction between traditional, complementary, and alternative medicine, which is problematic, since all three refer to different concepts of medical systems. However, a detailed criticism of this conflation is not our concern here. |
| 2 | Bunge speaks of emergentism instead of emergence as in his former publications. |
| 3 | He broadly distinguishes three kinds of causal hypotheses: (i) Null hypotheses of no association between two putatively causally connected variables. (ii) General hypotheses of the form “X is a cause of that disease” or “the mechanism of X is Y”. (iii) Particular hypotheses such as “that individual is likely to suffer from that disease”. |
| 4 | This sounds like an argument by definition. Bunge postulates a meaning for “probability” and then concludes that the Bayesian conception is absurd. However, we are not going to pursue this point further here. |
| 5 | Bunge seems to have missed that Bayesians of the personalist stripe are ontological determinists and epistemic probabilists. |
| 6 | We use the term positivist-empiricist referring to a conjunction of concepts of logical positivism and Humean empiricism. The former rejects any reference to unobservable (metaphysical) entities, while the latter describes the scientific endeavor to test causal hypotheses by finding quantitative associations between observed events. Indeed, the literature on the philosophical and methodological foundations of EBM emphasizes statistical methodologies and avoids any reference to a particular ontology [2,19]. |
| 7 | More precisely, we can speak of the degree of belief in the truth of the hypothesis; this unifies Bunge’s arguments about hypotheses being confirmed and hypotheses being assigned truth values. |
| 8 | The data generating process is covered by the auxiliary hypotheses which can be about mechanisms. These auxiliaries serve as links between theoretical entities of the system under study and observable features in nature, in this way generating observable predictions [36]. |
| 9 | The distinction between the Real and the Empirical is borrowed from Critical Realism which itself exhibits many features of systems thinking [37]. |
| 10 | An example is a recent case report of a patient with chronic kidney disease experiencing severe lactic acidosis from taking the widely prescribed anti-diabetic drug metformin [38]. In the case report, the authors state their background knowledge as follows: “In the setting of dehydration with resultant acute kidney injury, metformin can accumulate, leading to type B lactic acidosis, especially in the presence of other nephrotoxic agents (ACEi and loop diuretics)”. They conclude to “use this patient as an example of the population that actually needs dosing adjustments”, a theoretical generalization supported by the evidence obtained from observations on this single patient. |
| 11 | |
| 12 | See Klement [43] for such a qualitative medical application of the evidence/confirmation distinction. |
| 13 | Actually, the very significance of knowing the average treatment effect for medical practice may be questioned. See Subramanian et al. [45] for a brief commentary. |
| 14 | |
| 15 | See chapter 5 in Judea Pearl’s “Book of Why” [48] for a detailed historical summary on how causation between smoking and lung cancer became established, including the argument that a “smoking gene” might be the underlying confounding factor. |
| 16 | |
| 17 | Ketone bodies are produced under conditions of low insulin levels such as during fasting or very low carbohydrate intake; in this respect, ketogenic diets can mimic fasting without necessarily restricting energy intake. Ketone bodies are transported through the blood-brain barrier by monocarboxylate transporters; this transport mechanism is therefore completely insulin- and GLUT-independent. |
| 18 | Critical realism maintains the naïve realistic view of an independently existing world of objects and structures giving rise to events that do and do not occur, while at the same time acknowledging the epistemological limitations of our observations and knowledge that are relative to our time period and culture [37]. Emergence and the concept of systems are central themes in critical realism [37], similar to Bunge’s systemism. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klement, R.J.; Bandyopadhyay, P.S. Emergence and Evidence: A Close Look at Bunge’s Philosophy of Medicine. Philosophies 2019, 4, 50. https://doi.org/10.3390/philosophies4030050
Klement RJ, Bandyopadhyay PS. Emergence and Evidence: A Close Look at Bunge’s Philosophy of Medicine. Philosophies. 2019; 4(3):50. https://doi.org/10.3390/philosophies4030050
Chicago/Turabian StyleKlement, Rainer J., and Prasanta S. Bandyopadhyay. 2019. "Emergence and Evidence: A Close Look at Bunge’s Philosophy of Medicine" Philosophies 4, no. 3: 50. https://doi.org/10.3390/philosophies4030050
APA StyleKlement, R. J., & Bandyopadhyay, P. S. (2019). Emergence and Evidence: A Close Look at Bunge’s Philosophy of Medicine. Philosophies, 4(3), 50. https://doi.org/10.3390/philosophies4030050





