1. Introduction
The St. Petersburg paradox was first discussed in letters between Pierre Rémond de Montmort and Nicholas Bernoulli, dated from 1713, and was supposedly invented by the latter [
1]. The paradox has been since then one of the most famous examples in probability theory and has been generalized by economists, philosophers and mathematicians, being widely applied in decision theory and game theory. The paradox arises from a very simple coin tossing game. A player tosses a fair coin until it falls heads. If this occurs at the
ith toss, the player receives
money unities. However, the paradox appears when one engages in determining the fair quantity that should be paid by a player to play a trial of this game. Indeed, in the eighteenth century, when the paradox was first studied, the main goal of probability theory was to answer questions that involved gambling, especially the problem of defining fair amounts that should be paid to play a certain game or if a game was interrupted before its end. Those amounts were then named
moral value or
moral price and are what we call
expected utility nowadays. It is intuitive to take the expected gain at a trial of the game or the expected gain of a player if the game were not to end now, respectively, as
moral values, and that is what the first probabilists established as those fair amounts. Nevertheless, when the expected gain was not finite, they would not know what to do, and that is exactly what happens in the St. Petersburg game. In fact, let
X denote the gain of a player at a trial of the game. Then, the expected gain at a trial of the game is given by:
since the random variable that represents the toss in which the first heads appears has a geometric distribution with parameter
.
Besides the fact that the gain is indeed a random variable with infinite expected value, the St. Petersburg paradox has drawn the attention of many mathematicians and philosophers throughout the years because it deals with a game that nobody in his right state of mind would want to pay large amounts to play, and that is what has intrigued great mathematicians such as Laplace, Cramer, and the Bernoulli family. Indeed, at that time, random variables with infinite expected value were quite disturbing, for not even the simplest laws of large numbers had been proven and the difference between a random variable and its expected value was not yet clear. In this scenario, the St. Petersburg paradox emerged and took its place in the probability theory.
The magnitude of the paradox may be exemplified by the comparison between the odds of wining in the lottery and recovering the value paid to play the game, as shown in [
2], in the following way. Suppose a lottery that pays 50 million money unities to the gambler that hits the 6 numbers drawn out of sixty. For simplification, suppose that there is no possibility of a draw and that the winner always gets the whole 50 million. Now, presume a gambler can bet on 16 numbers, i.e., bet on
different sequences of 6 numbers, paying
money unities, and let
p be his probability of wining. Then, it is straightforward that:
On the other hand, if one pays
money unities to play the St. Petersburg game, he will get his money back (and eventually profit) if the first heads appears on the 14th toss or later. Therefore, letting
q be the probability of the gambler recovering its money, it is easy to see that:
and
. Then, winning the lottery can be more likely than recovering the money in a St. Petersburg game. Of course, it is true only for a
money unities (or more) lottery bet. Thus, if one is interested in investing some money, the lottery may be a better investment than the St. Petersburg game. I would rather take my chances on Wall Street, for
p and
q are far too small.
Nevertheless, the paradox gets even more interesting when we compare the lottery in the scenario above and the St. Petersburg game in terms of their expected gain. On the one hand, as seen before, the expected gain in the St. Petersburg game is infinite. On the other hand, the expected gain at the lottery on the scenario above is:
Here the St. Petersburg paradox is brought to a twenty-first century context, for which even the layman can understand its most intrinsic problem: how can one expect to win an infinite amount of money, but have at the same time less probability of winning anything at all than someone who expects to lose money? Now imagine the impact of this result on the eighteenth century mathematicians, who did not know the modern probability theory, which greatly facilitates understanding of the St. Petersburg paradox.
A first attempt to solve the paradox was made independently by Daniel Bernoulli in a 1738 paper translated in [
3] and by Gabriel Cramer in a 1728 letter to Nicholas Bernoulli available in [
1]. In Bernoulli’s approach,
the value of an item is not to be based on its price, but rather on the utility it yields. In fact, the price of an item depends solely on the item itself and is equal for every buyer, although the utility is dependent on the particular circumstances of the purchase and the person making it. In this context, we have his famous assertion that
a gain of one thousand ducats is more significant to a pauper than to a rich man though both gain the same amount.
In his approach, the gain in the St. Petersburg game is replaced by the utility it yields, i.e., a linear utility function that represents the monetary gain of the game is replaced by a logarithm utility function. If a logarithm utility function is used instead, the paradox disappears, for now the expected incremental utility is finite and, therefore, may be used to determine a fair amount to be paid to play a trial of the game. The logarithm utility function takes into account the total wealth of the person willing to play the game, which makes the utility function dependent on who is playing the game, and not only on the game itself, in the following way.
Let
w be the total wealth of a player, i.e., all the money he has available to gamble at a given moment. We define the utility of a monetary quantity
m as
, in which the logarithm is the natural one. Therefore, letting
c be the value that should be paid to play a trial of the game, the expected incremental utility, i.e., how much utility the player expects to gain, is given by:
and we have an implicit relation between the total wealth of a player and how much he must pay to expect to gain a finite utility
.
Table 1 shows the values of
c for which
, i.e., the maximum monetary unities someone must be willing to pay to play the game, for different values of
w.
Note that, if , one must be willing to give all his money and eventually take a loan to play the game. In fact, the game is advantageous for players that have little wealth and, the richer the player is, the lower the percentage of his wealth that he must be willing to pay to play the game.
Although the logarithm utility function solves the St. Petersburg paradox, the paradox immediately reappears if the gain when the first heads occurs at the
ith trial is changed from
to
, in which
is another function of
i and not the identity one. For example, if
the paradox holds even with the logarithm utility function. This fact was outlined by [
4] that created the so-called super St. Petersburg paradoxes, in which
may take different forms.
There are many others generalizations and solutions to the St. Petersburg paradox, as shown in [
5,
6,
7], for example. However, the main goal of this paper is to present and generalize W. Feller’s solution by the introduction of an entrance fee, as will be defined on the next section. We generalize his method for the game in which the coin used is not fair, i.e., its probability of heads is
, and for the case in which the coin is a random one, i.e., its probability
of heads is a random variable defined in
.
2. Entrance Fee
A way of ending the paradox, i.e., making the game fair in the sense discussed by [
8], is to define an entrance fee
that should be paid by a player so he can play
n trials of the St. Petersburg game. This solution differs from the solutions given above in the fact that it does not take into account the utility function of a player, although it is rather theoretical, for it determines the cost of the game based on the convergence in probability of a convenient random variable. Furthermore, Feller’s solution is given for the scenario in which the player pays to play
n trials of the game, i.e., he pays a quantity to play
n trials of the game described above and his gain is the sum of the gains at each trial. In Feller’s definition, the entrance fee
will be fair if
tends to 1 in probability, in which
is the gain at the
kth trial of the game and
. If the coin is fair, it was proved by [
9] that
.
Note that, of course, . However, gives the rate in which the accumulated gain at the trials of the game increases, so that paying the entrance fee may be considered fair, for it will be as close to the accumulated gain in n trials of the game as desired with probability 1 as the number of trials diverges. Although classic and well-known in probability theory, Feller’s solution may still be generalized to the case in which the coin used at the game is not fair, in the following way.
As a generalization of the St. Petersburg game, one could toss a coin with probability
of heads. If
the paradox still holds, for:
However, if
,
so there is no paradox. Applying the same method used by [
9], we have, for the game played with a coin with probability
of heads, the entrance fee presented in the theorem below. This has remained an open problem for the last decades and is originally solved in this paper. Proofs for all results are presented in the
Appendix A.
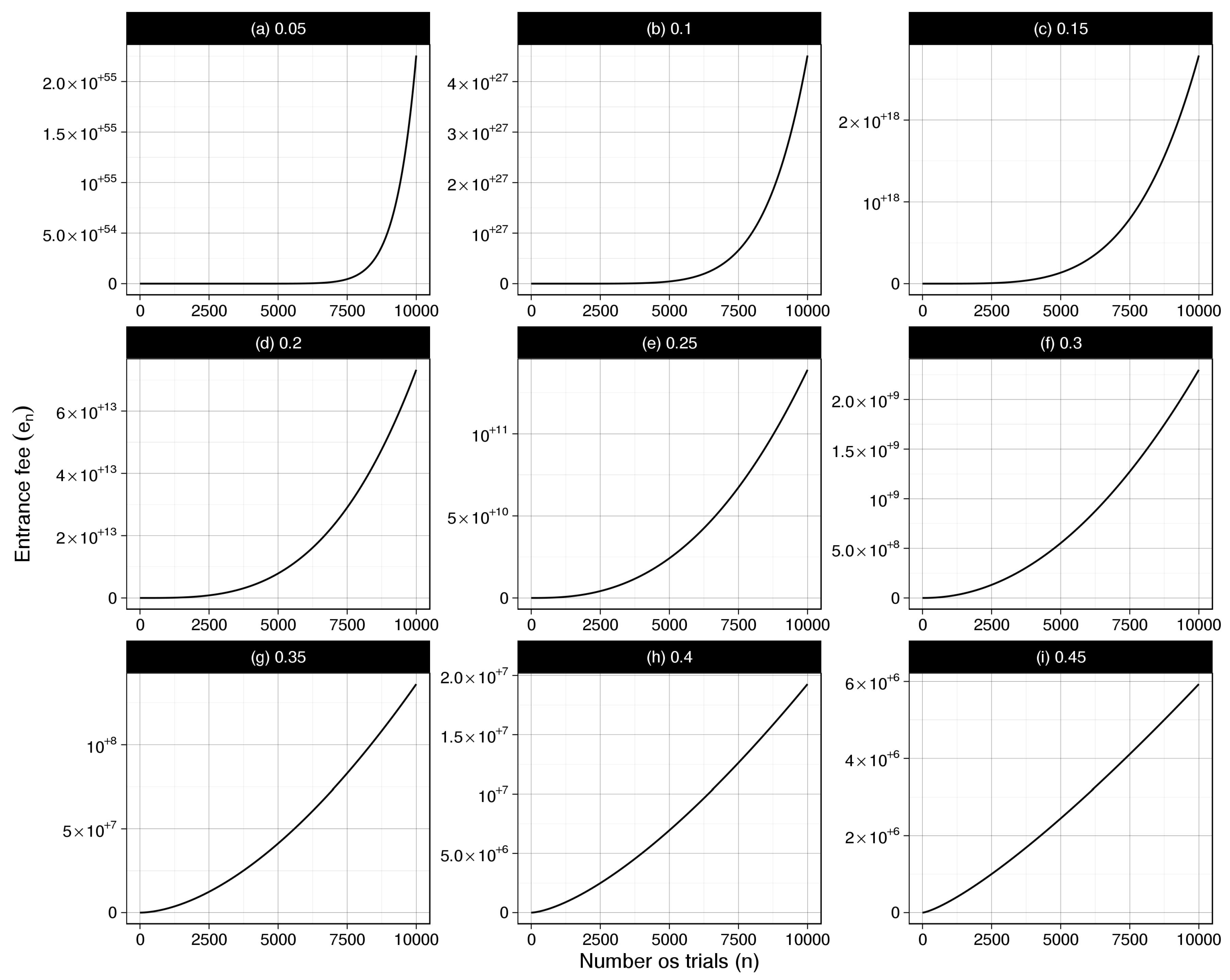
Theorem 1. Let . If and then Figure 1 shows the entrance fees for selected
n and
. It is important to note that the limit of
, as defined in Theorem 1, as
increases to
, does not equal the entrance fee
for the fair coin game. In fact,
for all values of
n. Therefore, the entrance fee has an interesting discontinuity property at
. Furthermore, as the value of
decreases, the entrance fee increases for each
n. This behaviour is expected for as the value of
decreases, it will take longer for the first heads to show up and the player can expect to gain more money.
3. Bayesian Approach
Persi Diaconis and Susan Holmes wrote that there is much further work to be done by incorporating uncertainty and prior knowledge into basic probability calculations and developed a Bayesian version of three classical problems in [
10]. Following this advice, we develop a Bayesian approach to the St. Petersburg paradox.
The Bayesian paradigm started with Reverend Thomas Bayes, whose work led to what is known today as Bayes theorem, and was first published posthumously in 1763 by Richard Price [
11]. Although his work inspired great probabilists and statisticians of the following centuries, it was not until the second half of the twentieth century that the Bayesian paradigm was popularized within the statistical society, for the development of computer technology made it possible to apply Bayesian analysis in a variety of theoretical and practical problems.
In the centuries following Bayes work, another branch of statistics, the frequentist one, was developed and exhaustively studied by probabilists, mathematicians and, of course, statisticians. The main characteristic of the frequentist statistics is that it treats the probability of an event as the limit of the ratio between the number of times the event occurs and the number of times the experiment, in which the event is a possible outcome, is repeated, the limit being taken as the latter diverges. The sharper reader may immediately conclude that this interpretation of probability has an intrinsic problem: not every experiment can be replicated. Consider, for example, the probability of rain tomorrow. By a frequentist perspective, this probability is the limit of the ratio between the number of times that rain occurs tomorrow and the number of times that tomorrow happens. However, it is naive to think of probability in this way, for tomorrow will happen only once. Therefore, there is a need for a more general interpretation of probability, and that is where the Bayesian approach comes into play.
In the Bayesian approach, the concept of probability may be interpreted as a measure of knowledge: how much is known about the odds of an event to occur. Of course, the concept of probability in Bayesian statistics may be considered by a frequentist statistician as subjective, for each person may have different knowledge about the likelihood of an event and, therefore, different people may have distinct conclusions analysing the same data. The debate between the Bayesian and the frequentist approach has been going on for the last decades, and we are not going to get into its merits. However, for a succinct and introductory presentation of the Bayesian approach see [
12].
In the context of the St. Petersburg paradox, the main difference between the frequentist and Bayesian approach manifests in the way in which the parameter
, i.e., the probability of heads of the game’s coin, is treated. In the frequentist approach,
is a
number in the interval
, either known or unknown. If it is known, as it was in
Section 1 and
Section 2, there is nothing to be done from a statistical point of view. However, if it is unknown, it may be estimated and hypotheses about it may be tested. On the other hand, in the Bayesian approach, the parameter
is a random variable, i.e, has a cumulative probability function
, that is called the priori distribution of
. The St. Petersburg game played with a coin with probability
may also be interpreted from a Bayesian point of view, as it is enough to take:
However, in this section, we will determine conditions on
F for which the paradox does not hold, i.e.,
. For this purpose, we have first to define the probability distribution of
X (the gain at a trial of the St. Petersburg game) from a Bayesian point of view. Applying basic properties of the probability measure we have:
for
has a geometric distribution with parameter
. Therefore, the expected gain
at a trial of the game is given, applying (4), by:
If
F is given by (3), it was proved in (1) and (2) that if
the paradox holds, whilst if
there is no paradox. This conclusion is the same from a frequentist point of view, and therefore is not of interest. The Bayesian approach gets more appealing when
F takes other forms, distinct from (3). As a motivation for the Bayesian approach, we present the case in which
is uniformly distributed in
, which raises some interesting questions about the Bayesian approach.
From (2), we know that if , the expected gain of the game is finite, therefore there is no paradox. However, suppose one incorporates prior knowledge to and takes it as a random variable assuming values in with probability 1 and distribution F. It would be expected that the paradox would not hold for any distribution F with such properties. However, this does not happen.
Suppose
is uniformly distributed in
. Then,
The result (5) raises a couple of interesting questions about the Bayesian approach to the St. Petersburg paradox. Firstly, one may ask for which prior distributions
F the paradox holds. Theorem 2 answers this question, giving a sufficient condition for the absence of paradox in the Bayesian approach. Then, one could inquire what is the entrance fee for the case in which
is a random variable uniformly distributed in
. In
Section 4, we establish the entrance fee for this case.
We now treat the case in which the probability
of heads in each trial of the game is a random variable, defined as
, taking values in the interval
with probability 1 and distribution
F. The case in which
is not of interest, for the paradox holds for any
F with this property. Therefore, in this scenario, the expected gain at a trial of the game is given by:
for any fixed
. From now on, consider
fixed in
, unless said otherwise. Now,
so that the paradox will exist if, and only if,
. The lemma below gives a sufficient condition for the absence of paradox and will be used to prove the main result of this section.
Lemma 1. Suppose that F is absolutely continuous in and . If and for some , there is no paradox.
Furthermore, the lemma bellow gives an obvious condition for the absence of paradox.
Lemma 2. If there exists an such that , then .
If F is discrete or singular on an -neighbourhood of , and there is no such that , then there may or may not be paradox. For example, if F is such that , the paradox does not hold. On the other hand, if is so that , the paradox holds. Now, if F is absolutely continuous in , the paradox holds if, and only if, the limit of the probability density of at is greater than zero.
Theorem 2. Suppose that F is absolutely continuous in and . There is no paradox if, and only if, .
In summary, there will be no paradox if there is no probability mass on nor around it. Then, if F is discrete or singular, there may or may not be paradox. However, if F is absolutely continuous in a neighbourhood of , there will be no paradox if, and only if, the probability density tends to zero as tends to . Otherwise, there would be a probability mass in every neighbourhood of .