The Geometry of Thought: Circling Through Concepts

Abstract

The goal of this paper is to shed light on the nature of mathematical practice, i.e., on “doing mathematics”. It explores Gödel’s perspective, which offers an approach to understanding mathematics centered on concepts, objects, and structures. The paper has two parts. In the first part, we situate Gödel’s reflections against the backdrop of formalism and Platonism. In the second part, we present the view shaped by Gödel’s ideas that resonates with contemporary discussions in the philosophy of mathematical practice, particularly in its attention to abstraction, generalization, and conceptual discovery, as essential components of mathematical reasoning. We illustrate this view through concrete examples from category theory and geometry. This approach reveals that mathematical practice, far from being merely formal, is a dynamic interplay of intuition, abstraction, structural, and conceptual reasoning. Such a focus underscores the need for developing the theory of concepts along the lines proposed by Gödel to provide a more natural framework for thinking about mathematics.

1. Introduction

The philosophy of mathematical practice has become a major area of inquiry in recent decades, with works such as [1,2] shaping contemporary debates. However, while much of this research has focused on figures like Pólya and Lakatos, Gödel’s views on mathematical practice remain underexplored. This paper aims to bridge this gap by analyzing Gödel’s insights into mathematical reasoning, particularly his emphasis on concepts, objects, and structures as fundamental to mathematical knowledge.

To discern Gödel’s views that inspired the position presented in this paper, we will primarily rely on his remarks from the recently published Max Phil notebooks. These remarks address philosophical issues that are not fully explored in Gödel’s published works, highlighting reflections on mathematical concepts. Although the notebooks have just begun to make their way into scholarly circles, they provide a rich and valuable source for rethinking the epistemology of mathematics and mathematical practice. In what follows, we will refer to specific passages and discuss their relevance to contemporary debates. In this regard, we found volumes I and III particularly informative (written between 1934 and 1941, during which period Gödel grappled with the philosophical implications of his incompleteness theorems and the problem of the Continuum Hypothesis), as well as volumes X and XII (written between 1943 and 1945, when he focused on his Russell paper [3], which examines the nature and role of concepts in mathematics and the possibility of solving the paradoxes by developing a formal theory of concepts).

Our approach contributes to two key discussions. First, we argue that Gödel’s perspective offers a non-formalist alternative to the formalist and constructivist views in the philosophy of mathematics. While Gödel engaged with Hilbert’s program, his reflections on intuition and conceptual understanding offer quite a distinct epistemology of mathematics. Second, this paper positions Gödel’s thought within the broader landscape of mathematical practice, showing how his emphasis on concepts and structures aligns with contemporary studies on the cognitive and structural aspects of mathematical discovery.

In doing so, we respond to the recent literature on mathematical practice while also clarifying Gödel’s stance on formalism, Platonism, and mathematical intuition. This study is thus both historical—in its examination of Gödel’s unpublished manuscripts—and systematic, in its effort to integrate Gödel’s insights into current debates.

Both philosophers and mathematicians, influenced as they are by logicism, finitism, and formalism, tend to assert the following:

(1)

Mathematical work consists of deductions carried out within a specific, predefined formal system.

The aforementioned philosophical standpoints, along with the projects they inspired, have underscored the importance of formalizing mathematics. Formalization is attributed not only the role of ensuring the logical correctness of proofs but also that of determining the nature and justification of mathematical knowledge. By formalizing a mathematical theory, its fundamental truths are distilled, enabling a critical examination of their nature.

The emphasis on formalization in mathematics finds its roots in the foundational crises of the late 19th and early 20th centuries. Figures such as Frege, Russell, and Hilbert sought to resolve ambiguities and paradoxes in mathematics by grounding it in formal logic. Hilbert’s formalist program, in particular, was motivated by a desire to secure the consistency and completeness of mathematical theories, a goal partially challenged by Gödel’s incompleteness theorems [4].

Within Hilbert’s program, the formalization was intended to assist in ensuring the consistency of the finitary aspect of mathematics. This served to justify classical mathematics by demonstrating it to be a conservative extension of its finitary part. Among these schools of thought, formalists advanced the most in appreciating the role of formal systems in mathematics. Some of them even equated mathematics with the manipulation of symbols, contending that mathematics consists solely of the knowledge and practice that can be encapsulated within a formal system.

However, the formalist agenda faced significant challenges, most notably Gödel’s incompleteness theorems, which demonstrated that any sufficiently rich, consistent formal system capable of expressing arithmetic would contain true statements that are unprovable within the system itself [4]. This result not only questioned the feasibility of Hilbert’s program but also underscored the limitations of purely formal approaches in capturing the entirety of mathematical knowledge:

So we are confronted with a strange situation. We set out to find a formal system for mathematics and instead of that found an infinity of systems, and whichever system you choose out of this infinity, there is one more comprehensive, i.e., one whose axioms are stronger. ([5], p. 47)

Apart from that, this emphasis on formalization in mathematics has led to an overestimation of its role, with mathematical work often equated to activity within the corresponding formal system. Although this perspective is flawed and heavily influenced by specific philosophical doctrines, it remains prevalent among philosophers. Among mathematicians, however, this standpoint is particularly problematic, as it stands in stark contrast to their actual practice, which can be more accurately described as follows:

(2)

Mathematical work consists of discovering the mathematical world and refining the view of the objects within it.

Contrary to formalist perspective, mathematical practice frequently relies on intuition and heuristic reasoning. For instance, the development of non-Euclidean geometry and the use of diagrammatic reasoning in topology demonstrate that much of mathematical discovery transcends formal manipulation. Similarly, the classification of finite simple groups, while formally expressible, was achieved through a combination of deep insights, intuition, and collaborative efforts spanning decades. Lakatos’ work on the methodology of mathematical proofs further illustrates how informal approaches contribute to the refinement and validation of mathematical theories [6].

The examples mentioned are by no means solitary. From a more foundational perspective, Gödel’s work on the Incompleteness theorems and the consistency and independence of the Continuum Hypothesis (CH) from Zermelo–Fraenkel set theory with the Axiom of Choice (ZFC) illustrates the limits of formal systems in resolving mathematical questions.

Some perspectives in the philosophy of mathematics approach mathematical practices at face value, offering their explanation in terms of the nature of mathematical objects or other entities involved in the development of mathematical knowledge. One such perspective is Gödel’s Platonist view, which asserts the objective existence not only of mathematical objects but also of mathematical concepts, whose comprehension he takes to be essential for advancing mathematical knowledge. In the second part of this paper, we will argue that this standpoint enables us to interpret mathematical practices as strategies for uncovering the interrelations of mathematical concepts.

It could then be gathered that a key tension in the philosophy of mathematics lies in the opposition between Gödel’s Platonism and Hilbert’s formalism. However, this tension is often misrepresented as a strict opposition. Gödel was not categorically opposed to Hilbert’s formalist approach; rather, he engaged critically with its assumptions while advocating for a broader conception of mathematical knowledge.

It is important to recognize that Hilbert’s program was not purely formalist in the sense of denying mathematical meaning beyond symbolic manipulation—as some brands of formalism stemming from Hilbert surely were. For instance, Curry ([7], p. 28) writes of the primitives of his formal systems (calling them ’tokens’) that we “can take for those tokens any objects we please, and similarly we can take for operators any ways of combining these objects which have the requisite formal properties”.

On the other hand, as Hilbert himself stated, axiomatization is not the discovery of new theorems but the systematic exploration of the conditions necessary and sufficient to ground them ([8], p. 88). This perspective leaves room for intuition and heuristic reasoning, which Gödel also considered essential to mathematical thought.

The key point of divergence was Hilbert’s belief in the solvability of all mathematical problems, famously articulated in his dictum that “every definite mathematical problem must necessarily be susceptible of an exact settlement” ([9], p. 444). Gödel’s incompleteness theorems demonstrated the impossibility of a complete, consistent formal system for arithmetic, thus challenging Hilbert’s program. However, Gödel himself acknowledged that Hilbert’s finitary proof methods remained valid within their domain.

The question, then, is not whether Gödel rejected formalism outright but rather how his Platonist epistemology provided an alternative justification for mathematical truth. Gödel’s view that mathematical objects have an independent existence suggests a practice of mathematics that is not merely formal, but conceptual, grounded in the discovery of objective structures rather than the mere manipulation of symbols. This perspective aligns with contemporary discussions on the cognitive and structural aspects of mathematical practice (cf. [10,11]).

The following remark of Gödel highlights the diverse range of activities that constitute mathematical practice:

Remark Mathematics: Important activities of the mathematician:

1.

Generalizing (theorem) = consider what is essential in a proof.

2.

Rendering precisely (an intuitive proof).

3.

Continuizing = assign continuous values to originally discrete variables.

3.1

Generalizing (concepts) = defining concepts in a broader area.

4.

Approximate concepts (by simpler ones) and theorems by weaker ones.

5.

Extensionalizing: transition from the intensional to the extensional, omitting certain peculiarities (examples: constructible set, axiom of replacement, Frege’s formalization of propositional calculus).

6.

Calcularizing = seeking out operations that can be used to “calculate”; that is, that satisfy certain commutativities.

4.1

Specializing (first give the proof of a general theorem for a special case). Very often, this special case is found through intuition; then prove abstractly and then render precisely. 1. For the general case; cf. below.

7.

Elegantizing (of proofs and definitions) = simplify; cf. 1.

8.

Finding out the “meaning” of a proposition (in order to find the proof).

9.

Constructivizing (of non-constructive proofs), that is, descending to lower types. ([12], pp. 230–231)

An adequate characterization of mathematical work, along with the knowledge it generates, becomes particularly crucial in instances where established mathematical practice fails to yield definitive results—for instance, in the paradigmatic case of the ZFC theory’s inability to resolve the CH. In such situations, mathematicians may find it necessary to clarify the nature of mathematical knowledge and the means by which it is acquired. This need for reflection may explain why Gödel turned his attention to the nature of mathematical knowledge.

According to Gödel, mathematical knowledge is grounded in an understanding of mathematical concepts, such as the concept of a set, and in deriving the properties of the mathematical objects that these concepts encompass. Our paper aims to clarify and substantiate this claim by proposing an analysis of mathematical language—specifically, the terminology employed by mathematicians that warrants philosophical scrutiny. The analysis seeks to elucidate the meanings of key terms such as concepts, objects, and the related notion of structure within the context of mathematics. This approach will enable us to determine the types of entities to which mathematical terms refer and better understand the descriptive objectives of mathematical theorems. By applying this analysis to examples drawn from mathematical practice, we aim to demonstrate that it offers a faithful representation of mathematical activity and provides valuable insights into the nature of mathematical work.

2. Concept–Structure–Object

In this section, we attempt to clarify the terminology employed throughout the paper. The central notion is the notion of concept, which we will use to elucidate the related notions of object and structure. Before presenting our understanding of the notion of concept, we will briefly examine how it has been utilized and explained in philosophy. This exploration highlights the richness of the notion and helps us unearth its core meaning, which will serve as the foundation for our analysis.

We do not attempt to address all debates surrounding the notion of concept. Instead, our focus is on the role that concepts play in the acquisition and expansion of knowledge. For our purposes, the critical aspect is the possibility of attaining objective knowledge through an understanding of conceptual content. Specifically, we are interested in the relationship between concepts and objects, as this connection enables knowledge derived from understanding concepts to be applied to the objects they encompass. We will justify our characterization of mathematical knowledge through an analysis of mathematical language using the notions of concept, object, and structure. This focus shapes and, by necessity, limits our overview of the various philosophical theories of concepts.

For instance, our approach inevitably excludes certain prominent contemporary analyses of concepts. Fodor’s representational theory of mind, which characterizes concepts as mental symbols structured and manipulated to facilitate reasoning and knowledge acquisition [13], is an example at hand. The same holds for Brandom’s and other inferentialist views, according to which the meaning of a concept is determined by its role in a network of inferential relations rather than by an internal essence [14]. This perspective is particularly relevant when analyzing the meaning of logical concepts, as we will emphasize in the second part of the paper. However, engaging with such views, despite their significance, lies outside the scope of this paper. Our objective is not to provide a comprehensive survey but to assemble perspectives that are most congenial to addressing the specific issues at hand.

2.1. Concepts in Philosophy

Throughout the history of philosophy, diverse vistas have emerged concerning the possibility of gaining knowledge about concepts—their nature, formal properties, and the founding of a coherent theory of concepts. Views on the nature of concepts are typically grounded in broader philosophical frameworks with concepts attributed varying ontological statuses. These include viewing concepts as independently existing abstract objects, mental representations of empirical reality, forms of human thought, or linguistic constructs. The ontological status ascribed to concepts fundamentally influences whether their understanding yields knowledge and whether this knowledge is considered objective or subjective.

Concepts have also been understood in different functional roles: as bundles of properties that objects falling under them satisfy; as functions mapping objects to truth values; or as functions from sets of possible worlds to sets of objects in those worlds. Each of these perspectives provides unique insights into how concepts relate to objects and to the broader epistemological projects based upon these foundations.

In what follows, we offer a concise overview of the theories most relevant to our purposes. Leaving out the details of the theories, we concentrate solely on their key idea. Each of the three theories we will mention addresses a specific aspect of concepts that we consider essential for understanding their role in mathematical practice. These theories address the nature of concepts, their epistemological significance, and their relationship to objects and the language through which they are expressed. Importantly, the perspectives discussed here have been particularly influential in shaping Gödel’s understanding of concepts, offering bridges connecting language, thought, and reality. This overview is thus supposed to place Gödel’s notion of concept within the philosophical context, while also motivating the subsequent discussion on the notion itself.

An important thing to bear in mind is that Gödel’s work suggests a deeply Platonist view, treating concepts as objective and independent of human cognition. He argued that mathematical concepts, such as the concept of set, are not mere linguistic constructs but possess an existence that transcends subjective interpretation [15]. We gain knowledge of mathematical objects by recognizing the concepts instantiated in them and improving our understanding of their content. This perspective underpins the relationship between concepts and the objects they describe, emphasizing the objective nature of mathematical truths.

2.1.1. Plato

In Plato’s philosophy, the notion of concept, referred to as Form or Idea, occupies a central role. Forms are universals that manifest themselves in individual objects—their imperfect copies—but exist independently from them. They are immutable and eternal essences of individual objects that make our sensory experience of the physical world intelligible. Objects in this world possess the characteristics they do to the extent to which they participate in or resemble the corresponding Forms.

Plato maintained that only Forms possess true existence, being eternal and changeless, while concrete objects are in the state of constant change and decay. Consequently, only Forms can serve as the objects of true knowledge that, according to Plato, must be of something stable and enduring. Our mind has the capacity to access and comprehend these Forms. The primary tools for this comprehension are reason and intellect.

By contrast, material objects, subject to change and apprehended through often deceiving sensory experience, cannot provide such knowledge but only unreliable belief. The only potential for understanding material objects lies in perceiving them as imperfect copies or shadows of the Forms, which makes knowledge of Forms applicable to the objects of the sensory world. Encountering imperfect manifestations of the Forms in our sensory experiences triggers a process of recollecting the perfect knowledge of Forms that our souls once possessed. Forms thus serve as the ultimate objects of understanding, providing a stable and reliable foundation for all epistemological endeavors.

Plato conceived of a distinct and separate conceptual sphere, the realm of Forms. This realm has a hierarchical structure, which culminates in the Form of the Good. This further implies a fundamental order and interconnectedness within the conceptual sphere, suggesting a unified and coherent system of reality. He recognized a profound connection between his realm of Forms and the realm of mathematical objects. Similar to the Forms, mathematical objects possess characteristics of perfection and immutability and are primarily apprehended through intellectual understanding rather than sensory experience. Mathematical truths are likewise universal and eternal (cf. Books VI and VII of The Republic).

This framework has had a profound influence on mathematical Platonism, advocated by Gödel, where mathematical entities are likened to abstract, immutable Forms. Plato’s theory of Forms aligns particularly well with Gödel’s version of mathematical Platonism, which acknowledges not only mathematical objects but also mathematical concepts as objective entities. For instance, the concept of a perfect circle, inaccessible in the physical world, aligns closely with Plato’s Form of circularity, serving as the basis for reasoning and mathematical proofs.

As we will explore further, Gödel also views the web or sphere of mathematical concepts as hierarchically structured. This hierarchy is defined by various relationships between concepts, each of which plays an important role in shaping our understanding of mathematical knowledge. The recognition of mathematical concepts and their relationships is crucial for acquiring this type of knowledge. Similarly, in Plato’s theory, identifying an object as a circle involves recognizing the underlying Form of circularity instantiated in it. This recognition enables us to apply the knowledge of this Form to its instances. Leibniz’s theory of concepts, which we examine next, can be seen as shedding light on the process of gaining and applying this knowledge.

2.1.2. Leibniz

Gödel’s understanding of the notion of concept appears to be deeply influenced by Leibniz’s theory of concepts and intensions (cf. [16]). According to Leibniz, concepts or ideas express the essence or nature of the objects subsumed under them. Complex concepts are composed of simpler ones, which are represented by characteristics or marks that collectively define the object’s nature. Leibniz referred to these bundles of essential marks, which are indispensable for the concept’s identity, as intensions. Knowledge, in this framework, is acquired by discerning the logical relationships and interconnections among the marks that constitute a concept. Thus, discovering the truth about a concept involves analyzing it into simpler, foundational components and uncovering their interrelations.

A proper understanding of a concept allows us to infer the properties of the object it defines. As Leibniz noted,

Although, therefore, the idea of a circle is not similar to the circle, truths can be derived from it which would be confirmed beyond doubt by investigating a real circle. ([17], p. 208)

A perfect understanding of a concept arises when it is sufficient to identify the objects falling under it through a clear list of marks and criteria, all of which are distinctly understood and present in the mind ([18], p. 23). This level of comprehension seems hardly attainable. Instead, knowledge is a process of progressive and endless clarification and illumination: the more we analyze and understand the relationships between concepts, the closer we come to grasping the truths of the world. The knowledge we arrive at is often incomplete. For instance, in Leibniz’s words,

Here is a circle: if you know that all the lines from the center to the circumference are equal, in my opinion, you consider its essence sufficiently clearly. Still, you have not comprehended in virtue of that innumerable theorems. (as cited in [19], p. 432)

This limitation arises because we are unable to immediately grasp all the relations a concept entails, as well as those it shares with other concepts. To achieve a more comprehensive understanding of a circle, we must consider it from various perspectives, relating it to different concepts, and thus, exploring its alternative definitions. Leibniz emphasized this point:

We do not have any idea of a circle, such as there is in God, who thinks all things at the same time … We think about a circle, we provide demonstrations about a circle, we recognize a circle: its essence is known to us—but only part by part. If we were to think of the whole essence of a circle at the same time, then we would have the idea of a circle. (as cited in [19], p. 432)

In this sense, attaining complete knowledge of a circle—or any concept for that matter—requires apprehending every possible property or expression of its essence. In other words, it involves fully understanding all of its definitions. The following remark testifies that Gödel was also concerned with the relationship between a concept and its definitions and illustrates his understanding of a concept’s definition as a description of its interrelation with other concepts:

Remark Philosophy: How is it possible to have clear (although not distinct) concepts without knowing their definition, if the definition constitutes the essence of the concept? It seems to follow from this that the concept is an entity that exists independently of the definition, which merely describes it (through its relations to other concepts). ([20], pp. 4–5)1

This subject will be revisited in the next section, where we will explore its implications in greater depth, particularly in relation to our primary objective.

2.1.3. Frege

Frege considers concepts primarily in their relationship to language, specifically through the meaning they impart to linguistic expressions, such as predicates (see [21]). In Frege’s framework, the meaning of an expression is characterized by two dimensions: reference (Bedeutung) and sense (Sinn). The reference of a linguistic expression is the specific object or entity it points to in the world, while its sense is the mode of representing this entity. The sense of an expression represents its reference in a specific way, effectively determining it. For one to identify the reference of an expression, it is essential to grasp its sense.

It is common to associate concepts in Frege’s theory with the reference of predicate expressions. However, concepts are also closely tied to Frege’s sense, which captures the intensional aspect of meaning. Concepts allow us to represent objects in a particular way and understand their characteristics. In Frege’s framework, this role is attributed to the sense of expressions referring to these objects. Gödel’s view on this matter is reflected in the following remark:

The neglect of the conceptual content of sentences (i.e., the ’sense’ according to Frege) also is responsible for the wrong view that the conclusion in logical inference, objectively contains no information beyond that contained in the premises. ([22], p. 350)

Associating concept with Frege’s sense allows us to view them not only as the references of predicates but also in relation to names—expressions that refer to mathematical objects. This is also suggested by Gödel’s following statement, which links concepts to the means of denoting, a notion that closely resembles Frege’s idea of sense:

Remark Philology: With every word, one must distinguish between what it denotes (e.g., the individual person) and that “by means of which” it denotes (the concept of a person). ([20], p. 19)2

Gödel approached concepts with a focus on their epistemological role in logical and mathematical reasoning. Such a role Frege ascribes primarily to the sense, positing that understanding the sense of an expression, and subsequently determining its reference, constitutes the process of gaining knowledge. For this reason, it seems more plausible to associate Gödel’s concepts with the senses of expressions rather than their references. Concepts might be understood as what we grasp when we comprehend the sense of an expression. This broader interpretation positions concepts as integral to understanding both the logical structure of language and the nature of mathematical truth. For a different interpretation of Gödel’s notion of concept, see [16].

2.2. Our Notion of Concept

A central argument of this paper is that mathematical reasoning is best understood through an interplay between concepts, objects, and structures. Gödel’s writings suggest that these three elements form a hierarchy: mathematical concepts define the essential characteristics of mathematical entities, mathematical objects instantiate these concepts, and mathematical structures describe the relationships between them. By ’structure’, we refer not merely to set-theoretic relational systems but also to the abstract patterns recognized in category theory. In other words, we take the structural properties of an object to be those that remain invariant under specific morphisms. As such, they can be viewed as properties that do not individuate an object but relate different instances of the same concept, which is determined by the preserved structural properties. We do not treat structures as distinct mathematical entities whose metaphysical nature should be clarified; rather, we study them as they emerge from mathematical practice (as in [23]). In what follows, we elaborate on how structural properties mediate our understanding of mathematical objects and concepts and argue that this triadic framework is crucial for understanding how mathematical knowledge develops in practice.

In modern philosophy of mathematics, this perspective aligns with recent discussions on structuralism and mathematical cognition. Structuralist approaches [24,25] emphasize that the primary objects of mathematics are structures rather than individual objects. Our understanding of structures aligns most closely with the variant of structuralism known as conceptual structuralism—by connecting structures to mathematical concepts [26] and category-theoretic structuralism—by its understanding of structural properties [27]. Research into the philosophy of mathematical practice [2,10] has likewise stressed the role of conceptual discovery and structural reasoning in mathematical work, moving beyond the narrow focus on formal derivations.

Gödel’s framework anticipates these developments. He argued that mathematical concepts have objective reality, independent from formal representations, and that mathematical objects are recognized through their structural properties rather than defined purely syntactically. This is particularly evident in category theory, where structures (such as adjunctions and functors) take precedence over specific object definitions.

To illustrate the relevance of this framework to mathematical practice, consider the classification of finite simple groups. While each group is formally defined through axioms, the real breakthrough came from understanding their structural relationships—such as the way they fit into the overarching “periodic table” of groups. Similarly, in algebraic geometry, different formulations of elliptic curves (Weierstrass equations, modular forms, homotopy types) instantiate the same underlying mathematical concept but highlight different structural properties depending on the context.

Thus, Gödel’s concept–structure–object framework captures a fundamental feature of mathematical practice: the process of refining and abstracting concepts through their structural manifestations. This approach not only aligns with Gödel’s Platonism but also resonates with modern views on mathematical reasoning as an interplay between formal and conceptual understanding (cf. [1]).

Arriving at, analyzing, or understanding a concept is essential for the acquisition of knowledge; yet these verbs seem misplaced when directly applied to objects. This mismatch becomes less apparent in the case of mathematical objects, due to their abstract nature. However, just as propositional knowledge of physical objects requires subsuming them under some concept, the same holds true for mathematical objects.

The first step in acquiring or expanding mathematical knowledge is thus to identify the concepts used to describe mathematical objects and to analyze these concepts to uncover their properties. This process underscores the fundamental distinction between concepts and objects, a distinction that is crucial for the epistemology of mathematics. Mathematical objects subsumed under the same concept have properties that individuate them from one another. For example, a circle as an object has a diameter of a specific length. However, knowing the length of a circle’s diameter represents a distinct kind of knowledge compared to the understanding that all its diameters are the same in length, which is a fundamental characteristic contained in the concept of a circle. In our view, while mathematics seeks knowledge of mathematical objects, this knowledge is invariably mediated by the concepts under which these objects are subsumed. Although we cannot grasp a mathematical object in itself, we can comprehend the structure it instantiates. This structure reveals the concept under which the object falls and serves as the key to understanding it. For example, recognizing the structural property of rotational invariance in a circle (or the identity of all its diameters) allows us to identify the concept of a circle instantiated in it, thereby deepening our understanding of the circle. As we will see later, there is a certain back-and-forth process at play here, underpinning our knowledge of mathematical objects and concepts.

Our perspective aligns with Gödel’s view, as articulated in the following remark:

The axioms correspond to the concepts, and the models which satisfy them correspond to the objects. The representations give the relation between concepts and objects. ([28], p. 141)

In this interpretation, models are the concrete representations of axioms, just as objects embody the concepts under which they fall. What determines an object as a representation of a particular concept is its structure. In other words, the structural properties of an object allow it to instantiate and represent a given concept, bridging the gap between abstract concepts and the objects they define.

The threefold relationship between objects, their structural properties, and the concepts they instantiate can appear somewhat vague at first glance. An additional example might illuminate the distinction, which Gödel regarded as highly significant.

In response to Reinhardt’s paper [29], which examined the formulation of new axioms for set theory grounded in reflection principles and elementary embeddings, Gödel’s comment was concise yet notably telling (our emphasis):

However, as to the justification of the axioms attempted here, Gödel feels that it is rather unsatisfactory and that something better could be achieved by a proper analysis of the notion of structural property of the concept of set, which would then lead to the reflection principles in the form ’any structural property of the concept of set is reflected by some set’. ([29], p. 189)

Gödel underscores the critical role of structural properties in our pursuit of mathematical knowledge. However, as evidenced by his remarks on Reinhardt’s paper, this emphasis on structural properties shifts its focus—from being tied to mathematical objects to being rooted in mathematical concepts. This shift might suggest a conceptual framework in which there exists a web or a sphere of concepts, with lower-level concepts serving as concrete instances (or reflections) of the structural properties inherent in higher-level ones. In this view, the conceptual realm itself, as far as formal concepts are concerned, appears somewhat stratified, with each “level” providing a foundation for understanding the abstract properties that define and shape the levels below.

Some further insight into the nature of the conceptual realm can be gathered from Gödel’s following remark:

In order to arrive at a structured perception, it is necessary to relate the currently given “sense object” [which changes from one moment to the next] to some concepts [the totality of all possible concepts, ordered by affinity, forms the space of understanding (or space of concepts)]. The objects of the space do not change, only the attention directed at them changes. It is apparently not possible to direct attention on some object of the space3 without at the same time directing it at an object of the sensory space “on which” or “through which” the respective concept is perceived (in the case of abstract concepts this is the word?)

An example for the most primitive sensory concepts are colours (primary colours). Or better, it is any state of affairs that involves the respective concept. It is a perception in the case of sensuous concepts, which means that we understand what it means that they “apply” to something [i.e., when a state of affairs involving them is true], though we do not see the concepts themselves. In this sense, every concept is perceived via the concept of “truth”. ([30], p. 211)

Although Gödel speaks of “sense objects” here, what he says closely aligns with the idea of gaining knowledge of mathematical objects by recognizing the concepts they instantiate. As we have emphasized, this is facilitated through the specific perception of these objects revealing their structural properties, which can be associated with the structured perception Gödel mentions here. This passage highlights the back-and-forth process underlying knowledge acquisition. Namely, to gain insight into the properties of an object, we must subsume it under a concept; but also, as Gödel suggests, we can only grasp a concept by recognizing particular objects as its instances. The concepts themselves are immutable. What does change is our attention directed at them. In the case of empirical concepts (the concept of a certain color would here provide a typical example), it is, Gödel tells us, not possible to focus on them without also directing our attention to an object instantiating the respective concept.

After echoing Plato’s view that the structured perception requires connecting transient sensory objects to stable concepts, Gödel offers some clues as to the nature of the conceptual sphere. This “space of understanding” or the “space of concepts” exhibits the hierarchy based on affinity between concepts. Concepts sharing some structural properties could be seen as providing an example of the affinity Gödel has in mind. However, this ordering by affinity need not be only horizontal, so to speak. It could also be that affinity between concepts is present when we are dealing with a lower-level concept instantiating some of the structural properties of a higher-level one:

Remark: This identification of the low by means of something higher (which is the essence of knowledge) takes place in many stages:

• Individual objects are known by means of empirical concepts.
• The empirical concepts are known by means of formal concepts (in physics).
• The formal concepts are known by means of higher formal concepts. For example, if one had the right definition of the natural numbers in terms of higher concepts, one would probably overlook number-theoretical regularity, just as one overlooks the optical laws by means of the proper definition of color as wavelength (and undulatory theory).4 This correct definition of number may be analytical (via analytical functions). ([12], p. 248)

This remark suggests that a similar process of gaining an insight into an object or a lower-level concept by identifying a concept instantiated in it is present in the case of abstract objects and formal concepts. Here, Gödel is considering whether ’to perceive’ would be the appropriate verb. In the case of empirical objects, it might be said that we do ’perceive’ the respective concepts through them—the focus here being on, say, the physical object instantiating the concept of redness. In the case of mathematical, abstract concepts, it would be congenial to Gödel’s philosophical views to say that we understand the concepts through the abstract objects instantiating them. The concept of truth plays an important role here. It is by ascertaining that a certain object really does fall under a specific concept that we come to understand the concept in question.

Remark Philosophy: Knowledge always consists in a connection between concepts, but the reason why this connection occurs (why the judgment is made or the knowledge is reached) does not always lie in the concepts alone, but often in something non-conceptual (in a having) [even in purely conceptual knowledge, such an externally forced evidence would be conceivable]. ([20], p. 47)5

Here, we are reminded of the Leibnizan idea that knowledge consists of recognizing and analyzing the relationships between concepts but also of the impossibility of dealing with them without considering their instances. For example, our understanding of the connections between specific metric, symmetric, and topological concepts is enhanced by observing that the same geometric object, such as a circle, instantiates all of them. It is, in a sense, not possible to understand a concept directly but only insofar as it is mediated by an object. In the case of abstract objects specifically, this mediation might consist of exhibiting an abstract structure tying the object to the concept it instantiates. This structure, which seems inseparable from the objects of thought, provides us with the epistemological basis of our mathematical knowledge. (Presumably, God would be able to understand the concepts directly, without the need of them being instantiated by objects.)

As Gödel suggests at the end of the quote, even purely conceptual knowledge could be mediated by the “externally forced evidence”. The hint as to the kind of this evidence is given in the text quoted above, where Gödel asks if the objects through which abstract concepts are perceived, i.e., understood, might be words. The paradigmatic examples of abstract concepts are logical concepts, such as connectives. Their understanding can be mediated by the symbols standing for them and their role in language or formal systems. Let us try to illustrate this through the following simple example:

$$\begin{array}{c}\underline{A\to C\frac{[A\wedge B]}{A}}\underline{B\to D\frac{[A\wedge B]}{B}}\\ \underline{CD}\\ \frac{C\wedge D}{(A\wedge B)\to (C\wedge D)}\end{array}$$

Here, we have a deduction of $(A\wedge B)\to (C\wedge D)$ from hypotheses $A\to C$ and $B\to D$ in Gentzen’s system of natural deduction. If, together with Gödel, we take the concepts of logical constants to be basic, fundamental building blocks within the space of understanding ([28], p. 277), then the above deduction—being just a linguistic representation of a proper mathematical object—is helping us gain a clearer insight into the nature of concepts it instantiates, i.e., conjunction and implication. What insight might this be?

First of all, it could be said that it helps us understand the proper use of connectives inside deductions—their deductive role. One way to encapsulate this role would be through the following inference rules:

$$\begin{array}{c}\Gamma ⊢A\Gamma ⊢B\\ =\\ \Gamma ⊢A\wedge B\end{array}({\wedge }_a)$$

and

$$\begin{array}{c}\Gamma ,A⊢B\\ =\\ \Gamma ⊢A\to B,\end{array}({\to }_a)$$

which are just sequent-style natural deduction rules for (intuitionistic) implication and conjunction. The double line indicates that there is a rule going from the upper sequent or sequents to the bottom one, as well as rules going from the bottom sequent to either of the upper ones. The notation used here is not a plain shorthand. It indicates that there is an equivalence between deductions represented by the upper sequent or sequents and deduction represented by the bottom sequent. These rules are tied to the notion of adjunction—which is a fundamental concept inside category theory—characterizing the respective logical constants [31].

Logical constants are characterized by their role in deductions, i.e., through the inferential relations in which the sentences formed by them stand. The example above illustrates how focusing on them and understanding logical constants from the inferentialist standpoint, such as that of Brandom, allows us to distinguish their structural properties. By understanding these and related properties of logical constants, we are becoming more aware of their place and relations to other concepts inside the space of understanding. For instance, far from being an isolated phenomenon, adjunction permeates the whole of mathematics and ties in a profound way the concepts of logical constants with other important mathematical notions ([32], Chapters IV and V).

However, how is it that we can use syntactical representation (essentially, words) to gain deeper understanding of the conceptual realm?

Remark Gr: The fact that the understanding of concepts becomes significantly clearer by the construction of their sensory images [i.e., words] seems absurd at first [could the perception of some landscape become clearer by sketching a picture of it?]. But the reason might be that the material (i.e., the finite combinatorics) already contains, in some way, the image of the conceptual so that only this can really be depicted (or depicted simply). This would mean: the truth is what has the simplest and the most beautiful symbolic expression. (This means: the finite combinatorics already contains a ‘picture of God’). ([33], p. 18)6

As Gödel suggests, it might indeed seem absurd to hope for a clearer understanding of concepts by forming their “sensory images”. However, if our imagery is such that it already contains certain structural aspects of the conceptual, our mediation of mathematical concepts through abstract, mathematical objects and their representations seems like an inevitable path we need to take in order to make the space of understanding clearer.

In the following sections, we explore two key ways of following this path and deepening our understanding of concepts in mathematics.

3. Two Ways of Navigating the Web of Concepts

Mathematical concepts can, in general, be identified through two principal methods: abstraction and generalization. In what follows, we will first outline these methods as derived from Gödel’s writings, followed by examples that illustrate the central points of our work.

Abstraction is the process of recognizing a concept reflected in an object or a concept of a lower level and directing our attention to it. The relation between the concepts participating in this hierarchy is that of subsumption of one concept under the other. That this relation obtains between a concept and either an object or a lower-level concept is indicated by their shared structure. This allows us to climb the hierarchy that orders concepts according to their structural affinities.

On the other hand, generalization is a way of arriving at and understanding simpler, more general concepts, taking complex concepts as a base. It allows us to climb another hierarchy made of concepts that contain one another. By generalizing, we arrive at a concept applicable in a broader area. A more general concept allows its structure to be seen more clearly, which can lead us to recognize a higher-level concept instantiated in it and the concepts from which it has been generalized.

We argue that both abstraction and generalization have an indispensable role in gaining mathematical knowledge, which no formal system can simulate. Some of Gödel’s reflections suggest that mathematical knowledge emerges from such processes. He emphasizes the importance of structural properties in gaining knowledge of mathematical concepts. Our notion of abstraction aligns with this perspective by illustrating how structure serves as a bridge between an object and the concept applicable to it, making it a valuable subject of mathematical investigation. On the other hand, Gödel also emphasizes the process of ’generalizing’ concepts to uncover underlying structures, a theme he identifies as central to the future development of a theory of concepts. Although one might argue that inferential relations or other forms of bridging the gap between concepts, objects, and structures could also be significant, our focus here is on abstraction and generalization because they most directly illustrate the transition from concrete examples to a unified structural understanding and seem to be closely related to Gödel’s views on mathematical practice. In what follows, we use examples from category theory (the product) and geometry (Erlangen Program, the notion of a circle, and the notion of configuration) to illustrate how these processes operate in practice.

3.1. Example: Product

An important example of generalization was hinted at in the preceding section. There, it was noted that logical constants can be characterized by double-line rules tied to the categorial notion of adjunction. Taking the connective of conjunction (either classical or intuitionistic—they are the same), we could generalize it to the algebraic notion of a lattice meet. Given the elements a and b of a Boolean algebra (or a more general Heyting algebra), their meet $a\cap b$ is defined as the greatest c such that $c\le a$ and $c\le b$. This sort of generalization is useful in that it allows one to model the whole of propositional logic, either classical or intuitionistic, using algebraic means.

However, if we take one step further, we can generalize the conjunction to a categorical notion of the product. To take the simplest example, in the category Set of sets and functions, the product is the usual Cartesian product of sets:

$$A\times B=\left\{\right(a,b)\mid a\in A,b\in B\}.$$

Tied to the product are the canonical projection arrows:

$${\pi }_1:A\times B\to A,{\pi }_2:A\times B\to B.$$

Apart from these, we have an operation of pairing on arrows that when applied to arrows $f:C\to A$ and $g:C\to B$ yields the arrow

$$\langle f,g\rangle :C\to A\times B,$$

which, together with projections, satisfies the following equalities (where h is an arbitrary arrow of type $C\to A\times B$):

$${\pi }_1\circ \langle f,g\rangle =f,{\pi }_2\circ \langle f,g\rangle =g,\langle {\pi }_1\circ h,{\pi }_2\circ h\rangle =h.$$

In the preceding section, we have introduced double line rule ${\wedge }_a$, which encapsulates the deductive role of conjunction. Going downwards, we have a natural deduction rule of conjunction introduction. Here, in the context of categorical product, that rule is mirrored by the partial operation of pairing $\langle \rangle$ on arrows. Going upwards via ${\wedge }_a$, we have a pair of natural deduction rules of conjunction elimination. Their role is here reflected by the projection arrows ${\pi }_1$ and ${\pi }_2$. The equalities given above, which characterize the notion of product, are closely tied to the reduction steps in normalization procedure for derivations inside natural deduction.

By now, we have considered the operation of the product as it applies to objects inside a category. This operation can also be extended so that it applies to arrows in the following way: if we have the arrows $f_1:A\to C$ and $f_2:B\to D$, then composing with appropriate projections and taking the pairing of the result, we obtain

$$f_1\times f_2{=}_{def}\langle f_1\circ {\pi }_1,f_2\circ {\pi }_2\rangle :A\times B\to C\times D.$$

This operation on arrows, together with the corresponding operation on objects, makes the product a biendofunctor inside a category (more details of these interesting constructions can be found in [34]).

By passing from the connective of conjunction, the simplest and arguably most fundamental logical connective, to the categorical notion of product, we gain far more than mere generality. It can be argued that we arrive at the right level of generality, uncovering the deep interconnectedness between one of the cornerstones of logic and other mathematical concepts that embody the same essence. These include the Cartesian product in set theory, the product of spaces in topology, the direct product in group theory, and more.

What makes this generalization particularly insightful is that it focuses on the structural properties of the conjunction connective, revealed in its role in deduction. By setting aside its other properties, such as its truth-functional interpretation, we gain a clearer view of the structure of the categorical product it reflects. As Gödel points out in some of the cited remarks, these structural properties play a crucial role in the pursuit of mathematical knowledge. They reveal higher-order concepts, in this case from category theory, that are instantiated in concepts from seemingly unrelated areas, thereby establishing connections between them. The notion of a product serves as a unifying concept, bridging disparate domains under a common framework. This perspective reveals how logical conjunction, often seen as elementary, resonates through the grander tapestry of mathematical thought.

In this unification, the rewards of studying mathematics become apparent: not just in the richness of individual concepts but in the profound order and regularity of the relationships between them. The product, as a categorical notion, exemplifies this harmony by linking logic to algebra, topology, and geometry, highlighting the elegance and interdependence of the mathematical universe.

3.2. Example: Erlangen Program

Klein’s Erlangen program [35] offers another example of unification achieved through the appropriate generalization.

The Erlangen program led to the unification of hitherto known geometries (Euclidean, projective, hyperbolic, etc.) by defining geometry as a study of symmetries–transformations that preserve important properties of the figures in a particular homogenous space. The symmetries acting upon a space form a group under composition. Different geometries can then be viewed as special cases of this general framework: they emerge by varying the underlying homogeneous space and the symmetry group. This not only provides a deeper insight into any particular geometry but also reveals a complex and multidimensional network, showing how different geometries are interconnected. For instance, if we are given ${\mathbb{R}}^2$ and a group acting on it, in the case of Euclidean geometry, this group consists of all transformations of the following form

$$x\mapsto Ax+b$$

where A is an orthogonal transformation and $b\in {\mathbb{R}}^2$. By varying A so that, for example, we consider only affine transformations (keeping parallelism, collinearity, and concurrence invariant), we pass to affine geometry, and so on.

In our terminology, the Erlangen program can be described as a generalization of the concept of transformation preserving some important properties of the figures in the given space. The generalization is achieved by disregarding the specific properties that are preserved and instead focusing solely on the relationships or interactions between the transformations that preserve them. Such a generalization allows us to identify key structural properties of these transformations and to observe the formal concept of a group reflected in different sets of transformations.

Some types of generalization can also be achieved by working inside an established axiomatic system of a mathematical theory, say, of geometry. Here, the generalization consists of loosening (or outright removing) a subset of axioms. Simple as this may be, it produces a non-trivial problem: finding the model that satisfies the reduced set of axioms but not the original one. This type of generalization is useful for exploring which sets of axioms are independent of one another, but it does not lead to the unifications discussed in this and the previous example. Therefore, it cannot replace the intuitive, informal reasoning that leads to such unifications.

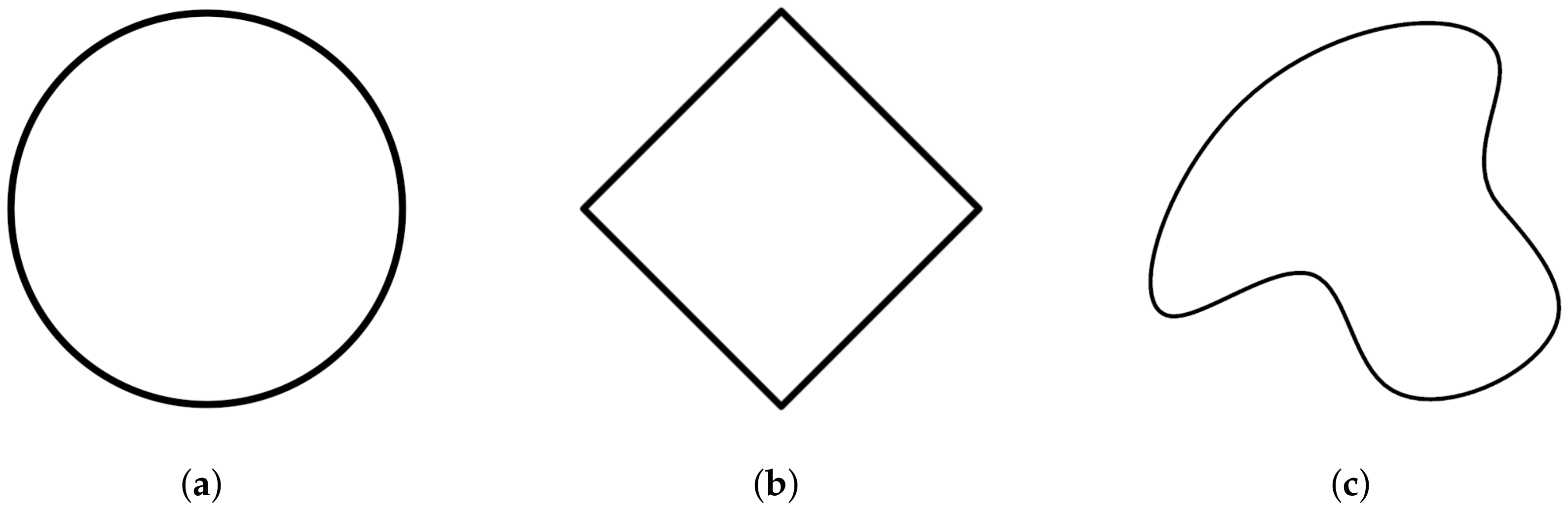
3.3. Example: Circle

One of the most familiar mathematical concepts is the concept of a circle. We arrive at it, usually, by observing everyday objects such as plates, cups, or sun and moon from which we identify the concept of a circle through simple abstraction.

Notice an important property of the abstraction process—it leads us to identify a concept, providing us with a definition of the concept as well. In the aforementioned example, the definition we obtain is the standard metric definition of a circle as a set of points equidistant from a particular point we call its center.

Abstracting is not a uniquely determined process. Different ways, i.e., different paths, can lead us to the same concept but to different definitions. Suppose we lived in an odd world in which all were blind but interacted daily with all sorts of circular controls such as dials, valves, etc. In such a world, we would arrive, again simply abstracting from such objects, at the concept of a circle, though the definition would likely not be the standard one, but one related to the rotational invariance of a circle. Namely, we would define a circle as that which is invariant under rotations (around its center) for all angles.

Starting from the metric definition, we can deduce the circle’s rotational invariance and vice versa. However, the definitions are different. Each offers a distinct perspective, linking the concept of a circle to various other concepts and thereby shedding new light on its place in the web of concepts. Figure 1 illustrates how a circle can appear differently depending on which definition of the concept is considered.

Different definitions, i.e., different “cross-sections” of the concept of a circle are useful because they not only open up a deeper understanding of the concept they define but also provide a springboard for exploring different concepts altogether. For example, considering the aforementioned definition of a circle, one may inquire into the nature of distance, i.e., how we measure it. Indeed, the concept of a metric is contained in it and once that insight is opened up, one can see that the definition of a circle can, when the underlying metric is changed, describe other objects that also fall under the concept of a circle. For example, in $l_1$ metric, the circle appears to us as square.

It is in the nature of the concept that no finite set of definitions exhausts it. While the two mentioned definitions of a circle already open manifold paths for the exploration of the circle and related concepts, there are yet more. For example, if one studies the behavior of functions from closed planar curves to the real numbers, one can see that it primarily depends on the number of intersections of this closed planar curve. That is, continuity does not distinguish between closed curves that do not intersect. They are all homeomorphic, and any one of them can rightly be called a (topological) circle.

It is important to notice that this new topological definition is not compatible with the metrical and “symmetrical” definitions in the way those two were with each other. We might then distinguish “metric circle” from “topological circle”, but this only underscores the fact that there is such a thing as a “circle”, of which both are manifestations.

Different understandings of the same mathematical concept, embodied in its various definitions, offer alternative perspectives on its place in the web of concepts. These multiple definitions illustrate how mathematical concepts emerge through abstraction. Gödel’s perspective on mathematical concepts suggests that these definitions do not simply describe different interpretations of a circle; rather, they reflect different structural properties of the same underlying mathematical reality. As Gödel argued, knowledge consists of recognizing connections between concepts. This example shows how abstraction can reveal mutual connections between the concept of a circle and that of a metric, symmetry, topology, etc. The process of abstraction starts with a particular object, in this case, a circle. This aligns with Gödel’s observation that the reason conceptual connections occur might lie in something non-conceptual, which suggests that the way we recognize connections between concepts is by observing objects in which they are reflected in some manner.

This observation has significant implications for mathematical practice. The process of concept crystallization in mathematics does not rely on a single method of abstraction but rather on a dialectical interplay between abstraction and generalization. In this way, Gödel’s framework aligns with modern studies on conceptual change in mathematical reasoning, as developed in cognitive science and the philosophy of mathematics (cf. [2,10]).

The axiomatic system comes in later in the course of developing an understanding of a concept, only after a particular view on the concept is established. The choice of axiomatic system—and thus, the particular perspective on the corresponding concept that a mathematician adopts—often depends on the specific problem being addressed or the objects under consideration. Its role in expanding mathematical knowledge is therefore limited: it sharpens a restricted view of the concept, focusing on one aspect while leaving others unexplored. Such a system does not reveal alternative definitions or their interconnections. Furthermore, it does not aid in identifying and exploring meaningful structures or uncovering what it reveals about the corresponding concept or objects instantiating it by reflecting this structure. This process, however, can be of great importance to mathematics, as the following example illustrates.

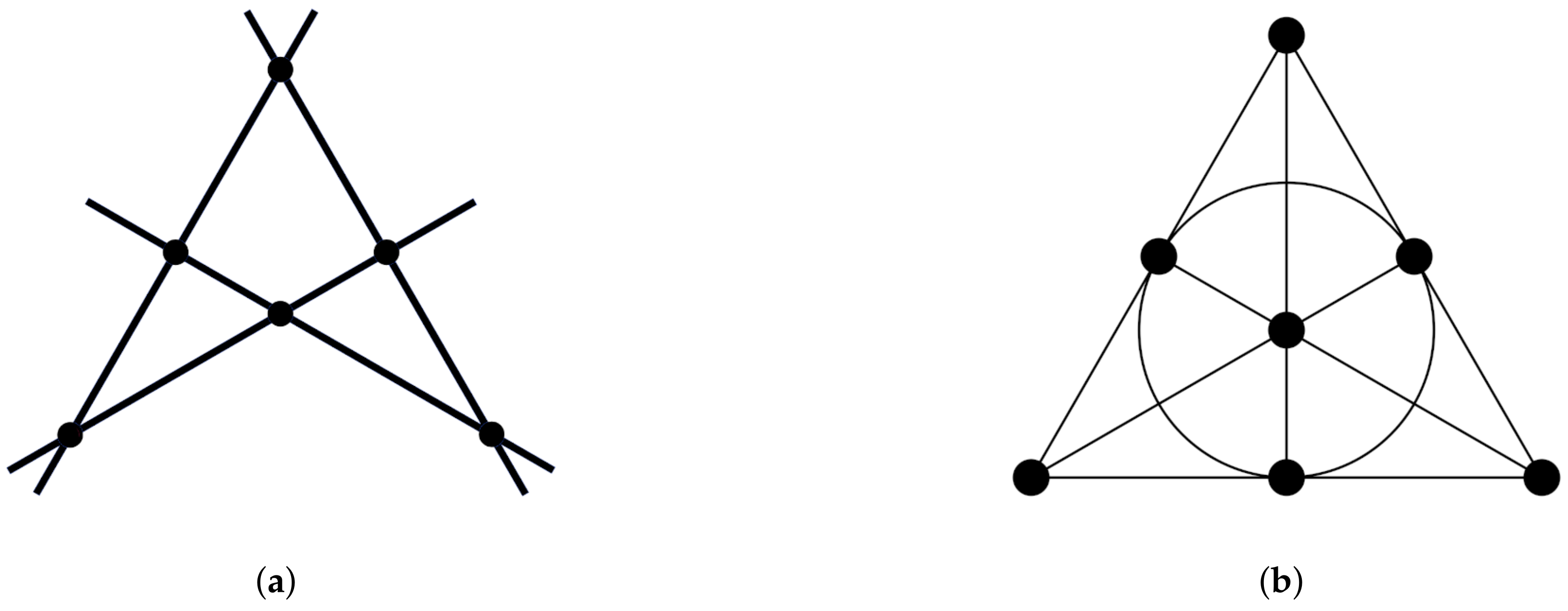
3.4. Example: Configuration

In the course of studying Euclidean geometry, we arrived at the notion of configuration that encapsulates certain combinatorial properties of (usually) projective spaces. It is highly questionable whether we could have arrived at it working solely within the confines of a formal system, such as one of Hilbert’s type. This notion, however, helps us expand our view of mathematical reality.

The examination of classical theorems in geometry leads to the realization that in many cases, what matters are not the metrical properties but only the incidences of lines and points. This leads to the identification of a structure we call configuration $\left(p_n{l}_m\right)$—a set of p points, each incident to n lines, and l lines, each incident to m points (see Figure 2 for examples of some important configurations). The configuration is a way of specifying a combinatorial relationship that need not be concerned with the specific distances or angles between the points and lines; instead, it focuses purely on the incidences, the patterns of intersection between points and lines. Such an approach reveals structural properties that are often independent of the particular geometrical space in which they are embedded.

As a structure, a configuration is a bridge between the concept of space, i.e., geometry, for points and lines are elements of some space and particular objects that instantiate them. Therefore, in studying configuration, one operates upon, or explores, both levels. On the level of objects, the exploration involves finding specific instances of a given configuration within a given space. The task is to identify whether certain arrangements of points and lines fit the given combinatorial structure and whether these instances are isomorphic (i.e., equivalent in terms of their incidence relations) or not. On the level of concepts, it involves asking what types of spaces can support a given configuration.

A good example is the famous $\left(7_3\right)=\left(7_3{7}_3\right)$ configuration. The question it gives rise to is as follows: what geometric spaces (or more abstract combinatorial structures) can accommodate this configuration? It turns out that this configuration is unrealizable in the Euclidean plane but can be realized as the smallest finite projective plane—the Fano plane. Studying the Fano plane offers valuable insights into the properties of finite projective planes and helps us understand more complex geometric and combinatorial structures.

In conclusion, configurations provide a bridge between the concept of geometric space, characterized by points, lines, and incidence relations, and the objects that inhabit these spaces. They thus illustrate the mediation between concepts and objects through a structure and show how the study of a structure can be valuable even when the particular concepts and objects it connects are unspecified. By focusing on the combinatorial properties of incidences, configurations help us explore spaces beyond the Euclidean realm. This approach fosters a deeper understanding of geometry that cannot be achieved through purely axiomatic reasoning, revealing the richness of mathematical reality.

4. Conclusions

According to the view presented in this article, although mathematical knowledge primarily concerns mathematical objects, it is mediated by the structures reflected in these objects, and the concepts they instantiate. The structure reflected in a mathematical object allows us to recognize the corresponding concept and gain a better understanding of it. Conversely, by enhancing our understanding of a concept, we expand our knowledge of the objects to which it applies.

This interpretation sheds new light on the epistemology of mathematics as conceived by Gödel within the framework of his mathematical Platonism. He is commonly criticized for positing a mystical ability that enables a direct perception of abstract, mathematical objects, by which we are to gain knowledge of them. As we have emphasized, no direct perception would ever be capable of explaining how we acquire mathematical knowledge. The foundation of this knowledge lies in an understanding of mathematical concepts in which only reason is involved. This understanding is capable of indefinite expansion and and refinement.

Developing an understanding of a mathematical concept entails connecting it to other concepts and thus observing its different definitions. (This is often facilitated by the objects that indicate the connections between concepts.) It also entails distinguishing more general concepts contained in it or subsuming it under the concepts of a higher level. In this respect, the most important are the subsumptions under the structural concepts, such as those studied in category theory.

The theory of concepts that Gödel envisioned is supposed to deal with the formal properties of concepts and the relation of concept application [36]. It is also supposed to study how complex concepts are built from simpler ones using logical concepts as connecting tissue. Given this, it is to be expected that it throws light on both processes we identified as crucial for mathematical practice: abstraction as a process of recognizing that the relation of application between a concept and particular objects obtains, and generalization as a process of distinguishing simpler concepts contained in a more complex one. This partly explains the significance Gödel attached to this theory, not only for the future of logic but also for our understanding of mathematics and its epistemological foundations.

This article has examined Gödel’s perspective on mathematical practice, arguing that his emphasis on concepts, objects, and structures provides a compelling alternative to purely formalist accounts of mathematics. While Gödel critically engaged with Hilbert’s program, his philosophy moves beyond syntactic formalism by positioning mathematical knowledge within a conceptual and structural framework. This view resonates with contemporary discussions in the philosophy of mathematical practice, particularly in its attention to abstraction, generalization, and conceptual discovery, as essential components of mathematical reasoning.

One of the key insights of this study is that Gödel’s work challenges the traditional opposition between formalism and mathematical intuition. Rather than dismissing formal systems, Gödel acknowledged their role in structuring mathematical knowledge, but he insisted that the understanding of mathematical concepts precedes and extends beyond mere formal manipulation. This is evident in how mathematicians engage with multiple definitions and representations of concepts, as seen in the case of the circle, where different approaches—metric, group-theoretic, and topological—capture distinct but interrelated aspects of the same mathematical object.

This conceptual approach to mathematics is not just of historical interest. As recent scholarship in the philosophy of mathematical practice has emphasized, mathematical reasoning is deeply tied to structural and cognitive processes that cannot be reduced to formal axiomatization alone. Gödel’s perspective offers an early articulation of this idea, reinforcing the view that mathematical knowledge is grounded in conceptual insight rather than purely symbolic derivation.

Further research should explore how Gödel’s framework aligns with contemporary cognitive models of mathematical thinking, as well as how it contrasts with other non-formalist perspectives, such as Lakatos’ fallibilism and Pólya’s heuristic approach. Additionally, Gödel’s theory of concepts—though still largely undeveloped—may provide a foundation for a richer epistemology of mathematics, one that acknowledges both the formal rigor of axiomatic systems and the intuitive processes underlying mathematical discovery.

Ultimately, Gödel’s perspective reminds us that mathematics is not merely a game of symbols but a conceptual exploration of an independent mathematical reality. By situating Gödel’s thought within contemporary debates, this paper highlights his relevance not only as a foundational logician but also as a philosopher of mathematical practice whose insights continue to shape our understanding of mathematics today.