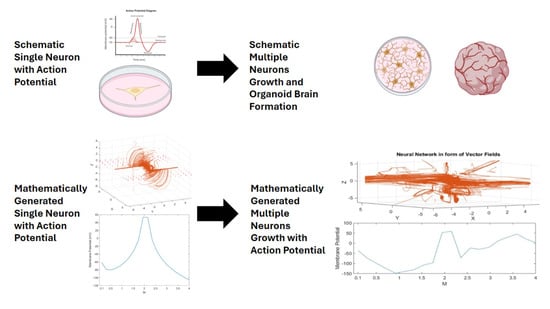
A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton
Abstract
1. Introduction
2. Method
3. Results
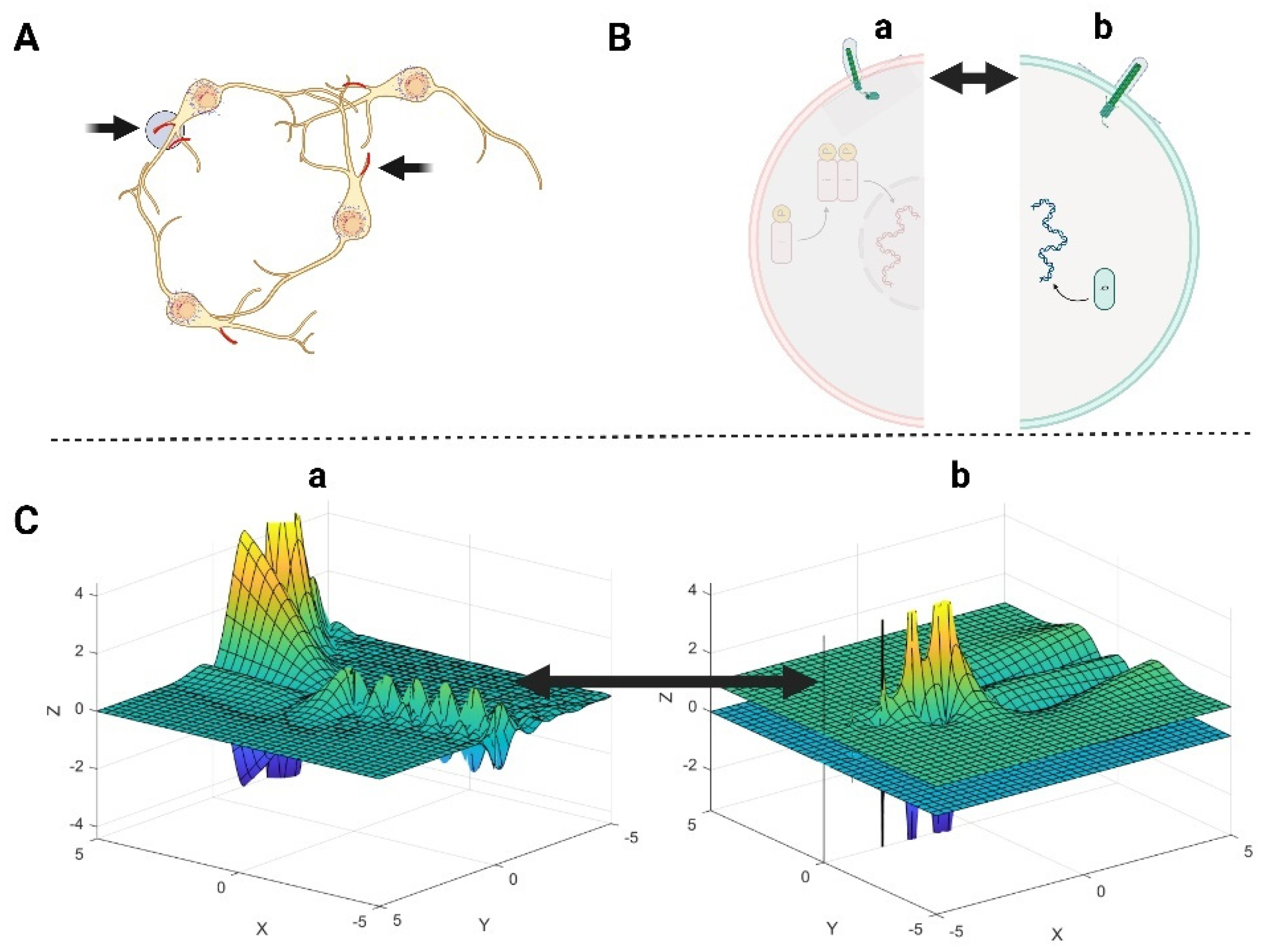
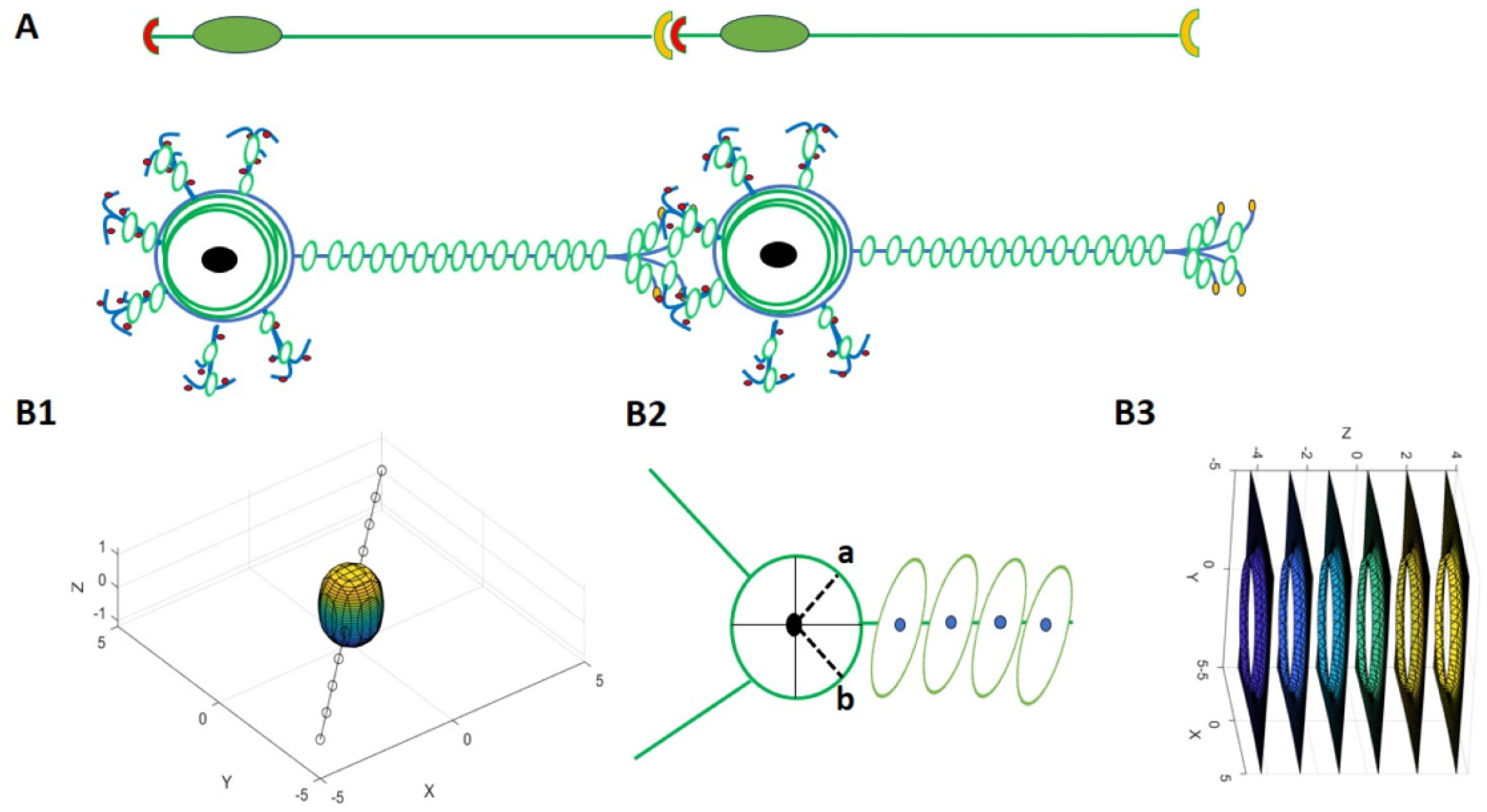
3.1. The Role of Primary Cilia and Actin Cytoskeleton in Signal Transduction Through the Cell Membrane
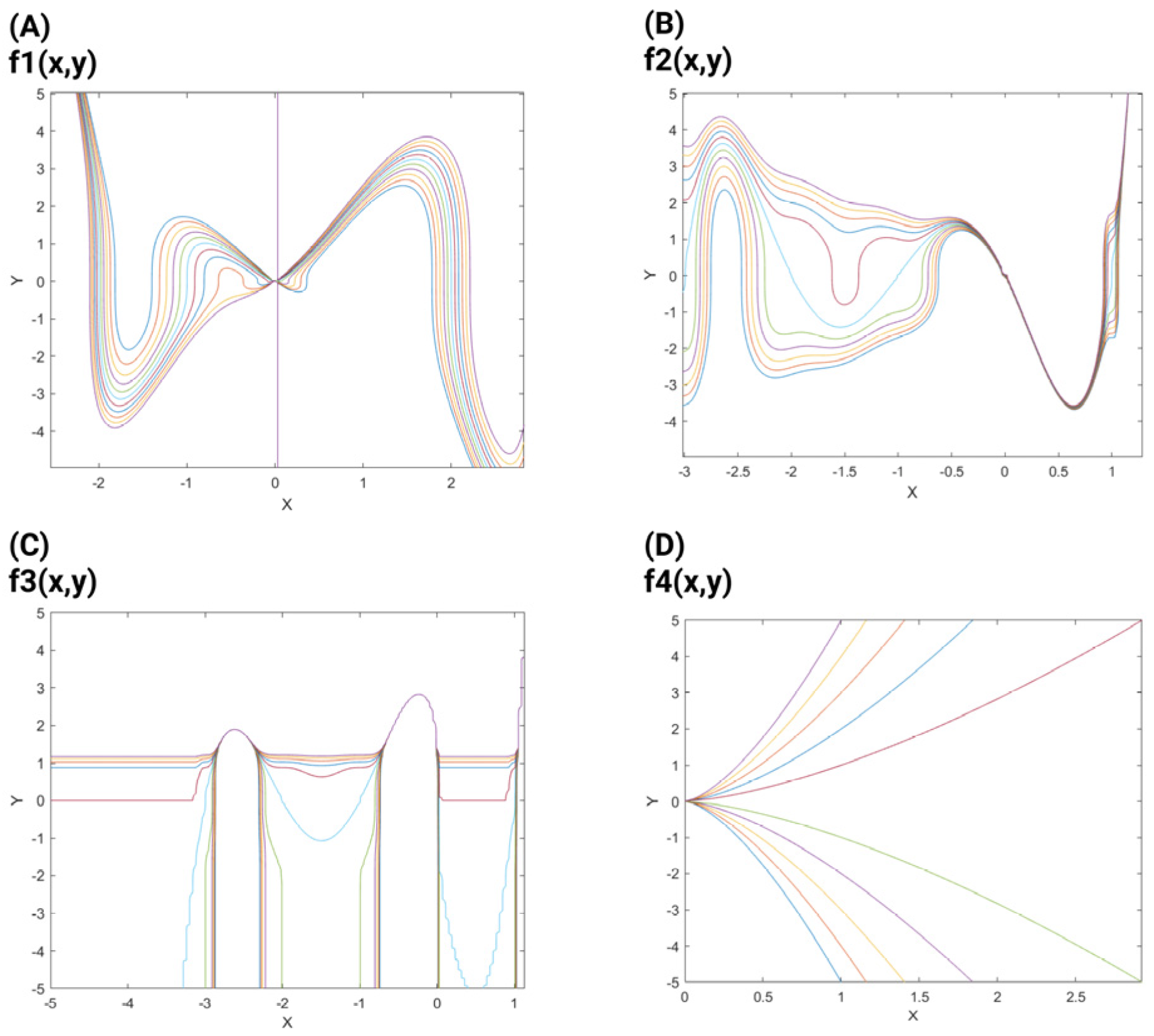
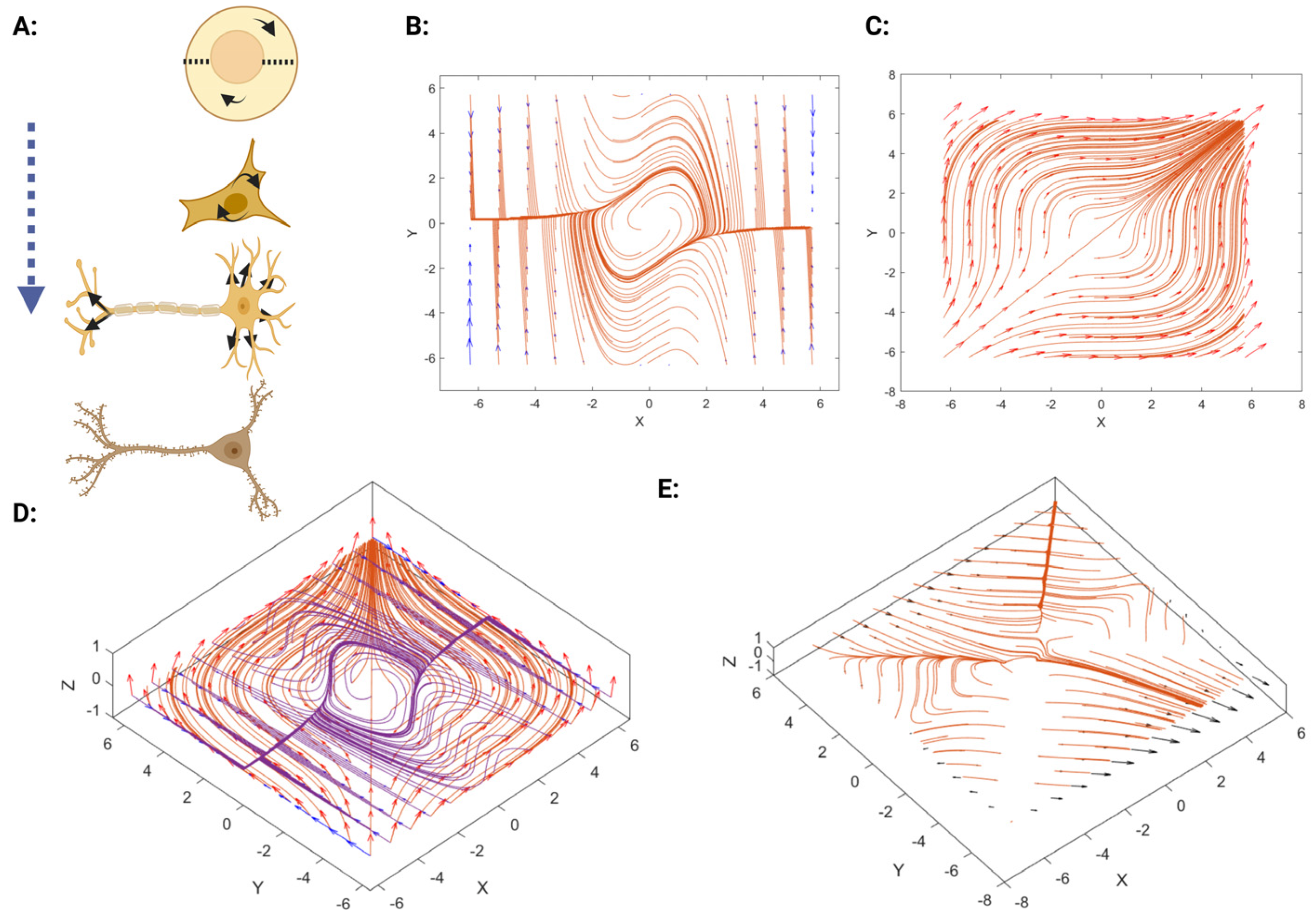
3.2. The Mathematical Model of Neuronal Branch and Soma Formation
3.2.1. Neuronal Branch and Soma Formation Based on Actin Cytoskeleton
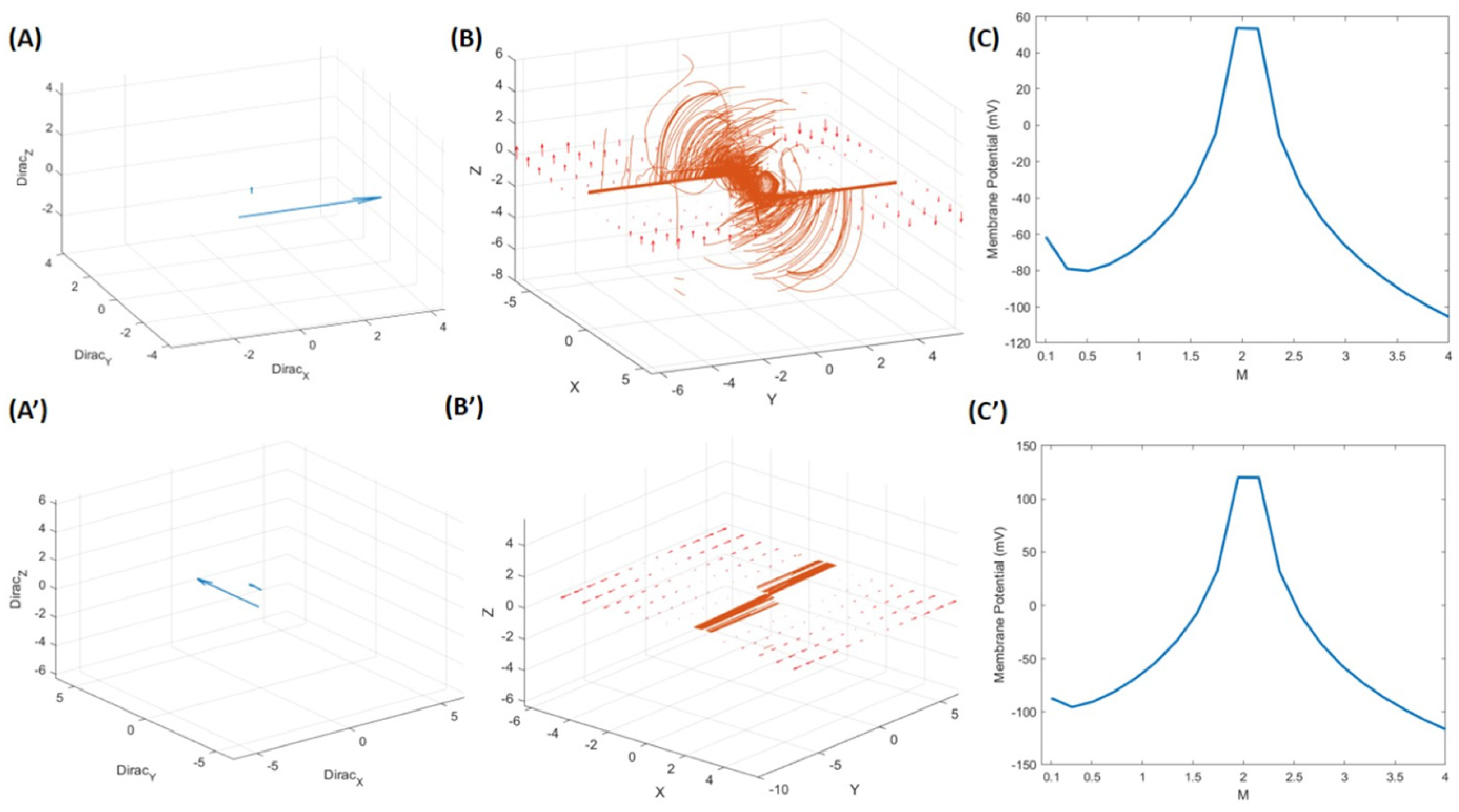
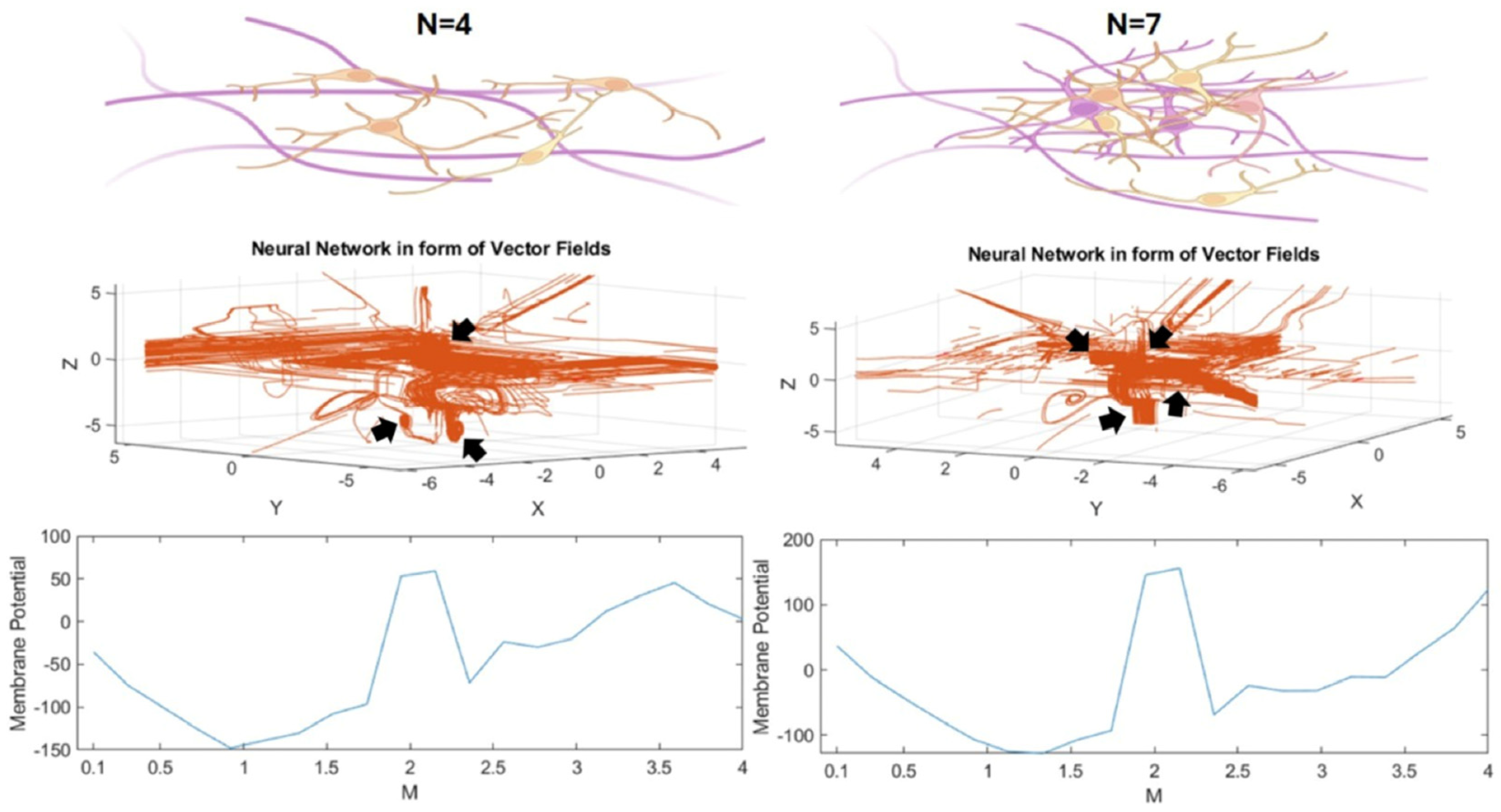
3.2.2. Role of Neuronal Electrical Activity in Conjunction with the Actin Cytoskeleton in Neuronal Branch and Soma Formation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lana, D.; Ugolini, F.; Nosi, D.; Wenk, G.L.; Giovannini, M.G. Alterations in the interplay between neurons, astrocytes and microglia in the rat dentate gyrus in experimental models of neurodegeneration. Front. Aging Neurosci. 2017, 9, 296. [Google Scholar] [CrossRef]
- Hua, J.Y.; Smith, S.J. Neural activity and the dynamics of central nervous system development. Nat. Neurosci. 2004, 7, 327–332. [Google Scholar] [CrossRef]
- Yamamoto, N.; López-Bendito, G. Shaping brain connections through spontaneous neural activity. Eur. J. Neurosci. 2012, 35, 1595–1604. [Google Scholar] [CrossRef]
- Visa, N.; Percipalle, P. Nuclear functions of actin. Cold Spring Harb. Perspect. Biol. 2010, 2, a000620. [Google Scholar] [CrossRef]
- Shim, S.; Goyal, R.; Panoutsopoulos, A.A.; Balashova, O.A.; Lee, D.; Borodinsky, L.N. Calcium dynamics at the neural cell primary cilium regulate Hedgehog signaling–dependent neurogenesis in the embryonic neural tube. Proc. Natl. Acad. Sci. USA 2023, 120, e2220037120. [Google Scholar] [CrossRef]
- Konietzny, A.; Bär, J.; Mikhaylova, M. Dendritic actin cytoskeleton: Structure, functions, and regulations. Front. Cell. Neurosci. 2017, 11, 147. [Google Scholar] [CrossRef]
- Oertner, T.G.; Matus, A. Calcium regulation of actin dynamics in dendritic spines. Cell Calcium 2005, 37, 477–482. [Google Scholar] [CrossRef]
- Kiss, J.Z.; Müller, D. Contribution of the neural cell adhesion molecule to neuronal and synaptic plasticity. Rev. Neurosci. 2001, 12, 297–310. [Google Scholar] [CrossRef]
- Drenckhahn, D.; Frotscher, M.; Kaiser, H.W. Concentration of F-actin in synaptic formations of the hippocampus as visualized by staining with fluorescent phalloidin. Brain Res. 1984, 300, 381–384. [Google Scholar] [CrossRef]
- Singla, V.; Reiter, J.F. The primary cilium as the cell’s antenna: Signaling at a sensory organelle. Science 2006, 313, 629–633. [Google Scholar] [CrossRef]
- Wheway, G.; Nazlamova, L.; Hancock, J.T. Signaling through the primary cilium. Front. Cell Dev. Biol. 2018, 6, 8. [Google Scholar] [CrossRef]
- Peng, T.; Cheng, Y.; Xiong, M.; Zhou, W.-H.; Cheng, G.-Q. Primary cilia in the development of the cerebral cortex: A literature. Pediatr. Med. 2022, 6, 26. [Google Scholar] [CrossRef]
- Smith, C.E.; Lake, A.V.; Johnson, C.A. Primary cilia, ciliogenesis and the actin cytoskeleton: A little less resorption, a little more actin please. Front. Cell Dev. Biol. 2020, 8, 622822. [Google Scholar] [CrossRef]
- Markram, H. The blue brain project. Nat. Rev. Neurosci. 2006, 7, 153–160. [Google Scholar] [CrossRef]
- Holmes, W.R.; Edelstein-Keshet, L. A comparison of computational models of the dendritic actin cytoskeleton. Cytoskeleton 2016, 73, 450–461. [Google Scholar] [CrossRef]
- Lynn, C.W.; Bassett, D.S. The physics of brain network structure, function and control. Nat. Rev. Phys. 2019, 1, 318–332. [Google Scholar] [CrossRef]
- Rafati, A.H.; Joca, S.; Vontell, R.T.; Wegener, G.; Ardalan, M. Approaches to embryonic neurodevelopment: From neural cell to neural tube formation through mathematical models. Brief. Bioinform. 2024, 25, bbae265. [Google Scholar] [CrossRef]
- van Hoeij, M.; Vidunas, R. Algorithms and differential relations for Belyi functions. arXiv 2018, arXiv:1305.7218. [Google Scholar]
- Opfer, G. Polynomial interpolation in nondivision algebras. Electron. Trans. Numer. Anal. 2015, 44, 660–670. [Google Scholar]
- Robbiano, L. Term orderings on the polynomial ring. In Proceedings of the European Conference on Computer Algebra, Linz, Austria, 1–3 April 1985; pp. 513–517. [Google Scholar]
- Berele, A. Homogeneous polynomial identities. Isr. J. Math. 1982, 42, 258–272. [Google Scholar] [CrossRef]
- Amitsur, S.A. On the characteristic polynomial of a sum of matrices. Linear Multilinear Algebra 1980, 8, 177–182. [Google Scholar] [CrossRef]
- Kaczmarek, L.K.; Zhang, Y. Kv3 channels: Enablers of rapid firing, neurotransmitter release, and neuronal endurance. Physiol. Rev. 2017, 97, 1431–1468. [Google Scholar] [CrossRef]
- Feleqi, E.; Rampazzo, F. Iterated Lie brackets for nonsmooth vector fields. Nonlinear Differ. Equ. Appl. NoDEA 2017, 24, 61. [Google Scholar] [CrossRef]
- Franci, A.; Drion, G.; Seutin, V.; Sepulchre, R. A novel phase portrait to understand neuronal excitability. arXiv 2011, arXiv:1112.2588. [Google Scholar]
- Barr, L. Membrane potential profiles and the Goldman equation. J. Theor. Biol. 1965, 9, 351–356. [Google Scholar] [CrossRef]
- Cavagna, G. Fundamentals of Human Physiology; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Balakrishnan, V. All about the Dirac delta function (?). Resonance 2003, 8, 48–58. [Google Scholar] [CrossRef]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Silverman, J.H.; Tate, J. Rational Points on Elliptic Curves; Springer: New York, NY, USA, 1992. [Google Scholar] [CrossRef]
- Silverman, J.H. The Arithmetic of Elliptic Curves; Springer: New York, NY, USA, 2009; Volume 106. [Google Scholar]
- Verde-Star, L. Inverses of generalized Vandermonde matrices. J. Math. Anal. Appl. 1988, 131, 341–353. [Google Scholar] [CrossRef]
- Breunig, J.J.; Sarkisian, M.R.; Arellano, J.I.; Morozov, Y.M.; Ayoub, A.E.; Sojitra, S.; Wang, B.; Flavell, R.A.; Rakic, P.; Town, T. Primary cilia regulate hippocampal neurogenesis by mediating sonic hedgehog signaling. Proc. Natl. Acad. Sci. USA 2008, 105, 13127–13132. [Google Scholar] [CrossRef]
- Derrick, D.J.; Wolton, K.; Currie, R.A.; Tindall, M.J. A mathematical model of the role of aggregation in sonic hedgehog signalling. PLoS Comput. Biol. 2021, 17, e1008562. [Google Scholar] [CrossRef]
- Reinartz, K.D. Chebychev interpolations of the Gamma and Polygamma Functions and their analytical properties. arXiv 2016, arXiv:1605.02776. [Google Scholar]
- Owolabi, K.M. Mathematical modelling and analysis of two-component system with Caputo fractional derivative order. Chaos Solitons Fractals 2017, 103, 544–554. [Google Scholar] [CrossRef]
- Stepanyants, A.; Hof, P.R.; Chklovskii, D.B. Geometry and structural plasticity of synaptic connectivity. Neuron 2002, 34, 275–288. [Google Scholar] [CrossRef]
- Arnold, D.N.; Rogness, J.P. Möbius transformations revealed. Not. Am. Math. Soc. 2008, 55, 1226–1231. [Google Scholar]
- Xu, K.; Zhong, G.; Zhuang, X. Actin, spectrin, and associated proteins form a periodic cytoskeletal structure in axons. Science 2013, 339, 452–456. [Google Scholar] [CrossRef]
- Giné, J. Limit cycle bifurcations from a non-degenerate center. Appl. Math. Comput. 2012, 218, 4703–4709. [Google Scholar] [CrossRef]
- Sabri, E.; Brosseau, C. Electromechanical interactions between cell membrane and nuclear envelope: Beyond the standard Schwan’s model of biological cells. Bioelectrochemistry 2024, 155, 108583. [Google Scholar] [CrossRef]
- Tuszyński, J.A.; Portet, S.; Dixon, J.M.; Luxford, C.; Cantiello, H.F. Ionic Wave Propagation along Actin Filaments. Biophys. J. 2004, 86, 1890–1903. [Google Scholar] [CrossRef]
- Connors, B.W.; Gutnick, M.J. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 1990, 13, 99–104. [Google Scholar] [CrossRef]
- McCormick, D.A. Chapter 12-Membrane Potential and Action Potential. In From Molecules to Networks; Academic Press: Cambridge, MA, USA, 2014; pp. 351–376. [Google Scholar] [CrossRef]
- Akin, E.J.; Solé, L.; Dib-Hajj, S.D.; Waxman, S.G.; Tamkun, M.M. Preferential targeting of Nav1. 6 voltage-gated Na+ channels to the axon initial segment during development. PLoS ONE 2015, 10, e0124397. [Google Scholar] [CrossRef]
- Kotnik, T.; Miklavčič, D. Analytical description of transmembrane voltage induced by electric fields on spheroidal cells. Biophys. J. 2000, 79, 670–679. [Google Scholar] [CrossRef]
- Shamsara, E.; Yamakou, M.E.; Atay, F.M.; Jost, J. Dynamics of neural fields with exponential temporal kernel. Theory Biosci. 2024, 143, 107–122. [Google Scholar] [CrossRef]
- Lin, C.-C.; Segel, L.A. Mathematics Applied to Deterministic Problems in the Natural Sciences; SIAM: Philadelphia, PA, USA, 1988. [Google Scholar]
- Marton, R.M.; Pașca, S.P. Organoid and assembloid technologies for investigating cellular crosstalk in human brain development and disease. Trends Cell Biol. 2020, 30, 133–143. [Google Scholar] [CrossRef]
- Quadrato, G.; Nguyen, T.; Macosko, E.Z.; Sherwood, J.L.; Min Yang, S.; Berger, D.R.; Maria, N.; Scholvin, J.; Goldman, M.; Kinney, J.P.; et al. Cell diversity and network dynamics in photosensitive human brain organoids. Nature 2017, 545, 48–53. [Google Scholar] [CrossRef]
- Zourray, C.; Kurian, M.A.; Barral, S.; Lignani, G. Electrophysiological properties of human cortical organoids: Current state of the art and future directions. Front. Mol. Neurosci. 2022, 15, 839366. [Google Scholar] [CrossRef]
- Kang, R.; Park, S.; Shin, S.; Bak, G.; Park, J.-C. Electrophysiological insights with brain organoid models: A brief review. BMB Rep. 2024, 57, 311. [Google Scholar] [CrossRef]
- Kirschen, G.W.; Xiong, Q. Primary cilia as a novel horizon between neuron and environment. Neural Regen. Res. 2017, 12, 1225. [Google Scholar]
- Berbari, N.F.; O’Connor, A.K.; Haycraft, C.J.; Yoder, B.K. The primary cilium as a complex signaling center. Curr. Biol. 2009, 19, R526–R535. [Google Scholar] [CrossRef]
- Anvarian, Z.; Mykytyn, K.; Mukhopadhyay, S.; Pedersen, L.B.; Christensen, S.T. Cellular signalling by primary cilia in development, organ function and disease. Nat. Rev. Nephrol. 2019, 15, 199–219. [Google Scholar] [CrossRef]
- Kaltenbacher, B.; Rundell, W. Recovery of multiple coefficients in a reaction-diffusion equation. J. Math. Anal. Appl. 2020, 481, 123475. [Google Scholar] [CrossRef]
- Moore, P.; Huxley, H.; DeRosier, D. Three-dimensional reconstruction of F-actin, thin filaments and decorated thin filaments. J. Mol. Biol. 1970, 50, 279–292. [Google Scholar] [CrossRef]
- Hu, J.; Othmer, H.G. A theoretical analysis of filament length fluctuations in actin and other polymers. J. Math. Biol. 2011, 63, 1001–1049. [Google Scholar] [CrossRef]
- e Silva, M.S.; Alvarado, J.; Nguyen, J.; Georgoulia, N.; Mulder, B.M.; Koenderink, G.H. Self-organized patterns of actin filaments in cell-sized confinement. Soft Matter 2011, 7, 10631–10641. [Google Scholar] [CrossRef]
- Gentile, J.E.; Carrizales, M.G.; Koleske, A.J. Control of Synapse Structure and Function by Actin and Its Regulators. Cells 2022, 11, 603. [Google Scholar] [CrossRef]
- Nechipurenko, I.V.; Doroquez, D.B.; Sengupta, P. Primary cilia and dendritic spines: Different but similar signaling compartments. Mol. Cells 2013, 36, 288–303. [Google Scholar] [CrossRef]
- Kress, G.J.; Mennerick, S. Action potential initiation and propagation: Upstream influences on neurotransmission. Neuroscience 2009, 158, 211–222. [Google Scholar] [CrossRef]
- Li, S.; Liu, N.; Zhang, X.; McLaughlin, D.W.; Zhou, D.; Cai, D. Dendritic computations captured by an effective point neuron model. Proc. Natl. Acad. Sci. USA 2019, 116, 15244–15252. [Google Scholar] [CrossRef]
- Ward, M.D. Asymptotic analysis of the Nörlund and Stirling polynomials. Appl. Anal. Discret. Math. 2012, 6, 95–105. [Google Scholar] [CrossRef]


| Symbol/Expression | Meaning | Units |
|---|---|---|
| Spatial coordinates (position) | µm (micrometers) | |
| Euclidean distance from origin | µm | |
| Nonlinear control parameter | dimensionless | |
| Vector Fields | mV/µm | |
| Lie bracket between and | mV/µm2 | |
| Lie bracket (recursive) | mV/µm2 | |
| Gradient of scalar potential field | mV/µm3 | |
| Activation-like potential field | dimensionless | |
| Membrane potential derived from the field | mV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafati, A.H.; Joca, S.; Vontell, R.T.; Mallard, C.; Wegener, G.; Ardalan, M. A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton. Methods Protoc. 2025, 8, 76. https://doi.org/10.3390/mps8040076
Rafati AH, Joca S, Vontell RT, Mallard C, Wegener G, Ardalan M. A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton. Methods and Protocols. 2025; 8(4):76. https://doi.org/10.3390/mps8040076
Chicago/Turabian StyleRafati, Ali H., Sâmia Joca, Regina T. Vontell, Carina Mallard, Gregers Wegener, and Maryam Ardalan. 2025. "A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton" Methods and Protocols 8, no. 4: 76. https://doi.org/10.3390/mps8040076
APA StyleRafati, A. H., Joca, S., Vontell, R. T., Mallard, C., Wegener, G., & Ardalan, M. (2025). A Model-Based Approach to Neuronal Electrical Activity and Spatial Organization Through the Neuronal Actin Cytoskeleton. Methods and Protocols, 8(4), 76. https://doi.org/10.3390/mps8040076