New Bioelectrical Impedance-Based Equations to Estimate Resting Metabolic Rate in Young Athletes
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Study Design
2.3. Anthropometrics
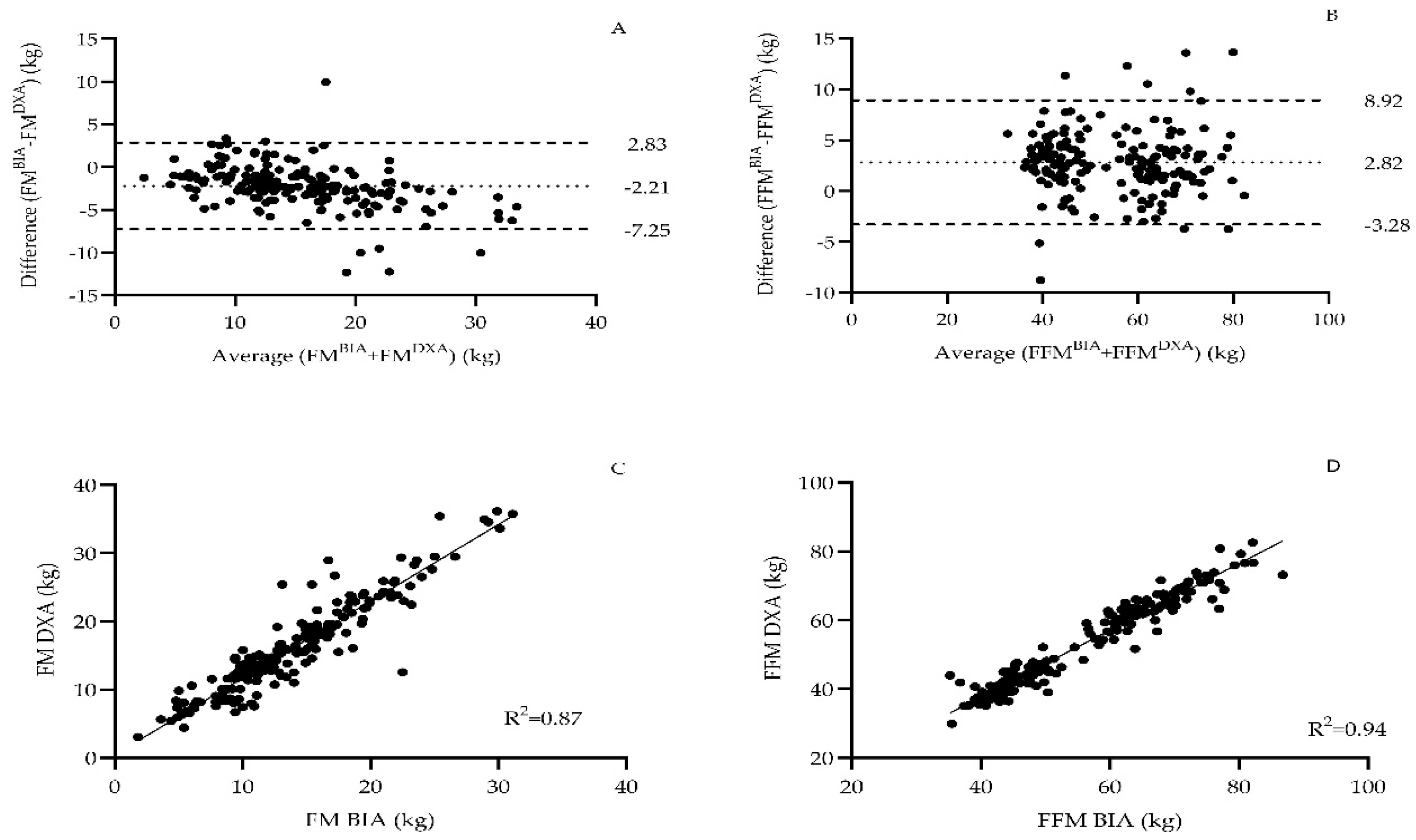
2.4. Dual Energy X-Ray Absorptiometry (DXA)
2.5. Bioelectrical Impedance Analysis (BIA)
2.6. Resting Metabolic Rate
2.7. Estimation of Resting Metabolic Rate
2.8. Statistical Analysis
3. Results
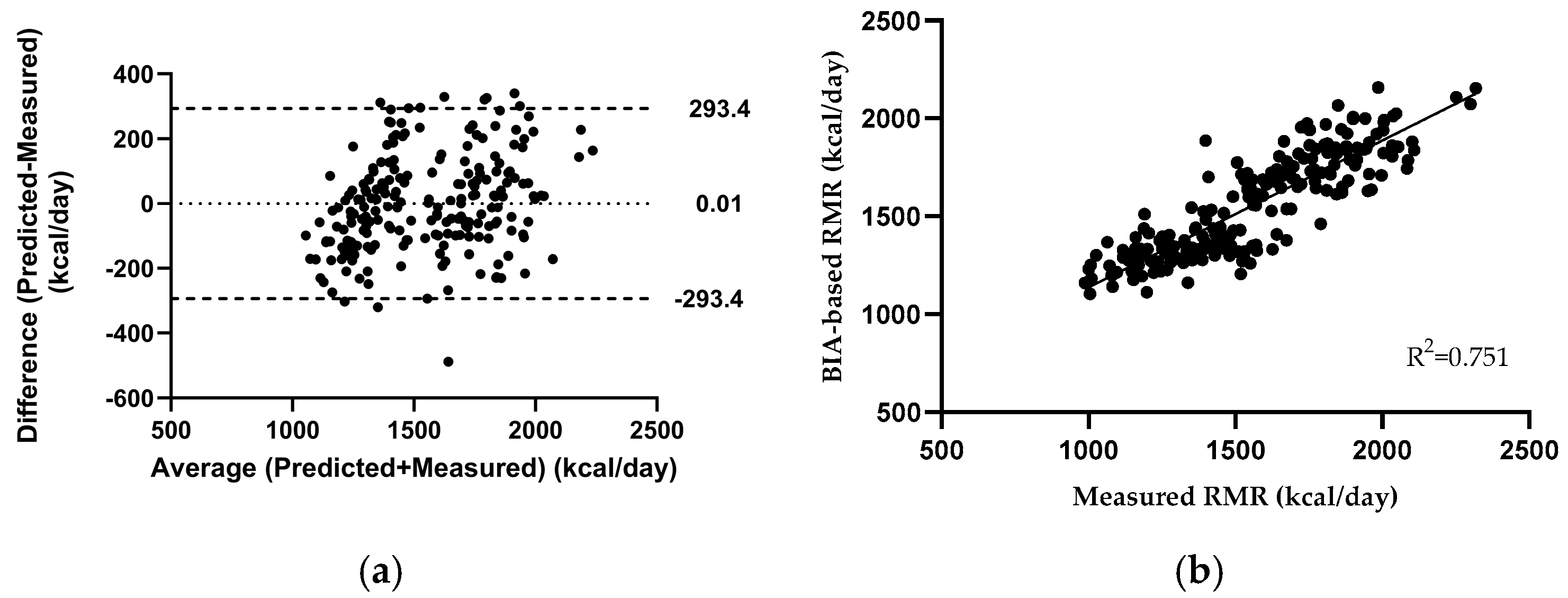
3.1. Developing a New Bioelectrical Impedance Analysis (BIA)-Based Predictive Equation
3.2. Development of New Gender-Dependent, Bioelectrical Impedance Analysis (BIA)-Based Equations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McMurray, R. Laboratory Methods for Determining Energy Expenditure of Athletes. In Nutritional Assessment of Athletes; Driskell, J.A., Wolinsky, I., Eds.; CRC Press: Boca Raton, FL, USA, 2002; pp. 203–224. [Google Scholar]
- Byrne, H.K.; Wilmore, J.H. The Relationship of Mode and Intensity of Training on Resting Metabolic Rate in Women. Int. J. Sport Nutr. Exerc. Metab. 2001, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Kang, J. Resting Metabolic Rate. In Bioenergetics Primer for Exercise Science; Human Kinetics: Champaign, IL, USA, 2008; Volume c2008, pp. 131–138. [Google Scholar]
- de Souza Marques, D.C.; Coelho, A.A.; de Oliveira, F.M.; de Souza, M.G.; Ferrari, A.; Mariano, I.R.; Branco, B.H.M. Resting Metabolic Rate: A Comparison between Different Measurement Methods Used in Male University Students. Sport Sci. Health 2021, 17, 449–457. [Google Scholar] [CrossRef]
- Schofield, K.L.; Thorpe, H.; Sims, S.T. Resting Metabolic Rate Prediction Equations and the Validity to Assess Energy Deficiency in the Athlete Population. Exp. Physiol. 2019, 104, 469–475. [Google Scholar] [CrossRef]
- Steinberg, A.; Manlhiot, C.; Cordeiro, K.; Chapman, K.; Pencharz, P.B.; McCrindle, B.W.; Hamilton, J.K. Determining the Accuracy of Predictive Energy Expenditure (PREE) Equations in Severely Obese Adolescents. Clin. Nutr. 2017, 36, 1158–1164. [Google Scholar] [CrossRef]
- Aristizabal, J.C.; Freidenreich, D.J.; Volk, B.M.; Kupchak, B.R.; Saenz, C.; Maresh, C.M.; Kraemer, W.J.; Volek, J.S. Effect of Resistance Training on Resting Metabolic Rate and Its Estimation by a Dual-Energy X-Ray Absorptiometry Metabolic Map. Eur. J. Clin. Nutr. 2015, 69, 831–836. [Google Scholar] [CrossRef]
- Schubert, M.M.; Clarke, H.E.; Seay, R.F.; Spain, K.K. Impact of 4 Weeks of Interval Training on Resting Metabolic Rate, Fitness, and Health-Related Outcomes. Appl. Physiol. Nutr. Metab. 2017, 42, 1073–1081. [Google Scholar] [CrossRef]
- Webb, P. Energy Expenditure and Fat-Free Mass in Men and Women. Am. J. Clin. Nutr. 1981, 34, 1816–1826. [Google Scholar] [CrossRef] [PubMed]
- Loucks, A.B. Energy Balance and Body Composition in Sports and Exercise. J. Sports Sci. 2004, 22, 1–14. [Google Scholar] [CrossRef]
- Ruggiero, C.; Ferrucci, L. The Endeavor of High Maintenance Homeostasis: Resting Metabolic Rate and the Legacy of Longevity. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2006, 61, 466–473. [Google Scholar] [CrossRef]
- Jeziorek, M.; Wronowicz, J.; Janek, Ł.; Kujawa, K.; Szuba, A. Development of New Predictive Equations for the Resting Metabolic Rate (RMR) of Women with Lipedema. Metabolites 2024, 14, 235. [Google Scholar] [CrossRef]
- Balci, A.; Badem, E.A.; Yılmaz, A.E.; Devrim-Lanpir, A.; Akınoğlu, B.; Kocahan, T.; Hasanoğlu, A.; Hill, L.; Rosemann, T.; Knechtle, B. Current Predictive Resting Metabolic Rate Equations Are Not Sufficient to Determine Proper Resting Energy Expenditure in Olympic Young Adult National Team Athletes. Front. Physiol. 2021, 12, 625370. [Google Scholar] [CrossRef] [PubMed]
- Jagim, A.R.; Camic, C.L.; Kisiolek, J.; Luedke, J.; Erickson, J.; Jones, M.T.; Oliver, J.M. Accuracy of Resting Metabolic Rate Prediction Equations in Athletes. J. Strength Cond. Res. 2018, 32, 1875–1881. [Google Scholar] [CrossRef]
- Fullmer, S.; Benson-Davies, S.; Earthman, C.P.; Frankenfield, D.C.; Gradwell, E.; Lee, P.S.P.; Piemonte, T.; Trabulsi, J. Evidence Analysis Library Review of Best Practices for Performing Indirect Calorimetry in Healthy and Non–Critically Ill Individuals. J. Acad. Nutr. Diet. 2015, 115, 1417–1446.e2. [Google Scholar] [CrossRef] [PubMed]
- Levine, J.A.; Schleusner, S.J.; Jensen, M.D. Energy Expenditure of Nonexercise Activity. Am. J. Clin. Nutr. 2000, 72, 1451–1454. [Google Scholar] [CrossRef]
- Bielinski, R.; Schutz, Y.; Jéquier, E. Energy Metabolism during the Postexercise Recovery in Man. Am. J. Clin. Nutr. 1985, 42, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Ferrannini, E. The Theoretical Bases of Indirect Calorimetry: A Review. Metabolism 1988, 37, 287–301. [Google Scholar] [CrossRef]
- Harris, J.A.; Benedict, F.G. A Biometric Study of Human Basal Metabolism. Proc. Natl. Acad. Sci. USA 1918, 4, 370–373. [Google Scholar] [CrossRef]
- Energy and Protein Requirements. In Report of a Joint FAO/WHO/UNU Expert Consultation; World Health Organization Technical Report Series; World Health Organization: Geneva, Switzerland, 1985; Volume 724, pp. 1–206.
- Cunningham, J.J. A Reanalysis of the Factors Influencing Basal Metabolic Rate in Normal Adults. Am. J. Clin. Nutr. 1980, 33, 2372–2374. [Google Scholar] [CrossRef]
- Schofield, W.N. Predicting Basal Metabolic Rate, New Standards and Review of Previous Work. Hum. Nutr. Clin. Nutr. 1985, 39 (Suppl. 1), 5–41. [Google Scholar]
- Marra, M.; Di Vincenzo, O.; Cioffi, I.; Sammarco, R.; Morlino, D.; Scalfi, L. Resting Energy Expenditure in Elite Athletes: Development of New Predictive Equations Based on Anthropometric Variables and Bioelectrical Impedance Analysis Derived Phase Angle. J. Int. Soc. Sports Nutr. 2021, 18, 68. [Google Scholar] [CrossRef]
- Martinho, D.; Naughton, R.; Faria, A.; Rebelo, A.; Sarmento, H. Predicting Resting Energy Expenditure among Athletes: A Systematic Review. Biol. Sport 2023, 40, 787–804. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, J.E.R.; Corish, C.A.; Horner, K. Accuracy of Resting Metabolic Rate Prediction Equations in Athletes: A Systematic Review with Meta-Analysis. Sports Med. 2023, 53, 2373–2398. [Google Scholar] [CrossRef] [PubMed]
- De Lorenzo, A.; Bertini, I.; Candeloro, N.; Piccinelli, R.; Innocente, I.; Brancati, A. A New Predictive Equation to Calculate Resting Metabolic Rate in Athletes. J. Sports Med. Phys. Fit. 1999, 39, 213–219. [Google Scholar]
- ten Haaf, T.; Weijs, P.J.M. Resting Energy Expenditure Prediction in Recreational Athletes of 18–35 Years: Confirmation of Cunningham Equation and an Improved Weight-Based Alternative. PLoS ONE 2014, 9, e108460. [Google Scholar] [CrossRef]
- Tinsley, G.M.; Graybeal, A.J.; Moore, M.L. Resting Metabolic Rate in Muscular Physique Athletes: Validity of Existing Methods and Development of New Prediction Equations. Appl. Physiol. Nutr. Metab. 2019, 44, 397–406. [Google Scholar] [CrossRef]
- Watson, A.D.; Zabriskie, H.A.; Witherbee, K.E.; Sulavik, A.; Gieske, B.T.; Kerksick, C.M. Determining a Resting Metabolic Rate Prediction Equation for Collegiate Female Athletes. J. Strength Cond. Res. 2019, 33, 2426–2432. [Google Scholar] [CrossRef]
- Wong, J.E.; Poh, B.K.; Nik Shanita, S.; Izham, M.M.; Chan, K.Q.; Tai, M.D.; Ng, W.W.; Ismail, M.N. Predicting Basal Metabolic Rates in Malaysian Adult Elite Athletes. Singap. Med. J. 2012, 53, 744–749. [Google Scholar]
- Freire, R.; Pereira, G.R.; Alcantara, J.M.A.; Santos, R.; Hausen, M.; Itaborahy, A. New Predictive Resting Metabolic Rate Equations for High-Level Athletes: A Cross-Validation Study. Med. Sci. Sports Exerc. 2022, 54, 1335–1345. [Google Scholar] [CrossRef]
- Abulmeaty, M.M.A.; Almajwal, A.; Elsayed, M.; Hassan, H.; Aldossari, Z.; Alsager, T. Development and Validation of Novel Equation for Prediction of Resting Energy Expenditure in Active Saudi Athletes. Medicine 2023, 102, e36826. [Google Scholar] [CrossRef]
- McKay, A.K.A.; Stellingwerff, T.; Smith, E.S.; Martin, D.T.; Mujika, I.; Goosey-Tolfrey, V.L.; Sheppard, J.; Burke, L.M. Defining Training and Performance Caliber: A Participant Classification Framework. Int. J. Sports Physiol. Perform. 2022, 17, 317–331. [Google Scholar] [CrossRef]
- Campa, F.; Toselli, S.; Mazzilli, M.; Gobbo, L.A.; Coratella, G. Assessment of Body Composition in Athletes: A Narrative Review of Available Methods with Special Reference to Quantitative and Qualitative Bioimpedance Analysis. Nutrients 2021, 13, 1620. [Google Scholar] [CrossRef]
- Ackland, T.R.; Lohman, T.G.; Sundgot-Borgen, J.; Maughan, R.J.; Meyer, N.L.; Stewart, A.D.; Müller, W. Current Status of Body Composition Assessment in Sport. Sports Med. 2012, 42, 227–249. [Google Scholar] [CrossRef] [PubMed]
- Sillanpää, E.; Cheng, S.; Häkkinen, K.; Finni, T.; Walker, S.; Pesola, A.; Ahtiainen, J.; Stenroth, L.; Selänne, H.; Sipilä, S. Body Composition in 18- to 88-Year-Old Adults—Comparison of Multifrequency Bioimpedance and Dual-Energy X-Ray Absorptiometry. Obesity 2014, 22, 101–109. [Google Scholar] [CrossRef] [PubMed]
- McLester, C.N.; Nickerson, B.S.; Kliszczewicz, B.M.; McLester, J.R. Reliability and Agreement of Various InBody Body Composition Analyzers as Compared to Dual-Energy X-Ray Absorptiometry in Healthy Men and Women. J. Clin. Densitom. 2020, 23, 443–450. [Google Scholar] [CrossRef] [PubMed]
- Nieman, D.C.; Austin, M.D.; Benezra, L.; Pearce, S.; McInnis, T.; Unick, J.; Gross, S.J. Validation of Cosmed’s FitMateTM in Measuring Oxygen Consumption and Estimating Resting Metabolic Rate. Res. Sports Med. 2006, 14, 89–96. [Google Scholar] [CrossRef]
- Jagim, A.R.; Camic, C.L.; Askow, A.; Luedke, J.; Erickson, J.; Kerksick, C.M.; Jones, M.T.; Oliver, J.M. Sex Differences in Resting Metabolic Rate Among Athletes. J. Strength Cond. Res. 2019, 33, 3008–3014. [Google Scholar] [CrossRef]
- Reale, R.J.; Roberts, T.J.; Lee, K.A.; Bonsignore, J.L.; Anderson, M.L. Metabolic Rate in Adolescent Athletes: The Development and Validation of New Equations, and Comparison to Previous Models. Int. J. Sport Nutr. Exerc. Metab. 2020, 30, 249–257. [Google Scholar] [CrossRef]
- Jagim, A.R.; Jones, M.T.; Askow, A.T.; Luedke, J.; Erickson, J.L.; Fields, J.B.; Kerksick, C.M. Sex Differences in Resting Metabolic Rate among Athletes and Association with Body Composition Parameters: A Follow-Up Investigation. J. Funct. Morphol. Kinesiol. 2023, 8, 109. [Google Scholar] [CrossRef]

| Equations | Formula |
|---|---|
| De Lorenzo [27] | RMR (kcal/day) = −857 + [9∗BW (in kg)] + [11.7∗H (in cm)] |
| Ten Haaf_BW [28] | RMR (kcal/day) = 29.279 + ([11.936∗BW (in kg)] + [587.728∗H (in m)] − [8.129∗Age (years)] + [191.027∗Gender (M = 1, F = 0)]) |
| Ten Haaf_FFM [28] | RMR (kcal/day) = 484.264 + [22.771∗FFM (in kg)] |
| Jagim_BW [38] | M: RMR (kcal/day) = 775.33 + [19.46∗BW (in kg)] F: RMR (kcal/day) = 288.6 + [21.10∗BW (in kg)] |
| Total (n = 219) | Male (n = 104) | Female (n = 115) | p-Value | ||||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | ||
| Age (years) | 20.35 | 1.47 | 20.52 | 1.57 | 20.20 | 1.35 | 0.108 |
| Height (cm) | 173.16 | 10.17 | 181.3 | 7.25 | 165.81 | 5.94 | <0.001 |
| Weight (kg) | 69.73 | 13.13 | 79.74 | 10.19 | 60.67 | 7.86 | <0.001 |
| BMI (kg/m2) | 23.09 | 2.72 | 24.24 | 2.55 | 22.05 | 2.44 | <0.001 |
| BFM (kg) | 14.14 | 5.51 | 12.17 | 5.55 | 15.92 | 4.85 | <0.001 |
| BFP (%) | 20.60 | 7.55 | 14.82 | 5.27 | 25.83 | 5.09 | <0.001 |
| SMM (kg) | 30.73 | 7.78 | 37.68 | 5.16 | 24.44 | 2.82 | <0.001 |
| Protein (kg) | 11.60 | 5.63 | 13.85 | 1.40 | 9.56 | 7.07 | <0.001 |
| RHMM (kg) | 3.05 | 0.97 | 3.93 | 0.58 | 2.26 | 0.40 | <0.001 |
| LHMM (kg) | 3.01 | 0.96 | 3.88 | 0.58 | 2.23 | 0.38 | <0.001 |
| RHFM (kg) | 0.59 | 0.30 | 0.47 | 0.28 | 0.70 | 0.25 | <0.001 |
| LHFM (kg) | 0.58 | 0.29 | 0.46 | 0.28 | 0.69 | 0.25 | <0.001 |
| TMM (kg) | 24.75 | 5.70 | 30.00 | 3.21 | 20.00 | 2.22 | <0.001 |
| TFM (kg) | 6.95 | 3.01 | 6.75 | 3.19 | 7.14 | 2.84 | 0.334 |
| RLMM (kg) | 8.52 | 2.46 | 10.41 | 2.24 | 6.81 | 0.91 | <0.001 |
| LLMM (kg) | 8.43 | 2.04 | 10.24 | 1.15 | 6.80 | 1.03 | <0.001 |
| RLFM (kg) | 2.40 | 1.20 | 1.61 | 1.04 | 3.11 | 0.83 | <0.001 |
| LLFM (kg) | 2.39 | 1.20 | 1.56 | 0.93 | 3.14 | 0.88 | <0.001 |
| ICW (L) | 25.59 | 5.97 | 31.23 | 2.98 | 20.49 | 2.18 | <0.001 |
| ECW(L) | 15.00 | 3.33 | 18.09 | 1.82 | 12.21 | 1.26 | <0.001 |
| PhA (degrees) | 6.16 | 0.76 | 6.70 | 0.50 | 5.68 | 0.62 | <0.001 |
| Total (n = 219) | Male (n = 104) | Female (n = 115) | p-Value | ||||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | ||
| RMR (kcal) | |||||||
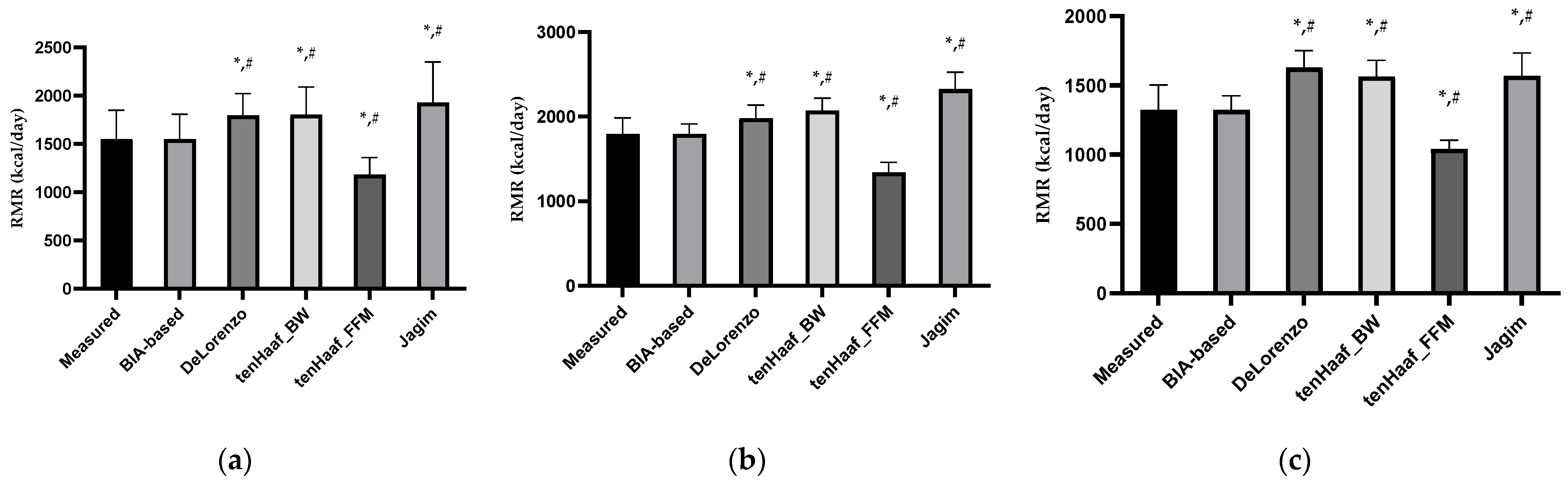
| Measured | 1548.06 | 299.92 | 1797.45 | 187.34 | 1322.51 | 179.57 | <0.001 |
| BIA-based | 1548.04 | 259.88 | 1797.45 | 115.32 | 1322.53 | 103.96 | <0.001 |
| De Lorenzo_BW | 1796.55 | 224.68 | 1981.85 | 155.63 | 1628.97 | 122.47 | <0.001 |
| Ten Haaf_BW | 1804.55 | 286.42 | 2070.83 | 148.94 | 1563.74 | 116.86 | <0.001 |
| Ten Haaf_FFM | 1183.95 | 177.24 | 1342.16 | 117.52 | 1040.87 | 64.09 | <0.001 |
| Jagim_BW | 1928.89 | 420.71 | 2327.08 | 198.29 | 1568.78 | 165.77 | <0.001 |
| Total (n = 51) | Male (n = 24) | Female (n = 27) | p-Value | ||||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | ||
| Age (years) | 20.55 | 1.60 | 21.04 | 1.73 | 20.11 | 1.37 | 0.037 |
| Height (cm) | 173.37 | 10.84 | 181.75 | 8.84 | 165.93 | 5.88 | <0.001 |
| Weight (kg) | 71.88 | 15.62 | 84.57 | 11.38 | 60.61 | 8.61 | <0.001 |
| BMI (kg/m2) | 23.41 | 3.26 | 25.21 | 3.19 | 21.81 | 2.41 | <0.001 |
| BFM (kg) | 15.39 | 6.26 | 15.23 | 7.80 | 15.54 | 4.63 | 0.865 |
| BFP (%) | 21.65 | 7.33 | 17.38 | 6.84 | 25.44 | 5.50 | <0.001 |
| SMM (kg) | 30.70 | 8.90 | 37.56 | 7.99 | 24.60 | 3.72 | <0.001 |
| Protein (kg) | 11.41 | 2.93 | 14.21 | 1.11 | 8.93 | 1.35 | <0.001 |
| RHMM (kg) | 3.11 | 1.01 | 4.06 | 0.44 | 2.27 | 0.50 | <0.001 |
| LHMM (kg) | 3.04 | 0.99 | 3.95 | 0.47 | 2.23 | 0.49 | <0.001 |
| RHFM (kg) | 0.65 | 0.33 | 0.63 | 0.41 | 0.66 | 0.24 | 0.684 |
| LHFM (kg) | 0.64 | 0.33 | 0.61 | 0.42 | 0.66 | 0.24 | 0.565 |
| TMM (kg) | 25.08 | 6.05 | 30.78 | 2.52 | 20.00 | 2.82 | <0.001 |
| TFM (kg) | 7.71 | 3.58 | 8.51 | 4.39 | 7.00 | 2.56 | 0.135 |
| RLMM (kg) | 8.58 | 2.12 | 10.50 | 1.02 | 6.87 | 1.11 | <0.001 |
| LLMM (kg) | 8.59 | 2.09 | 10.48 | 1.05 | 6.90 | 1.10 | <0.001 |
| RLFM (kg) | 2.58 | 1.20 | 2.06 | 1.32 | 3.03 | 0.88 | <0.001 |
| LLFM (kg) | 8.59 | 2.09 | 2.05 | 1.34 | 3.17 | 1.06 | <0.001 |
| ICW (L) | 25.94 | 6.37 | 31.97 | 2.56 | 20.57 | 2.94 | <0.001 |
| ECW(L) | 15.22 | 3.51 | 18.52 | 1.46 | 12.29 | 1.71 | <0.001 |
| PhA (degrees) | 6.18 | 0.77 | 6.74 | 0.48 | 5.68 | 0.62 | <0.001 |
| Total (n = 51) | Male (n = 24) | Female (n = 27) | |||
|---|---|---|---|---|---|
| Measured | BIA-based | Measured | RMRM | Measured | RMRF |
| 1621.84 ± 434.01 | 1568.91 ± 283.59 | 1943.00 ± 349.94 | 1841.03 ± 106.69 | 1336.37 ± 272.16 | 1323.12 ± 124.52 |
| p = 0.165 | p = 0.116 | p = 0.767 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stampoulis, T.; Avloniti, A.; Draganidis, D.; Balampanos, D.; Chalastra, P.E.; Gkachtsou, A.; Pantazis, D.; Retzepis, N.-O.; Protopapa, M.; Poulios, A.; et al. New Bioelectrical Impedance-Based Equations to Estimate Resting Metabolic Rate in Young Athletes. Methods Protoc. 2025, 8, 53. https://doi.org/10.3390/mps8030053
Stampoulis T, Avloniti A, Draganidis D, Balampanos D, Chalastra PE, Gkachtsou A, Pantazis D, Retzepis N-O, Protopapa M, Poulios A, et al. New Bioelectrical Impedance-Based Equations to Estimate Resting Metabolic Rate in Young Athletes. Methods and Protocols. 2025; 8(3):53. https://doi.org/10.3390/mps8030053
Chicago/Turabian StyleStampoulis, Theodoros, Alexandra Avloniti, Dimitrios Draganidis, Dimitrios Balampanos, Polyxeni Efthimia Chalastra, Anastasia Gkachtsou, Dimitrios Pantazis, Nikolaos-Orestis Retzepis, Maria Protopapa, Athanasios Poulios, and et al. 2025. "New Bioelectrical Impedance-Based Equations to Estimate Resting Metabolic Rate in Young Athletes" Methods and Protocols 8, no. 3: 53. https://doi.org/10.3390/mps8030053
APA StyleStampoulis, T., Avloniti, A., Draganidis, D., Balampanos, D., Chalastra, P. E., Gkachtsou, A., Pantazis, D., Retzepis, N.-O., Protopapa, M., Poulios, A., Zaras, N., Michalopoulou, M., Fatouros, I. G., & Chatzinikolaou, A. (2025). New Bioelectrical Impedance-Based Equations to Estimate Resting Metabolic Rate in Young Athletes. Methods and Protocols, 8(3), 53. https://doi.org/10.3390/mps8030053








