Energy-Resolved Mass Spectrometry and Mid-Infrared Spectroscopy for Purity Assessment of a Synthetic Peptide Cyclised by Intramolecular Huisgen Click Chemistry
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals and Sample Preparation
2.2. Energy Resolved Mass Spectrometry
2.3. Infrared Microscopy
3. Results and Discussion
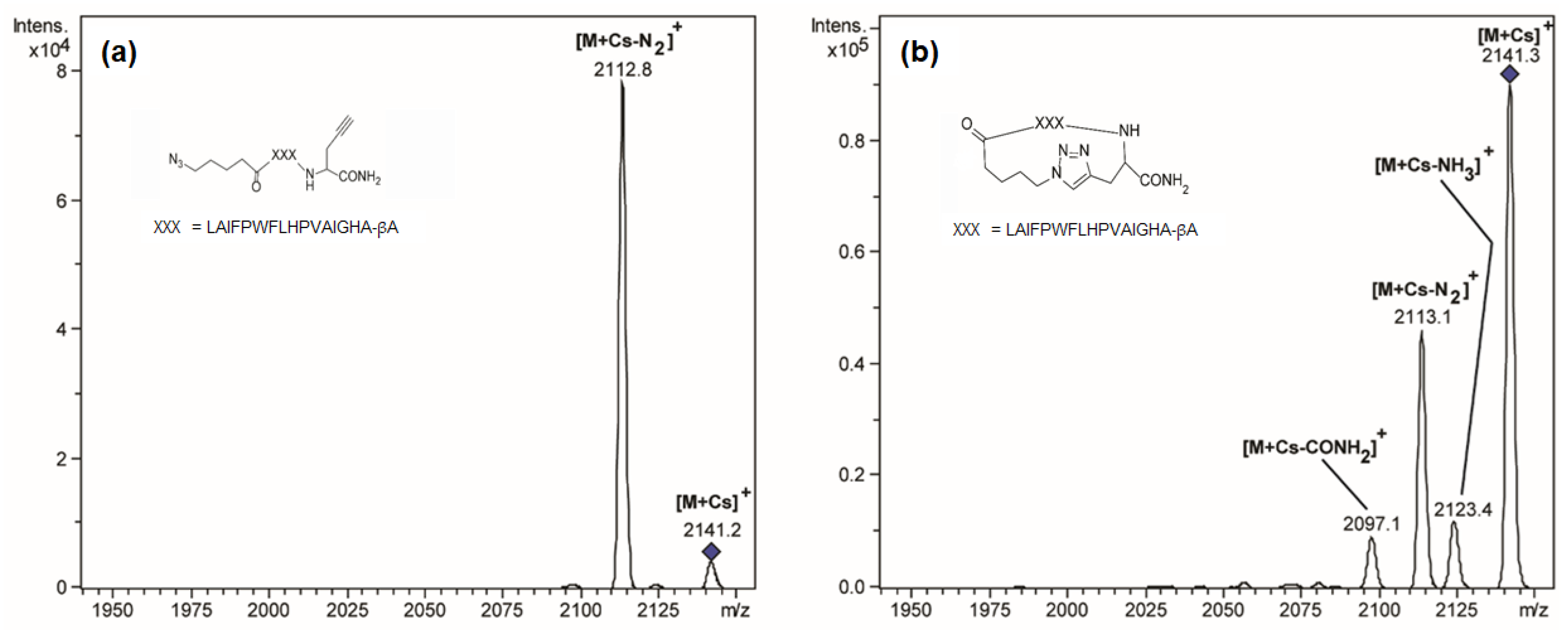
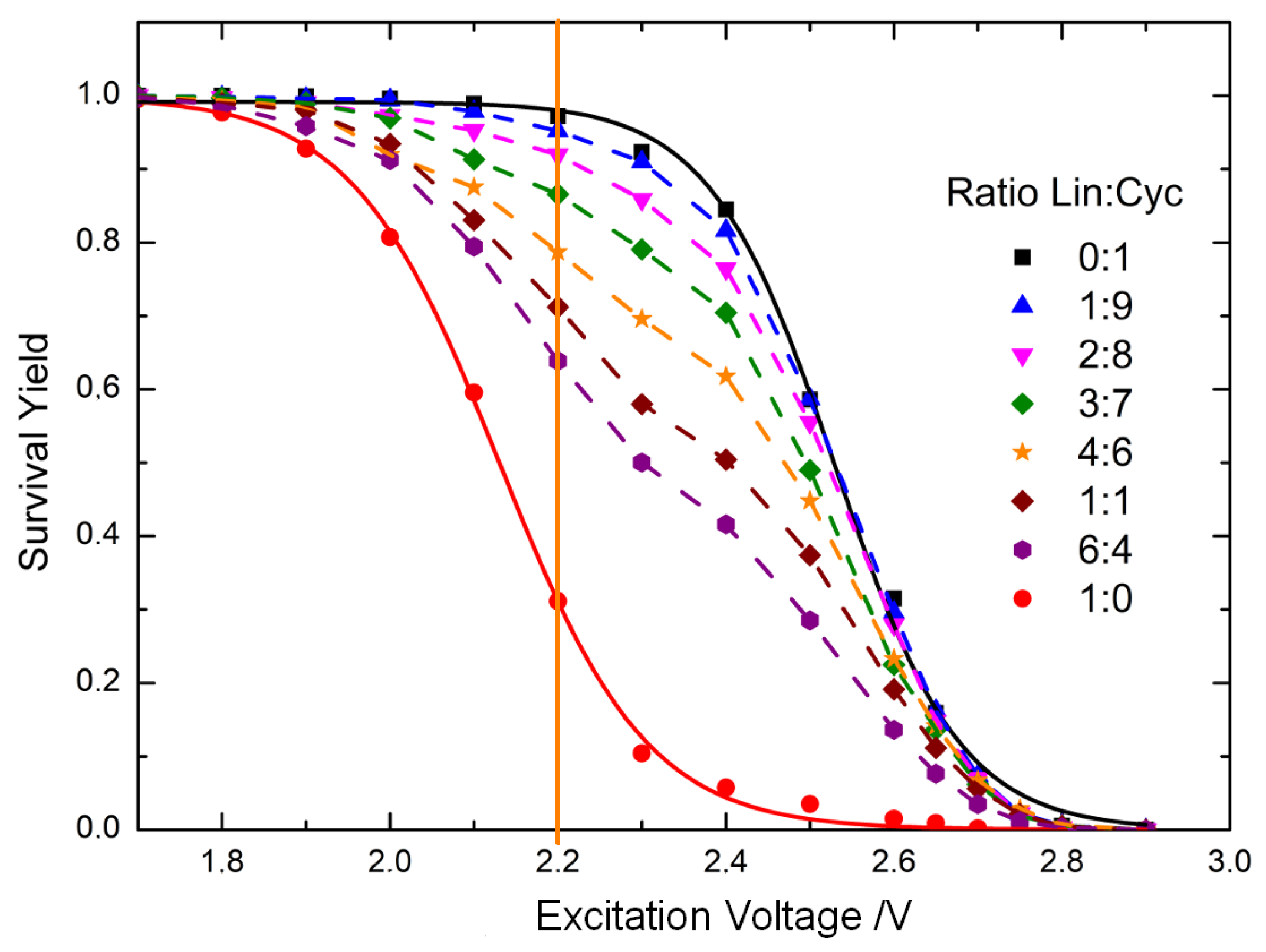
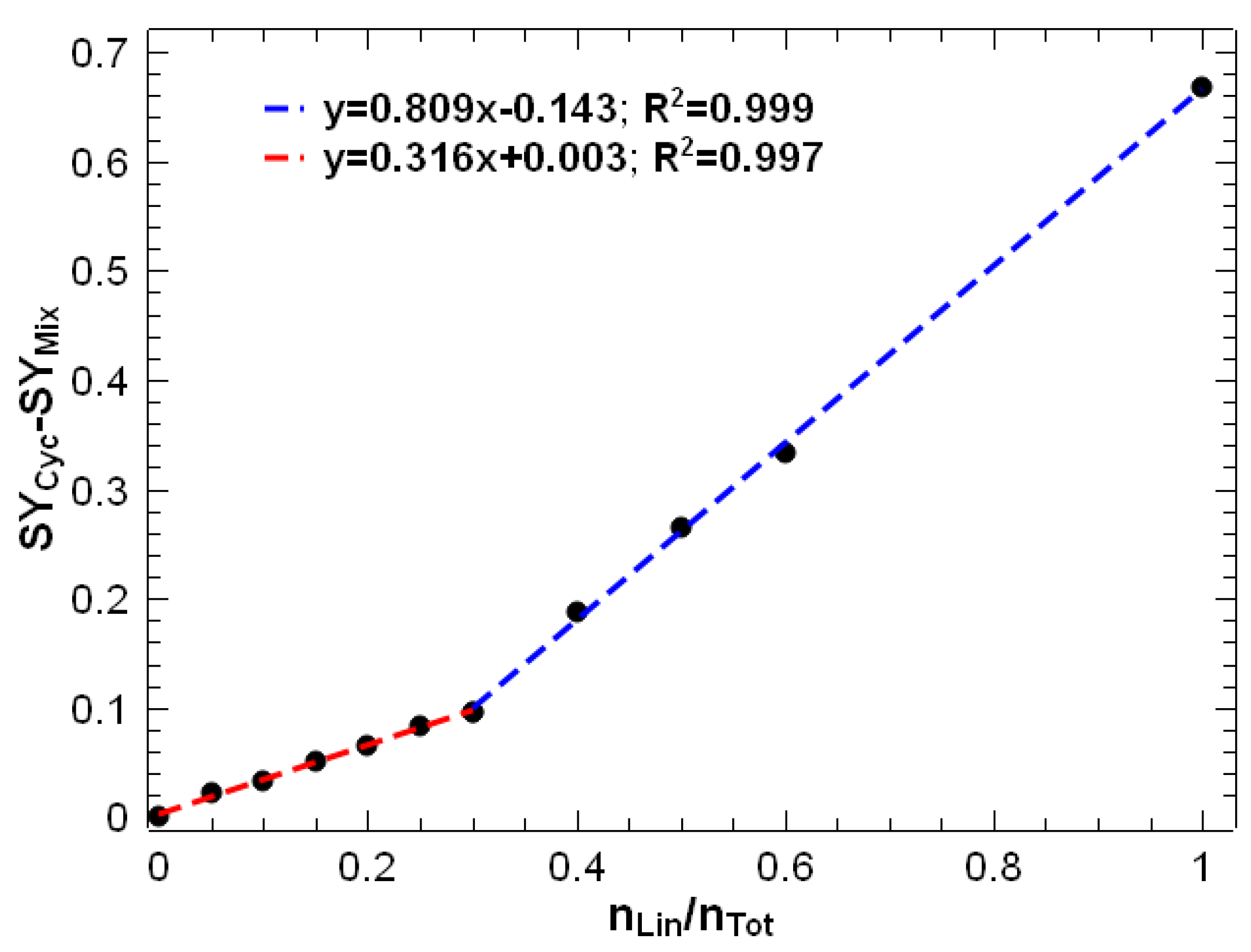
3.1. Energy-Resolved Mass Spectrometry and the Survival Yield Technique
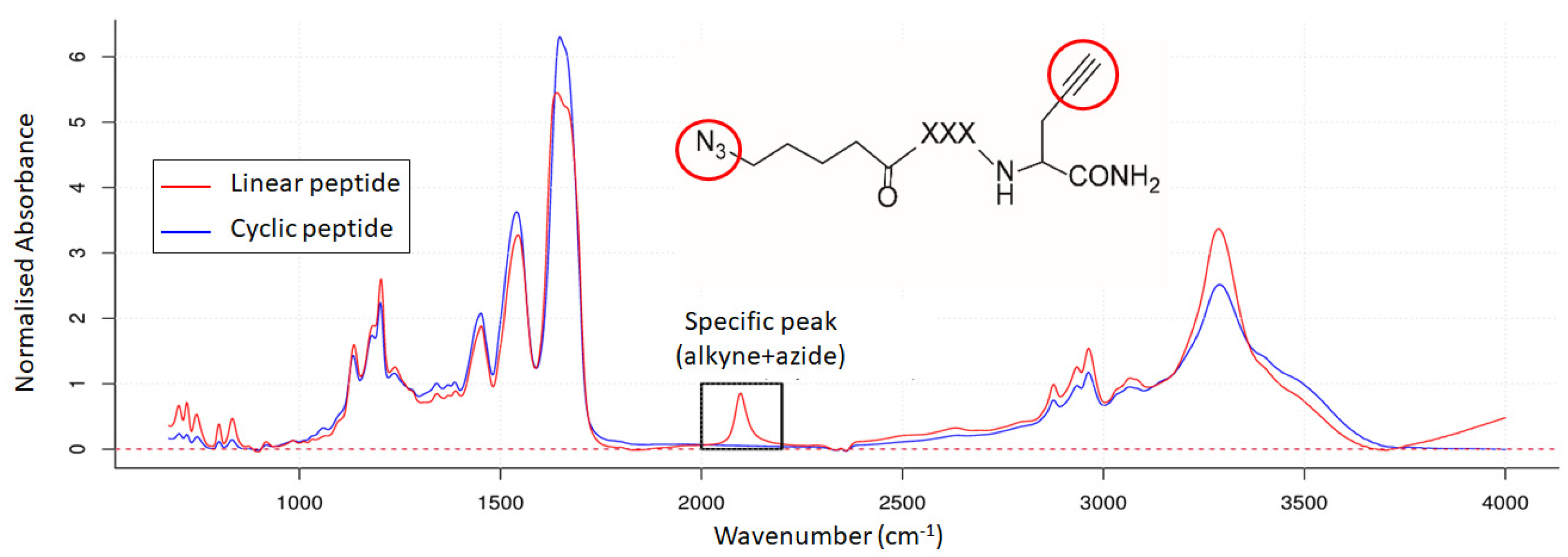
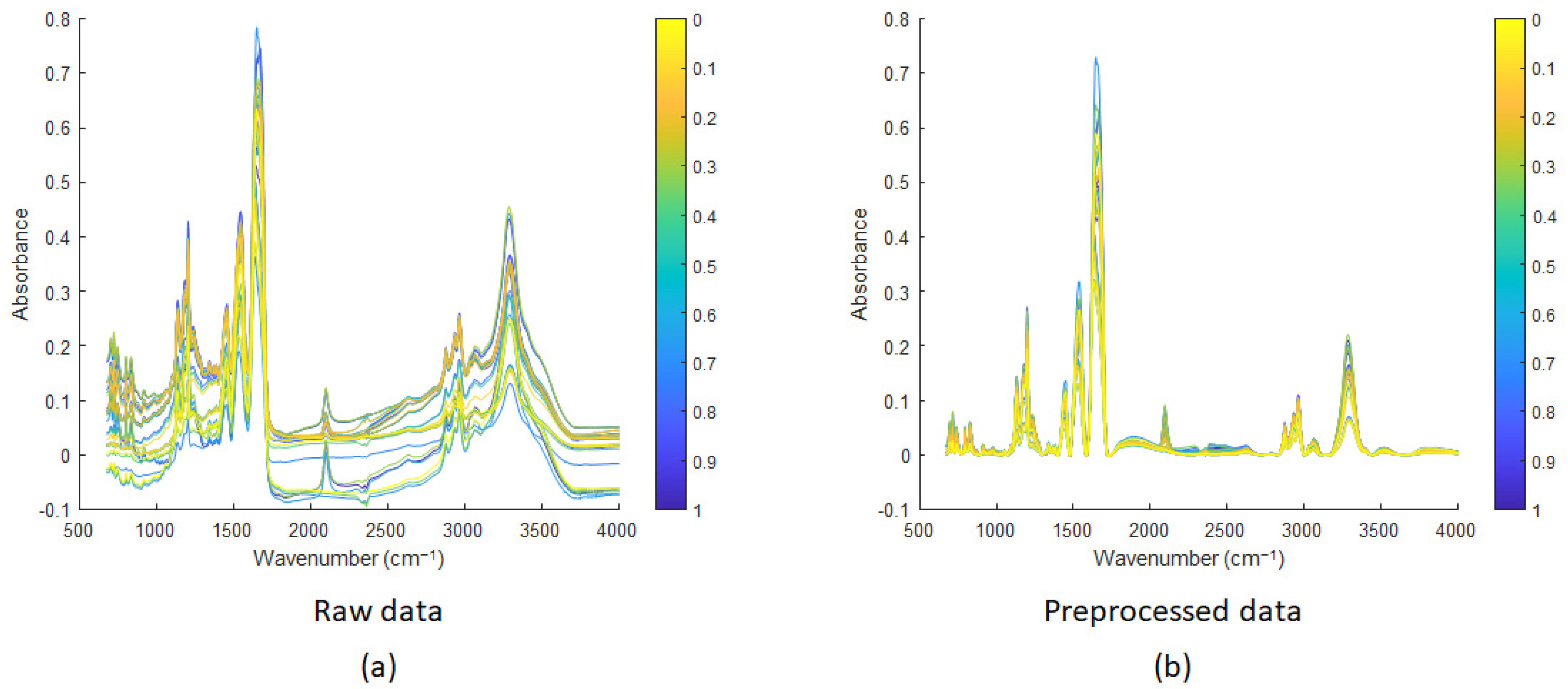
3.2. Mid-Infrared Microscopy
3.3. Comparison of Energy-Resolved Mass Spectrometry and Mid-Infrared Microscopy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdalla, M.A.; McGaw, L.J. Natural Cyclic Peptides as an Attractive Modality for Therapeutics: A Mini Review. Molecules 2018, 23, 2080. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Nielsen, A.L.; Heinis, C. Cyclic Peptides for Drug Development. Angew. Chem. Int. Ed. 2024, 63, e202308251. [Google Scholar] [CrossRef] [PubMed]
- Ramadhani, D.; Maharani, R.; Gazzali, A.M.; Muchtaridi, M. Cyclic Peptides for the Treatment of Cancers: A Review. Molecules 2022, 27, 4428. [Google Scholar] [CrossRef] [PubMed]
- Gisemba, S.A.; Ferracane, M.J.; Murray, T.F.; Aldrich, J.V. A Bicyclic Analog of the Linear Peptide Arodyn Is a Potent and Selective Kappa Opioid Receptor Antagonist. Molecules 2024, 29, 3109. [Google Scholar] [CrossRef]
- Li, P.; Roller, P.P. Cyclization Strategies in Peptide Derived Drug Design. Curr. Top. Med. Chem. 2002, 2, 325–341. [Google Scholar] [CrossRef]
- Li, H.; Aneja, R.; Chaiken, I. Click Chemistry in Peptide-Based Drug Design. Molecules 2013, 18, 9797–9817. [Google Scholar] [CrossRef]
- Jagasia, R.; Holub, J.M.; Bollinger, M.; Kirshenbaum, K.; Finn, M.G. Peptide Cyclization and Cyclodimerization by CuI-Mediated Azide−Alkyne Cycloaddition. J. Org. Chem. 2009, 74, 2964–2974. [Google Scholar] [CrossRef] [PubMed]
- Tahoori, F.; Balalaie, S.; Sheikhnejad, R.; Sadjadi, M.; Boloori, P. Design and Synthesis of Anti-Cancer Cyclopeptides Containing Triazole Skeleton. Amino Acids 2014, 46, 1033–1046. [Google Scholar] [CrossRef]
- Uclés, S.; Lozano, A.; Sosa, A.; Parrilla Vázquez, P.; Valverde, A.; Fernández-Alba, A.R. Matrix Interference Evaluation Employing GC and LC Coupled to Triple Quadrupole Tandem Mass Spectrometry. Talanta 2017, 174, 72–81. [Google Scholar] [CrossRef]
- Yan, Z.; Maher, N.; Torres, R.; Cotto, C.; Hastings, B.; Dasgupta, M.; Hyman, R.; Huebert, N.; Caldwell, G.W. Isobaric Metabolite Interferences and the Requirement for Close Examination of Raw Data in Addition to Stringent Chromatographic Separations in Liquid Chromatography/Tandem Mass Spectrometric Analysis of Drugs in Biological Matrix. Rapid Commun. Mass Spectrom. 2008, 22, 2021–2028. [Google Scholar] [CrossRef]
- Josse, T.; Winter, J.D.; Dubois, P.; Coulembier, O.; Gerbaux, P.; Memboeuf, A. A Tandem Mass Spectrometry-Based Method to Assess the Architectural Purity of Synthetic Polymers: A Case of a Cyclic Polylactide Obtained by Click Chemistry. Polym. Chem. 2014, 6, 64–69. [Google Scholar] [CrossRef]
- Jeanne Dit Fouque, D.; Maroto, A.; Memboeuf, A. Purification and Quantification of an Isomeric Compound in a Mixture by Collisional Excitation in Multistage Mass Spectrometry Experiments. Anal. Chem. 2016, 88, 10821–10825. [Google Scholar] [CrossRef] [PubMed]
- Jeanne Dit Fouque, D.; Lartia, R.; Maroto, A.; Memboeuf, A. Quantification of Intramolecular Click Chemistry Modified Synthetic Peptide Isomers in Mixtures Using Tandem Mass Spectrometry and the Survival Yield Technique. Anal. Bioanal. Chem. 2018, 410, 5765–5777. [Google Scholar] [CrossRef] [PubMed]
- Tao, W.A.; Cooks, R.G. Peer Reviewed: Chiral Analysis by MS. Anal. Chem. 2003, 75, 25 A–31 A. [Google Scholar] [CrossRef]
- Majumdar, T.K.; Clairet, F.; Tabet, J.C.; Cooks, R.G. Epimer Distinction and Structural Effects on Gas-Phase Acidities of Alcohols Measured Using the Kinetic Method. J. Am. Chem. Soc. 1992, 114, 2897–2903. [Google Scholar] [CrossRef]
- Tao, W.A.; Wu, L.; Cooks, R.G. Differentiation and Quantitation of Isomeric Dipeptides by Low-Energy Dissociation of Copper(II)-Bound Complexes. J. Am. Soc. Mass Spectrom. 2001, 12, 490–496. [Google Scholar] [CrossRef]
- Crotti, S.; Menicatti, M.; Pallecchi, M.; Bartolucci, G. Tandem Mass Spectrometry Approaches for Recognition of Isomeric Compounds Mixtures. Mass Spectrom. Rev. 2023, 42, 1244–1260. [Google Scholar] [CrossRef] [PubMed]
- Hanozin, E.; Morsa, D.; De Pauw, E. Energetics and Structural Characterization of Isomers Using Ion Mobility and Gas-Phase H/D Exchange: Learning from Lasso Peptides. Proteomics 2015, 15, 2823–2834. [Google Scholar] [CrossRef]
- Lapthorn, C.; Pullen, F.; Chowdhry, B.Z. Ion Mobility Spectrometry-Mass Spectrometry (IMS-MS) of Small Molecules: Separating and Assigning Structures to Ions. Mass Spectrom. Rev. 2013, 32, 43–71. [Google Scholar] [CrossRef]
- Morsa, D.; Defize, T.; Dehareng, D.; Jérôme, C.; De Pauw, E. Polymer Topology Revealed by Ion Mobility Coupled with Mass Spectrometry. Anal. Chem. 2014, 86, 9693–9700. [Google Scholar] [CrossRef]
- Hanozin, E.; Grifnée, E.; Gattuso, H.; Matagne, A.; Morsa, D.; Pauw, E.D. Covalent Cross-Linking as an Enabler for Structural Mass Spectrometry. Anal. Chem. 2019, 91, 12808–12818. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Wang, J.-Y.; Han, D.-Q.; Yao, Z.-P. Recent Advances in Differentiation of Isomers by Ion Mobility Mass Spectrometry. TrAC Trends Anal. Chem. 2020, 124, 115801. [Google Scholar] [CrossRef]
- Menicatti, M.; Guandalini, L.; Dei, S.; Floriddia, E.; Teodori, E.; Traldi, P.; Bartolucci, G. The Power of Energy-Resolved Tandem Mass Spectrometry Experiments for Resolution of Isomers: The Case of Drug Plasma Stability Investigation of Multidrug Resistance Inhibitors. Rapid. Commun. Mass Spectrom. 2016, 30, 423–432. [Google Scholar] [CrossRef] [PubMed]
- Menicatti, M.; Guandalini, L.; Dei, S.; Floriddia, E.; Teodori, E.; Traldi, P.; Bartolucci, G. Energy Resolved Tandem Mass Spectrometry Experiments for Resolution of Isobaric Compounds: A Case of Cis/Trans Isomerism. Eur. J. Mass Spectrom. 2016, 22, 235–243. [Google Scholar] [CrossRef]
- Menicatti, M.; Pallecchi, M.; Bua, S.; Vullo, D.; Di Cesare Mannelli, L.; Ghelardini, C.; Carta, F.; Supuran, C.T.; Bartolucci, G. Resolution of Co-Eluting Isomers of Anti-Inflammatory Drugs Conjugated to Carbonic Anhydrase Inhibitors from Plasma in Liquid Chromatography by Energy-Resolved Tandem Mass Spectrometry. J. Enzyme Inhib. Med. Chem. 2018, 33, 671–679. [Google Scholar] [CrossRef]
- Pallecchi, M.; Lucio, L.; Braconi, L.; Menicatti, M.; Dei, S.; Teodori, E.; Bartolucci, G. Isomers Recognition in HPLC-MS/MS Analysis of Human Plasma Samples by Using an Ion Trap Supported by a Linear Equations-Based Algorithm. Int. J. Mol. Sci. 2023, 24, 11155. [Google Scholar] [CrossRef]
- Memboeuf, A.; Jullien, L.; Lartia, R.; Brasme, B.; Gimbert, Y. Tandem Mass Spectrometric Analysis of a Mixture of Isobars Using the Survival Yield Technique. J. Am. Soc. Mass Spectrom. 2011, 22, 1744–1752. [Google Scholar] [CrossRef]
- Jeanne Dit Fouque, D.; Maroto, A.; Memboeuf, A. Internal Standard Quantification Using Tandem Mass Spectrometry of a Tryptic Peptide in the Presence of an Isobaric Interference. Anal. Chem. 2018, 90, 14126–14130. [Google Scholar] [CrossRef]
- Dong, X.; Mayes, H.B.; Morreel, K.; Katahira, R.; Li, Y.; Ralph, J.; Black, B.A.; Beckham, G.T. Energy-Resolved Mass Spectrometry as a Tool for Identification of Lignin Depolymerization Products. ChemSusChem 2023, 16, e202201441. [Google Scholar] [CrossRef]
- Maroto, A.; Jeanne Dit Fouque, D.; Memboeuf, A. Ion Trap MS Using High Trapping Gas Pressure Enables Unequivocal Structural Analysis of Three Isobaric Compounds in a Mixture by Using Energy-Resolved Mass Spectrometry and the Survival Yield Technique. J. Mass Spectrom. 2020, 55, e4478. [Google Scholar] [CrossRef]
- Maroto, A.; Jeanne Dit Fouque, D.; Lartia, R.; Memboeuf, A. Removal of Isobaric Interference Using Pseudo-Multiple Reaction Monitoring and Energy-Resolved Mass Spectrometry for the Isotope Dilution Quantification of a Tryptic Peptide. J. Mass Spectrom. 2024, 59, e5025. [Google Scholar] [CrossRef] [PubMed]
- Maroto, A.; Jeanne Dit Fouque, D.; Lartia, R.; Memboeuf, A. LC-MS Accurate Quantification of a Tryptic Peptide Co-Eluted with an Isobaric Interference by Using in-Source Collisional Purification. Anal. Bioanal. Chem. 2023, 415, 7211–7221. [Google Scholar] [CrossRef] [PubMed]
- Katon, J.E. Infrared Microspectroscopy. A Review of Fundamentals and Applications. Micron 1996, 27, 303–314. [Google Scholar] [CrossRef]
- Muchaamba, F.; Stephan, R. A Comprehensive Methodology for Microbial Strain Typing Using Fourier-Transform Infrared Spectroscopy. Methods Protoc. 2024, 7, 48. [Google Scholar] [CrossRef]
- Bunaciu, A.A.; Fleschin, Ş.; Aboul-Enein, H.Y. Biomedical Investigations Using Fourier Transform-Infrared Microspectroscopy. Crit. Rev. Anal. Chem. 2014, 44, 270–276. [Google Scholar] [CrossRef]
- Türker-Kaya, S.; Huck, C.W. A Review of Mid-Infrared and Near-Infrared Imaging: Principles, Concepts and Applications in Plant Tissue Analysis. Molecules 2017, 22, 168. [Google Scholar] [CrossRef]
- Lin, S.-Y.; Chu, H.-L. Fourier Transform Infrared Spectroscopy Used to Evidence the Prevention of Beta-Sheet Formation of Amyloid Beta(1-40) Peptide by a Short Amyloid Fragment. Int. J. Biol. Macromol. 2003, 32, 173–177. [Google Scholar] [CrossRef]
- Ayvaz, H.; Plans, M.; Riedl, K.M.; Schwartz, S.J.; Rodriguez-Saona, L.E. Application of Infrared Microspectroscopy and Chemometric Analysis for Screening the Acrylamide Content in Potato Chips. Anal. Methods 2013, 5, 2020–2027. [Google Scholar] [CrossRef]
- Santos, P.M.; Pereira-Filho, E.R.; Rodriguez-Saona, L.E. Rapid Detection and Quantification of Milk Adulteration Using Infrared Microspectroscopy and Chemometrics Analysis. Food Chem. 2013, 138, 19–24. [Google Scholar] [CrossRef]
- Download LibreOffice|LibreOffice—Free and Private Office Suite—Based on OpenOffice—Compatible with Microsoft. Available online: https://www.libreoffice.org/download/download-libreoffice/ (accessed on 19 September 2024).
- SciDAVis. Available online: https://scidavis.sourceforge.net/ (accessed on 19 September 2024).
- Sargent, M. (Ed.) Guide to Achieving Reliable Quantitative LC-MS Measurements; RSC Analytical Methods Committee: London, UK, 2013. [Google Scholar]
- Kruve, A.; Rebane, R.; Kipper, K.; Oldekop, M.-L.; Evard, H.; Herodes, K.; Ravio, P.; Leito, I. Tutorial Review on Validation of Liquid Chromatography–Mass Spectrometry Methods: Part I. Anal. Chim. Acta 2015, 870, 29–44. [Google Scholar] [CrossRef]
- Evard, H.; Kruve, A.; Leito, I. Tutorial on Estimating the Limit of Detection Using LC-MS Analysis, Part I: Theoretical Review. Anal. Chim. Acta 2016, 942, 23–39. [Google Scholar] [CrossRef] [PubMed]
- Currie, L.A. Detection and Quantification Limits: Origins and Historical Overview. Anal. Chim. Acta 1999, 391, 127–134. [Google Scholar] [CrossRef]
- Massart, D.L.; Vandeginste, B.G.M.; Buydens, L.M.C.; De Jong, S.; Lewi, P.J.; Smeyers-Verbeke, J. Handbook of Chemometrics and Qualimetrics: Part A; Elsevier: Amsterdam, The Netherlands, 1997; ISBN 0-444-89724-0. [Google Scholar]
- Eilers, P.; Boelens, H. Baseline Correction with Asymmetric Least Squares Smoothing. Leiden Univ. Med. Cent. Rep. 2005, 1, 5. [Google Scholar]
- Eilers, P.H.C. A Perfect Smoother. Anal. Chem. 2003, 75, 3631–3636. [Google Scholar] [CrossRef] [PubMed]

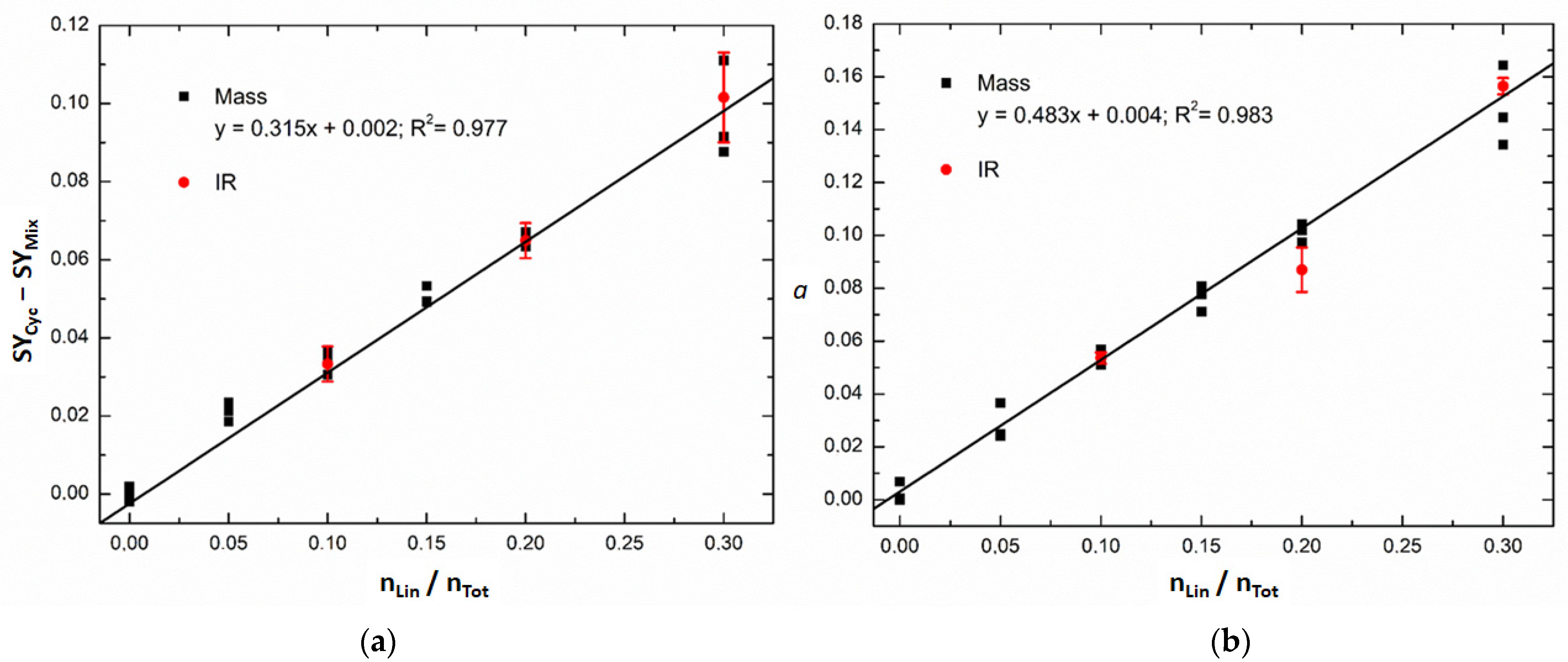

| Analytical Technique | Calibration Model | Linearity Interval | R2 | Fit Error (RMSEC) | Intermediate Precision | Detection Limit (LD) |
|---|---|---|---|---|---|---|
| ER MS | Univariate | 0–0.3 | 0.977 | 0.015 | 1.71 × 10−2 | 0.053 |
| Multivariate (CLS) | 0–0.3 | 0.983 | 0.013 | 1.58 × 10−2 | 0.045 | |
| IR microscopy | Univariate | 0–1 | 0.961 | 0.062 | 5.06 × 10−2 | 0.21 |
| Multivariate (PLS) | 0–1 | 0.987 | 0.036 | 2.63 × 10−2 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maroto, A.; Boqué, R.; Jeanne Dit Fouque, D.; Memboeuf, A. Energy-Resolved Mass Spectrometry and Mid-Infrared Spectroscopy for Purity Assessment of a Synthetic Peptide Cyclised by Intramolecular Huisgen Click Chemistry. Methods Protoc. 2024, 7, 97. https://doi.org/10.3390/mps7060097
Maroto A, Boqué R, Jeanne Dit Fouque D, Memboeuf A. Energy-Resolved Mass Spectrometry and Mid-Infrared Spectroscopy for Purity Assessment of a Synthetic Peptide Cyclised by Intramolecular Huisgen Click Chemistry. Methods and Protocols. 2024; 7(6):97. https://doi.org/10.3390/mps7060097
Chicago/Turabian StyleMaroto, Alicia, Ricard Boqué, Dany Jeanne Dit Fouque, and Antony Memboeuf. 2024. "Energy-Resolved Mass Spectrometry and Mid-Infrared Spectroscopy for Purity Assessment of a Synthetic Peptide Cyclised by Intramolecular Huisgen Click Chemistry" Methods and Protocols 7, no. 6: 97. https://doi.org/10.3390/mps7060097
APA StyleMaroto, A., Boqué, R., Jeanne Dit Fouque, D., & Memboeuf, A. (2024). Energy-Resolved Mass Spectrometry and Mid-Infrared Spectroscopy for Purity Assessment of a Synthetic Peptide Cyclised by Intramolecular Huisgen Click Chemistry. Methods and Protocols, 7(6), 97. https://doi.org/10.3390/mps7060097









