Abstract
(1) Background: Radial RARE-EPI MRI facilitates simultaneous T2 and T2* mapping (2in1-RARE-EPI). With modest undersampling (R = 2), the speed gain of 2in1-RARE-EPI relative to Multi-Spin-Echo and Multi-Gradient-Recalled-Echo references is limited. Further reduction in scan time is crucial for clinical studies investigating T2 and T2* as imaging biomarkers. We demonstrate the feasibility of further acceleration, utilizing compressed sensing (CS) reconstruction of highly undersampled 2in1-RARE-EPI. (2) Methods: Two-fold radially-undersampled 2in1-RARE-EPI data from phantoms, healthy volunteers (n = 3), and multiple sclerosis patients (n = 4) were used as references, and undersampled (Rextra = 1–12, effective undersampling Reff = 2–24). For each echo time, images were reconstructed using CS-reconstruction. For T2 (RARE module) and T2* mapping (EPI module), a linear least-square fit was applied to the images. T2 and T2* from CS-reconstruction of undersampled data were benchmarked against values from CS-reconstruction of the reference data. (3) Results: We demonstrate accelerated simultaneous T2 and T2* mapping using undersampled 2in1-RARE-EPI with CS-reconstruction is feasible. For Rextra = 6 (TA = 01:39 min), the overall MAPE was ≤8% (T2*) and ≤4% (T2); for Rextra = 12 (TA = 01:06 min), the overall MAPE was <13% (T2*) and <5% (T2). (4) Conclusion: Substantial reductions in scan time are achievable for simultaneous T2 and T2* mapping of the brain using highly undersampled 2in1-RARE-EPI with CS-reconstruction.
1. Introduction
Brain lesions in multiple sclerosis (MS) have MRI characteristics that can be used to aid diagnosis and to discriminate among different lesion types. Given these features, parametric mapping of multiple MR contrasts would be highly clinically relevant [1,2,3]. Nevertheless, routine clinical practice demands that scan acquisition times are kept to a minimum. It is therefore conceptually appealing to establish methods to simultaneously acquire multiple MR contrasts, and to explore approaches to accelerate this as much as possible. To realize this, we previously presented a radially-sampled RARE-EPI hybrid that facilitates simultaneous T2 and T2* mapping (2in1-RARE-EPI) [4]. Similar to previously proposed RARE-EPI combined-acquisition-techniques [5,6,7], the MR signal in 2in1-RARE-EPI is acquired with a RARE module followed by an EPI module to capture the T2 and T2* decay simultaneously after each excitation. The radial sampling of k-space data implemented in 2in1-RARE-EPI promotes acceleration through undersampling. This approach reduces scan time and eliminates the risk of slice misregistration, as the T2 and T2* maps are inherently co-registered. In general, the benefits of quantitative mapping come with the drawback of increased scan time, since multiple images with different contrast weightings need to be acquired. This limits the implementation of quantitative mapping in routine clinical practice and broader clinical studies. In our previous study, the acquisition time for simultaneous T2 and T2* mapping was reduced to 77% of the comparable reference methods Multi-Spin-Echo (MSE) and Multi-Gradient-Recalled-Echo (MGRE) due to the use of the hybrid acquisition and a modest radial undersampling factor (R = 2) [4]. Unlike previous methods for simultaneous T2 and T2* mapping, such as Spin- and Gradient-Echo (SAGE) [8,9,10,11] and 3D Echo Planar Time-Resolved Imaging (3D EPTI) [12], which utilize multiple EPI readouts before and after 180° refocusing pulses to obtain multiple images with different contrast weightings for T2 and T2* mapping, 2in1-RARE-EPI samples k-space spokes in a hybrid acquisition in an echo train consisting of a RARE module followed by an EPI module.
Additional reduction in scan time will further enhance patient comfort and compliance, and is a fundamental precursor for broader clinical studies on the potential of T2 and T2* as imaging biomarkers in MS, including application in a drug trial [13]. A promising approach to accelerate quantitative mapping in MRI is the use of compressed sensing (CS) reconstruction of highly undersampled data [14,15,16,17,18]. CS has revolutionized MRI by exploiting the inherent sparsity of natural images to allow high k-space undersampling factors [19,20]. First commercial applications have recently achieved clinical approval [21,22,23]. Previous contributions have shown accelerated quantitative measurements in vivo for T2 mapping in cartilage and liver [18], single point imaging T2* mapping of a mouse tumor [15], and T2 mapping of the mouse heart [14]. However, little has been reported to confirm the effectiveness of CS for relaxation time mapping and to evaluate the effect of undersampling rates on the reliability of quantitative mapping of neurodegenerative and neuroinflammatory disease in vivo.
Here, we demonstrate the first application of CS reconstruction for simultaneous T2 and T2* mapping with accelerated 2in1-RARE-EPI, in phantoms, healthy volunteers, and MS patients, and provide practical recommendations.
2. Materials and Methods
2.1. MR Data Acquisition
In 2in1-RARE-EPI, the MR signal is first acquired with a RARE module (T2 decay), followed by the acquisition with an EPI module (T2* decay). A pulse sequence diagram of 2in1-RARE-EPI is depicted in Figure 1. In the EPI module, transitions between the k-space spokes are realized by small blip gradients.
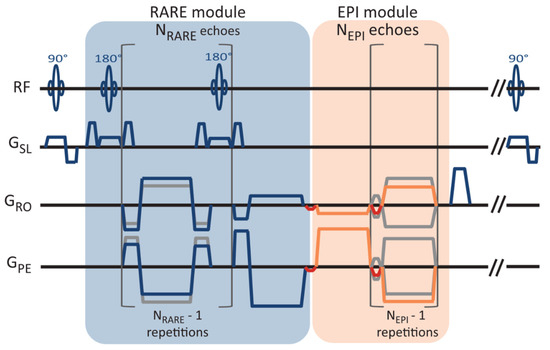
Figure 1.
Pulse sequence diagram of the radially-sampled RARE-EPI hybrid, which facilitates simultaneous T2 and T2* mapping (2in1-RARE-EPI). The magnetic resonance signal is first acquired with a RARE module with NRARE echoes, followed by the acquisition with an EPI module of NEPI echoes. NRARE = 14 and NEPI = 18 were used in this study. The transition between the spokes in the EPI module are realized with small blip gradients (marked in red).
The MR data were acquired with 2in1-RARE-EPI at 3.0 T (Siemens Magnetom SkyraFit, Erlangen, Germany, maximum gradient strength, 43 mT/m; maximum slew rate 180.18 mT/m/ms) using the body RF coil for transmission and a 32-channel head RF coil (Siemens, Erlangen, Germany) for signal reception. The radial k-space data were corrected for gradient delays based on a calibration scan acquired prior to each scan (TACalib = 32 s). The following imaging parameters were used: FOV = (232 × 232) mm2, matrix size = 256 × 256, slice thickness = 5 mm, no. of slices = 3, TR = 2000 ms, NRARE = 14, NEPI = 18, echo-spacing (RARE/EPI) = 6.5 ms/2.3 ms, receiver bandwidth = 610 Hz/px, no. of shots (NS) = 200, acquisition time (TA) = TACalib + NS*TR = 07:12 min. For the phantom study, a single slice and FOV = (212 × 212) mm2 were used. The acquisition of 200 shots with a matrix size of 256 × 256 corresponds to an undersampling factor of R = 2 for the TE images.
2.2. Phantom Study
The phantom was designed to mimic the T2 and T2* of brain tissue, and contained 12 plastic tubes (volume = 15 mL, diameter = 15 mm), filled with water-based solutions of the iron oxide nanoparticle-based contrast agent Resovist (Schering, Berlin, Germany). The iron oxide nanoparticles decrease T2 and T2* of the solvent, depending on their concentration in the solution. For the phantom, different solutions with iron concentrations ranging between 2.3 to 12.3 μg Fe/mL were used. Specifically, the tubes were filled with solutions of the following iron concentrations (from left to right and top to bottom): 5.9, 4.6, 6.15, 6.15, 4.01, 4.01, 2.95, 2.95, 2.3, 2.3, 12.3, 8.02 μg Fe/mL and 3.51 μg Fe/mL outside the tubes.
2.3. In Vivo Study
The in vivo feasibility study included three healthy volunteers (1 female/2 male, age = 31–46 years, body mass index (BMI) = 23.6–25.9 kg/m2) and four MS patients (3 female/1 male, age = 30–39 years, BMI = 22.3–34.9 kg/m2). For the in vivo study including healthy volunteers, three slices were acquired, which covered the lateral ventricles. For the in vivo study including MS patients, three slices covering MS specific lesions were acquired, which were selected based on a 2D T2-weighted RARE scan.
2.4. T2 and T2* Mapping
In 2in1-RARE-EPI, the MR signal is first acquired with a RARE module (T2 decay), followed by the acquisition with an EPI module (T2* decay). For T2 and T2* mapping, a linear least-square fit was applied to the images reconstructed from k-space data acquired at the same echo times (TEs) within the echo train. For T2 mapping, the first echo was excluded from the fit to limit the effect of stimulated echoes. This approach is generally effective at reducing stimulated echo contamination, however, it may still result in erroneous estimations of T2, particularly for very low T2 values [24].
2.5. Undersampling, Data Pre-Processing, and CS-Reconstruction
The two-fold radially-undersampled 2in1-RARE-EPI data, used as reference, were undersampled at each TE by removing every nth k-space spoke. Undersampling factors of Rextra = 1, 2, 4, 6, 8, 10, and 12 were investigated. This undersampling scheme corresponds to an effective acceleration of Reff = 2–24. For each receive channel, non-regularized reconstructions of the first TE images were obtained with the Michigan Image Reconstruction Toolbox (MIRT) NUFFT [25,26] for the RARE and EPI modules. Based on these images, coil sensitivities were computed with the ESPIRiT method [27,28] implemented in the Berkeley Advanced Reconstruction Toolbox (BART, v0.7.00) [29,30,31] for each undersampling factor and module. K-space noise levels and correlations were estimated from background regions in the 1D inverse Fourier transform along the frequency encoding direction. Noise pre-whitening using the Cholesky decomposition of the inverse covariance matrix was performed [32,33]. Individual echo parallel imaging CS-reconstructions were computed with wavelet regularization using the Fast Iterative Soft-Thresholding Algorithm implemented in BART [34,35,36,37]. Automatic optimization of the regularization strength (λ) is essential to ensure reproducibility and reliability of the results [38]. We employed an adapted version of the discrepancy principle [39,40,41]. Given radial non-uniform Fourier transform and coil sensitivities S, the expected quadratic deviation of a true, but unknown, image rt from the measured data y is
where is the number of frequency encoding points, the number of spokes, the number of channels, and the noise standard deviation in the real and imaginary channels. The discrepancy principle consists of finding a value of λ such that
for CS-reconstruction . However, implementation of the discrepancy principle, and the CS-reconstruction in general, requires use of a non-uniform fast Fourier transform () to limit computation times, and data-derived coil sensitivities , both of which introduce errors, such that the minimal attainable deviation exceeds the noise level for high SNR data:
The NUFFT and coil sensitivity induced errors are proportional to the signal level, and thus highest in the k-space center, while the measurement noise is uniformly distributed. We exploited this fact by considering only the k-space periphery in the computation of the deviation of the reconstruction from the measured data. For this purpose, we selected only the highest spatial frequencies on each spoke using masking matrix . The discrepancy principle condition thus becomes
where is an additional factor to fine tune the degree of smoothing, which was set to 0.97 in our study [41]. Importantly, this masking is only applied during the computation of the deviation from the data and not during the CS-reconstruction itself. The Illinois algorithm was employed to find the fitting value of λ with a tolerance of 0.1% in the data deviation. Using this adapted form of the discrepancy principle, high reconstruction quality could be achieved with automatic tuning for most images. The above condition could not be met for the highest SNR echoes in the RARE module, and for the first echoes of the EPI module without retrospective undersampling. In these cases, a small, fixed λ value of 2.5 × 10−5 was employed to ensure the reduction of aliasing artifacts with only minimal deviation from the measured data.
2.6. Assessment of the Effect of Acceleration on T2 and T2* Mapping
To assess the feasibility of undersampling, regression and Bland–Altman plot analyses were performed for every undersampling factor. T2 and T2* derived from CS-reconstruction of the undersampled data were benchmarked against T2 and T2* obtained from CS-reconstruction of the reference data (Rextra = 1). For analysis of the phantom study, seven ROIs (size = 9 × 9 pixels) were placed within the phantom (Figure 2a), corresponding to the position of the plastic tubes containing the varying iron concentrations. For analysis of the T2 and T2* maps obtained from healthy volunteers, six ROIs (size = 7 × 7 pixels) were selected for each subject, which were placed within the following anatomical brain regions: the globus pallidus, thalamus, and frontal (periventricular) white matter, in both, the left and right hemisphere (Figure 2b,c). For analysis of the T2 and T2* maps obtained from the patient cohort, eight ROIs (size = 7 × 7 pixels) were selected to cover MS lesions identified in four patients.
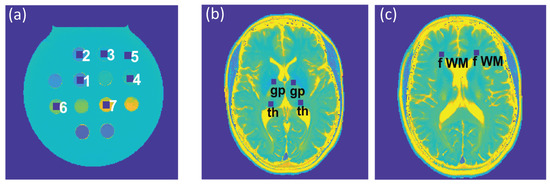
Figure 2.
(a) Regions of interest (ROIs) (size: 9 × 9 pixels), corresponding to tubes with varying iron concentrations in the phantom, which were used for the regression and Bland–Altman plot analyses and the calculation of the median absolute percentage error (MAPE). (b,c) ROIs (size: 7 × 7 pixels) used for further analysis of the in vivo study involving healthy volunteers were placed within the globus pallidus (gp) and thalamus (th) (b) and periventricular frontal white matter (fWM) (c), in the left and right hemispheres.
Multiple linear regression was used to assess the agreement between the reference and undersampled data, which also takes into account the effects of ROI and subject, and their interaction. For the Bland–Altman plot analyses, the median of the T2 and T2* differences, and and the interquartile range (IQR) were used to calculate the limits-of-agreement (LOAs) according to . since it was observed that the differences of T2 and T2* values among the reference and undersampled data did not follow a Gaussian distribution in all cases.
Furthermore, the median absolute percentage error (MAPE) of T2 and T2* derived from undersampled 2in1-RARE-EPI was calculated relative to the corresponding T2 and T2* deduced from the CS-reconstruction of the 2in1-RARE-EPI reference (Rextra = 1) according to:
where M denotes the median and T2(*)(Rextra) and T2(*) the T2 and T2* values derived from 2in1-RARE-EPI with and without retrospective undersampling, respectively. The calculation of the MAPE was performed for the same ROIs used for the regression and Bland–Altman plot analyses. Differences in MAPE among Rextra factors were analyzed using the non-parametric repeated-measures Friedman test, followed by the Dunn’s post-hoc test with the Benjamini–Hochberg correction for multiple comparisons. Data were analyzed using R v.3.6.3.
3. Results
Figure 3 shows T2 and T2* maps of the phantom and in vivo studies obtained with 2in1-RARE-EPI for Rextra = 1–12. Figure 3a shows the T2 and T2* maps of the phantom. For the T2 maps, increasing the undersampling rate to Rextr ≥ 6 (TA reduced to ≤01:39 min) resulted in a minor increase in T2 for low iron concentrations (T2(Rextra) ≥ 100 ms). Despite this, no visible change in the T2 maps was apparent. In the T2* maps, undersampling artifacts were apparent at Rextra = 8 and became more pronounced with increasing undersampling.
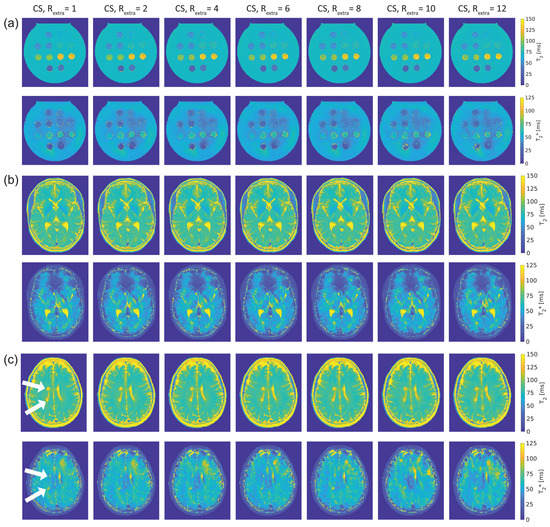
Figure 3.
T2 and T2* maps obtained from 2in1-RARE-EPI using extra undersampling factors of Rextra = 1–12 (Rextra = 1 is used as a reference). The undersampling factor Rextra increases from left to right. (a): T2 (top) and T2* (bottom) maps of a phantom containing tubes filled with solutions of different iron concentration, which mimics typical T2 and T2* values of brain tissue. (b): T2 (top) and T2* (bottom) maps covering the lateral ventricles of the brain of a healthy 30-year-old female volunteer. (c): T2 (top) and T2* (bottom) maps depicting two periventricular lesions in the right cerebral hemisphere of a 30-year old female multiple sclerosis (MS) patient (white arrows).
Figure 3b shows T2 and T2* maps of the brain of a healthy 30-year-old female volunteer. Increasing undersampling to Rextra = 10 (TA reduced to 01:12 min) resulted in a minor reduction of high spatial frequency information, which became apparent in the small gyri of the brain.
The T2 and T2* maps of the brain of a 30-year-old female MS patient are depicted in Figure 3c. As in the case of the healthy volunteers, increasing undersampling to Rextra = 10 resulted in a minor reduction of high spatial frequency information. The periventricular MS lesions were clearly delineated up to Rextra = 12 in the T2 maps. In T2* maps, these lesions were clearly delineated up to Rextra = 10.
For closer examination, the results of the regression and Bland–Altman analyses are depicted in Figure 4, Figure 5 and Figure 6.
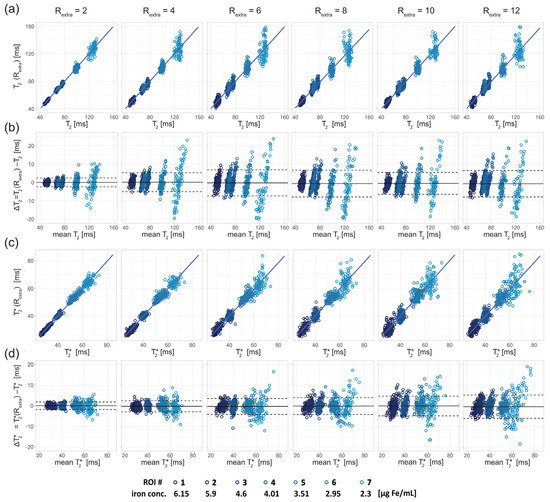
Figure 4.
Scatter and Bland–Altman plots of T2 and T2* calculated from seven ROIs (size: 9 × 9 pixel) placed within the phantom (corresponding to seven different iron concentrations) for undersampling factors Rextra = 2–12, increasing from left to right. (a) Scatter plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2 (Rextra), against T2 obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2. (b) Bland–Altman plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2 (Rextra), against T2 obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2. (c) Scatter plots comparing T2* derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2* (Rextra), against T2* obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2*. (d) Bland–Altman plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2* (Rextra), against T2* obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2*. In the scatter plots, the regression line obtained from multiple linear regression is depicted as a solid line. In the BA plots, the median of the T2/T2* differences and the limits-of-agreement are depicted as solid and dashed lines, respectively.
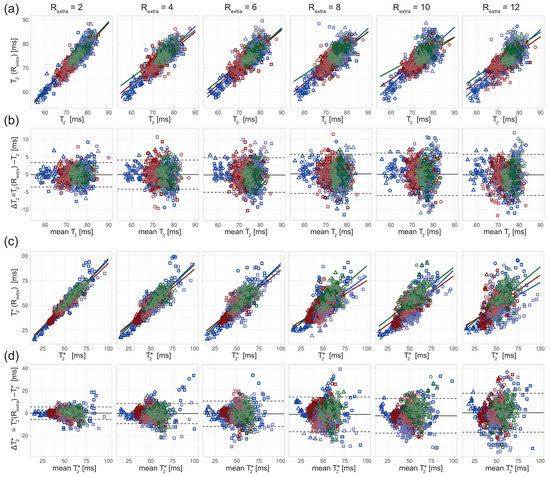
Figure 5.
Scatter and Bland–Altman plots of T2 and T2* calculated from brain scans of 3 healthy volunteers (denoted by square, circle, and triangle) for extra undersampling factors Rextra = 2–12, increasing from left to right. The color of the data points denotes the anatomical locations of the ROIs (size: 7 × 7 pixel, blue: thalamus; red: globus pallidus; green: frontal white matter; dark/light = left/right hemisphere). (a) Scatter plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2 (Rextra), against T2 obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2. (b) Bland–Altman plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2 (Rextra), against T2 obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2. (c) Scatter plots comparing T2* derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2* (Rextra), against T2* obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2*. (d) Bland–Altman plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2* (Rextra), against T2* obtained from 2in1-RARE-EPI reference (Rextra = 1), denoted T2*. In the scatter plots, separate regression lines for each anatomical region are depicted (solid lines), which were obtained from multiple linear regression. In the BA plots, the median of the T2/T2* differences and the limits-of-agreement are depicted as solid and dashed lines, respectively.
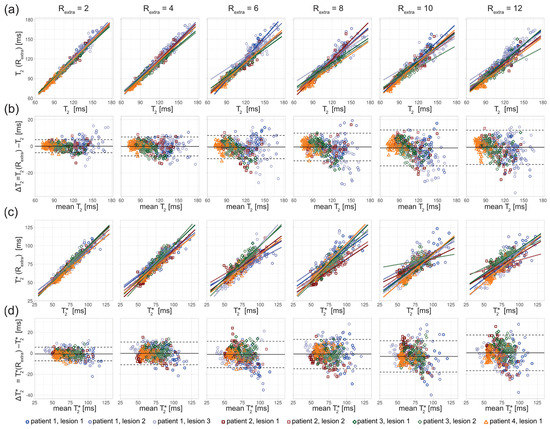
Figure 6.
Scatter and Bland–Altman plots of T2 and T2* calculated from eight ROIs covering lesions in three MS patients, for undersampling factors Rextra = 2–12, increasing from left to right. (a) Scatter plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2 (Rextra), against those obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2. (b) Bland–Altman plots comparing T2 derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2 (Rextra), against T2 obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2. (c) Scatter plots comparing T2* derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2* (Rextra), against T2*obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2*. (d) Bland–Altman plots comparing T2* derived from retrospectively undersampled 2in1-RARE-EPI, denoted T2* (Rextra), against T2* obtained from the 2in1-RARE-EPI reference (Rextra = 1), denoted T2*. In the scatter plots, separate regression lines for each lesion are depicted (solid lines), which were obtained from multiple linear regression. In the BA plots, the median of the T2/T2* differences and the limits-of-agreement are depicted as solid and dashed lines, respectively.
For the phantom study, T2 depicted in the scatter (Figure 4a) and Bland–Altman plots (Figure 4b) showed increased variance with increasing undersampling. The multiple linear regression showed a decrease in the adjusted R2 with increased undersampling for T2 (0.99, 0.97, 0.92, 0.94, 0.93, 0.92 for Rextra = 2–12, respectively) and T2* (0.99, 0.99, 0.96, 0.95, 0.94, 0.89 for Rextra = 2–12, respectively). This corresponds to a decrease of the adjusted R2 of 7% and 10% for the T2 and T2*, respectively, when increasing Rextra from 2 to 12. For T2, a minor increase of the limits-of-agreement (LOAs) from −2.35 ms and 2.46 ms at Rextra = 2 to −7.41 ms and 6.16 ms at Rextra = 12 (TA reduced to 01:06 min) was observed. The median of the T2 differences showed a minor decrease from 0.05 ms at Rextra = 2 to −0.62 ms at Rextra = 12. These results show that 2in1-RARE-EPI-based T2 mapping supports high undersampling in conjunction with CS reconstruction. For T2*, the scatter plots (Figure 4c) and Bland–Altman plots (Figure 4d) revealed an increase in the variance. T2* showed a minor increase of the LOAs from −1.80 ms and 1.81 ms at Rextra = 2 to −6.07 ms and 5.07 ms at Rextra = 12. The median of the T2* differences decreased from −0.01 ms at Rextra = 2 to −0.50 ms at Rextra = 12. These results demonstrate that 2in1-RARE-EPI-based T2* mapping supports high undersampling in conjunction with CS reconstruction.
The in vivo study in healthy volunteers showed increased variance of T2 and T2* with increasing undersampling (Figure 5). The multiple linear regression showed a decrease in the adjusted R2 with increased undersampling for T2 (0.85, 0.79, 0.72, 0.69, 0.67, 0.70 for Rextra = 2–12, respectively) and T2* (0.90, 0.79, 0.71, 0.59, 0.71, 0.41 for Rextra = 2–12, respectively). This corresponds to a decrease of the adjusted R2 of 18% and 54% for the T2 and T2*, respectively, when increasing Rextra from 2 to 12. The adjusted R2 of T2* at Rextra = 8 is decreased by 34% relative to Rextra = 2. The results of the Bland–Altman plot analysis of T2 showed a minor increase of the LOAs from −3.62 ms and 3.36 ms at Rextra = 2 to −6.00 ms and 5.71 ms at Rextra = 12. The median of the T2 differences was −0.13 ms at Rextra = 2 and −0.15 at Rextra = 12. The Bland–Altman plot analysis of T2* showed an increase of the LOAs from −5.48 ms and 5.55 ms at Rextra = 2 to −16.95 ms and 17.76 ms at Rextra = 12. The median of the T2* differences increased from −0.04 ms at Rextra = 2 to 0.40 ms at Rextra = 12.
The in vivo study in MS patients revealed an increase in the T2 variance with increasing undersampling for the ROIs covering the lesions (Figure 6). The scatter plots show a decrease of the slope of the regression lines with increased undersampling for T2 and T2* (Figure 6a,c). The multiple linear regression showed a decrease in the adjusted R2 with increased undersampling for T2 (0.98, 0.97, 0.94, 0.92, 0.91, 0.92 for Rextra = 2–12, respectively) and T2* (0.94, 0.88, 0.80, 0.81, 0.73, 0.75 for Rextra = 2–12, respectively). This corresponds to a decrease of the adjusted R2 of 6% and 20% for the T2 and T2*, respectively, when increasing Rextra from 2 to 12. The Bland–Altman plot analysis showed an increase of the LOAs from −4.86 ms and 4.94 ms at Rextra = 2 to −13.65 ms and 12.09 ms at Rextra = 12. The median decreased from −0.04 ms at Rextra = 2 to −0.78 ms at Rextra = 12. For T2*, the LOAs obtained from the Bland–Altman analysis increased from −7.27 ms and 5.76 ms at Rextra = 2 to −16.67 ms and 17.42 ms at Rextra = 12. The median of the T2* differences increased from −0.75 ms at Rextra = 2 to 0.37 ms at Rextra = 12.
Figure 7A shows the MAPE analysis of T2 and T2* for the phantom study. There was a significant difference in the MAPE of T2 of the 7 ROIs placed within the phantom among different undersampling factors Rextra (p = 3.8 × 10−5, Friedman test). There were significant differences of the MAPE of T2 between Rextra = 6, 8, and 12 and Rextra = 2 (p = 4.7 × 10−3, 3.2 × 10−3, 2.1 × 10−3, respectively, Dunn’s post-hoc test). The overall MAPE of T2 (Figure 7B) for Rextra = 8 was only 3.7%. For T2*, there were significant differences in the MAPE among the various undersampling factors (p = 3.1 × 10−6). There were significant differences between Rextra = 10–12 and Rextra = 2 (2.3 × 10−2, 4.6 × 10−4, respectively). The overall MAPE of T2* (Figure 7B) for Rextra = 12 was 4.7%.
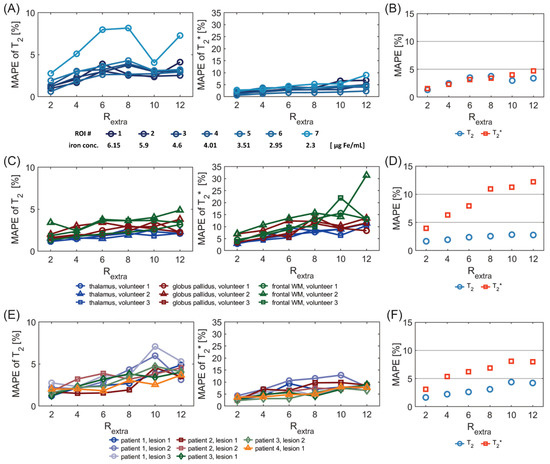
Figure 7.
MAPE of T2 and T2* derived from undersampled 2in1-RARE-EPI (Rextra = 2–12), relative to the corresponding T2 and T2* values obtained from the 2in1-RARE-EPI reference (Rextra = 1). MAPEs were calculated for the same ROIs as used for the scatter and Bland–Altman plot analysis (Figure 2, Figure 3 and Figure 4). (A) MAPE of T2 (left) and T2* (right) for seven ROIs placed within the phantom (corresponding to seven different iron concentrations) (B) Overall MAPE of T2 and T2* comprising all seven ROIs placed within the phantom. (C) MAPE of T2 and T2* values derived from brain scans of 3 healthy volunteers. The MAPE was calculated based on the combined ROIs of the left and right hemisphere for each brain region. (D) Overall MAPE of T2 and T2* comprising all ROIs and all healthy volunteers. (E) MAPE of T2 and T2* for eight ROIs covering lesions in four MS patients. (F) Overall MAPE of T2 and T2* comprising all ROIs covering the eight lesions.
Figure 7C shows the MAPE of T2 and T2* for the in vivo study with healthy volunteers. For the MAPE of T2, significant differences were obtained among different undersampling factors Rextra (p = 1.0 × 10−4) for the six ROIs placed in the brain. There were significant differences of the MAPE of T2 between Rextra = 8–12 and Rextra = 2 (p = 7.5 × 10−3, 5.3 × 10−3, 7.2 × 10−3, respectively). This shows the consistency of the T2 measurement within subjects for Rextra below 8. For T2*, there were significant differences in the MAPE among the various undersampling factors (p = 7.3 × 10−7). There were significant differences of the MAPE of T2* between Rextra = 6–12 and Rextra = 2 (p = 1.0 × 10−2, 2.4 × 10−4, 3.1 × 10−4, 3.2 × 10−5). This shows the consistency of the T2* measurement within subjects for Rextra below 6. The overall MAPE of T2 and T2*(Figure 7D) for Rextra = 6 was as small as 2.4% and 7.9%, respectively.
Figure 7E shows the MAPE of T2 and T2* for the in vivo study with MS patients. There was a significant difference of the MAPE of T2 values of the eight ROIs, covering MS lesions, among different undersampling factors Rextra (p = 1.5 × 10−5). There were significant differences of the MAPE of T2 between Rextra = 8–12 and Rextra = 2 (p= 1.0 × 10−2, 1.7 × 10−4, 1.0 × 10−4, respectively). This shows the consistency of the T2 measurement within subjects for Rextra below 8. For T2*, there were significant differences in the MAPE among the various undersampling factors (p = 1.8 × 10−4). There were significant differences of the MAPE of T2* between Rextra = 6–12 and Rextra =2 (p = 9.4 × 10−3, 6.7 × 10−3, 7.4 × 10−5, 7.7 × 10−5, respectively,). This shows the consistency of the T2* measurement within subjects for Rextra below 6. The overall MAPE of T2 and T2* (Figure 7F) for Rextra = 6 was 2.6% and 6.2%, respectively.
4. Discussion
In this study, we demonstrated the feasibility of highly accelerated simultaneous T2 and T2* mapping using a radially-undersampled RARE-EPI hybrid in conjunction with CS-reconstruction. The findings from this feasibility study support the application of quantitative T2 and T2* mapping of the brain in clinical practice, which could be utilized for broader clinical studies on the potential of T2 and T2* as imaging biomarkers in MS.
The regression and Bland–Altman analysis revealed an increase of the variance of the T2 and T2* values with increasing undersampling for both the phantom experiments and the in vivo studies. The Bland–Altman analysis showed that the median of the differences of T2 and T2* values were close to zero in all cases, for all investigated undersampling factors, which suggests that an increase in undersampling does not introduce a systematic bias in T2 and T2*.
The higher variance in ROIs 6 and 7 can be attributed to the fact that there is a large and sharp signal drop at the edge of the plastic tubes for these ROIs due to the difference in T2 values of the solution within the tube and that in the surrounding body of the phantom. This leads to increased variance of T2 values caused by more pronounced Gibbs ringing artifacts. Furthermore, residual aliasing artifacts which are not fully compensated by the CS reconstruction might have a higher impact on ROIs 6 and 7, as the mislocated signal stemming from the phantom body deviates more in T2/T2* than for the other ROIs.
In addition, the higher variance in ROI 6 can be attributed to the higher T2 and T2* values within the ROI, i.e., the relative variance of the T2 and T2* values corresponding to ROI 6 does not substantially differ from the relative variances in ROIs 1–5. For ROI 7, the relative variance is increased compared to the other ROIs, which emphasizes the stronger influence of Gibbs ringing and aliasing artifacts in this ROI.
The Bland–Altman plots of the T2 values of MS lesions showed that the T2 differences follow a negative trend, with increasing mean T2 values for higher undersampling factors (Rextra = 8–12). This can likely be explained by the reduction of high spatial frequency information in highly undersampled images, leading to smoothing of the lesion sharpness, and reduced contrast between the lesions and surrounding tissue with lower T2.
The smaller relative decrease of the adjusted R2 of T2 and T2* with increased undersampling in the phantom study compared to the in vivo studies can be explained by the higher degree of sparsity in the phantom images compared to images of the brain, which promotes accurate recovery of true signal intensities for higher undersampling factors [42]. We observed that the relative decrease of the adjusted R2 of T2 and T2* was lower for the in vivo study with MS patients compared to the healthy volunteers. This can be attributed to the fact that in the case of MS patients, the T2 and T2* values within all ROIs have a larger range than in the ROIs of the healthy volunteers, and thus the additional variance contributed by the undersampling is proportionally smaller.
A previous study that investigated the performance of R2* mapping based on 3D single point imaging (SPI) with CS reconstruction in ex vivo rat tissue and an in vitro cell phantom [15] shows a relative decrease of the R2 of about 10–12% for an increase of the undersampling factor from 2 to 10, which is lower than the values observed in our in vivo studies. However, there a number of differences between the two studies that can explain these discrepancies. In the SPI approach, only one k-space point is sampled within a TR, which increases the accuracy of R2* measurements, due to a higher sampling rate of the signal decay, but at the expanse of considerably longer scan times. Furthermore, the 3D single point sampling of k-space allows for a higher degree of freedom in the undersampling pattern, which can substantially increase the performance of CS reconstruction at high undersampling factors [36,43]. This motivates the future investigation of 2in1-RARE-EPI using 3D k-space sampling schemes.
The analysis showed that the MAPE of T2* is higher and increases more strongly with increasing undersampling compared to the MAPE of T2. This can be explained by the hybrid acquisition of the MR signal in 2in1-RARE-EPI, in which the MR signal is first acquired with a RARE module to capture the T2 decay, followed by the acquisition with an EPI echo-train to capture the T2* decay. This results in a lower SNR of the TE images used for T2* mapping, which manifests as an increased MAPE of T2*. Notwithstanding this SNR constraint, the overall MAPE of T2* was <5% in the phantom studies for Rextra ≤ 12, and <8% in the in vivo studies for Rextra ≤ 6. The overall MAPE of T2 remained <4.4% for Rextra ≤ 12 in the phantom and in vivo studies.
Due to the consecutive sampling of the T2 and T2* decay within each TR, the measurement of T2* values could be impaired for tissues exhibiting very low T2 values. This could be due, e.g., as a result of increased iron deposition, which is a pathological feature of some neurodegenerative diseases, including MS. The lowest T2 values of the tissues investigated in the current study are about 60 ms, which does not impact the T2* measurement. Evaluating simultaneous T2 and T2* mapping with 2in1-RARE-EPI for lower T2 values will require further studies, including an adaptation of the length of the RARE and EPI module to achieve optimal results.
In this study, we used a limited slice coverage (n = 3, slice thickness = 5 mm) to demonstrate the feasibility of our approach. This could be easily scaled up to meet the needs of clinical applications, by reducing the slice thickness and increasing the total number of slices acquired. Reduced slice thickness would also mitigate partial volume effects and result in a better coverage of lesions. Given the high SNR we observed for the 2in1-RARE-EPI using the imaging parameters of the current study, we expect the results presented here to also hold for lower slice thicknesses. The long TR used in the 2in1-RARE-EPI will allow for acquisition of additional slices without increasing the acquisition time.
The scan time reduction shown in this work will benefit patient compliance, and enhances the robustness to bulk motion. With an extra undersampling factor of Rextra = 6 (Reff = 12), the acquisition time for simultaneous T2 and T2* mapping can be reduced from 07:12 min to 01:39 min. An extra undersampling of Rextra = 12 (Reff = 24) permits a scan time as short as 01:06 min. The 2in1-RARE-EPI approach is compatible with the concept of using different undersampling rates for the RARE module and for the EPI module. This approach would permit an improvement of the RF deposition economy of the RARE module. Even further scan time reductions could be achieved by employing simultaneous multi-slice imaging techniques which are compatible with 2in1-RARE-EPI [6,44,45,46].
The current study is a proof-of-concept demonstration of the feasibility of using undersampled 2in1-RARE-EPI in a realistic clinical context, and was not designed or powered to detect group differences. Further clinical studies with larger numbers of patients will be needed to robustly test the sensitivity to group differences.
5. Conclusions
We demonstrate that the scan time for simultaneous T2 and T2* mapping can be substantially reduced, by utilizing high radial undersampling in 2in1-RARE-EPI together with CS-reconstruction. This improvement comes at the cost of only minor reductions of high spatial frequency information, and provides a proof-of-concept technical foundation to support the implementation of quantitative mapping in routine clinical practice. This approach could also be applied to broader clinical studies on the potential use of T2 and T2* as imaging biomarkers of neuroinflammatory and neurodegenerative diseases, thereby expanding previous work [47,48,49] using these imaging biomarkers. Furthermore, 2in1-RARE-EPI can also be adapted to simultaneously provide temperature maps in addition to T2 and T2* maps. The potential range of clinical applications for accelerated 2in1-RARE-EPI for T2 and T2* mapping extends well beyond MS to several other pathologies in the brain and other target organs.
Author Contributions
Conceptualization, C.J.J.H. and T.N.; Methodology, C.J.J.H., L.S. and J.M.M.; Software, C.J.J.H. and L.S.; Validation, C.J.J.H.; Formal Analysis, C.J.J.H. and J.M.M.; Investigation, C.J.J.H.; Resources, J.K. and F.P.; Data Curation, C.J.J.H.; Writing—Original Draft Preparation, C.J.J.H. and L.S.; Writing—Review and Editing, C.J.J.H., J.M.M., T.N., J.K. and F.P.; Visualization, C.J.J.H.; Supervision, T.N.; Project Administration, C.J.J.H.; Funding Acquisition, T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program, grant number 743077 (ThermalMR). The APC was funded by the Max Delbrück Center for Molecular Medicine in the Helmholtz Association, Berlin, Germany.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the local ethics committee (Charité—University Medicine, Berlin, Germany, EA1/191/19).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on reasonable request from the corresponding author.
Acknowledgments
We thank Eckart Grönerwäller and Beate Endemann (Berlin Ultrahigh Field Facility, Max Delbrück Center for Molecular Medicine in the Helmholtz Association) for expert radiology support. We thank Antje Els (Berlin Ultrahigh Field Facility, Max Delbrück Center for Molecular Medicine in the Helmholtz Association) for supporting the acquisition of the in vivo data presented in this study.
Conflicts of Interest
Thoralf Niendorf is founder and CEO of MRI.TOOLS, Berlin, Germany.
References
- Maranzano, J.; Dadar, M.; Rudko, D.; De Nigris, D.; Elliott, C.; Gati, J.; Morrow, S.; Menon, R.; Collins, D.; Arnold, D. Comparison of multiple sclerosis cortical lesion types detected by multicontrast 3T and 7T MRI. Am. J. Neuroradiol. 2019, 40, 1162–1169. [Google Scholar] [CrossRef] [PubMed]
- Sinnecker, T.; Mittelstaedt, P.; Dörr, J.; Pfueller, C.F.; Harms, L.; Niendorf, T.; Paul, F.; Wuerfel, J. Multiple sclerosis lesions and irreversible brain tissue damage: A comparative ultrahigh-field strength magnetic resonance imaging study. Arch. Neurol. 2012, 69, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Kuchling, J.; Paul, F. Visualizing the Central Nervous System: Imaging Tools for Multiple Sclerosis and Neuromyelitis Optica Spectrum Disorders. Front. Neurol. 2020, 11, 450. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, C.; Els, A.; Boehmert, L.; Periquito, J.; Eigentler, T.W.; Millward, J.M.; Waiczies, S.; Kuchling, J.; Paul, F.; Niendorf, T. Simultaneous T2 and T2* Mapping of Multiple Sclerosis Lesions with Radial RARE-EP. Magn. Reson. Med. 2021, 86, 1383–1402. [Google Scholar] [CrossRef] [PubMed]
- Hillenbrand, C.; Hahn, D.; Haase, A.; Jakob, P. MR CAT scan: A modular approach for hybrid imaging. MAGMA 2000, 10, 183–199. [Google Scholar] [CrossRef] [PubMed]
- Paul, K.; Huelnhagen, T.; Oberacker, E.; Wenz, D.; Kuehne, A.; Waiczies, H.; Schmitter, S.; Stachs, O.; Niendorf, T. Multiband diffusion-weighted MRI of the eye and orbit free of geometric distortions using a RARE-EPI hybrid. NMR Biomed 2018, 31, e3872. [Google Scholar] [CrossRef] [PubMed]
- Biller, A.; Choli, M.; Blaimer, M.; Breuer, F.A.; Jakob, P.M.; Bartsch, A.J. Combined Acquisition Technique (CAT) for Neuroimaging of Multiple Sclerosis at Low Specific Absorption Rates (SAR). PLoS ONE 2014, 9, e91030. [Google Scholar] [CrossRef] [PubMed]
- Schmiedeskamp, H.; Straka, M.; Newbould, R.D.; Zaharchuk, G.; Andre, J.B.; Olivot, J.M.; Moseley, M.E.; Albers, G.W.; Bammer, R. Combined spin-and gradient-echo perfusion-weighted imaging. Magn. Reson. Med. 2012, 68, 30–40. [Google Scholar] [CrossRef]
- Manhard, M.K.; Bilgic, B.; Liao, C.; Han, S.; Witzel, T.; Yen, Y.F.; Setsompop, K. Accelerated whole-brain perfusion imaging using a simultaneous multislice spin-echo and gradient-echo sequence with joint virtual coil reconstruction. Magn. Reson. Med. 2019, 82, 973–983. [Google Scholar] [CrossRef]
- Schmiedeskamp, H.; Straka, M.; Bammer, R. Compensation of slice profile mismatch in combined spin-and gradient-echo echo-planar imaging pulse sequences. Magn. Reson. Med. 2012, 67, 378–388. [Google Scholar] [CrossRef]
- Zhang, Z.; Cho, J.; Wang, L.; Liao, C.; Shin, H.G.; Cao, X.; Lee, J.; Xu, J.; Zhang, T.; Ye, H. Blip up-down acquisition for spin-and gradient-echo imaging (BUDA-SAGE) with self-supervised denoising enables efficient T2, T2*, para-and dia-magnetic susceptibility mapping. Magn. Reson. Med. 2022, 88, 633–650. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Dong, Z.; Reese, T.G.; Bilgic, B.; Katherine Manhard, M.; Chen, J.; Polimeni, J.R.; Wald, L.L.; Setsompop, K. Echo planar time-resolved imaging (EPTI). Magn. Reson. Med. 2019, 81, 3599–3615. [Google Scholar] [CrossRef] [PubMed]
- de Stefano, N.; Barkhof, F.; Montalban, X.; Achiron, A.; Derfuss, T.; Chan, A.; Hodgkinson, S.; Prat, A.; Leocani, L.; Schmierer, K. Early reduction of MRI activity during 6 months of treatment with cladribine tablets for highly active relapsing multiple sclerosis: MAGNIFY-MS. Neurol.-Neuroimmunol. Neuroinflammation 2022, 9. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, W.; Jiang, K.; Wang, C.Y.; Yu, X. Rapid T2 mapping of mouse heart using the carr–purcell–meiboom–gill sequence and compressed sensing reconstruction. J. Magn. Reson. Imaging 2016, 44, 375–382. [Google Scholar] [CrossRef] [PubMed]
- Rioux, J.A.; Beyea, S.D.; Bowen, C.V. 3D single point imaging with compressed sensing provides high temporal resolution R 2* mapping for in vivo preclinical applications. MAGMA 2017, 30, 41–55. [Google Scholar] [CrossRef]
- Zibetti, M.V.; Helou, E.S.; Sharafi, A.; Regatte, R.R. Fast multicomponent 3D-T1ρ relaxometry. NMR Biomed 2020, 33, e4318. [Google Scholar] [CrossRef]
- Doneva, M.; Börnert, P.; Eggers, H.; Stehning, C.; Sénégas, J.; Mertins, A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med. 2010, 64, 1114–1120. [Google Scholar] [CrossRef]
- Huang, C.; Graff, C.G.; Clarkson, E.W.; Bilgin, A.; Altbach, M.I. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn. Reson. Med. 2012, 67, 1355–1366. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Ye, J.C. Compressed sensing MRI: A review from signal processing perspective. BMC Biomed. Eng. 2019, 1, 8. [Google Scholar] [CrossRef]
- FDA. 510k Premarket Notification of HyperSense (GE Medical Systems). 2017. Available online: https://www.accessdata.fda.gov/cdrh_docs/pdf16/K162722.pdf (accessed on 7 December 2021).
- FDA. 510k Premarket Notification of Compressed Sensing Cardiac Cine (Siemens). 2017. Available online: https://www.accessdata.fda.gov/cdrh_docs/pdf16/K163312.pdf (accessed on 7 December 2021).
- FDA. 510k Premarket Notification of Compressed SENSE (Philips). 2018. Available online: https://www.accessdata.fda.gov/cdrh_docs/pdf17/K173079.pdf (accessed on 7 December 2021).
- McPhee, K.C.; Wilman, A.H. Limitations of skipping echoes for exponential T2 fitting. J. Magn. Reson. Imaging 2018, 48, 1432–1440. [Google Scholar] [CrossRef] [PubMed]
- Fessler, J.A. Michigan Image Reconstruction Toolbox. Available online: https://web.eecs.umich.edu/~fessler/code/ (accessed on 23 April 2021).
- Fessler, J.A.; Sutton, B.P. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process. 2003, 51, 560–574. [Google Scholar] [CrossRef]
- Uecker, M.; Lai, P.; Murphy, M.J.; Virtue, P.; Elad, M.; Pauly, J.M.; Vasanawala, S.S.; Lustig, M. ESPIRiT—An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014, 71, 990–1001. [Google Scholar] [CrossRef] [PubMed]
- Uecker, M.; Virtue, P.; Vasanawala, S.S.; Lustig, M. ESPIRiT Reconstruction Using Soft SENSE. Proc. Intl. Soc. Mag. Reson. Med. 2013, 21, 127. [Google Scholar]
- Uecker, M.; Ong, F.; Tamir, J.I.; Bahri, D.; Virtue, P.; Cheng, J.Y.; Zhang, T.; Lustig, M. Berkeley Advanced Reconstruction Toolbox. Proc. Intl. Soc. Mag. Reson. Med. 2015, 23, 2486. [Google Scholar]
- Uecker, M.; Virtue, P.; Ong, F.; Murphy, M.J.; Alley, M.T.; Vasanawala, S.S.; Lustig, M. Software toolbox and programming library for compressed sensing and parallel imaging. In Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona, AZ, USA, 3–6 February 2013; p. 41. [Google Scholar]
- Tamir, J.I.; Ong, F.; Cheng, J.Y.; Uecker, M.; Lustig, M. Generalized Magnetic Resonance Image Reconstruction using The Berkeley Advanced Reconstruction Toolbox. In Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona, AZ, USA, 17–20 January 2016. [Google Scholar]
- Hansen, M.S.; Kellman, P. Image reconstruction: An overview for clinicians. J. Magn. Reson. Imaging 2015, 41, 573–585. [Google Scholar] [CrossRef]
- Hansen, M.S. Nuts & Bolts of Advanced Imaging: Image Reconstruction—Parallel Imaging. Available online: http://hansenms.github.io/sunrise/sunrise2014/ (accessed on 7 December 2021).
- Liang, D.; Liu, B.; Wang, J.; Ying, L. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 2009, 62, 1574–1584. [Google Scholar] [CrossRef]
- Block, K.T.; Uecker, M.; Frahm, J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 2007, 57, 1086–1098. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Varela-Mattatall, G.; Baron, C.A.; Menon, R.S. Automatic determination of the regularization weighting for wavelet-based compressed sensing MRI reconstructions. Magn. Reson. Med. 2021, 86, 1403–1419. [Google Scholar] [CrossRef] [PubMed]
- Morozov, V.A. On the Solution of Functional Equations by the Method of Regularization. In Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1966; pp. 510–512. [Google Scholar]
- Kilmer, M.E.; O’Leary, D.P. Choosing regularization parameters in iterative methods for ill-posed problems. SIAM J. Matrix Anal. Appl. 2001, 22, 1204–1221. [Google Scholar] [CrossRef]
- Starke, L.; Pohlmann, A.; Prinz, C.; Niendorf, T.; Waiczies, S. Performance of compressed sensing for fluorine-19 magnetic resonance imaging at low signal-to-noise ratio conditions. Magn. Reson. Med. 2020, 84, 592–608. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Feng, L.; Benkert, T.; Block, K.T.; Sodickson, D.K.; Otazo, R.; Chandarana, H. Compressed sensing for body MRI. J. Magn. Reson. Imaging 2017, 45, 966–987. [Google Scholar] [CrossRef]
- Norris, D.G.; Boyacioglu, R.; Schulz, J.; Barth, M.; Koopmans, P.J. Application of PINS radiofrequency pulses to reduce power deposition in RARE/turbo spin echo imaging of the human head. Magn. Reson. Med. 2014, 71, 44–49. [Google Scholar] [CrossRef]
- Norris, D.G.; Koopmans, P.J.; Boyacioglu, R.; Barth, M. Power Independent of Number of Slices (PINS) radiofrequency pulses for low-power simultaneous multislice excitation. Magn. Reson. Med. 2011, 66, 1234–1240. [Google Scholar] [CrossRef]
- Gagoski, B.A.; Bilgic, B.; Eichner, C.; Bhat, H.; Grant, P.E.; Wald, L.L.; Setsompop, K. RARE/turbo spin echo imaging with Simultaneous Multislice Wave-CAIPI. Magn. Reson. Med. 2015, 73, 929–938. [Google Scholar] [CrossRef]
- Pasquier, B.; Borisow, N.; Rasche, L.; Bellmann-Strobl, J.; Ruprecht, K.; Niendorf, T.; Derfuss, T.J.; Wuerfel, J.; Paul, F.; Sinnecker, T. Quantitative 7T MRI does not detect occult brain damage in neuromyelitis optica. Neurol.-Neuroimmunol. Neuroinflammation 2019, 6. [Google Scholar] [CrossRef]
- Sinnecker, T.; Schumacher, S.; Mueller, K.; Pache, F.; Dusek, P.; Harms, L.; Ruprecht, K.; Nytrova, P.; Chawla, S.; Niendorf, T. MRI phase changes in multiple sclerosis vs neuromyelitis optica lesions at 7T. Neurol.-Neuroimmunol. Neuroinflammation 2016, 3. [Google Scholar] [CrossRef]
- Sinnecker, T.; Clarke, M.A.; Meier, D.; Enzinger, C.; Calabrese, M.; De Stefano, N.; Pitiot, A.; Giorgio, A.; Schoonheim, M.M.; Paul, F. Evaluation of the central vein sign as a diagnostic imaging biomarker in multiple sclerosis. JAMA Neurol. 2019, 76, 1446–1456. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).