Characterizing Errors in Pharmacokinetic Parameters from Analyzing Quantitative Abbreviated DCE-MRI Data in Breast Cancer
Abstract
:1. Introduction
2. Methodology
2.1. ACRIN 6883 Trial DCE-MRI Acquisition
2.2. Single-Site DCE-MRI Acquisition
2.3. DCE-MRI Data Analysis
2.4. DCE-MRI Simulated Data Analysis
2.5. Statistical Analysis
3. Results
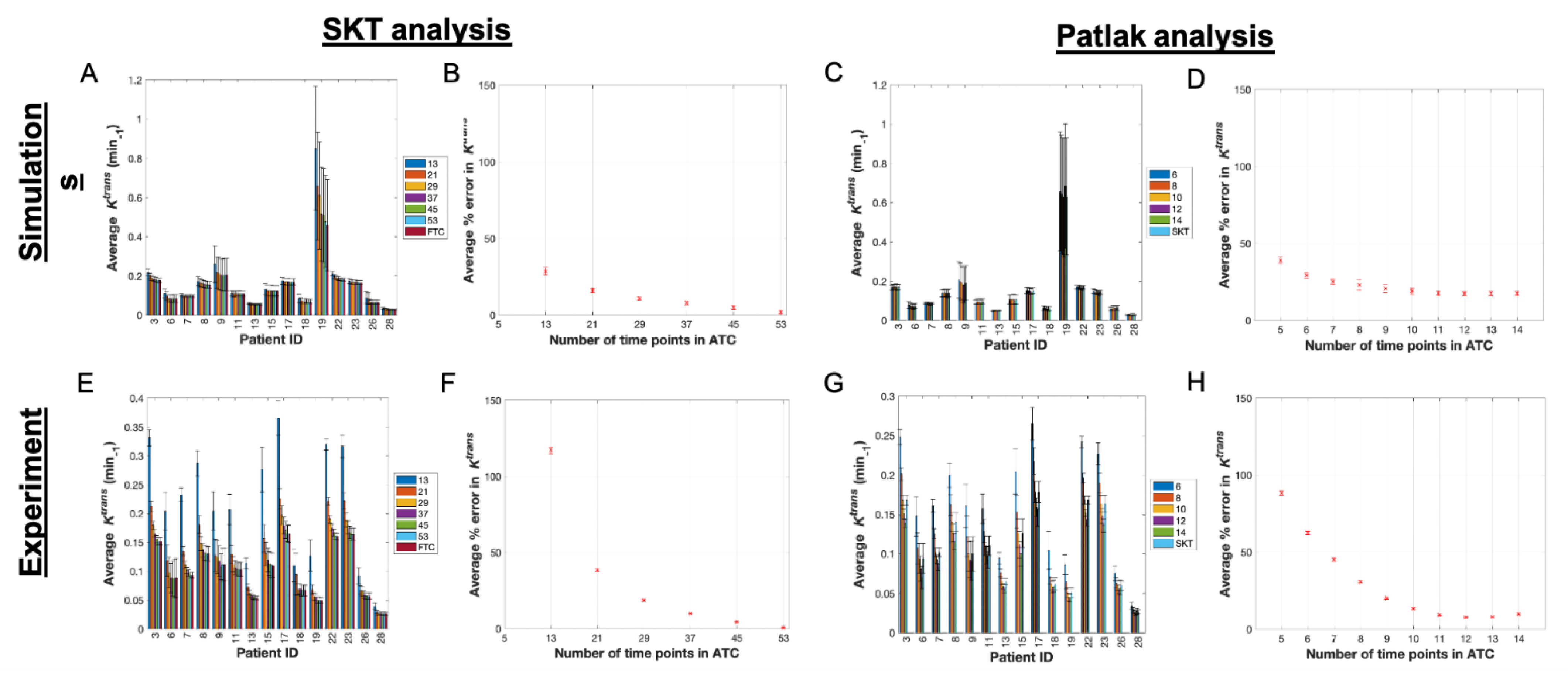
3.1. Pharmacokinetic Assessment of ACRIN-Based Simulated Data
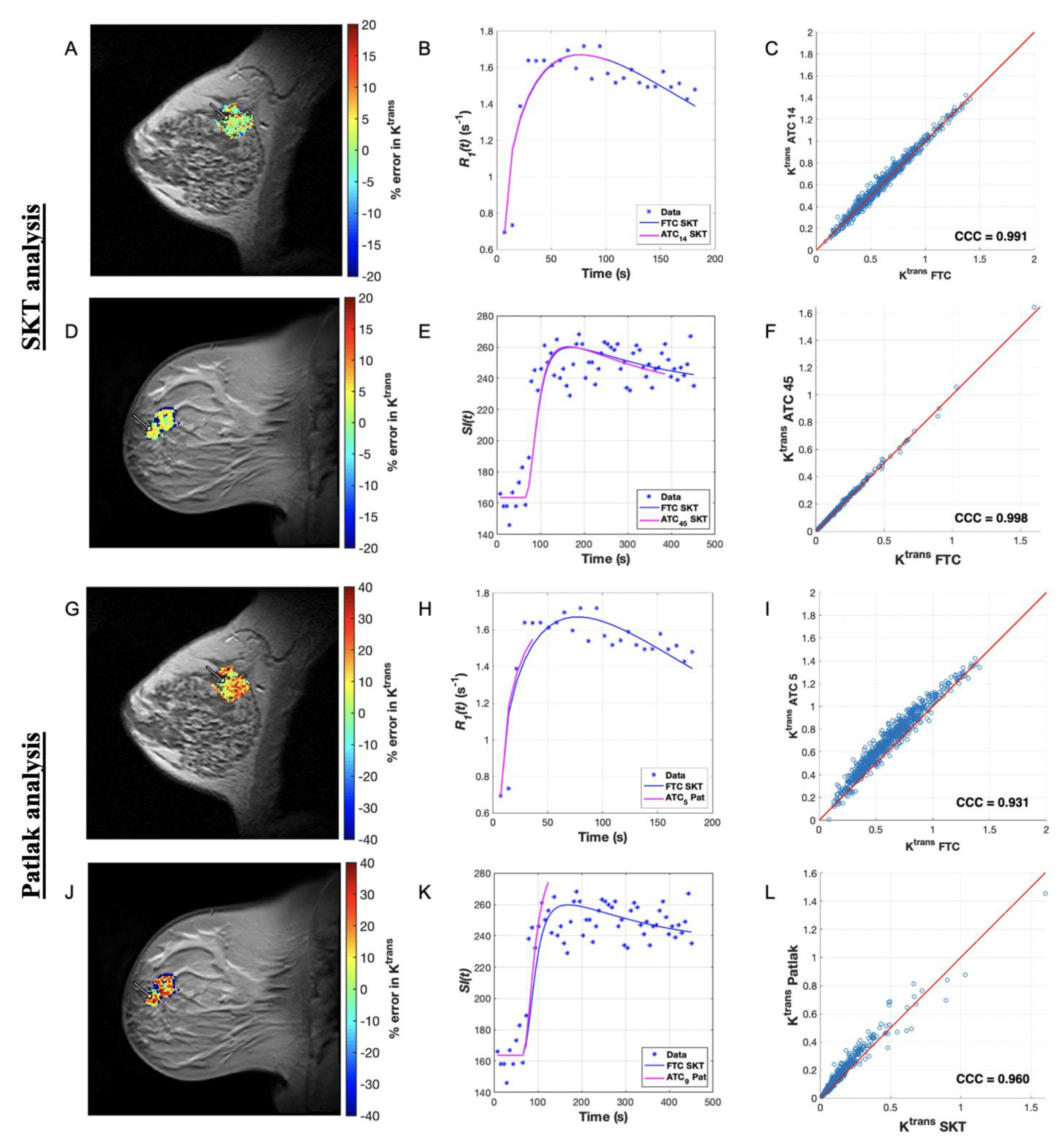
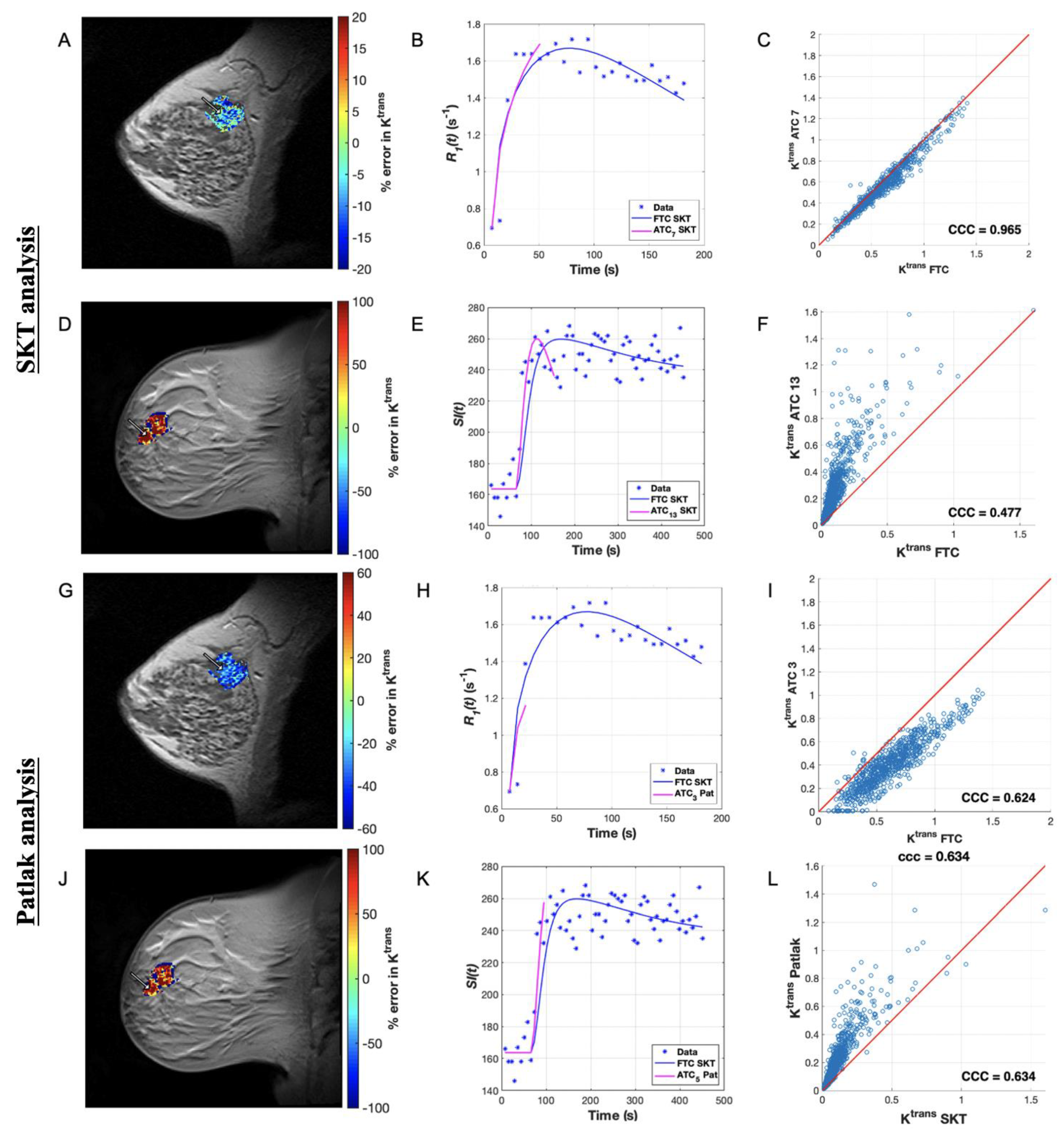
3.2. Pharmacokinetic Assessment of ACRIN Clinical Data
3.3. Pharmacokinetic Assessment of Single-Site-Based Simulated Data
3.4. Pharmacokinetic Assessment of Single-Site Clinical Data
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DCE-MRI | dynamic contrast-enhanced MRI |
| FTC | full time course |
| ATC | abbreviated time course |
| GRAPPA | generalized autocalibrating partial parallel acquisition |
| BI-RADS | breast imaging reporting and data system |
| IBMC | International Breast MR Consortium |
| ACRIN | American College of Radiology Imaging Network |
| ROI | region of interest |
| SPGR | spoiled gradient echo |
References
- Sardanelli, F.; Podo, F.; Santoro, F.; Manoukian, S.; Bergonzi, S.; Trecate, G.; Vergnaghi, D.; Federico, M.; Cortesi, L.; Corcione, S.; et al. Multicenter surveillance of women at high genetic breast cancer risk using mammography, ultrasonography, and contrast-enhanced magnetic resonance imaging (the high breast cancer risk italian 1 study): Final results. Investig. Radiol. 2011, 46, 94–105. [Google Scholar] [CrossRef]
- Moy, L.; Elias, K.; Patel, V.; Lee, J.; Babb, J.S.; Toth, H.K.; Mercado, C.L. Is breast MRI helpful in the evaluation of inconclusive mammographic findings? Am. J. Roentgenol. 2009, 193, 986–993. [Google Scholar] [CrossRef] [PubMed]
- Kuhl, C.K.; Schrading, S.; Leutner, C.C.; Morakkabati-Spitz, N.; Wardelmann, E.; Fimmers, R.; Kuhn, W.; Schild, H.H. Mammography, breast ultrasound, and magnetic resonance imaging for surveillance of women at high familial risk for breast cancer. J. Clin. Oncol. 2005, 23, 8469–8476. [Google Scholar] [CrossRef] [PubMed]
- Leach, M.O.; Boggis, C.R.; Dixon, A.K.; Easton, D.F.; Eeles, R.A.; Evans, D.G.R.; Gilbert, F.J.; Griebsch, I.; Hoff, R.J.C.; Kessar, P.; et al. Screening with magnetic resonance imaging and mammography of a UK population at high familial risk of breast cancer: A prospective multicentre cohort study (MARIBS). Lancet 2005, 365, 1769–1778. [Google Scholar]
- Li, K.; Machireddy, A.; Tudorica, A.; Moloney, B.; Oh, K.Y.; Jafarian, N.; Partridge, S.C.; Li, X.; Huang, W. Discrimination of Malignant and Benign Breast Lesions Using Quantitative Multiparametric MRI: A Preliminary Study. Tomography 2019, 6, 148–159. [Google Scholar] [CrossRef]
- Schnall, M.D.; Blume, J.; Bluemke, D.A.; Deangelis, G.A.; Debruhl, N.; Harms, S.; Heywang-Köbrunner, S.H.; Hyltono, N.; Kuhl, C.K.; Pisanoo, E.D.; et al. MRI detection of distinct incidental cancer in women with primary breast cancer studied in IBMC 6883. J. Surg. Oncol. 2005, 92, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Sippo, D.A.; Burk, K.S.; Mercaldo, S.F.; Rutledge, G.M.; Edmonds, C.; Guan, Z.; Hughes, K.S.; Lehman, C.D. Performance of Screening Breast MRI across Women with Different Elevated Breast Cancer Risk Indications. Radiology 2019, 292, 51–59. [Google Scholar] [CrossRef]
- Kuhl, C.K.; Weigel, S.; Schrading, S.; Arand, B.; Bieling, H.; König, R.; Tombach, B.; Leutner, C.; Rieber-Brambs, A.; Nordhoff, D.; et al. Prospective multicenter cohort study to refine management recommendations for women at elevated familial risk of breast cancer: The EVA trial. J. Clin. Oncol. 2010, 28, 1450–1457. [Google Scholar] [CrossRef] [Green Version]
- Heller, S.L.; Moy, L. MRI breast screening revisited. J. Magn. Reson. Imaging 2019, 49, 1212–1221. [Google Scholar] [CrossRef]
- Kuhl, C.K.; Schrading, S.; Strobel, K.; Schild, H.H.; Hilgers, R.D.; Bieling, H.B. Abbreviated Breast Magnetic Resonance Imaging (MRI): First Postcontrast Subtracted Images and Maximum-Intensity Projection—A Novel Approach to Breast Cancer Screening With MRI. J. Clin. Oncol. 2014, 32, 2304–2310. [Google Scholar] [CrossRef]
- Greenwood, H.I. Abbreviated protocol breast MRI: The past, present, and future. Clin. Imaging 2019, 53, 169–173. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.Q.; Huang, M.; Shen, Y.Y.; Liu, C.L.; Xu, C.X. Abbreviated MRI protocols for detecting breast cancer in women with dense breasts. Korean J. Radiol. 2017, 18, 470–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sorace, A.G.; Partridge, S.C.; Li, X.; Virostko, J.; Barnes, S.L.; Hippe, D.S.; Huang, W.; Yankeeloov, T.E. Distinguishing benign and malignant breast tumors: Preliminary comparison of kinetic modeling approaches using multi-institutional dynamic contrast-enhanced MRI data from the International Breast MR Consortium 6883 trial. J. Med. Imaging 2018, 5, 011019. [Google Scholar]
- Wu, C.; Pineda, F.; Hormuth, D.A.; Karczmar, G.S.; Yankeelov, T.E. Quantitative analysis of vascular properties derived from ultrafast DCE-MRI to discriminate malignant and benign breast tumors. Magn. Reson. Med. 2019, 81, 2147–2160. [Google Scholar] [CrossRef] [PubMed]
- Grimm, L.J.; Soo, M.S.; Yoon, S.; Kim, C.; Ghate, S.V.; Johnson, K.S. Abbreviated Screening Protocol for Breast MRI. A Feasibility Study. Acad. Radiol. 2015, 22, 1157–1162. [Google Scholar] [CrossRef] [PubMed]
- Leithner, D.; Moy, L.; A Morris, E.; A Marino, M.; Helbich, T.H.; Pinker, K. Abbreviated MRI of the Breast: Does It Provide Value? J. Magn. Reson. Imaging 2019, 49, e85–e100. [Google Scholar] [CrossRef] [PubMed]
- Li, H.-N.; Chen, C.-H. Ultrasound-Guided Core Needle Biopsies of Breast Invasive Carcinoma: When One Core is Sufficient for Pathologic Diagnosis and Assessment of Hormone Receptor and HER2 Status. Diagnostics 2019, 9, 54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hormuth, D.A.; Sorace, A.G.; Virostko, J.; Abramson, R.G.; Bhujwalla, Z.M.; Enriquez-Navas, P.; Gillies, R.; Hazle, J.D.; Mason, R.P.; Quarles, C.C.; et al. Translating preclinical MRI methods to clinical oncology. J. Magn. Reson. Imaging 2019, 50, 1377–1392. [Google Scholar] [CrossRef] [PubMed]
- Tofts, P.; Kermode, A.G. Measurement of the blood-brain barrier permeability and leakage space using dynamic MR imaging. 1. Fundamental concepts. Magn. Reson. Med. 1991, 17, 357–367. [Google Scholar] [CrossRef]
- Lawrence, K.S.; Lee, T.Y. An adiabatic approximation to the tissue homogeneity model for water exchange in the brain: I. Theoretical derivation. J. Cereb. Flow Metab. 1998, 18, 1365–1377. [Google Scholar] [CrossRef]
- Planey, C.R.; Welch, E.B.; Xu, L.; Chakravarthy, A.B.; Gatenby, J.C.; Freehardt, D.; Mayer, I.; Meszeoly, I.; Kelley, M.; Means-Powell, J.; et al. Temporal sampling requirements for reference region modeling of DCE-MRI data in human breast cancer. J. Magn. Reson. Imaging JMRI 2009, 30, 121–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jajamovich, G.H.; Huang, W.; Besa, C.; Li, X.; Afzal, A.; Dyvorne, H.A.; Taouli, B. DCE-MRI of hepatocellular carcinoma: Perfusion quantification with Tofts model versus shutter-speed model—Initial experience. Magma Magn. Reson. Mater. Phys. Biol. Med. 2015, 29, 49–58. [Google Scholar] [CrossRef] [Green Version]
- Karakatsanis, N.A.; Zhou, Y.; Lodge, M.A.; Casey, M.E.; Wahl, R.L.; Zaidi, H.; Rahmim, A. Generalized whole-body Patlak parametric imaging for enhanced quantification in clinical PET. Phys. Med. Biol. 2015, 60, 8643–8673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pineda, F.D.; Medved, M.; Wang, S.; Fan, X.; Schacht, D.; Sennett, C.; Aytekin, O.; Newstead, G.M.; Hiroyuki, A.; Karczmar, G.S. Ultrafast bilateral DCE-MRI of the breast with conventional Fourier sampling: Preliminary evaluation of semi-quantitative analysis. Acad. Radiol. 2016, 23, 1137–1144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Welch, E.B.; Chakravarthy, A.B.; Xu, L.; Arlinghaus, L.R.; Farley, J.; Mayer, I.A.; Kelley, M.C.; Meszoely, I.M.; Means-Powell, J.; et al. Statistical comparison of dynamic contrast-enhanced MRI pharmacokinetic models in human breast cancer. Magn. Reson. Med. 2012, 68, 261–271. [Google Scholar] [CrossRef] [Green Version]
- Amarnath, J.; Sangeeta, T.; Mehta, S.B. Role of quantitative pharmacokinetic parameter (transfer constant: K(trans)) in the characterization of breast lesions on MRI. Indian J. Radiol. Imaging 2013, 23, 19–25. [Google Scholar]
- Chung, S.; Kim, D.; Breton, E.; Axel, L. Rapid B1+ mapping using a preconditioning RF pulse with TurboFLASH readout. Magn. Reson. Med. 2010, 64, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Giger, M.L.; Bick, U. A fuzzy c-means (FCM)-based approach for computerized segmentation of breast lesions in dynamic contrast-enhanced MR images. Acad. Radiol. 2006, 13, 63–72. [Google Scholar] [CrossRef]
- Partridge, S.C.; Nissan, N.; Rahbar, H.; Kitsch, A.E.; Sigmund, E.E. Diffusion-weighted breast MRI: Clinical applications and emerging techniques. J. Magn. Reson. Imaging 2017, 45, 337–355. [Google Scholar] [CrossRef]
- Shin, H.J.; Chae, E.Y.; Choi, W.J.; Ha, S.M.; Park, J.Y.; Shin, K.C.; Cha, J.H.; Kim, H.H. Diagnostic performance of fused diffusion-weighted imaging using unenhanced or postcontrast T1-weighted MR imaging in patients with breast cancer. Medicine 2016, 95, e3502. [Google Scholar] [CrossRef]
- Barnes, S.L.; Quarles, C.C.; Yankeelov, T.E. Modeling the effect of intra-voxel diffusion of contrast agent on the quantitative analysis of dynamic contrast enhanced magnetic resonance imaging. PLoS ONE 2014, 9, e108726. [Google Scholar] [CrossRef] [PubMed]
- Cronenweth, C.M.; Shellock, F.G. Assessment of MRI Issues at 3 Tesla for a New Metallic Tissue Marker. Int. J. Breast Cancer 2015, 2015, 823759. [Google Scholar] [CrossRef]
- Huang, W.; Li, X.; Chen, Y.; Li, X.; Chang, M.C.; Oborski, M.J.; Malyarenko, D.I.; Muzi, M.; Jajamovich, G.H.; Fedorov, A.; et al. Variations of dynamic contrast-enhanced magnetic resonance imaging in evaluation of breast cancer therapy response: A multicenter data analysis challenge. Transl. Oncol. 2014, 7, 153–166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H. Variability in Quantitative DCE-MRI: Sources and Solutions. South Pac. J. Nat. Appl. Sci. 2018, 4, 1–16. [Google Scholar]

| Patient | Site | Length | SNR | Diagnosis (benign = 0/malig = 1) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 1 | 19 | 14 | 0 | |||||||||||
| 22 | 1 | 24 | 22 | 0 | |||||||||||
| 183 | 1 | 24 | 26 | 1 | |||||||||||
| 276 | 1 | 27 | 26 | 0 | |||||||||||
| 310 | 1 | 27 | 24 | 1 | |||||||||||
| 718 | 1 | 27 | 25 | 0 | |||||||||||
| 724 | 3 | 25 | 16 | 1 | |||||||||||
| 770 | 1 | 31 | 30 | 1 | |||||||||||
| 867 | 2 | 22 | 18 | 1 | |||||||||||
| 882 | 2 | 22 | 22 | 1 | |||||||||||
| 439 | 3 | 25 | 22 | 0 | |||||||||||
| 84 | 1 | 20 | 13 | 1 | |||||||||||
| 27 | 1 | 21 | 28 | 0 | |||||||||||
| 143 | 1 | 24 | 33 | 1 | |||||||||||
| 725 | 1 | 29 | 6 | 0 | |||||||||||
| Patient | 3 | 6 | 7 | 8 | 9 | 11 | 13 | 15 | 17 | 18 | 19 | 22 | 23 | 26 | 28 |
| SNR | 19 | 19 | 26 | 19 | 14 | 27 | 24 | 21 | 26 | 19 | 8 | 21 | 25 | 22 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slavkova, K.P.; DiCarlo, J.C.; Kazerouni, A.S.; Virostko, J.; Sorace, A.G.; Patt, D.; Goodgame, B.; Yankeelov, T.E. Characterizing Errors in Pharmacokinetic Parameters from Analyzing Quantitative Abbreviated DCE-MRI Data in Breast Cancer. Tomography 2021, 7, 253-267. https://doi.org/10.3390/tomography7030023
Slavkova KP, DiCarlo JC, Kazerouni AS, Virostko J, Sorace AG, Patt D, Goodgame B, Yankeelov TE. Characterizing Errors in Pharmacokinetic Parameters from Analyzing Quantitative Abbreviated DCE-MRI Data in Breast Cancer. Tomography. 2021; 7(3):253-267. https://doi.org/10.3390/tomography7030023
Chicago/Turabian StyleSlavkova, Kalina P., Julie C. DiCarlo, Anum S. Kazerouni, John Virostko, Anna G. Sorace, Debra Patt, Boone Goodgame, and Thomas E. Yankeelov. 2021. "Characterizing Errors in Pharmacokinetic Parameters from Analyzing Quantitative Abbreviated DCE-MRI Data in Breast Cancer" Tomography 7, no. 3: 253-267. https://doi.org/10.3390/tomography7030023
APA StyleSlavkova, K. P., DiCarlo, J. C., Kazerouni, A. S., Virostko, J., Sorace, A. G., Patt, D., Goodgame, B., & Yankeelov, T. E. (2021). Characterizing Errors in Pharmacokinetic Parameters from Analyzing Quantitative Abbreviated DCE-MRI Data in Breast Cancer. Tomography, 7(3), 253-267. https://doi.org/10.3390/tomography7030023






