Bone Evaluation with Micro Finite Element Analysis in Animal Models
Abstract
1. Introduction
2. Materials and Methods
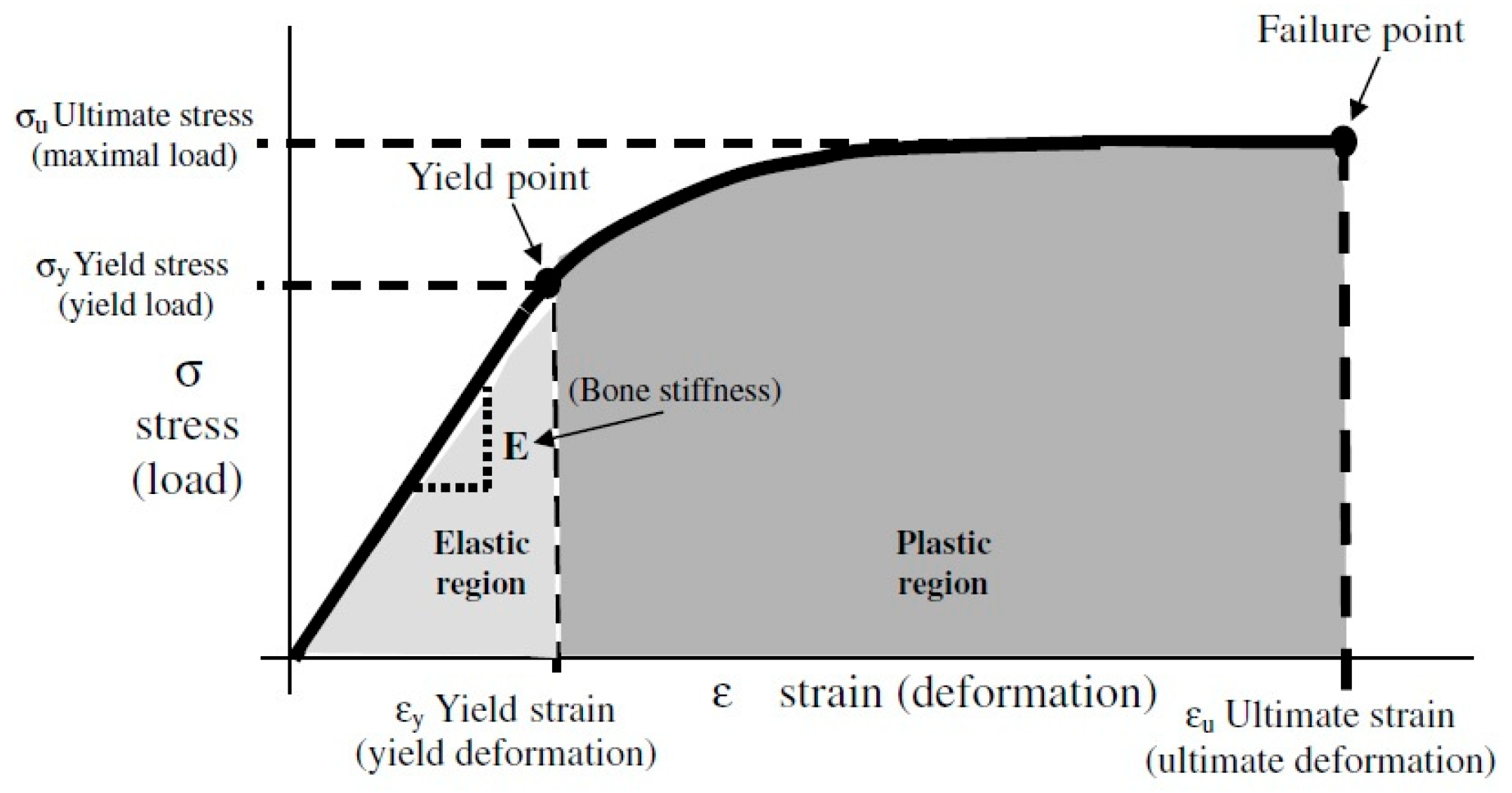
3. Mechanical Properties and Concept
| Mechanical Parameters | Formula | Definition | Schematics |
|---|---|---|---|
| Normal stress | The magnitude of the force applied on the unit area, perpendicular to the force direction | 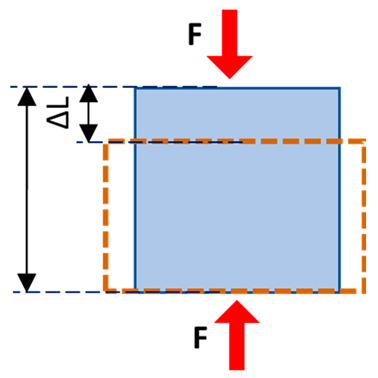 | |
| Normal strain | The change in length of the sample per its original unit length, parallel to the force direction | ||
| Young’s modulus | Normal stress to normal strain ratio, as the elasticity defined in applied force direction but perpendicular to the unit volume surface | ||
| Shear stress | The magnitude of the force applied on the unit area, parallel to the force direction | 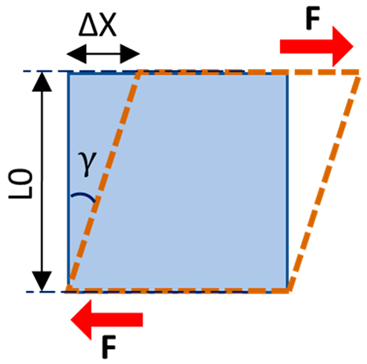 | |
| Shear strain | The angular change in the original right angles of the unit volume after shear stress application | ||
| Shear modulus | Shear stress to shear strain ratio, as the elasticity defined in applied force direction and parallel to the unit volume surface | ||
| Poisson’s ratio | The negative ratio of the transverse strain component to the longitudinal strain component | 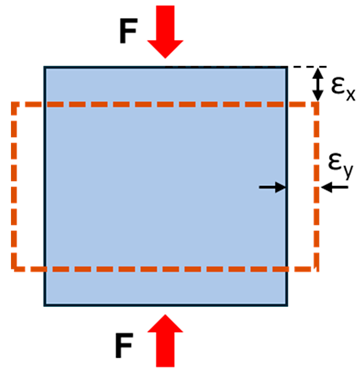 |
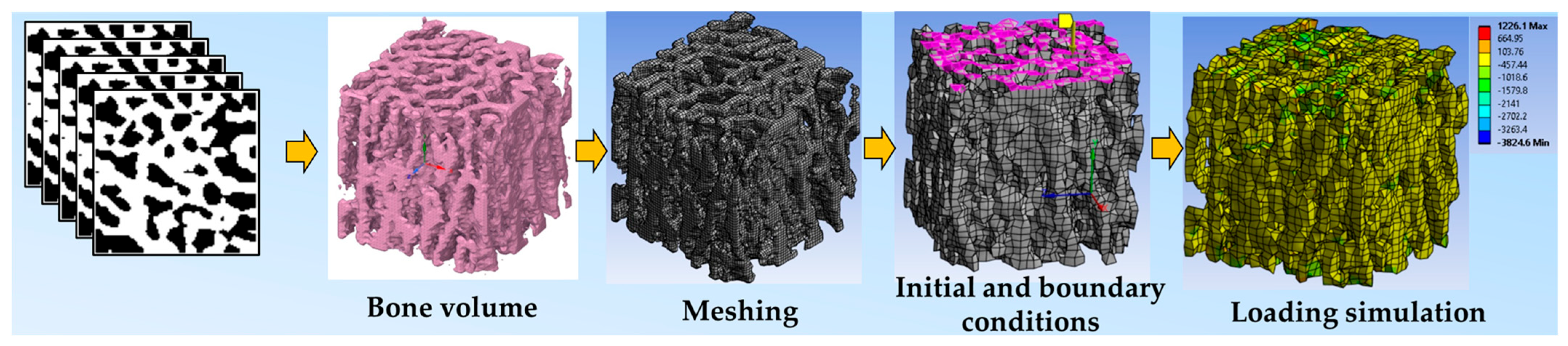
4. FE Modeling Principles
5. FEA of Animal Models
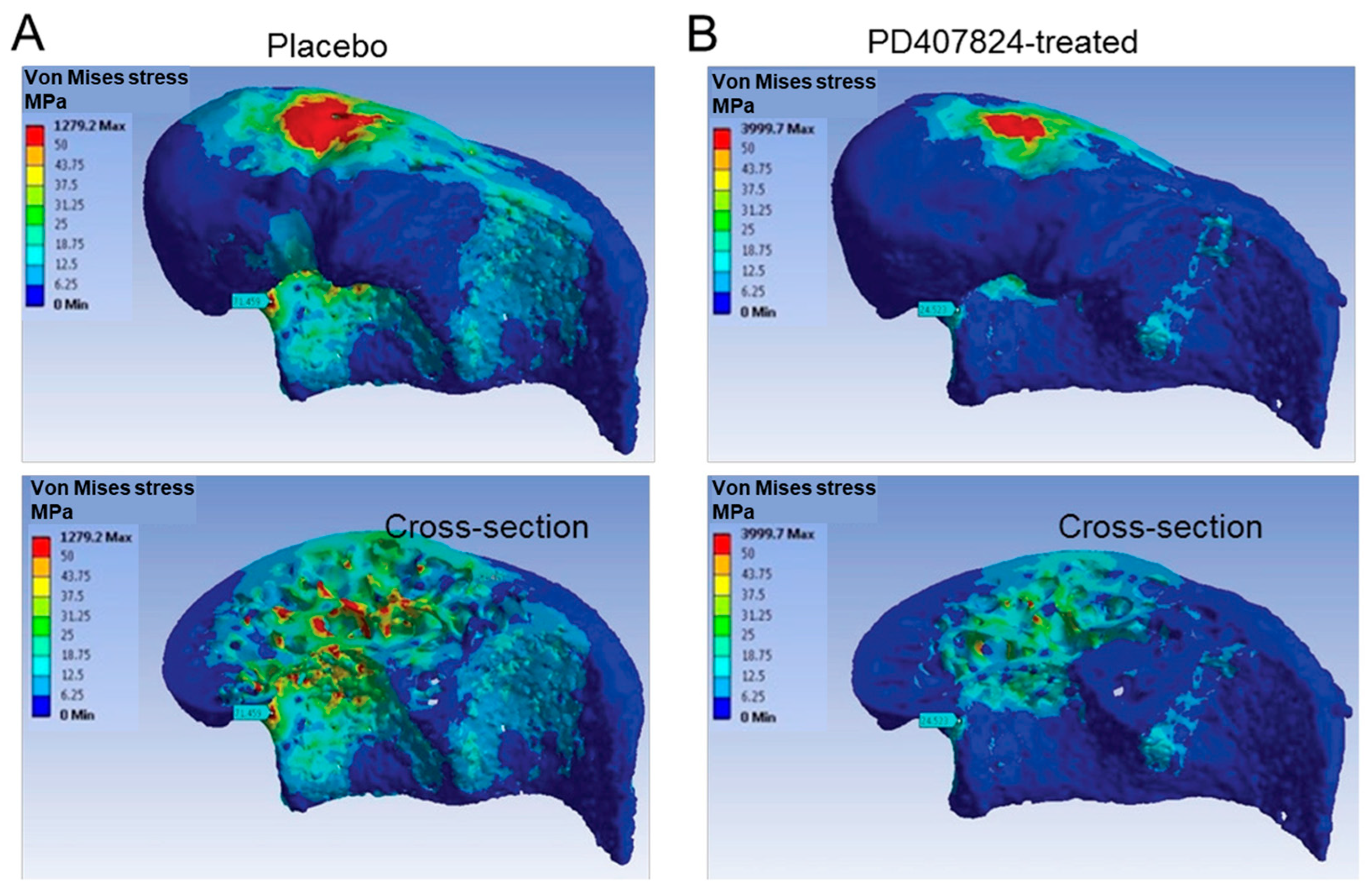
5.1. Using FEA to Examine Impacts of Therapies
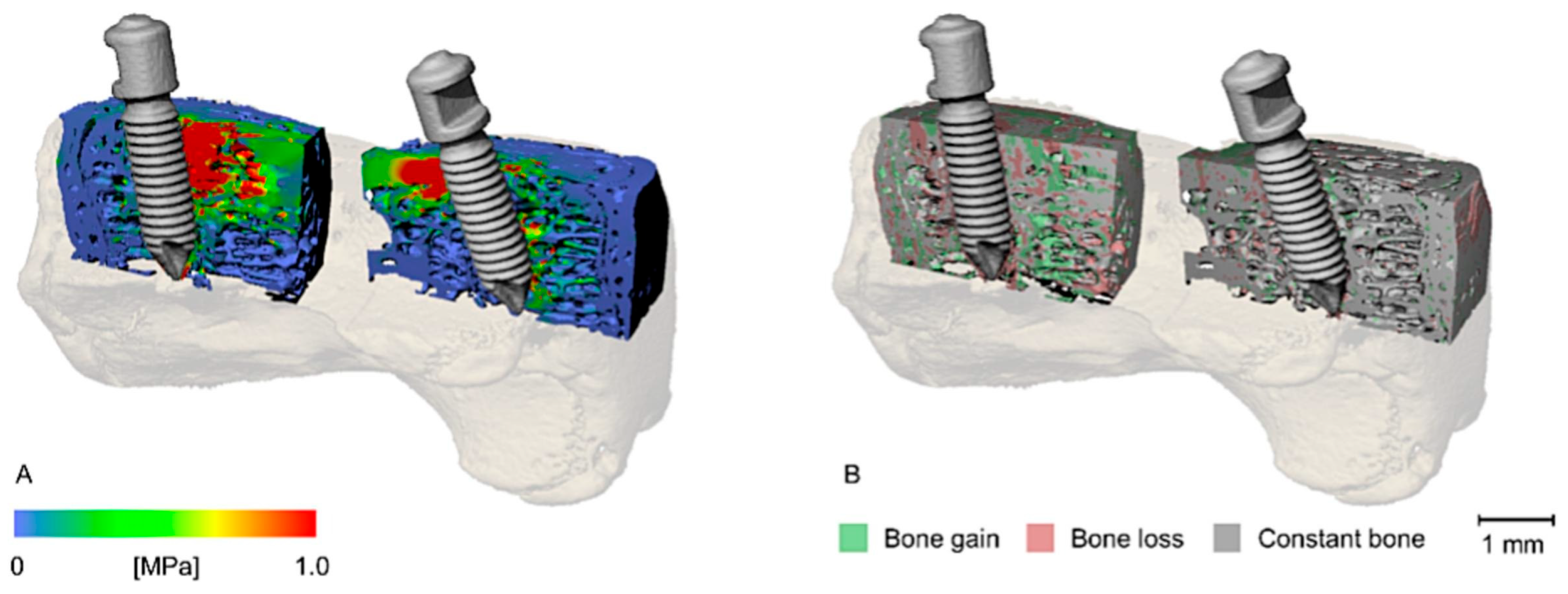
5.2. Using FEA to Examine Impacts of Implants and Surgical Interventions
5.3. Using FEA to Investigate Mechanical Loading Effects and Bone Fracture Mechanisms
5.4. Miscellaneous Bone FEA Studies
6. Continuous Improvements in FEA
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rho, J.; Liisa, K.-S.; Peter, Z. Mechanical Properties and the Hierarchical Structure of Bone. Med. Eng. Phys. 1998, 20, 92–102. [Google Scholar] [CrossRef]
- Wehrli, F.W. Structural and Functional Assessment of Trabecular and Cortical Bone by Micro Magnetic Resonance Imaging. J. Magn. Reson. Imaging 2007, 25, 390–409. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, X.; Fujita, H.; Onozuka, M.; Kubo, K.Y. Age-Related Changes in Trabecular and Cortical Bone Microstructure. Int. J. Endocrinol. 2013, 2013, 213234. [Google Scholar] [CrossRef] [PubMed]
- Engelke, K.; Libanati, C.; Fuerst, T.; Zysset, P.; Genant, H.K. Advanced CT Based in Vivo Methods for the Assessment of Bone Density, Structure, and Strength. Curr. Osteoporos. Rep. 2013, 11, 246–255. [Google Scholar] [CrossRef] [PubMed]
- Zysset, P.K.; Dall’ara, E.; Varga, P.; Pahr, D.H. Finite Element Analysis for Prediction of Bone Strength. Bonekey Rep. 2013, 2, 386. [Google Scholar] [CrossRef]
- Brandi, M.L. Microarchitecture, the Key to Bone Quality. Rheumatology 2009, 48, iv3–iv8. [Google Scholar] [CrossRef] [PubMed]
- Benca, E.; Amini, M.; Pahr, D.H. Effect of CT Imaging on the Accuracy of the Finite Element Modelling in Bone. European Radiol. Exp. 2020, 4, 51. [Google Scholar] [CrossRef]
- Bauer, J.S.; Sidorenko, I.; Mueller, D.; Baum, T.; Issever, A.S.; Eckstein, F.; Rummeny, E.J.; Link, T.M.; Raeth, C.W. Prediction of Bone Strength by μCT and MDCT-Based Finite-Element-Models: How Much Spatial Resolution Is Needed? Eur. J. Radiol. 2014, 83, e36–e42. [Google Scholar] [CrossRef]
- Sharir, A.; Barak, M.M.; Shahar, R. Whole Bone Mechanics and Mechanical Testing. Vet. J. 2008, 177, 8–17. [Google Scholar] [CrossRef]
- Parashar, S.K.; Sharma, J.K. A Review on Application of Finite Element Modelling in Bone Biomechanics. Perspect. Sci. 2016, 8, 696–698. [Google Scholar] [CrossRef]
- Kim, C.H.; Takai, E.; Zhou, H.; Von Stechow, D.; Müller, R.; Dempster, D.W.; Guo, X.E. Trabecular Bone Response to Mechanical and Parathyroid Hormone Stimulation: The Role of Mechanical Microenvironment. J. Bone Miner. Res. 2003, 18, 2116–2125. [Google Scholar] [CrossRef]
- MacNeil, J.A.; Doschak, M.R.; Zernicke, R.F.; Boyd, S.K. Preservation of Periarticular Cancellous Morphology and Mechanical Stiffness in Post-Traumatic Experimental Osteoarthritis by Antiresorptive Therapy. Clin. Biomech. 2008, 23, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Jerban, S.; Barrère, V.; Andre, M.; Chang, E.Y.; Shah, S.B. Quantitative Ultrasound Techniques Used for Peripheral Nerve Assessment. Diagnostics 2023, 13, 956. [Google Scholar] [CrossRef] [PubMed]
- Rhee, Y.; Hur, J.H.; Won, Y.Y.; Lim, S.K.; Beak, M.H.; Cui, W.Q.; Kim, K.G.; Kim, Y.E. Assessment of Bone Quality Using Finite Element Analysis Based upon Micro-CT Images. Clin. Orthop. Surg. 2009, 1, 40–47. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Shahnazari, M.; Yao, W.; Dai, W.; Wang, B.; Ionova-Martin, S.S.; Ritchie, R.O.; Heeren, D.; Burghardt, A.J.; Nicolella, D.P.; Kimiecik, M.G.; et al. Higher Doses of Bisphosphonates Further Improve Bone Mass, Architecture, and Strength but Not the Tissue Material Properties in Aged Rats. Bone 2010, 46, 1267–1274. [Google Scholar] [CrossRef][Green Version]
- Liang, Y.; Yuan, X.; Dai, X.; Zhang, G.; Li, C.; Yang, H.; Zhang, T.; Qin, J. The Effects of Simvastatin on the Bone Microstructure and Mechanics of Ovariectomized Mice: A Micro-CT and Micro-Finite Element Analysis Study. BMC Musculoskelet. Disord. 2024, 25, 748. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Z.; Li, C.; Ma, C.; Chen, J.; Wang, M.; Gao, D.; Wu, Y.; Wang, H. Effect of Bisphosphonate on Bone Microstructure, Mechanical Strength in Osteoporotic Rats by Ovariectomy. BMC Musculoskelet. Disord. 2024, 25, 725. [Google Scholar] [CrossRef]
- Wu, T.; Bonnheim, N.B.; Pendleton, M.M.; Emerzian, S.R.; Keaveny, T.M. Radiation-Induced Changes in Load-Sharing and Structure-Function Behavior in Murine Lumbar Vertebrae. Comput. Methods Biomech. Biomed. Eng. 2023, 27, 1278–1286. [Google Scholar] [CrossRef]
- Huang, X.; Zheng, L.; Zheng, D.; Li, S.; Fan, Y.; Lin, Z.; Huang, S. Studying Trabecular Bone Samples Demonstrates a Power Law Relation between Deteriorated Structure and Mechanical Properties—A Study Combining 3D Printing with the Finite Element Method. Front. Endocrinol. 2023, 14, 1061758. [Google Scholar] [CrossRef]
- Du, J.; Li, S.; Silberschmidt, V.V. Trabecular Bone Remodelling: Finite-Element Simulation. Procedia Struct. Integr. 2020, 28, 577–583. [Google Scholar] [CrossRef]
- Ju, Y.-I.; Choi, H.-J.; Ohnaru, K.; Sone, T. Differential Effects of Jump versus Running Exercise on Trabecular Bone Architecture and Strength in Rats. Phys. Act. Nutr. 2020, 24, 1–8. [Google Scholar] [CrossRef]
- Santaella, B.L.; Tseng, Z.J. Hole in One: An Element Reduction Approach to Modeling Bone Porosity in Finite Element Analysis. PeerJ 2019, 7, e8112. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Liu, S.; Chen, A.; Li, B.-Y.; Robling, A.G.; Chen, J.; Yokota, H. Finite Element Analysis of the Mouse Distal Femur with Tumor Burden in Response to Knee Loading. Int. J. Orthop. 2018, 5, 863–871. [Google Scholar] [CrossRef]
- Cabal, A.; Williams, D.S.; Jayakar, R.Y.; Zhang, J.; Sardesai, S.; Duong, L.T. Long-Term Treatment with Odanacatib Maintains Normal Trabecular Biomechanical Properties in Ovariectomized Adult Monkeys as Demonstrated by Micro-CT-Based Finite Element Analysis. Bone Rep. 2017, 6, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Pei, S.; Lucas Lu, X.; Wang, L. A Multiscale 3D Finite Element Analysis of Fluid/Solute Transport in Mechanically Loaded Bone. Bone Res. 2016, 4, 16032. [Google Scholar] [CrossRef]
- Wu, Y.; Adeeb, S.; Doschak, M.R. Using Micro-CT Derived Bone Microarchitecture to Analyze Bone Stiffness—A Case Study on Osteoporosis Rat Bone. Front. Endocrinol. 2015, 6, 80. [Google Scholar] [CrossRef]
- Lin, L.; Oon, H.Y.; Lin, W.; Qin, Y.-X. Principal Trabecular Structural Orientation Predicted by Quantitative Ultrasound Is Strongly Correlated with μ FEA Determined Anisotropic Apparent Stiffness. Biomech. Model. Mechanobiol. 2014, 13, 961–971. [Google Scholar] [CrossRef]
- Spatz, J.M.; Ellman, R.; Cloutier, A.M.; Louis, L.; Van Vliet, M.; Suva, L.J.; Dwyer, D.; Stolina, M.; Ke, H.Z.; Bouxsein, M.L. Sclerostin Antibody Inhibits Skeletal Deterioration Due to Reduced Mechanical Loading. J. Bone Miner. Res. 2013, 28, 865–874. [Google Scholar] [CrossRef]
- Cabal, A.; Jayakar, R.Y.; Sardesai, S.; Phillips, E.A.; Szumiloski, J.; Posavec, D.J.; Mathers, P.D.; Savitz, A.T.; Scott, B.B.; Winkelmann, C.T.; et al. High-Resolution Peripheral Quantitative Computed Tomography and Finite Element Analysis of Bone Strength at the Distal Radius in Ovariectomized Adult Rhesus Monkey Demonstrate Efficacy of Odanacatib and Differentiation from Alendronate. Bone 2013, 56, 497–505. [Google Scholar] [CrossRef]
- Liu, X.S.; Stein, E.M.; Zhou, B.; Zhang, C.A.; Nickolas, T.L.; Cohen, A.; Thomas, V.; McMahon, D.J.; Cosman, F.; Nieves, J.; et al. Individual Trabecula Segmentation (ITS)-Based Morphological Analyses and Micro finite Element Analysis of HR-pQCT Images Discriminate Postmenopausal Fragility Fractures Independent of DXA Measurements. J. Bone Miner. Res. 2012, 27, 263–272. [Google Scholar] [CrossRef]
- Liu, X.S.; Ardeshirpour, L.; VanHouten, J.N.; Shane, E.; Wysolmerski, J.J. Site-Specific Changes in Bone Microarchitecture, Mineralization, and Stiffness during Lactation and after Weaning in Mice. J. Bone Miner. Res. 2012, 27, 865–875. [Google Scholar] [CrossRef]
- Harrison, N.M.; McHugh, P.E. Comparison of Trabecular Bone Behavior in Core and Whole Bone Samples Using High-Resolution Modeling of a Vertebral Body. Biomech. Model. Mechanobiol. 2010, 9, 469–480. [Google Scholar] [CrossRef]
- Nagaraja, S.; Couse, T.L.; Guldberg, R.E. Trabecular Bone Microdamage and Microstructural Stresses under Uniaxial Compression. J. Biomech. 2005, 38, 707–716. [Google Scholar] [CrossRef]
- Jaecques, S.V.N.; Van Oosterwyck, H.; Muraru, L.; Van Cleynenbreugel, T.; De Smet, E.; Wevers, M.; Naert, I.; Vander Sloten, J. Individualised, Micro CT-Based Finite Element Modelling as a Tool for Biomechanical Analysis Related to Tissue Engineering of Bone. Biomaterials 2004, 25, 1683–1696. [Google Scholar] [CrossRef]
- Kerberger, R.; Brunello, G.; Drescher, D.; van Rietbergen, B.; Becker, K. Micro Finite Element Analysis of Continuously Loaded Mini-Implants – A Micro-CT Study in the Rat Tail Model. Bone 2023, 177, 116912. [Google Scholar] [CrossRef]
- Gerasimov, O.V.; Kharin, N.V.; Fedyanin, A.O.; Bolshakov, P.V.; Baltin, M.E.; Statsenko, E.O.; Fadeev, F.O.; Islamov, R.R.; Baltina, T.V.; Sachenkov, O.A. Bone Stress-Strain State Evaluation Using CT Based FEM. Front. Mech. Eng. 2021, 7, 688474. [Google Scholar] [CrossRef]
- Bouxsein, M.L.; Boyd, S.K.; Christiansen, B.A.; Guldberg, R.E.; Jepsen, K.J.; Müller, R. Guidelines for Assessment of Bone Microstructure in Rodents Using Micro-Computed Tomography. J. Bone Miner. Res. 2010, 25, 1468–1486. [Google Scholar] [CrossRef]
- Soltanmohammadi, R.; Faroughi, S.A. A Comparative Analysis of Super-Resolution Techniques for Enhancing Micro-CT Images of Carbonate Rocks. Appl. Comput. Geosci. 2023, 20, 100143. [Google Scholar] [CrossRef]
- Gu, A.; Andreyev, A.; Terada, M.; Rodgers, T.; Viswanathan, V. A Deep Learning Reconstruction Technique and Workflow to Enhance 3D X-ray Imaging Resolution and Speed for Electronics Package Failure Analysis. In Proceedings of the 2023 International Conference on Electronics Packaging (ICEP), Kumamoto, Japan, 19–22 April 2023; pp. 69–70. [Google Scholar] [CrossRef]
- Lee, A.H.; Moore, J.M.; Covarrubias, B.V.; Lynch, L.M. Segmentation of Cortical Bone, Trabecular Bone, and Medullary Pores from Micro-CT Images Using 2D and 3D Deep Learning Models. Anat. Rec. 2025, 1–23. [Google Scholar] [CrossRef] [PubMed]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022. [CrossRef]
| First Author, Year | Micro-CT Voxel (Element Size) | Element Properties | Finite Element Software | Ex/In Vivo, Bone Site |
|---|---|---|---|---|
| Liang et al., 2025 [16] | 15 µm3 | Hexahedron element Elastic modulus, E = 15 GPa | ANSYS, Ver 17 | - ex vivo - mice vertebra - trabecular |
| Wang et al., 2024 [17] | 10 µm3 | Quadratic tetrahedron element E = 13 GPa | ABAQUS Ver 2020 | - ex vivo - rat femoral condyle - trabecular |
| Wu et al., 2023 [18] | 10 µm3 | Eight-noded brick element E = 10 GPa | custom-written code | - ex vivo - mice vertebrae - trabecular |
| Huang et al., 2023 [19] | 15 µm3 | Tetrahedral element E = 3 GPa | custom-written code | - ex vivo - rat femur - trabecular |
| Du et al., 2020 [20] | 60 µm3 | Tetrahedral element E = 12 GPa | ABAQUS Ver 6.4 | - ex vivo - bovine femoral head - trabecular |
| Ju et al., 2020 [21] | 18 µm3 | Not mentioned | TRI/3D-FEM64 (Version not reported) | - ex vivo - rat femur - trabecular |
| Santaella et al., 2019 [22] | Tetrahedral element E = 20 GPa | Strand 7 Ver 2.4.6 | - ex vivo - carnivoran - trabecular | |
| Jiang et al., 2018 [23] | 9 µm3 | Tetrahedral element E = 8.9 GPa | ANSYS Ver 14.5 | - ex vivo - mouse distal femur - trabecular |
| Cabal et al., 2017 [24] | 20 µm3 | Tetrahedral element E = 12 GPa | ANSYS (Version not reported) | - ex vivo - monkey vertebra - trabecular |
| Fan et al., 2016 [25] | 20 µm3 | Tetrahedral element E = 20 GPa | Altair HyperWorks (Version not reported) | - in vivo - mouse tibia - cortical and trabecular |
| Wu et al., 2015 [26] | 18 µm3 | Hexahedral element E = 24.5 GPa | ABAQUS Ver 6.10 | - ex vivo - rat lumbar vertebra - trabecular |
| Lin et al., 2014 [27] | 18 µm3 | Tetrahedral element E = 15.9 GPa | ABAQUS Ver 6.10 | - ex vivo - bovine femur - trabecular |
| Spatz et al., 2013 [28] | 12 µm3 | E = 10 GPa | Scanco Medical AG (Version not reported) | - ex vivo - mice tibia - trabecular and cortical |
| Cabal et al., 2013 [29] | 41 μm3 | E = 18 GPa | ANSYS (Version not reported) | - ex vivo - monkey - trabecular and cortical |
| Liu et al., 2012 [30] | 10.5 µm3 | Eight-noded brick element E =15 GPa | custom-written code | - ex vivo - mice tibia, spine, femur - trabecular |
| Liu et al., 2012 [31] | 38 µm3 | Hexahedron element E = 15 GPa | custom-written code | - ex vivo - rabbit femur - trabecular |
| Harrison et al., 2010 [32] | 36 µm3 | Tetrahedral element E = 8.5 GPa | custom-written code | - ex vivo - ovine vertebra - trabecular |
| Shahnazari et al., 2010 [15] | 10.5 µm3 | Eight-noded prismatic E = 18 GPa | custom-written code | - ex vivo - rat lumbar vertebra - trabecular and cortical |
| Rhee et al., 2009 [14] | 21.3 µm3 | Hexahedron element E = 1 GPa | ANSYS Ver 09 | - ex vivo - rat vertebra - trabecular |
| Nagaraja et al., 2005 [33] | 20 µm3 | Hexahedral element E = 18.4 GPa | Scanco Medical AG (Version not reported) | - ex vivo - bovine proximal tibia - trabecular |
| Jaecques et al., 2004 [34] | 15.9 µm3 | Tetrahedral element E = 11 GP | MSC Nastran/Pattern (Version not reported) | - in vivo - guinea pig tibia - trabecular |
| Kim et al., 2003 [11] | 34 µm3 | Eight-noded brick element E = 18 GPa | custom-written code | - ex vivo - rat tail vertebra - trabecular |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Namiranian, B.; Doi, K.; Alenezi, S.; Shah, S.B.; Jerban, S.; Chang, E.Y. Bone Evaluation with Micro Finite Element Analysis in Animal Models. Tomography 2025, 11, 101. https://doi.org/10.3390/tomography11090101
Namiranian B, Doi K, Alenezi S, Shah SB, Jerban S, Chang EY. Bone Evaluation with Micro Finite Element Analysis in Animal Models. Tomography. 2025; 11(9):101. https://doi.org/10.3390/tomography11090101
Chicago/Turabian StyleNamiranian, Behnam, Kenichiro Doi, Salem Alenezi, Sameer B. Shah, Saeed Jerban, and Eric Y. Chang. 2025. "Bone Evaluation with Micro Finite Element Analysis in Animal Models" Tomography 11, no. 9: 101. https://doi.org/10.3390/tomography11090101
APA StyleNamiranian, B., Doi, K., Alenezi, S., Shah, S. B., Jerban, S., & Chang, E. Y. (2025). Bone Evaluation with Micro Finite Element Analysis in Animal Models. Tomography, 11(9), 101. https://doi.org/10.3390/tomography11090101





