STANet: A Novel Spatio-Temporal Aggregation Network for Depression Classification with Small and Unbalanced FMRI Data
Abstract
1. Introduction
1.1. fMRI-Informed Depression Diagnosis
1.2. fMRI-Informed Feature Integration
1.3. Data Imbalance in fMRI-Based Classification Task
1.4. The Proposed Method
2. Materials and Methods
2.1. Dataset
2.2. Pipeline of Data Processing
2.2.1. Pre-Processing
2.2.2. Model Architecture
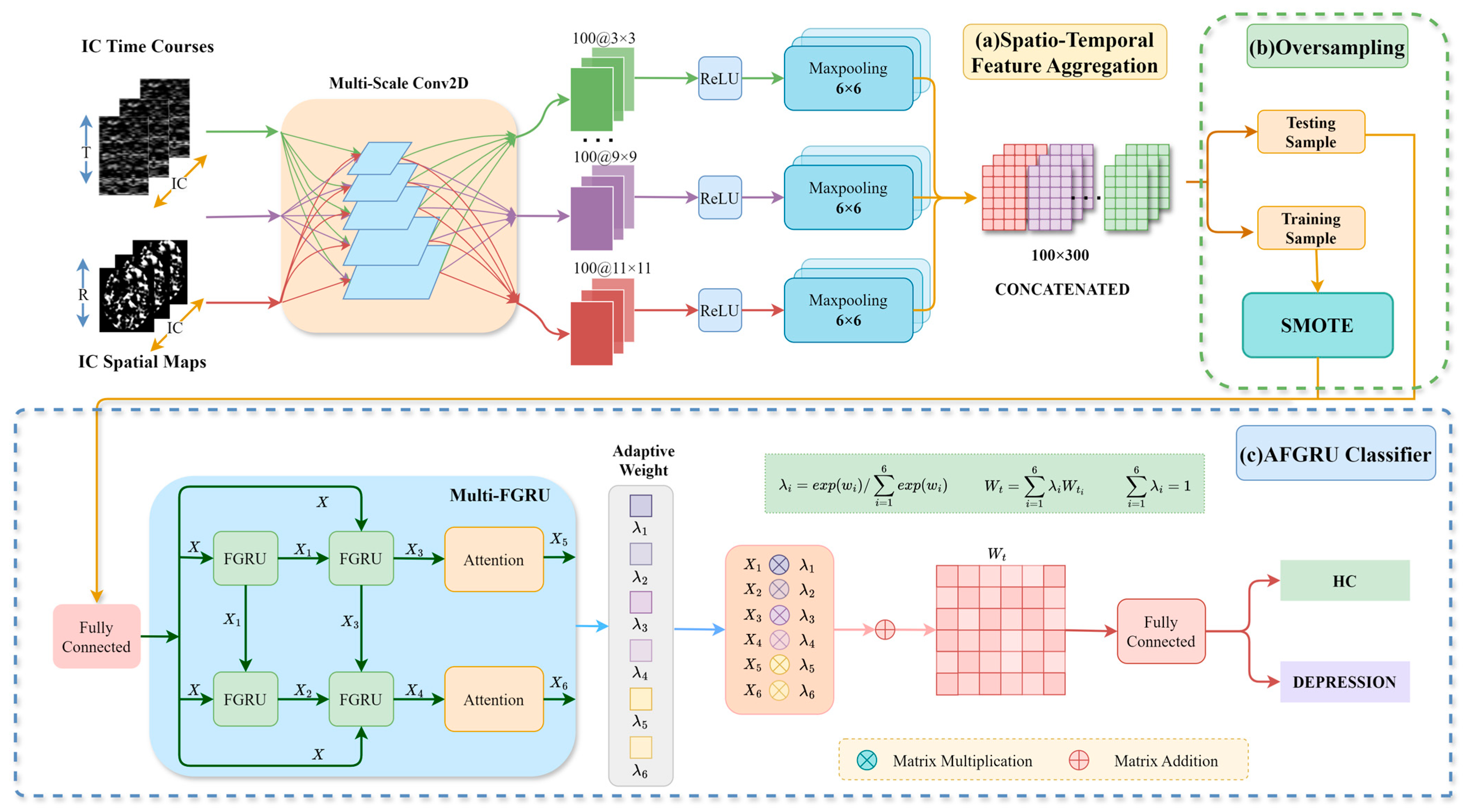
2.3. STANet
2.3.1. STFA Module
Independent Component Analysis
Multiple Linear Regression
Multi-Scale Convolution Layer
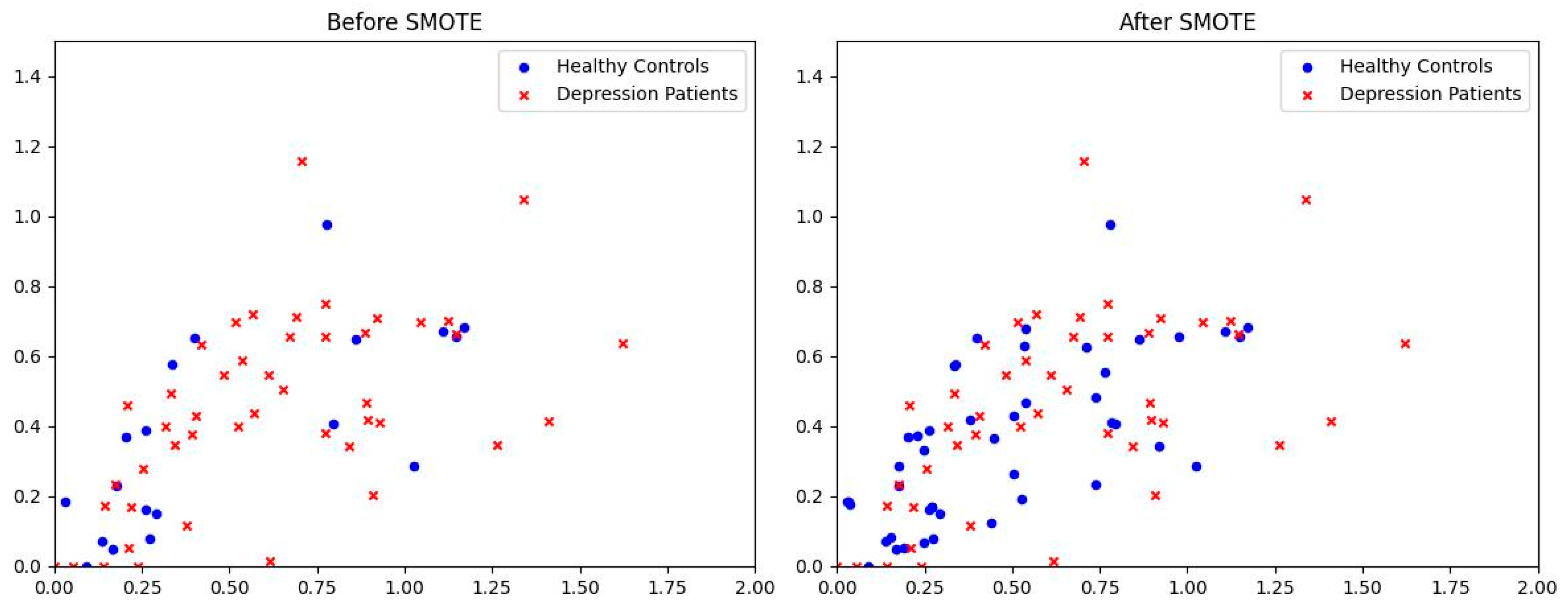
2.3.2. SMOTE
2.3.3. AFGRU Classifier
Multi-FGRU
Adaptive Weighting
| Algorithm 1: Adaptive Weighting | ||
| Input: Sample data (, ), sample data weights , training iteration number | ||
| Output: Optimal model | ||
| Initialization: Set to Gaussian distribution random number and | ||
| Start: | ||
| For i from 0 to : | ||
| #Train the model using the current weights | ||
| model = Train ((, ), ) | ||
| #Calculate the loss function | ||
| Loss = MSE (model, (, )) | ||
| #Update sample weights to minimize the loss function | ||
| For j = 1 to 6: | ||
| Prediction value = model. predict () | ||
| Truth value = | ||
| = *exp (−lr * (Prediction value—Truth value)) | ||
| End for | ||
| #Normalize sample weights | ||
| For k = 1 to 6: | ||
| = / | ||
| End for | ||
| End for | ||
| Return | ||
2.4. Performance Metrics
3. Results
3.1. Experimental Setting
3.2. Performance Assessment of STFA Module in STANet
3.2.1. Performance Comparison Without STFA Module
3.2.2. Performance Comparison with STFA Module
3.3. Performance Assessment of AFGRU Classifier in STANet
3.4. Oversampling Strategy Impact on STANet
3.5. Order Number Impact on STANet
3.6. Comparison with Other Competing Methods
4. Discussion
4.1. Performance Analysis
4.2. Diagnostic Analysis of Depression
4.3. Limitation and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Traditional Classifiers Based on the FC Matrix
| Methods | Accuracy | F1-Score | Recall | AUC |
|---|---|---|---|---|
| Adaboost | 52.50% | 61.43% | 59.00% | 48.67% |
| Bayes | 63.75% | 76.12% | 84.33% | 48.33% |
| DT | 59.46% | 66.81% | 66.67% | 55.00% |
| RF | 62.14% | 75.11% | 84.00% | 40.33% |
| LG | 51.25% | 65.12% | 68.33% | 32.00% |
| SVM | 60.89% | 73.92% | 65.65% | 47.17% |
Appendix B. Results of Group ICA
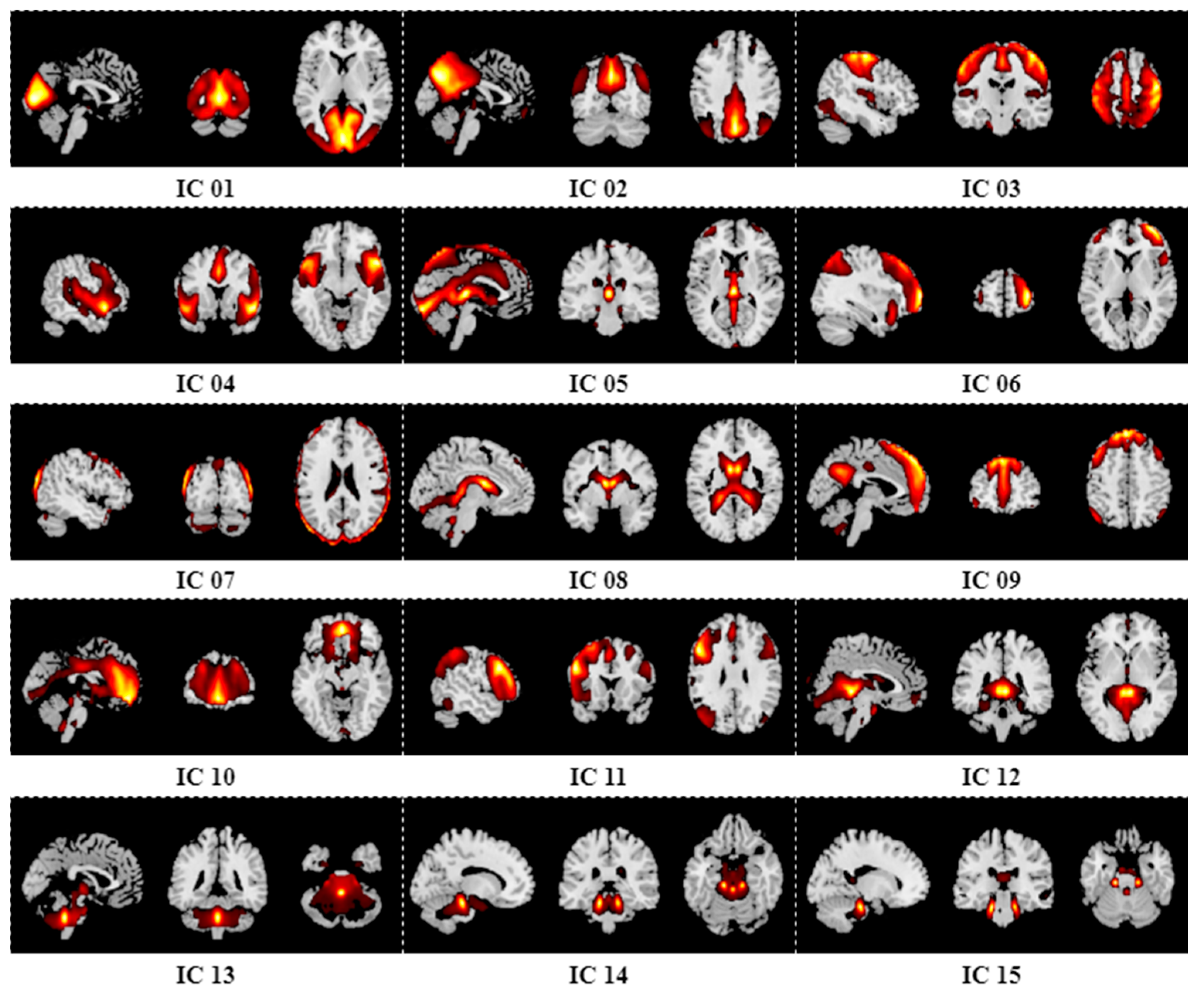
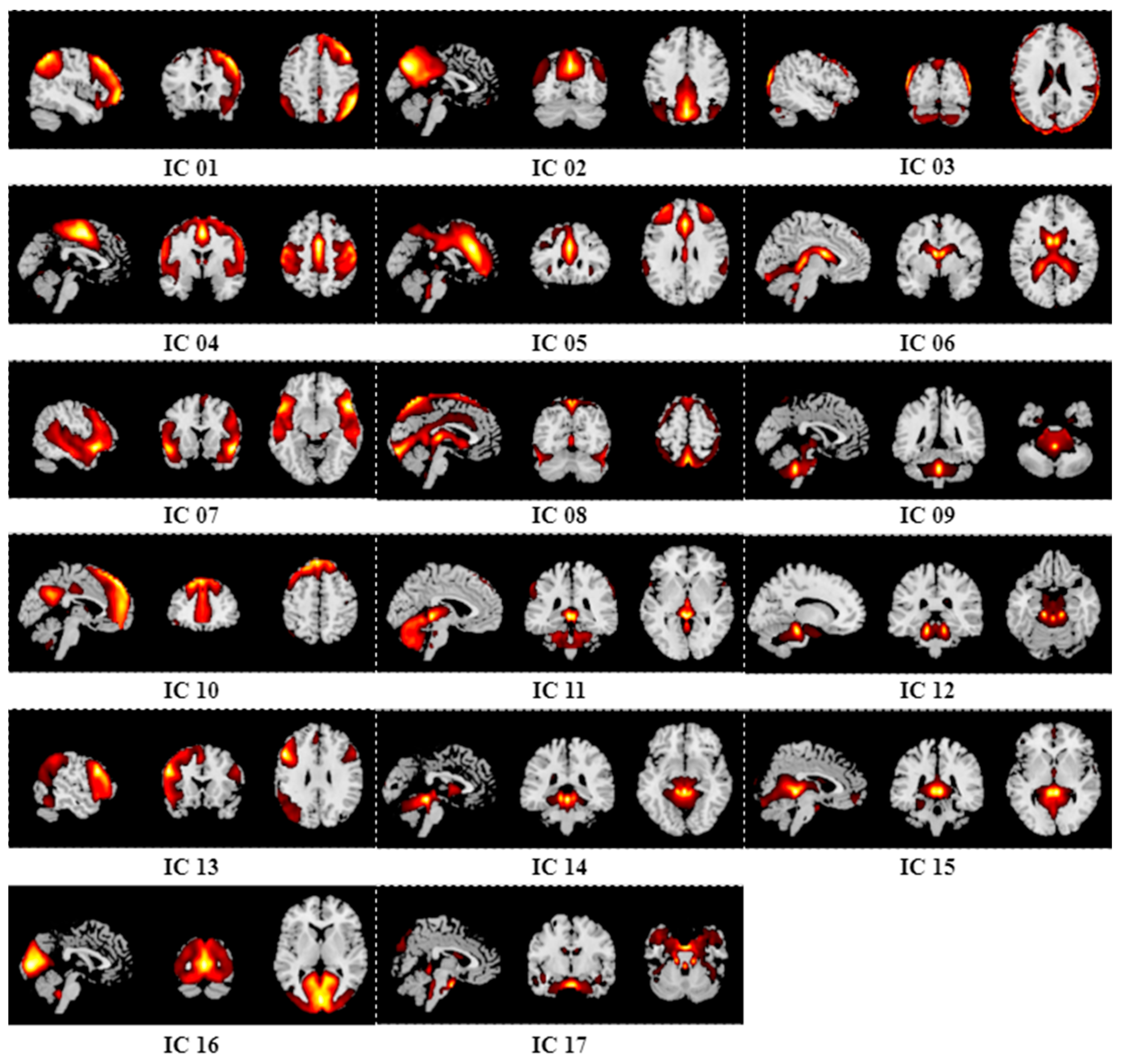
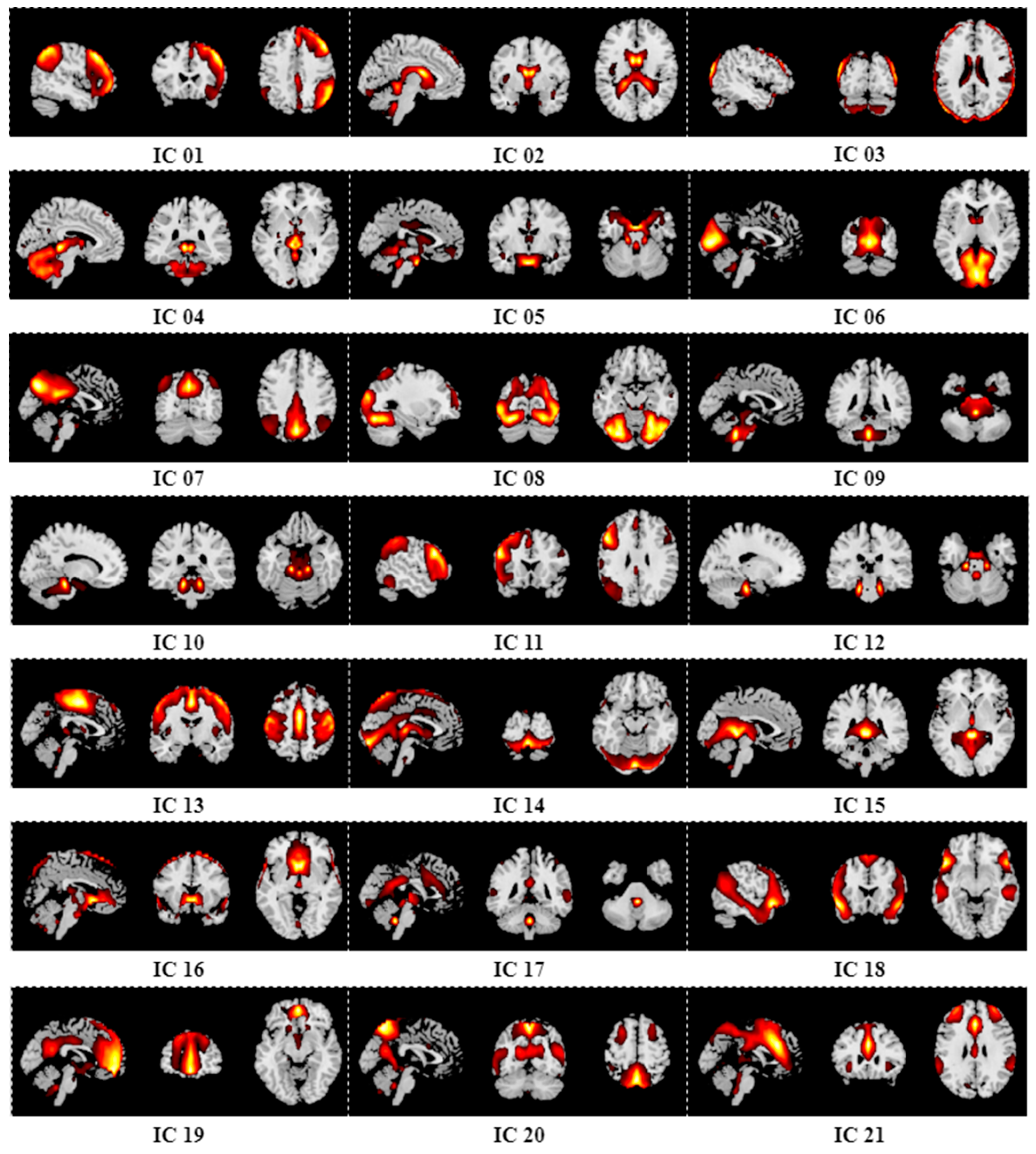
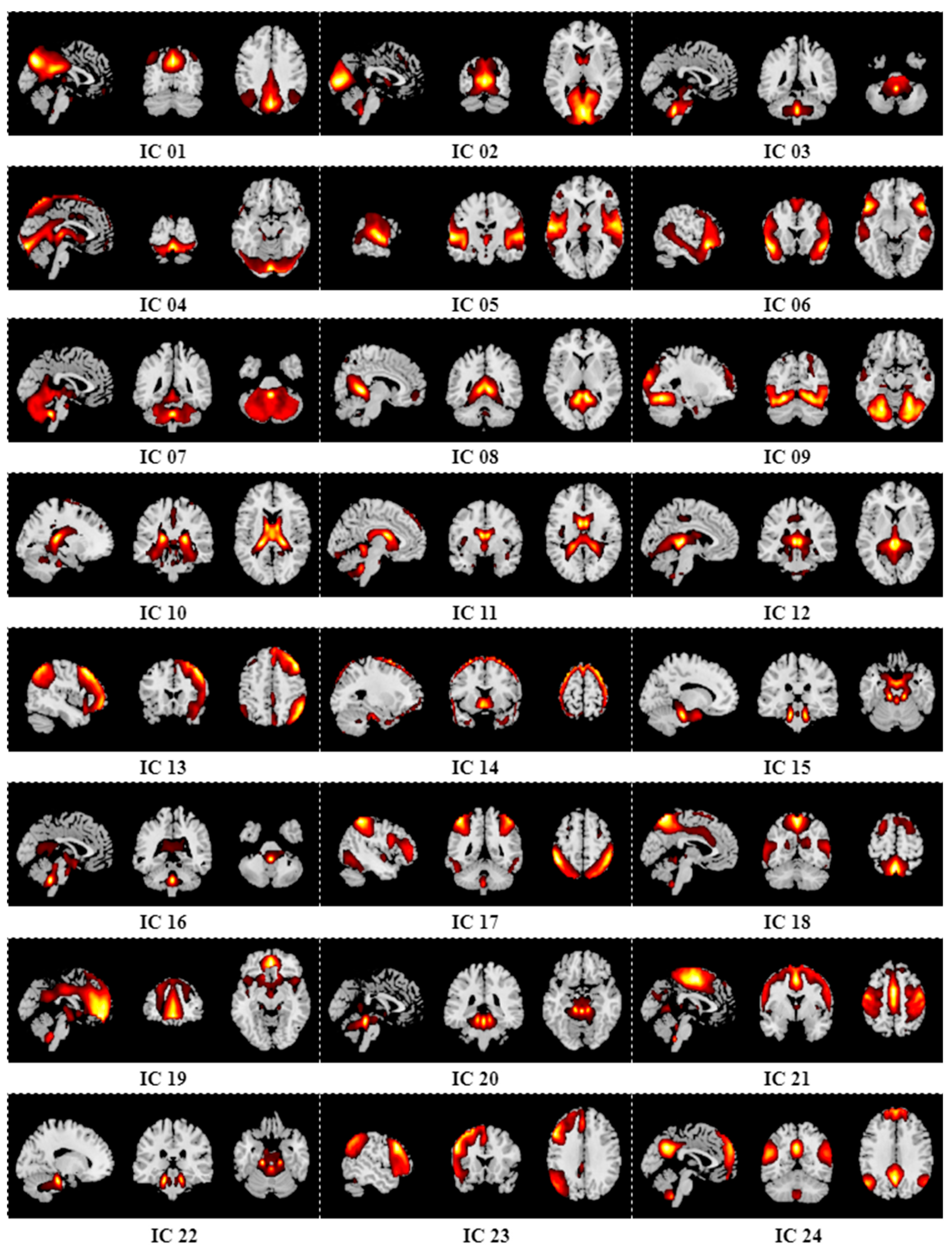
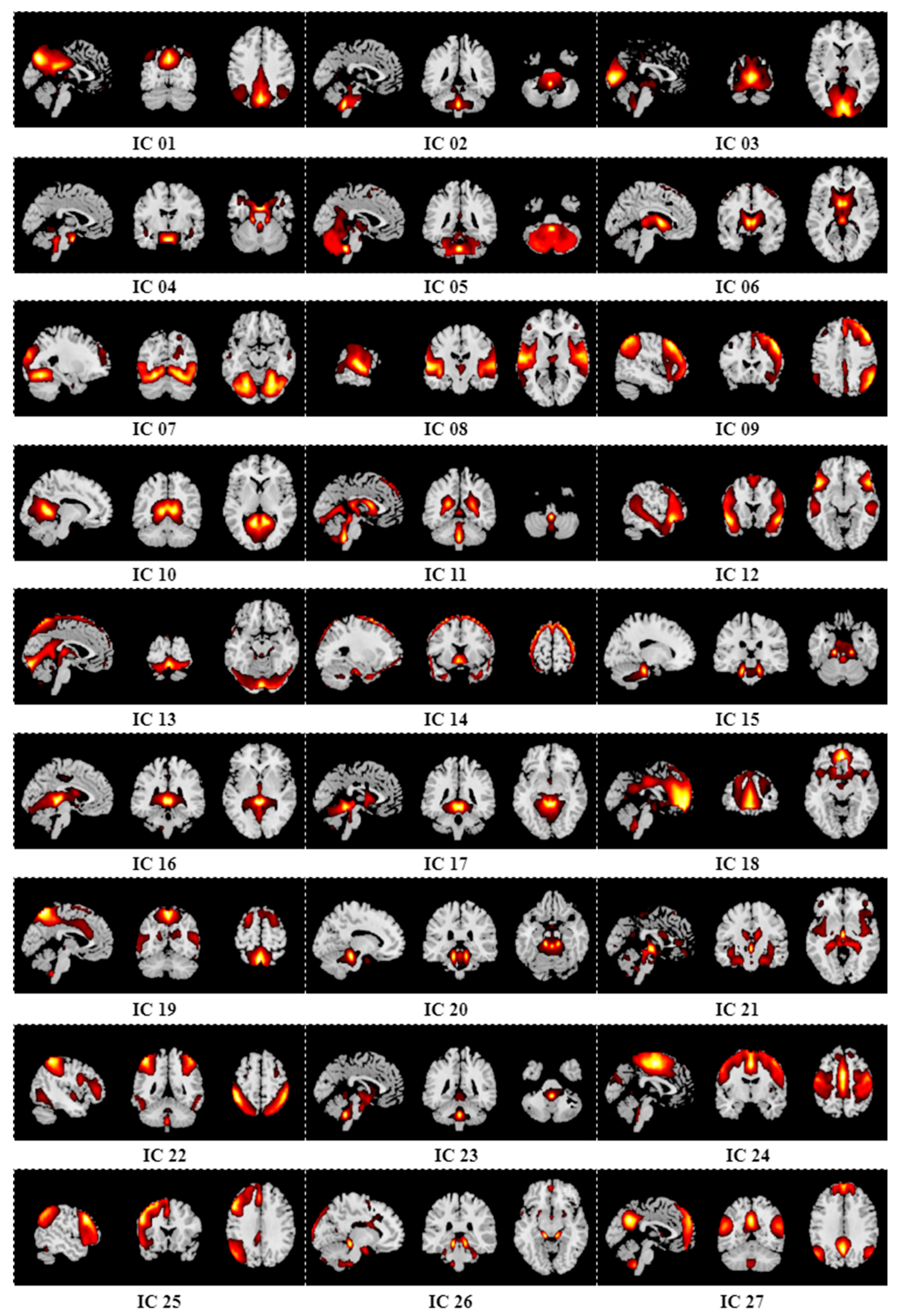
References
- GBD 2019 Mental Disorders Collaborators. Global, regional, and national burden of 12 mental disorders in 204 countries and territories, 1990–2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet Psychiatry 2022, 9, 137–150. [Google Scholar] [CrossRef]
- Hatami, A.; Ranjbar, A.; Azizi, S. Utilizing fMRI and Deep Learning for the Detection of Major Depressive Disorder: A MobileNet V2 Approach. In Proceedings of the 2024 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Istanbul, Turkey, 23–25 May 2024; pp. 1–5. [Google Scholar]
- Lee, D.J.; Shin, D.H.; Son, Y.H.; Han, J.W.; Oh, J.H.; Kim, D.H.; Jeong, J.H.; Kam, T.E. Spectral Graph Neural Network-Based Multi-Atlas Brain Network Fusion for Major Depressive Disorder Diagnosis. IEEE J. Biomed. Health 2024, 28, 2967–2978. [Google Scholar] [CrossRef] [PubMed]
- Sen, B.; Cullen, K.R.; Parhi, K.K. Classification of Adolescent Major Depressive Disorder via Static and Dynamic Connectivity. IEEE J. Biomed. Health Inf. 2021, 25, 2604–2614. [Google Scholar] [CrossRef]
- Gordon, E.M.; Chauvin, R.J.; Van, A.N.; Rajesh, A.; Nielsen, A.; Newbold, D.J.; Lynch, C.J.; Seider, N.A.; Krimmel, S.R.; Scheidter, K.M.; et al. A somato-cognitive action network alternates with effector regions in motor cortex. Nature 2023, 617, 351–359. [Google Scholar] [CrossRef] [PubMed]
- Raimondo, L.; Oliveira, I.A.F.; Heij, J.; Priovoulos, N.; Kundu, P.; Leoni, R.F.; van der Zwaag, W. Advances in resting state fMRI acquisitions for functional connectomics. Neuroimage 2021, 243, 13. [Google Scholar] [CrossRef] [PubMed]
- Noman, F.; Ting, C.M.; Kang, H.; Phan, R.C.W.; Ombao, H. Graph Autoencoders for Embedding Learning in Brain Networks and Major Depressive Disorder Identification. IEEE J. Biomed. Health Inf. 2024, 28, 1644–1655. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Zhang, Z. DDN-Net: Deep Residual Shrinkage Denoising Networks with Channel-Wise Adaptively Soft Thresholds for Automated Major Depressive Disorder Identification. ICASSP 2024–2024. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 1626–1630. [Google Scholar]
- Chen, F.; Wang, L.; Ding, Z. Alteration of whole-brain amplitude of low-frequency fluctuation and degree centrality in patients with mild to moderate depression: A resting-state functional magnetic resonance imaging study. Front. Psychiatry 2022, 13, 1061359. [Google Scholar] [CrossRef] [PubMed]
- Barandas, M.; Folgado, D.; Fernandes, L.; Santos, S.; Abreu, M.; Bota, P.; Liu, H.; Schultz, T.; Gamboa, H. TSFEL: Time series feature extraction library. SoftwareX 2020, 11, 100456. [Google Scholar] [CrossRef]
- Shi, Y.; Zeng, W.; Wang, N. SCGICAR: Spatial concatenation based group ICA with reference for fMRI data analysis. Comput. Methods Programs Biomed. 2017, 148, 137–151. [Google Scholar] [CrossRef]
- Zang, Y.; He, Y.; Zhu, C.; Cao, Q.; Sui, M.; Liang, M.; Tian, L.; Jiang, T.; Wang, Y. Altered baseline brain activity in children with ADHD revealed by resting-state functional MRI. Brain Dev. 2007, 29, 83–91. [Google Scholar]
- Zou, Q.; Zhu, C.; Yang, Y.; Zuo, X.; Long, X.; Cao, Q.; Wang, Y.; Zang, Y. An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: Fractional ALFF. J. Neurosci. Methods 2008, 172, 137–141. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Cai, Z.; Li, C.; Xiong, Y.; Yang, Y.; He, S.; Tang, H.; Zhang, B.; Du, S.; Yan, H.; et al. A novel spectrum contrast mapping method for functional magnetic resonance imaging data analysis. Front. Hum. Neurosci. 2021, 15, 739668. [Google Scholar] [CrossRef]
- Yan, W.Z.; Calhoun, V.; Song, M.; Cui, Y.; Yan, H.; Liu, S.F.; Fan, L.Z.; Zuo, N.M.; Yang, Z.Y.; Xu, K.B.; et al. Discriminating schizophrenia using recurrent neural network applied on time courses of multi-site FMRI data. EBioMedicine 2019, 47, 543–552. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Duan, F.; Zhang, M.X. Convolution-GRU Based on Independent Component Analysis for fMRI Analysis with Small and Imbalanced Samples. Appl. Sci. 2020, 10, 17. [Google Scholar] [CrossRef]
- Mao, Z.; Su, Y.; Xu, G.; Wang, X.; Huang, Y.; Yue, W.; Sun, L.; Xiong, N. Spatio-temporal deep learning method for adhd fmri classification. Inf. Sci. 2019, 499, 1–11. [Google Scholar] [CrossRef]
- Liu, R.; Huang, Z.-A.; Hu, Y.; Zhu, Z.; Wong, K.-C.; Tan, K.C. Spatial–temporal co-attention learning for diagnosis of mental disorders from resting-state fMRI data. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 10591–10605. [Google Scholar] [CrossRef]
- Lim, M.; Heo, K.-S.; Kim, J.-M.; Kang, B.; Lin, W.; Zhang, H.; Shen, D.; Kam, T.-E. A Unified Multi-Modality Fusion Framework for Deep Spatio-Temporal-Spectral Feature Learning in Resting-State fMRI Denoising. IEEE J. Biomed. Health 2024, 28, 2067–2078. [Google Scholar] [CrossRef] [PubMed]
- Kaur, H.; Pannu, H.S.; Malhi, A.K. A systematic review on imbalanced data challenges in machine learning: Applications and solutions. ACM Comput. Surv. 2019, 52, 1–36. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, L. Clustering-based undersampling with random over sampling examples and support vector machine for imbalanced classification of breast cancer diagnosis. Comput. Assist. Surg. 2019, 24 (Suppl. S2), 62–72. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Eslami, T.; Saeed, F. Auto-ASD-network: A technique based on deep learning and support vector machines for diagnosing autism spectrum disorder using fMRI data. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, New York, NY, USA, 7–10 September 2019; pp. 646–651. [Google Scholar]
- Riaz, A.; Asad, M.; Alonso, E.; Slabaugh, G. Fusion of fMRI and non-imaging data for ADHD classification. Comput. Med. Imaging Graph. 2018, 65, 115–128. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Zeng, M.; Zou, B.; Wei, F.; Liu, X.; Wang, L. Effective prediction of three common diseases by combining SMOTE with Tomek links technique for imbalanced medical data. In Proceedings of the 2016 IEEE International Conference of Online Analysis and Computing Science (ICOACS), Chongqing, China, 28–29 May 2016; pp. 225–228. [Google Scholar]
- Wang, J.; Zou, C.; Fu, G. AWSMOTE: An SVM-Based Adaptive Weighted SMOTE for Class-Imbalance Learning. Sci. Program 2021, 2021, 9947621. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE IJCNN, Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Chen, Y.; Chang, R.; Guo, J. Effects of data augmentation method borderline-SMOTE on emotion recognition of EEG signals based on convolutional neural network. IEEE Access 2021, 9, 47491–47502. [Google Scholar] [CrossRef]
- Koh, J.E.W.; Jahmunah, V.; Pham, T.-H.; Oh, S.L.; Ciaccio, E.J.; Acharya, U.R.; Yeong, C.H.; Fabell, M.K.M.; Rahmat, K.; Vijayananthan, A.; et al. Automated detection of Alzheimer’s disease using bi-directional empirical model decomposition. Pattern Recognit. Lett. 2020, 135, 106–113. [Google Scholar] [CrossRef]
- Bezmaternykh, D.D.; Melnikov, M.Y.; Savelov, A.A.; Kozlova, L.I.; Petrovskiy, E.D.; Natarova, K.A.; Shtark, M.B. Brain Networks Connectivity in Mild to Moderate Depression: Resting State fMRI Study with Implications to Nonpharmacological Treatment. Neural Plast. 2021, 2021, 8846097. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Holmes, A.; Worsley, K.J.; Poline, J.-B.; Frith, C.D.; Frackowiak, R.S.J. Statistical parametric maps in functional imaging: A general linear approach. Hum. Brain Mapp. 1994, 2, 189–210. [Google Scholar] [CrossRef]
- Correa, N.; Adali, T.; Li, Y.O.; Calhoun, V.D. Comparison of blind source separation algorithms for FMRI using a new Matlab toolbox: GIFT. In Proceedings of the IEEE ICASSP, Philadelphia, PA, USA, 23 March 2005. [Google Scholar]
- Erhardt, E.B.; Rachakonda, S.; Bedrick, E.J.; Allen, E.A.; Adali, T.; Calhoun, V.D. Comparison of Multi-Subject ICA Methods for Analysis of fMRI Data. Hum. Brain Mapp. 2011, 32, 2075–2095. [Google Scholar] [CrossRef]
- Himberg, J.; Hyvarinen, A. Icasso: Software for investigating the reliability of ICA estimates by clustering and visualization. In Proceedings of the 2003 IEEE Workshop on Neural Networks for Signal Processing, Toulouse, France, 17–19 September 2003; pp. 259–268. [Google Scholar]
- Li, Y.O.; Adalı, T.; Calhoun, V.D. Estimating the number of independent components for functional magnetic resonance imaging data. Hum. Brain Mapp. 2007, 28, 1251–1266. [Google Scholar] [CrossRef]
- Smith, S.M.; Fox, P.T.; Miller, K.L.; Glahn, D.C.; Fox, P.M.; Mackay, C.E.; Filippini, N.; Watkins, K.E.; Toro, R.; Laird, A.R.; et al. Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl. Acad. Sci. USA 2009, 106, 13040–13045. [Google Scholar] [CrossRef]
- Shi, Y.; Zeng, W.; Wang, N.; Zhao, L. A new method for independent component analysis with priori information based on multi-objective optimization. J. Neurosci. Methods 2017, 283, 72–82. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Zeng, W.; Chen, L. A fast-FENICA method on resting state fMRI data. J. Neurosci. Methods 2012, 209, 1–12. [Google Scholar]
- Wang, N.; Zeng, W.; Chen, L. SACICA: A sparse approximation coefficient-based ICA model for functional magnetic resonance imaging data analysis. J. Neurosci. Methods 2013, 216, 49–61. [Google Scholar] [CrossRef]
- Wang, N.; Zeng, W.; Shi, Y.; Ren, T.; Jing, Y.; Yin, J.; Yang, J. WASICA: An effective wavelet-shrinkage based ICA model for brain fMRI data analysis. J. Neurosci. Methods 2015, 246, 75–96. [Google Scholar] [PubMed]
- Wang, N.; Chang, C.; Zeng, W.; Shi, Y.; Yan, H. A novel feature-map based ICA model for identifying the individual, intra/inter-group brain networks across multiple fMRI datasets. Front. Neurosci. 2017, 11, 510. [Google Scholar] [CrossRef]
- Li, Q.; Wu, X.; Liu, T.M. Differentiable neural architecture search for optimal spatial/temporal brain function network decomposition. Med. Image Anal. 2021, 69, 14. [Google Scholar] [CrossRef]
- Ahmad, T.; Wu, J. SDIGRU: Spatial and Deep Features Integration Using Multilayer Gated Recurrent Unit for Human Activity Recognition. IEEE Trans. Comput. 2024, 11, 973–985. [Google Scholar] [CrossRef]
- Che, Z.P.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Ma, Q.; Sun, X.; Xu, Z.; Zhang, J.; Liao, X.; Wang, X.; Wei, D.; Chen, Y.; Liu, B.; et al. Frequency-resolved connectome alterations in major depressive disorder: A multisite resting fMRI study. J. Affect. Disord. 2023, 328, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Su, J.; Gan, M.; Zhang, Y.; Fan, Z.; Zeng, L.L. Co-Teaching Learning from Noisy Labeled FMRI Data for Diagnostic Classification of Major Depression. In Proceedings of the 2023 7th Asian Conference on Artificial Intelligence Technology (ACAIT), Quzhou, China, 10–12 November 2023; pp. 404–409. [Google Scholar]
- Jie, B.; Liu, M.; Lian, C.; Shi, F.; Shen, D. Designing weighted correlation kernels in convolutional neural networks for functional connectivity based brain disease diagnosis. Med. Image Anal. 2020, 63, 101709. [Google Scholar] [CrossRef]
- Li, Y.; Song, X.; Chai, L. Classification of Alzheimer’s Disease via Spatial-Temporal Graph Convolutional Networks. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 838–843. [Google Scholar]
- Dai, P.; Xiong, T.; Zhou, X.; Ou, Y.; Li, Y.; Kui, X.; Chen, Z.; Zou, B.; Li, W.; Huang, Z. The alterations of brain functional connectivity networks in major depressive disorder detected by machine learning through multisite rs-fMRI data. Behav. Brain Res. 2022, 435, 114058. [Google Scholar] [CrossRef] [PubMed]
- Fair, D.A.; Cohen, A.L.; Dosenbach, N.U.F.; Church, J.A.; Miezin, F.M.; Barch, D.M.; Raichle, M.E.; Petersen, S.E.; Schlaggar, B.L. The maturing architecture of the brain’s default network. Proc. Natl. Acad. Sci. USA 2008, 105, 4028–4032. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.X.; Chen, X.; Shen, Y.Q.; Li, L.; Chen, N.X.; Zhu, Z.C.; Castellanos, F.X.; Yan, C.G. Rumination and the default mode network: Meta-analysis of brain imaging studies and implications for depression. Neuroimage 2020, 206, 9. [Google Scholar] [CrossRef] [PubMed]
- Klug, M.; Enneking, V.; Borgers, T.; Jacobs, C.M.; Dohm, K.; Kraus, A.; Grotegerd, D.; Opel, N.; Repple, J.; Suslow, T.; et al. Persistence of amygdala hyperactivity to subliminal negative emotion processing in the long-term course of depression. Mol. Psychiatry 2024, 29, 1501–1509. [Google Scholar] [CrossRef] [PubMed]
- Mousavian, M.; Chen, J.; Greening, S. Depression Detection Using Feature Extraction and Deep Learning from sMRI Images. In Proceedings of the 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 1731–1736. [Google Scholar]
- Kipli, K.; Kouzani, A.Z.; Xiang, Y. An Empirical Comparison of Classification Algorithms for Diagnosis of Depression from Brain SMRI Scans. In Proceedings of the 2013 International Conference on Advanced Computer Science Applications and Technologies, Kuching, Malaysia, 23–24 December 2013; pp. 333–336. [Google Scholar]
- Qu, X.; Xiong, Y.; Zhai, K.; Yang, X.; Yang, J. An Efficient Attention-Based Network for Screening Major Depressive Disorder with sMRI. In Proceedings of the 2023 29th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Queenstown, New Zealand, 21–24 November 2023; pp. 1–6. [Google Scholar]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef]

| Methods | Accuracy | F1-Score | Recall | AUC |
|---|---|---|---|---|
| Adaboost | 51.25% | 63.47% | 62.33% | 43.67% |
| DT | 52.86% | 64.74% | 64.67% | 44.83% |
| GRU | 52.68% | 60.19% | 55.33% | 45.50% |
| LSTM | 47.32% | 55.41% | 51.33% | 48.17% |
| LG | 65.54% | 78.69% | 92.33% | 51.33% |
| RF | 63.75% | 77.20% | 90.00% | 51.17% |
| SVM | 66.61% | 79.54% | 94.00% | 50.33% |
| STANet | 82.38% | 88.18% | 82.38% | 90.72% |
| Method | Accuracy | F1-Score | Recall | AUC |
|---|---|---|---|---|
| STFA-Adaboost | 77.86% | 83.31% | 82.67% | 74.67% |
| STFA-DT | 76.61% | 82.39% | 82.67% | 72.17% |
| STFA-GRU | 63.93% | 73.03% | 74.67% | 52.83% |
| STFA-LSTM | 43.04% | 41.82% | 44.00% | 49.67% |
| STFA-LG | 75.18% | 83.30% | 88.33% | 75.83% |
| STFA-SVM | 67.14% | 72.22% | 82.17% | 28.42% |
| STFA-RF | 68.21% | 77.45% | 80.67% | 79.67% |
| STFA-Transformer | 72.38% | 82.21% | 75.86% | 83.72% |
| STANet | 82.38% | 88.18% | 82.38% | 90.72% |
| Methods | Accuracy | F1-Score | Recall | AUC |
|---|---|---|---|---|
| STFA-sLSTM | 43.04% | 41.82% | 44.00% | 49.67% |
| STFA-sGRU | 63.93% | 73.03% | 74.67% | 52.83% |
| STFA-dGRU | 66.67% | 71.54% | 69.76% | 77.72% |
| STFA-AtFGRU | 73.49% | 81.26% | 82.33% | 86.33% |
| STFA-AdFGRU | 76.34% | 84.03% | 79.17% | 87.11% |
| STFA(s)-AFGRU | 77.78% | 85.19% | 80.40% | 74.78% |
| STFA-AGRU | 79.52% | 86.24% | 81.81% | 89.72% |
| STANet(t) | 66.67% | 77.76% | 69.81% | 46.50% |
| STANet(s) | 73.81% | 82.84% | 77.67% | 81.44% |
| STANet | 82.38% | 88.18% | 82.38% | 90.72% |
| Method | Accuracy | F1-Score | Recall | AUC |
|---|---|---|---|---|
| Random Oversampling | 76.67% | 84.53% | 78.38% | 81.06% |
| SMOTE | 82.38% | 88.18% | 82.38% | 90.72% |
| ADASYN | 75. 24% | 82. 04% | 85.14% | 86.39% |
| Borderline-SMOTE | 78.10% | 85.75% | 79.52% | 85.39% |
| SMOTE Tomek | 74.92% | 83.58% | 79.52% | 88.06% |
| SVMSMOTE | 72.38% | 81.56% | 75.10% | 80.00% |
| Number of ICs | Accuracy | F1-Score | Recall | AUC |
|---|---|---|---|---|
| 15 | 72.38% | 82.62% | 74.81% | 63.78% |
| 17 (estimated) | 82.38% | 88.18% | 82.38% | 90.72% |
| 21 | 68.10% | 80.34% | 69.76% | 63.33% |
| 24 | 63.81% | 76.18% | 69.00% | 60.00% |
| 27 | 69.52% | 81.15% | 73.71% | 66.61% |
| Method | Input | Accuracy | F1-Score | Recall |
|---|---|---|---|---|
| Convolution-GRU | Time Courses | 65.24% | 77.58% | 69.24% |
| Auto-ASD-Network | Time Courses | 75.24% | 83.67% | 79.57% |
| MsRNN | Time Courses | 73.81% | 82.72% | 76.48% |
| Co-Teaching Learning | FC Matrix | 70.95% | 79.40% | 79.19% |
| Spectral-GNN | FC Matrix | 69.59% | 70.07% | 68.99% |
| wck-CNN | FC Matrix | 63.04% | 59.84% | 58.69% |
| STCAL | Spatio-Temporal | 76.67% | 84.75% | 79.19% |
| STANet | Spatio-Temporal | 82.38% | 88.18% | 82.38% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zeng, W.; Chen, H.; Liu, J.; Yan, H.; Zhang, K.; Tao, R.; Siok, W.T.; Wang, N. STANet: A Novel Spatio-Temporal Aggregation Network for Depression Classification with Small and Unbalanced FMRI Data. Tomography 2024, 10, 1895-1914. https://doi.org/10.3390/tomography10120138
Zhang W, Zeng W, Chen H, Liu J, Yan H, Zhang K, Tao R, Siok WT, Wang N. STANet: A Novel Spatio-Temporal Aggregation Network for Depression Classification with Small and Unbalanced FMRI Data. Tomography. 2024; 10(12):1895-1914. https://doi.org/10.3390/tomography10120138
Chicago/Turabian StyleZhang, Wei, Weiming Zeng, Hongyu Chen, Jie Liu, Hongjie Yan, Kaile Zhang, Ran Tao, Wai Ting Siok, and Nizhuan Wang. 2024. "STANet: A Novel Spatio-Temporal Aggregation Network for Depression Classification with Small and Unbalanced FMRI Data" Tomography 10, no. 12: 1895-1914. https://doi.org/10.3390/tomography10120138
APA StyleZhang, W., Zeng, W., Chen, H., Liu, J., Yan, H., Zhang, K., Tao, R., Siok, W. T., & Wang, N. (2024). STANet: A Novel Spatio-Temporal Aggregation Network for Depression Classification with Small and Unbalanced FMRI Data. Tomography, 10(12), 1895-1914. https://doi.org/10.3390/tomography10120138






