Identifying Brain Network Structure for an fMRI Effective Connectivity Study Using the Least Absolute Shrinkage and Selection Operator (LASSO) Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects, Experimental Design, MRI Collection, and fMRI Image Pre-Processing
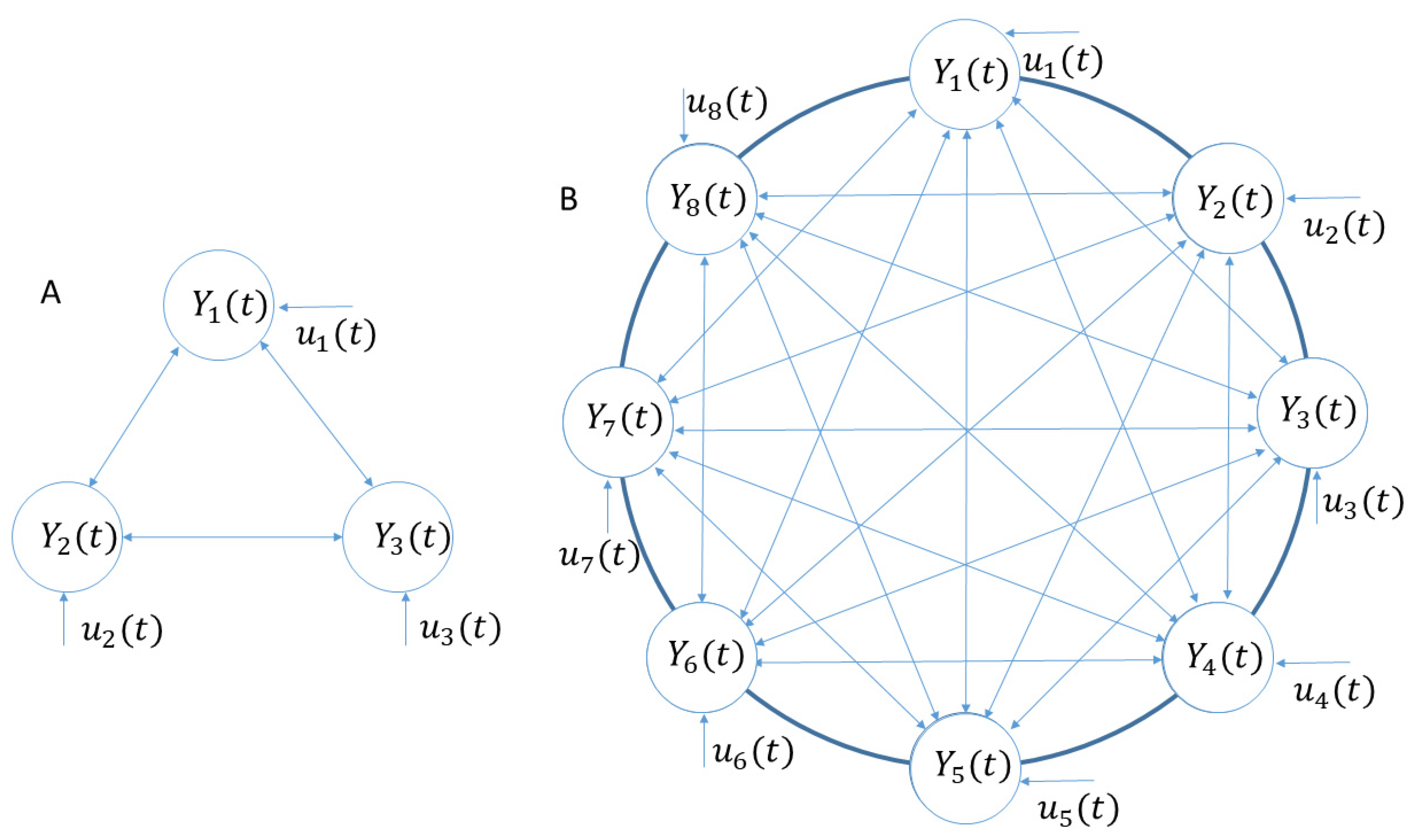
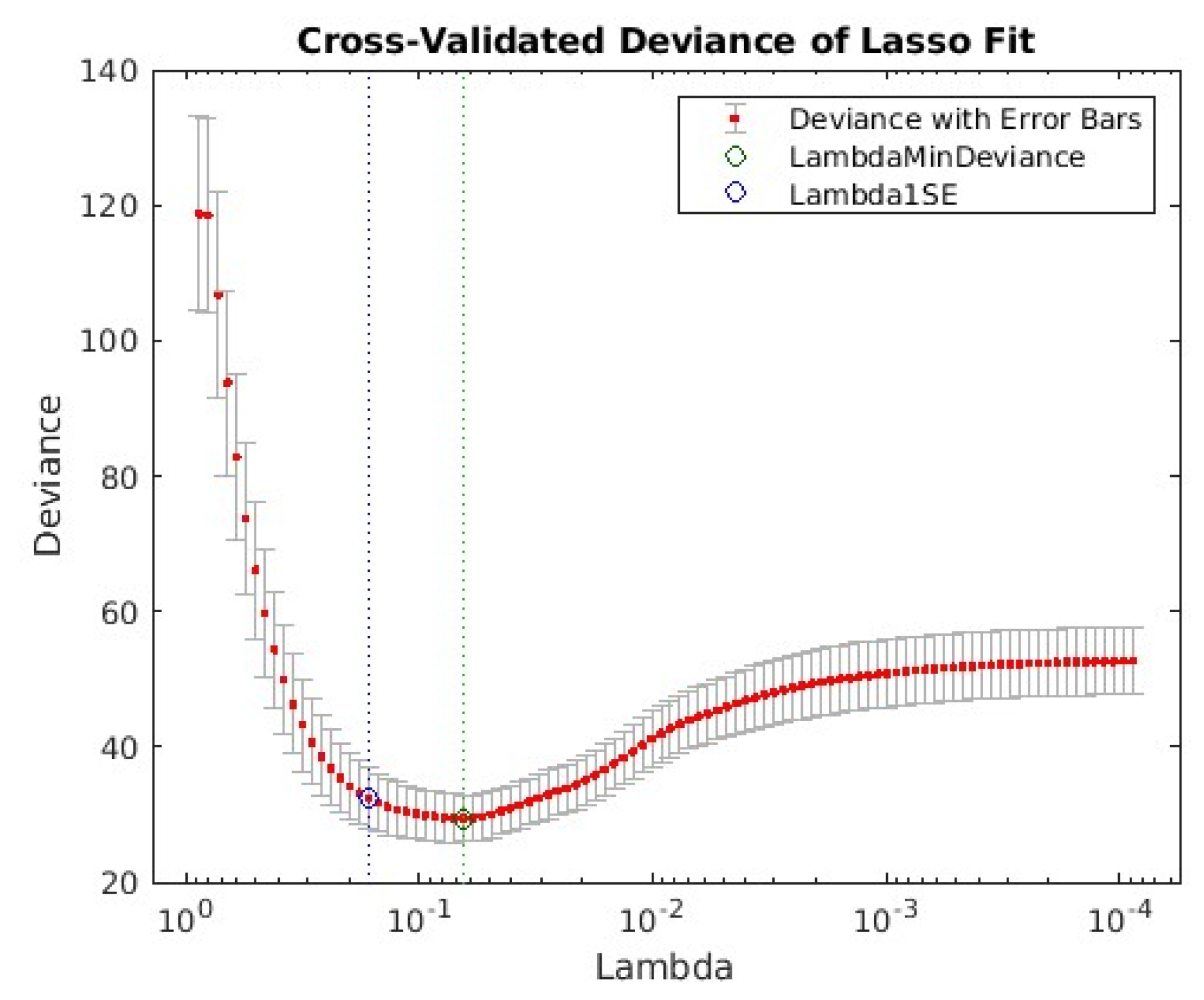
2.2. Theory
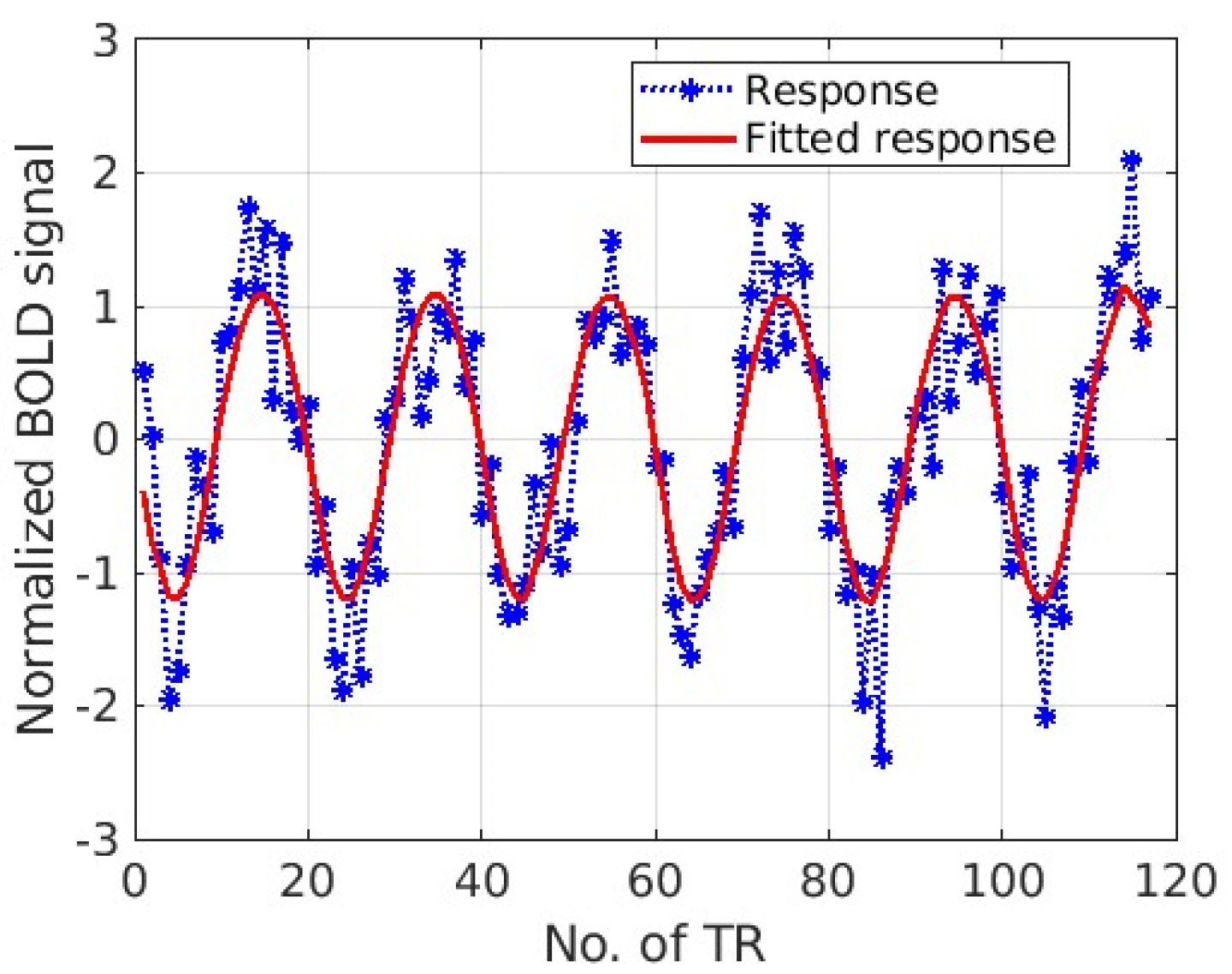
2.3. Visual System
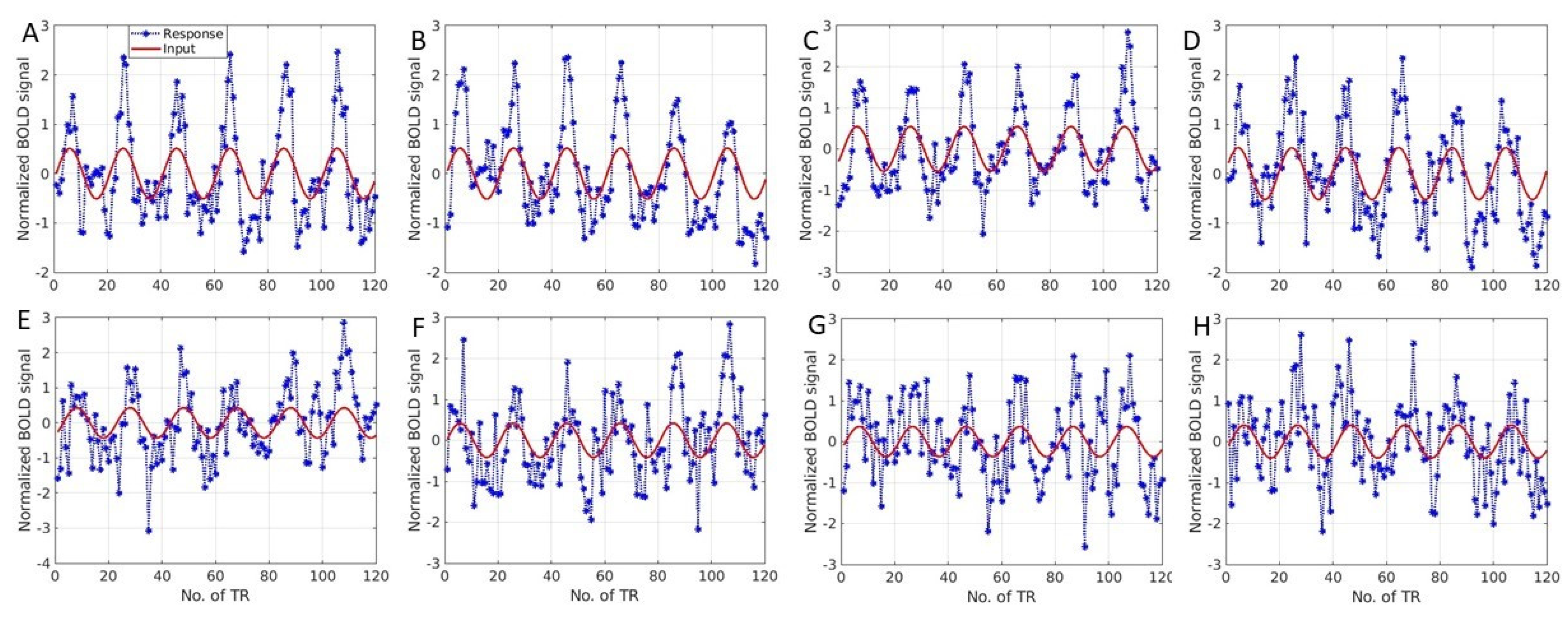
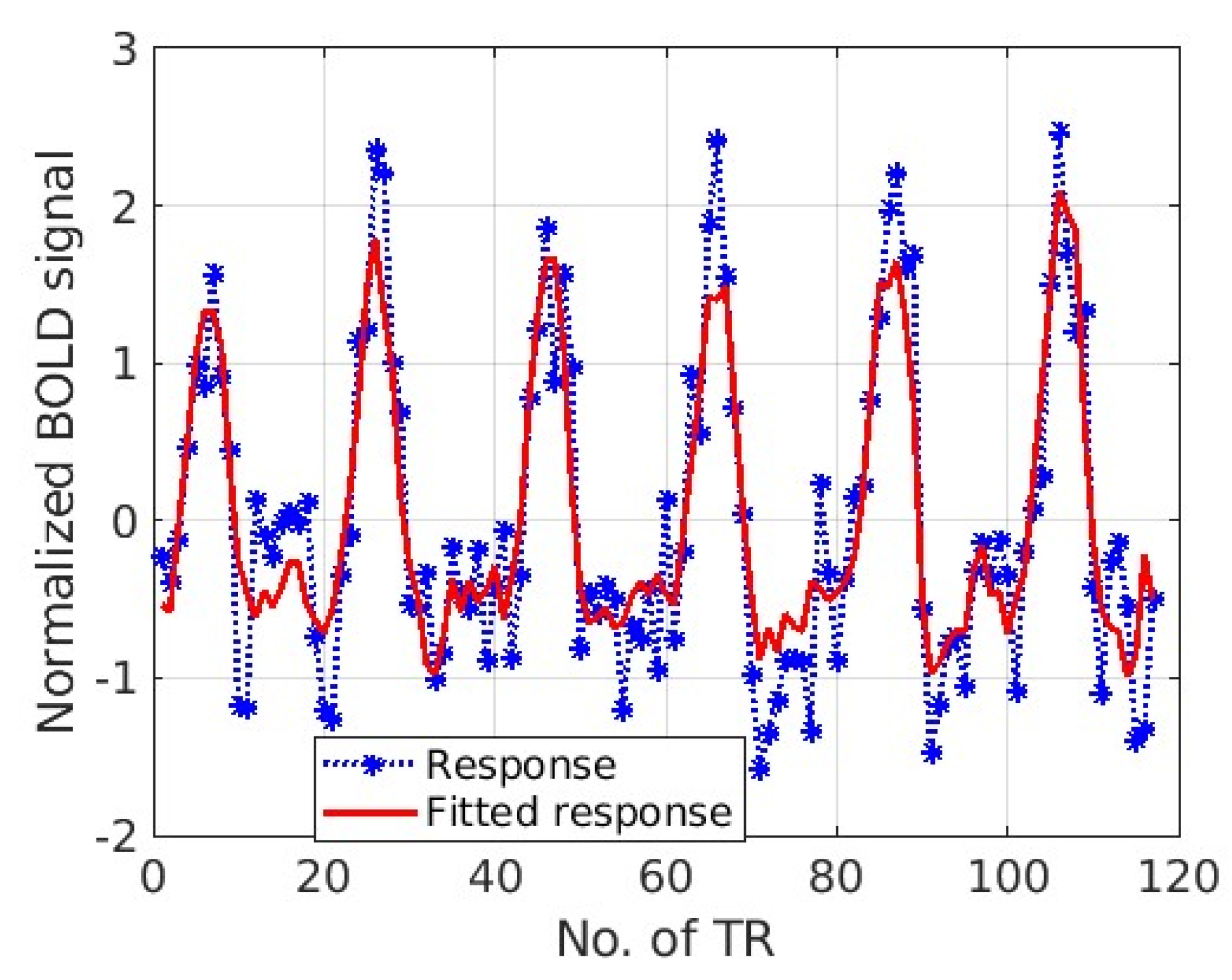
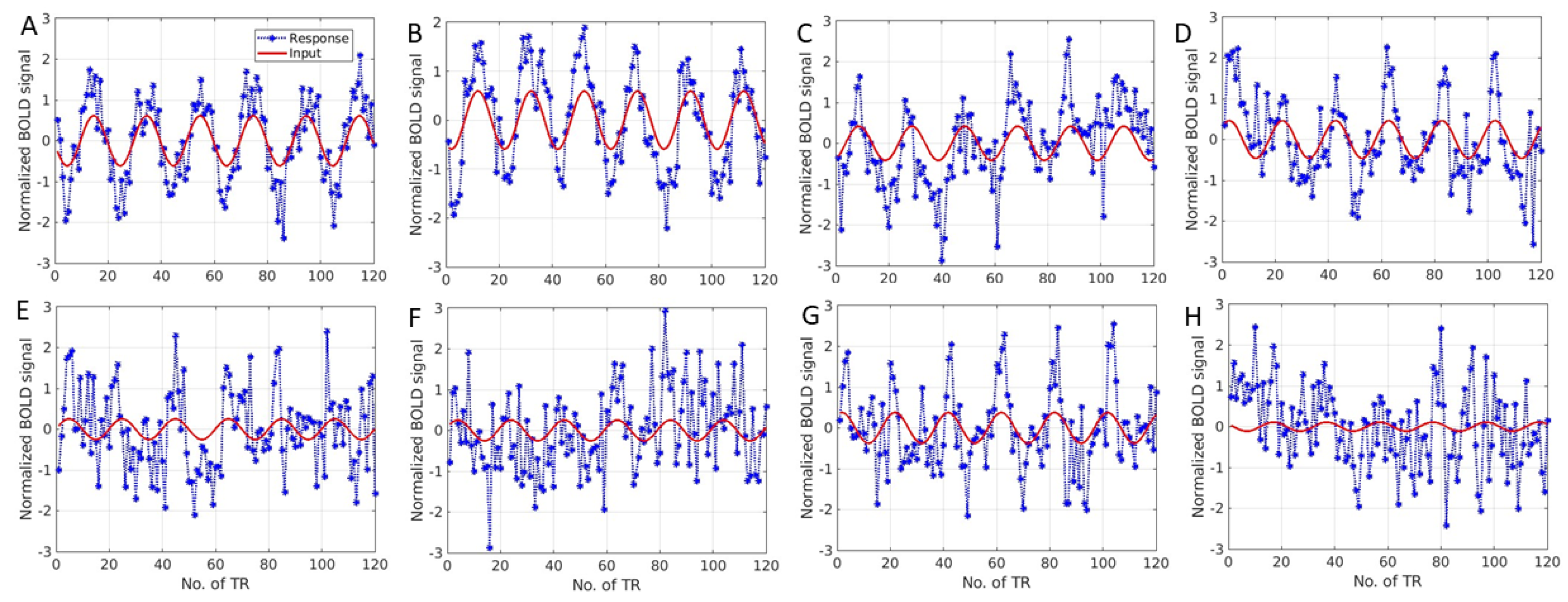
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Ogawa, S.; Lee, T.M.; Kay, A.R.; Tank, D.W. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc. Natl. Acad Sci. USA 1990, 87, 9868–9872. [Google Scholar] [CrossRef]
- Rugh, W.J. Nonlinear System Theory—The Volterra-Wiener Approach, Web version prepared in 2002; Johns Hopkins University Press: Baltimore, MD, USA, 1981; Chapter 1; pp. 1–53. ISBN O-8018-2549-0. [Google Scholar]
- Boynton, G.M.; Engel, S.A.; Glover, G.H.; Heeger, D.J. Linear Systems Analysis of Functional Magnetic Resonance Imaging in Human V1. J. Neurosci. 1996, 16, 4207–4221. [Google Scholar] [CrossRef]
- Schetzen, M. Nonlinear system modeling based on the Wiener theory. Proc. IEEE 1981, 69, 1557–1573. [Google Scholar] [CrossRef]
- Li, X.; Marrelec, G.; Hess, R.F.; Benali, H. A nonlinear identification method to study effective connectivity in functional MRI. Med. Image Anal. 2010, 14, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Goebel, R.; Roebroeck, A.F.; Kim, D.-S.; Formisano, E. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magn. Reason. Imaging 2003, 21, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Harrison, L.; Penny, W.; Friston, K.; Harrison, L.; Penny, W.; Friston, K.; Harrison, L.; Penny, W.; Friston, K. Multivariate autoregressive modeling of fMRI time series. NeuroImage 2003, 19, 1477–1491. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Yang, L.; Sarrigiannis, P.G.; Blackburn, D.; Zhao, Y. Dementia classification using a graph neural network on imaging of effective brain connectivity. Comput. Biol. Med. 2024, 168, 107701. [Google Scholar] [CrossRef]
- Bressler, S.L.; Kumar, A.; Singer, I. Brain Synchronization and Multivariate Autoregressive (MVAR) Modeling in Cognitive Neurodynamics. Front. Syst. Neurosci. 2021, 15, 638269. [Google Scholar] [CrossRef]
- Nagle, A.; Gerrelts, J.P.; Krause, B.M.; Boes, A.D.; Bruss, J.E.; Nourski, K.V.; Banks, M.I.; Van Veen, B. High-dimensional multivariate autoregressive model estimation of human electrophysiological data using fMRI priors. NeuroImage 2023, 277, 120211. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Calhoun, V.D.; Pham, T.D.; Iraji, A. Exploring Nonlinear Dynamics in Brain Functionality through Phase Portraits and Fuzzy Recurrence Plots. bioRxiv 2024. [Google Scholar] [CrossRef]
- Ponce-Alvarez, A.; Deco, G. The Hopf whole-brain model and its linear approximation. Sci. Rep. 2024, 14, 2615. [Google Scholar] [CrossRef] [PubMed]
- Abbaspourazad, H.; Erturk, E.; Pesaran, B.; Shanechi, M.M. Dynamical flexible inference of nonlinear latent factors and structures in neural population activity. Nat. Biomed. Eng. 2024, 8, 85–108. [Google Scholar] [CrossRef] [PubMed]
- Åström, K.J.; Eykhoff, P. System identification—A survey. Automatica 1971, 7, 123–162. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Valdés-Sosa, P.A.; Sánchez-Bornot, J.M.; Lage-Castellanos, A.; Vega-Hernández, M.; Bosch-Bayard, J.; Melie-García, L.; Canales-Rodríguez, E. Estimating brain functional connectivity with sparse multivariate autoregression. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 969–981. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Chen, X.; McKeown, M.J.; Wang, Z.J. A Sticky Weighted Regression Model for Time-Varying Resting-State Brain Connectivity Estimation. IEEE Trans. Biomed. Eng. 2015, 62, 501–510. [Google Scholar] [CrossRef] [PubMed]
- Shojaie, A.; Michailidis, G. Discovering graphical Granger causality using the truncating lasso penalty. Bioinformatics 2010, 26, i517–i523. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Coyle, D.; Maguire, L.; McGinnity, T.M.; Benali, H. A Model Selection Method for Nonlinear System Identification Based fMRI Effective Connectivity Analysis. IEEE Trans. Med. Imaging 2011, 30, 1365–1380. [Google Scholar] [CrossRef] [PubMed]
- Pongrattanakul, A.; Lertkultanon, P.; Songsiri, J. Sparse system identification for discovering brain connectivity from fMRI time series. In The SICE Annual Conference; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Haufe, S.; Müller, K.R.; Nolte, G.; Krämer, N. Sparse causal discovery in multivariate time series. In Proceedings of the 2008th International Conference on Causality: Objectives and Assessment, Vancouver, BC, Canada, 12 December 2008; JMLR.org: Whistler, BC, Canada, 2008; Volume 6, pp. 97–106. [Google Scholar]
- Ryali, S.; Chen, T.; Supekar, K.; Menon, V. Estimation of functional connectivity in fMRI data using stability selection-based sparse partial correlation with elastic net penalty. NeuroImage 2012, 59, 3852–3861. [Google Scholar] [CrossRef]
- Shojaie, A.; Fox, E.B. Granger Causality: A Review and Recent Advances. Annu. Rev. Stat. Its Appl. 2022, 9, 289–319. [Google Scholar] [CrossRef] [PubMed]
- Teipel, S.J.; Grothe, M.J.; Metzger, C.D.; Grimmer, T.; Sorg, C.; Ewers, M.; Franzmeier, N.; Meisenzahl, E.; Klöppel, S.; Borchardt, V.; et al. Robust Detection of Impaired Resting State Functional Connectivity Networks in Alzheimer’s Disease Using Elastic Net Regularized Regression. Front. Aging Neurosci. 2017, 8, 318. [Google Scholar] [CrossRef] [PubMed]
- Siggiridou, E.; Kugiumtzis, D. Granger Causality in Multivariate Time Series Using a Time-Ordered Restricted Vector Autoregressive Model. IEEE Trans. Signal Process. 2016, 64, 1759–1773. [Google Scholar] [CrossRef]
- Tang, W.; Bressler, S.L.; Sylvester, C.M.; Shulman, G.L.; Corbetta, M. Measuring Granger Causality between Cortical Regions from Voxelwise fMRI BOLD Signals with LASSO. PLoS Comput. Biol. 2012, 8, e1002513. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Babadi, B. Non-Asymptotic Guarantees for Reliable Identification of Granger Causality via the LASSO. IEEE Trans. Inf. Theory 2023, 69, 7439–7460. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Dumoulin, S.O.; Mansouri, B.; Hess, R.F. Cortical Deficits in Human Amblyopia: Their Regional Distribution and Their Relationship to the Contrast Detection Deficit. Investig. Ophthalmol. Vis. Sci. 2007, 48, 1575–1591. [Google Scholar] [CrossRef] [PubMed]
- Nozari, E.; Bertolero, M.A.; Stiso, J.; Caciagli, L.; Cornblath, E.J.; He, X.; Mahadevan, A.S.; Pappas, G.J.; Bassett, D.S. Macroscopic resting-state brain dynamics are best described by linear models. Nat. Biomed. Eng. 2023, 8, 68–84. [Google Scholar] [CrossRef]
- Pattanaik, R.K.; Mohanty, M.N. Nonlinear System Identification Using Robust Fusion Kernel-Based Radial basis function Neural Network. In Proceedings of the 2022 International Conference on Emerging Smart Computing and Informatics (ESCI), Pune, India, 9–11 March 2022. [Google Scholar]
- Gedon, D.; Wahlström, N.; Schön, T.B.; Ljung, L. Deep state space models for nonlinear system identification. IFAC-PapersOnLine 2021, 54, 481–486. [Google Scholar] [CrossRef]
- Hutchison, R.M.; Womelsdorf, T.; Allen, E.A.; Bandettini, P.A.; Calhoun, V.D.; Corbetta, M.; Della Penna, S.; Duyn, J.H.; Glover, G.H.; Gonzalez-Castillo, J.; et al. Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage 2013, 80, 360–378. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, Y. Identifying Brain Network Structure for an fMRI Effective Connectivity Study Using the Least Absolute Shrinkage and Selection Operator (LASSO) Method. Tomography 2024, 10, 1564-1576. https://doi.org/10.3390/tomography10100115
Li X, Zhang Y. Identifying Brain Network Structure for an fMRI Effective Connectivity Study Using the Least Absolute Shrinkage and Selection Operator (LASSO) Method. Tomography. 2024; 10(10):1564-1576. https://doi.org/10.3390/tomography10100115
Chicago/Turabian StyleLi, Xingfeng, and Yuan Zhang. 2024. "Identifying Brain Network Structure for an fMRI Effective Connectivity Study Using the Least Absolute Shrinkage and Selection Operator (LASSO) Method" Tomography 10, no. 10: 1564-1576. https://doi.org/10.3390/tomography10100115
APA StyleLi, X., & Zhang, Y. (2024). Identifying Brain Network Structure for an fMRI Effective Connectivity Study Using the Least Absolute Shrinkage and Selection Operator (LASSO) Method. Tomography, 10(10), 1564-1576. https://doi.org/10.3390/tomography10100115





